Lifelong Dynamic Timed A* (LTA*) for Fastest Path Retrieval in

Congested Road Networks Using Predicted Speeds

Kartikey Sondhi, Poulami Dalapati

and Saurabh Kumar

Department of Computer Science and Engineering, The LNM Institute of Information Technology Jaipur, India

Keywords:

Intelligent Transportation Systems, Trafﬁc Congestion Management, Trafﬁc Modelling and Simulation,

Dynamic A*.

Abstract:

Efﬁcient transportation systems are crucial for the ever-growing smart cities. With the increasing urbanization

and growth in vehicular trafﬁc, congestion has become a signiﬁcant challenge. This research paper addresses

the critical issue of identifying the fastest, least congested path in road transport networks, aiming to enhance

overall travel efﬁciency and reduce the negative impact of trafﬁc congestion. The study employs an improved

version of the Lifelong Planning A* (LPA*) that helps ﬁnd the fastest route between two points in dynamic

changing environments. The proposed methodology is called the Lifelong Dynamic Timed A

∗

(LTA

∗

) algo-

rithm with an optimal bound weight factor integrated with it to make the search more guided and efﬁciently

predict optimized trafﬁc paths to provide real-time recommendations. To validate the effectiveness of the de-

veloped algorithm, extensive simulations and case studies are conducted on a small area in Washington as well

as on Grid Worlds. The experimental results show that LTA*, within accurate weight bounds, always managed

to ﬁnd the fastest path, and in some cases, the time taken was close to half of that produced by A*.

1 INTRODUCTION

Heuristic based searches have been widely used to

compute the shortest paths in graphs, which extends

is usage to grid world planning problems, mazes and

even road networks. To ﬁnd solutions to various prob-

lems algorithms are frequently used to add robustness

to the the search. The search algorithms in the lit-

erature often give results with different costs, where

costs are often measured in time to generate ﬁrst so-

lutions, deviation from ideal outcomes, computational

units exhausted as well as total nodes expanded to ﬁnd

these solutions.

The A* algorithm being a special case of the

Breadth First Search is often deployed in such prob-

lems, ﬁrst proposed in (Hart et al., 1968), utilizes

the heuristic to perform a guided search as compared

to the unguided alternative being the Djikstra’s algo-

rithm, which also is a special case of the BFS. The

conditions that the these algorithms will ﬁnd the opti-

mal solution if any, are that, ﬁrstly the heuristic func-

tion is admissible, meaning it never over-estimates the

cost to the goal and the secondly, the edges within

https://orcid.org/0000-0003-0539-3029

https://orcid.org/0000-0002-1786-1056

the graph are non negative. In 1970, Pohl proposed

the inclusion of a weighted constant w, when mul-

tiplied to the heuristic in A* would speed up search

by compromising with the optimal solution and re-

ceiving a sub-optimal one(Pohl, 1970), when w was

greater than 1. This sub-optimal nature of the solu-

tion is bounded by the weight w, in cases where h

is admissible , meaning the solution produced is to be

not more than w times the optimal solution(Likhachev

et al., 2005). This inﬂated heuristic search paved

way for a new class of searching algorithms called

the Anytime Algorithms. In these algorithms, a in-

ﬂated value of w is chosen, that allows the algorithm

to generate a ﬁrst sub-optimal solution very quickly,

and reﬁnes over its search by iterating over smaller

values of w to produce subsequent better solutions as

the search progresses. The way these ﬁrst values of w

are chosen and the magnitude of their decrements is

something that varies greatly from one problem to the

other, but someone interested in reading can refer to

(Richter et al., 2010)(Stern et al., 2014)(Van Den Berg

et al., 2011). When speaking about urban transporta-

tion systems the actions taken now, greatly reﬂect the

next possible choices we can possibly make. For these

very reasons we ponder through the paper the reasons

and lengths to which the weighted constant has been

Sondhi, K., Dalapati, P. and Kumar, S.

Lifelong Dynamic Timed A* (LTA*) for Fastest Path Retrieval in Congested Road Networks Using Predicted Speeds.

DOI: 10.5220/0012629900003702

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2024), pages 293-298

ISBN: 978-989-758-703-0; ISSN: 2184-495X

293

applied.

These anytime algorithms designed are great for

generating the quickest ﬁrst solutions but often fail

to perform well in dynamic environments like trans-

portation systems and robot path ﬁnding, where the

edge costs are prone to change. The D* (Dynamic

A*) (Likhachev et al., 2005), D* Lite and LPA* (Life-

long Planning A*) (Koenig et al., 2004) are dynamic

versions that are adapted to the changing edge cost

that may occur in the environment. They compute

a ﬁrst shortest path and then based on the f values

of remaining states, calculates alternate optimal paths

when current optimal trajectories get obstructed. The

difference between the D* Lite and LPA* algorithms

is the cost associated with computing the solution in

real time, with the D* Lite being the optimised and re-

ﬁned version, with signiﬁcantly lesser push and pops

from the priority queue and the restarting nature of

the LPA*.

To extend the knowledge of such algorithms into

Intelligent Transportation System (ITS), we must ad-

dress that there are critical challenges to ITS like ﬂuc-

tuations in road mobility volumes, sensitive to irregu-

lar patterns and real time trafﬁc control, which, due to

the highly stochastic nature of congestion on road net-

works, creates planning problems. Path ﬁnding in the

case of vehicles not only requires shortest routes to

the destination, but a path that avoids excessive con-

gestion, includes better quality roads and exhibit bet-

ter or even the fastest travel times possible. To tackle

these spatio-temporal factors, congestion data needs

to be captured from road networks and processed.

For this, in (Ma et al., 2015), Ma et al propose a

Long Short Term Memory Neural Network that evalu-

ates trafﬁc data collected through microwave sensors,

that produced speed predictions better than Support

Vector Machines and Non-Linear Auto-Regressive

Neural Networks, with the model proposed deliver-

ing speed prediction with less than 4% Mean Ab-

solute Percentage Error(MAPE). Another such state

of the art method was proposed by Zhang et al in

2020 in (Zhang et al., 2020) where the trafﬁc was

predicted using a Structured Learning Convolutional

Neural Networks. Reﬂecting upon the possibilities of

NN’s to assist in the prediction problem of this highly

dynamic nature of trafﬁc on road networks, a novel

Lifelong Planning Timed A* (LTA*) is proposed, that

shall produce fastest paths in real time, even in cases

of accidents or abrupt road closures.

The remaining paper is organized as follows: Sec-

tion 2 proposes the novel LTA* with the mathematical

model and the algorithmic approach. The theoretical

analysis with challenges and the experimental results

and comparative analysis have been discussed in Sec-

tion 3. Finally Section 4 concludes the proposed re-

search work and discusses the future scope.

2 METHODOLOGY

2.1 Problem Statement

The goal of this paper is to propose and develop an al-

gorithm that suggests the fastest route to be taken be-

tween two points on a real world road network map.

Our proposed algorithm encapsulates the challenges

faced in real road networks, like the unreliability of

congestion that may be present on roads, and it mod-

iﬁes itself in times of uncertain trafﬁc conditions in

real time.

The problem involves receiving a map of city, that

can be represented as a graph with the vertices repre-

sent intersections and edges represent the roads con-

necting them. If a person wants to travel from one in-

tersection to the other, the algorithms returns the path,

which takes the shortest time to travel. The algorithms

uses historical speed data and predictive models, de-

veloped for certain cities using sensors and machine

learning in real time to retrieve the fastest path.

2.2 Proposed LTA*

In this section we will introduce the working of our

LTA* algorithm, which tackles the problem of the

stochastic nature of congestion that might be present

on road networks, then deriving a shortest time con-

suming path from within such a network with great

accuracy. Doing so requires

• A time dependent value for each edge, containing

values for every 10 minute time interval or real

time generated values. These values need to be

updated using the sensors in the environment or

through online maps that show road closures.

• A hash map is used that stores the speed data for

the different times of the day, and is only up-

dated in cases of signiﬁcant difference between

predicted values or sudden road closures.

• Further the LTA* algorithm proposed is inspired

from the Lifelong Planning Problem in (Koenig

et al., 2004). The given algorithm uses an ad-

ditional variable for each node and that is it’s t

also called the t-score, a parallel drawn from the

g score and f score, that stores the time at which

a certain node can be reached at.

• The g also called g score, for a node u, is updated

based on the least time it takes to get to u from

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

294

its predecessors. Intuitively doing so would make

the dimensions of this physical quantity to that of

. To change the dimensions back to those of

distance, we multiply the MaxSpeed of the entire

network so that we are logically diving the dis-

tance between two intersections by a quantity be-

tween (0, 1] and then updating the g.

Assuming we have to update the g value for some

state s which has a predecessor s

′

, so in equation 1.

(

g(s

′

) = g(s) +

c(s,s

′

)∗MaxSpeed

Speed(s

′

,s,t(s

′

))

f (s

′

) = g(s

′

) + w ∗ h(s

′

)

(1)

Algorithm 1: LTA

∗

Main().

procedure Main( )

Initialize

Repeat ▷ forever

location ← getLocation()

currTime ← getTime()

ComputeFastestPath()

wait for change in predicted values

for all updated edges from (u,v)

UpdateNode(v)

end procedure

The working of the algorithm is similar to the op-

timised LPA* proposed in (Koenig et al., 2004), but

the overview of the algorithm is as follows:

• The edge costs are updated as per the normalised

distance from t values of the predecessors instead

of the directly added edge costs.

• The lifelong planning approach utilizes the con-

cept of restarting searches from current node, so

whenever there is an update to a node’s intersec-

tion’s t and g value, all nodes with them as pre-

decessors get updated, causing a chain of changes

within the values.

• The core of the algorithm lies in the speed func-

tion that calculates the speed for an intersection

from it’s t value. So instead of using the cur-

rent congestion information for a an intersection,

which may be occupied by the vehicle 1 hour

later, using the estimate t value at that time makes

sense, as it reduces computation to update the

speeds dynamically. The only time there are any

change in the predicted speeds and t values, are

when there are unexpected road closures or acci-

dents. We assume that our vehicle will reach our

intersection at the time that is equivalent to the t

value.

Algorithm 2: LTA

∗

Dependencies.

procedure CalculateKey(s)

return [w*h(s) + min (g(s), rhs g(s)),

min (g(s), rhs g(s))]

end procedure

procedure Initialize( )

U=φ

for all s ∈ S, rhs g(s), g(s), rhs t(s) ← ∞

rhs g(start) , rhs t(start) ← 0

U.insert(start, [h(start), 0]

end procedure

procedure UpdateNode(v)

if (v ̸= start)

rhs t(v) = min

′

∈pred(v)

(

c(s

′

,v)

speed(v,s

′

,T (s

′

))

T (s

′

) ▷ T Value Updation

rhs g(v) = min

′

∈pred(v)

(

c(s

′

,v)

speed(v,s

′

,T (s

′

))

g(s

′

) ▷ G Value Updation

end

if (u ∈ v)

U.remove(u)

end

if (g(u) ̸= rhs(u)

u.insert(u, calculateKey(u))

end

end procedure

procedure ComputeShortestPath( )

while (U.TopKey() < CalculateKey (S goal)

or rhs g(S goal) ̸= g(S goal)

or rhs t(S goal) ̸= t(S goal))

▷ Termination Checking

u = U.pop()

if (g(u) > rhs(u))

g(u) ← rhs g(u)

t(u) ← rhs t(u)

for all s ∈ succ(u), updateNode(s)

end

else

g(u) ← ∞

for all s ∈ succ(u) ∪ u, updateNode(s)

end

end procedure

Lifelong Dynamic Timed A* (LTA*) for Fastest Path Retrieval in Congested Road Networks Using Predicted Speeds

295

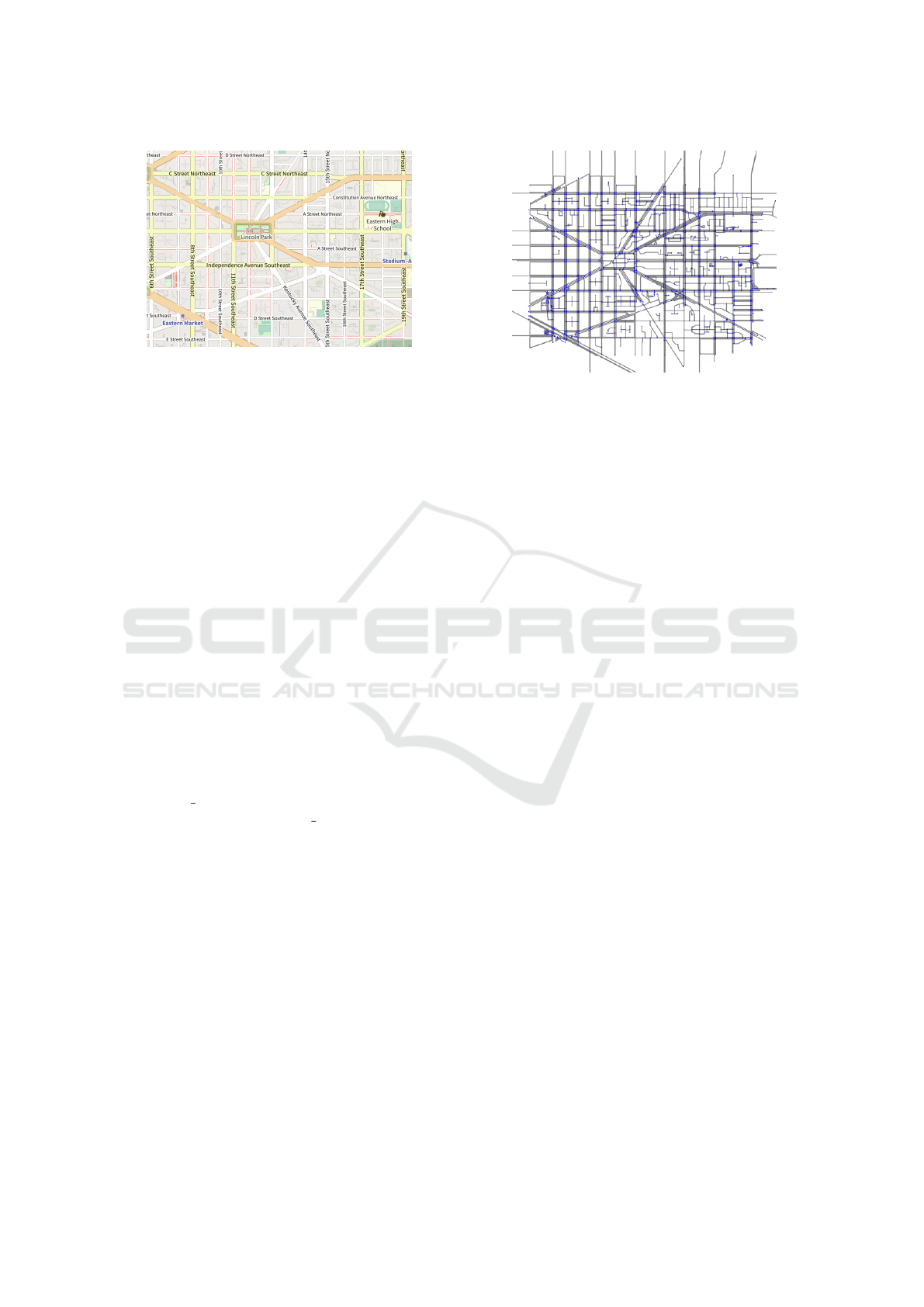
Figure 1: Road transport network of Washington City area.

3 RESULT AND ANALYSIS

3.1 Theoretical Analysis

3.1.1 Challenges

Incremental search algorithms like the one proposed

are best suited for environment with changing fea-

tures which in our case is the congestion present on

the road. The algorithm proposed utilises the time de-

rived values of speeds for different edges which are

garnered through the t values. The algorithm cur-

rently runs on Restarting the A* search which re-

quires the re-computation of edges for their g and

t values whenever there is a change. Certain ap-

proaches from within the literature would seem log-

ical to be applied in such cases to boost the search:

1. Bidirectional search: The following LTA* ap-

proach cannot be applied using a bidirectional A*

because the core of the LTA* algorithm lies in us-

ing the time based speed of an edge to estimate a

node’s g cost at a given time, and it is practically

impossible to estimate the t cost of node’s in the

opposite direction in the same order as they are

from the start to ﬁnish.

2. D* Lite: Following the intuition from the bidirec-

tional search as well, we can see that if the node

encounters an unexpected blockage, which may

occur in trafﬁc systems, the recovery/repair part

of the D* Lite from that time on can compute the

shortest path from the goal to current position of

the vehicle, as it designed to do, but it may en-

counter issues in computing the fastest path, due

to failing to collect accurate time based speeds for

each edge due to the t values getting changed due

to changes in g values.

Figure 2: Graphical grid model of Washington City area.

3.2 Observation and Analysis

The proposed algorithm is implemented using a 500×

500, 1000 × 1000, as shown in Table 1 Grid World

systems with constant lengths equal to 200 meters,

with 5 − 10% nodes and corresponding edges ran-

domly removed from the grid to mimic a real world

like city road map. The algorithm is also tested on

an urban area of Washington, US, depicted in Figure

1 and Figure 2 to validate the efﬁciency of the pro-

posed methods. To calculate the distance between the

nodes on the map, the longitudinal and latitudinal co-

ordinates are used to compute the distance.

The analysis of time base values for the differ-

ent times of the days has been conducted using ran-

dom integer values for speeds generated between the

range of 2m/s or 7.2km/hr, and 15m/s or 54km/hr and

dynamically updated for an edge for 10 minute in-

tervals within a day. The observations in all three

examples taken (see Table 1) show that the shortest

route every time isn’t the fastest route, not that it isn’t

possible, which in contradiction with the popular be-

lief and trend present in the literature where all algo-

rithms focus on shortest routes. The numbers show

how effective this algorithm can be in certain situa-

tions where shortest paths are extremely congested,

and how choosing alternative paths as shown in ex-

amples can even reduce travel times by half.

Numerous observations were conducted, both on

the grid world example as well as on the map of Wash-

ington, and it was found out that on an average, even

though using a weight equal to w equal to 1.6 was

used to overestimate the heuristic function, it rarely

compromised with the optimal solution. The observa-

tion were run for various simulations and it was found

that the number of nodes traversed decreased by al-

most a factor of 10 when employing a weight of 1.6.

These results are recorded in the graphs, depicted in

Figure 3, Figure 4, Figure 5, and Figure 6. This value

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

296

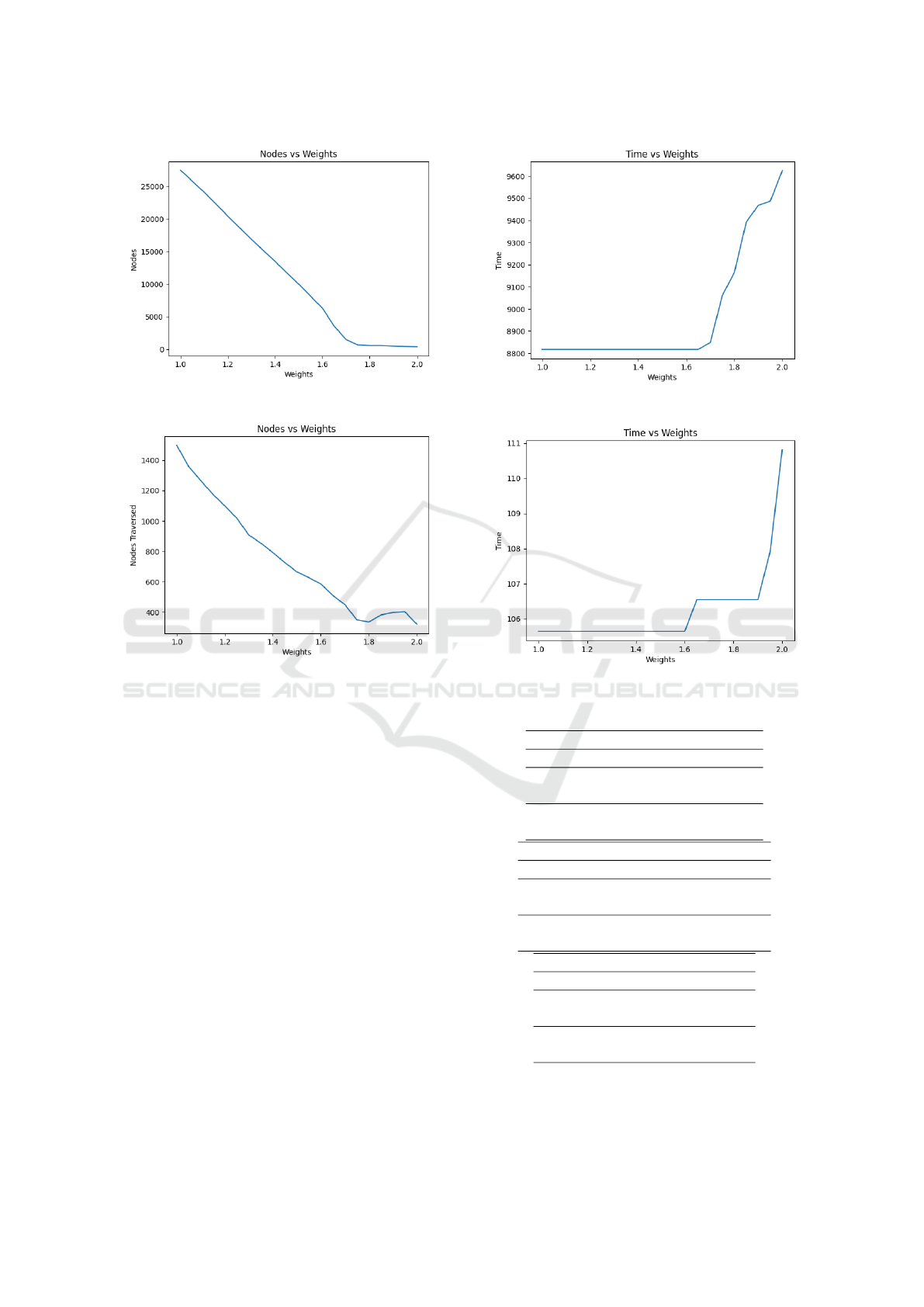
Figure 3: Nodes Searched in the Grid Vs Weight for LTA*.

Figure 4: Nodes Searched on the Map Vs Weight for LTA*.

of the weight, might suit some grid-worlds or maps

but isn’t in any way a generalization to all kinds of

maps.

4 CONCLUSION

This research addresses a critical aspect of urban

transportation by focusing on the identiﬁcation of the

fastest least congested path in road transport networks

using a novel timed weighted A

∗

algorithm. Through

the modelling and implementation of LTA* that in-

corporates real-time trafﬁc data and dynamic vari-

ables, this research work demonstrates a signiﬁcant

improvement in identifying optimal routes. The ex-

tensive simulations and case studies conducted on ur-

ban road networks provides valuable insights into the

adaptability and robustness of the proposed algorithm

to sudden road closures. The positive outcomes ob-

served in 1000x1000 Grid Worlds demonstrates the

algorithms potential to address the complex and dy-

namic nature of urban trafﬁc, making it a practical

tool for urban planners, transportation authorities, and

Figure 5: Fastest Time in the Grid Vs Weight for LTA*.

Figure 6: Fastest Time on the Map Vs Weight for LTA*.

Table 1: LTA* Observations on different test cases.

GridWorld: 500x500

Observation Distance Time

A* 112.2Km 18563 s

LTA* 114.6Km 10484 s

A* 65.2Km 11186 s

LTA* 65.6Km 5789 s

GridWorld: 1000x1000

Observation Distance Time

A* 143Km 23684 s

LTA* 144.6Km 13190 s

A* 222.6 Km 36723.9 s

LTA* 225.8 Km 20695.3 s

Washington Map

Observation Distance Time

A* 1.788Km 275 s

LTA* 2.233Km 195 s

A* 1.554Km 221 s

LTA* 1.646Km 152 s

commuters seeking more efﬁcient travel routes. This,

in turn, aligns with the broader goal of achieving

Lifelong Dynamic Timed A* (LTA*) for Fastest Path Retrieval in Congested Road Networks Using Predicted Speeds

297

sustainable urban mobility and improving the overall

quality of modern transportation systems.

The current LTA* algorithm works great in dy-

namic environments without actually restarting the

search throughout the search space but for only the

successor intersections where the edge speeds had

been predicted wrongly. To further speed up the

search we can employ algorithms like ANA* to pro-

duce even faster ﬁrst outputs search results.

REFERENCES

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE transactions on Systems Science and

Cybernetics, 4(2):100–107.

Koenig, S., Likhachev, M., and Furcy, D. (2004). Lifelong

planning a star. Artiﬁcial Intelligence, 155(1-2):93–

146.

Likhachev, M., Ferguson, D. I., Gordon, G. J., Stentz, A.,

and Thrun, S. (2005). Anytime dynamic a*: An

anytime, replanning algorithm. In ICAPS, volume 5,

pages 262–271.

Ma, X., Tao, Z., Wang, Y., Yu, H., and Wang, Y. (2015).

Long short-term memory neural network for trafﬁc

speed prediction using remote microwave sensor data.

Transportation Research Part C: Emerging Technolo-

gies, 54:187–197.

Pohl, I. (1970). Heuristic search viewed as path ﬁnding in a

graph. Artiﬁcial intelligence, 1(3-4):193–204.

Richter, S., Thayer, J., and Ruml, W. (2010). The joy of

forgetting: Faster anytime search via restarting. In

Proceedings of the International Conference on Au-

tomated Planning and Scheduling, volume 20, pages

137–144.

Stern, R., Felner, A., Van Den Berg, J., Puzis, R., Shah, R.,

and Goldberg, K. (2014). Potential-based bounded-

cost search and anytime non-parametric a

. Artiﬁcial

Intelligence, 214:1–25.

Van Den Berg, J., Shah, R., Huang, A., and Goldberg, K.

(2011). Anytime nonparametric a. In Proceedings

of the AAAI conference on artiﬁcial intelligence, vol-

ume 25, pages 105–111.

Zhang, Q., Chang, J., Meng, G., Xiang, S., and Pan, C.

(2020). Spatio-temporal graph structure learning for

trafﬁc forecasting. In Proceedings of the AAAI con-

ference on artiﬁcial intelligence, volume 34, pages

1177–1185.

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

298