Mitigating Outlier Activations in Low-Precision Fine-Tuning of

Language Models

Alireza Ghaffari

, Justin Yu

, Mahsa Ghazvini Nejad

, Masoud Asgharian

, Boxing Chen

and

Vahid Partovi Nia

Huawei Noah’s Ark Lab, Montreal, Canada

Department of Mathematics and Statistics, McGill University, Montreal, Canada

Keywords:

Accelerated Training, Compressed Training, Low-Precision Fine-Tuning, Language Models.

Abstract:

Low-precision ﬁne-tuning of language models has gained prominence as a cost-effective and energy-efﬁcient

approach to deploying large-scale models in various applications. However, this approach is susceptible to

the existence of outlier values in activation. The outlier values in the activation can negatively affect the

performance of ﬁne-tuning language models in the low-precision regime since they affect the scaling factor

and thus make representing smaller values harder. This paper investigates techniques for mitigating outlier

activation in low-precision integer ﬁne-tuning of the language models. Our proposed novel approach enables

us to represent the outlier activation values in 8-bit integers instead of ﬂoating-point (FP16) values. The beneﬁt

of using integers for outlier values is that it enables us to use operator tiling to avoid performing 16-bit integer

matrix multiplication to address this problem effectively. We provide theoretical analysis and supporting

experiments to demonstrate the effectiveness of our approach in improving the robustness and performance of

low-precision ﬁne-tuned language models.

1 INTRODUCTION

Language models have achieved remarkable success

in various NLP tasks, owing to their ability to capture

the intricacies of text data. Fine-tuning large language

models, however, often requires substantial computa-

tional resources and memory bandwidth that hinder

its accessibility to users with limited computational

resources. To make large language models accessible

and efﬁcient for real-world applications, researchers

have explored various techniques for making ﬁne-

tuning pre-trained models more efﬁcient on devices

with lower computational power. To mitigate these

challenges, low-precision ﬁne-tuning has emerged as

a promising approach.

Low-precision ﬁne-tuning involves representing

the model’s weights, activations, and also gradients

to lower bit-width representations, such as 8-bit inte-

ger or ﬂoating-point numbers. This approach reduces

memory and computational requirements, making it

feasible to ﬁne-tune and deploy large-scale models on

resource-constrained devices. However, both in ﬁne-

tuning and inference, this approach introduces the

problem of outlier activation, where a small number

of activations exhibit extreme values, causing numer-

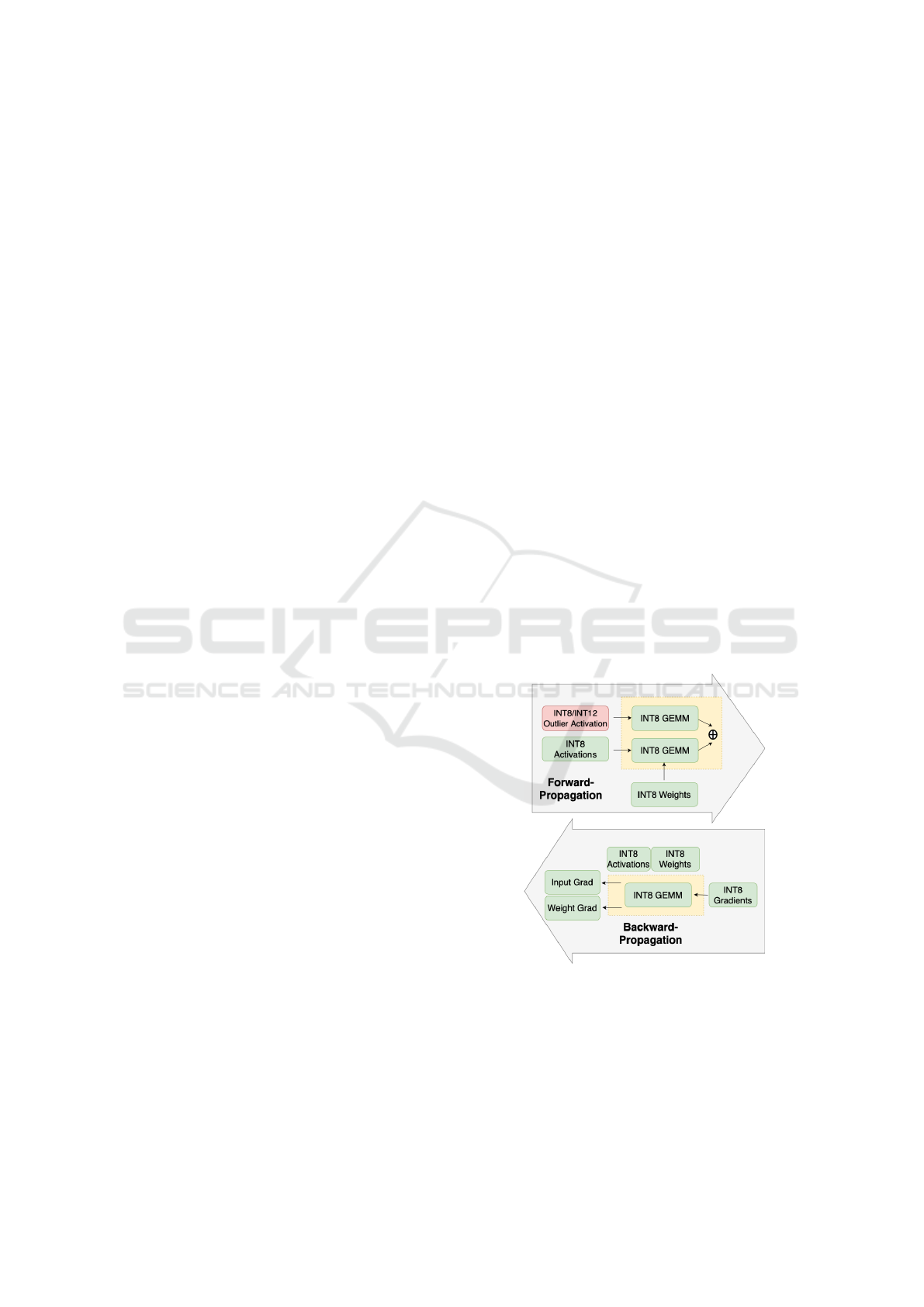
Figure 1: Computation ﬂow of proposed linear layers for

forward and backward propagation. Integer computation

signiﬁcantly reduces the computational cost of compute-

intensive linear layers.

ical instability and degradation in model performance.

In this paper, we delve into the problem of outlier

activation in low-precision ﬁne-tuning of language

models. In our proposed approach, weights, activa-

478

Ghaffari, A., Yu, J., Nejad, M., Asgharian, M., Chen, B. and Nia, V.

Mitigating Outlier Activations in Low-Precision Fine-Tuning of Language Models.

DOI: 10.5220/0012567700003654

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2024), pages 478-484

ISBN: 978-989-758-684-2; ISSN: 2184-4313

tions, and gradients of all compute-intensive linear

layers are represented using integer number formats.

Instead of quantization approaches used in the litera-

ture, we propose a comprehensive approach that uses

various hardware design techniques to address this is-

sue effectively. Our contributions are as follows.

• We analyze the causes and consequences of out-

lier activation in low-precision ﬁne-tuning. We

ﬁnd that outlier activations are more important in

the forward pass. Thus, we keep all the gradients

in the back-propagation of linear layers in 8-bit

integers.

• Instead of quantizing the ﬂoating point values, we

switch the number format of weights, activations,

and gradients to an adaptive-integer number for-

mat which considers different integer lengths (e.g.

INT12 or INT16) for activation outliers (less than

5% of all parameters) and keeps all the other pa-

rameters in INT8 format.

• Using the advantage of integer number formats,

we present a tiling strategy that enables the pos-

sibility of using int8 GEMM for all the compu-

tation of linear layers. Note that such tiling strat-

egy is not easily possible for ﬂoating-point num-

ber formats such as (FP16 and FP8)

• We provide theoretical analysis on how treating

outliers separately helps to preserve the informa-

tion in low-precision regime.

In Figure 1, we present an overview of our novel

linear layers, highlighting the innovative handling of

outlier activations in an integer number format while

maintaining gradient computation in low-precision

integer format. Notably, to the best of our knowl-

edge, this is the ﬁrst fully INT8 linear layer designed

to manage outlier features in integer format, while si-

multaneously preserving gradient calculations in low-

precision integer format.

2 RELATED WORKS

The emergence of Large Language Models (LLMs)

has revolutionized natural language processing, yet

their formidable size poses signiﬁcant computational

challenges for training, ﬁne-tuning, and deployment.

To address these challenges, intensive research has

focused on quantization techniques, low-precision

arithmetic, and compression methods. This Sec-

tion investigates these approaches and their efﬁcacy

in mitigating outlier activation during inference and

back-propagation, offering insights into the evolv-

ing landscape of techniques designed to make LLMs

more efﬁcient and accessible in resource-constrained

environments.

2.1 Handling Outliers in Low-Precision

Inference

Most of the research efforts in the literature are fo-

cused on studying the effect of outlier activations in

the forward propagation i.e. inference. For instance,

LLM.int8() proposed by (Dettmers et al., 2022) de-

compose the outlier activations and their correspond-

ing weights to a separate matrix multiplication that

is performed in FP16 format while keeping the val-

ues that are not outlier in INT8 format. They also

show that using a threshold is enough for detecting the

outlier features. GPTQ presented by (Frantar et al.,

2022) is a one-shot post-training quantization (PTQ)

scheme that is based on approximate second-order in-

formation. GPTQ quantizes the weights while keep-

ing the activations in ﬂoating point format. AWQ pro-

posed by (Lin et al., 2023) is another PTQ scheme

that focuses on protecting salient activations by ap-

plying normalizing scales for weights and activa-

tion tensors. These scales are determined by only

analyzing activation tensors. (Dettmers and Zettle-

moyer, 2023) proposed an outlier-dependent quanti-

zation scheme called proxy quantization which quan-

tizes the weights corresponding to the outliers into a

higher precision number format. Proxy quantization

exploits the standard deviation of each layer’s hidden

unit weights as a proxy for which dimensions have

outlier features. Outlier channel splitting (OCS) pro-

posed by (Zhao et al., 2019) tackle the problem of out-

lier features by duplicating channels containing out-

liers, then halves the channel values. Morover, norm

tweaking is proposed by (Li et al., 2023) to reverse

the magniﬁcation of outliers by normalization layers

i.e. LayerNorm as discovered by (Wei et al., 2022).

SmoothQuant proposed by (Xiao et al., 2023) offers

an 8-bit quantization scheme for weights and activa-

tion. SmoothQuant deals with outlier features by mi-

grating the quantization difﬁculty from activation to

weights using scaling factors for weights and activa-

tions. Furthermore, (Dettmers et al., 2023) proposed

SpQR that isolates outlier weights, which may cause

large quantization errors, and stores them in higher

precision, an then compresses all other weights to in-

teger format. (Yuan et al., 2023) suggested RPTQ

method which reorders the channels with outliers and

group them in order to reduce the quantization error.

Mitigating Outlier Activations in Low-Precision Fine-Tuning of Language Models

479

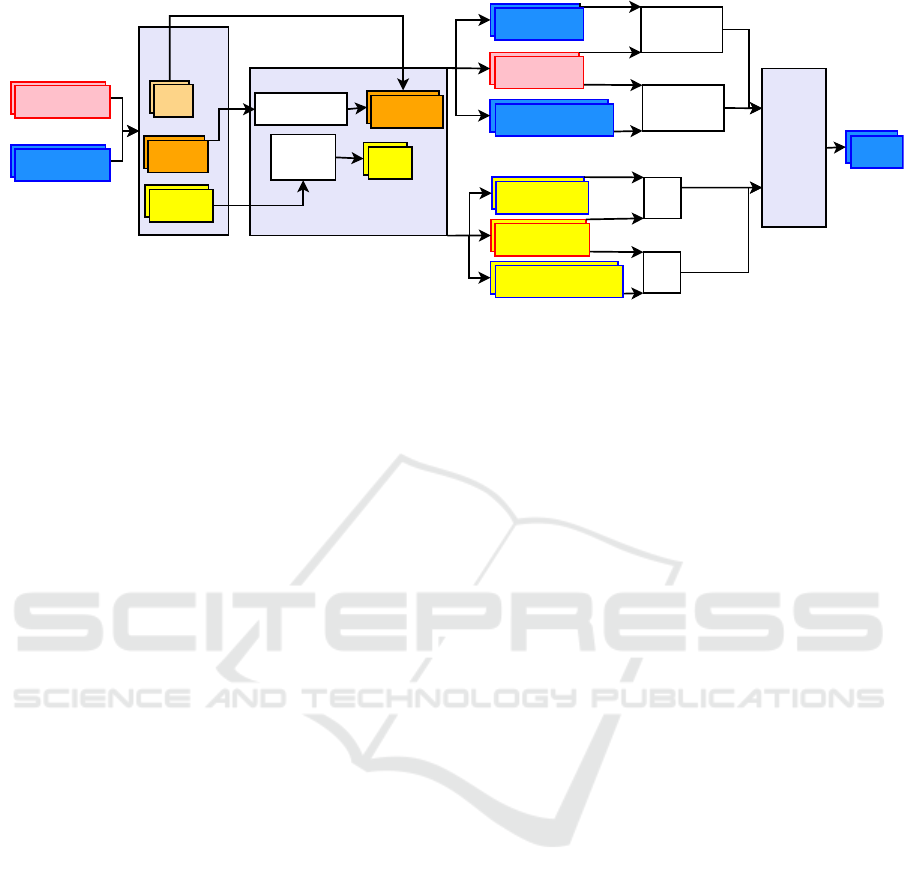
Fixed-point Mapping

Parameter FP16

FP16 Activation

Unpack

Floating-point

Sign

Matinssa

Exponent

Round to b bits

Maximum

Exponent

Signed INT

Scale

INT Activation

INT Parameter

Activation scale

Parameter scale

Add

Matrix

Multiplication

Nonlinear

Inverse

Mapping

Sign

Matinssa

Exponent

Signed INT

Scale

Output

INT Oulier Activation

Activation Outlier scale

Matrix

Multiplication

Add

Parameter FP16

FP16 Activation

INT Activation

INT Parameter

INT Oulier Activation

Activation scale

Parameter scale

Activation Outlier scale

Figure 2: Inference operations in an integer-only linear layer. The bottom panel shows the linear ﬁxed-point mapping for the

input tensors, which can adapt different bit-widths for activation outliers and other parameters in the layer.

2.2 Handling Outliers in Low-Precision

Back-Propagation

Over the past few years, low-precision training of

deep learning models has gained popularity in reduc-

ing the training cost. For instance, FP16 mixed preci-

sion training (Micikevicius et al., 2017) is nowadays

a commonplace methodology to ﬁne-tune language

models. Integer data type has also been extensively

studied for back-propagation computations by (Zhang

et al., 2020; Zhao et al., 2021; Zhu et al., 2020; Ghaf-

fari et al., 2022). Moreover, using higher-bit integer

formats such as INT12 for both back-propagation and

forward propagation is proposed by (Tayaranian et al.,

2023).

Nonetheless, the majority of literature pertinent to

low-precision back-propagation and training does not

address the emergence of outliers in language mod-

els. As a result, our paper is dedicated to investigating

the impact of outliers in low-precision integer training

of language models. In the remainder of the paper,

we demonstrate the signiﬁcance of outlier features in

the forward pass. Additionally, we establish that the

forward pass can be entirely computed using integer

arithmetic. Finally, we emphasize that handling out-

lier separately is only important in the forward pass.

As for the back-propagation, all the parameters can

remain in INT8 format.

3 METHODOLOGY

This section delves into our proposed methodology

for mitigating outlier values in the low-precision

training of language models. We consider keeping

all the parameters in the back-propagation in INT8

format while treating the outlier activation separately

in the forward pass. We found that the outlier ac-

tivation does not need to be treated differently (i.e.

representing outliers in higher precision) in the back-

propagation.

3.1 Number Representation

We employ the dynamic ﬁxed-point format, also re-

ferred to as block ﬂoating-point (Williamson, 1991),

to convert ﬂoating-point numbers into integer data

types. In this format, ﬂoating-point numbers are

mapped into blocks of integer values, each assigned

a unique scale.

To perform this conversion, we utilize a lin-

ear ﬁxed-point mapping function, which transforms

a ﬂoating-point tensor F into a tensor of integers

along with a single scale factor. The integer val-

ues are derived by rounding the ﬂoating-point man-

tissas, while the scale is determined as the maximum

of the ﬂoating-point exponents within F. The oper-

ational details of the linear ﬁxed-point mapping are

illustrated in the lower section of Figure 2.

To convert the ﬁxed-point integers back into

ﬂoating-point representation, we employ a non-

linear inverse mapping function. This inverse map-

ping function converts integer values into normal-

ized ﬂoating-point mantissas, associating each integer

with its respective scale before packaging them into a

ﬂoating-point number.

For a more comprehensive insight into the rep-

resentation mapping functions, readers can refer to

(Ghaffari et al., 2022). It is worth noting that our

approach deviates from existing methods by intro-

ducing various bit-widths for outlier activations in

the ﬁne-tuning of transformer-based language mod-

els. This strategy enables us to explore different bit-

width conﬁgurations for handling outlier activations,

ultimately facilitating the determination of the min-

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

480

imum memory band-width required for ﬁne-tuning

language models both in forward and backward prop-

agations.

3.2 Proposed Methods

In this subsection, we present two approaches de-

signed to mitigate the impact of outliers in the con-

text of low-precision language model ﬁne-tuning. The

ﬁrst approach, the uniﬁed scale for outliers, seeks to

provide a consistent scaling mechanism for outlier ac-

tivations. The second approach, splitting outlier ac-

tivations (Tiling), explores a novel strategy to iso-

late and manage outlier activations effectively, taking

advantage of having two scaling factors for outliers.

Also note that in both approaches, we used a thresh-

old γ = 5 to isolate the outlier activations for all the

linear layers.

3.2.1 Approach 1. Uniﬁed Scale for Outliers

In this approach, we completely isolate the outlier ac-

tivations and their corresponding weights and quan-

tize them to INT12 while the rest are quantized to

INT8. Let us assume X denotes the activation tensor,

and Q() is the quantization function, then

Q(X) = S

INT8

+ S

outlier

INT12

outlier

. (1)

3.2.2 Approach 2. Splitting Outlier Activations

(Tiling)

In the second approach, the value of outliers are split

into two values

INT8

outlier SP1

and X

INT8

outlier SP2

and the

quantization scheme is as follows

Q(X) = (2)

INT8

+ X

INT8

outlier SP1

) + S

outlier

INT8

outlier SP2

In this quantization scheme, we extract ﬂoating-

point outlier activations X

outlier

from original ﬂoating-

point activations X using threshold γ and then, split

them as shown in the following equations,

outlier SP2

= ⌊

outlier

+ γ

2γ

⌋ × 2γ (3)

outlier SP1

= X

outlier

− X

outlier SP2

and then we quantize them to get X

INT8

outlier SP1

and

INT8

outlier SP2

. The beneﬁt of this method is that we can

keep the computation of forward pass completely in

INT8 format while treating the outlier separately from

the no-outlier activation values.

4 THEORETICAL ANALYSIS

In this section, we delve into the implications of low-

precision number formats on information preserva-

tion. The utilization of reduced bit-width represen-

tations in deep learning, while advantageous for ef-

ﬁciency and resource conservation, inevitably intro-

duces the issue of information loss. We explore the

nuances of this phenomenon and employ sensitivity

analysis to quantify the extent to which information

is altered or discarded in the transition from high pre-

cision to low precision.

Furthermore, we extend our investigation to con-

sider distribution distances, such as the χ

-divergence

and the Hammersley–Chapman–Robbins bound.

4.1 Information Loss in Low-Precision

Number Formats

The concept of sample informativeness is a well-

established notion within the ﬁeld of statistics. For

example, (Tukey, 1965) introduced a dimensionless

metric for measuring informativeness, which proves

particularly valuable for our analysis. To measure the

informativeness, (Tukey, 1965) deﬁnes the concept of

leverage and linear sensitivity as

lev

(X) =

∂

∂θ

(X)

sens

(X) =

(lev

(X))

V(X)

, (4)

where θ is the parameters of X distribution.

Thus, we can re-write the equation (4) in the low-

precision number formats

X if we consider a low pre-

cision number has a rounding error of δ in a way that

X = X + δ. Note that we assume δ and X are indepen-

dent random variables and E(δ) = ε ≃ 0.

lev

(

lev

(X)

≃ 1 s.t E(δ) ≃ 0

sens

(

sens

(X)

V(X)

V(X) + V(δ)

≤ 1. (5)

Inequality (5) shows that in the case of unbi-

ased rounding, low-precision representation always

increases the variance and therefore decreases the in-

formativeness of the sample.

It is noteworthy to mention that the sensitivity

measure deﬁned in equation (4) is closely related to

Hammersley-Chapman-Robbins lower-bound (Chap-

Mitigating Outlier Activations in Low-Precision Fine-Tuning of Language Models

481

man and Robbins, 1951),



E(X) − E(



≤



E(X) − E(



V(X)

≤ χ

( f

|| f

), (6)

which provides a lower-bound for χ

-divergence of

X and

X distributions. Note that χ

-divergence is a

measure to quantify the divergence between two dis-

tributions and for distributions P and Q is deﬁned as,

(P||Q) =

(

− 1)

dQ. (7)

4.2 Analysing Outlier Activations as a

Mixture Distribution

Treating outlier activations separately as explained in

Section 3.2 closely resembles having a mixture distri-

bution as shown in Figure 3. This means that we con-

sider the outlier activations are samples that are drawn

from a different distribution function than non-outlier

activations. Let us assume the original distribution of

X as f

and a threshold γ that separates outliers f

from the rest of activations f

. deﬁne F

as the coef-

ﬁcients of X such that

(x) = p f

(x) + (1 − p) f

(x),

p = F

(γ),

(x) =

(x)I

{X≤γ}

(γ)

(x) =

(x)I

{X>γ}

1 − F

(γ)

. (8)

Let us further assume Y = I

{X≤γ}

, then

E(X) = E (E(X|Y ))

= pE

(X) + (1 − p)E

(X), (9)

and,

E(X

) = pE

) + (1 − p)E

). (10)

Furthermore, by subtracting the pE

(X) + (1 −

p)E

(X) from (10) and using Jensen’s inequality we

have

V(X) ≥ pV

(X) + (1 − p)V

(X). (11)

Figure 3: Outliers modeled as a mixture distribution.

Remark 1. The inequality (11) shows that weighted

average of variances of distibutions is less than total

variance of a mixture distribution. Therefore, treating

outlier separately reduces the variance and hence it in-

creases the informativeness i.e. sensitivity according

to equation (4).

4.3 Informativeness of Mixture

Distribution in Low-Precision

Number Formats

In this section, we try to re-establish the results of

Section 4.2 for low-precision number formats. To do

so, we need to show equation (8) holds in the low-

precision number format.

Let us consider the following low-precision repre-

sentations,

X = X + δ,

= X

+ δ and

= X

+ δ,

where δ is the rounding error and is independent from

X. The moment generating function m

(t) = E(e

) = E(e

)E(e

tδ

)

= m

(t)m

(t). (12)

Now,

(t) =

∞

−∞

(x)

= p

∞

−∞

(x)

+ (1 − p)

∞

−∞

(x)

= pm

(t)+ (1 − p)m

(t). (13)

and thus, using equations (12) and (13),

(t) = m

(t)m

(t)

= pm

(t)m

(t)+ (1 − p)m

(t)m

(t)

= pm

(t)+ (1 − p)m

(t). (14)

which means,

(x) = p f

(x) + (1 − p) f

(x). (15)

Remark 2. Establishing equation (15) conﬁrms that

inequality (11) holds for the low-precision regime and

thus, treating outlier activations separately in low-

precision reduces the quantization variance (i.e. quan-

tization noise) and increases the informativeness.

Remark 3. The equation (15) holds if the moement

generative functions exist. This is a valid assumption

since the distribution of activation has bounded sup-

port.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

482

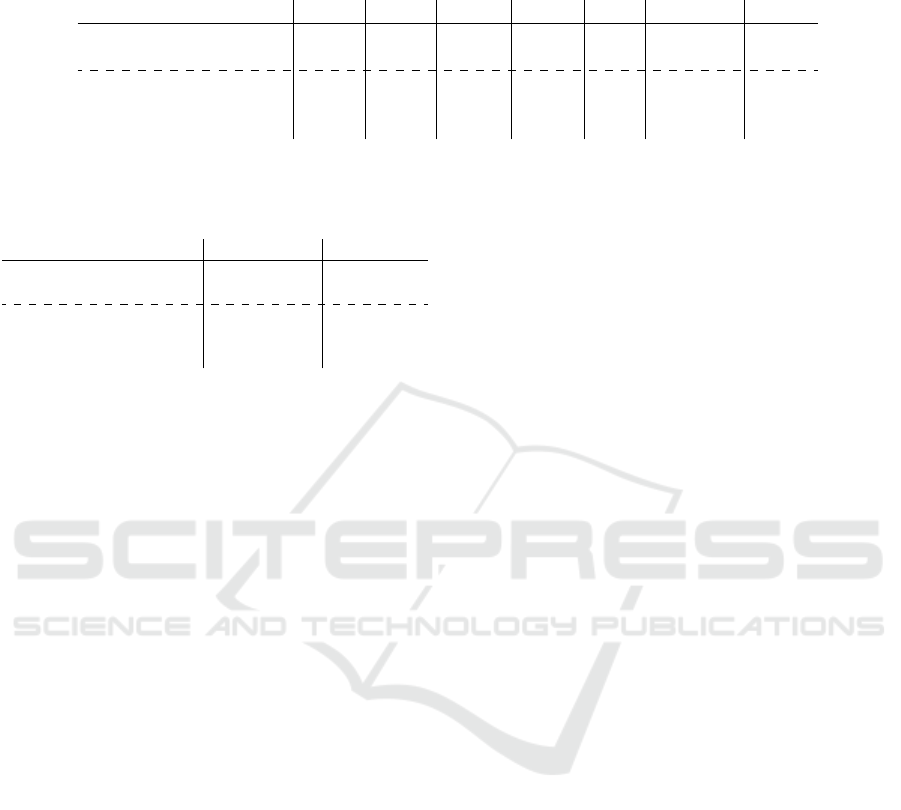
Table 1: Metric performance of integer ﬁne-tuning of BERT on selected GLUE tasks. The reported metric for MRPC is

accuracy and F1 score, for QNLI, MNLI, RTE, and SST-2 is accuracy, for STSB is the Pearson-Spearman correlation, and for

CoLA is the Matthews correlation.

STSB QNLI MNLI SST-2 RTE MRPC CoLA

FP32 87.6 89.9 83.5 91.9 61.7 78.7/85.3 55.3

FP16 88.6 90.1 83.2 91.7 59.6 77.7/85.1 56.0

Proposed Approach 1 85.2 89.9 82.6 91.5 55.6 75.2/83.7 53.4

Proposed Approach 2 81.6 89.6 82.6 91.5 59.2 74.3/83.5 52.2

INT8 Untreated Outliers 80.9 86.4 80.9 91.8 58.5 69.9/81.9 43.5

Table 2: Metric performance of ﬁne-tuning BERT on

SQuAD v1.1 and v2.0 datasets. For both datasets, the exact

match metrics and F1 scores are reported.

SQuAD v1.1 SQuAD v2

FP32 79.6/87.5 71.5/74.8

FP16 79.6/87.5 69.1/72.2

Proposed Approach 1 76.2/85.2 67.7/71.2

Proposed Approach 2 74.9/84.1 65.5/69.0

INT8 Untreated Outliers 69.8/80.2 60.9/64.6

5 EXPERIMENTAL RESULTS

5.1 Experiment Setup

We conducted ﬁne-tuning on the BERT base model

across a series of downstream tasks to facilitate a

performance comparison between our integer ﬁne-

tuning method and the FP16 and FP32 ﬁne-tuning ap-

proaches. The ﬁne-tuning process encompassed spe-

ciﬁc tasks selected from the GLUE benchmark (Wang

et al., 2018), in addition to the Stanford Question

Answering Datasets, speciﬁcally SQuAD v1.1 and

SQuAD v2.0 (Rajpurkar et al., 2016).

Each ﬁne-tuning setup was standardized with

identical hyper-parameters and an equivalent number

of training epochs. To ensure result stability, reported

metrics represent the average of ﬁve runs, each ini-

tialized with a different random seed to mitigate the

impact of random variations.

Our ﬁne-tuning experiments were executed using

the ﬁne-tuning scripts provided by the Hugging Face

library (Wolf et al., 2019). In the case of GLUE exper-

iments, ﬁne-tuning spanned ﬁve epochs, with a learn-

ing rate set to 2 × 10

−5

, and a per-device ﬁne-tuning

batch size of 32. Meanwhile, the ﬁne-tuning of BERT

on the SQuAD datasets comprised two epochs, with a

learning rate of 5 ×10

−5

and a per-device ﬁne-tuning

batch size of 12. Notably, all experiments were con-

ducted on a computational infrastructure consisting of

eight NVIDIA V100 GPUs, each equipped with 32

gigabytes of VRAM.

5.2 Results

The results of ﬁne-tuning BERT base on GLUE

benchmark and SQuAD datasets are presented in

Table 1 and Table 2 respectively. Our proposed

solution signiﬁcantly improves the robustness of

low-precision ﬁne-tuning for BERT on GLUE and

SQuAD datasets. Comparing the results of the pro-

posed approaches with INT8 ﬁne-tuning with un-

treated outliers shows that representing outliers sep-

arately almost always improves the ﬁne-tuning per-

formance of the model. Additionally, we emphasize

again that, the results presented in this paper com-

prise of having both back-propagation and forward-

propagation in low-precision number formats and

show that low-precision arithmetic are promising av-

enue to reduce the computational complexity of lan-

guage models.

6 CONCLUSION

This paper explored means to mitigate the outlier acti-

vations in low-precision language model ﬁne-tuning.

We have introduced a novel methodology for miti-

gating the challenges posed by outlier activations, of-

fering effective approaches as effective approaches to

enhance the stability of the ﬁne-tuning phase in low

precision number format where gradients, weights,

and activations are in INT8 format. Additionally, we

provided a theoretical analysis to understand the in-

tricacies of information loss in low-precision num-

ber formats. Our sensitivity analysis has unveiled

the trade-offs between variance and informativeness

while considering distribution distances like the χ

divergence and the Hammersley–Chapman–Robbins

bound has deepened our insights into these trans-

formations. In a landscape where the deployment

of large language models is increasingly resource-

constrained, our work contributes to the ongoing ef-

forts to make these models more accessible and ef-

ﬁcient. By addressing the challenges of outliers and

information loss, we pave the way for the continued

evolution of low-precision back-propagation in lan-

Mitigating Outlier Activations in Low-Precision Fine-Tuning of Language Models

483

guage model ﬁne-tuning. Our ﬁndings not only have

implications for natural language processing but also

hold relevance for broader applications across data

analysis and machine learning.

REFERENCES

Chapman, D. G. and Robbins, H. (1951). Minimum vari-

ance estimation without regularity assumptions. The

Annals of Mathematical Statistics, pages 581–586.

Dettmers, T., Lewis, M., Belkada, Y., and Zettlemoyer,

L. (2022). Llm. int8 (): 8-bit matrix multipli-

cation for transformers at scale. arXiv preprint

arXiv:2208.07339.

Dettmers, T., Svirschevski, R., Egiazarian, V., Kuznedelev,

D., Frantar, E., Ashkboos, S., Borzunov, A., Hoeﬂer,

T., and Alistarh, D. (2023). Spqr: A sparse-quantized

representation for near-lossless llm weight compres-

sion. arXiv preprint arXiv:2306.03078.

Dettmers, T. and Zettlemoyer, L. (2023). The case for 4-bit

precision: k-bit inference scaling laws. In Interna-

tional Conference on Machine Learning, pages 7750–

7774. PMLR.

Frantar, E., Ashkboos, S., Hoeﬂer, T., and Alistarh, D.

(2022). Gptq: Accurate post-training quantization for

generative pre-trained transformers. arXiv preprint

arXiv:2210.17323.

Ghaffari, A., Tahaei, M. S., Tayaranian, M., Asgharian,

M., and Partovi Nia, V. (2022). Is integer arith-

metic enough for deep learning training? Advances

in Neural Information Processing Systems, 35:27402–

27413.

Li, L., Li, Q., Zhang, B., and Chu, X. (2023). Norm tweak-

ing: High-performance low-bit quantization of large

language models. arXiv preprint arXiv:2309.02784.

Lin, J., Tang, J., Tang, H., Yang, S., Dang, X., and Han, S.

(2023). Awq: Activation-aware weight quantization

for llm compression and acceleration. arXiv preprint

arXiv:2306.00978.

Micikevicius, P., Narang, S., Alben, J., Diamos, G., Elsen,

E., Garcia, D., Ginsburg, B., Houston, M., Kuchaiev,

O., Venkatesh, G., et al. (2017). Mixed precision train-

ing. arXiv preprint arXiv:1710.03740.

Rajpurkar, P., Zhang, J., Lopyrev, K., and Liang, P. (2016).

Squad: 100,000+ questions for machine comprehen-

sion of text. arXiv preprint arXiv:1606.05250.

Tayaranian, M., Ghaffari, A., Tahaei, M. S., Reza-

gholizadeh, M., Asgharian, M., and Nia, V. P. (2023).

Towards ﬁne-tuning pre-trained language models with

integer forward and backward propagation. In Find-

ings of the Association for Computational Linguistics:

EACL 2023, pages 1867–1876.

Tukey, J. W. (1965). Which part of the sample contains the

information? Proceedings of the National Academy

of Sciences, 53(1):127–134.

Wang, A., Singh, A., Michael, J., Hill, F., Levy, O., and

Bowman, S. R. (2018). Glue: A multi-task bench-

mark and analysis platform for natural language un-

derstanding. arXiv preprint arXiv:1804.07461.

Wei, X., Zhang, Y., Zhang, X., Gong, R., Zhang, S., Zhang,

Q., Yu, F., and Liu, X. (2022). Outlier suppres-

sion: Pushing the limit of low-bit transformer lan-

guage models. Advances in Neural Information Pro-

cessing Systems, 35:17402–17414.

Williamson, D. (1991). Dynamically scaled ﬁxed point

arithmetic. In [1991] IEEE Paciﬁc Rim Conference

on Communications, Computers and Signal Process-

ing Conference Proceedings, pages 315–318. IEEE.

Wolf, T., Debut, L., Sanh, V., Chaumond, J., Delangue, C.,

Moi, A., Cistac, P., Rault, T., Louf, R., Funtowicz,

M., et al. (2019). Huggingface’s transformers: State-

of-the-art natural language processing. arXiv preprint

arXiv:1910.03771.

Xiao, G., Lin, J., Seznec, M., Wu, H., Demouth, J., and Han,

S. (2023). Smoothquant: Accurate and efﬁcient post-

training quantization for large language models. In In-

ternational Conference on Machine Learning, pages

38087–38099. PMLR.

Yuan, Z., Niu, L., Liu, J., Liu, W., Wang, X., Shang, Y., Sun,

G., Wu, Q., Wu, J., and Wu, B. (2023). Rptq: Reorder-

based post-training quantization for large language

models. arXiv preprint arXiv:2304.01089.

Zhang, X., Liu, S., Zhang, R., Liu, C., Huang, D., Zhou, S.,

Guo, J., Guo, Q., Du, Z., Zhi, T., et al. (2020). Fixed-

point back-propagation training. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 2330–2338.

Zhao, K., Huang, S., Pan, P., Li, Y., Zhang, Y., Gu, Z., and

Xu, Y. (2021). Distribution adaptive int8 quantization

for training cnns. In Proceedings of the AAAI Con-

ference on Artiﬁcial Intelligence, volume 35, pages

3483–3491.

Zhao, R., Hu, Y., Dotzel, J., De Sa, C., and Zhang, Z.

(2019). Improving neural network quantization with-

out retraining using outlier channel splitting. In In-

ternational conference on machine learning, pages

7543–7552. PMLR.

Zhu, F., Gong, R., Yu, F., Liu, X., Wang, Y., Li, Z., Yang,

X., and Yan, J. (2020). Towards uniﬁed int8 training

for convolutional neural network. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 1969–1979.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

484