The Traveling Tournament Problem:

Rows-First versus Columns-First

Kristian Verduin

1,2 a

, Ruben Horn

2,3 b

, Okke van Eck

1,2 c

Reitze Jansen

1 d

, Thomas Weise

4 e

and Daan van den Berg

1,2 f

Department of Computer Science, University of Amsterdam, The Netherlands

Department of Computer Science, VU Amsterdam, The Netherlands

Helmut-Schmidt-University, Hamburg, Germany

Institute of Applied Optimization, Hefei University, China

Keywords:

Traveling Tournament Problem, Genetic Algorithms, Evolutionary Computing, Constraints, Constraint

Hierarchy.

Abstract:

At the time of writing, there is no known deterministic time algorithm to uniformly sample initial valid solu-

tions for the traveling tournament problem, severely impeding any evolutionary approach that would need a

random initial population. Repeatedly random sampling initial solutions until we ﬁnd a valid one is apparently

the best we can do, but even this rather crude method still requires exponential time. It does make a difference

however, if one chooses to generate initial schedules column-by-column or row-by-row.

1 INTRODUCTION

Even though both are proven to be NP-hard (Thielen

and Westphal, 2011; Verduin et al., 2023a), the trav-

eling tournament problem (TTP) is much harder than

the likesounding traveling salesman problem (TSP).

Being NP-hard means any exact algorithm requires

exponential time

, but for the TSP, we can at least

uniformly sample random solutions in deterministic

linear time, and perform mutations that transitively

connect all valid solutions in deterministic constant

time. The availability of an efﬁcient sampling algo-

rithm and efﬁcient transitive mutations for TSP make

the problem amenable to a broad variety of evolution-

ary algorithms. For TTP, both such algorithms are

currently not available, and it is really the question

whether they ever will.

The root of the issue lies in the constraints. The

TTP entails scheduling a tournament of an even num-

https://orcid.org/0009-0005-8754-7635

https://orcid.org/0000-0001-6643-5582

https://orcid.org/0000-0002-3600-5183

https://orcid.org/0009-0007-0029-2882

https://orcid.org/0000-0002-9687-8509

https://orcid.org/0000-0001-5060-3342

In the worst case instance, and assuming P ̸= NP

ber of (baseball) teams (n

teams

), containing 2 ·n

teams

−

2 rounds (Easton et al., 2001). Each team needs

to play all other teams exactly twice in the sched-

ule (once at home, once away), which is known as

the double round-robin constraint. Additionally,

when team A plays team B in one round, the inverse

match (B playing A) cannot be scheduled in the im-

mediate consecutive round, which is known as the

noRepeat constraint. Finally, there is the maximum

number of consecutive games any team can play at

home (or away), the maxStreak constraint

. Usually,

maxStreak = 3 meaning any team can at most play

three consecutive rounds at home or away anywhere

in the schedule (Thielen and Westphal, 2011). Only

three constraints, but they can be violated many times

per schedule (Fig.1, especially for larger numbers of

teams

. And as constraints go, it only takes one viola-

tion to render the entire schedule invalid.

But the actual problem is not about satisfying

these constraints. The TTP, like the TSP, has a dis-

tance matrix which holds the travel time between sta-

diums, and the main task is actually to minimize the

total travel time. The three constraints however, are so

asphyxiating, that travel time optimization almost be-

comes auxiliary to ﬁnding a valid schedule in the ﬁrst

Terminology varies slightly across literature.

Verduin, K., Horn, R., van Eck, O., Jansen, R., Weise, T. and van den Berg, D.

The Traveling Tournament Problem: Rows-First versus Columns-First.

DOI: 10.5220/0012557700003690

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 26th International Conference on Enterprise Information Systems (ICEIS 2024) - Volume 1, pages 447-455

ISBN: 978-989-758-692-7; ISSN: 2184-4992

447

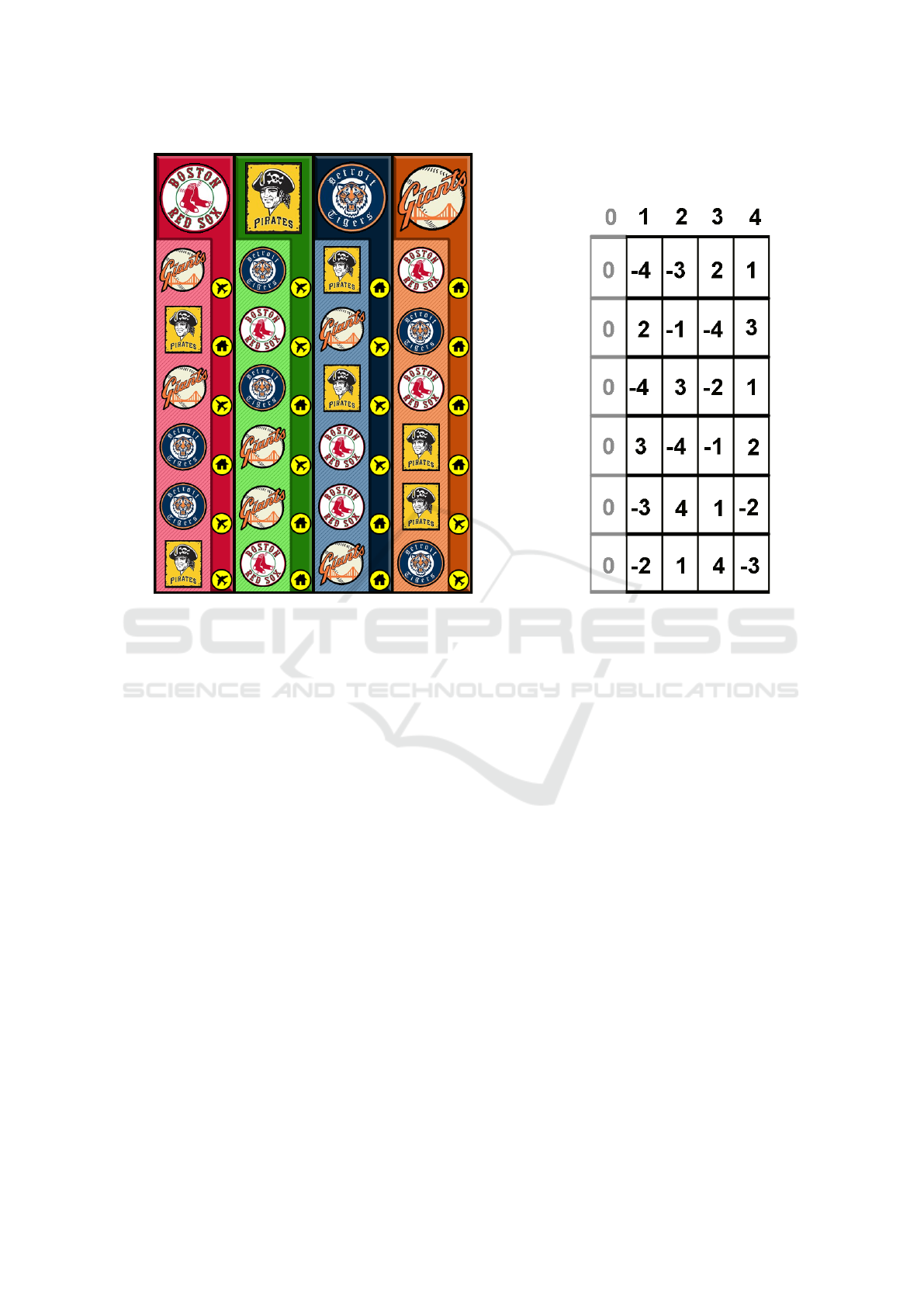
Figure 1: Left: A 4-team TTP schedule, generated in rows-ﬁrst order. It has one doubleRoundRobin violation in column 1

(playing the Giants away twice), one maxStreak violation in column 4, and no less than 4 noRepeat violations on row 5 in all

columns. Right: Internal representation of the same schedule. The padding the ﬁrst column of the matrix with unused zeroes

assures that all team numbers are nonzero, and thereby facilitates the use of negative numbers in the source code.

place. This is a real head breaker because NP-hard

problems, practically unsolvable by exact algorithms,

are usually attacked with some kind of metaheuristic,

which usually requires an initial population of valid

individuals, preferably uniformly sampled from the

solution space, to even start its optimizing process.

2 SAMPLING TTP SOLUTIONS

To be completely clear: we think that uniform random

sampling, which is so much needed for unbiased op-

eration of metaheuristic algorithms, is not possible in

deterministic polynomial time for TTP. Furthermore,

we suspect that ‘eligible’ mutations, that connect all

valid solutions into one traversable neighbourhood,

might not be possible either. Finally, we think that

an ‘eligible’ crossover operator might also not exist.

We are aware that this is a very strong and poten-

tially falsiﬁable position, but we also think that the

current state of consensus pertaining the TTP needs

it. The challenge to our colleagues therefore is: prove

us wrong, and bring your best game. Supply either a

deterministic polynomial sampling algorithm, an eli-

gible mutation or crossover operator. To the best of

our knowledge, none such methods exist.

Of course we dove into literature, and we encoun-

tered a lot of reccurring patterns. Many of the stud-

ies use small values for n

teams

, often from Michael

Trick’s benchmark (Trick, 2022). Many of these

even smaller than the real-life Major League base-

ball, which ‘only’ holds 30 teams at the time of writ-

ing. The world cup soccer however, typically played

in multiple countries, will hold 48 teams from 2026

onward, and is expected to grow from there.

While multiple of the papers implicitly or even

explicitly acknowledge the sparseness of the solution

landscape, none of them report the number of infea-

sible schedules that are generated. This suggests two

things:

1. New schedules (e.g. by mutation or crossover) are

made in stochastic time: if a mutation produces an

invalid schedule, simply retry. This is different,

and less reliable, than a mutation in determinis-

tic time, such as a 2-opt in the traveling salesman

problem.

2. The number of necessary tries in obtaining a valid

mutated schedule might increase exponentially,

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

448

similar to the generation of random initial valid

solutions as reported by Verduin et al. (Verduin

et al., 2023a). A very disheartening outlook might

therefore be that for larger problem instances,

even simply mutating a valid schedule into an-

other valid schedule in deterministic feasible time

is not possible. In some cases, we think this might

have been observed but not reported by the au-

thors, as it would explain the low number of n

teams

in many studies.

Often, a non-uniform initialization procedure is used

(usually the polygon method (de Werra, 1988; Dinitz

et al., 2006)), which is a deterministic scheduling pro-

cess, but of course only produces solutions from a

tiny portion of the combinatorial space. It is notewor-

thy however that the original proposal of this method

by (de Werra, 1988) considers creating a schedule

with one game between any two opponents and al-

lows breaks.

Finally, a number of papers pertain the mirrored

traveling tournament problem (mTTP), in which the

lower half of the schedule is identical to the up-

per half, with the home/away designations reverted.

Although this subset of TTP-solutions has a (su-

per)exponentially smaller search space than the reg-

ular TTP, it is still estimated to be far beyond

the reaches of explicit enumeration for any reason-

able values of n

teams

. But it might still be eas-

ier, even for metaheuristic algorithms, because the

doubleRoundRobin constraint is less likely to be vi-

olated. An open question however, is to what extent

that observation ties into the results reported in our

study.

3 RELATED WORK: EAs FOR

TTP

In a 2006 study, Biajoli and Lorena apply a genetic

algorithm together with simulated annealing to the

mTTP in which the doubleRoundRobin constraint is

satisﬁed by repeating the ﬁrst half of the schedule

with home/away designations reversed (Biajoli and

Lorena, 2006). The population is initialized using the

polygon method (de Werra, 1988) by expansion from

a compact chromosome representation which is a per-

mutation of the teams. Their possible mutations are:

swapping the home/away roles for a match, swapping

two matches, or swapping the entire match plan for

the two teams. The last mutation can produce invalid

schedules, causing a cascade of changes to the sched-

ule which is not further elaborated upon in this pa-

per. During the initialization, only the home/away

swap mutation is applied using a randomized non-

ascend method. Recombination is implemented us-

ing block order crossover, whereby the parent from

which to inherit a gene is determined by a uniform

random bitmask, resulting in an increase from O(n) to

O(2

) potential different offspring compared to one-

point crossover (Syswerda, 1989). An individual pro-

duced by recombination may undergo the mutations

of swapping home and away roles for a match, swap-

ping opponents for a match, or the entire itinerary

for two teams. This can result in invalid individ-

uals, which is not further addressed in the paper

(Ribeiro and Urrutia, 2007). Before selection, the lo-

cal search is applied using simulated annealing, and

the home/away and team swap mutations. Both fea-

sible and infeasible schedules are considered as the

‘neighborhood’ of an individual in this step. Their

largest instance comes from real world sports and has

24 teams, which, according to the authors, is large

compared to other instances used in the literature. We

agree.

In another study from 2006, Anagnostopoulos et

al. desginate doubleRoundRobin as a hard constraint,

while noRepeat and maxStreak are considered soft

constraints, and then apply simulated annealing with

reheating to the TTP (Anagnostopoulos et al., 2006).

Soft constraints may be violated as the algorithm tra-

verses the search space, and both feasible and infea-

sible neighborhood of schedules are explored. Us-

ing three mutation operations being the swapping two

rounds, swapping the home/away roles in one pair of

games, swapping opponents for a pair of teams, or

swapping rounds for one or two teams. The number of

violations is incorporated into the objective function

with a parameter ω to balance the exploration of both

feasible and infeasible regions. The initial schedule

is generated in a greedy recursive algorithm, and their

maximum n

teams

is 16, taken from Trick’s benchmark.

To us, this sounds like a promising approach, but the

big question is how long the algorithm stays in the

invalid space for values of ω, and whether a suitable

value for the parameter actually exists.

Tajbakhsh et al. present an approach with particle

swarm optimization improved by simulated anneal-

ing to the TTP modelled using binary integer pro-

gramming in which infeasible schedules are penal-

ized (Tajbakhsh et al., 2009). The generated individu-

als are only guaranteed to satisfy one hard constraint,

being the doubleRoundRobin constraint. The neigh-

borhood explored by simulated annealing is generated

using the same three mutation operations as in Anag-

nostopoulos et al. (Anagnostopoulos et al., 2006).

The largest instance from (Trick, 2022) used for eval-

uation has 10 teams. We suspect that the TTP is sig-

The Traveling Tournament Problem: Rows-First versus Columns-First

449

niﬁcantly easier without its maxStreak constraint.

Uthus et al. propose ant colony optimization with

forward checking and conﬂict-directed backjumping

for the TTP (Uthus et al., 2009). Schedules are gener-

ated round by round from the team with the fewest

possible opponents remaining. Unsafe backjump-

ing, at the cost of potentially missing feasible sched-

ules, helps the algorithm to leave unfeasible partial

ones. The algorithm generates and applies all possi-

ble home/away sequences for teams not violating the

corresponding constraint. Feasible solutions are im-

proved using tabu search. This approach is evaluated

using instances of up to 20 teams from Trick’s bench-

mark.

Nitin Choubey proposes symbolic chromosomes

with a unique character for each team as an encod-

ing scheme of all matches in a single string for TTP

using a genetic algorithm (Choubey, 2010). The ran-

dom initialization process is not described in detail

and may consist of forming a random permutation

of all pairs of teams. The approach uses bit-swap

mutation and two-point crossover with internal swap-

ping. Violations of constraints are penalized in the ﬁt-

ness calculation. The inclusion of the required num-

ber of slots in the penalty suggests that their method

also creates schedules with ‘holes’ such that not every

team plays a match in every round. It is evaluated us-

ing TTP instances of up to just 8 teams from Trick’s

online benchmark repository (Trick, 2022).

Saul and Adewumi investigate an artiﬁcial bee

colony algorithm for the TTP (Saul and Adewumi,

2012). They use the polygon method to create ini-

tial schedules, and their experiment uses a population

of 20 individuals over 20 cycles (only). Similar to

Anagnostopoulos et al., they use mutation operations

for swapping home/away conﬁgurations, opponents,

rounds and a partial swap of rounds but not of teams.

Their largest test instance consists of 16 teams, but

they note that “the algorithm [does] not perform well

on larger instances”. To mitigate this, they propose

to develop more the neighborhood relations to search

through, however, they do not mention their approach

to infeasible schedules.

Gupta et al. present a grey wolf optimizer for

the TTP (Gupta et al., 2015). The polygon method

is used to initialize the population, and simulated an-

nealing using the same ﬁve mutation types as Saul and

Adewumi (Saul and Adewumi, 2012) to optimize the

schedules. For the TTP, individuals are updated by

changing a single position in the initial permutation

of teams according to the best schedule. If a feasi-

ble schedule cannot be generated from this, the move

is not applied. Unfortunately, they do not report how

often this happens, a common theme in TTP papers.

Besides, for larger number of n

teams

, the algorithm

might be stuck in invalid space forever, and maybe

therefore the approach is evaluated using instances

from Trick’s benchmark with a size of only up to 16

teams. In their conclusion, the authors acknowledge

that the doubleRoundRobin constraint presents a sig-

niﬁcant difﬁculty and hint at the possible unfeasibility

of generating schedules in real world scenarios within

a short timeframe. We agree with this observation;

it could well be that without the doubleRoundRobin

constraint, ﬁnding valid TTP-schedules is easy.

Rutjanisarakul and Jiarasuksakun also tackle the

mTTP using a genetic algorithm (Rutjanisarakul and

Jiarasuksakun, 2017). They separate the binary

home/away and categorical opponents for all matches

into two matrices, but the algorithm only operates on

the former. During initialization, the second half of

the teams in the home/away matrix are assigned the

inverse of the ﬁrst half. Mutation is applied by ﬂip-

ping the binary value in the same cell of all four quad-

rants. Recombination is performed by selecting the

ﬁrst half of the teams using crossover and again ﬁll-

ing the second half with the inverse, as in the initial-

ization. The opponent matrix is then created using

an iterative scheduling algorithm. They evaluate their

approach using TTP instances up to n

teams

= 20. The

authors acknowledge that crossover without ﬁlling the

second half of the teams with the inverse of the ﬁrst

may result in invalid schedules, requiring repeated at-

tempts. However, they do not address the fact that

the mutation operation could also introduce violations

and how they handle this.

Kehilfa et al. propose an “enhanced genetic algo-

rithm for the TTP” (Khelifa et al., 2017). They ini-

tialize the population using the polygon method (de

Werra, 1988; Dinitz et al., 2006) and then choose

the best schedule from its neighborhood created by

mutation. They use the same mutations as Bai-

joli et al. (Biajoli and Lorena, 2006), but intro-

duce a new crossover that takes the partial itinerary

with the lowest cost from the ﬁrst parent and iter-

atively generate the remaining rounds from a min-

imum weight pairing of the graph of teams, with

the away/home assignment from the second parent

if possible. Additionally, their method includes vari-

able neighborhood search consisting of the mutations

described previously. Their test instances are taken

from Trick’s benchmark and have at most 10 teams.

They note that “it is not easy to create the remaining

rounds of an incomplete schedule without breaking

the [doubleRoundRobin] constraint”, but the treat-

ment of invalid schedules is not described further.

Also, the mutation types as described on page 2 of

their paper might introduce violations, but we were

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

450

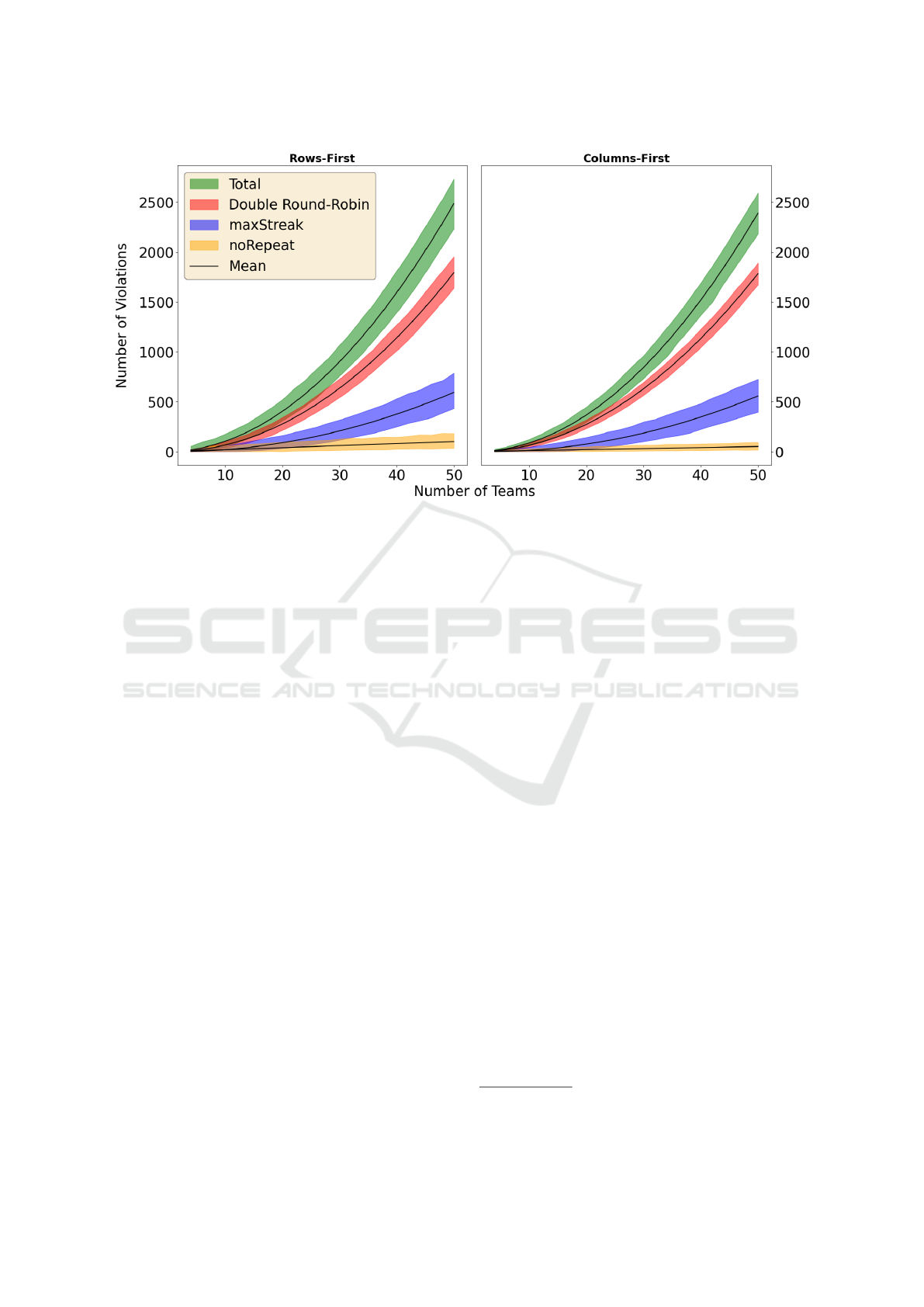
Figure 2: Whether random TTP schedules are generated in rows-ﬁrst or columns-ﬁrst order, the number of total violations

increases quadratically. However, the number of noRepeat-violations is almost half for columns ﬁrst, but the effect on its

linear increase is barely noticeable against the quadratic total.

as yet unable to reach the authors for comments or

source code.

A recent approach by Haldar et al. compares a

genetic algorithm and a particle swarm optimization

for the TTP (Haldar et al., 2022). Algorithms use the

same representation as Choubey for their candidate

schedules, but, since it is not described how new gen-

erations are created or how violations are treated, we

assume that it is also similar to the approach taken

in that paper. Supposedly, the particle swarm outper-

forms the genetic algorithm on the test instances with

up to n

teams

= 16 from teams Trick’s benchmark.

4 EXPERIMENT: ROWS-FIRST

VERSUS COLUMNS-FIRST

So as it turns out, we have a problem on our hands:

the TTP cannot be solved by exact algorithms for any

feasible n

teams

because it is NP-hard, but it can ALSO

not be solved by evolutionary algorithms, since they

need a uniformly sampled random initial population

of solutions – which can also not be done in any sort

of feasible time. At the time of writing, it seems

that uniform random sampling initial solutions to the

TTP can only be done in stochastic time: resampling

time and time again, hoping to ﬁnd a solution with

zero constraint violations. Sadly, this stochastic time

appears to be of exponential nature (Verduin et al.,

2023b; Verduin et al., 2023a), making it practically

impossible to solve TTP-instances with any substan-

tial n

teams

Nonetheless, we would like to press efforts in this

direction, and the most straightforward approach is

to build up a schedule round by round. A single

round can be randomly generated in deterministic lin-

ear time: ﬁrst make a ‘remaining’-list of all teams,

then randomly select a team, remove it from the list

randomly select a second team, also remove that team

from the ‘remaining’-list and insert these as oppo-

nents in the round, one of the two randomly assigned

their home venue, the other as playing away. Repeat

the procedure by choosing a second pair of opponents,

then a third pair and so on until the list is empty.

This round-by-round, or “rows-ﬁrst” generation guar-

antees, in deterministic linear time, that every round

in itself is valid: every team plays exactly one oppo-

nent, which is not itself, and home and away assign-

ments are conﬂict-free. As each round is uniform ran-

domly generated, the resulting schedule is also fully

uniformly random, but nonetheless not free of viola-

tions.

An alternative approach would be to do a column-

by-column (“columns-ﬁrst”) generation. Each col-

umn should hold all teams twice (once at home, once

away), except for the column’s own team, which can

not play against itself. A columns-ﬁrst generation can

also be done in deterministic linear time, which in-

This intermittent removal step might look superﬂuous,

but is necessary for the deterministic-time claim.

The Traveling Tournament Problem: Rows-First versus Columns-First

451

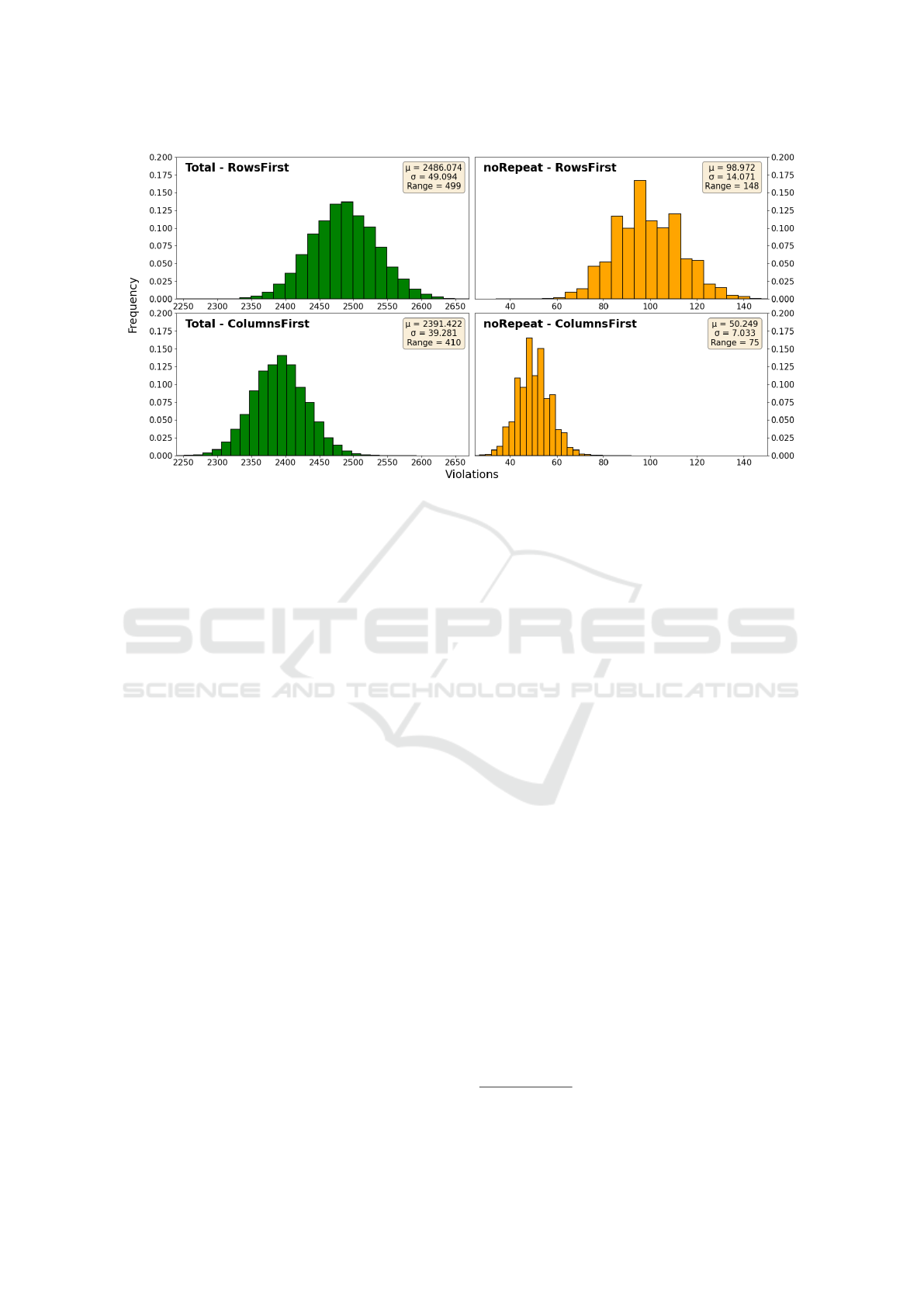
Figure 3: Using rows-ﬁrst generation or columns-ﬁrst generation for TTP schedules has a signiﬁcant impact on the number of

noRepeat violations for the traveling tournament problem. The number of total violations however, remains largely the same,

even though the range of values decreases with approximately 20%. In this ﬁgure, n

teams

= 50, and both experiments consist

of 5 million samples.

volves creating a ‘remaining’-list for team T . Other

than in rows-ﬁrst generation, it is speciﬁc to teams T

by containing all teams twice, once at home and once

away but not T itself. Internally, the ‘remaining’-

list is a set containing numbers {1, 2...n

teams

} twice:

positive for an ‘at home’-opponents, negative for an

‘away’-opponent. For this reason, the list contains

no zeroes, and the zero-column of the matrix contain-

ing the schedule is padded with unused zeroes (Fig.

1). It also allows the integer value in a matrix cell

to be immediately used as a column number for op-

posing teams. A for-loop randomly picking a team

from the ‘remaining’-list, placing them in the sched-

ule in the ﬁrst open slot of column T , and then remov-

ing them from the same list, effectively generating a

random permutation in deterministic linear time. Of

course, this can be done in stochastic time too, with

a while-loop, but we ﬁnd that approach sloppy, and

possibly more time consuming. After the procedure

is completed for the last column, the resulting com-

plete schedule is uniformly random, in deterministic

linear time, but again not free of violations. Strangely

enough though, the number and type of violations cre-

ated by columns-ﬁrst differs substantially from rows-

ﬁrst.

Our experiment entails generating 240 million

random TTP schedules: 5 million for each n

teams

∈

{4, 6,8...48, 50} using the rows-ﬁrst method totalling

to 120 million, and another 120 million for the same

teams

, each 5 million, but with columns-ﬁrst. After

completely ﬁlling up a schedule, the constraint viola-

tions are counted. All work was done in 48 threads

on SURF’s Snellius Compute Cluster

running De-

bian Linux in approximately 30 hours, and our Python

source code is publicly available (Anonymous, 2024).

For the noRepeat constraint, a violation is counted

for every team if a round’s opponent is the same as

the opponent from the previous round, regardless of

the home or away designation: playing the same team

in two subsequent rounds means one more noRepeat

violation. Internally, this is done by a for-loop that

compares the absolute values (thereby neglecting the

home/away designations) of two consecutive rows in

a column. For the maxStreak = 3 constraint, every

home or away game after the third is counted as one

constraint violation.

The doubleRoundRobin constraint is a little less

straightforward though. Historically, constructive

approaches (such as Frohner et al.’s beam search

(Frohner et al., 2020)) use round-ﬁrst generation only

hold valid partial schedules, i.e. having zero viola-

tions. But when it comes to allowing invalid sched-

ules, counting doubleRoundRobin violations is not

entirely straightforward. Departing from the only

known previous counting methods (Verduin et al.,

2023b) and (Verduin et al., 2023a), we count the

doubleRoundRobin constraint violations as follows:

every column T should hold every team twice, once

home once away, (internally denoted as once posi-

https://www.surf.nl/en/dutch-national-supercomputer-

snellius

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

452

tive, once negative), except T itself. For every team

missing, one column-violation is counted. Simultane-

ously, every row should hold each team exactly once,

in either home or away assignment (internally repre-

sented by the absolute value). For each team miss-

ing from a round, one row violation is counted. The

number of doubleRoundRobin violations is then the

sum of all row violations and all column violations. It

should be noted however, that columns-ﬁrst produces

only row violations, and the rows-ﬁrst produces only

column violations. It is an open problem whether a

deterministic time algorithm exists that does produce

a uniform random schedule with neither column vio-

lations nor row violations. We think it does not, and

also have doubts on whether it even can exist.

5 RESULTS

After the 5 million rows-ﬁrst random schedules for

a value of n

teams

were generated and violation-

counted, the mean number of violations was taken for

each violation type (doubleRoundRobin, maxStreak,

noRepeat, total) for every n

teams

, and characteriza-

tions were made through polynomial function ﬁtting

(Fig. 2). The same technique was then applied for

columns-ﬁrst generation, yielding another set of poly-

nomial characterizations.

The results show a very clear pattern: for

the expected number of doubleRoundRobin vio-

lations O(0.74(n

teams

)

) and maxStreak violations

O(0.25(n

teams

)

), it really doesn’t matter whether

to use rows-ﬁrst or columns-ﬁrst generation – their

characterizations are almost identical. Although

columns-ﬁrst generation is slightly better than rows-

ﬁrst overall, the difference converges to 1% for

doubleRoundRobin and < 6% for maxStreak. But re-

markably enough, this does not hold for the number

of noRepeat violations which is almost 94% higher

when using rows-ﬁrst generation, than with columns-

ﬁrst generation, in O(7.88 ·n

teams

) and O(4.07 · n

teams

respectively. For all eight characterizations, the R

quality-of-ﬁt was at least 0.9999.

Another striking difference is in the range (max-

min) and the standard deviation (σ) for the total num-

ber of violations (Figure 3). Although both are signiﬁ-

cantly higher in rows-ﬁrst, both values appear to con-

verge to 125% of the values for columns-ﬁrst, even

though this percentage is naturally a bit wobblier for

the range, which depends on individual outliers.

6 INTERMEZZO: TO MATCH OR

NOT TO MATCH

During the ﬁnalization of this manuscript, one discus-

sion popping up between the authors was the asym-

metry of matching between rows-ﬁrst and columns-

ﬁrst. In rows-ﬁrst, the teams are selected as pairs, in-

serted in both corresponding columns, one randomly

designated as ‘away’, the other ‘at home’. This means

that for rows-ﬁrst, not only the appearance of “every

team once per row” is satisﬁed, but also their opposi-

tion in pairs, and even their home-away designation.

These possible violations were not counted,

and thereby might present columns-ﬁrst as more

favourable than it actually is. On the other hand, it

might be possible to do the matching for columns-ﬁrst

also, although at the time of writing we are not sure

whether it leads to better schedules, or to a deadlock

later in the assignment.

This incompleteness of thought was one reason

not to endeavour in this direction yet, but another rea-

son is given by the existence of (approximate) random

sampling of magic squares (Jacobson and Matthews,

1996). Though the approach is not without difﬁcul-

ties, it is principally possible to uniformly randomly

sample magic squares. Although it is possible to

transform any mirrored TTP schedule into a magic

square, the converse is not necessarily true: not every

magic square is transformable into a (mirrored) TTP-

schedule – even though some are. Still, we feel that

these results are so deeply connected they could shed

new light on the problem of uniformly randomly sam-

pling TTP schedules. The current way of counting vi-

olations in TTP is almost directly suitable for count-

ing violations in randomly sampled magic squares.

We will explore these, and several other avenues, in

future work.

7 CONCLUSION

Columns-ﬁrst generation is better than rows-ﬁrst gen-

eration. It scores lower for all violation types, but

whereas the difference in doubleRoundRobin viola-

tions and maxStreak violations tends to zero for in-

creasing n

teams

, the true gain for columns-ﬁrst is in

noRepeat, which converges to about half the number

compared to rows-ﬁrst – for the same time complex-

ity.

Great, we just cut the amount of expected

noRepeat violations in half. But does it really strike

a dent in the problem as a whole? Both the number

of doubleRoundRobin violations and maxStreak vi-

olations increase quadratically, dwarving the linearly

The Traveling Tournament Problem: Rows-First versus Columns-First

453

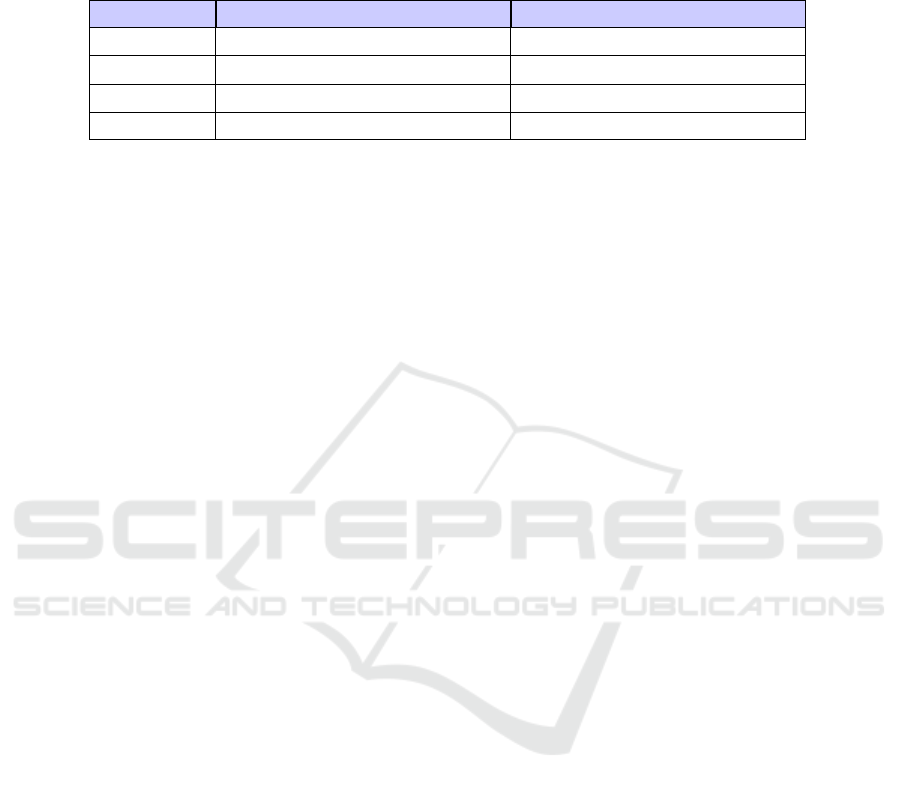
Table 1: Expected numbers of violations can be characterized by a quadratric polynomial (x substitutes n

teams

for readability).

The resulting functions are nearly identical for either generation method, except for the expected number of noRepeat viola-

tions, which doubles from columns-ﬁrst to rows-ﬁrst. Note that the exact same function was ﬁt to all three violation types, but

for noRepeat, the ﬁrst constant just ﬁt to zero, dropping the quadratic term.

Rows-First Columns-First

Total 0.9855x

+ 0.4725x − 1.3570 0.9862x

− 1.5050x + 1.1980

dRR 0.7357x

− 0.9178x − 0.0610 0.7360x

+ 1.1140x − 0.1436

maxStreak 0.2500x

− 0.6251x − 0.0021 0.2502x

− 1.3890x − 1.3180

noRepeat 2.0150x − 1.2840 0.9855x + 0.0239

increasing number of noRepeat violations as n

teams

increases. So for speciﬁc obscure variants of the TTP

it might help a bit, but for now, the progress on just

generating valid initial solutions for the TTP is very

meagre, practically speaking. Still, it is a principal

step forward in ﬁnding a feasible-time random sam-

pling algorithm for the problem.

A more important takeaway from this investiga-

tion is that it is very hard, if not impossible, to gener-

ate uniform random valid TTP-schedules in any sort

of deterministic time, even when completely ignor-

ing the maxStreak and noRepeat constraints. For the

best uniform algorithm we know, columns-ﬁrst gen-

eration, the expected number of constraint violations

for the TTP still increases quadratically in the number

of teams. In computer science, a polynomial increase

is usually considered innocuous but remember that in

this case, all constraints need to be satisﬁed before

even considering a minimized travel distance – the

real task at hand. Besides, the stochastic quadratic

increase in violations might give rise to a stochastic

exponential number of required samples for a ﬁnding

a single valid initial schedule, as suggested by earlier

studies (Verduin et al., 2023b; Verduin et al., 2023a).

Furthermore, the TTP is not the only problem having

this difﬁculty; HP-protein folding also seems to be af-

fected by it, but to a lesser extent (Dill, 1985; van Eck

and van den Berg, 2023; Jansen et al., 2023).

It is for this reason, the unavailability of a fea-

sible random sampling algorithm (in either stochas-

tic or deterministic time), that we argue that the

TTP is harder than the TSP, even though both are

listed as NP-hard. The TSP can still be ‘solved’

with hill climbing, simulated annealing or evolution-

aryc algorithms (Koppenhol et al., 2022), whereas the

TTP probably cannot, simply because random ini-

tial solutions can not be produced in feasible time.

And whether eligible feasible-time mutations and

crossovers exist also remains to be seen. It looks

like ﬁnding valid schedules in itself is quite a chal-

lenge, and might be amenable to approaches such as

frequency ﬁtness assignment or local optima network

analysis before even thinking about minimizing travel

distance (de Bruin et al., 2023; Liang et al., 2022;

Thomson et al., 2023; Thomson et al., 2022).

ACKNOWLEDGEMENT

Logos in this paper were remade by

melling2293@Flickr, and distributed under cre-

ative commons license. We also thank Reviewer#1

from ICEIS 2024 for reading our paper so well.

REFERENCES

Anagnostopoulos, A., Michel, L., Hentenryck, P. V., and

Vergados, Y. (2006). A simulated annealing ap-

proach to the traveling tournament problem. Journal

of Scheduling, 9(2):177–193.

Anonymous (2024). Repository containing source material:

https://anonymous.4open.science/r/TTP-Column-vs-

Row-Constraints-46FE/README.md.

Biajoli, F. L. and Lorena, L. A. N. (2006). Mirrored

traveling tournament problem: An evolutionary ap-

proach. In Sichman, J. S., Coelho, H., and Rezende,

S. O., editors, Advances in Artiﬁcial Intelligence -

IBERAMIA-SBIA 2006, pages 208–217, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Choubey, N. (2010). A novel encoding scheme for traveling

tournament problem using genetic algorithm. Interna-

tional Journal of Computer Applications, ecot.

de Bruin, E., Thomson, S. L., and Berg, D. v. d. (2023).

Frequency ﬁtness assignment on jssp: A critical re-

view. In International Conference on the Applications

of Evolutionary Computation (Part of EvoStar), pages

351–363. Springer.

de Werra, D. (1988). Some models of graphs for scheduling

sports competitions. Discrete Applied Mathematics,

21(1):47–65.

Dill, K. A. (1985). Theory for the folding and stability of

globular proteins. Biochemistry, 24(6):1501–1509.

Dinitz, J. H., Froncek, D., Lamken, E. R., and Wallis, W. D.

(2006). Scheduling a tournament. In Handbook of

Combinatorial Designs. Chapman and Hall/CRC.

Easton, K., Nemhauser, G., and Trick, M. (2001). The

traveling tournament problem description and bench-

marks. In Principles and Practice of Constraint Pro-

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

454

gramming—CP 2001: 7th International Conference,

CP 2001 Paphos, Cyprus, November 26–December 1,

2001 Proceedings 7, pages 580–584. Springer.

Frohner, N., Neumann, B., and Raidl, G. (2020). A beam

search approach to the traveling tournament problem.

In Evolutionary Computation in Combinatorial Op-

timization, pages 67–82. Springer International Pub-

lishing.

Gupta, D., Anand, C., and Dewan, T. (2015). Enhanced

heuristic approach for traveling tournament problem

based on grey wolf optimizer. In 2015 Eighth In-

ternational Conference on Contemporary Computing

(IC3), pages 235–240.

Haldar, A., Mondal, S., Mukherjee, A., and Chatterjee,

K. (2022). A comparative analysis of application of

genetic algorithm and particle swarm optimization in

solving traveling tournament problem (ttp). Interna-

tional Journal of Bioinformatics and Intelligent Com-

puting.

Jacobson, M. T. and Matthews, P. (1996). Generating uni-

formly distributed random latin squares. Journal of

Combinatorial Designs, 4(6):405–437.

Jansen, R., Horn, R., van Eck, O., Verduin, K., Thomson,

S., and van den Berg, D. (2023). Can hp-protein fold-

ing be solved with genetic algorithms? maybe not.

In Proceedings of the 15th International Joint Confer-

ence on Computational Intelligence ECTA - Volume 1,

pages 131–140.

Khelifa, M., Boughaci, D., and A

ımeur, E. (2017). An en-

hanced genetic algorithm with a new crossover opera-

tor for the traveling tournament problem. In 2017 4th

International Conference on Control, Decision and

Information Technologies (CoDIT), pages 1072–1077.

Koppenhol, L., Brouwer, N., Dijkzeul, D., Pijning, I.,

Sleegers, J., and Van Den Berg, D. (2022). Exactly

characterizable parameter settings in a crossoverless

evolutionary algorithm. In Proceedings of the Genetic

and Evolutionary Computation Conference Compan-

ion, pages 1640–1649.

Liang, T., Wu, Z., L

assig, J., van den Berg, D., and Weise, T.

(2022). Solving the traveling salesperson problem us-

ing frequency ﬁtness assignment. In 2022 IEEE Sym-

posium Series on Computational Intelligence (SSCI),

pages 360–367. IEEE.

Ribeiro, C. C. and Urrutia, S. (2007). Heuristics for the mir-

rored traveling tournament problem. European Jour-

nal of Operational Research, 179(3):775–787.

Rutjanisarakul, T. and Jiarasuksakun, T. (2017). A sport

tournament scheduling by genetic algorithm with

swapping method. Journal of Engineering and Ap-

plied Sciences, 13.

Saul, S. and Adewumi, A. (2012). An artiﬁcial bees colony

algorithm for the traveling tournament problem. In

41st Annual Conference of the Operations Research

Society of South Africa, page 10.

Syswerda, G. (1989). Uniform crossover in genetic algo-

rithms. In Proc. 3rd Intl Conference on Genetic Algo-

rithms 1989.

Tajbakhsh, A., Eshghi, K., and Shamsi, A. (2009). A hybrid

pso-sa algorithm for the traveling tournament prob-

lem. In 2009 International Conference on Computers

& Industrial Engineering, pages 512–518.

Thielen, C. and Westphal, S. (2011). Complexity of the

traveling tournament problem. Theoretical Computer

Science, 412(4-5):345–351.

Thomson, S. L., Ochoa, G., and Verel, S. (2022). The frac-

tal geometry of ﬁtness landscapes at the local optima

level. Natural Computing, pages 1–17.

Thomson, S. L., Veerapen, N., Ochoa, G., and van den

Berg, D. (2023). Randomness in local optima net-

work sampling. In Proceedings of the Companion

Conference on Genetic and Evolutionary Computa-

tion, pages 2099–2107.

Trick, M. A. (2022). Challenge traveling tournament prob-

lems.

Uthus, D. C., Riddle, P. J., and Guesgen, H. W. (2009). An

ant colony optimization approach to the traveling tour-

nament problem. In Proceedings of the 11th Annual

Conference on Genetic and Evolutionary Computa-

tion, GECCO ’09, page 81–88, New York, NY, USA.

Association for Computing Machinery.

van Eck, O. and van den Berg, D. (2023). Quantifying

instance hardness of protein folding within the hp-

model. (accepted for publication at CIBCB’23).

Verduin, K., Thomson, S. L., and van den Berg, D.

(2023a). Too constrained for genetic algorithms. too

hard for evolutionary computing. the traveling tour-

nament problem. In Proceedings of the 15th Inter-

national Joint Conference on Computational Intelli-

gence ECTA - Volume 1, pages 246–257.

Verduin, K., Weise, T., and van den Berg, D. (2023b). Why

is the traveling tournament problem not solved with

genetic algorithms?

The Traveling Tournament Problem: Rows-First versus Columns-First

455