The Robustness of a Twisted Prisoner’s Dilemma for Incorporating

Memory and Unlikeliness of Occurrence

Akihiro Takahara

and Tomoko Sakiyama

Information Systems Science, Graduate School of Science and Engineering, Soka University, Hachioji, Japan

Department of Information Systems Science, Soka University, Hachioji, Japan

Keywords: Spatila Prisoner’s Dilemma, Memory, System-Size Analysis.

Abstract: In classical game theory, because players having Defector (D) strategy tend to survive, many studies have

been conducted to determine the survival of players with Cooperator (C) strategy. Recently, we have tackled

the problem of the evolution of cooperators by proposing a new model called the twisted prisoner’s dilemma

(TPD) model. In the proposed model, each player is given a memory length. In situations where neighbors

had the same strategy as a player and a higher score than that of the player, the player updated their strategy

by ignoring the classical SPD update rule. This new strategy was difficult to choose before the update.

Consequently, cooperators could survive even if their memory length was small. In this study, by focusing on

the system sizes, performance of the TPD model was determined. Similar results were obtained for various

system sizes, except when the system size was extremely small.

1 INTRODUCTION

Cooperative behavior is the characteristic present in a

population as per the game theory (Smith & Price,

1973). In game theory, propagation as a population in

the interaction of cooperative and defective behavior

is described (Nowak & May, 1992; Jusup et al.,

2022). In classical game theory, there are two

strategies, Cooperator (C) and Defector (D), both of

which interact to obtain a payoff. The earned payoff

differs depending on the owner and opponent’s

payoff. Therefore, a player’s strategy with a high

payoff is easily passed onto the next generation.

However, in classical game theory, cooperators have

difficulty surviving and are sensitive to the

parameters.

The payoff matrix parameter in classical game

theory significantly affects system evolution

(Killingback and Coebeli, 1996; Smith and Price,

1973; Szabó and Toké, 1998). Thus, many studies

have been conducted on the survival of cooperators

(Qin et al., 2018; Sakiyama & Arizono, 2019;

Sakiyama, 2021). Among them, the prisoner’s

dilemma is particularly used. Recently, the twisted

prisoner’s dilemma (TPD) model, which considers

the player’s memory of their past strategy and

https://orcid.org/ 0000-0002-2687-7228

sometimes ignores the conventional strategy update

rule, has been developed (Takahara & Sakiyama,

2023). This model calculates the frequency of

strategies’ appearance using each memory. Then, the

strategy of low adoption rate is easily adopted by

ignoring the classical strategy update rule of the

spatial prisoner’s dilemma (SPD) model. Several

studies have focused on player’s past information or

the time delay effect (Deng et al., 2017; Danku et al.,

2019). However, most of these studies assume that

players can access the “long past.” Conversely, unlike

previous studies, our model assumes that players can

access only recent memories. Thus, our proposed

TPD model is more realistic than the classical SPD

model. In our previous study using this model, we

found that it was insensitive to the payoff matrix

parameter and could maintain the cooperators

(Takahara & Sakiyama, 2023). In this study, the

model’s performance was further investigated by

focusing on the system size. Many studies on spatial

game theory have investigated the effect of varying

system sizes (Sakiyama & Arizono, 2019; Frey,

2010).

Takahara, A. and Sakiyama, T.

The Robustness of a Twisted Prisoner’s Dilemma for Incorporating Memory and Unlikeliness of Occurrence.

DOI: 10.5220/0012537800003708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 9th Inter national Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2024), pages 13-16

ISBN: 978-989-758-698-9; ISSN: 2184-5034

2 METHODS

2.1 Simulation Environments

A lattice space was formed with players in every

square. The system size of the lattice space could be

changed: 10 × 10, 30 × 30, 100 × 100, 100 ×

200, 𝑎𝑛𝑑 200 × 200 sizes were used in this study.

All squares of any system size were initially assigned

either the Cooperator (C) or Defector (D) strategy.

The initial distribution of the strategies was set to 0.5

for the initial defector density. Thus, both strategies

were distributed with the same probability.

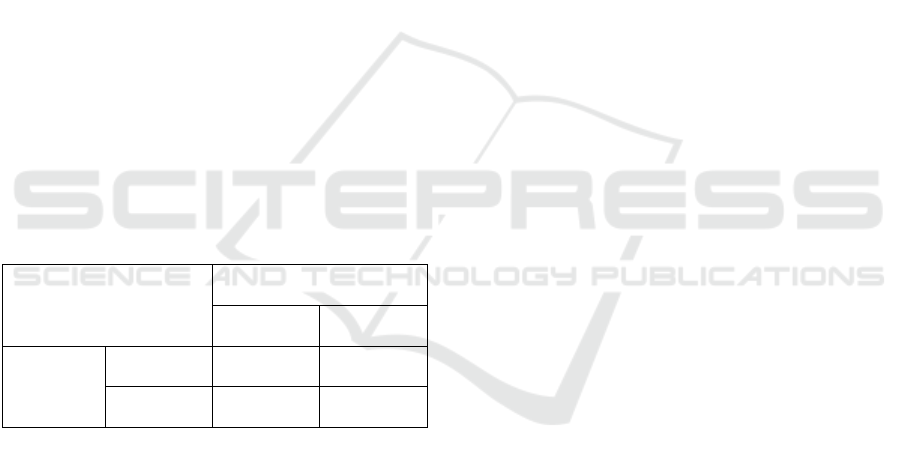
The payoffs were arranged as T=b, R=1, S=P=0,

according to the payoff matrix depicted in Table 1,

where T>R>P=S. The parameter 𝑏 determining 𝑇

was set to 1<𝑏<2 (Nowak & May, 1992). If a

neighboring player adopted strategy C, a player

employing strategy D would receive T as a

temptation. Conversely, if a neighboring player

employed strategy D, a player using strategy C would

receive S as a sucker. A player received P as a

punishment if both strategies were D. A player

received R as a reward if both strategies were C. We

used the Neumann neighborhood and periodic

boundary conditions. Each trial included 1000 time

steps.

Table 1: Payoff matrix.

neighbor

C D

Player

C 𝑅(1) 𝑆(0)

𝑇(𝑏) 𝑃(0)

2.2 Description of Spatial Prisoner’s

Dilemma Model

After assigning strategies to the players, the iteration

began, during which the players compared their

strategies with those of their neighbors based on the

payoff matrix and calculated their scores. Then, the

players compared their own scores with their

neighbors’ scores and memorized the neighbor’s

strategy with the highest score. All players’ strategies

were then synchronously updated to their memorized

strategies. Their strategies remained unchanged in

cases where multiple neighbors attained the highest

score while employing different strategies.

2.3 Description of the Twisted

Prisoner’s Dilemma Model

In a previous study, the TPD model has been

described (Takahara & Sakiyama, 2023). Every

player was allocated a constant memory length value,

denoted as 𝜃, which remained unchanged across trials.

After every player calculated their scores, they

reviewed their previous strategies. The past duration

considered spanned from 𝑡 (current) to 𝑡−𝜃, and the

parameter n_c represented the count of cooperative

strategies experienced during that period.

If their neighbor’s strategy was the same as theirs,

while their own score was lower, the player updated

the strategy to either C or D using the following two

probabilities:

For C:

1 − (𝑛_𝑐)/𝜃

For D:

(𝑛_𝑐)/𝜃

If the aforementioned conditions were not met, the

strategy update rule of the SPD model was

implemented. The strategy of each player is

synchronously updated. In the proposed TPD model,

the strategy update rule, which uses the 𝑝 -values

excluded from the SPD model, was not executed until

𝑡 > 𝜃.

3 RESULTS

One hundred trials were performed using thousand-

time steps as one trial. The defector density at the

1000-time steps for each trial was calculated and

averaged over 100 trials.

First, the proposed TPD model was compared with

the conventional SPD model. The system size was

100 × 100. Figure 1 shows the results. The proposed

model had a defector density higher than that of the

conventional model for 1.0 < 𝑏 < 1.5 . However,

after the parameter b passed 1.5, the proposed model

had a lower value than the conventional model,

suggesting that the proposed model contributed to the

maintenance of the cooperator (Takahara &

Sakiyama, 2023).

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

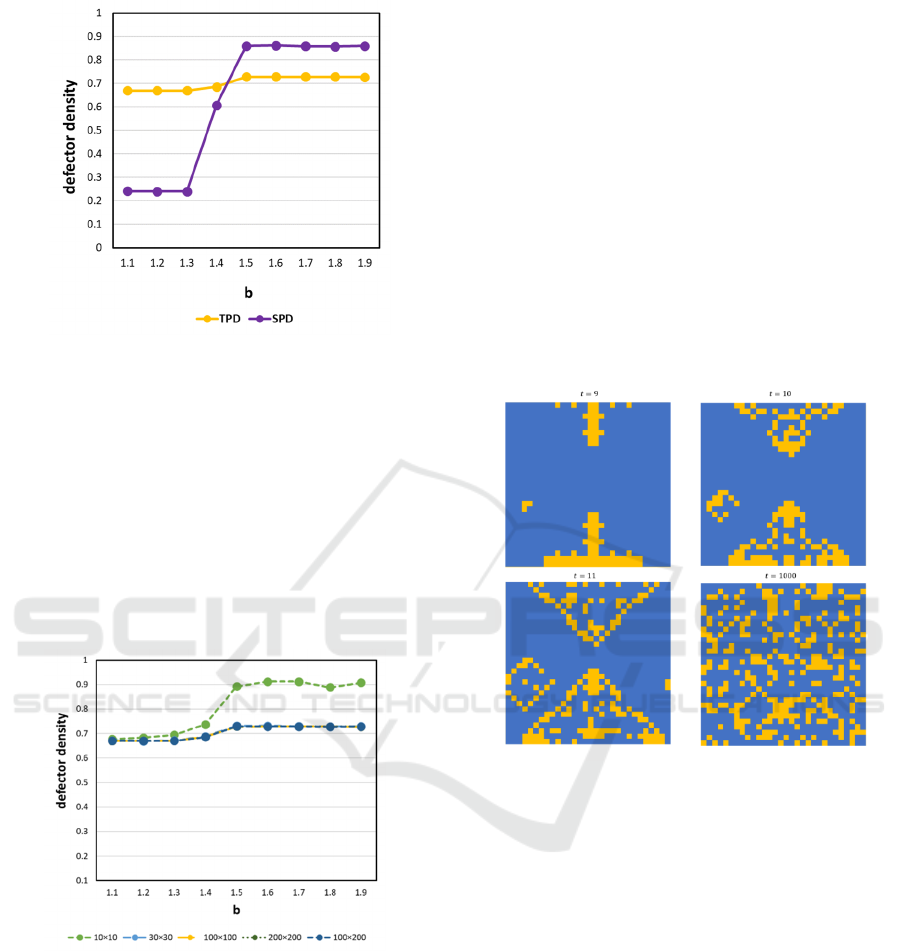
Figure 1: Defector density for the two models—SPD and

TPD.

Next, the system-size effects were evaluated by

comparing the various system sizes of the TPD model

with its 100 × 100 size. Figure 2 shows the results.

Most of the system sizes had similar defector density

values. The results indicate that the TPD model is

unaffected by changes in the system size and that a

certain number of cooperators are maintained even at

a certain small system size. However, the defector

density of the system size with 10 × 10 was higher

than that of the other system sizes.

Figure 2: Defector density of the proposed TPD model for

various sizes.

Hereafter, the spatial distribution of the small

system size was checked to investigate why an

extremely small system size affects the performance

of the TPD model.

In this study, two different system sizes were

investigated. The system size was either 10 × 10 or

30 × 30. The spatial distribution was displayed for

several time steps ( 𝑡  9, 𝑡  10, 𝑡  11, 𝑎𝑛𝑑 𝑡 

1000).

Figure 3 shows the results. Given that 𝑝10 in

this case, the C was maintained at 𝑡9 as in the SPD

model. In this model, the C is characterized by a form

that is maintained as a two-column cross, which is

similar to the classical SPD model. However, the

player near a cooperator then updated their strategy to

C at 𝑡10. It also spread like a wave with each time

step. Since a defector in the neighborhood of a

cooperator had a smaller score than another defector

in the same neighborhood, they had a chance to

become cooperators. Also, some of the players who

had their original strategy as C updated their

strategies to D according to the SPD rules. These

strategy updates extended further by forming a

characteristic pattern. Finally, C was maintained as

sparsely as a 1000-time step.

Figure 3: Spatial distribution for mutiple times in the

30 × 30 system size.

The 10 × 10 system size results are shown in

Figure 4. Similarly, 𝑝10 was set for this system

size. Two patterns were found for this system size. In

Figure 4A, some cooperators survived until the end.

However, wavy spreading could not be observed

at 𝑡  9 , 𝑡10, and 𝑡11. Therefore, it was

considered more difficult for C to survive in than in

other system sizes. In addition, the cooperators did

not appear at all times in Figure 4B, which is

supposedly related to the initial placement as per C.

Supposedly, they did not form clumps to survive, as

shown in Figure 4B. Some trials created a spatial

pattern that resembled those in Figure 4A and 4B,

resulting in the high defector density shown in Figure

The pattern of early C extinction was observed for

small system sizes such as 10 × 10, whereas it was

rarely observed for other larger system sizes.

The Robustness of a Twisted Prisoner’s Dilemma for Incorporating Memory and Unlikeliness of Occurrence

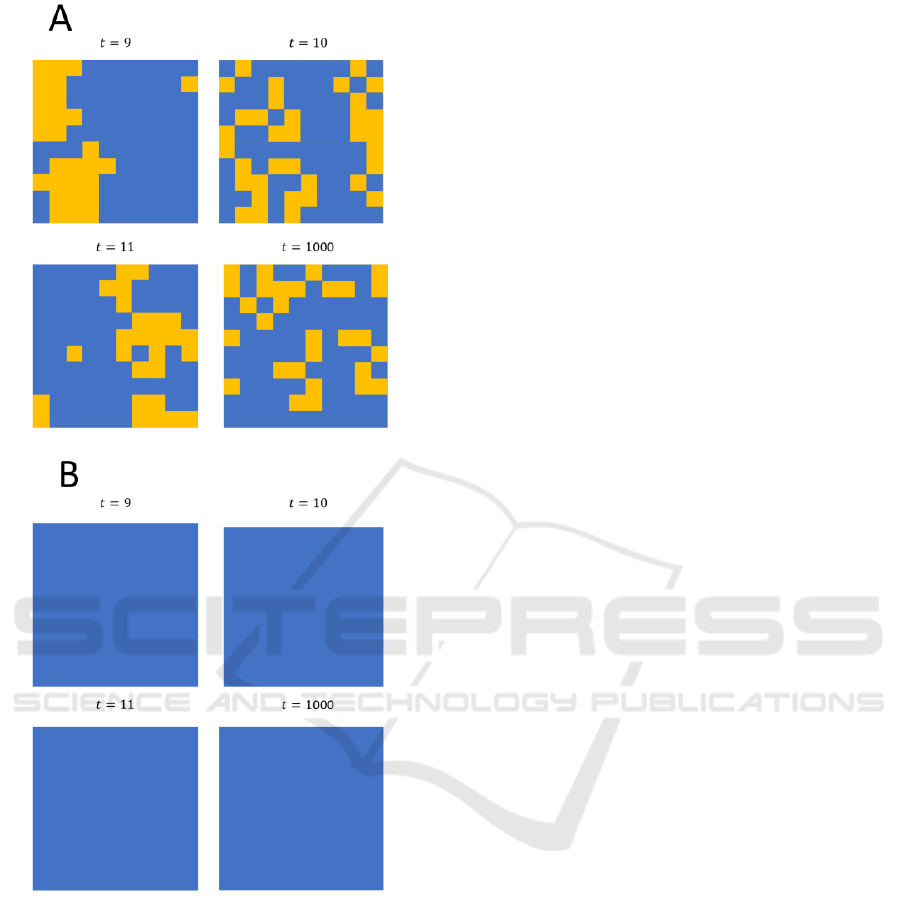
Figure 4: Spatial distribution for mutiple times in the

10 × 10 system size. Two different examples are shown in

A and B panels.

4 CONCLUSIONS

In this study, the TPD model was compared with the

conventional SPD model, and the effect of system

size on the proposed TPD model was investigated.

The system sizes of 10 × 10, 30 × 30, 100 ×

100, 100 × 200, 𝑎𝑛𝑑 200 × 200 were compared,

and the spatial distributions of the two smaller system

sizes were compared. Consequently, the defector

density results for all system sizes differed

insignificantly except for the 10 × 10 system size,

and the strategy C is maintained. In this model, the

spatial distribution shows that the C spreads like a

wave in a diamond shape (Takahara & Sakiyama,

2023). Even with a spatial distribution of the 30 × 30

system size, the C spreads like a diamond shape.

However, the spatial distribution of the 10 × 10

system size makes it difficult to form such a wave.

This leads to the results shown in Figure 2. In

summary, it is found that the proposed model is

inventive for various system sizes.

In the future, we will confirm the impact on the

model by increasing the system size and changing the

network topology.

REFERENCES

Deng, Z., Ma, C., Mao, X., Wang, S., Niu, Z., Gao, L.

(2017). Historical payoff promotes cooperation in the

prisoner’s dilemma game. Chaos, Solitons & Fractals.

104, 1–5.

Danku, Z., Perc, M., Szolnoki, A. (2019). Knowing the past

improves cooperation in the future. Scientific Reports.

9, 262.

Frey, E. (2010). Evolutionary game theory: Theoretical

concepts and applications to microbial communities.

Physica. Part A. 389, 4265–4298.

Killingback, T., Coebeli, M. (1996). Spatial evolutionary

game theory: Hawks and Doves revisited. Proceedings

of the Royal Society of London. Series B. 263, 1135–

1144.

Jusup, M., Holme, P., Kanazawa, K., Takayasu, M., Romić,

I., Wang, Z., Geček, S., Lipić, T., Podobnik, B., Wang,

L., Luo, W., Klanjšček, T., Fan, J., Boccaletti, S., Perc,

M. (2022). Social physics. Physics Reports. 948, 1–

148.

Nowak, M. A., May, R. M. (1992). Evolutionary games and

spatial chaos. Nature. 359, 826–829.

Qin, J., Chen, Y., Fu, W., Kang, Y., Perc, M. (2018).

Neighborhood diversity promotes cooperation in

social dilemmas. IEEE Access. 6, 5003–5009.

Sakiyama, T. (2021). A power law network in an

evolutionary hawk–dove game. Chaos, Solitons &

Fractals. 146, 110932.

Sakiyama, T., Arizono, I. (2019). An adaptive replacement

of the rule update triggers the cooperative evolution in

the Hawk–Dove game. Chaos, Solitons & Fractals.

121, 59–62.

Smith, J. M., Price, G. R. (1973). The logic of animal

conflict. Nature. 246, 15–18.

Szabó, G., Toké, C. (1998). Evolutionary prisoner’s

dilemma game on a square lattice. Physical Review.

Part E. 58, 69–73.

Takahara, A., Sakiyama, T. (2023). Twisted strategy may

enhance the evolution of cooperation in spatial

prisoner’s dilemma. Physica. Part A, 129212.

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk