
Detection of Local Symmetry Polylines of Polygons Based on Sweeping
Paradigm
Martin Safko
1,3 a
, Luka Luka
ˇ
c
2 b
, Borut
ˇ
Zalik
2 c
and Ivana Kolingerov
´
a
3 d
1
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Praha 2, Czech Republic
2
Faculty of Electrical Engineering and Computer Science, University of Maribor,
Koro
ˇ
ska cesta 46, SI-2000 Maribor, Slovenia
3
Department of Computer Science and Engineering, University of West Bohemia,
Technick
´
a 8, 306 14 Plze
ˇ
n, Czech Republic
Keywords:
Symmetry, Polygon, Sweeping, Segmentation, Characterization, Computer Graphics.
Abstract:
Symmetry is a fundamental property of many objects of interest allowing us to simplify computation or re-
duce complexity and is also a contributing factor of beauty for a human brain. In this work, we try to identify
polylines satisfying the local reflection symmetry of polygons and show how to use them for shape character-
ization, segmentation or to find global approximate reflection symmetries. We describe an algorithm based on
a sweep-line paradigm to efficiently compute the polylines by scanning through a polygon at various angles.
1 INTRODUCTION
Symmetry is one of the crucial features of geomet-
ric shapes, indicating their invariance to various ge-
ometric transformations or their combinations (Sun
and Bhanu, 2011). People perceive symmetrical pat-
terns as more attractive than their asymmetrical coun-
terparts (Enquist and Arak, 1994). Symmetry repre-
sents one of the main visible properties of objects and
is easily recognizable to the human eye. Unlike hu-
mans, the detection of symmetries is a considerably
challenging task for computers (
ˇ
Zalik et al., 2022).
As the identification of symmetries in shapes can sig-
nificantly simplify further tasks of shape processing,
such as polygon segmentation or shape characteriza-
tion, numerous approaches for symmetry detection in
shapes have been proposed thus far.
Existing approaches for the detection of sym-
metries in shapes are often complex and resource-
intensive. Therefore, in this paper, we propose a
fast and simple method that extracts local features of
a shape using the concepts of sweeping and reflec-
tion symmetry. The shape, described by polygons, is
swept with sweep-lines at different angles. During
a
https://orcid.org/0009-0005-9403-8185
b
https://orcid.org/0000-0003-4691-5401
c
https://orcid.org/0000-0003-4372-5020
d
https://orcid.org/0000-0003-4556-2771
this procedure, polylines are obtained, which char-
acterize symmetrical areas of the shape. After the
sweeping part of the method, the polylines are fil-
tered and combined to obtain a feature vector of the
shape. Due to the design of the method, the trans-
formations of input shapes do not influence the detec-
tion of local features. Furthermore, smaller degrees of
noise, present in a shape, do not significantly impact
the sweeping process.
The remainder of this paper is structured as fol-
lows. In Section 2, previous work from the fields
of symmetry detection, polygon segmentation, shape
characterization, and sweeping are summarised. Sec-
tion 3 describes the proposed method and its appli-
cations. In Section 4, results of the local feature de-
tection method are presented. Section 5 discusses the
future work. The paper is concluded in Section 6.
2 RELATED WORK
This section consists of four parts. In the first part, the
sweeping technique is explained shortly. The symme-
try detection methods are described and briefly sur-
veyed in the second part. After that, methods for poly-
gon segmentation are discussed. Lastly, shape charac-
terization methods are described.
Safko, M., Luka
ˇ
c, L., Žalik, B. and Kolingerová, I.
Detection of Local Symmetry Polylines of Polygons Based on Sweeping Paradigm.
DOI: 10.5220/0012473400003660
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 1: GRAPP, HUCAPP
and IVAPP, pages 329-336
ISBN: 978-989-758-679-8; ISSN: 2184-4321
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
329

2.1 Sweeping
Sweeping is a well-established technique for effi-
cient solutions to geometric problems (Preparata and
Shamos, 1985). The basic element of sweeping in
2D is a sweep-line, which moves through a geomet-
ric space and stops at event points, specific to various
geometric problems. A local part of the problem is
solved during the stop. All local solutions are stored
in a data structure called sweep-line status. When all
event points have been reached by the sweep-line, the
geometric problem is completely solved. The same
approach is utilized in 3D, where a sweep-plane is
used for sweeping instead of a sweep-line.
The sweeping concept has been used in many dif-
ferent fields, such as the construction of a Delau-
nay triangulation (
ˇ
Zalik, 2005; Domiter and
ˇ
Zalik,
2008), the construction of Voronoi diagrams (For-
tune, 1986; Jin et al., 2006), convex hull computa-
tion (Borna, 2019), state space exploration (Chris-
tensen et al., 2001; Jensen et al., 2012), spatial clus-
tering (
ˇ
Zalik and
ˇ
Zalik, 2009), and image segmenta-
tion (Wu et al., 2014).
2.2 Symmetry Detection
In 2D, there are four basic symmetry types: reflection,
rotational, translational, and glide-reflection (Liu
et al., 2010). In the continuation, only reflection sym-
metry is considered. Symmetry can be either global
or local (also referred to as partial). Global symmetry
indicates that the whole shape is symmetric while lo-
cal symmetry signifies that the shape contains smaller
symmetrical segments.
There are plenty of methods, dealing with the de-
tection of global symmetries. Various techniques are
used, such as: finding symmetry axes from potential
fields (Prasad and Yegnanarayana, 2004), building ro-
bust structure descriptors (Atadjanov and Lee, 2016),
grid splitting (
ˇ
Zalik et al., 2022), and applying Hough
transforms (Lei and Wong, 1999).
Local symmetry detection is even more challeng-
ing. Still, many methods were proposed: correlation-
based (Masuda et al., 1993), voxelisation-based
(Podgorelec et al., 2023), approach using surface
descriptors (Gal and Cohen-Or, 2006), neural net-
works (Tsogkas and Kokkinos, 2012), and other.
2.3 Polygon Segmentation
The procedure for partitioning a complex polygon
into simpler polygons is called polygon segmenta-
tion. In the past, the main motivation for this task
was speed improvement of various triangulation algo-
rithms (O’Rourke, 1998). Despite that, the segmenta-
tion of polygons often represents a standalone task.
There are several approaches to polygon segmenta-
tion: monotone partitioning (Lee and Preparata, 1977;
Wei et al., 2012), triangulation (Chazelle, 1991),
trapezoidation (Hain and Langan, 2005), and division
into convex polygons (Fern
´
andez et al., 2000).
2.4 Shape Characterization
One of the main topics in the field of image process-
ing is the characterization of geometric shapes. The
main idea behind this procedure is to detect important
features in a shape, extract them, and store them in
a feature vector (Zhang and Lu, 2004). Such shape
representations can be used for various tasks, e.g.
classification of a shape, detection of similar shapes,
and data preprocessing in machine learning. Unfor-
tunately, the selection of appropriate features is not
a trivial task. Numerous approaches were proposed
to solve this issue. However, many of the existing
methods possess some weaknesses, such as sensitiv-
ity to noise (Blum, 1967), non-unique characteriza-
tion of equal shapes with different transformations
(e.g. translation, rotation, scaling) (Grosky et al.,
1992), and inability to successfully process shapes
with holes (Iivarinen and Visa, 1996).
Generally, characterization methods can be classi-
fied into two larger groups (Loncaric, 1998). Exter-
nal methods process the shape boundary and perform
the characterization upon boundary points. Internal
methods extract features from the shape interior.
External methods use various approaches for
shape characterization: boundary representation with
1D function (Bennett and Mac Donald, 1975; Wang
et al., 1994), Fourier transform of the boundary (Zahn
and Roskies, 1972; Pinkowski, 1993), stochastic al-
gorithms (Das et al., 1990), detection of critical
points in chain codes (Freeman, 1978), scale-space
representation (Witkin, 1987), and many others. Most
common internal characterisation methods are medial
axis transform (Blum, 1967; Peleg and Rosenfeld,
1981; Makem et al., 2020), shape decomposition into
simpler shapes (Bjorklund and Pavlidis, 1981; Attene
et al., 2009), and detection of shape features using
sweep-line (
ˇ
Zalik et al., 2023).
Nowadays, shape characterization methods often
rely on deep neural networks. They are used in agri-
culture (Toda et al., 2020), medicine (Xu et al., 2020;
Hasan et al., 2022), physics (Bisheh et al., 2023), ar-
chitecture (Yan et al., 2019), and many others. De-
spite yielding great characterization accuracy, the dis-
advantage of those methods is the need for huge
datasets during the training phase of their models.
GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications
330
3 SWEEP-LINE METHOD
Let P = {p
1
,..., p
n
}, p
i
∈ R
2
be a polygon represent-
ing the input shape in the Euclidean plane. Our goal
is to find a suitable set of polylines, also referred to
as chains, {M
1
,..., M
k
} that in some sense character-
ize local symmetry of the input polygon and can be
used to efficiently compute geometric properties such
as generalized reflection symmetry, polygon segmen-
tation or shape characterization, described later.
The algorithm works, as the name suggests, by
sweeping a line over the polygon several times with
increasing angle. The resulting polylines from each
run are then filtered and combined to produce the final
solution. We describe each part in more detail in the
following text. The main structure of the algorithm is
shown in Alg. 1.
Function generatePolygonChains
Input : polygon P
Output: set of chains from all angles C
C ← ∅;
angle ← 0;
while angle ≤ 2π do
polygon ← rotate(angle,P);
chains ← f indChains(polygon);
C ← C ∪ chains;
angle ← increment(angle);
end
C ← f ilter(C);
C ← combine(C);
return C;
end
Function findChains
Input : polygon P = {p
1
,.. . , p
n
}
Output: chains = {M
1
,.. . ,M
t
}
chains ← ∅;
sortedPoints ← sort(points(P));
for k = 1, . .., n do
p
k
← sortedPoints[k];
p
k−1
, p
k+1
← neighbors(p
k
, P);
M ← selectChain(chains, p
k−1
, p
k+1
);
p
int
← intersect(P, p
k
);
m
i
← (p
k
+ p
int
)/2;
M ← M ∪ m
i
;
assignChain(M, p
k
);
end
return chains;
end
Algorithm 1: Sweep line symmetry pseudocode.
3.1 Sweeping Procedure
In this section, we will assume a horizontal sweep line
since sweeping a line at an angle over a polygon is
equivalent to sweeping a horizontal line over a rotated
polygon. The f indChains procedure starts by sorting
the input vertices by their y coordinate. The sweep
line starts at the bottom-most vertex of the polygon.
If such vertices are multiple we pick the middle point.
Next, we move the line upward, vertex by vertex, pro-
gressively building local symmetry polylines until we
reach the last vertex.
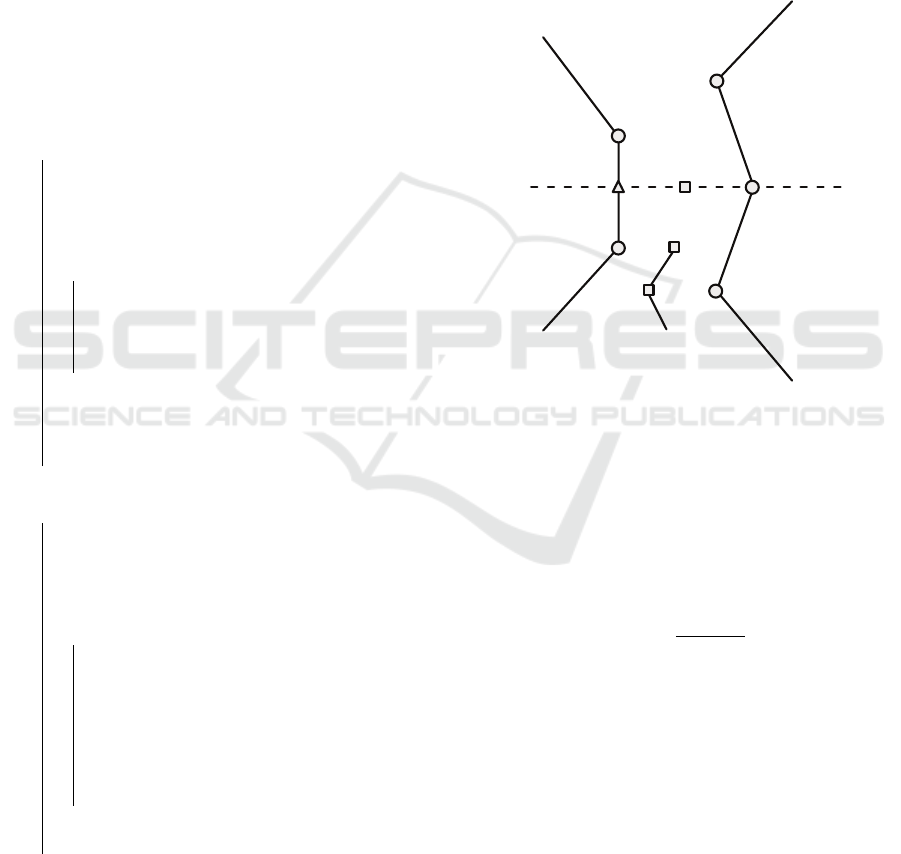
s
p
k
p
int
p
k+1
p
k-1
m
i-1
m
i
m
i-2
e
Figure 1: One step of the sweeping procedure.
Consider a sweep line s passing through point p
k
(see Fig. 1), where m
i−1
and m
i−2
are symmetry poly-
line points from the previous iterations. Let us define
e as the closest edge of the polygon intersecting with
the sweep line s such that the resulting line segment is
inside P, and define p
int
as the intersection point. We
extend the symmetry polyline {.. .,m
i−2
,m
i−1
} with
the midpoint
m
i
:=
p
int
+ p
k
2
and continue on the next iteration.
3.1.1 Polyline Selection
At each iteration, a chain M is selected ac-
cording to the neighboring polygon vertices
(selectChain(chains, p
k−1
, p
k+1
). Since every
vertex can be associated with only one chain, we can
store the chain index with each point. It is important
to notice that there are cases where several chains
can be selected for extension as can be seen in Fig 2.
There are three cases to consider:
1. no neighboring vertices have been processed yet
Detection of Local Symmetry Polylines of Polygons Based on Sweeping Paradigm
331

2. one of the neighbors has been processed
3. both neighboring vertices have been processed
In the first case, we create a new chain starting at
the current vertex. In the second case, we extend the
chain belonging to the neighboring vertex. In the third
case, there are multiple choices to consider. We could
either extend both chains, select just one according to
some criterion, or create a new chain. We decided on
extending both chains, which gave us the best results.
Figure 2: Both chains being extended (left) or a completely
new chain created (right).
3.1.2 External Chains
A small modification of the polygon intersection rou-
tine yields chains outside of the polygon (Fig. 3)
and can provide additional information about the in-
put shape, which is useful in some applications.
The intersect(P, p
k
) function is changed to choose
a line segment outside the polygon if it exists. More
specifically, we pick the closest edge e such that the
resulting line segment L satisfies L ∩ P = ∅. This is
equivalent to running the unmodified algorithm on the
complement of an input polygon.
Figure 3: Left: internal chains Right: external chains.
3.2 Chain Filtering and Combining
After all the chains have been created for each sweep
angle, they are further processed to produce the final
symmetry polylines. This processing includes filter-
ing, combining and separating chains to suit the needs
of subsequent use cases, see examples in Fig 4.
First, short chains with only a few points that
resulted from small convex/concave irregularities on
the polygon boundary are discarded. The threshold
for the number of discarded points can be adjusted
based on a desired sensitivity to noise. Next, chains
with long jumps between successive points are split
into individual chains. What is considered too long
depends on the distance between points before the
jump. Finally, if enabled, chains are combined to
form larger structures, useful namely to find global
properties such as generalized reflection symmetry,
described next.
3.3 Generalized Reflection Symmetry
We define symmetry as any transformation T (X) such
that T (X) = X, i.e. applying the transformation yields
the same object. However, in the real world, no ob-
ject is perfectly symmetric, so we replace the strict
equality sign with approximate equality.
Reflection or mirror symmetry is defined over a
straight line l : n · p − d = 0, where n is the normal
vector and d is the distance from the origin to the line.
The resulting transformation can then be defined as
r(p
i
, l) := p
i
− 2(n · (p
i
− dn))n
where p
i
is a point we want to reflect. If the condition
r(p
i
, l) = p
j
holds for all points of a polygon then
we say it has a reflection symmetry. Since we are not
interested in perfect but in approximate symmetry, we
can rewrite it as an optimization problem where we
try to find a line that minimizes the residual, namely
min
l
∑
i̸= j
∥ r(p
i
, l) − p
j
∥
.
We generalize this definition by replacing the
straight line with a curve. This introduces the prob-
lem of having many different curves with wild shapes
satisfying the symmetry condition. So, we add a loss
function for the shape of a curve with a straight line
being a minimum. The ideal function satisfying these
properties is a curvature. Therefore, we can specify
the solution to generalized reflection symmetry as an
optimization problem
min
C
Z
C
κ(s)ds
where κ(s) is the curvature at point s and the curve C
satisfies the reflection condition. We can combine all
conditions into one loss function such as
min
C
∑
i̸= j
∥ r(p
i
, C) − p
j
∥ +α
Z
C
κ(s)ds
where α ≥ 0 is a user-defined parameter controlling
the straightness of the reflection curve.
Symmetry chains enable us to easily find suitable
solutions to the generalized symmetry of a polygon.
First, chains are combined based on their distance and
tangent directions of endpoints. These larger pieces
GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications
332
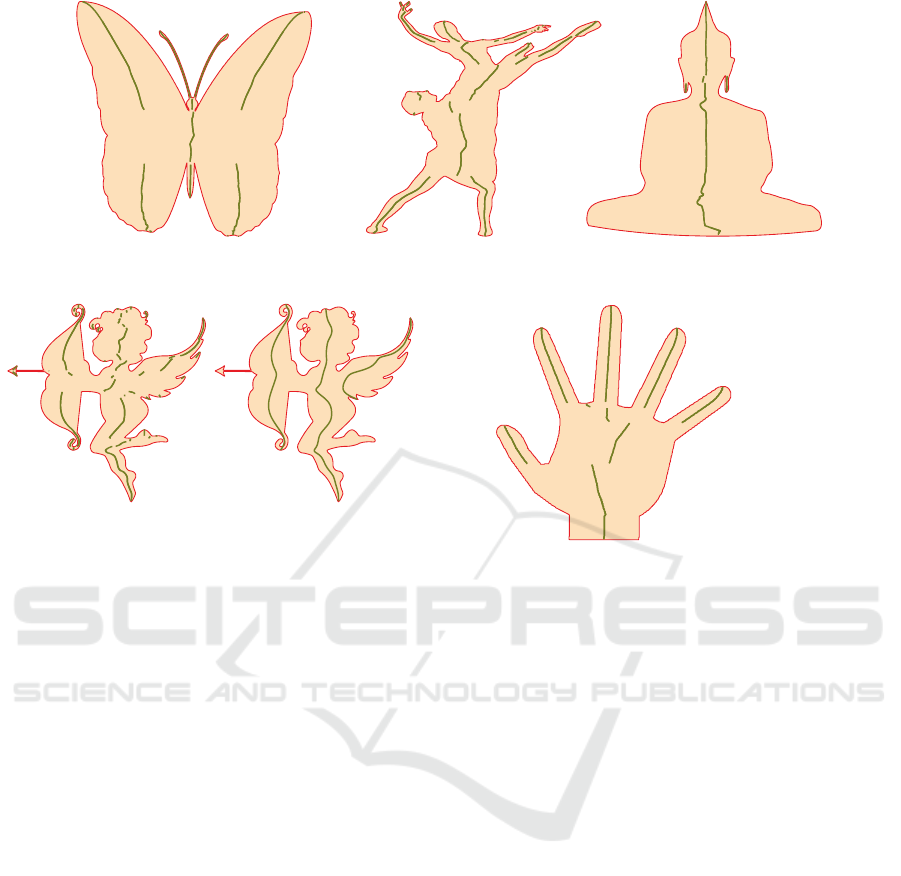
Figure 4: Example of different objects with their symmetry chains.
Figure 5: Individual chains (left) and approximate general-
ized reflection symmetry (right).
then have curvature reduced by smoothing to decrease
the general symmetry loss function. This process is
repeated until the loss improvement stops and so the
result is only a local optimum. Still, the results for our
data are satisfactory, see Fig.5.
3.4 Polygon Segmentation
Polygon segmentation is the process of partitioning
a polygon into individual parts with geometric sig-
nificance. We use the symmetry chains computed
by our algorithm to find regions of interest specified
by custom filter rules. These rules describe proper-
ties used to select chains associated with desired seg-
ments, e.g. min/max length, width of the segments,
or chain sweep line angle. Consider a shape in Fig.
6. Choosing long chains with small widths yields the
fingers part of the hand. Additionally, a constraint on
chain angle allows us to select any of the five fingers.
Similarly, picking wide chains results in the selection
of the palm. Incorporating external chains even al-
lows us to specify empty space between solid parts.
3.5 Shape Characterization
The input polygon is moved so that its center of mass
coincides with the origin and is scaled to range [−1, 1]
to ensure output chain invariance to scale and transla-
tion, which is necessary for a practical shape charac-
Figure 6: A shape with several narrow sections at different
orientations and a wide section at the base.
terization procedure. We follow the steps of (
ˇ
Zalik
et al., 2023) and implement similar length-based fea-
tures. Additionally, we include the total curvature of
a chain to improve the original approach. The feature
vector of the object i is therefore defined as
V
i
=
n
f (M
1
), g(M
1
)
, ...,
f (M
k
), g(M
k
)
o
where f (M) is the length and g(M) is the total curva-
ture of the chain M. Two objects i and j are consid-
ered equal when the two feature vectors V
i
and V
j
are
compatible within a reasonable margin of error, i.e.
|V
i
| = |V
j
| and V
i
k
≈ V
j
k
for all indices k.
External chains can be used to augment the exist-
ing features, or separately, when the input shape con-
tains self-intersections or other imperfections that af-
fect the internal structure of the polygon.
4 RESULTS
We present several examples that showcase our algo-
rithm. Fig. 7 compares simple shapes with more com-
plex ones. Notice how the front wheel on the bicycle
produces the same chain as in the simple circle. In
Fig. 8 we show examples of generalized symmetry
curves. In Fig. 9 we demonstrate the robustness of
Detection of Local Symmetry Polylines of Polygons Based on Sweeping Paradigm
333
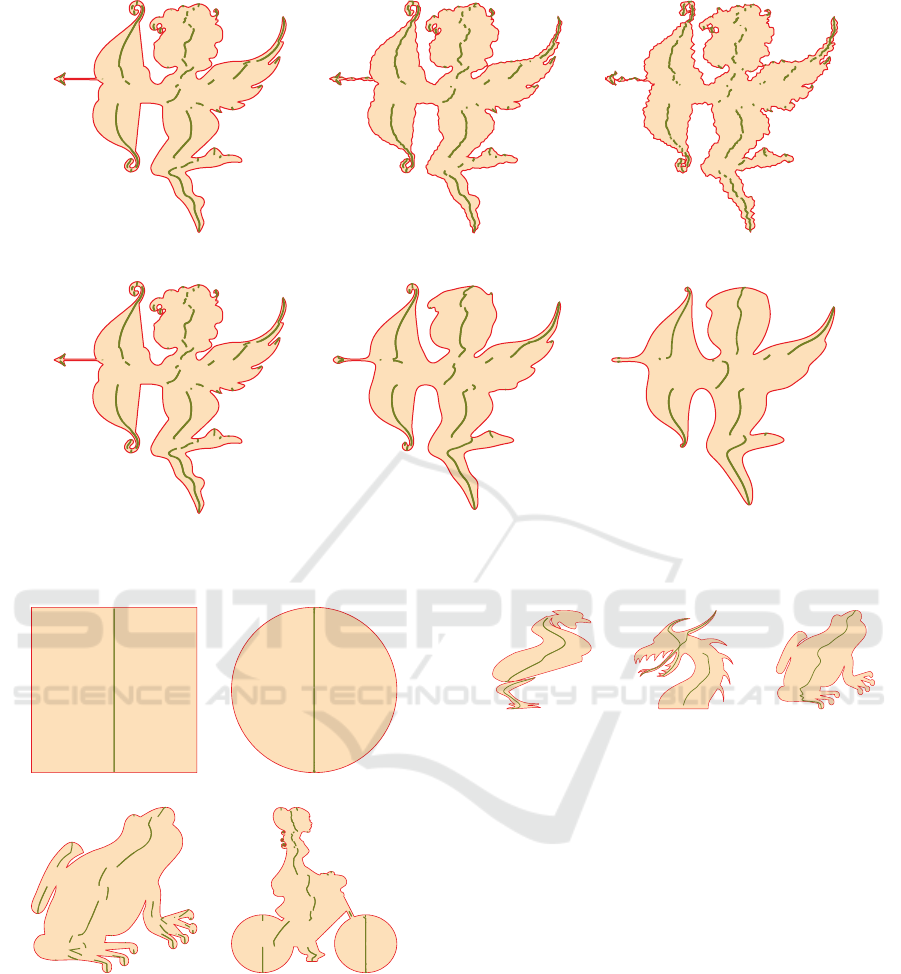
Figure 9: Invariance of local symmetry chains to small changes in boundary. Top: boundary noise is increased from left to
right. Bottom: boundary is smoothed out from left to right.
Figure 7: A selection of chains shown with various shape
complexities. Chains are split at places where it would re-
sult in a long jump.
local symmetry chains to the noise of polygon bound-
ary. In the first row, the boundary gets progressively
noisier with minimal distortion to chains. Similarly,
the second row shows a smoothing effect. Again,
the chains are mostly intact, which illustrates the re-
silience of the algorithm in poor conditions, which is
useful especially for shape characterization.
All images were generated and exported as SVG
Figure 8: Generalized symmetry curves computed on se-
lected objects.
files by our algorithm. Input data was taken from pre-
vious work done by (
ˇ
Zalik et al., 2023). Original input
data was converted from chain codes to a list of float-
ing point vertex coordinates to make the actual com-
putation easier. This freed us from having to work on
a pixel lattice and allowed processing of an arbitrary
rotated input shape.
We evaluate our method on different shapes and
compare time performance with other method in Ta-
ble 1. The experiments were done on a laptop with an
Intel i7-8550U CPU @ 1.80GHz and 8GB RAM.
5 FUTURE WORK
The algorithm can be further extended to process
smooth shapes with boundaries represented by curves
and to produce chains also represented as curves
which might have other interesting applications.
Other possible ventures might be local deformation
GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications
334

Table 1: Performance comparison with (
ˇ
Zalik et al., 2023).
Shape #points
ˇ
Zalik et.al. [ms] Ours [ms]
Bird 2372 693 95
Dolphin 2870 1098 136
Hand 3798 936 170
Buddha 10146 24693 941
Ballet 14438 15590 1737
Cupid 20646 35302 3232
Spider 23900 36513 4112
of the input shape controlled by the symmetry chains,
which could be helpful for animating polygons.
6 CONCLUSION
We presented an algorithm that extracts symmetry
chains of a polygonal shape by utilizing the local re-
flection symmetry. The algorithm is based on the
sweep-line paradigm for efficient processing of the
polygon. Due to its generality, resulting local sym-
metry chains can be used for polygon segmentation,
shape characterization and finding generalized reflec-
tion symmetry. We demonstrated resilience to local
changes in boundary due to noise or smoothing, and
described possible future applications.
ACKNOWLEDGEMENTS
This research was supported by the Czech Sci-
ence Foundation under research project 21-08009K,
the Slovene Research and Innovation Agency un-
der research project N2-0181, Research Programme
P2-0041, and the Charles University grant SVV
260699/2023.
REFERENCES
Atadjanov, I. R. and Lee, S. (2016). Reflection symmetry
detection via appearance of structure descriptor. In
Computer Vision–ECCV 2016: 14th European Con-
ference, Amsterdam, The Netherlands, October 11-14,
2016, Proceedings, Part III 14, pages 3–18. Springer.
Attene, M., Robbiano, F., Spagnuolo, M., and Falci-
dieno, B. (2009). Characterization of 3d shape parts
for semantic annotation. Computer-Aided Design,
41(10):756–763. Selected Papers from the 2007 New
Advances in Shape Analysis and Geometric Modeling
Workshop.
Bennett, J. and Mac Donald, J. (1975). On the measure-
ment of curvature in a quantized environment. IEEE
Transactions on Computers, C-24(8):803–820.
Bisheh, M. N., Wang, X., Chang, S. I., Lei, S., and Ma, J.
(2023). Image-based characterization of laser scribing
quality using transfer learning. Journal of Intelligent
Manufacturing, 34(5):2307–2319.
Bjorklund, C. M. and Pavlidis, T. (1981). Global shape
analysis by k-syntactic similarity. IEEE Transactions
on Pattern Analysis and Machine Intelligence, PAMI-
3(2):144–155.
Blum, H. (1967). A Transformation for Extracting New De-
scriptors of Shape. M.I.T. Press.
Borna, K. (2019). Sweep line algorithm for convex hull
revisited. Journal of Algorithms and Computation,
51(1):1–14.
Chazelle, B. (1991). Triangulating a simple polygon in
linear time. Discrete & Computational Geometry,
6(3):485–524.
Christensen, S., Kristensen, L. M., and Mailund, T. (2001).
A sweep-line method for state space exploration. In
International Conference on Tools and Algorithms for
the Construction and Analysis of Systems, pages 450–
464. Springer.
Das, M., Paulik, M., and Loh, N. (1990). A bivariate au-
toregressive technique for analysis and classification
of planar shapes. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 12(1):97–103.
Domiter, V. and
ˇ
Zalik, B. (2008). Sweep-line algo-
rithm for constrained Delaunay triangulation. Interna-
tional Journal of Geographical Information Science,
22(4):449–462.
Enquist, M. and Arak, A. (1994). Symmetry, beauty and
evolution. Nature, 372(6502):169–172.
Fern
´
andez, J., C
´
anovas, L., and Pelegrın, B. (2000). Algo-
rithms for the decomposition of a polygon into convex
polygons. European Journal of Operational Research,
121(2):330–342.
Fortune, S. (1986). A sweepline algorithm for Voronoi dia-
grams. In Proceedings of the Second Annual Sympo-
sium on Computational Geometry, pages 313–322.
Freeman, H. (1978). Shape description via the use of critical
points. Pattern Recognition, 10(3):159–166. The Pro-
ceedings of the IEEE Computer Society Conference.
Gal, R. and Cohen-Or, D. (2006). Salient geometric fea-
tures for partial shape matching and similarity. ACM
Transactions on Graphics (TOG), 25(1):130–150.
Grosky, W. I., Neo, P., and Mehrotra, R. (1992). A pictorial
index mechanism for model-based matching. Data &
Knowledge Engineering, 8(4):309–327.
Hain, T. and Langan, D. (2005). A fast, practical algorithm
for the trapezoidation of simple polygons. In CISST,
pages 98–108. Citeseer.
Hasan, M. I., Ali, M. S., Rahman, M. H., Islam, M. K., et al.
(2022). Automated detection and characterization of
colon cancer with deep convolutional neural networks.
Journal of Healthcare Engineering, 2022.
Iivarinen, J. and Visa, A. J. (1996). Shape recognition
of irregular objects. In Intelligent Robots and Com-
puter Vision XV: Algorithms, Techniques, Active Vi-
sion, and Materials Handling, volume 2904, pages
25–32. SPIE.
Detection of Local Symmetry Polylines of Polygons Based on Sweeping Paradigm
335

Jensen, K., Kristensen, L. M., and Mailund, T. (2012). The
sweep-line state space exploration method. Theoreti-
cal Computer Science, 429:169–179.
Jin, L., Kim, D., Mu, L., Kim, D.-S., and Hu, S.-M. (2006).
A sweepline algorithm for Euclidean Voronoi diagram
of circles. Computer-Aided Design, 38(3):260–272.
Lee, D. T. and Preparata, F. P. (1977). Location of a point in
a planar subdivision and its applications. SIAM Jour-
nal on Computing, 6(3):594–606.
Lei, Y. and Wong, K. C. (1999). Detection and locali-
sation of reflectional and rotational symmetry under
weak perspective projection. Pattern Recognition,
32(2):167–180.
Liu, Y., Hel-Or, H., Kaplan, C. S., Van Gool, L., et al.
(2010). Computational symmetry in computer vision
and computer graphics. Foundations and Trends® in
Computer Graphics and Vision, 5(1–2):1–195.
Loncaric, S. (1998). A survey of shape analysis techniques.
Pattern Recognition, 31(8):983–1001.
Makem, J. E., Fogg, H. J., and Mukherjee, N. (2020).
Automatic feature recognition using the medial axis
for structured meshing of automotive body panels.
Computer-Aided Design, 124:102845.
Masuda, T., Yamamoto, K., and Yamada, H. (1993).
Detection of partial symmetry using correlation
with rotated-reflected images. Pattern Recognition,
26(8):1245–1253.
O’Rourke, J. (1998). Computational Geometry in C. Cam-
bridge Tracts in Theoretical Computer Science. Cam-
bridge University Press.
Peleg, S. and Rosenfeld, A. (1981). A min-max medial axis
transformation. IEEE Transactions on Pattern Analy-
sis and Machine Intelligence, PAMI-3(2):208–210.
Pinkowski, B. (1993). Multiscale Fourier descriptors
for classifying semivowels in spectrograms. Pattern
Recognition, 26(10):1593–1602.
Podgorelec, D., Luka
ˇ
c, L., and
ˇ
Zalik, B. (2023). Reflection
symmetry detection in Earth observation data. Sen-
sors, 23(17).
Prasad, V. and Yegnanarayana, B. (2004). Finding axes of
symmetry from potential fields. IEEE Transactions on
Image Processing, 13(12):1559–1566.
Preparata, F. P. and Shamos, M. I. (1985). Computational
Geometry: An Introduction. Springer Science & Busi-
ness Media.
Sun, Y. and Bhanu, B. (2011). Reflection symmetry-
integrated image segmentation. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
34(9):1827–1841.
Toda, Y., Okura, F., Ito, J., Okada, S., Kinoshita, T., Tsuji,
H., and Saisho, D. (2020). Training instance seg-
mentation neural network with synthetic datasets for
crop seed phenotyping. Communications Biology,
3(1):173.
Tsogkas, S. and Kokkinos, I. (2012). Learning-based
symmetry detection in natural images. In Computer
Vision–ECCV 2012: 12th European Conference on
Computer Vision, Florence, Italy, October 7-13, 2012,
Proceedings, Part VII 12, pages 41–54. Springer.
Wang, S.-S., Chen, P.-C., and Lin, W.-G. (1994). Invari-
ant pattern recognition by moment Fourier descriptor.
Pattern Recognition, 27(12):1735–1742.
Wei, X., Joneja, A., and Mount, D. M. (2012). Optimal uni-
formly monotone partitioning of polygons with holes.
Computer-Aided Design, 44(12):1235–1252.
Witkin, A. P. (1987). Scale-space filtering. In Readings in
Computer Vision, pages 329–332. Elsevier.
Wu, J., Zhao, Y., Zhu, J.-Y., Luo, S., and Tu, Z. (2014).
Milcut: A sweeping line multiple instance learning
paradigm for interactive image segmentation. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 256–263.
Xu, Q., Zeng, Y., Tang, W., Peng, W., Xia, T., Li, Z.,
Teng, F., Li, W., and Guo, J. (2020). Multi-task joint
learning model for segmenting and classifying tongue
images using a deep neural network. IEEE Journal
of Biomedical and Health Informatics, 24(9):2481–
2489.
Yan, X., Ai, T., Yang, M., and Yin, H. (2019). A graph con-
volutional neural network for classification of building
patterns using spatial vector data. ISPRS Journal of
Photogrammetry and Remote Sensing, 150:259–273.
Zahn, C. T. and Roskies, R. Z. (1972). Fourier descriptors
for plane closed curves. IEEE Transactions on Com-
puters, C-21(3):269–281.
ˇ
Zalik, B. (2005). An efficient sweep-line Delaunay
triangulation algorithm. Computer-Aided Design,
37(10):1027–1038.
ˇ
Zalik, B., Strnad, D., Podgorelec, D., Kolingerov
´
a, I., Nerat,
A., Luka
ˇ
c, N., Kohek,
ˇ
S., and Luka
ˇ
c, L. (2023).
Geometric shape characterisation based on a multi-
sweeping paradigm. Symmetry, 15(6).
ˇ
Zalik, K. R. and
ˇ
Zalik, B. (2009). A sweep-line algorithm
for spatial clustering. Advances in Engineering Soft-
ware, 40(6):445–451.
Zhang, D. and Lu, G. (2004). Review of shape representa-
tion and description techniques. Pattern Recognition,
37(1):1–19.
ˇ
Zalik, B., Strnad, D., Kohek,
ˇ
S., Kolingerov
´
a, I., Nerat, A.,
Luka
ˇ
c, N., and Podgorelec, D. (2022). A hierarchical
universal algorithm for geometric objects’ reflection
symmetry detection. Symmetry, 14(5).
GRAPP 2024 - 19th International Conference on Computer Graphics Theory and Applications
336
