Formal Analysis of Uncertain Continuous Markov Chains in Systems

Biology

Krishnendu Ghosh

and Caroline Goodman

Department of Computer Science, College of Charleston, SC, U.S.A.

Keywords:

Probabilistic Model Checking, Uncertain Continuous-Time Markov Chain, Computational Feasibility,

Tractable, Phylogenetic Tree.

Abstract:

Data dependent abstraction for continuous-time Markov chain is often challenging given the incompleteness

and imprecision of data. Uncertainty in the environment is modeled in the form of uncertain continuous-time

Markov chain. In this work, a tractable model checking methodology, stochastic partial model set checking is

formalized by approximation of the uncertain continuous-time Markov chain. The methodology was applied in

querying to infer on a phylogenetic tree, constructed under uncertainty. Queries were posed on the formalism

using continuous stochastic logic formula. Experimental results demonstrate the computational feasibility of

the model.

1 INTRODUCTION

Modeling of biological processes is an important re-

search direction in systems biology. One of the prob-

lems in systems biology is the correct construction

of phylogenetic trees from biological data. Phylo-

genetic studies are key in understanding the evolu-

tion of species. Often the construction of phylo-

genetic tree is not precise because of imprecision

and uncertainty in the data. Stochastic models such

as discrete-time Markov chains and continuous-time

Markov chain have been used as modeling tools in

problems in systems biology and formal veriﬁca-

tion methods such as model checking. Discrete-time

Markov chain (DTMC) have been used as stochas-

tic model in systems biology. The order of the pro-

cesses in biology is abstracted in the order of the states

in the dtmc. However biological applications, time

runs continuously, and so discrete-time mathematical

models are not always appropriate models. This is es-

pecially true in biology where organisms reproduce,

infect each other, etc. in continuous time. There-

fore, continuous-time Markov chains (CTMC) are of-

ten more suited to model abstraction. Continuous-

time Markov chains (CTMC) are one of the founda-

tional structure to model continuous probabilities in

the modeling processes such as in- rates of execution

https://orcid.org/0000-0002-8471-6537

https://orcid.org/0009-0009-1592-6029

of chemical reaction and rates of epidemiology as in

spread of diseases. However, rates are imprecise and

are uncertain because it is challenging to get precise

data given the experimental conditions are not always

possible to replicate exactly and there is presence of

noise. Parameter synthesis in formal modeling have

been applied to address imprecise data. However, of-

ten times the modeler would introduce imprecision to

quantify error and evaluate the constructed model ab-

straction in comparison with the real phenomena that

is modeled. In this work, we create a tractable for-

malism for model checking on uncertain continuous-

time Markov chain and evaluate the computational

feasibility of the application of the model in infer-

ence of phylogenetic tree, by posing temporal logic

queries.

1. A novel inference formalism for temporal logic

reasoning on uncertain continuous-time Markov

chain is described. A stochastic partial model set

is deﬁned that provides the modeler the perfor-

mance of the models. The methodology is an ap-

proximation to perform model checking on uncer-

tain continuous-time Markov chain.

2. The formalism has been applied to model phylo-

genetic tree and computational feasibility of the

abstraction on a published dataset of phylogenetic

tree is evaluated.

Ghosh, K. and Goodman, C.

Formal Analysis of Uncertain Continuous Markov Chains in Systems Biology.

DOI: 10.5220/0012466000003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 1, pages 519-526

ISBN: 978-989-758-688-0; ISSN: 2184-4305

519

2 BACKGROUND

The foundation of this work is the intersection of

probabilistic model checking for uncertain stochastic

structures, formal modeling and inference of phylo-

genetic tree under uncertainty.

2.1 Formal Veriﬁcation of Stochastic

Models

Computation of reachability probabilities (Delahaye

et al., 2016) for parametric Markov model has been

studied by a closed form function (Hahn et al., 2011).

Given the imprecision in data, models require param-

eters for effective inference. Computation of param-

eters and its estimation is an active area of research.

The modeler executes temporal logic queries on the

model and computes the parameter (Han et al., 2008).

There are synthesis based approaches that have ad-

dressed uncertainty in data (Shavit et al., 2016). Ap-

proximations for analysis of biological systems us-

ing probabilistic model checking by removing the un-

likely states, thereby reducing the state space has been

studied (Neupane et al., 2019). Interval form of rep-

resentation of probabilities on Markov chains to in-

corporate uncertainty has been formalized (Sproston,

2018). Here the intervals were open intervals. In our

work, we focus on closed intervals of uncertain ki-

netic rates. Sampling techniques have been used to

learn CTMC (Sen et al., 2004). In our formalism

we use sampling on the subintervals after discretiza-

tion of the interval representing the rates. Sampling

having been applied to uncertain parametric CTMCs

with parametric transition rates and scalability of the

model is evaluated (Badings et al., 2022).

2.2 Formal Analysis in Systems Biology

There is a body of literature that described formal

analysis of stochastic models of biochemical path-

ways using continuous-time Markov chains using

probabilistic model checking (Calder et al., 2010;

Calder et al., 2006; Heath et al., 2008) and different

formalisms to address uncertainty in the environment.

Quantitative analysis using continuous-time stochas-

tic logic and have been compared with ordinary dif-

ferential equation based model(Calder et al., 2006).

However, the models do not take into account envi-

ronmental variations in which the rate of reactions,

i.e the speeds at which pathway (biochemical reac-

tion) will execute is assumed to be exact. Recent work

incorporating imprecision in CTMC is the formaliza-

tion of uncertain CTMCs (Cardelli et al., 2023). The

rates of the CTMCs have been assumed to vary non-

deterministically with time represented by continuous

intervals. The states of the CTMC are partitioned and

the states are lifted in a standard CTMC setting but

under uncertainty. The reﬁnements were based on

bisimulation of stochastic models (Baier et al., 2003;

Neuhäußer and Katoen, 2007). Uncertain kinetic

rates using probabilistic model checking has been de-

scribed by creating a novel semantics (Barbuti et al.,

2012). Model checking of uncertain continuous-time

Markov chains have been reported(Bortolussi et al.,

2016). Chemical reaction network has been modeled

as parametric CTMC integrating with learning mod-

els with the goal of applying statistical model check-

ing (Molyneux and Abate, 2020).

2.3 Construction of Phylogenetic Tree

Under Uncertainty

Monte Carlo based method was studied as an in-

ference method on phylogenetic tree by represent-

ing CTMC and approximate transition probabilities

and compute the parameters (Hajiaghayi et al., 2014).

Bayesian phylogenetic inference using annealed se-

quential Monte Carlo method have been proposed

(Wang et al., 2020). This direction of research is on-

going and there is no substantial approximation that

has been accepted as the standard in the community.

3 PRELIMINARIES

In this section, we state the mathematical preliminar-

ies that are foundations of our formalism. A contin-

uous time Markov chain is a stochastic model with

a discrete states with a continuous time as a parame-

ter. In formal modeling, the continuous time Markov

chain is described in the form of a state based sys-

tem, called a labeled continuous-time Markov chain.

For consistency throughout the paper, we will denote

a labeled continuous-time Markov chain as CTMC.

Deﬁnition 1. A labeled CTMC (Baier et al., 2000) is

a tuple,M = ⟨S, S

, R,AP,L⟩ where:

1. S is a set of states.

2. S

⊂ S is the set of initial states.

3. R : S × S → R

≥0

as the rate matrix.

4. L : S ← 2

is the labeling function.

The labeled CTMC described in Deﬁnition 2 elim-

inates the requirement R(s, s) =

∑

s̸=s

′

R(s, s

′

), unlike

non-state based deﬁnition of CTMCs. Self-loops are

modeled by R(s, s

′

) > 0.

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

520

Deﬁnition 2. (Labeled Uncertain Continuous-time

Markov Chain) A labeled uncertain CTMC (UCTMC)

is a tuple, K = ⟨S, S

, R, A, AP, L⟩ where:

1. S is a set of states.

2. S

⊂ S is the set of initial states.

3. A is the the set of actions.

4. R : S × A × S → R

≥0

as the rate matrix and

each,R

i, j

is an interval,(m, n), m ≤ n and m, n ∈ Q.

5. L : S → 2

is a state labeling function.

A path in a UCTMC is a non-empty sequence,

... where R(s

, a

, s

i+1

) > 0 and t

∈ R

for all i ≤ 0. The value of t ∈ (

). The open interval

is a way to add imprecision.

3.1 Probabilistic Model Checking

Model checking is performed on labeled ﬁnite state

machine in the form of Kripke structure, M . For-

mally,

Deﬁnition 3. (Model Checking (Clarke, 1997)) Given

a model, M and formula,φ , model checking is the

process of deciding whether a formula φ is true in the

model, written M |= φ.

Here, φ represents a temporal logic formula that rep-

resents the properties of a system. The model, M

represents the description of the system. The system

description when represented by a stochastic struc-

ture, M

, then the model checking is performed on

a stochastic structure and the validity of the formula

is quantiﬁed by probability.

Deﬁnition 4. (Probabilistic Model Checking) Given

a model, M

and formula,φ , model checking is the

process of deciding whether a formula φ is true in the

model, written M |= φ and quantiﬁed by a probability.

Details on probabilistic computational tree logics can

be found in the literature (Baier et al., 2008; Aziz

et al., 1996) Probabilistic model checking on un-

certain stochastic structures such as interval discrete

Markov chains have been shown to be in PSPACE and

NP-hard (Benedikt et al., 2013; Sen et al., 2006).

3.1.1 Continuous Stochastic Logic

Stochastic Model Checking have been described

(Kwiatkowska et al., 2007). Model checking on

CTMC is performed by the logics known as contin-

uous stochastic logic (CSL) (Aziz et al., 1996; Baier

et al., 1999) The syntax of CSL (Aziz et al., 1996)

Syntax of CSL is:

φ ::= true | a | φ ∧ φ | ¬φ | P

⊕p

[ψ] | S

⊕p

[φ]

ψ ::= X φ | φU

≤k

φ |φUφ

where a is an atomic proposition,⊕ ∈ {≤, <, ≥, >

}, p ∈ [0, 1] and k ∈ R

≥0

. φ, ψ are state and path for-

mula respectively. P

⊕p

ψ represents the probability of

φ satisﬁed from a given state satisﬁes the bound ⊕p.

The bounded until operator φ

≤

kφ

is valid if φ

for

a time instant in the interval [0, k] and φ

is valid at all

preceding time instants. The path formula,Xφ is true

if φ is satisﬁed in the next state. The formula φ

≤k

is true if φ

is satisﬁed within k time-steps and φ

true at that point. Similar is the description of φ

Uφ

where φ

is true some point in future till then φ

true. φ

is satisﬁed at some time instant in the interval

[0, k] and φ

holds at all preceding time steps. The

S operator describes the steady-state behaviour of the

CTMC. S

⊕

p[φ] asserts that the steady-state probabil-

ity of being in a state satisfying φ meets the bound

⊕p

The semantics of CSL are deﬁned on CTMC and

can be found (Aziz et al., 1996; Baier et al., 1999) for

further reading.

4 STOCHASTIC PARTIAL

MODEL SET CHECKING

Probabilistic model checking is performed on

stochastic structures such as DTMC or CTMC. Model

checking on UCTMC is challenging because the in-

tervals for rates can generate inﬁnite number of rates.

The following are keys to approximate the UCTMC

denoted by M

and construct a tractable computa-

tional model. A ﬁnite set of stochastic partial model,

= {M

, M

, . . . M

} where n ∈ N. Each stochas-

tic partial model M ∈ M

has identical state space

that of M

with the intervals for rates of M are the

subintervals for rates in M

The model checking problem is phrased as given

a model M

and a formula, φ, model checking is the

process of deciding whether a formula φ is true in the

model and represented by M

|= φ. The generalization

of the model checking on probabilistic partial models

will be denoted by probabilistic partial model check-

ing problem. Formally, given a set of probabilistic

partial models, M and a formula, φ model checking is

the process of deciding whether a formula is true for

each M ∈ M

. and denoted by M |= φ.

4.1 Model Abstraction

The model abstraction is two step process: Initially, a

UCTMC is constructed from the data. The next step

is to construct set of stochastic partial models from

the UCTMC is constructed.

Construction of UCTMC Representing Phylogenetic

Tree: Given a set of species , G and set of rate of evo-

lution (transitions), R = {I

, ..., I

}where n ∈ N and

Formal Analysis of Uncertain Continuous Markov Chains in Systems Biology

521

Input: K

⟨S

, S, R, A, AP, L⟩ Number of

subintervals, k

Output: Set of Stochastic Partial Models, K

1: S = {s

S =

I ; {S

is the initial set and

T is

the set of transitions.}

2: IntervalSet ←

3: OrderedSetRate ←

4: for each s

i j

−→ s

where s

, s

∈ S do

5: Construct k subintervals for each r

i j

6: IntervalSet ← IntervalSet ∪ (r

i j

, r

i j

, . . . , r

i j

)

where r

i j

is a subinterval.

7: end for

8: OrderdedTuples ←

|IntervalSet|

∏

IntervalSet

9: K ←

10: for each T ∈ OrderedTuples do

11: R ← T

12: K

⟨S

, S, T, A, AP, L⟩

13: K ← K ∪ K

14: end for

15: K

Algorithm 1: StochasticPartialModel.

is the interval representing mth. clade. UCTMC

is constructed in the following way: Each state,s is

labeled as specie and a transition to another state,s

′

implies species A evolves into species B. The label

on the transition, I

is the interval that represents the

range of values the rate of evolution from species A

to species B. The state, s

′

is labeled with species.

Construction of Stochastic Partial Model Set: In the

construction of a set of stochastic partial models, each

intervals for rates on the transition in UCTMC is par-

titioned into subintervals. The partitions of the inter-

vals are user deﬁned value, k amd k ∈ N. For exam-

ple, an interval in K

between a transition s → s

′

given by I = (a, b) where a, b ∈ (N) and a < b, the

intervals where s, s

′

∈ K

. For k = 2, the subinter-

vals are: (a,

a+b

], (

a+b

, b). Similarly, for n intervals

in K

, there will be nk subintervals and each stochastic

partial model will represent a UCTMC with a series

of subinterval from a series of intervals of transition

rates in K

. There are k

stochastic partial models. k

can be varied. Algorithm 1 shows the construction of

set of stochastic partial model set. The ﬁxed point al-

gorithm constructs the set of stochastic partial models

with subintervals.

4.2 Construction of Simulation Model

The transition rates for probabilistic partial models

are represented in the form of intervals. In order to

make the models tractable, sampling on the intervals

are performed. Notation for upper bound and lower

bound of an interval in a stochastic partial model is

given by ub(I

) and lb(I

), respectively and I

repre-

sents an interval in a stochastic partial model and the

set of intervals is

. Algorithm 2 demonstrates the

sampling of the rates from each intervals in a stochas-

tic partial model. The models in the set,K form the

basis of probabilistic model checking. If the values

of the probabilities for consecutive subintervals are

close to each other, then the intervals can be merged

and hence, the number of models get reduced. The

algorithm terminates because the number of intervals

are ﬁnite and there are ﬁnite states in each stochastic

partial model in the ﬁnite set, K. Each K

sim

∈ K

sim

is a CTMC, an approximation of K

∈ K and hence,

CSL logic queries can be executed. The computa-

tional complexity of model checking is polynomial in

the size of the model. Therefore, for a partial model

set of size n, the model checking complexity is poly-

nomial as the model checking is performed on each

of the partial model.

Input: K

Output: Set of Sampled Stochastic Partial Models,

sim

1: K

sim

← 0

2: for each K ∈ K do

3: for each r ∈ R do

4: if r is partly closed interval then

5: Generate random value, r such that

lb(I

) < r ≤ up(I

)

6: else

7: Generate random value, r such that

lb(I

) ≤ r ≤ up(I

)

8: SRate ← SRate ∪ r where i =|

9: end if

10: K

sim

⟨S

, S, srate, A, AP, L⟩.srate ∈ SRate.

11: end for

12: K

sim

← K

sim

∪ K

sim

13: end for

14: K

sim

Algorithm 2: Sampled Stochastic Partial Models.

5 APPLICATION OF UCTMC IN

PHYLOGENETIC TREE

The steps involved in reasoning for an abstraction of

phylogenetic tree under uncertainty is given by :

1. Construct an UCTMC, K

representing a phyloge-

netic tree,T .

2. Construct the set of stochastic partial models

from the UTMC, K

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

522

3. Perform probabilistic model checking by posing

queries using continuous stochastic logic on the

set of sampled stochastic partial models.

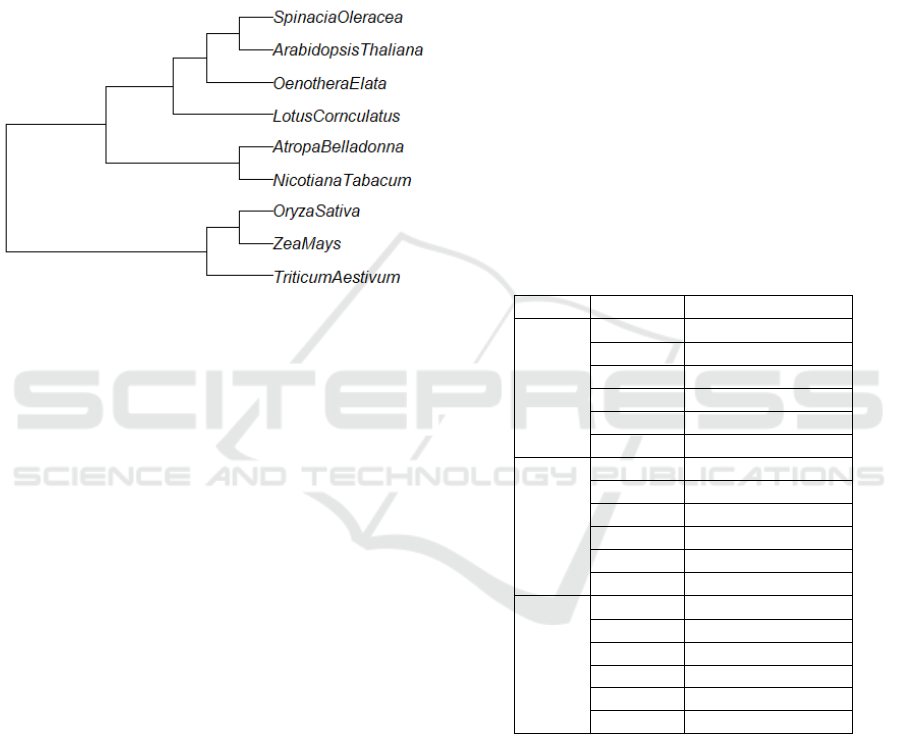
The data used as the phylogenetic tree model was

from published data by Baele et al. (Baele et al.,

2021), as shown in Figure 1. The models were con-

structed and evaluated in PRISM (Kwiatkowska et al.,

2011) The states in the model are labeled symboli-

cally with species.

Figure 1: Fragment of Phylogenetic tree representing the

speciation of eudicots, angiosperms, and seed plants (Baele

et al., 2021).

Notation: The various species of plants are

Arabidopsis Thaliana(at), Spinacia Oleracea(so),

Oenothera Elata(oe), Lotus Corniculatus(lc), Nico-

tiana Tabacum(nt), and Atropa Belladonna(ab) in the

model.

In the Figure 2, the boxplots show the variation

amongst each model variation. The data is based

on the randomly generated rates based on the ranges

speciﬁed. The ﬁgure is provided for the sole purpose

of conveying the variations among a select few mod-

els involved in the total calculations.

5.1 Evaluation of Temporal Logic

Properties

The evaluation of speciﬁcations, represented by

probabilistic temporal logics is performed using

PRISM (https://www.prismmodelchecker.org/)

model checker. The simulation was performed in a

Mac with 2.3 GHz with quad core Intel i5 proces-

sor and 8GB RAM. In this model, we are focused

on reachability properties and temporal logic proper-

ties. A sample of reachability biological queries rep-

resented as continuous stochastic logic formula are as

follows:

Property 1: P=? (ab & nt & oe). The meaning of

the statement is: Is there a state where all three

species ab, nt and oe are present? Note: This

property’s result will always evaluate to 0.0 be-

cause our model checks to see if a single species

formed, but not multiple species.

Property 2: P=? ( nt = true) The meaning of the

logic formula- is it possible to reach a state where

species nt is present in the model.

Property 3: P=? ( ab = true ) The meaning of the

logic formula- is it possible to reach a state where

species ab is present in the model.

Property 4: P=? ( at = true ). The meaning of the

logic formula- is it possible to reach a state where

species at is present in the model.

Property 5: P=? ( so = true ) The meaning of the

logic formula- is it possible to reach a state where

species so is present in the model.

Property 6: P=? ( oe = true ) This is a reachability

property asking if it is possible to reach a state

where species oe is present in the model.

Table 1: Execution Time of CSL Queries.

Model Property Time (in seconds)

n=6 1 0.088

2 0.009

3 0.001

4 0.001

5 0.001

6 0

n=10 1 0.018

2 0.202

3 0.202

4 0.245

5 0.23

6 0.227

n=13 1 0.453

2 41.65

3 40.76

4 53.945

5 52.851

6 45.922

Table 1 shows of the results obtained for model

checking for different problem sizes input sizes and

properties. The data consists of results obtained for

seven different input sizes: n=6, n=10, and n=13, with

varying properties. There are over 40 models, which

refer to the varied rates speciﬁed earlier. Each vari-

ation has been checked for the same set of proper-

ties. For n=6, the results are further broken down into

seven different variations of the input. For each input

size and property combination, the "Time" for exe-

cution of the queries are presented. The properties

checked are numbered from 1 to 6. The time taken

Formal Analysis of Uncertain Continuous Markov Chains in Systems Biology

523

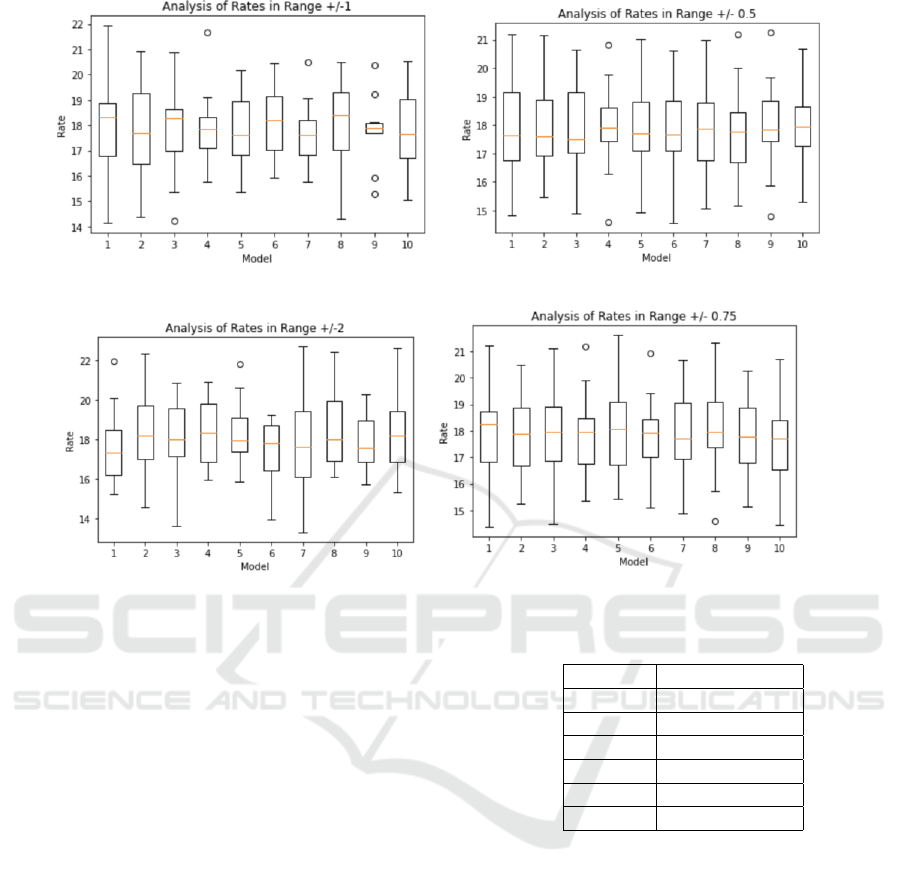
Figure 2: Random Rates of Phylogenetic Tree.

for model checking is recorded in seconds, and the

result indicates whether the model satisﬁes the prop-

erty checked. For example, for n=6 and property 2,

the time taken for model checking was 0.009 seconds,

and the result was 0.212459016, indicating that the

model satisﬁed the property. The times of the ex-

ecution of the logic queries demonstrate a correla-

tion with the increase in the input sizes. For exam-

ple, the time taken for model checking n=6 is signif-

icantly less than the time taken for n=13. However,

there are some variations in time taken for the same

input size, indicating that the properties of the input

can also have an impact on the time taken for model

checking.

5.2 Analysis of Properties

Table 2 shows some properties are satisﬁed for all

values of n, while others are not. Property 1 seems

to be satisﬁed for all values of n, as indicated by the

result of 0 for all entries. Here is the table with the

average result for each individual property (averages

are rounded to four decimal places):

The average result of each property reveals that

some properties are more likely to be present in

some models than others. Property 7 has the highest

average probability of presence, with a 34.9% chance

Table 2: Computed Probabilities from Properties.

Property Average Result

1 0.0

2 0.227723931

3 0.160131871

4 0.077751529

5 0.078001573

6 0.160862186

of eventually being present at some point in the

model checking process. This could be due to various

reasons, including but not limited to, the particular

organism speciﬁed in the property and the values of

the rates of transition associated with the property.

Analysis Results of Temporal Logic Queries: Table

3 shows the comparison of a property across all the

models. Property 2 is deﬁned as follows: P=? [F nt =

true]. This property checks whether the state with nt

is eventually reached during the execution of the sys-

tem. The result of the property veriﬁcation for differ-

ent problem sizes. For the model with n=6, the model

checker took 0.009 seconds to verify the property and

returned a result of 0.212459. This means that there

is a 21.25% chance that the system will eventually

reach the state labeled with nt during execution. For

the model with n=10, the model checker took 0.202

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

524

Table 3: Comparison of time of execution (in seconds) across different models.

Model Property Time (seconds) Result

n =6 2 0.009 0.212459

n =10 2 0.202 0.310325

n =13 2 40.76 0.220842

n =6 (variation 1) 2 0.001 0.187863

seconds to verify the property and returned a result of

0.310325. This means that there is a 31.03% chance

that the system will eventually reach the state nt dur-

ing execution. For the model with n=13, the model

checker took 40.76 seconds to verify the property and

returned a result of 0.220842649. This means that

there is a 22.08% chance that the system will even-

tually reach the state nt during execution. The model

with n=6 (variation 1) represents a larger size (size

of ± 2 ) of the interval for rates. The model checker

took 0.001 seconds to verify the property and returned

a result of 0.18786327, implying there is a 18.79%

chance that the system will eventually reach the state

nt during execution. The change in the size of the in-

terval of the rates did not inﬂuence the time for veriﬁ-

cation of the speciﬁcation. These results remain simi-

lar for each property, as the input size and model vari-

ables are altered. Based on these results, we can con-

clude that the larger the size of the model, the longer

it takes for the model checker to verify the property.

Additionally, we can see that the probability of reach-

ing the nt state during system execution is higher in

the model with n=10 compared to the other models.

This information can be useful in determining the fea-

sibility of the system and making design decisions to

optimize the system performance.

6 CONCLUSION

In this paper, we describe an abstraction of feasible

models, an approximation of a given uncertain

continuous-time Markov chain. The approximated

set of CTMC constructed is used for stochastic partial

model set checking. The computational feasibility

is evaluated on continuous stochastic logic queries,

on a prototype of a phylogenetic tree from published

data. The modeling technique can be improved

by quantifying error for model checking of partial

models and identiﬁability of the partial models

(Browning et al., 2020). The formalism is promising

to model other problems in systems biology where

there data is imprecise and provide the modeler a tool

to provide insights to the biological questions.

ACKNOWLEDGEMENTS

The ﬁrst author, KG was supported by NSF CCF

2227898 during the research. The second author,

CG was supported by SC-INBRE funds in summer

of 2022. Research reported in this publication was

supported by the National Institute of General Medi-

cal Sciences of the National Institutes of Health under

Award Number P20GM103499. The content is solely

the responsibility of the authors and does not neces-

sarily represent the ofﬁcial views of the National In-

stitutes of Health.

REFERENCES

Aziz, A., Sanwal, K., Singhal, V., and Brayton, R. (1996).

Verifying continuous time markov chains. In Inter-

national Conference on Computer Aided Veriﬁcation,

pages 269–276. Springer.

Badings, T. S., Jansen, N., Junges, S., Stoelinga, M.,

and Volk, M. (2022). Sampling-based veriﬁcation of

ctmcs with uncertain rates. In Computer Aided Ver-

iﬁcation: 34th International Conference, CAV 2022,

Haifa, Israel, August 7–10, 2022, Proceedings, Part

II, pages 26–47. Springer.

Baele, G., Gill, M. S., Bastide, P., Lemey, P., and Suchard,

M. A. (2021). Markov-modulated continuous-time

markov chains to identify site-and branch-speciﬁc

evolutionary variation in beast. Systematic biology,

70(1):181–189.

Baier, C., Haverkort, B., Hermanns, H., and Katoen, J.-

P. (2000). Model checking continuous-time markov

chains by transient analysis. In International Confer-

ence on Computer Aided Veriﬁcation, pages 358–372.

Springer.

Baier, C., Haverkort, B., Hermanns, H., and Katoen, J.-P.

(2003). Model-checking algorithms for continuous-

time markov chains. IEEE Transactions on software

engineering, 29(6):524–541.

Baier, C., Katoen, J.-P., and Hermanns, H. (1999). Approx-

imative symbolic model checking of continuous-time

markov chains. In International Conference on Con-

currency Theory, pages 146–161. Springer.

Baier, C., Katoen, J.-P., and Larsen, K. G. (2008). Princi-

ples of model checking. MIT press.

Barbuti, R., Caravagna, G., Maggiolo-Schettini, A., Mi-

lazzo, P., and Tini, S. (2012). Foundational aspects of

Formal Analysis of Uncertain Continuous Markov Chains in Systems Biology

525

multiscale modeling of biological systems with pro-

cess algebras. Theoretical Computer Science, 431:96–

116.

Benedikt, M., Lenhardt, R., and Worrell, J. (2013). Ltl

model checking of interval markov chains. In Inter-

national Conference on Tools and Algorithms for the

Construction and Analysis of Systems, pages 32–46.

Springer.

Bortolussi, L., Milios, D., and Sanguinetti, G. (2016).

Smoothed model checking for uncertain continuous-

time markov chains. Information and Computation,

247:235–253.

Browning, A. P., Warne, D. J., Burrage, K., Baker, R. E.,

and Simpson, M. J. (2020). Identiﬁability analy-

sis for stochastic differential equation models in sys-

tems biology. Journal of the Royal Society Interface,

17(173):20200652.

Calder, M., Gilmore, S., Hillston, J., and Vyshemirsky, V.

(2010). Formal methods for biochemical signalling

pathways. In Formal Methods: State of the Art and

New Directions, pages 185–215. Springer.

Calder, M., Vyshemirsky, V., Gilbert, D., and Orton, R.

(2006). Analysis of signalling pathways using con-

tinuous time markov chains. In Transactions on Com-

putational Systems Biology VI, pages 44–67. Springer.

Cardelli, L., Grosu, R., Larsen, K. G., Tribastone, M.,

Tschaikowski, M., and Vandin, A. (2023). Algo-

rithmic minimization of uncertain continuous-time

markov chains. IEEE Transactions on Automatic Con-

trol.

Clarke, E. M. (1997). Model checking. In Foundations of

Software Technology and Theoretical Computer Sci-

ence: 17th Conference Kharagpur, India, December

18–20, 1997 Proceedings 17, pages 54–56. Springer.

Delahaye, B., Lime, D., and Petrucci, L. (2016). Param-

eter synthesis for parametric interval markov chains.

In International Conference on Veriﬁcation, Model

Checking, and Abstract Interpretation, pages 372–

390. Springer.

Hahn, E. M., Hermanns, H., and Zhang, L. (2011). Proba-

bilistic reachability for parametric markov models. In-

ternational Journal on Software Tools for Technology

Transfer, 13(1):3–19.

Hajiaghayi, M., Kirkpatrick, B., Wang, L., and Bouchard-

Côté, A. (2014). Efﬁcient continuous-time markov

chain estimation. In International Conference on Ma-

chine Learning, pages 638–646. PMLR.

Han, T., Katoen, J.-P., and Mereacre, A. (2008). Ap-

proximate parameter synthesis for probabilistic time-

bounded reachability. In 2008 Real-Time Systems

Symposium, pages 173–182. IEEE.

Heath, J., Kwiatkowska, M., Norman, G., Parker, D., and

Tymchyshyn, O. (2008). Probabilistic model checking

of complex biological pathways. Theoretical Com-

puter Science, 391(3):239–257.

Kwiatkowska, M., Norman, G., and Parker, D. (2007).

Stochastic model checking. In International School

on Formal Methods for the Design of Computer, Com-

munication and Software Systems, pages 220–270.

Springer.

Kwiatkowska, M., Norman, G., and Parker, D. (2011).

PRISM 4.0: Veriﬁcation of probabilistic real-time sys-

tems. In Gopalakrishnan, G. and Qadeer, S., edi-

tors, Proc. 23rd International Conference on Com-

puter Aided Veriﬁcation (CAV’11), volume 6806 of

LNCS, pages 585–591. Springer.

Molyneux, G. W. and Abate, A. (2020). Abc (smc): Si-

multaneous inference and model checking of chem-

ical reaction networks. In International Conference

on Computational Methods in Systems Biology, pages

255–279. Springer.

Neuhäußer, M. R. and Katoen, J.-P. (2007). Bisimulation

and logical preservation for continuous-time markov

decision processes. In International Conference on

Concurrency Theory, pages 412–427. Springer.

Neupane, T., Zhang, Z., Madsen, C., Zheng, H., and Myers,

C. J. (2019). Approximation techniques for stochas-

tic analysis of biological systems. In Automated Rea-

soning for Systems Biology and Medicine, pages 327–

348. Springer.

Sen, K., Viswanathan, M., and Agha, G. (2004). Learning

continuous time markov chains from sample execu-

tions. In First International Conference on the Quan-

titative Evaluation of Systems, 2004. QEST 2004. Pro-

ceedings., pages 146–155. IEEE.

Sen, K., Viswanathan, M., and Agha, G. (2006). Model-

checking markov chains in the presence of uncertain-

ties. In International Conference on Tools and Algo-

rithms for the Construction and Analysis of Systems,

pages 394–410. Springer.

Shavit, Y., Yordanov, B., Dunn, S.-J., Wintersteiger, C. M.,

Otani, T., Hamadi, Y., Livesey, F. J., and Kugler, H.

(2016). Automated synthesis and analysis of switch-

ing gene regulatory networks. Biosystems, 146:26–34.

Sproston, J. (2018). Qualitative reachability for open in-

terval markov chains. In International Conference on

Reachability Problems, pages 146–160. Springer.

Wang, L., Wang, S., and Bouchard-Côté, A. (2020). An

annealed sequential monte carlo method for bayesian

phylogenetics. Systematic biology, 69(1):155–183.

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

526