Towards Self-Adaptive Resilient Swarms Using Multi-Agent

Reinforcement Learning

Rafael Pina

, Varuna De Silva

and Corentin Artaud

Institute for Digital Technologies, Loughborough University London, 3 Lesney Avenue, London, U.K.

Keywords:

Cooperative Swarms, Multi-Agent Reinforcement Learning, Adaptation.

Abstract:

Cooperative swarms of intelligent agents have been used recently in several different ﬁelds of application.

The ability to have several units working together to accomplish a task can drastically extend the range of

challenges that can be solved. However, these swarms are composed of machines that are susceptible to

suffering external attacks or even internal failures. In cases where some of the elements of the swarm fail, the

others must be capable of adjusting to the malfunctions of the teammates and still achieve the objectives. In

this paper, we investigate the impact of possible malfunctions in swarms of cooperative agents through the use

of Multi-Agent Reinforcement Learning (MARL). More speciﬁcally, we investigate how MARL agents react

when one or more teammates start acting abnormally during their training and how that transfers to testing.

Our results show that, while common MARL methods might be able to adjust to simple ﬂaws, they do not

adapt well when these become more complex. In this sense, we show how independent learners can be used

as a potential direction of future research to adapt to malfunctions in swarms using MARL. With this work,

we hope to motivate further research to create more robust intelligent swarms using MARL.

1 INTRODUCTION

Cooperative swarms play an important role in multi-

ple applications in the modern world (Liekna et al.,

2014; Dias et al., 2021). When we think about it,

there is a wide range of different ﬁelds that come to

mind: manufacturing, defence and security, agricul-

ture, and healthcare, to name a few (Jahanshahi et al.,

2017; Rodriguez et al., 2021; Hildmann and Kovacs,

2019; Hunjet et al., 2018). Swarms can be naturally

seen in assembly lines in factories, or when consid-

ering human-machine cooperation in warehouses. In

agriculture, it is common to see swarms of agents for

smart applications (Qu et al., 2022), or in healthcare

to monitor certain complex cases (Jahanshahi et al.,

2017). In the context of defence, swarms of intelligent

drones can be used to control certain areas and ensure

better communication (Hunjet et al., 2018). Regard-

less of the ﬁeld of application, it is always important

to ensure that the systems are functioning properly.

In other words, it is important to ensure that the ele-

ments in the swarm are performing as expected and

https://orcid.org/0000-0003-1304-3539

https://orcid.org/0000-0001-7535-141X

https://orcid.org/0009-0002-0387-235X

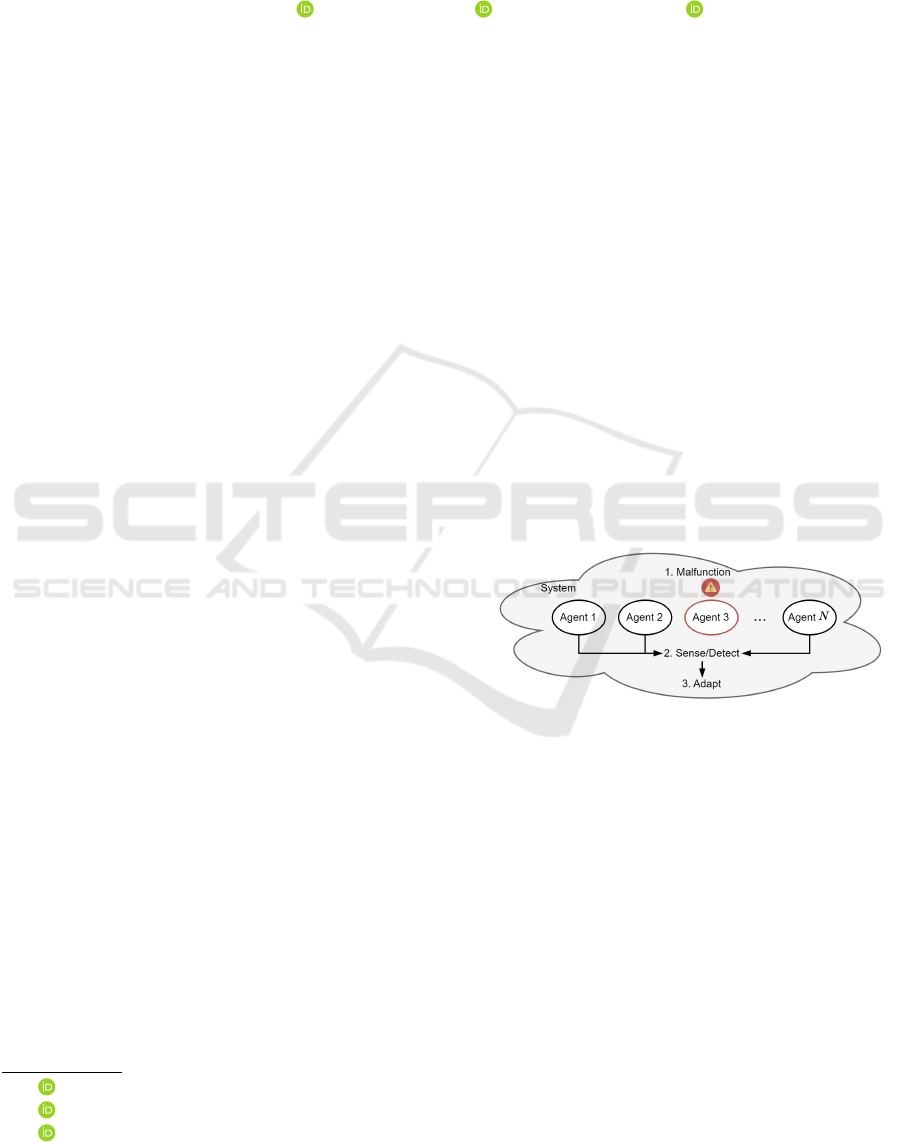
Figure 1: Illustration of the considered scenarios. When a

malfunction affects the elements of a swarm, the remaining

ones must be able to understand that and adapt.

are cooperating with the others.

Note the case of malfunctions that might occur in

some of the elements of a certain swarm. These can

be caused, for example, by external cyberattacks, by

failures in a communication network, or even sim-

ply by internal unexpected ﬂaws of one of the ele-

ments. These types of malfunctions can cause se-

rious problems in the tasks that the swarm is try-

ing to accomplish. If one of the entities is affected,

it might also affect the performance of the rest of

the swam, resulting in catastrophic consequences that

could be avoided (Christensen et al., 2009; Revill,

2016). In this paper, we investigate precisely this

problem, from a Multi-Agent Reinforcement Learn-

ing (MARL) perspective. MARL allows the devel-

410

Pina, R., De Silva, V. and Artaud, C.

Towards Self-Adaptive Resilient Swarms Using Multi-Agent Reinforcement Learning.

DOI: 10.5220/0012462800003654

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2024), pages 410-417

ISBN: 978-989-758-684-2; ISSN: 2184-4313

opment of extremely advanced and specialised be-

haviours within a swarm of cooperative agents (Al-

brecht et al., 2024). However, what if one of the

agents incurs into a ﬂaw? Are the other agents pre-

pared to adapt to it? It is crucial that agents are ca-

pable of demonstrating this type of behaviour and are

able to not only identify but also positively react to

potential malfunctions of one or more of the elements

of the swarm. In the case of such ﬂaws, maintaining

the good functioning of the swarm can prevent major

consequences.

Along these lines, in this paper, we investigate

scenarios where a swarm of agents attempts to solve

a cooperative task. We aim to evaluate where the

agents can naturally react to unexpected ﬂaws in the

behaviours of the teammates. In complex cases where

they cannot adapt, we hypothesise a solution for them

to adjust themselves and still be able to hold and per-

form reasonably until the others either recover or are

replaced. Achieving this optimal behaviour can be

key to address real problems where groups of agents

need to improvise and react to unexpected situations

where one of their reliable teammates incurs into an

unforeseen impairment.

Overall, in this paper, we discuss potential prob-

lems that might occur within swarms and affect their

performance holistically. As illustrated in Figure 1,

when a malfunction incurs into one agent in a swarm,

the others must understand that and adapt to it in or-

der to still achieve their objectives. Through MARL,

in this work, we delve into the implications of mal-

functions in swarms and we identify future ways of

research as a product of our results.

2 RELATED WORK

Swarms have been tipped to solve multiple emerging

applications, including precision agriculture, search

and rescue, disaster response and relief, surveillance

and land administration and wildlife protection. In

(Jurt et al., 2022), a swarm of warehouse robots was

programmed to safely transport large and arbitrarily

shaped objects towards a target direction that did not

require prior knowledge of the object or the number of

agents required. Some of these applications include

very novel methods to address global challenges, such

as climate change related scenarios. For example, a

forest ﬁreﬁghting system based on the use of a swarm

of hundreds of UAVs able to generate a continuous

ﬂow of extinguishing liquid on the ﬁre front is con-

ceptualised in (Ausonio et al., 2021).

In the same context of UAV swarms, to execute

reconnaissance and strike tasks under insufﬁcient en-

emy information and potential synergy between tar-

gets, a distributed task allocation method is proposed

for heterogeneous UAV swarms in (Deng et al., 2023).

The distributed system of the allocation of tasks does

not depend on a highly reliable network nor a cen-

tral node of control and thus improves the reliability

and scalability of the swarm. In (Deng et al., 2023),

all the task allocations and task executions are imple-

mented as online optimisation and hardcoded heuris-

tic algorithms for conﬂict resolution, negotiation and

planning.

Most of the networked UAV swarm control

methodologies are based on the mathematical model

of ﬂocking, in which three basic rules of, separa-

tion, alignment, and cohesion are simulated to achieve

ﬂocking-like behaviour. A model-free distributed

intelligent controller is designed in (Jafari and Xu,

2018) to maintain the motion of all agents in the ﬂock

in the events of network-induced delay. The low com-

plexity learning-based method is developed based on

the computational model of emotional learning ob-

served in the mammalian limbic system (Mor

en and

Balkenius, 2000).

In (Hildmann et al., 2019), the authors addressed

the scenarios where several UAVs are operating as a

single functional unit, which is a swarm, to provide

real-time data from their individual directed sensing

equipment. The partial coverage from individual de-

vices is to be combined with data from other devices

to offer full coverage of a target object or area. This is

a typical application of UAV swarms for surveillance

such as reconnaissance, search and rescue, and data

collection tasks such as precision agriculture. In the

algorithm proposed in (Hildmann et al., 2019), a UAV

swarm is able to autonomously adapt to changing res-

olution requirements for speciﬁc locations within the

area under surveillance. The algorithm is inspired

by how termites construct their nests, where without

direct inter-agent communication, the members of a

colony allow their decision-making to be guided by

their environment.

In (Majd et al., 2020), the authors addressed the

problem of safe and efﬁcient routing of a swarm of

drones through a parallel evolutionary-based swarm

mission planning algorithm (Majd et al., 2020). Evo-

lutionary computing allowed to plan and optimize the

routes of the drones at run-time to maximize safety

while minimising travelling distance as the efﬁciency

objective.

Besides the biological-inspired approaches de-

scribed, Reinforcement Learning (RL) has also been

used in the context of swarms. For instance, in

(Thumiger and Deghat, 2021) a MARL-based decen-

tralised collision avoidance system in a swarm of ho-

Towards Self-Adaptive Resilient Swarms Using Multi-Agent Reinforcement Learning

411

mogenous agents is proposed, where a trained con-

troller is tested in simulation and in a real-world 3-

dimensional drone environment. Similarly, strategies

in multi-UAV collaborative air combat scenarios can

be learned through MARL (Li et al., 2022). MARL-

based cooperative navigation of a swarm of UAVs is

developed through MARL and Curriculum learning

to facilitate and expedite convergence, under different

task complexities.

With the potential threat of UAV swarms in mod-

ern battleﬁelds, developing countermeasures against

them as a form of defence has been studied. There

are two broad categories of harming swarms: hard

kill where the physical components are destroyed by

means such as high-power RF signals that destroy

UAV components, or soft-kill methods that employ

hacking tactics to interfere with the robot’s control

mechanisms such as providing false navigation com-

mands (Zhang et al., 2023). For example, when

achieving cooperative ﬂight by the swarm of UAVs,

moments prior to it, the system is in a disordered

state and vulnerable to a malicious attack. In (Zhang

et al., 2023), authors develop countermeasures against

a UAV swarm by developing a low intensity continu-

ous radio inference scheme to degrade the communi-

cation between the drones.

Despite all the applications in swarms here men-

tioned, these are still liable to several threats to their

normal behaviour and performance by means such as

the ones described previously. Under such scenarios

of attacks, the agents must still be able to recover and

react accordingly to potential ﬂaws. In this sense, in

this paper, we investigate the robustness of swarm in-

telligence. Speciﬁcally, we are interested in dynamic

behaviour learned through MARL and how agents re-

act and adapt to potential malfunctions that might oc-

cur within their trusted swarm.

3 BACKGROUND

3.1 Decentralised Partially Observable

Markov Decision Processes

(Dec-POMDPs)

In this paper, we model our scenarios as Decen-

tralised Partially Observable Markov Decision Pro-

cesses (Dec-POMDPs). The reason to do so is be-

cause in most of the realistic scenarios involving

swarms of agents they only have partial perceptions

of the surroundings and cannot observe everything at

any moment. Additionally, swarms naturally model

interactions among agents. In our setting, we focus

speciﬁcally on cooperative settings to evaluate how

agents react to failures within their swarm.

Thus, we consider a problem deﬁned by the tu-

ple G = (S, A,r, N, Z, P, O,γ), where S represents the

state of the environment, from which each agent i ∈

N ≡ {1, . . . , N} draws an observation o

∈ O(s, i) :

S ×N → Z at each timestep t. At each timestep, each

agent chooses an action a

∈ A, forming a joint action

a ≡ a

, . .. , a

that is performed at state s of the envi-

ronment, resulting in a transition of state according to

the probability function P(s

′

|s, a) : S ×A × S → [0, 1],

where s

′

is the next resulting state, and γ ∈ [0, 1)

is a discount factor. During learning, each agent i

holds an observation-action history τ

such that τ

∈

T = (Z × A)

∗

. The policies of the agents are condi-

tioned on the respective history, π(a

|τ

) : T × A →

[0, 1]. At each timestep t the team receives a joint re-

ward r(s, a) : S × A → R, leading to the objective of

ﬁnding a joint policy π that maximises the objective

, a

) = E

, a

], where R

∑

∞

k=0

t+k

the discounted return.

3.2 Deep Reinforcement Learning

Reinforcement Learning (RL) has been around for

some time (Sutton and Barto, 2018). One of the ﬁrstly

proposed methods is named Q-learning (Watkins and

Dayan, 1992). This algorithm follows the lines of

dynamic programming and aims to learn an optimal

Q-function that dictates the best actions to execute at

each moment of a certain problem, based on its cur-

rent state. The updates of the Q-function are made

following the equation

Q(s, a) ← (1 − α)Q(s, a) + α(r + γmax

Q(s

′

, a)).

(1)

However, working on the tabular case has limita-

tions (Albrecht et al., 2024). For instance, tabular

Q-learning cannot approximate states that it has not

seen before, even if they are simply slightly different.

Thus, in (Mnih et al., 2015) the authors have extended

simple Q-learning to Deep Q-Networks (DQNs) that

use deep learning approaches and hence are capable

of learning outside of tabular settings. This extends

drastically the range of problems that can be solved

using reinforcement learning, allowing to learn an ap-

proximation for potentially inﬁnite spaces. The DQN

is trained to minimise the loss

L(θ) = E

b∼B



r + γmax

′

Q(s

′

, a

′

) − Q(s, a; θ)



(2)

where θ and θ

′

are the parameters of a learning net-

work and its target, respectively, and b is some sample

sampled from a batch B.

Following the foundations of these approaches,

the authors in (Tan, 1993) have demonstrated how

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

412

DQN can be used to train multiple agents indepen-

dently, giving rise to one of the ﬁrst MARL ap-

proaches. In this work, we explore cooperative en-

vironments that can be solved using MARL and use

more complex recent approaches. Additionally, these

also adopt recurrent DQNs in order to account for

partial observability, as per (Hausknecht and Stone,

2015). In the experiments in this paper, we use in-

dependent learners that use recurrent DQNs. We re-

fer to this method as Independent Deep Q-Learning

(IDQL).

3.3 Value Function Factorisation in

MARL

There are several types of methods in the literature of

MARL suitable to solve cooperative problems such

as the ones portrayed in this paper. Amongst them,

we opt to focus on value function factorisation meth-

ods (Sunehag et al., 2017; Rashid et al., 2020; Pina

et al., 2022). The key idea of these methods is to

learn an efﬁcient decomposition of a joint Q-function

into a set of individual action-value functions. This al-

lows the agents to have partial access to the policies of

the others during training, but they execute actions in

the environment following only their individual pol-

icy functions.

Thus, we can summarise this decomposition pro-

cess as the following:

tot

(τ, a) = f (Q

(τ

, a

), . . . , Q

(τ

, a

)), (3)

where f represents a function (neural network) that

learns a mix that should adhere to a factorisation

condition named Individual Global-Max (IGM). This

condition can be deﬁned as

argmax

tot

(τ, a) =







argmax

(τ

, a

)

argmax

(τ

, a

)







(4)

In our experiments, we make use of QMIX

(Rashid et al., 2020), one of the most popular value

function factorisation methods in the MARL litera-

ture. This method complies with the IGM condition

in (4) due to a structural constraint inherent to its fac-

torisation process, referred to as a monotonicity con-

straint, deﬁned as

∂Q

tot

(τ,a)

∂Q

(τ

)

> 0, ∀i ∈ {1, . . . , N}. In-

tuitively, this means that the joint and all individual

functions should be evolving in the same direction

(Rashid et al., 2020).

Figure 2: Lumberjacks environment with 6 agents (blue cir-

cles). The number inside the green squares represents the

level of the tree, i.e., the number of agents needed to cut it.

4 METHODS AND SETTING

To evaluate our hypothesis, we use MARL with the

objective of studying the level of robustness of swarm

intelligence. Speciﬁcally, we intend to investigate the

issue of malfunctioning agents within a swarm of co-

operative agents, i.e., all agents expect every other

agent to cooperate in a given task, but, in the case of

malfunction, the agents should understand to ignore

the potentially malicious agents. The objective is that

the resultant agents are robust for the perturbations

caused by an individual or a subset of malfunctioning

agents.

4.1 The MARL Environment

The environment used in the experiments is named

Lumberjacks and, in this environment, a team of 6

agents must learn cooperative strategies in order to

cut all the existing trees in the world of the map (Fig-

ure 2). Every time a tree is cut, there is a reward of

+5 for each agent. Note that these rewards are then

summed and given as the team reward that is shared

by the agents. The task becomes challenging because

each tree has a pre-deﬁned assigned level that dictates

the number of agents needed at the same time to cut

that speciﬁc tree. Logically, this requires their coop-

eration as a group. In addition, there is a step penalty

of –0.01 that is given to each agent at every time step

until the end of the episode. The episode terminates

either when all the trees are gone or when a limit of

100 timesteps is reached. Logically, the higher the

number of agents cooperating, the higher will be the

reward received by the team.

Towards Self-Adaptive Resilient Swarms Using Multi-Agent Reinforcement Learning

413

4.2 Experimental Setup

To evaluate our hypothesis, we design an experimen-

tal setup that consists of two main stages: 1) training

the MARL agents in the described environment with-

out any changes and 2) testing the learned policies

in the same environment but one of the agents of the

team starts executing random actions instead of fol-

lowing the learned policy (agent malfunction). Addi-

tionally, to test the hypothesis, we also train a varia-

tion of the training stage 1, where part of the agents

fail during training, that is, part of the agents start

executing random actions at a certain interval during

training. We refer to this training scheme as Adap-

tive Training. With this additional experiment, we in-

tend to investigate whether we can train the agents to

anticipate during training these kinds of unexpected

situations of system failures. In all the experiments

we use the centralised training decentralised execu-

tion (CTDE) method QMIX, as described in section

3.3.

5 EXPERIMENTS AND

DISCUSSIONS

With the experiments presented in this section we in-

tend to evaluate the following hypothesis: if we train

a team of N MARL agents to solve a certain cooper-

ative task, the team will struggle to re-adapt if one or

more of the N elements start acting unexpectedly after

the entire team is trained (that is, at evaluation/testing

time).

5.1 Main Results

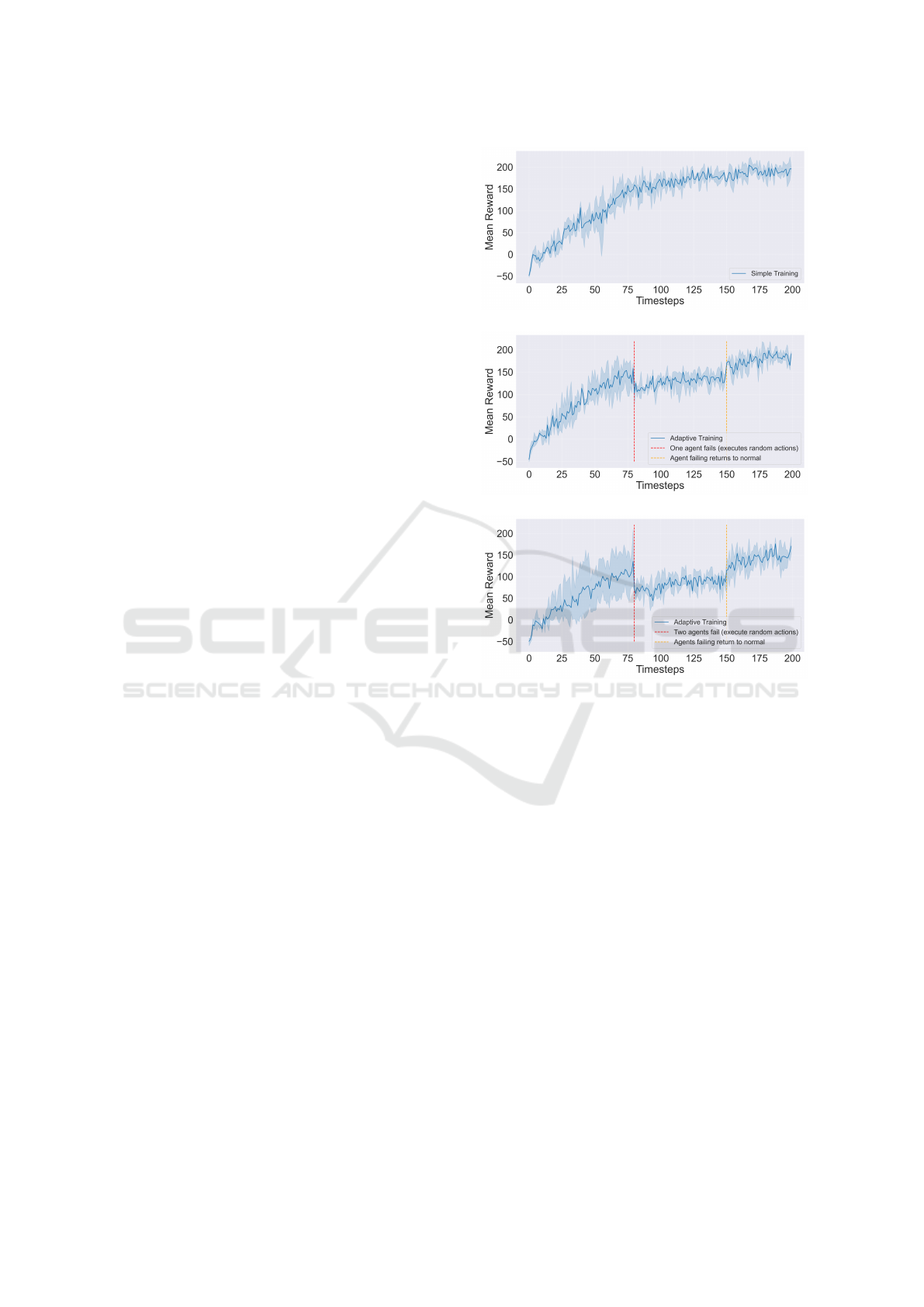
Figure 3 illustrates the results of the experimental

stage 1 (as described in section 4.2). We can see that

the agents can achieve a high reward in this task when

they are trained using a strong MARL algorithm such

as QMIX (Figure 3(a)). However, when we move the

learned policies to the second stage (testing, as de-

scribed in section 4.2), we can see that the induced

changes in the scenario have an impact on the agents’

behaviour (Figure 4). By looking at Figure 4, we ob-

serve that, while the agents still perform at a high level

under normal conditions, when we make one agent act

randomly the performance of the team decreases sub-

stantially. This raises the need for creating intelligent

agents that are capable of actively reacting to these

kinds of unexpected events. For instance, in certain

real scenarios that require multi-agent cooperation, if

there is a system malfunction in one of the agents, the

remaining agents should be able to react to the prob-

(a)

(b)

(c)

Figure 3: Training rewards over 2M timesteps. From top

to bottom, (a) shows the performance of QMIX in an envi-

ronment without malfunctions. (b) shows the performance

of QMIX but during a period of timesteps (800k-1M) one

agent acts randomly. (c) show the performance of QMIX

but during a period of timesteps (800k-1.5M) two agents

act randomly.

lem and adapt to the failure that occurred within the

team.

Conversely, when we introduce one failure dur-

ing the training of the team (Figure 3(b)), we can see

that, although during training there is a break of per-

formance that concurs with the moment of the intro-

duction of the failure, the team will be better prepared

to react to unexpected failures during the evaluation

time (second stage) (Figure 4). Figure 3(b) shows a

performance decrease from the moment of the intro-

duction of a failure until roughly the moment when

the agent recovers, that is, when the malfunctioning

agent stops doing random actions and returns to act-

ing according to the policy being learned. From the

moment the failure ends, the team ends up achiev-

ing the same optimal performance as achieved by the

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

414

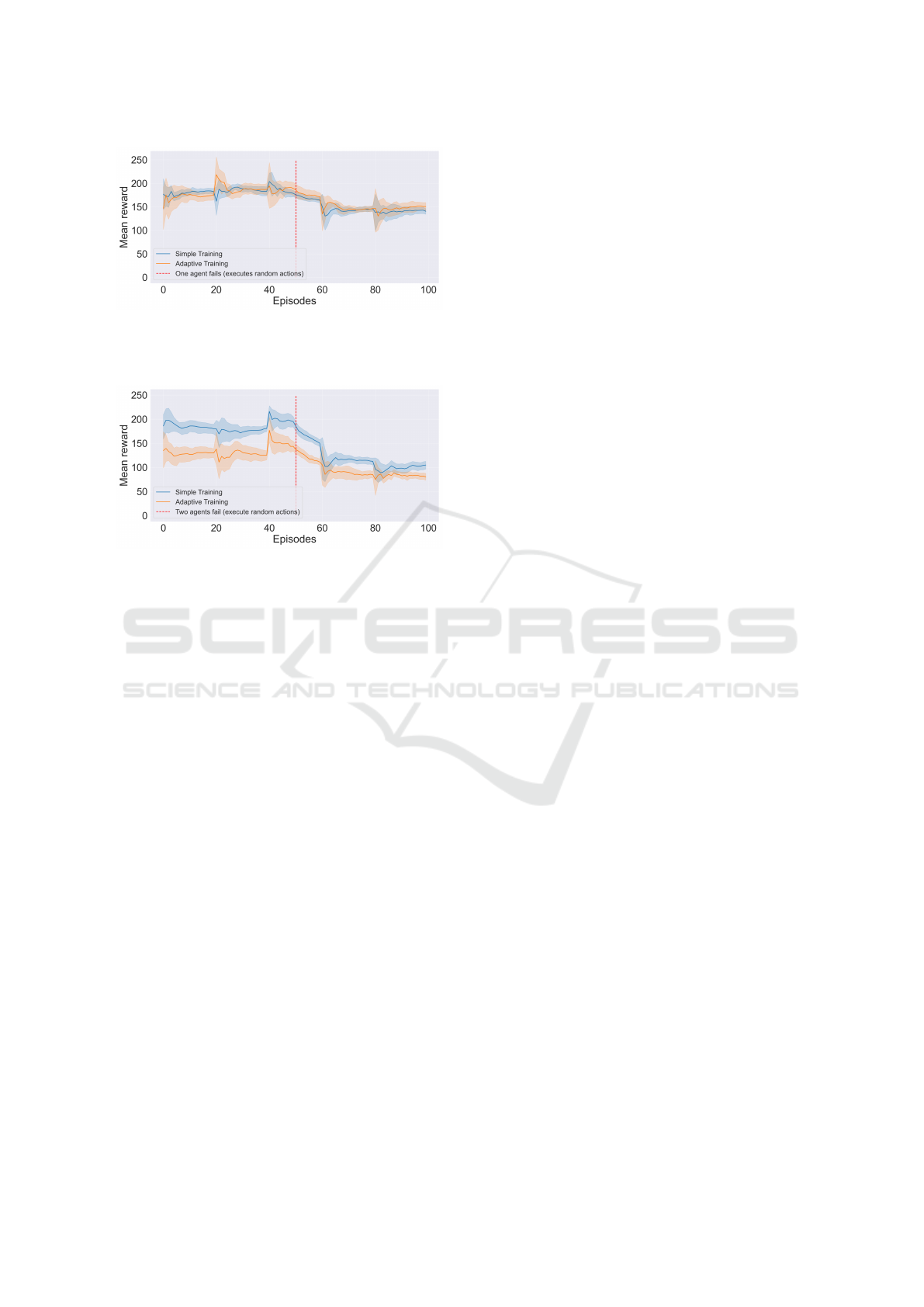
Figure 4: Evaluation of the agents over 100 episodes, but

after 50 episodes one of the agents starts doing random ac-

tions (failure).

Figure 5: Evaluation of the agents over 100 episodes, but

after 50 episodes two of the agents start doing random ac-

tions (two failures).

normal training as depicted in Figure 4. When the

learned policies are transferred to the evaluation phase

(stage 2), we can see that the team demonstrates good

behaviour not only under normal environment con-

ditions but also when a failure is introduced during

the evaluation phase. When compared to the policies

naively trained, the policies trained that encountered a

failure during training achieve the same performance

under normal conditions. Importantly, these policies

also allow to improve the reward received when a fail-

ure occurs in the system. The presented results en-

force the need for training more conscious agents in

MARL that can react to unexpected failures in the el-

ements of the team and still be capable of operating

successfully when the others fail.

5.2 Additional Experiments

To further investigate our hypothesis, we extend the

experiments carried out in the previous section to

make two agents fail instead of only one. Following

the same logic, we evaluate the performance of the

agents trained under normal conditions in this setting

(Figure 3(a)) and the performance of agents that have

experienced the failure of two agents during training

(as depicted in Figure 3(c)). While during training the

evolution of the rewards achieved over time is simi-

lar to the previous experiments, Figure 5 shows that,

when we evaluate the agents after training in a sce-

nario where two elements fail, the rewards achieved

decrease substantially for both training methods (nor-

mal and adaptive with two failures). In fact, the adap-

tive training that has seen two failures during training

seems to be even more affected in this case, as op-

posed to the results with only one failure in Figure 4.

This observation suggests that the occurrence of

two failures during training becomes confusing for

the agents when learning the task as a team. This

opens space for further research on how we can create

more robust methods that are capable of accounting

for an arbitrary number of failures and still perform

well.

5.3 Results with Independent Learners

(IDQL)

We have seen in the previous sections how the training

phase of QMIX method is drastically affected when

there is a malfunction in some of the agents of the

swarm. We hypothesise that this performance drop

can be due to the mixer of this method that is de-

scribed in section 3.3. Since some of the agents incur

into failures and perform random actions, the factori-

sation process during the centralised stage will be af-

fected. This leads us to think that, one step towards

improving reactions to these failures can be to use

fully independent learners instead of using a mixer

during a centralised step.

In Figure 6 we demonstrate the results for the

same scenario, but now using fully independent learn-

ers (IDQL, as described in section 3.2). That is, these

agents are trained in a fully decentralised and inde-

pendent manner, by simply updating their Q-networks

following the loss in (2). As the ﬁgure shows, the

signiﬁcant drops in performance during training that

we observed in the previous ﬁgures do not exist any-

more. Now, the performances are somewhat consis-

tent between normal training (Figure 6(a)) and train-

ing with malfunctions of the agents (one malfunction

in Figure 6(b) and two in Figure 6(c)). However, it

is important to note that the rewards achieved in this

case are far from being optimal. With the previous

method, the agents can achieve much higher rewards

in the task, meaning that, despite naive independent

learners seeming to be more robust to malfunctions

within the team, they are still not good enough to op-

timally solve complex tasks such as the one hereby

presented. Thus, these insights highlight the need to

develop stronger methods that can act in a fully inde-

pendent manner. Novel strong independent methods

can in fact be key to solve complex tasks, providing

improved robustness at the same time.

Towards Self-Adaptive Resilient Swarms Using Multi-Agent Reinforcement Learning

415

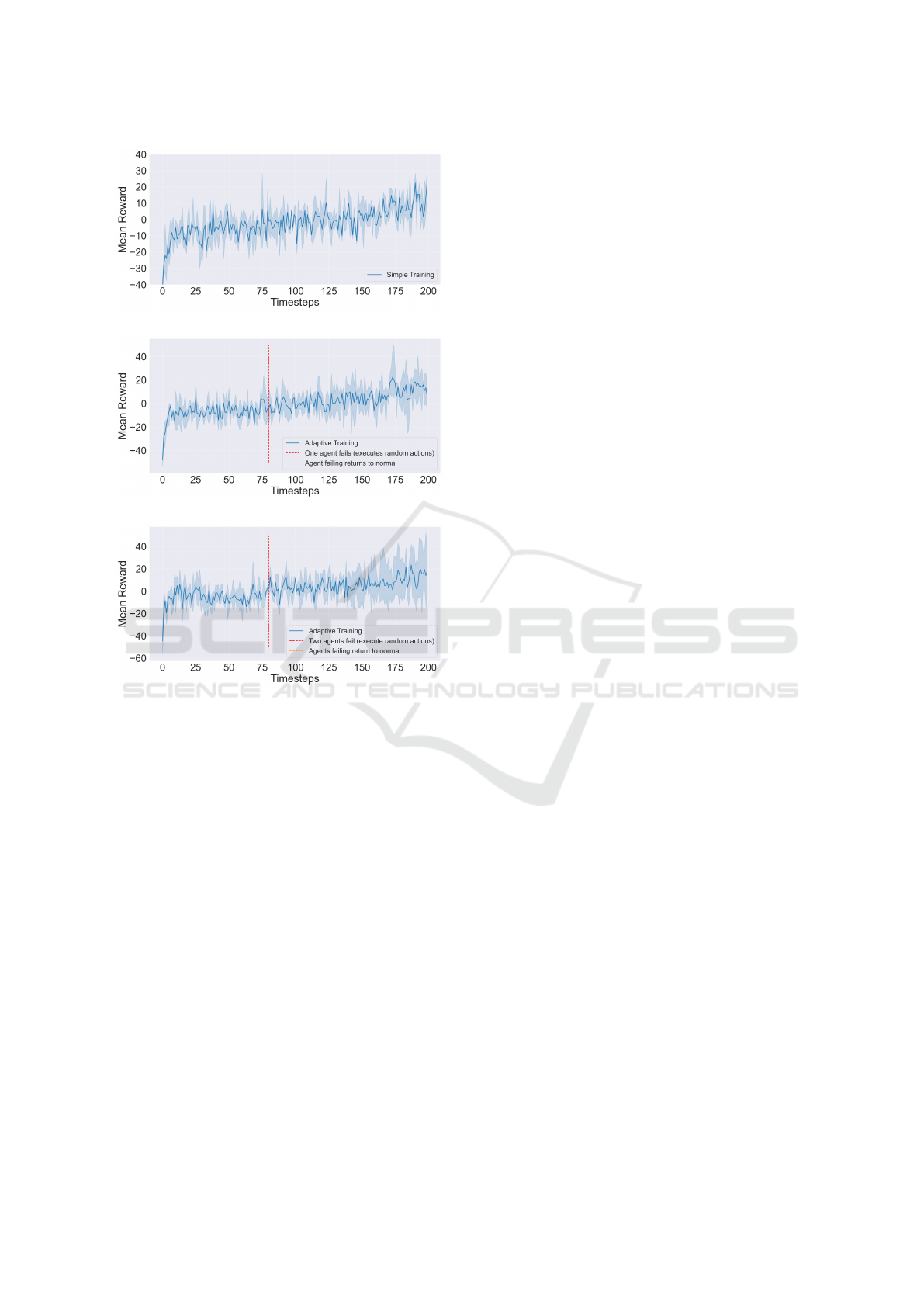
(a)

(b)

(c)

Figure 6: Training rewards over 2M timesteps. From top

to bottom, (a) shows the performance of IDQL in an envi-

ronment without malfunctions. (b) shows the performance

of IDQL but during a period of timesteps (800k-1M) one

agent acts randomly. (c) show the performance of IDQL

but during a period of timesteps (800k-1.5M) two agents

act randomly.

6 CONCLUSION AND FUTURE

WORK

Swarms of intelligent agents are becoming increas-

ingly popular in diverse applications. Despite their

notorious advantages, they are still subject to poten-

tial attacks or internal ﬂaws that they may not be able

to control. Creating robust units that can positively

react to these malfunctions can be key to developing

stronger cooperative swarms.

In this paper, we investigated the effect of mal-

functions within a trusted swarm of agents from a co-

operative MARL perspective. We demonstrated that

agents may not recover when some of their teammates

incur into failures and start acting abnormally. While

the proposed training scheme seems to be robust to

simple failures (one agent), when these become more

complex, it fails. Our results show that using indepen-

dent learners can be a solution to create more resilient

agents, but these may not be good enough to learn

complex tasks properly. This motivates further work

to ﬁnd a middle ground between independent learners

and other non-independent complex methods that can

be both resilient and solve complex problems.

Along these, it is important to train entities that

can not only ﬁnd the patterns that correspond to po-

tential malfunctions within their trusted swarm but are

also able to react and adapt to them. With our results,

we hope to motivate further research in this matter. In

the future, we intend to further investigate this prob-

lem by creating more robust independent agents. Ad-

ditionally, we aim to test these methods in real scenar-

ios.

ACKNOWLEDGEMENTS

This work was funded by the Engineering and Physi-

cal Sciences Research Council in the United Kingdom

(EPSRC), under the grant number EP/X028631/1.

REFERENCES

Albrecht, S. V., Christianos, F., and Sch

afer, L. (2024).

Multi-Agent Reinforcement Learning: Foundations

and Modern Approaches. MIT Press.

Ausonio, E., Bagnerini, P., and Ghio, M. (2021). Drone

swarms in ﬁre suppression activities: A conceptual

framework. Drones, 5(1):17.

Christensen, A. L., OGrady, R., and Dorigo, M. (2009).

From ﬁreﬂies to fault-tolerant swarms of robots.

IEEE Transactions on Evolutionary Computation,

13(4):754–766.

Deng, H., Huang, J., Liu, Q., Zhao, T., Zhou, C., and Gao, J.

(2023). A distributed collaborative allocation method

of reconnaissance and strike tasks for heterogeneous

uavs. Drones, 7(2):138.

Dias, P. G. F., Silva, M. C., Rocha Filho, G. P., Vargas, P. A.,

Cota, L. P., and Pessin, G. (2021). Swarm robotics: A

perspective on the latest reviewed concepts and appli-

cations. Sensors, 21(6):2062.

Hausknecht, M. and Stone, P. (2015). Deep recurrent q-

learning for partially observable mdps. In 2015 aaai

fall symposium series.

Hildmann, H. and Kovacs, E. (2019). Using unmanned

aerial vehicles (uavs) as mobile sensing platforms

(msps) for disaster response, civil security and public

safety. Drones, 3(3):59.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

416

Hildmann, H., Kovacs, E., Saffre, F., and Isakovic, A.

(2019). Nature-inspired drone swarming for real-time

aerial data-collection under dynamic operational con-

straints. Drones, 3(3):71.

Hunjet, R., Fraser, B., Stevens, T., Hodges, L., Mayen,

K., Barca, J. C., Cochrane, M., Cannizzaro, R., and

Palmer, J. L. (2018). Data ferrying with swarming uas

in tactical defence networks. In 2018 IEEE interna-

tional conference on robotics and automation (ICRA),

pages 6381–6388. IEEE.

Jafari, M. and Xu, H. (2018). Biologically-inspired intel-

ligent ﬂocking control for networked multi-uas with

uncertain network imperfections. Drones, 2(4):33.

Jahanshahi, M. R., Shen, W.-M., Mondal, T. G., Abdelbarr,

M., Masri, S. F., and Qidwai, U. A. (2017). Recon-

ﬁgurable swarm robots for structural health monitor-

ing: a brief review. International Journal of Intelligent

Robotics and Applications, 1:287–305.

Jurt, M., Milner, E., Sooriyabandara, M., and Hauert, S.

(2022). Collective transport of arbitrarily shaped ob-

jects using robot swarms. Artiﬁcial Life and Robotics,

27(2):365–372.

Li, S., Jia, Y., Yang, F., Qin, Q., Gao, H., and Zhou, Y.

(2022). Collaborative decision-making method for

multi-uav based on multiagent reinforcement learn-

ing. IEEE Access, 10:91385–91396.

Liekna, A., Grundspenkis, J., et al. (2014). Towards practi-

cal application of swarm robotics: overview of swarm

tasks. Engineering for rural development, 13:271–

277.

Majd, A., Loni, M., Sahebi, G., and Daneshtalab, M.

(2020). Improving motion safety and efﬁciency of

intelligent autonomous swarm of drones. Drones,

4(3):48.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-

ness, J., Bellemare, M. G., Graves, A., Riedmiller, M.,

Fidjeland, A. K., Ostrovski, G., et al. (2015). Human-

level control through deep reinforcement learning. na-

ture, 518(7540):529–533.

Mor

en, J. and Balkenius, C. (2000). A computational model

of emotional learning in the amygdala. From animals

to animats, 6:115–124.

Pina, R., De Silva, V., Hook, J., and Kondoz, A. (2022).

Residual q-networks for value function factorizing in

multiagent reinforcement learning. IEEE Transac-

tions on Neural Networks and Learning Systems.

Qu, C., Boubin, J., Gafurov, D., Zhou, J., Aloysius, N.,

Nguyen, H., and Calyam, P. (2022). Uav swarms

in smart agriculture: Experiences and opportunities.

In 2022 IEEE 18th International Conference on e-

Science (e-Science), pages 148–158. IEEE.

Rashid, T., Samvelyan, M., De Witt, C. S., Farquhar, G., Fo-

erster, J., and Whiteson, S. (2020). Monotonic value

function factorisation for deep multi-agent reinforce-

ment learning. The Journal of Machine Learning Re-

search, 21(1):7234–7284.

Revill, M. B. (2016). UAV swarm behavior modeling for

early exposure of failure modes. PhD thesis, Mon-

terey, California: Naval Postgraduate School.

Rodriguez, I., Mogensen, R. S., Schjørring, A., Razza-

ghpour, M., Maldonado, R., Berardinelli, G., Adeo-

gun, R., Christensen, P. H., Mogensen, P., Madsen,

O., et al. (2021). 5g swarm production: Advanced

industrial manufacturing concepts enabled by wire-

less automation. IEEE Communications Magazine,

59(1):48–54.

Sunehag, P., Lever, G., Gruslys, A., Czarnecki, W. M.,

Zambaldi, V., Jaderberg, M., Lanctot, M., Sonnerat,

N., Leibo, J. Z., Tuyls, K., et al. (2017). Value-

decomposition networks for cooperative multi-agent

learning. arXiv preprint arXiv:1706.05296.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-

ing: An introduction. MIT press.

Tan, M. (1993). Multi-agent reinforcement learning: Inde-

pendent vs. cooperative agents. In Proceedings of the

tenth international conference on machine learning,

pages 330–337.

Thumiger, N. and Deghat, M. (2021). A multi-agent deep

reinforcement learning approach for practical decen-

tralized uav collision avoidance. IEEE Control Sys-

tems Letters, 6:2174–2179.

Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine

learning, 8:279–292.

Zhang, X., Bai, Y., and He, K. (2023). On countermea-

sures against cooperative ﬂy of uav swarms. Drones,

7(3):172.

Towards Self-Adaptive Resilient Swarms Using Multi-Agent Reinforcement Learning

417