Preserving Privacy in High-Dimensional Data Publishing
Narges Alipourjeddi and Ali Miri
Department of Computer Science, Toronto Metropolitan University, Toronto, Canada
Keywords:
High-Dimensional Data, Privacy Preservation, Persistent Homology, Differential Privacy, Data Publishing,
Topological Data Analysis.
Abstract:
As the era of big data unfolds, high-dimensional datasets with complex structures have become increasingly
prevalent in various fields, including healthcare, finance, and social sciences. Extracting valuable insights
from such data is essential for scientific discovery and decision-making. However, the publication of these
datasets is full of privacy concerns, as they often contain sensitive and personally identifiable information. In
this paper, we introduce a novel approach that addresses the delicate balance between data privacy and the
exploration of high-dimensional data’s underlying structure. We leverage the power of persistent homology,
a topological data analysis method, to unveil hidden patterns and captures the persistent topological features
of the data, allowing us to study its shape and structure across different scales. Adding noise into the low di-
mensional embedding and provide private persistence diagram with differential privacy, offers a rigorous and
well-established framework to ensure that individuals’ privacy in the dataset is protected. We synthetically
generate high-dimensional data with a focus on differential privacy-preserved persistence diagrams, ensuring
privacy in our publication of the synthesized dataset. We conduct extensive experiments on three real-world
datasets and the experimental results demonstrate that our mechanism can significantly improve the data struc-
ture of the published data while satisfying differential privacy.
1 INTRODUCTION
In our data-driven era, high-dimensional datasets have
become ubiquitous, permeating fields as diverse as
healthcare, finance, and social sciences. The informa-
tion encapsulated within these data sets holds the key
to crucial scientific discoveries, informed decision-
making, and innovation. However, sharing this data
is not without its challenges, and among the most sig-
nificant is the need to navigate the delicate balance
between data publishing and data privacy.
The advent of big data has brought forth a press-
ing concern: how can we unlock the valuable insights
hidden within high-dimensional datasets, while safe-
guarding the sensitive and personally identifiable in-
formation they contain? This question is central to
our research as we delve into the intersection of data
privacy and data publishing. Our approach, built upon
the powerful foundations of persistent homology and
differential privacy, seeks to address this fundamental
question.
Privacy-Preserving Data Publishing (PPDP) has
gained significant attentions in recent years as a
promising approach for information sharing while
preserving data privacy. There exists standard meth-
ods such as k-anonymity (Mahanan et al., 2021), l-
diversity (Binjubeir et al., 2019) and t-closeness (Bin-
jubeir et al., 2019) that data collectors (sometimes
also referred to as curators) can apply to protect and
anonymize datasets. However, these methods can still
leak information when analysis involves additional
datasets or auxiliary information from other sources.
One also needs to able to formally measure informa-
tion leakage and privacy protection. A commonly
used methodology to provide a framework for pre-
serving and measuring privacy is Differential Privacy
(DP) (Dwork et al., 2014). DP can be used to pro-
vide privacy guarantees using an information theoret-
ical approach. The main idea in this approach is that
what can be learned from the published data is (ap-
proximately) the same, whether or not any particular
individual was included in the input database. This
model is mathematical foundation with a formal defi-
nition and rigorous proof while making the assump-
tion that an attacker has the maximum background
knowledge.
Nonetheless, ensuring differential privacy in the
publication of high-dimensional data continues to be
a powerful challenge, primarily due to the “Curse
Alipourjeddi, N. and Miri, A.
Preserving Privacy in High-Dimensional Data Publishing.
DOI: 10.5220/0012455600003648
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 10th International Conference on Information Systems Security and Privacy (ICISSP 2024), pages 845-852
ISBN: 978-989-758-683-5; ISSN: 2184-4356
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
845

of High-Dimensionality”. This phenomenon signi-
fies that as the dimensionality of the data grows, the
complexity and computational cost of handling and
analysing multidimensional data experience exponen-
tial growth.
One promising way to address high dimensional-
ity is to disassemble the dataset into a group of lower
dimensional datasets. One of the traditional approach
for disassembling the dataset into a group of lower
dimension dataset presented by Zhang et al. (Zhang
et al., 2017). They used a Bayesian network to deal
with high dimensionality. They assumed some corre-
lations between attributes exist and, if these correla-
tions can be modelled, the model can be used to gen-
erate a set of marginal datasets to simulate the dis-
tribution of the original dataset. The disadvantage of
this solution is that it consumes too much of the pri-
vacy budget during network construction and, hence,
makes the approximation of the distribution inaccu-
rate.
In this work, we employ a non-linear dimen-
sionality reduction method grounded in the mani-
fold hypothesis, which posits that real-world data sets
may reside on a non-linear, low-dimensional man-
ifold embedded within a high-dimensional ambient
vector space. In many real-world datasets, the char-
acteristics of this underlying manifold are initially un-
known. The process of manifold learning is employed
to endeavour the extraction of this hidden manifold
by mapping the data into a lower-dimensional space.
One of the current tools in this era is Topological Data
Analysis (TDA), utilized for the analysis of both geo-
metric and topological information within datasets.
TDA represents an innovative field of data anal-
ysis that was developed to capture the underlying
topological structures within data. Over the past few
decades, TDA has undergone extensive research and
exploration. This approach has proven invaluable
in handling complex, high-dimensional datasets that
challenge the capabilities of traditional data analysis
methods.
Persistent homology is a powerful tool for dimen-
sionality reduction from the field of TDA. In high-
dimensional data analysis, the manifold hypothesis
suggests that many datasets naturally lie on or near
lower-dimensional manifolds. These manifolds repre-
sent the underlying structure of the data, even though
the data is observed in a higher-dimensional space.
Persistent homology detect topological features that
represent the various components of the data, includ-
ing the lower-dimensional manifolds. These features
can include connected components (0-dimensional
manifolds), loops (1-dimensional manifolds), voids
(2-dimensional manifolds) and so on.
In this paper, we present a novel approach that ob-
tain topological features for our datasets and captures
how long these topological features persist privately.
This makes it possible to generate and publish high
dimensional data privately. Specifically, we make the
following contributions:
1) We use persistent homology technique to analyse
theoretical meaning behind our datasets and cre-
ating persistence diagram.
2) We implement differential privacy measures on
the persistence diagram to make private features.
3) We generate synthetic dataset based on the private
persistent diagram.
We commence with a preliminaries section, lay-
ing the groundwork with essential background infor-
mation and the introduction of the notations we will
use (Section 2). In Section 3, we delve into an exami-
nation of the related work in the field. Our framework
is presented comprehensively in Section 4, while Sec-
tion 5 showcases its practical capabilities. The paper
concludes with a summary and insights in Section 6.
2 PRELIMINARIES
In this section we review some of the standard con-
cepts from topology, algebraic topology and differen-
tial privacy. We want to use these methods to synthe-
size private high-dimensional datasets.
2.1 Differential Privacy Fundamentals
The protection of individuals’ privacy in the con-
text of data publishing and analysis has become a
paramount concern with the increasing availability of
large and sensitive datasets. Differential privacy of-
fers a rigorous and effective approach to address this
concern by ensuring that individual privacy is main-
tained while allowing for meaningful data publishing.
This section introduces the core concepts and termi-
nology related to differential privacy. Formally, dif-
ferential privacy is defined as follows:
Definition 2.1 (ε-differential Privacy). A randomized
mechanism M gives ε-differential privacy for every set
of outputs Ω, and for any neighbouring datasets of D
and D
′
, if M satisfies
Pr[M(D) ∈ Ω] ≤ exp(ε) · Pr[M(D
′
) ∈ Ω]
In other words, the probability of obtaining a spe-
cific outcome from the mechanism M is only slightly
influenced by the inclusion or exclusion of any indi-
vidual’s data.
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
846

Two fundamental components of differential pri-
vacy are the sensitivity of a function and the privacy
parameter ε. The sensitivity of a function f quanti-
fies how much the function’s output can change when
a single data point is added or removed from the
dataset. The parameter ε refers to the privacy budget,
which controls the level of privacy guarantee achieved
by mechanism M. A smaller ε represents a stronger
privacy level. For a strong privacy guarantee, we need
the privacy budget to be small with an ideal in the
range of zero and one.
To achieve differential privacy, various privacy
mechanisms introduce controlled randomness into
data analysis. Common mechanisms include the
Laplace mechanism and the exponential mechanism.
The Laplace mechanism (Dwork et al., 2016)
means perturbing the output of a function with
Laplace-distributed noise to achieve differential pri-
vacy. Lap(b) to represent the noise sampled from a
Laplace distribution with a scaling of b.
Definition 2.2. For a function f : D → R over
a dataset D, the mechanism Min provides the ε-
differential privacy
M(D) = f (D) +Lap(
∆ f
ε
)
In Definition 2.2, the parameter ∆ f refers to the
global sensitivity, which determine how much pertur-
bation is required for a particular query in a mecha-
nism. This property is defined as the largest differ-
ence between the outputs of query q for any pair of
neighbouring datasets which means that
∆
q
= max||q(D) − q(D
′
)||
1
where ||.||
1
is the L
1
norm.
The Exponential Mechanism (McSherry and Tal-
war, 2007) is employed when you need to select an
item from a set or make a decision based on data, and
you want to ensure that the process is differentially
private. This means that the probability of selecting
one item over another should be adjusted to protect
privacy while preserving the utility of the selection.
Definition 2.3. Let q(D,φ) be a score function of
dataset D that measures the quality of output φ, ∆ f
represents the sensitivity of f. The exponential mech-
anism M satisfies ε-differential privacy if
M(D) = (returnφ ∝ exp(
εq(D,Φ)
2∆ f
)
2.2 Persistent Homology
As per the manifold distribution hypothesis (Goodfel-
low et al., 2016), real-world high-dimensional data is
often situated on a lower-dimensional manifold hid-
den within the broader high-dimensional space. This
underlying manifold is believed to possess a highly
intricate non-linear structure, making its explicit defi-
nition challenging. Nonetheless, it is possible to scru-
tinize and analyze this manifold by considering its
topological properties.
Topological Data Analysis (TDA) serves as a
framework that integrates techniques from algebraic
topology and statistical learning, providing a quanti-
tative foundation for understanding these topological
properties. Among the array of tools hailing from al-
gebraic topology used in TDA, persistent homology
stands out as a pivotal method. To compute the per-
sistent homology of a space, it is necessary to ini-
tially express the space as a simplicial complex. Fig-
ure 1 shows example of simplices and one simpli-
cial complex. A simplicial complex is essentially a
collection of simplicial homology. Simplicial homol-
ogy employs matrix reduction algorithms to assign K
a family of groups, the homology groups. The d
th
homology group H
d
(K) of K contains d-dimensional
topological features, such as connected components
(d = 0), cycles/tunnels (d = 1), and voids (d = 2).
Homology groups are typically summarised by their
ranks, thereby obtaining a simple invariant “signa-
ture” of a manifold. For example, a circle in R
2
has
one feature with d = 1 (a cycle), and one feature with
d = 0 (a connected component).
0-simplex
1-simplex
2-simplex
3-simplex
Figure 1: Example of one simplicial complex with differ-
ent simplices. Two 0-simplex are vertex points, 1-simplex
is a pair of vertex points which bound a line segment, a
2-simplex is a collection of vertex points which live on a
triangle and a 3-dimensional simplex is a tetrahedron.
In practice scenarios, the underlying manifold M
is often unknown and we are working with a point
cloud X := x
1
,...,x
n
⊂ R
d
and a metric distance X ×
X → R such as the Euclidean distance. Persistent
homology adopts simplicial homology to this con-
text. Instead of attempting to approximate M trough
a single simplicial complex, which can be unstable
due to the discrete nature of X, persistent homology
monitors changes in homology groups across various
scales of the metric. A distance function on the un-
derlying space corresponds to a filtration of the sim-
plicial complex. One common method of doing this
is using the Vietoris-Rips construction. A Vietoris-
Rips complex of parameter d is the simplicial com-
Preserving Privacy in High-Dimensional Data Publishing
847

plex with finite set of points that has diameter at most
d. The Vietoris–Rips complex of X at scale d con-
tains all simplices of X whose elements x
0
,x
1
,... sat-
isfy dist(x
i
,x
j
) ≤ d for all i, j.
We consider all distances d, then each homology
appears at a particular value of d and disappear at an-
other value of d. We represent the persistence of this
hole as a pair, for example (d
1
,d
2
) and visualize this
pair as a bar from d
1
to d
2
. A collection of bars is
a barcode. We can represent the persistent homology
with a barcode or persistence diagram. A barcode rep-
resents each persistent generator with a horizontal line
beginning at the first filtration level where it appears,
and ending at the filtration level where it disappears.
(a)d
1
(b)d
2
(c)d
3
Figure 2: The three step filtration of Vietoris-Rips complex
on the set of 10 points with increasing radius 0 < d
1
< d
2
<
d
3
.
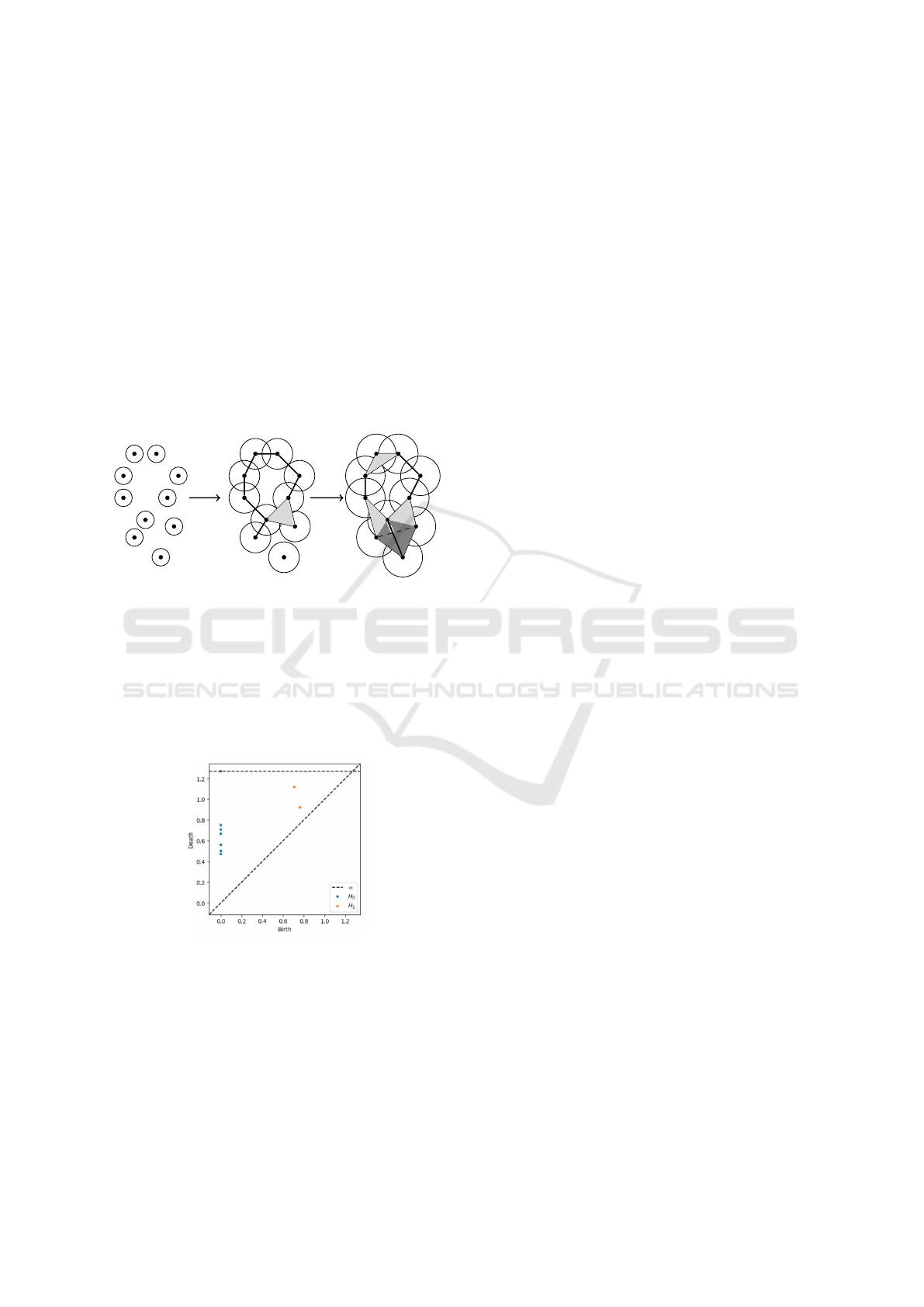
Figure 2 shows the The Vietoris–Rips complex
of a point cloud X at different scales d
1
,d
2
and
d
3
. As the distance threshold increases, the connec-
tivity changes. The creation and destruction of d-
dimensional topological features is recorded in the d
th
persistence diagram which is showed in the Figure 3.
Figure 3: The persistent diagram corresponding to the fil-
tration in the figure on top. Blue points represent persistent
homology groups of dimension 0, and the orange ones of
dimension 1.
A persistence diagram P = (b
i
,d
i
) is essentially
a multiset of birth-death pairs b
i
and d
i
, which sat-
isfy b
i
≤ d
i
. There are numerous ways to “vectoriz”
a persistence diagram into an element in some vec-
tor space. One of the most popular ways is to rep-
resent each birth-death pair (b,d) by the Dirac mea-
sure δ
(b,d)
at (b,d), and represent the whole diagram
P by the point measure
∑
m
i=1
δ
(b
i
,d
i
)
which is a mea-
sure on the set T := {(x; y) : 0 ≤ x ≤ y ≤ ∞} (Owada,
2022). By realizing a persistence diagram as a mea-
sure, it is possible to define the distance between two
persistence diagrams by means of a distance between
measures. One of the most popular choices is using
the L
∞
Wasserstein distance of the measures, which
is called the bottleneck distance. Specifically, let P,
P
′
be two persistence diagrams. Then the bottleneck
distance between P and P
′
is defined as
W
∞
(P,P
′
) := inf
η:P→P
sup
t∈P
||t − η(t)||
∞
where η ranges over bijections between P and P
′
.
A small perturbation in the input filtration leads to
a small perturbation of its persistence diagram in the
bottleneck distance. It means that for our work a key
property of the bottleneck distance is stability prop-
erty (Chazal et al., 2016). In this paper, our objec-
tive is to generate a differentially private persistence
diagram for our dataset and subsequently generalize
synthetic data based on its insights.
3 RELATED WORK
The field of publishing high-dimensional data has
garnered significant attention from researchers seek-
ing effective methods to balance the disclosure of
information with the imperative to preserve privacy.
Researchers have investigated the application of dif-
ferential privacy mechanisms for publishing high-
dimensional data. Dimensionality reduction is a piv-
otal step in managing high-dimensional datasets. A
powerful approach of dimensionality reduction is the
Bayesian network model proposed in (Zhang et al.,
2017), in which Zhang developed a differentially pri-
vate scheme PrivBayes for publishing high dimen-
sional data. PrivBayes first constructs a Bayesian
network to approximate the distribution of the orig-
inal dataset. It adds noise into each marginal of the
Bayesian network to guarantee differential privacy. It
constructs an approximate distribution of the original
dataset, and samples the tuples from the approximate
distribution to construct a synthetic dataset. DP2-Pub
algorithm (Jiang et al., 2023) is another method which
is based on the Bayesian network and propose an in-
variant post randomization method (PRAM) to apply
it to each attribute cluster. Another approach involves
analyzing attribute correlations and utilizing a depen-
dency graph to generate synthetic data that aligns with
the joint distribution. (Chen et al., 2015). These solu-
tions have a drawback as it significantly consume too
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
848

much of the privacy budget during network construc-
tion.
Computational topology and persistent homology
(PH) have started gaining traction in several areas of
data analysis. In (Alipourjeddi and Miri, 2023), PH is
employed to assess synthetic datasets, enhancing ac-
curacy. The integration of PH into graph analysis, as
indicated in (Alipourjeddi and Miri, 2022) contributes
to more precise synthetic datasets. Further, the fu-
sion of PH with neural networks (Moor et al., 2020)
facilitates dimensionality reduction. Additionally, in-
corporating differential privacy with PH enables dif-
ferentially private Topological Data Analysis (Kang
et al., 2023). These studies collectively concentrate
on the manifold hypothesis and preserving topologi-
cal structures of the input space.
In light of the above analysis, we present the
novel method to generate synthetic data with differ-
entially private persistence diagram. To the best of
our knowledge, our work is the first attempt of pub-
lishing high dimensional dataset privately with topo-
logical approach.
4 METHODOLOGY
The well-known Manifold Hypothesis (Cao et al.,
2020) states that in high dimensional data such as
census data are concentrated on a low dimensional
manifold in a Euclidean space embedded in the high-
dimensional background space. Based on this hypoth-
esis, we focus the following problem in this paper:
We have a high-dimensional dataset with r attributes,
and our strategy involves publishing and releasing the
dataset to the public while satisfying differential pri-
vacy. We consider persistent homology to preserves
the homology structure of our dataset accurately.
First, we propose how to add differential privacy
into the persistence diagram of our dataset. In this
step we need to consider the method which is sensi-
tive to outlier. Due to the differential privacy princi-
ple, the specific data of any one individual should not
have a significant effect on the outcome of the anal-
ysis to achieve privacy protection sensitivity (Avella-
Medina, 2021). We examine the sensitivity of the bot-
tleneck distance of persistence diagrams, which is the
most widely used presentation of persistent homol-
ogy. Because the magnitude of outlier-robustness af-
fects the rate of sensitivity of the bottleneck distance,
We use L
1
-DTM in order to achieve a minimal sensi-
tivity (Kang et al., 2023). We apply the exponential
mechanism which utility function is defined in terms
of the bottleneck distance of L
1
-DTM persistence di-
agrams in order to produce differentially privatized
persistence diagrams.
Second, we generate the synthetic dataset from the
private persistence diagram. In this step, we choose
randomly an initial hole from our persistence diagram
or persistence barcode and sampling the attributes.
We terminate this process when all attributes have
been sampled.
4.1 Differentially Private Persistence
Diagram Construction
In the realm of differential privacy algorithms, it is
commonplace to quantify the extent to which the
value of a statistic changes when altering a single
point within a given dataset. This maximal potential
change in the statistic is commonly referred to as the
sensitivity of the statistic. It is necessary that the sen-
sitivity goes to 0 as the size of the data grows.
In our work, we use a persistence diagram con-
structed from a dataset D as a statistic that provides
an estimation of the homological structure underlying
the data. To measure distances between persistence
diagrams, we employ the bottleneck distance, defin-
ing a metric on the space of these diagrams. Conse-
quently, when applying a differential privacy mecha-
nism to persistence diagrams, our initial step involves
estimating the sensitivity of persistence diagrams in
terms of the bottleneck distance. Specifically, we
need to analyse the maximum potential magnitude
of the bottleneck distance, where the pair (D, D
′
) de-
notes an adjacent pair of datasets. The sensitivity of
the persistence diagrams of VietorisRips complexes
cannot converge to 0 even if the size of data grows
to infinity (Kang et al., 2023). Weighted Vietoris-
Rips filtration can be useful to highlight topological
features against outliers and noise. In this regard,
Chazal propose using the notion called distance to a
measure (DTM), to get outlier-robust persistence dia-
grams(Chazal et al., 2017; Anai et al., 2020).
Definition 4.1. Given a probability measure P , for
0 < m < 1, the distance-to-measure (DTM) at resolu-
tion m is defined by
δ(x) = δ
P,m
(x) =
r
1
m
Z
m
0
(G
−1
x
(u))
2
du
where G
x
(t) = P(||X − x|| ≤ t).
The definition is L
2
type of DTM where the sen-
sitivity is bounded by O(n
−1/2
). We focus on L
1
type
DTM for getting fastest decrease rate for sensitivity
which is bounded by O(n
−1
) (Kang et al., 2023).
To generate differential private persistence dia-
gram, employ exponential mechanism with utility
Preserving Privacy in High-Dimensional Data Publishing
849

function with the bottleneck distance
u
D
(P
0
,...,P
l
) =
l
∑
q=0
u
q
D
P
q
where
u
q
D
(P) = −d
B
(P,P
q
(D))
More specifically, we use negative bottleneck dis-
tance between private and non-private persistence di-
agrams as a utility function.
4.2 Synthetic Data by Differential
Privacy Persistence Diagram
Our approach focuses on leveraging persistent dia-
grams to generate synthetic data that preserves the
essential topological features of the original high-
dimensional dataset. Analysing the differentially pri-
vate persistent diagrams provide valuable insights
into the homological characteristics inherent in the
data privately.
In the first step, we translate and understand the
persistent points corresponding to connected compo-
nents. A clear trend emerges, showcasing the birth
and death of connected components across different
scales. Such persistence indicates the robustness of
specific structural elements in the original dataset. Fo-
cusing on loops and voids, we identify regions of sus-
tained persistence, signifying the presence of consis-
tent topological patterns. Peaks and valleys in the
diagrams provide valuable insights into the lifetimes
of these features, aiding in the understanding of their
relevance and stability. All analysing help us to for-
mulate synthesis rules for generating synthetic data.
For our datasets, we prioritize components with long
persistence (we define a threshold for determining the
persistence) and simulate the birth and death events of
topological features. We need to ensure that the dis-
tribution of synthetic points are aligned with the topo-
logical structure. These results allowing us to recreate
the topological patterns in a low-dimensional space.
Secondly, we transform the synthetic points from the
low dimensional space to match the dimensionality
of the original dataset. To generate synthetic data, we
apply the topological autoencoders method (TopoAE)
(Moor et al., 2020). this paper evaluates the topologi-
cal loss in term of distance matrix for each persistence
diagram A
X
[π
X
]. Hence, L
t
= L
X→Z
+ L
Z→X
(Moor
et al., 2020) where,
L
X→Z
=
1
2
||A
X
[π
X
]] − A
Z
[π
X
]||
2
and
L
Z→X
=
1
2
||A
Z
[π
Z
]] − A
X
[π
Z
]||
2
The key idea for both terms is to align and preserve
topologically relevant distances from both spaces.
5 EXPERIMENTAL EVALUATION
In this part, we carry out extensive experiments
to demonstrate the performance of our mechanism
and compare it with two benchmark approaches,
PrivBayes (Zhang et al., 2017) and DP2-Pub (Jiang
et al., 2023). Note that our comparative study fo-
cuses on PrivBayes and DP2-Pub because these meth-
ods share a common approach of decomposing high-
dimensional data into a set of low-dimensional repre-
sentations. The evaluation is based on the three real
high-dimension datasets: the Adult dataset (Asuncion
and Newman, 2007), the Poker-Hand dataset (Asun-
cion and Newman, 2007) and the Cleveland dataset
(Asuncion and Newman, 2007).
Adult dataset contains personal information such
as gender, salary, and education level of 45222
records extracted from the 1994 US Census, where
each record has 15 attributes. Each record of Poker-
Hand dataset is an example of a hand consisting of
five playing cards drawn from a standard deck of 52.
Each card is described using two attributes (suit and
rank), for a total of 11 predictive attributes. There is
one Class attribute that describes the“Poker Hand”.
Cleveland Heart Disease dataset presents the heart
disease in the patient and contains 14 attributes.
Initially, we assess the persistent homology of our
datasets. Table 2 illustrates the count of homology
in various dimensions of these datasets, presented on
persistent diagrams. Notably, our analysis focuses on
a subset of both the Adult and Poker-Hand datasets.
Table 1: Persintent barcodes in different dimensions.
Datasets H
0
H
1
H
2
Adult 1000 27 0
Poker-Hand 800 863 564
Cleveland 303 199 34
To obtain the private persistence diagrams for each
dataset, we set the resolution of the L
1
-DTM as m =
0.05, the privacy budget ε = 1 and we consider 1-
dimension of topological feature in figures. Figure
4, Figure 5 and Figure 6 show the results of com-
paring the L
1
-DTM persistence diagram correspond-
ing to Adult, Poker-Hand and Cleveland datasets and
their differentially private diagrams respectively.
After getting the differential private persistence
diagram, we generate the synthetic data. We use
Monte carlo (MC) method to align the distributions.
The threshold for persistence of component H
0
are
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
850

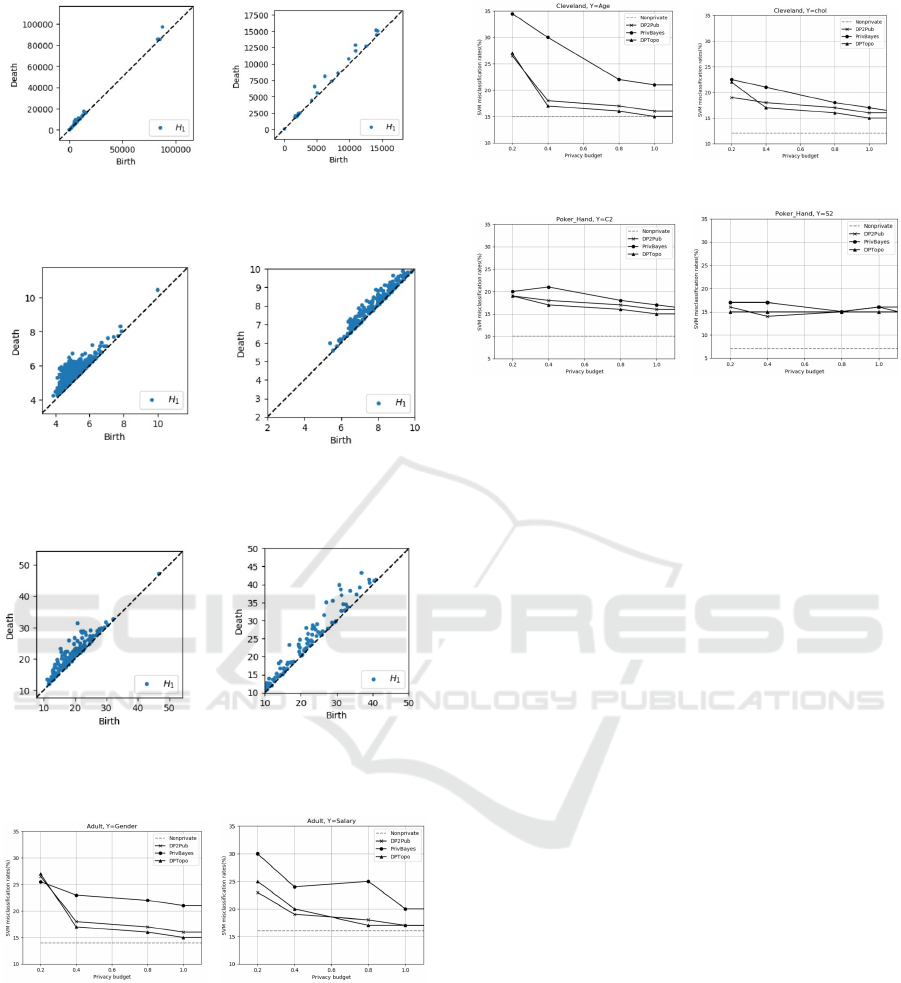
(a) Original PD. (b) Private PD.
Figure 4: Persistent diagrams(PDs) of Original and private
Adult dataset.
(a) Original PD. (b) Private PD.
Figure 5: Persistent diagrams(PDs) of Original and private
Poker-Hand dataset.
(a) Original PD. (b) Private PD.
Figure 6: Persistent diagrams(PDs) of Original and private
Cleveland dataset.
Figure 7: Multiple SVM classifiers on Adult dataset.
vary for each datasets. We set the threshold for Adult,
T
Adult
= 50000, for Poker-Hand T
PK
= 5, and for
Cleveland T
Celeland
= 25. Also, we use our differen-
tially private persistence diagram in the TopoAE al-
gorithm and generate the synthetic dataset.
For the second task, we evaluate the performance
of PrivBayes, DP2-Pub1, our work DPTopo, and
Non-Private (no DP is considered) for SVM classi-
fication. Figure 7 , Figure 8 and Figure 9 show the
Figure 8: Multiple SVM classifiers on Cleveland dataset.
Figure 9: Multiple SVM classifiers on Poker-Hand dataset.
misclassification rate of three datasets at different lev-
els of privacy protection or privacy budgets. The mis-
classification rate of the original dataset (denoted as
Non Private) stands for the best performance we can
achieve. It means that the lowest misclassification
rate is better result. We observe that our result out-
performs compared to others. Moreover, A lower pri-
vacy budget typically means stronger privacy protec-
tion but may lead to a higher misclassification rate.
Another notable observation is that the misclassifica-
tion rate of SVM decreases with the increase in the
privacy budget. This finding is in line with the theo-
retical expectation that as the privacy budget expands,
privacy protection weakens, leading to an increase in
the availability of data and a consequent reduction in
misclassification rates.
6 CONCLUSIONS
In this paper, we presented a novel approach to
generating private synthetic data leveraging insights
from persistent homology. Our methodology success-
fully replicated the essential topological features ob-
served in the high-dimensional original dataset. By
applying the weighted Vietoris-Rips complex algo-
rithm, we computed persistent homology and ex-
tracted meaningful diagrams. We produced differ-
ential private persistence diagrams by applying ex-
ponential mechanism. We used a negative bottle-
neck distance between private and non-private per-
sistence diagram as a utility function. we used L
1
-
DTM to achieve minimal sensitivity. For generating
synthetic data based on differentially private persis-
tence diagram, we kept similar birth and death events
for persistent points with the same distribution. We
Preserving Privacy in High-Dimensional Data Publishing
851

transformed the low-dimensional space with synthetic
points to high-dimensional space by topological au-
toencoders method. Our research highlights the ef-
ficacy of persistent homology-inspired synthesis in
producing differential private synthetic data with sig-
nificant topological structures. As the field of Topo-
logical Data Analysis (TDA) progresses, exploring al-
ternative metrics for computing the persistence dia-
gram, such as the persistence landscape, becomes cru-
cial. Adopting an alternative privacy framework like
zero-concentrated Differential Privacy has also shown
to yield lower errors in the privacy mechanism.
ACKNOWLEDGEMENTS
This work was supported in parts by funds from the
Natural Sciences and Engineering Research Coun-
cil of Canada (NSERC) Discovery and the Canada
First Research Excellence Fund (CFREF) Bridging
Divides programs.
REFERENCES
Alipourjeddi, N. and Miri, A. (2022). Publishing private
high-dimensional datasets: A topological approach.
In the 2022 International Wireless Communications
and Mobile Computing (IWCMC), pages 1142–1147.
IEEE.
Alipourjeddi, N. and Miri, A. (2023). Evaluating gener-
ative adversarial networks: A topological approach.
In the 2023 International Conference on Computing,
Networking and Communications (ICNC), pages 202–
206. IEEE.
Anai, H., Chazal, F., Glisse, M., Ike, Y., Inakoshi, H., Tinar-
rage, R., and Umeda, Y. (2020). Dtm-based filtrations.
In Topological Data Analysis: The Abel Symposium
2018, pages 33–66. Springer.
Asuncion, A. and Newman, D. (2007). UCI machine learn-
ing repository.
Avella-Medina, M. (2021). Privacy-preserving parametric
inference: a case for robust statistics. Journal of the
American Statistical Association, 116(534):969–983.
Binjubeir, M., Ahmed, A. A., Ismail, M. A. B., Sadiq, A. S.,
and Khan, M. K. (2019). Comprehensive survey on
big data privacy protection. IEEE Access, 8:20067–
20079.
Cao, W., Yan, Z., He, Z., and He, Z. (2020). A comprehen-
sive survey on geometric deep learning. IEEE Access,
8:35929–35949.
Chazal, F., De Silva, V., Glisse, M., and Oudot, S. (2016).
The structure and stability of persistence modules.
Springer.
Chazal, F., Fasy, B., Lecci, F., Michel, B., Rinaldo, A., Ri-
naldo, A., and Wasserman, L. (2017). Robust topo-
logical inference: Distance to a measure and kernel
distance. The Journal of Machine Learning Research,
18(1):5845–5884.
Chen, R., Xiao, Q., Zhang, Y., and Xu, J. (2015). Dif-
ferentially private high-dimensional data publication
via sampling-based inference. In the proceedings of
the 21th ACM SIGKDD international conference on
knowledge discovery and data mining, pages 129–
138. ACM.
Dwork, C., McSherry, F., Nissim, K., and Smith, A. (2016).
Calibrating noise to sensitivity in private data analysis.
Journal of Privacy and Confidentiality, 7(3):17–51.
Dwork, C., Roth, A., et al. (2014). The algorithmic founda-
tions of differential privacy. Foundations and Trends®
in Theoretical Computer Science, 9(3–4):211–407.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
learning. MIT press.
Jiang, H., Yu, H., Cheng, X., Pei, J., Pless, R., and Yu,
J. (2023). DP2-Pub: Differentially private high-
dimensional data publication with invariant post ran-
domization. IEEE Transactions on Knowledge and
Data Engineering.
Kang, T., Kim, S., Sohn, J., and Awan, J. (2023). Differen-
tially private topological data analysis. arXiv preprint
arXiv:2305.03609.
Mahanan, W., Chaovalitwongse, W. A., and Natwichai, J.
(2021). Data privacy preservation algorithm with k-
anonymity. World Wide Web, 24:1551–1561.
McSherry, F. and Talwar, K. (2007). Mechanism design
via differential privacy. In the proceeding of 48th An-
nual IEEE Symposium on Foundations of Computer
Science (FOCS’07), pages 94–103. IEEE.
Moor, M., Horn, M., Rieck, B., and Borgwardt, K. (2020).
Topological autoencoders. In the proceeding of In-
ternational conference on machine learning, pages
7045–7054. PMLR.
Owada, T. (2022). Convergence of persistence diagram in
the sparse regime. The Annals of Applied Probability,
32(6):4706–4736.
Zhang, J., Cormode, G., Procopiuc, C. M., Srivastava, D.,
and Xiao, X. (2017). PrivBayes: Private data re-
lease via bayesian networks. ACM Transactions on
Database Systems (TODS), 42(4):1–41.
ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy
852