Parking Scheduling Optimisation at Paris Charles de Gaulle

International Airport

Thibault Falque

1,2 a

, Christophe Lecoutre

2 b

, Bertrand Mazure

2 c

and Romain Wallon

2 d

Exakis Nelite, France

CRIL, Univ. Artois & CNRS, France

Keywords:

Constraint Programming, Optimization, Planning, Application.

Abstract:

Before the COVID-19 health crisis, the International Air Transport Association (IATA) forecasted that air

passengers would almost double by 2036, reaching 7.8 billion people. More than ever, air transport players

such as airline and airport companies, in a strongly competitive climate, need to beneﬁt from a carefully

optimized management of the airport resources in order to improve the quality of services and to control the

induced costs. For example, the allocation of parking spaces for landing aircrafts remains a central issue at

the airports, while optimizing an economic function determined by some business rules. In this paper, we

investigate the Airport Parking Assignment Problem (APAP) with a Constraint Programming (CP) approach.

We introduce a CP model, under the form of a Constraint Optimization Problem, and present some promising

preliminary experimental results from data coming from ADP (Aeroports de Paris).

1 INTRODUCTION

Before the COVID-19 health crisis, the International

Air Transport Association (IATA) forecasted that air

passengers would almost double by 2036, reaching

7.8 billion people. In such a context, optimizing the

management of the airport resources remains essen-

tial to control induced costs while keeping a good

quality of services. For many planning and schedul-

ing air transport problems, techniques and tools devel-

oped from mathematical and constraint programming

remain essential. Speciﬁcally, when airline compa-

nies have access to the resources delivered at the air-

port, the consumption of these resources (e.g., check-

in banks, aircraft parkings) must be carefully planned

while optimizing an objective function determined by

some business rules; see, for example, (Mangoubi and

Mathaisel, 1985) (Lim et al., 2005) (Diepen et al.,

2007). At airports, one of the signiﬁcant combina-

torial problems that need to be solved is the Stand

Allocation Problem. This problem is closely re-

lated to the Gate Allocation Problem, and both

have been extensively studied since the 1980s (Man-

https://orcid.org/0000-0003-2803-1530

https://orcid.org/0000-0002-2205-6545

https://orcid.org/0000-0002-3508-123X

https://orcid.org/0000-0001-7200-4279

goubi and Mathaisel, 1985) (Dincbas and Simonis,

1991) (Dorndorf et al., 2008) (Simonis, 2007). In

the following, we will refer to both problems with-

out distinction. The main objective of the Stand

Allocation Problem is to ﬁnd an optimal assign-

ment of aircraft serving different ﬂights to the avail-

able stands (gates) at the airport. Each ﬂight requires

a speciﬁc stand for various tasks, such as passenger

boarding, baggage handling, and refueling.

Deﬁnition 1 (Stand). A stand p ∈ S is an aircraft po-

sition. The ﬁrst type of stands is contact stands (or

hard stand) connected to a terminal by a door and a

gateway while the second type requires a bus to reach

the terminal (remote stands).

Deﬁnition 2 (Flight turnaround or rotation). A ﬂight

turnaround (or rotation) φ ∈ Φ comprises at least one

arrival or departure ﬂight or both. We note a

and d

the rotation’s start and end time, respectively (i.e., the

arrival time of the ﬂight at the airport and the depar-

ture time of the ﬂight from the airport).

Deﬁnition 3 (Stand operations). The stand operations

of a ﬂight turnaround can be divided into three parts:

(i) operations about the arrival ﬂight composed of the

unboarding of passengers and luggages, (ii) waiting

time, and (iii) operations of the departure ﬂight com-

posed of the boarding of passengers and luggages.

Note that during these operations, we also have air-

Falque, T., Lecoutre, C., Mazure, B. and Wallon, R.

Parking Scheduling Optimisation at Paris Charles de Gaulle International Airport.

DOI: 10.5220/0012437800003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 1119-1126

ISBN: 978-989-758-680-4; ISSN: 2184-433X

1119

craft ground handling operations: catering, refueling,

cabin services, etc.

Deﬁnition 4 (Operation). An operation, denoted by

, is deﬁned by its commencement at time a

and its

conclusion at time d

at the designated stand for op-

eration t

. Each operation is associated with an air-

craft of a speciﬁc model, such as an A320 or a B757.

The aircraft type for operation t

is identiﬁed by k

The aggregate of all ﬂight operations is denoted as

T . For a speciﬁed rotation, φ, its related set of activ-

ities, also known as the set of tasks, is represented as

. This set comprises n individual tasks, expressed

as {t

| i ∈ 1..n}. We also introduce sets T

which con-

sist of tuples of tasks, each tuple containing n tasks.

Depending on the waiting time and for operational

reasons, the aircraft may be moved to another stand,

creating several ﬂight operations. Figures 1 illustrate

the possible cases. This movement requires a towing

tractor and involves a cost for the operator. Figure 1a

presents the case where the arrival and the departure

ﬂight are the same operations. Figures 1b and 1c show

that the waiting time is enough to consider a decom-

position on two or three operations, respectively.

In the context of airport operations, stand assign-

ments are crucial and must be both aligned with the

airport’s services and convenient for passengers. Ac-

cording to (Dorndorf et al., 2007), these assignments

are governed by stringent rules, such as ensuring that

each stand is allocated to only one ﬂight at a time, ad-

hering to spatial limitations for adjacent stands, and

considering the speciﬁc preferences of certain air-

crafts for particular stand positions. The literature re-

veals a variety of objectives for addressing this prob-

lem. For example, studies have focused on mini-

mizing passenger walking distances through meth-

ods like binary integer programming (Bihr, 1990)

(Yan et al., 2002), or stochastic models (Yan and

Tang, 2007). Another objective is to minimize the

occurrence of off-gate events, as discussed in (Van-

derstraeten and Bergeron, 1988). Moreover, multi-

objective approaches have been explored:

• (Lim et al., 2005) applied integer programming to

optimize both the reduction of delay penalties and

the total walking distance.

• (Prem Kumar and Bierlaire, 2014) utilized binary

integer programming for threefold optimization:

maximizing the rest time between two turns at a

gate, minimizing the towing cost for aircraft with

extended turns, and reducing overall costs, includ-

ing penalties for not assigning preferred gates to

speciﬁc turns.

• Finally, (Dorndorf et al., 2012) employed a clique

partitioning formulation to address four objec-

tives: maximizing the total assignment prefer-

ence score, minimizing the number of unassigned

ﬂights and tows, and enhancing the robustness of

the schedule.

The rest of this paper is organized as follows. In

Section 2, we give some preliminaries regarding con-

straint programming and solving and the stand allo-

cation problem as deﬁned at Paris Airports. In Sec-

tion 3, we present some modeling for the stand allo-

cation problem. Before concluding, we present a few

promising experimental results in Section 4.

2 PRELIMINARIES

2.1 Constraint Optimization Problem

CP (Constraint Programming) (Apt, 2003) (Rossi

et al., 2006) (Lecoutre, 2009) is a powerful and rec-

ognized paradigm for modeling and solving every-

day problems (for example, the timeschedule prob-

lem can be modeled using constraint programming),

as well as combinatorial problems ranging from con-

ﬁguration and planning to bioinformatics. CP offers

generic methods for modeling and solving this type

of problems. It aims to reduce modeling complexity

by being as close to the natural language description

of the problem as possible. In the CP approach, users

deﬁne the problem by specifying decision variables

and constraints that deﬁne the relationships between

these variables. The objective is to ﬁnd an assignment

for all variables that satisﬁes all the given constraints.

This is known as a Constraint Satisfaction Problem

(CSP). The task is then solved by employing special-

ized solvers which use generic methods to efﬁciently

explore the search space and ﬁnd solutions that satisfy

all the constraints. A constraint network (CN) is com-

posed of a ﬁnite set of variables and a ﬁnite set of con-

straints. Each variable X takes its value in a ﬁnite set

called domain of X, denoted dom(X). Each constraint

deﬁnes a relation on a set of variables. A solution of

a CN is an assignment of values to all its variables

such that all the constraints of the CN are satisﬁed. A

CN is said to be consistent if it has at least one solu-

tion, and the corresponding decision problem, called

Constraint Satisfaction Problem (CSP), is to deter-

mine whether a CN is consistent. Deciding whether a

CSP is satisﬁable is an NP-complete problem (Mack-

worth, 1977). Other combinatorial tasks may interest:

enumerating or counting the set of solutions, calcu-

lating an optimal solution according to a given objec-

tive, etc. We conclude this section by deﬁning one

such task: the constraint optimization problem. A

Constraint Optimization Problem (COP) instance can

be interpreted as a CSP instance with an associated

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1120

Operation

Unboarding

Waiting

Boarding

(a) Short waiting time – do not split

the rotation.

Unboarding

Waiting

Boarding

Operation 1 Operation 2

(b) Medium waiting time – split in 2

operations.

Unboarding

Waiting

Boarding

Operation 1 Operation 2 Operation 3

erations.

Figure 1: Number of operations depending on waiting time.

cost function. This function gives a numerical value

to each solution of the instance, thereby quantifying

its quality. The objective is to ﬁnd the solution that

maximizes or minimizes this function. For example,

such a function may maximize (resp. minimize) the

sum or product of certain variables (possibly associ-

ated with coefﬁcients) of the problem.

2.2 Resolution Methods and Heuristics

Backtracking search is a conventional method for ad-

dressing COP instances, functioning as a complete

procedure. It conducts a depth-ﬁrst exploration of the

search tree, facilitated by a backtracking mechanism

alongside a sequence of decisions and propagations.

There are also incomplete search techniques which do

not ensure algorithmic completeness, but can still be

more effective at locating solutions. Backtrack search

for COP relies on CSP solving: the principle is to

add a special objective constraint obj < ∞ to the con-

straint network (although it is initially trivially satis-

ﬁed), and to update the limit of this constraint when-

ever a new solution is found. It means that any time

a solution S is found with cost B = obj(S), the objec-

tive constraint becomes obj < B. Hence, a sequence

of better and better solutions is generated (satisﬁabil-

ity is systematically proved with respect to the cur-

rent limit of the objective constraint) until no more

exists (unsatisﬁability is eventually proved with re-

spect to the limit imposed by the last found solution),

guaranteeing that the last found solution is optimal.

The order in which variables are chosen during the

depth-ﬁrst traversal of the search space is decided by

a variable ordering heuristic. Each heuristic asso-

ciates to a variable a score computed statically, dy-

namically or adaptatively. In this paper we focus

on two heuristics. dom/wdeg is a classical heuristics

(Boussemart et al., 2004) that aggregates by a divi-

sion operator the dom heuristics with a dynamic de-

gree of the variable wdeg. We also use a recent heuris-

tics called Frba/dom (Li et al., 2021) based on the

fail ﬁrst principle and exploiting two aspects of fail-

ure information collected during the search: the fail-

ure proportion after the propagations of assignments

of variables and the failure length heuristics consid-

ering the length of failures, which is the number of

ﬁxed variables composing a failure. Similar to vari-

able selection heuristics, a value ordering heuristic

is essential to determine the subsequent value to as-

sign. A straightforward heuristic approach involves

utilizing the initial value in the domain, symbolized

by First. This method is frequently adopted due

to its robustness. Recently, a heuristic strategy sug-

gesting the use of the value having the most signiﬁ-

cant effect on the objective function was introduced

in (Fages and Prud’Homme, 2017), labeled as Bivs.

For COPs, it is often advantageous to prioritize the

value observed in the most recent solution using so-

lution saving, as mentioned in works like (Vion and

Piechowiak, 2017) (Demirovic et al., 2018).

2.3 Stand Allocation Formulation

In this section, we consider the formulation of the

Gate Allocation Problem proposed by (Dorndorf

et al., 2008) and (Gu

epet et al., 2015) which we will

adapt for a Stand Allocation Problem (without

any loss of generality) and to the case of Paris Air-

ports. The previous section explains that the rotation

can be decomposed in several operations. At Paris

Airports, there can only be two movements for the

same aircraft, i.e., a maximum of 3 parking positions,

and the conditions for determining whether a rotation

must be decomposed depend on certain processing

times. Some physical constraints exist, as imposed

by the airport infrastructure.

Rule 1 (Capacity). The capacity

constraints prevent certain aircraft types

from being placed on some parking.

Rule 2 (No-Overlap). The No-Overlap

constraints reﬂect the physical impossibil-

ity of assigning two operations (two ﬂights) to the

same parking. An operation t

∈ T overlaps with

another operation t

∈ T if a

< d

∧ a

< d

. The

set of operations overlapping with t

is denoted by O

and so, contains all operations t

overlapping with i.

Rule 3 (Shading constraints). The shading

constraints block the positioning of an aircraft

Parking Scheduling Optimisation at Paris Charles de Gaulle International Airport

1121

on some nearby parking (regardless of the type of

aircrafts, e.g., two aircrafts cannot be simultaneously

assigned to adjacent stands due to space limitations).

Example 1 (Shading constraints). For example, Fig-

ure 2 shows that, if an aircraft is placed on parking

A14 then the parking A16 is “shaded” and vice-versa

(it is symmetrical).

Figure 2: Example for the shading constraint.

Rule 4 (Reduction). The reduction

constraints are similar to the shading

constraints except that they consider aircraft

types. These constraints can be deﬁned by 4-tuples

(k, p,k

′

,∆) with ∆ ⊂ S being a set of parkings. For

every parking p

′

in ∆, a plane of type k

′

is allowed on

′

if a plane of type k is placed on p. We note D the

set of all such reductions (all 4-tuples).

Example 2 (Reduction constraint). As an illustration,

considering Figure 3, shading will only be effective if

a speciﬁc aircraft type has been placed on A10, then

the reduction will still allow a subset of aircraft types

to be placed on A8 and A12.

Figure 3: Example for the reduction constraint.

Rule 5 (Order). The order constraints im-

pose for two parkings p

that the aircraft put on

must arrive and leave before that put on p

, if the

two aircrafts have an overlapping time.

Example 3 (Order constraint). Terminal 1 of CDG

(Charles de Gaulle) has a speciﬁc infrastructure that

imposes an order constraint. Let us take a

look at Figure 4: if a plane is placed on Y07 and an-

other plane is placed on Y 06, we need to make sure

that the plane on Y07 leaves before the plane on Y 06,

because planes arrive on the outside (route marked by

A) and leave on the inside (route A3). Note that the

direction is reversed if we take stands Z02 and Z01.

We note OR the set of pair of parking p

while p

is before p

Figure 4: Example of a special trafﬁc situation linked to the

CDG1 infrastructure.

Frequently, some stands are unavailable for sev-

eral hours to several days (for example, for mainte-

nance reasons).

Rule 6 (Unavailable constraints). The

unavailable constraints ensure that

certain stands are not available for a period of time

(which may be periodic). Said differently, we must

remove from the domain the stand for each operation

that overlaps with the period of exclusion. We note

u = (p,s,e) a triplet where p is the stand to exclude, s

and e is the start and end time of the excluded period.

Another type of unavailability, speciﬁc to certain

rotations, consists in declaring a list of prohibited

stands for a given rotation.

Rule 7 (Exclusion). The exclusion cons-

traints ensures that certain stands are excluded

from certain rotations under some conditions.

The components for the stand allocation problem

formulation at Paris Airports are given below:

• T the set of operations. The previous section ex-

plains that an operation t

∈ T is deﬁned by a start

time a

and an end time d

. For each operation

, we also have the set of operations that overlap

with t

: O

• S the set of the stands.

• S

⊂ S the set of compatible stands (stands with a

capacity compatible with t

) for operation t

• OR the set of pair of parkings for order rules.

• U the set of unavailable rules (i.e., the set of all

triplet (p,s, e)).

• E

the set of excluded stands for an operation t

• Q ⊆ S

the set of shadow restrictions. If

) ∈ Q then two operations that overlap can-

not be placed at the same time on p

and p

• D the set of reductions. For a quadruplet

(k, p,k

′

,∆) ∈ D and an operation t

∈ T with an

aircraft type k, if the operation t

is assigned to the

parking p, then only operations with an aircraft

type k

′

are allowed to parkings of the set ∆.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1122

• M P = (m

i,p

)

T ×S

the afﬁnity matrix, i.e., m

i,p

the airline satisfaction realized if operation t

∈ T

is assigned to stand p.

An assignment I is a mapping between opera-

tions T and stands S . The quality Obj(I) of an as-

signment I is deﬁned by Obj(I) = C(I ) where C is

the total operation-stand afﬁnity. Our objective is

to ﬁnd an assignment maximizing Obj(I) while re-

specting operation-stand compatibilities, shadowing,

reduction restrictions and overlapping constraints.

3 MODELING

For modeling COP, we have chosen to use the re-

cently developed Python library PyCSP

(Lecoutre

and Szczepanski, 2020) that permits to generate spe-

ciﬁc instances (after providing ad hoc data) in XCSP3

(Boussemart et al., 2020), which is recognized by

CP solvers such as ACE (AbsCon Essence) (Lecoutre,

2023) and Choco (Prud’homme et al., 2016). In the

following, we show how to model the stand alloca-

tion problem in the context of Paris Airports.

First, we need to introduce the variables of our

model. Actually, in addition to a stand-alone vari-

able used to count the number of rotations that are not

splitted, we need two arrays of variables to represent

assigned stands and their associated rewards:

• x is a matrix of |T | variables having the set of val-

ues {0, ... ,|S| − 1} as domain; x

represents the

index (code) of the stand assigned to the task t

• r is a matrix of |T | variables having the set of val-

ues {0, ... ,100} as domain; r

represents the sat-

isfaction of the company for task t

We now introduce constraints for this problem.

An illustration is now given to facilitate the under-

standing of the various constraints of the model.

Example 4. Let us consider an example with a set

of 5 rotations {φ

,. ..,φ

}, and a set of 4 stands

,. ..,p

}. where p

and p

are assumed to be re-

mote stands; so, we have S

= {p

}. Information

concerning rotations is given in Table 1.

In the next sections we introduce different model-

ing for the problem. Given the nature of the prob-

lem (and data), it is natural to post so-called ex-

tensional constraints, which explicitly enumerate ei-

ther the allowed tuples (positive table) or the disal-

lowed tuples (negative table) for a sequence of vari-

ables (representing the scope of a constraint). Over

the last decade, efﬁcient algorithms have been devel-

oped to handle such table constraints (Lecoutre, 2011)

(Lecoutre et al., 2015) (Demeulenaere et al., 2016)

(Verhaeghe et al., 2017).

Classical Variant

Model 1 (Classical variant).

∈ S

remote

,∀(t

) ∈ T

)

⟨x

⟩ ∈ S

)

⟨x

⟩ /∈ {(p

),∀p

∈ Q }

∀t

∈ T ,∀t

∈ O

)

⟨x

⟩ /∈ {(p

) | p

∈ δ},∀t

∈ T ,

∀⟨k, p

′

,δ⟩ ∈ D | k = kind(i),

∀ j ∈ O

| k

′

̸= kind( j)

)

⟨x

⟩ ∈ {(p

) | p

∈ S

},∀t

∈ T (C

)

⟨x

⟩ /∈ OR ,∀t

∈ T ,∀ j ∈ O

)

̸= p, ∀t

∈ T ,

∀(p,s, e) ∈ U | overlap(t

,s, e)

)

/∈ s,∀i ∈ T , ∀s ∈ E

)

Note that Constraint C

forces the middle parking

to be remote.

Example 5. For our example: T

= {φ

}, T

{φ

,φ

}, T

= {φ

,φ

}. The set of operations

T is composed of each tasks from each rotation:

,. ..,t

} where t

corresponds to the only task

of φ

while t

corresponds to the third tasks of φ

So we must post the constraints: x

∈ S

remote

and

∈ S

remote

To enforce capacity rules, we post unary con-

straints (see Constraint C

Example 6. Table 2 provides each parking

capacity for our example. Based on this ta-

ble, we must post the following unary con-

straints: For φ

: x

∈ {p

}. For φ

∈ {p

},x

∈ {p

}. For

: x

∈ {p

},x

∈ {p

For φ

: x

∈ {p

},x

∈ {p

},x

∈

}. For φ

: x

∈ {p

},x

∈

},x

∈ {p

Let us recall that when a parking p

is shaded by

a parking p

then these two values cannot be assigned

together to any pair of overlapping tasks. This leads

to binary negative table constraints. Although not ex-

plicitly shown below, assigning the same value twice

for any pair of overlapping operations is also forbid-

den (see Constraint C

). Constraint C

represents the

reduction constraint and is deﬁned with binary

negative tables.

Parking Scheduling Optimisation at Paris Charles de Gaulle International Airport

1123

Table 1: Data about rotations.

Rot. airline ntasks kind a

1 k

8h 10h

2 k

8h 12h

2 k

12h 16h

3 k

9h 15h

3 k

12h 18h

Example 7. For our example, suppose

that a reduction constraint exists be-

tween the stands p

and p

, given by D =

{(k

,{p

}),(k

,{p

})}. We also have

= {(t

),(t

)} and S

= {p

}. Task

1 from φ

overlaps Task 1 of φ

. Recall that

kind(φ

) = k

. So, for the reduction imposed by φ

we add the constraint that forbid the pair of values

) for the pair of variables ⟨x

⟩. In other

words, it is forbidden to use p

with the rotation φ

because φ

does not have the kind allowed by p

after placing φ

on p

(its capacity is reduced), i.e.,

⟨x

⟩ /∈ {(p

)}. Although φ

overlaps with φ

there are no restrictions to consider with φ

as φ

has

a capacity of type k

(see Table 1) which is allowed

in relation to the reduction.

According to the airlines preferences from afﬁn-

ity matrix M P , we can post binary table constraints

to “compute” rewards when ﬁltering such constraints

(see Constraint C

Table 3: Afﬁnity matrix.

Airline / Parking p

75 75 100 50 50

60 0 100 50 50

0 100 80 50 50

Example 8. For our example, let us assume that re-

wards are given by the matrix in Table 3. From the

data in this table, we post the following constraint for

the ﬁrst rotation (the same principle is adopted for the

other rotations):

⟨x

⟩ ∈

{(p

,75),(p

,100),(p

,50),(p

,50)},

Considering the reward variables we can express

the objective function as follows:

maximize

∑

∈T

· r

This function aims to optimize the cumulative

weighted rewards across all tasks within each rota-

tion. In this context, w

is the weight attributed to the

task t

. This weight quantiﬁes the importance or pri-

ority of each task. The term r

represents the decision

Table 2: Capacity.

Pkg Capacity

}

variables from the matrix r, speciﬁcally the weight

allocated to the resources assigned for task t

. Thus,

the objective function is to maximize the total value

by strategically allocating resources to tasks based on

their importance and the associated rewards.

AllDifferent Variant

In this variant, we propose to modify the shading con-

straint by posting AllDifferent constraints in ad-

dition to the table constraints already proposed, as it

is often done in the state-of-the-art (Simonis, 2007)

(Dincbas and Simonis, 1991). In these approaches, an

AllDifferent constraint is added between all over-

lapping pairs of tasks, but this cannot work here, as it

would be less restrictive than the shadow constraint.

Indeed, an AllDifferent constraint would force two

operations t

and t

to be assigned different parkings.

However, by assigning p

and p

as parkings for these

tasks, the constraint would be respected but would vi-

olate the shadow constraint if p

shaded p

Figure 5: Interval graph based on data from Table 1.

Nevertheless, it is possible to use AllDifferent

constraints with an interval graph. Each vertex of the

graph represents a task (the task’s time interval) and is

connected by an edge to another vertex if and only if

there is an overlap between the two intervals. Figure 5

represents an interval graph G for our example, each

vertex represents an interval and there is an edge be-

tween intervals when they intersect. From this graph,

we need to post an AllDifferent constraint for each

maximum clique in the graph.

Deﬁnition 5 (Maximum clique). A maximum clique

of G has the greatest number of vertices, which is

maximal for the cardinal. We note C

the set of all

maximum cliques.

For the set of maximum cliques, we can post the

constraints: allDifferent({x

,∀t

∈ c}),∀c ∈ C

For our example and based on our interval graph

(Figure 5), the maximum cliques are: {φ

,φ

} and

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1124

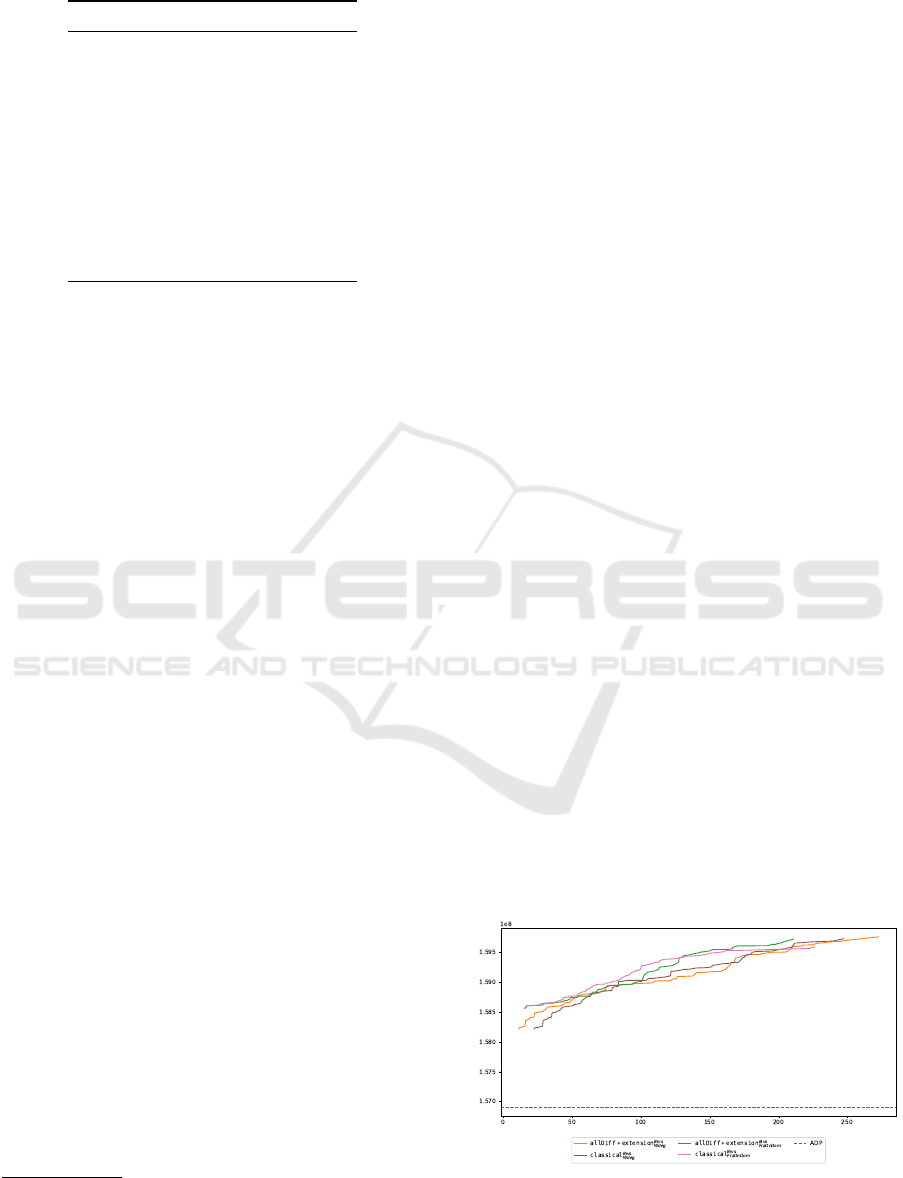
Table 4: General information about the parking planning.

Airport Terminals Week #Rot

CDG T2B T2D WE29 755

CDG T1 T3 WE29 888

CDG T2B T2D WE30 763

CDG T1 T3 WE30 903

CDG T1 T3 WE34 941

CDG T1 T3 WE35 960

CDG T2B T2D WE36 785

CDG T1 T3 WE36 884

CDG T2B T2D WE37 757

CDG T1 T3 WE37 868

CDG T2B T2D WE38 765

CDG T1 WE38 643

{φ

,φ

4 EXPERIMENTAL RESULTS

This section presents some experimental results of

our modeling presented in the previous sections. In

the context of our experiments, we used instances in

XCSP format (Boussemart et al., 2020) generated with

PyCSP

(Lecoutre and Szczepanski, 2020). Table 4

presents some factual information about the differ-

ent plannings used for these experiments. The ﬁrst

two columns indicate the area of the planning (i.e.,

Airport and Terminals concerning the planning).

The third column gives the date of the planning. Fi-

nally, the last column displays the number of rota-

tions. For each planning, we have considered the two

variants of the problem: classical which contains

the constraints given in Modeling 1 and alldiff in

which we add the allDifferent constraint based on

the maximum cliques (see Section 3).

We use different conﬁgurations of the solver ACE

as presented below and the current solution used by

ADP for planning ressources. We call this approach

ADP. ACE-based solvers are named as follows:

(

valh

varh



f ∈ {classical,alldiff,notbreak}

varh ∈ {Frba/dom,Wdeg}

valh ∈ {first,Bivs}

)

All solvers have been run on a cluster of comput-

ers equipped with 128 GB of RAM and two quadcore

Intel XEON E5-2637 (3.5 GHz). The time was lim-

ited to 5 minutes and the memory to 64 GB of RAM.

Figure 6 displays the evolution of solver-

determined bounds for some instances, chosen due to

space constraints

. This ﬁgure uses the x-axis to rep-

resent the elapsed time and the y-axis to indicate the

All the experiments data will be made publicly avail-

able if the paper is accepted

value of the bound. The blue dashed line marks the

bounds set by the previous ADP system, which had

an average response time of 7.5 seconds. This system

adopted a strategy of accepting the ﬁrst solution and

then applying localized optimization. On all tested in-

stances, our approach consistently outperformed the

ADP system in terms of achieving superior bounds.

It is important to note, however, that the attainment

of optimal bounds might occur later in our process.

The ﬁgure also shows that the AllDifferent-based

method, labeled as allDiff+extension, closely par-

allels the traditional approach. It should be mentioned

that the time taken to convert each instance into XML

format is not reﬂected in the timelines shown in this

ﬁgure. The exclusion of this compilation time is due

to its inclusion of data processing durations, which are

expected to be absent in the ﬁnal production version.

In the production environment, this processing will be

conducted prior to utilizing the PyCSP

compiler and

will employ a faster programming language.

5 CONCLUSION AND

PERSPECTIVES

In this paper, various models – mainly exploiting ta-

ble constraints – addressing the stand allocation prob-

lem have been introduced. This problem is a funda-

mental aspect of airport operations that has implica-

tions for both efﬁciency and airline satisfaction. We

put forward two distinct formulations of the problem:

the classical variant which mainly uses extensional

constraints and the allDifferent variant which adds

allDifferent constraints for each maximum clique

of the interval graph formed from overlapping tasks.

Subsequently, we conducted an analysis of different

conﬁgurations for the ACE solver and compared the

results with the current ADP method. The value se-

lection heuristic Bivs shows very good performance

and always obtains a better bound than that found by

Figure 6: Evolution of the bound for instance of CDG T1

T3 and planning for week 29.

Parking Scheduling Optimisation at Paris Charles de Gaulle International Airport

1125

ADP. An important aspect of our current approach is

its foundation on open-source tools, which presents

a signiﬁcant advantage over the former solution that

was commercial. This transition not only offers po-

tential cost savings but also enhances adaptability and

accessibility of the tools, as desired by the direction of

Paris Airports. In the future, we plan to make further

experiments and to study the interest of using multi-

objective constraint solvers like Choco.

REFERENCES

Apt, K. R. (2003). Principles of Constraint Programming.

Cambridge University Press.

Bihr, R. A. (1990). A conceptual solution to the aircraft

gate assignment problem using 0, 1 linear program-

ming. Computers & Industrial Engineering, 19(1-

4):280–284.

Boussemart, F., Hemery, F., Lecoutre, C., and Sais, L.

(2004). Boosting systematic search by weighting con-

straints. pages 146–150.

Boussemart, F., Lecoutre, C., Audemard, G., and Piette,

C. (2020). XCSP3-core: A format for representing

constraint Satisfaction/Optimization problems. CoRR,

abs/2009.00514.

Demeulenaere, J., Hartert, R., Lecoutre, C., Perez, G., Per-

ron, L., R

egin, J.-C., and Schaus, P. (2016). Compact-

Table: Efﬁciently Filtering Table Constraints with Re-

versible Sparse Bit-Sets. In Proceedings of CP’16,

pages 207–223.

Demirovic, E., Chu, G., and Stuckey, P. (2018). Solution-

based phase saving for CP: A value-selection heuristic

to simulate local search behavior in complete solvers.

In Proceedings of CP’18, pages 99–108.

Diepen, G., Akker, J., Hoogeveen, J., and Smeltink, J.

(2007). Using column generation for gate planning

at Amsterdam Airport Schiphol.

Dincbas, M. and Simonis, H. (1991). APACHE - A con-

straint based, automated stand allocation system. Au-

tomated Stand Allocation System Proc. Of Advanced

Software Technology in Air Transport (ASTAIR’91)

Royal Aeronautical Society, pages 267–282.

Dorndorf, U., Drexl, A., Nikulin, Y., and Pesch, E. (2007).

Flight gate scheduling: State-of-the-art and recent de-

velopments. Omega, 35(3):326–334.

Dorndorf, U., Jaehn, F., and Pesch, E. (2008). Modelling

Robust Flight-Gate Scheduling as a Clique Partition-

ing Problem. Transportation Science, 42(3):292–301.

Dorndorf, U., Jaehn, F., and Pesch, E. (2012). Flight gate

scheduling with respect to a reference schedule. An-

nals of Operations Research, 194(1):177–187.

Fages, J.-G. and Prud’Homme, C. (2017). Making the First

Solution Good! In ICTAI 2017, pages 1073–1077,

Boston, MA. IEEE.

epet, J., Acuna-Agost, R., Briant, O., and Gayon, J.

(2015). Exact and heuristic approaches to the airport

stand allocation problem. European Journal of Oper-

ational Research, 246(2):597–608.

Lecoutre, C. (2009). Constraint Networks: Techniques and

Algorithms. ISTE/Wiley.

Lecoutre, C. (2011). STR2: Optimized Simple Tabular Re-

duction for Table Constraints. Constraints : an inter-

national journal, 16(4):341–371.

Lecoutre, C. (2023). ACE, a generic constraint solver.

CoRR, abs/2302.05405.

Lecoutre, C., Likitvivatanavong, C., and Yap, R. (2015).

STR3: A path-optimal ﬁltering algorithm for table

constraints. Artiﬁcial Intelligence, 220:1–27.

Lecoutre, C. and Szczepanski, N. (2020). PyCSP3: Mod-

eling combinatorial constrained problems in Python.

CoRR, abs/2009.00326.

Li, H., Yin, M., and Li, Z. (2021). Failure Based Vari-

able Ordering Heuristics for Solving CSPs. In Michel,

L. D., editor, CP 21, volume 210, pages 9:1–9:10.

Lim, A., Rodrigues, B., and Zhu, Y. (2005). Airport Gate

Scheduling with Time Windows. Artiﬁcial intelli-

gence review, 24(1):5–31.

Mackworth, A. K. (1977). Consistency in networks of rela-

tions. Artiﬁcial Intelligence, 8(1):99–118.

Mangoubi, R. S. and Mathaisel, D. F. X. (1985). Optimizing

Gate Assignments at Airport Terminals. Transporta-

tion Science, 19(2):173–188.

Prem Kumar, V. and Bierlaire, M. (2014). Multi-objective

airport gate assignment problem in planning and

operations. Journal of Advanced Transportation,

48(7):902–926.

Prud’homme, C., Fages, J.-G., and Lorca, X. (2016).

Choco-solver, TASC, INRIA Rennes, LINA, Cosling

S.A.

Rossi, F., van Beek, P., and Walsh, T., editors (2006). Hand-

book of Constraint Programming. Elsevier.

Simonis, H. (2007). Models for global constraint ap-

plications. Constraints : an international journal,

12(1):63–92.

Vanderstraeten, G. and Bergeron, M. (1988). Automatic as-

signment of aircraft to gates at a terminal. Computers

& Industrial Engineering, 14(1):15–25.

Verhaeghe, H., Lecoutre, C., and Schaus, P. (2017). Extend-

ing Compact-Table to Negative and Short Tables. In

Proceedings of AAAI’17, pages 3951–3957.

Vion, J. and Piechowiak, S. (2017). Une simple heuristique

pour rapprocher DFS et LNS pour les COP. In Pro-

ceedings of JFPC’17, pages 39–45.

Yan, S., Shieh, C.-Y., and Chen, M. (2002). A simu-

lation framework for evaluating airport gate assign-

ments. Transportation Research Part A: Policy and

Practice, 36(10):885–898.

Yan, S. and Tang, C.-H. (2007). A heuristic approach

for airport gate assignments for stochastic ﬂight de-

lays. European Journal of Operational Research,

180(2):547–567.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1126