Multidimensional Compressed Sensing for Spectral Light Field Imaging

Wen Cao

, Ehsan Miandji

and Jonas Unger

Media and Information Technology, Department of Science and Technology, Link

oping University,

SE-601 74 Norrk

oping, Sweden

Keywords:

Spectral Light Field, Compressive Sensing.

Abstract:

This paper considers a compressive multi-spectral light ﬁeld camera model that utilizes a one-hot spectral-

coded mask and a microlens array to capture spatial, angular, and spectral information using a single

monochrome sensor. We propose a model that employs compressed sensing techniques to reconstruct the

complete multi-spectral light ﬁeld from undersampled measurements. Unlike previous work where a light

ﬁeld is vectorized to a 1D signal, our method employs a 5D basis and a novel 5D measurement model, hence,

matching the intrinsic dimensionality of multispectral light ﬁelds. We mathematically and empirically show

the equivalence of 5D and 1D sensing models, and most importantly that the 5D framework achieves or-

ders of magnitude faster reconstruction while requiring a small fraction of the memory. Moreover, our new

multidimensional sensing model opens new research directions for designing efﬁcient visual data acquisition

algorithms and hardware.

1 INTRODUCTION

Computational cameras for light ﬁeld capture, (Levoy

and Hanrahan, 1996; Gortler et al., 1996), post cap-

ture editing and scene analysis have become increas-

ingly popular and found applications ranging from

photography and computer vision to capture of neu-

ral radiance ﬁelds. Light ﬁeld imaging aims to ob-

tain multidimensional optical information including

spatial, angular, spectral, and temporal sampling of

the scene. Inherent to most light ﬁeld capture sys-

tems is the trade-off between the complexity and cost

of the acquisition system and the output image qual-

ity in terms of spatial and angular resolution. On

one hand camera arrays, (Wilburn et al., 2005), offer

high resolution but comes with high cost and complex

bulky mechanical setups, while systems based on mi-

crolens, or lenslet, arrays placed in the optical path,

(Ng et al., 2005), sacriﬁces resolution for the beneﬁt

of light weight systems and lower costs.

A key goal in the development of next generation

light ﬁeld imaging systems is to enable high quality

multispectral measurements of complex scenes based

on a minimum amount of input measurements. Fo-

cusing on cameras with lenslet arrays, such optical

https://orcid.org/0000-0002-2507-7288

https://orcid.org/0000-0002-4435-6784

https://orcid.org/0000-0002-7765-1747

systems capture 2D projections of the full 5D (spa-

tial, angular, spectral) light ﬁeld image data. Recon-

struction of the high dimensional 5D data from the 2D

measurements is challenging, due to the dimension-

ality gap and high compression ratio resulting from

undersampling of, e.g., the spectral domain. Com-

pressed sensing (CS) has emerged as a popular ap-

proach for light ﬁeld reconstruction, however, cur-

rent systems are either not designed for multispec-

tral reconstruction, (Marwah et al., 2013; Miandji

et al., 2019), and/or fundamentally rely on 1D CS

reconstruction, (Marquez et al., 2020), disregarding

the original signal dimensionality. Since a light ﬁeld

is fundamentally a 5D object, a vectorized 1D rep-

resentation of such data will prohibit the exploita-

tion of data coherence along each dimension, which

has been observed in a number of previous works

on sparse representation of multidimensional data

(Miandji et al., 2019). Another problem with 1D re-

construction is that it inherently leads to prohibitively

large storage costs for the dictionary and sensing ma-

trices as well as long reconstruction times.

In this paper, we formulate the light ﬁeld capture

and reconstruction as a multidimensional, nD, com-

pressed sensing problem. As a ﬁrst step, see Fig. 1,

we learn a 5D dictionary ensemble (Miandji et al.,

2019) from the spatial (2D), angular (2D), and spec-

tral (1D) domains of a light ﬁeld training set. Using a

Cao, W., Miandji, E. and Unger, J.

Multidimensional Compressed Sensing for Spectral Light Field Imaging.

DOI: 10.5220/0012431300003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 4: VISAPP, pages

349-356

ISBN: 978-989-758-679-8; ISSN: 2184-4321

349

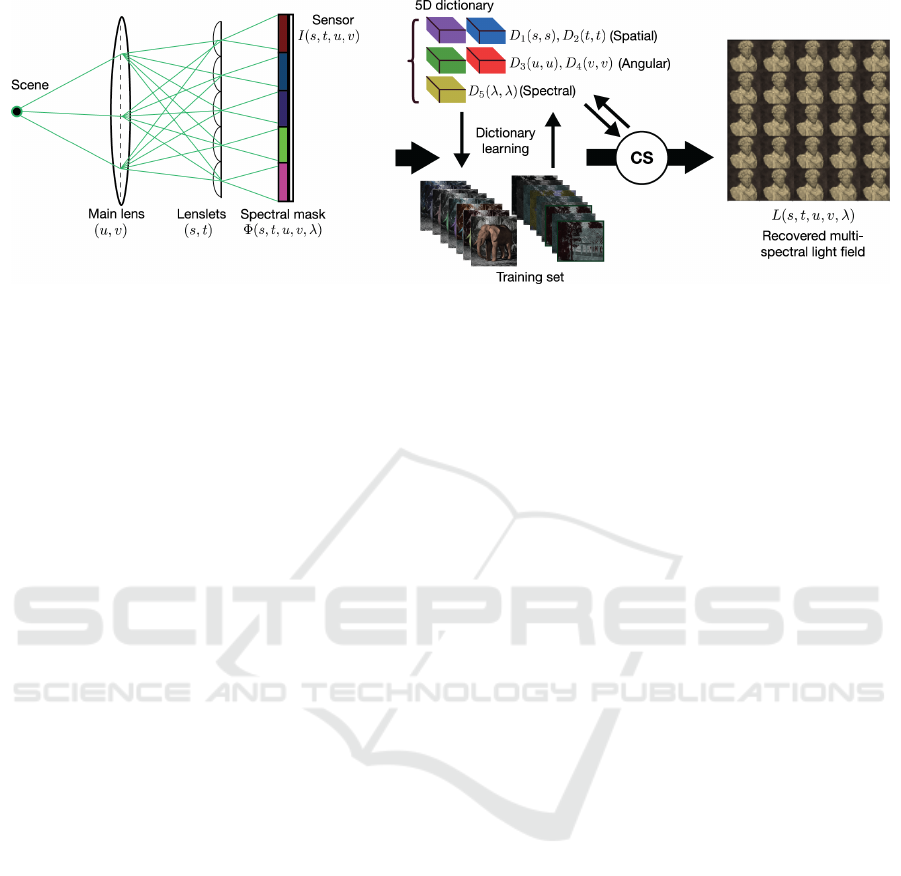
Figure 1: Illustrates the proposed compressed sensing framework for multi-spectral light ﬁeld capture and reconstruction.

Compressed light ﬁelds are captured using a lenslet array placed in the optical path and a one-hot spectral CFA mask placed

on the sensor. Our proposed nD compressed sensing formulation improves the reconstruction time by orders of magnitude as

compared to the commonly used 1D compressed sensing techniques without any quality degradation.

novel 5D sensing model based on a one-hot sampling

pattern (implemented as a multispectral color ﬁlter ar-

ray (CFA) on the sensor), we obtain measurements of

a light ﬁeld in the test set. The 5D sensing model

is composed of 5 measurement matrices, each corre-

sponding to one dimension of the light ﬁeld. By ran-

domizing the one-hot measurement for each measure-

ment matrix, we promote the incoherence of the mea-

surement matrices with respect to the 5D dictionary.

The one-hot spectral sampling mask allows us to de-

sign a spectral light ﬁeld camera with a monochrome

sensor. Another advantage of the one-hot mask is

cost-effectiveness, since it has a similar manufac-

turing complexity compared to a Color Filter Array

(CFA), which is commonly used in consumer-level

digital cameras. Finally, we extend the Smoothed-ℓ

(SL0) method for 2D signals (Ghaffari et al., 2009) to

5D signals, enabling fast reconstructions of the light

ﬁeld from the measurements without the need for ma-

nipulating the dimensionality of the light ﬁeld.

The main contributions are:

• A novel nD formulation for a single sensor

compressive spectral light ﬁeld camera design,

where a one-hot sensing model together with a

learned multidimensional sparse representation is

utilized.

• An nD recovery method that is more than two or-

ders of magnitude faster than the widely used 1D

formulation and recovery.

• We show, both theoretically and experimentally,

that the nD formulation is far superior to the 1D

variant both in terms of memory and speed.

Our sensing model derivation shows that the nD

sensing is mathematically equivalent to 1D sensing

with the same number of samples. Experimental re-

sults conﬁrm such equivalence in terms of reconstruc-

tion quality. Most importantly, the evaluations show

that the proposed novel formulation produces high

quality results orders of magnitude faster compared to

methods based on 1D compressed sensing. Our multi-

dimensional sensing model opens up ﬂexible sensing

mask designs where each dimension can be treated

individually.

2 RELATED WORK

Common approaches for light ﬁeld imaging include

the use of coded apertures (Liang et al., 2008; Baba-

can et al., 2009) and lenslet arrays (Ng et al., 2005),

and more recently combinations of the two (Marquez

et al., 2020). Combining compressive sensing with

spectrometers, coded aperture snapshot spectral im-

agers are also known as compressive spectral imagers

(CASSI). In general, a CASSI system consists of a

coded mask, prisms, and an imaging sensor. Exam-

ples of capture systems are for example described

by (Hua et al., 2022), and (Xiong et al., 2017). Based

on the detector measurements and the coded mask in-

formation the ﬁnal spectral images or light ﬁelds are

then typically reconstructed using compressed sens-

ing methods (Arce et al., 2014; Marquez et al., 2020;

Yuan et al., 2021). Recently, deep learning based

methods have shown promising results for the appli-

cation of multispectral image reconstruction, for an

overview, see the survey by (Huang et al., 2022). Re-

lated to our approach (Schambach et al., 2021) pro-

posed a multi-task deep learning method to estimate

the center view and depth from the coded measure-

ments. The approach yields good results, but is not di-

rectly comparable to our approach since the aim here

is to recover the full 5D light ﬁeld and not a depth

map.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

350

Compared to previous work, our nD formulation

presents several beneﬁts such as ﬂexible design of the

5D light ﬁeld sensing masks as well as orders of mag-

nitude speed up without any quality degradation as

compared to the 1D sensing used in previous work.

One of the key insights, and contributions, enabling

the nD CS framework is the sensing mask formulation

illustrated in Fig. 2, where the Kronecker product of a

set of small design matrices lead to the one-hot CFA

mask used for nD compressed sampling. This as well

as our general formulation are described in detail in

the next section.

3 MULTIDIMENSIONAL

COMPRESSIVE LIGHT FIELDS

Our capture system, see Fig. 1, records a set of an-

gular views as produced by the lenslet array, where a

one-hot spectral coded mask at the resolution of the

lenslet is placed on the sensor. In the design, we as-

sume that there are n different types of ﬁlters with dif-

ferent spectral characteristics available, and that the

goal is to formulate a one-hot coded mask such that

each measurement, or pixel on the sensor, integrates

the incoming light rays modulated by one of the n dif-

ferent ﬁlter types. This is motivated by the fact that

we want to enable capture of a well deﬁned set of

spectral bands, typically deﬁned by the imaging ap-

plication.

3.1 The Measurement Model

Our camera design measures the spatial and angular

information, while the spectral information, due to the

one-hot mask, is compressed to a single value. Let

L(s,t,u,v,λ) represent the light ﬁeld function follow-

ing the commonly used two-plane parameterization,

where (s,t) and (u, v) denotes the spatial and angu-

lar dimensions, and λ the spectral dimension. More-

over, let I(s,t,u,v) be the compressed measurements

recorded by the sensor. We formulate the multispec-

tral compressive imaging pipeline as follows

I(s,t,µ,ν) =

Φ(s,t, u,v,λ)L(s,t,u,v,λ)dλ, (1)

where Φ(s,t,u, v,λ) is the 5D sensing operator, as

shown in Fig. 2. Speciﬁcally, due to our design of

the one-hot binary mask, we have

∑

λ=1

Φ[s,t, u,v,λ] = 1, (2)

making sure that only one spectral channel is sampled

for every pixel on the monochrome sensor.

Figure 2: Illustration of Kronecker-based coded attenuation

masks.

According to (1), our goal is to recover the full

multispectral light ﬁeld L from its measurements I

and with the knowledge of the measurement operator

Φ constructed from the one-hot mask. Indeed, since

(1) is a linear measurement model, we can rewrite it

as I = ΦL, where L is the light ﬁeld arranged in a vec-

tor and Φ is the measurement matrix. In this case,

recovering L amounts to solving an underdetermined

system of linear equations, which is a topic addressed

by compressed sensing (Candes and Wakin, 2008).

3.2 Compressed Sensing

The underdetermined system of linear equations I =

ΦL can be solved by regularizing the problem based

on sparsity of the light ﬁeld in a suitable basis or dic-

tionary D as follows

argmin

∥α∥

s.t. ||I − ΦDα||

≤ ε, (3)

where ε is a user-deﬁned threshold for the data ﬁdelity

and ∥.∥

denotes the ℓ

pseudo-norm. The dictionary

D can be obtained from analytical basis function, e.g.,

Discrete Cosine Transform (DCT), or by training-

based algorithms, e.g., K-SVD (Aharon et al., 2006).

Equation (3) can be solved by several algorithms and

in this paper we use Smoothed-ℓ

(SL0) (Mohimani

et al., 2010). We note that (3) solves a 1D compressed

sensing problem, and therefore utilizes a 1D dictio-

nary. As mentioned, our goal is to solve (3) using

multidimensional dictionaries and a multidimensional

sensing model.

3.3 Learning-Based Multidimensional

Dictionary

To this end, we utilize the Aggregated Multidimen-

sional Dictionary Ensemble (AMDE) (Miandji et al.,

2019) to train an ensemble of 5D orthogonal dictio-

naries to efﬁciently represent spatial, angular, and

spectral dimensions of a light ﬁeld. In particu-

lar, we have D

∈ R

s×s

∈ R

t×t

∈ R

u×u

∈

v×v

∈ R

λ×λ

. The 1D dictionary, used in (3), can

be obtained from a 5D dictionary using the Kronecker

Multidimensional Compressed Sensing for Spectral Light Field Imaging

351

product (Duarte and Baraniuk, 2012) as follows

D = D

⊗ D

, (4)

where D ∈ R

stuvλ×stuvλ

. Indeed, the storage cost of D

is prohibitively large compared to the per-dimension

dictionaries D

. The memory requirement ratio be-

tween a 1D and a 5D dictionary is

(stuvλ)

+λ

This further motivates a multidimensional dictionary

and sensing model.

3.4 Multidimensional Measurement

Model

In multidimensional sensing, a requirement is to in-

troduce a separate sensing operator for each dimen-

sion of the signal. Since a light ﬁeld is 5D, we need

to design 5 sensing operators to obtain measurements

from the spatial, angular, and spectral domains. Let

, j = 1,...,5 be the set of sensing matrices (or op-

erators) for a 5D light ﬁeld. Utilizing the n-mode

product between a tensor and a matrix (Kolda and

Bader, 2009), we can formulate the multidimensional

measurement model as follows

I = L ×

(5)

where L ∈ R

s×t×u×v×λ

is the light ﬁeld tensor and

I ∈ R

s×t×u×v

is the compressed measurements on the

sensor. The choice of sensing matrices Φ

is of utmost

importance in any compressive acquisition setup. Due

to our camera design in Fig. 1, i.e. the use of a lenslet

array, we do not perform compression on spatial and

angular domains. As a result, Φ

, j = 1,. ..,4, are

identity matrices. However, we would like to maxi-

mize the incoherence between the dictionary and the

sensing matrices (Candes and Wakin, 2008). There-

fore, as illustrated in Fig. 2, we perform a random

row-shufﬂing of the identity matrices to form Φ

, j =

1,. ..,4. On the other hand, since we perform spec-

tral compression using the one-hot mask, Φ

∈ R

1×n

contains only one nonzero value, where n is the to-

tal number of spectral bands. In our experiments, we

used data sets where n = 13.

The multidimensional measurement model in (5)

can be converted to a 1D measurement model as fol-

lows

I = (Φ

⊗ Φ

)

| {z }

L, (6)

where L and I are vectorized forms of the tensors L

and I , respectively. An illustration of the Kronecker

product of sensing matrices Φ

is shown in Fig. 2.

Note that the key beneﬁt of the nD sensing model re-

quires several orders of magnitude less memory com-

pared to the Kronecker 1D sensing model in (6). Re-

call from Section 3.3 that our 5D AMDE dictionary

also exhibits such beneﬁts. The nD approach also

comes with the beneﬁt that the sensing mask can be

designed using only ﬁve small matrices.

The psuedo-code in Algorithm 1 illustrates nD

SL0 reconstruction given the measurements I and the

matrices A

(i)

= Φ

as presented in Section 3.5.

Algorithm 1: Multidimensional SL0 algorithm.

Require: Input tensor I , input matrices A

(1...n)

, limit

parameter σ

min

, decreasing factor σ

, iteration L,

step µ

Ensure: S as sparse solution of S ×

1...n

(1...n)

= I

1: S ← I ×

1...n

(1...n)†

{initial estimate, † de-

notes pseudo-inverse}

2: σ ← largest absolute element of I

3: while σ > σ

min

4: for k = 1 .. .L do

5: ∆S = −

◦ exp



−

S ◦S

2σ



S ← µ · ∆S {Steepest ascent step}

S ←

S − (

S ×

1...n

(1...n)

− I ) ×

1...n

(1...n)†

8: end for

9: S ←

10: σ = σ

· σ

11: end while

3.5 Reconstruction

Given the AMDE dictionary in Section 3.3 and the

multidimensional measurement model in Section 3.4,

we formulate the 5D light ﬁeld recovery algorithm

from its measurements as follows

argmin

∥S ∥

s.t. ∥I − S ×

∥

≤ ε, (7)

where S ∈ R

s×t×u×v×λ

is a sparse coefﬁcient vector.

Once the coefﬁcients are obtained, the full light ﬁeld

is computed as

L = S ×

. To solve (7), we extend the 2D SL0 algorithm

(Ghaffari et al., 2009) for higher dimensional signals.

A pseudo-code of the 5D SL0 algorithm is provided

in Algorithm 1.

4 EVALUATION AND RESULTS

We evaluate our multispectral light ﬁeld camera de-

sign and CS framework using the multispectral data

set published by (Schambach and Heizmann, 2020).

As training set we randomly choose 60 out of the 500

random scenes, and as test set we use the ﬁve hand-

crafted scenes. The [512 × 512 × 5 × 5 × 13] light

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

352

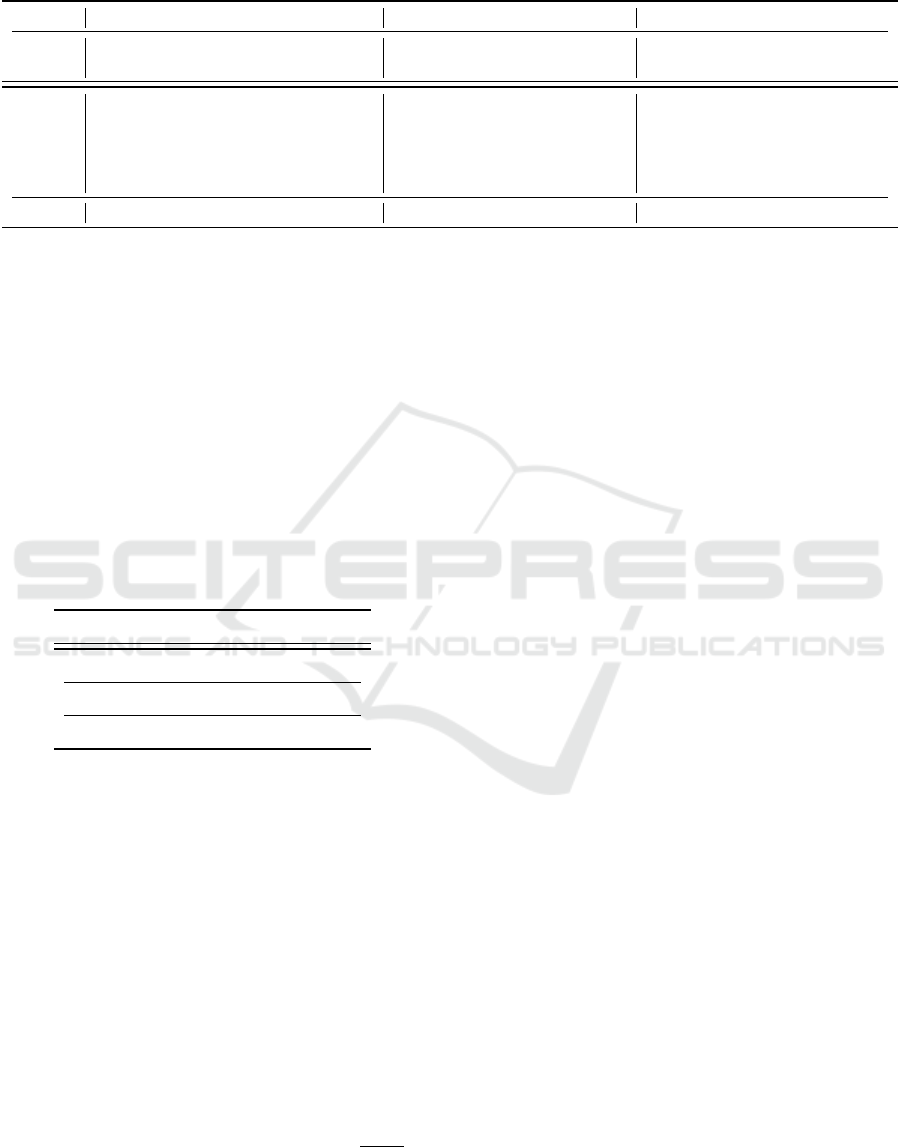
Table 1: Comparing 5D DCT, 1D AMDE and 5D AMDE using ﬁve test spectral light ﬁelds under ONE snapshot. Proposed

Method in blue. Best values in bold.

Test Methods PSNR /dB SSIM SA/(

◦

)

Scenes 5D 1D 5D 5D 1D 5D 5D 1D 5D

DCT AMDE AMDE DCT AMDE AMDE DCT AMDE AMDE

Bust 25.388 31.944 31.944 0.741 0.812 0.812 22.6658 10.853 10.853

Cabin 15.798 20.275 20.2754 0.302 0.636 0.636 53.767 26.977 26.977

Circles 15.459 18.494 18.494 0.313 0.530 0.530 35.216 29.588 29.588

Dots 15.454 23.485 23.485 0.247 0.738 0.738 24.661 10.668 10.668

Elephants 18.108 24.880 24.880 0.5761 0.743 0.7435 23.161 17.356 17.356

Average 14.631 22.398 22.398 0.324 0.627 0.627 35.54 24.804 24.804

ﬁelds exhibit a spatial resolution of 512 × 512 pix-

els and an angular resolution of 5 × 5 views sampled

in 13 spectral bands in steps of 25 nm from 400 nm

to 700 nm. For all experiments we use a patch size of

5×5×4×4×13, where the one-hot encoded mask il-

lustrated in Fig. 2 samples the spectral domain using a

single sample per pixel, leading to a compression ratio

of 1/13 corresponding to 7.69% of the original sam-

ples. We also report our results with multiple shots,

i.e. when multiple shots are taken by the camera sys-

tem in Fig. 1, where the mask pattern is changed for

each shot.

Table 2: Average Reconstruction Time of 5D DCT, 1D

AMDE and 5D AMDE per spectral light ﬁeld using ONE

snapshot.

Methods Reconstruction Time

5D DCT 40.3 seconds

1D AMDE 2.4 hour

5D AMDE 79.5 seconds

Table 1 compares 5D CS using the AMDE basis

described above to 1D CS using AMDE in terms of

peak signal-to-noise ratio (PSNR), structural similar-

ity index measure (SSIM), and spectral angle (SA).

We also include 5D DCT as representative for com-

monly used analytical bases in compressed sensing.

The results show that our novel nD formulation and

the resulting 5D multidimensional sensing mask per-

form as expected with PSNR, SSIM, and SA on par

with the 1D approach. The important difference, how-

ever, is that the nD formulation is orders of magni-

tude faster, speciﬁcally 106 times faster, running on

a machine with 16 CPU cores operating at 4.5GHz.

The average reconstruction time comparison of the

5D CS and 1D CS is provided in Table 2. More im-

portantly, our 5D sensing and reconstruction require

only a fraction of the memory, speciﬁcally

107729

9.2825e − 06.

Generally, an imaging system can take more snap-

shots to get more measurements. This can yield better

results for compressive sensing methods (Yuan et al.,

2021). As all previous evaluations were conducted

under a single snapshot condition, we can signiﬁ-

cantly enhance the reconstruction quality by employ-

ing additional snapshots as shown in Fig. 3. Speciﬁ-

cally, when utilizing ﬁve snapshots for recovering the

elephant scene with the 5D AMDE basis, the recov-

ered spectral light ﬁeld exhibits accurate colors. Al-

though the 5D DCT basis also shows improved re-

construction with an increased number of snapshots,

it fails in accurately reproducing colors.

Furthermore, Fig. 4 presents a comparative visu-

alization of the reconstruction results of the spectral

light ﬁeld for all scenes in Table 1 using three snap-

shots. As expected, 5D CS using the AMDE basis

achieves visually identical results when compared to

1D AMDE. And 5D AMDE outperforms the 5D CS

with the DCT basis as 5D DCT cannot faithfully re-

cover spectral information.

5 CONCLUSIONS

This paper introduced a sensing and reconstruction

method for fast multispectral light ﬁeld acquisition.

We believe that our novel nD formulation, and in par-

ticular the one-hot sampling strategy, opens up new

research directions for fast acquisition of other data

modalities in computer graphics, e.g. BRDFs, BTF,

and light ﬁeld videos. Multidimensional sensing and

dictionary learning allows us to have different sam-

pling strategies for each dimension. For instance, one

can choose to take full spectral information and sub-

sample the angular information. Hence, our nD for-

mulation facilitates the design of new visual data ac-

quisition devices. Another interesting aspect of the

proposed method is the utilization of learned dictio-

naries, which we show to outperform analytical dic-

tionaries such as DCT.

Multidimensional Compressed Sensing for Spectral Light Field Imaging

353

Ground Truth 1 Snapshot 3 Snapshots 5 Snapshots 7 Snapshots

5D DCT

PSNR 18.1089 18.3892 19.4972 21.2688

5D AMDE

PSNR 24.8808 25.0373 26.4341 28.7968

Figure 3: 5D CS Performance comparison (5D DCT, 5D AMDE) of reconstruction results using different number of snapshots

of Elephant scene. Captions are identical to Fig. 4.

ACKNOWLEDGEMENTS

This project has received funding from the European

Union’s Hori- zon 2020 research and innovation pro-

gram under Marie Skłodowska- Curie grant agree-

ment No956585. We thank the anonymous reviewers

for their feedback.

REFERENCES

Aharon, M., Elad, M., and Bruckstein, A. (2006). K-SVD:

An algorithm for designing overcomplete dictionaries

for sparse representation. IEEE Transactions on Sig-

nal Processing, 54(11):4311–4322.

Arce, G. R., Brady, D. J., Carin, L., Arguello, H., and Kittle,

D. S. (2014). Compressive Coded Aperture Spectral

Imaging: An Introduction. IEEE Signal Processing

Magazine, 31(1):105–115. Conference Name: IEEE

Signal Processing Magazine.

Babacan, S. D., Ansorge, R., Luessi, M., Molina, R., and

Katsaggelos, A. K. (2009). Compressive sensing of

light ﬁelds. In Proceedings of the 16th IEEE ICIP,

ICIP’09, page 2313–2316. IEEE Press.

Candes, E. J. and Wakin, M. B. (2008). An Introduction

To Compressive Sampling. IEEE Signal Processing

Magazine, 25(2):21–30. Conference Name: IEEE

Signal Processing Magazine.

Duarte, M. F. and Baraniuk, R. G. (2012). Kronecker Com-

pressive Sensing. IEEE Transactions on Image Pro-

cessing, 21(2):494–504. Conference Name: IEEE

Transactions on Image Processing.

Ghaffari, A., Babaie-Zadeh, M., and Jutten, C. (2009).

Sparse decomposition of two dimensional signals. In

2009 IEEE International Conference on Acoustics,

Speech and Signal Processing, pages 3157–3160.

Gortler, S. J., Grzeszczuk, R., Szeliski, R., and Cohen, M. F.

(1996). The lumigraph. In Proceedings of the 23rd an-

nual conference on Computer graphics and interac-

tive techniques, SIGGRAPH ’96, pages 43–54, New

York, NY, USA. ACM.

Hua, X., Wang, Y., Wang, S., Zou, X., Zhou, Y., Li,

L., Yan, F., Cao, X., Xiao, S., Tsai, D. P., Han, J.,

Wang, Z., and Zhu, S. (2022). Ultra-compact snapshot

spectral light-ﬁeld imaging. Nature Communications,

13(1):2732. Number: 1 Publisher: Nature Publishing

Group.

Huang, L., Luo, R., Liu, X., and Hao, X. (2022). Spectral

imaging with deep learning. Light: Science & Appli-

cations, 11(1):61.

Kolda, T. G. and Bader, B. W. (2009). Tensor decomposi-

tions and applications. SIAM Review, 51(3):455–500.

Levoy, M. and Hanrahan, P. (1996). Light ﬁeld render-

ing. In Proceedings of the 23rd annual conference on

Computer graphics and interactive techniques - SIG-

GRAPH ’96, pages 31–42, Not Known. ACM Press.

Liang, C.-K., Lin, T.-H., Wong, B.-Y., Liu, C., and Chen,

H. H. (2008). Programmable aperture photogra-

phy: Multiplexed light ﬁeld acquisition. ACM Trans.

Graph., 27(3):1–10.

Marquez, M., Rueda-Chacon, H., and Arguello, H. (2020).

Compressive Spectral Light Field Image Reconstruc-

tion via Online Tensor Representation. IEEE Trans-

actions on Image Processing, 29:3558–3568.

Marwah, K., Wetzstein, G., Bando, Y., and Raskar, R.

(2013). Compressive light ﬁeld photography using

overcomplete dictionaries and optimized projections.

ACM Transactions on Graphics, 32(4):1–12.

Miandji, E., Hajisharif, S., and Unger, J. (2019). A Uniﬁed

Framework for Compression and Compressed Sens-

ing of Light Fields and Light Field Videos. ACM

Transactions on Graphics, 38(3):1–18.

Mohimani, H., Babaie-Zadeh, M., Gorodnitsky, I., and Jut-

ten, C. (2010). Sparse Recovery using Smoothed

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

354

Ground Truth 5D DCT 1D AMDE 5D AMDE

Bust

PSNR 25.4520 32.1021 32.1021

Cabin

PSNR 16.1041 21.5743 21.5743

Circles

PSNR 15.6698 18.9974 18.9974

Dots

PSNR 16.1914 24.7977 24.7977

Elephant

PSNR 18.3892 25.0373 25.0373

Figure 4: Performance comparison of Reconstruction Results of 5D DCT, 1D AMDE and 5D AMDE of ﬁve test spectral light

ﬁelds using three snapshots. Evaluation metric PSNR in dB. The multi-spectral channels are converted to RGB according to

CIE 1913 and CIE D65. The images are chosen as the angular image [2 3] out of the 5 × 5 reconstructed views.

Multidimensional Compressed Sensing for Spectral Light Field Imaging

355

(SL0): Convergence Analysis. arXiv:1001.5073 [cs,

math].

Ng, R., Levoy, M., Br

edif, M., Duval, G., Horowitz, M., and

Hanrahan, P. (2005). Light Field Photography with

a Hand-held Plenoptic Camera. Tech Report CSTR

2005-02, Stanford university.

Schambach, M. and Heizmann, M. (2020). A Multispectral

Light Field Dataset and Framework for Light Field

Deep Learning. IEEE Access, 8:193492–193502.

Conference Name: IEEE Access.

Schambach, M., Shi, J., and Heizmann, M. (2021). Spectral

Reconstruction and Disparity from Spatio-Spectrally

Coded Light Fields via Multi-Task Deep Learning.

arXiv:2103.10179 [cs].

Wilburn, B., Joshi, N., Vaish, V., Talvala, E.-V., Antunez,

E., Barth, A., Adams, A., Horowitz, M., and Levoy,

M. (2005). High performance imaging using large

camera arrays. ACM Trans. Graph., 24(3):765–776.

Xiong, Z., Wang, L., Li, H., Liu, D., and Wu, F. (2017).

Snapshot Hyperspectral Light Field Imaging. In 2017

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 6873–6881, Honolulu,

HI. IEEE.

Yuan, X., Brady, D. J., and Katsaggelos, A. K. (2021).

Snapshot Compressive Imaging: Theory, Algorithms,

and Applications. IEEE Signal Processing Magazine,

38(2):65–88.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

356