Visualizing Group Structure in Compound Graphs: The Current State,

Lessons Learned, and Outstanding Opportunities

Henry Ehlers

1 a

, Diana Marin

2 b

, Hsiang-Yun Wu

3 c

and Renata G. Raidou

1 d

Visualization Group, Institute of Visual Computing and Human-Centered Technology, TU Wien,

Favoritenstr. 9-11 / E193-02, A-1040 Vienna, Austria

Rendering and Modeling Group, Institute of Visual Computing and Human-Centered Technology, TU Wien,

Favoritenstr. 9-11 / E193-02, A-1040 Vienna, Austria

St. P

olten University of Applied Sciences, Department of Media and Digital Technologies,

Campus-Platz 1, St. P

olten, A-3100, Austria

Keywords:

Compound Graph Visualization, Literature Survey, Group Structure Visualization.

Abstract:

Compound graphs are common across domains, from social science to biochemical pathway studies, and their

visualization is important to both their exploration and analysis. However, effectively visualizing a com-

pound graph’s topology and group structure requires careful consideration, as evident by the many different

approaches to this particular problem. To better understand the current advancements in compound graph

visualization, we have consolidated and streamlined existing surveys’ taxonomies. More speciﬁcally, we aim

to disentangle the visual relationship between graph topology and group structure from the visual encoding

used to visualize its group structure in order to identify interesting gaps in the literature. In so doing, we are

able to enumerate a number of lessons learned and gain a better understanding of the outstanding research

opportunities and practical implications across domains.

1 INTRODUCTION

Compound graph data, their visualization, and anal-

ysis are common across many different ﬁelds: from

social networks (Federico et al., 2011), to biochemi-

cal pathways (Partl et al., 2013), to business analytics

(Adomavicius and Bockstedt, 2008) and transporta-

tion logistics (Mesa-Arango and Ukkusuri, 2015). In

social network analysis, for example, researchers are

interested in understanding a person’s role across so-

cial groups. Here, compound graphs can be used

to model individuals as nodes and their relationships

as edges, as well as their place in various types of

groups, such as circles of friends, roles within a

workplace, or associations with organizations. For

another example, in the context of biological path-

ways, domain experts are interested in understanding

the mechanistic relationships between individual and

groups of genes and metabolites, in order to under-

stand the biochemical underpinnings of disease or cell

https://orcid.org/0000-0002-5994-1492

https://orcid.org/0000-0002-8812-9719

https://orcid.org/0000-0003-1028-0010

https://orcid.org/0000-0003-2468-0664

function. No matter their application area, compound

graphs are a useful framework for probing and un-

derstanding networks whose nodes also share group-

level relationships.

However, compound graphs are challenging to vi-

sualize, as researchers are interested in understanding

such graphs on both a topological and a group level

for increasingly large datasets. Thus, any visualiza-

tion of compound graphs must tackle the challenge

born of trying to balance the visual communication

of both entity topology and group structure. Various

visualization approaches and systems have been put

forth in literature, each tackling this challenge dif-

ferently: Some forgo interactivity in the interest of

scalability (De Domenico et al., 2015), others aim

to combine the two using summarization or linked

views (Dunne and Shneiderman, 2013), while others

yet build upon domain-speciﬁc visual conventions to

better serve a particular user group (Lex et al., 2010).

While existing reviews have taxonomically sum-

marized these various visualization approaches for

compound (Vehlow et al., 2015), multivariate (Nobre

et al., 2019), multilayered (McGee et al., 2019), and

dynamic (Beck et al., 2014) graphs, we note that none

Ehlers, H., Marin, D., Wu, H. and Raidou, R.

Visualizing Group Structure in Compound Graphs: The Current State, Lessons Learned, and Outstanding Opportunities.

DOI: 10.5220/0012431200003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 1: GRAPP, HUCAPP

and IVAPP, pages 697-708

ISBN: 978-989-758-679-8; ISSN: 2184-4321

697

had classiﬁed compound graph visualization strate-

gies along the more abstract axes of general (compar-

ative) visualization (Kim et al., 2017). We argue that

doing so allows for a more general understanding of

literature gaps and the identiﬁcation of new, interest-

ing research opportunities.

In this position paper, we identify and discuss

lessons learned and novel research opportunities

within the context of group structure visualization in

compound graphs. To better understand the current

state-of-the-art, we draw upon existing taxonomies

developed in recent surveys, namely i) (Vehlow et al.,

2015), (Beck et al., 2014), (Nobre et al., 2019), and

(McGee et al., 2019)’s reports on (particular types of)

compound graphs, ii) (Alsallakh et al., 2016)’s survey

on set-typed data, and ﬁnally iii) in order to position

compound graph visualization within a comparison-

oriented framework, (Kim et al., 2017)’s report on

comparative strategies. These reviews were selected

as, based on their impact on the ﬁeld, we believe them

to be authoritative and representative. These state-

of-the-art reports and their taxonomies share notable

overlap and all shed light on various facets of the

group structure visualization challenge in compound

graphs. We argue, however, that none, by themselves,

provide a complete view of the current opportunities.

Instead of providing a meta-review, here, we consol-

idate and extend these taxonomies to provide a com-

prehensive overview of the topic. This is to aid us in

identifying both major lessons learned from past re-

search in the ﬁeld as well as open challenges across

compound graph visualization domains not yet dis-

cussed by these aforementioned reports.

Speciﬁcally, we identify three core axes along

which to categorize literature, namely

1. the visual relationship between group and topo-

logical information, inspired by (Kim et al.,

2017),

2. the visual encoding chosen for the graph’s group

structure, inspired by (Alsallakh et al., 2016),

3. the kind of group-level relationships admitted

by the approach in question, as investigated by

(Vehlow et al., 2015).

We collect 167 references, partially based on the bib-

liographies of existing reviews, and place them within

our taxonomy. Based on our ﬁndings, we identify

gaps in the literature, outstanding challenges, and

lessons that can be useful for domain researchers. We

also identify several novel research opportunities.

2 RELATED WORK

2.1 Compound Graph Visualization

Dynamic Graphs. Dynamic graphs describe the

evolution of entities and their relationships over time.

(Beck et al., 2014) survey and taxonomically clas-

sify current approaches to the visualization of such

graphs. They identify three families of approaches,

namely i) animation, i.e. the mapping of time to time,

as seen in the work of (Ma et al., 2015), ii) timelines,

i.e. the mapping of time to space, exempliﬁed by Ma-

trixFlow (Perer and Sun, 2012), and iii) hybrid ap-

proaches that combine the two, such as Small Multi-

ples (Bach et al., 2015). While these families of ap-

proaches can indeed be utilized for general compound

graph visualization, their work naturally does not dis-

cuss this in much detail. Nonetheless, they identify a

large set of relevant techniques, approaches, and ap-

plications of dynamic graph visualization, and a num-

ber of their ﬁndings are mirrored in more general sur-

veys (Vehlow et al., 2015; McGee et al., 2019).

Multilayer Graphs. Multilayer networks are a gen-

eral framework describing various group-level rela-

tionships of both edges and nodes (Kivel

a et al.,

2014). (McGee et al., 2019) survey the state-of-the-

art of visualizing such networks. They classify papers

collected based on the visualization method: i) 1D

representations, e.g. circular (Bothorel et al., 2013) or

axis-based (Krzywinski et al., 2012) approaches, ii) 2,

2.5, and 3D node-link diagrams which often use color

(Archambault et al., 2007b) or linked views (Renoust

et al., 2015) to communicate group structure, iii)

matrix-based visualizations, such as Termite (Chuang

et al., 2012) or MuxVis (De Domenico et al., 2015), iv)

hybrid approaches, such as the matrix/node-link dia-

gram NodeTrix (Henry et al., 2007), and v) summary

approaches, such as Graph Thumbnails (Yoghourd-

jian et al., 2018).

Multivariate Graphs. Multivariate graphs are col-

lections of nodes and edges with additional data at-

tached to them, such as group-level associations.

Here, (Nobre et al., 2019) classify existing multivari-

ate graph techniques along their view-, layout-, data-

operations, and layouts. While they do not speciﬁ-

cally address the visualization of group-level informa-

tion, a number of their taxonomy categories are mir-

rored by other surveys discussed here. Most notably

they discuss three types of view operations; juxta-

posed, integrated, and overloaded. Nonetheless, their

recent publication contains a number of papers fea-

IVAPP 2024 - 15th International Conference on Information Visualization Theory and Applications

698

tured in other state-of-the-art reports that are worth

classifying in our own taxonomy.

Compound Graphs. Finally, (Vehlow et al., 2015)

survey approaches to the visual communication of

group structure of compound graphs. They ultimately

identify four meta-categories to describe different ap-

proaches with which to visualize such group struc-

tures, namely i) visual node attributes, i.e. the en-

coding of group structure in the form of glyphs or

color in the compound graph’s embedding, exempli-

ﬁed by TopicPanorama (Wang et al., 2016) and Net-

workAnalyst (Xia et al., 2015), respectively, ii) jux-

taposition, i.e. the separate visualizing group struc-

ture in either a linked view or attached to the graph’s

embedding, as seen in the works of (Burch et al.,

2013) and (Zhou et al., 2015), respectively, iii) su-

perimposition, i.e. the overlaying of group struc-

ture atop the graph’s embedding using regions or

lines, such as Kelp Diagrams (Dinkla et al., 2012)

and LineSets (Paduano and Forbes, 2015), respec-

tively, iv) embedding, i.e. the drawing of a separate

graph with which to communicate group structure re-

lations, using, for example, hypernode summarization

(Chaturvedi et al., 2014) or hybrid graph embeddings

(Henry et al., 2007; Angori et al., 2019).

Summary. All four of these categorizations, while

useful, are complementary to each other, and all, to

some extent or another, conﬂate i) the visual rela-

tionship between topological and group-level infor-

mation, i.e. how a graph’s group structure is visu-

alized relative to the topology’s visualization, and ii)

the group structure’s chosen visual encoding, i.e. how

a graph’s group structure, not its topology, is visu-

ally represented. Subsequently, we aim to build upon,

unify, and extend them to produce a novel perspective

on the current state of compound graph visualization.

2.2 Visualizing Group Structure

(Alsallakh et al., 2016) study different strategies for

visualizing group-level information for sets and their

elements. While this taxonomy was not developed

with compound graphs in mind, there is notable over-

lap with, and opportunities for extending, the afore-

mentioned compound graph visualization taxonomies

(Section 2.1). They identify six types of visualiza-

tion strategies with which to encode group structure,

namely i) Euler/Venn diagrams that represent each

set as a closed curve and intersections as the over-

lap between them, ii) Overlays, which, given some

embedding of each element as a point in 2D (or

3D) space, overlay set-membership using (colored)

glyphs, lines, or region overlays, iii) node-link dia-

grams that represent each set and element as a node

and draw bipartite edges between to communicate set-

element-membership, iv) matrices which place either

elements and sets along rows and columns to com-

municate identity, or will place sets/elements along

both rows and columns to communicate similarity, v)

aggregation-based representations that do not visual-

ize all elements, but instead only show the number

of elements per set in order to provide an effective

overview of larger datasets, vi) scatter plots, a spe-

cial type of aggregation, which embeds each set as a

single point in 2D or 3D space as a function of some

similarity metric or data attribute.

2.3 Comparative Visualization

Lastly, (Kim et al., 2017) describe four differ-

ent approaches to comparative visualization of 3D

and 4D spatial data. While not complete on their

own, we argue that these abstract classes of com-

parative visualization can be meaningfully mapped

to group-structure visualization approaches in com-

pound graphs. More speciﬁcally, we argue that the

compound graph visualization problem can be under-

stood as a comparison of graph topology on the one

hand and group structure on the other. Four classes

of approaches to comparative visualization are iden-

tiﬁed. Juxtaposition describes the side-by-side visu-

alization of objects to be compared. Superimposition

describes overlaying the objects to be compared. In-

terchangeability describes the interactive or animated

scrubbing through objects. Finally, explicit visualiza-

tion is the visualization of some derived (summary)

quantity instead of the objects directly.

3 PAPER COLLECTION

In order to obtain a representative set of papers and

applications, key references selected from the bib-

liographies of four relevant state-of-the-art reports,

(Nobre et al., 2019), (McGee et al., 2019), (Vehlow

et al., 2015), and (Beck et al., 2014) were consoli-

dated. Interestingly, despite the relatedness of the top-

ics, we note little overlap in general between these

four reviews, with the possible exception of (Beck

et al., 2014) and (Vehlow et al., 2015) (Figure 1. It

should, however, be noted that the inclusion of ref-

erences from existing works may introduce a certain

bias to our literature review. Thus, in order to in-

clude more recent papers not present in these afore-

mentioned works, we additionally manually curated

an additional set of references from relevant venues,

Visualizing Group Structure in Compound Graphs: The Current State, Lessons Learned, and Outstanding Opportunities

699

Figure 1: Sources and overlap of the selected papers col-

lected from (Beck et al., 2014), (Nobre et al., 2019),

(Vehlow et al., 2015), and (McGee et al., 2019) illustrated

as an area-proportional Euler diagram. Among other goals,

we aim to unify their collected references in addition to ex-

tending this collection of literature.

such as IEEE TVCG, Computer Graphics Forum,

PaciﬁcVis, Graph Drawing and Network Visualiza-

tion, and Information Visualization. In total, 167 pa-

pers were collected and subsequently manually cat-

egorized based on their visual relationship (Section

4.1), visual encoding (Section 4.2), group structure

(Section 4.3), as well as their application area. The

ﬁnal set of papers and their categorization have been

made publicly available on GitHub.

4 THE CURRENT STATE

Drawing upon these taxonomies, we propose to cate-

gorize papers along three main “axes”, namely i) the

chosen visual relationship between groups and their

elements, ii) the selected visual encoding with which

to communicate the graph’s group structure itself, and

iii) the group structure of the data.

4.1 Visual Relationships

A compound graph’s visual relationship describes

how a graph’s group structure is visualized relative

to its topology - Figure 2. Here, combining (Kim

et al., 2017) and (Vehlow et al., 2015)’s taxonomies,

we identify ﬁve possible visual relationships.

Separate. Deﬁned by (Vehlow et al., 2015) as “Par-

titioned”, a separate visual relationship, describes the

visualization of group structure in a separate (possi-

bly linked) view, such that the graph’s global topol-

ogy and group structure can be investigated indepen-

dently. Such representations are especially useful if

the graph’s group structure is too complex to visualize

atop or within its topological embedding. Consider,

for example, the tree attached to a node-link diagram

seen in ASK-GraphView (Abello et al., 2006).

Juxtaposed. Equivalently found in (Vehlow et al.,

2015)’s taxonomy under “Superimposed / Parti-

tioned”, a juxtaposed visual relationship (Kim et al.,

2017) describes the side-by-side visualization of each

group’s subgraph’s embedding in separate, possibly

linked, views. Such representations are beneﬁcial

when a set of topologically similar graphs are to be

compared side-by-side. For example, Entourage (Lex

et al., 2013) opts to visualize different pathways side-

by-side in a juxtaposed manner.

Embedded. Deﬁned as “Superimposed” by (Kim

et al., 2017) and “Visual Node Attribute” as well as

“Superimposed / Overlay” by (Vehlow et al., 2015),

an embedded visual relationship deﬁnes the simul-

taneous visualization of graph topology and group

structure in a single view, be it through color or re-

gion overlays or an explicit axis. Such representa-

tions can be useful, especially in explorative analysis

endeavors, where one must ﬁrst locate areas of simul-

taneous topological or group-structural interest. Top-

icPanorama (Wang et al., 2016), for example, visual-

izes group assignments as embedded glyphs.

Interchangeable. Not explicitly found in (Vehlow

et al., 2015), an interchangeable visual relationship

(Kim et al., 2017) describes the visualization of each

group’s subgraph as a separate “slice” in a pile of lin-

early arranged slices that are traversed interactively,

or automatically, using animation. Similar to juxta-

posed representations, such visual relationships lend

themselves well to immediate comparisons of pairs

of subgraphs, especially when a compound graph’s

group structure can be linearly arranged, e.g. time

slices in dynamic graphs. Consider, for example, the

small multiples of adjacency matrices presented in the

work of (Bach et al., 2015).

Explicit. Deﬁned by (Vehlow et al., 2015) as “Em-

bedded”, an explicit visual relationship (Kim et al.,

2017) describes the visualization of some computed

characteristic, such as differences or averages or sim-

ilarity, in order to provide a simpler summary visu-

alization. These representations are especially useful

for highly complex or large compound graphs, where

IVAPP 2024 - 15th International Conference on Information Visualization Theory and Applications

700

(a) Separate (b) Juxtaposed (c) Embedded (d) Interchangeable (e) Explicit

Figure 2: Examples showcasing the ﬁve identiﬁed visual relationships between group-level and topological encodings. (a)

Separate relationships describe the visualization of group structure independently of any (topological) embedding of the

compound graph. (b) Juxtaposed relationships place each group’s subgraph side-by-side, allowing for straightforward com-

parisons between them. (c) Embedded relationships embed group-level information within/atop a compound graph’s draw-

ing. If a particular node forms an intersection between two groups, its glyph is accordingly colored. (d) Interchangeable

relationships only visualize one group’s subgraph’s topology at a time but allow for a user to scrub through them linearly. (e)

Explicit relationships, rather than displaying all topological and group-level relationships, visualize only a composite of the

two.

the simultaneous visualization of group structure and

topology (in a single view) is not feasible or useful.

For example, (Sallaberry et al., 2010) opt to visualize

each group and their intersections as hypernodes and

regular nodes, respectively.

4.2 Visual Encoding

The visual encoding describes here how a graph’s

group structure—not its topology—is visually repre-

sented, i.e. how set membership, intersections, and

exclusions are visually communicated to the user, as

seen in Figure 3. Drawing primarily from (Vehlow

et al., 2015) and (Alsallakh et al., 2016) we identify

and deﬁne eight approaches with which to visually

communicate nodes’ group associations.

Node Attribute. Described as “Overlays” by Alsal-

lakh et al. (Alsallakh et al., 2016), node attributes

(Vehlow et al., 2015) are characteristics, here group

membership(s), of a compound graph’s elements,

which can be utilized to alter the visual attributes of

each node during the embedding of the graph. Color

is arguably the most common such node attribute with

which to communicate group/set/cluster membership

as it is simple to implement and understand. Sim-

ilarly, shapes can also be used. Lastly, glyphs are

useful for more complex element-set-memberships

and relationships, as they can, for example, express

such relationships as pie charts instead of simple

shapes or colors, as seen in TopicPanorama (Wang

et al., 2016). In general, node attributes are a non-

invasive, if limited, approach to visually communicat-

ing group memberships and relations without affect-

ing the graph’s topological embedding.

Overlay. Given some embedding of elements in

2D, overlays, described by (Vehlow et al., 2015) as

“Line/Region-based overlays”, add visual informa-

tion atop elements/nodes to communicate set mem-

bership. This commonly takes the form of a

hulls/regions overlaid atop grouped vertices (Alsal-

lakh et al., 2016), as seen in (Partl et al., 2013)’s

enRoute. A key disadvantage of region-based over-

lays is the ambiguity that can arise from overlapping,

but non-intersecting, contiguous regions (Alper et al.,

2011). Line overlays avoid such ambiguity by encod-

ing group membership to line-node-intersections, as

seen in (Alper et al., 2011)’s LineSets. Lines, how-

ever, can require a lot of “ink” when connecting ver-

tices close to each other, resulting in more visual clut-

ter than a simple region. In an effort to leverage the

advantages of both, hybrid overlays combine both re-

gions and lines, as exempliﬁed by (Meulemans et al.,

2013)’s KelpFusion. In general, overlays can be an

effective means of communicating (disjoint) vertex-

group membership, though they struggle to effec-

tively communicate denser or more complex group-

level relationships.

Bipartite Node-Link Diagram. Thus far, group-

level relationships have not affected the topological

embedding, thereby communicating topological rela-

tionships clearly at the potential cost of group-level

clarity. Here, (bipartite) node-link diagrams (Alsal-

lakh et al., 2016; Vehlow et al., 2015) represent both

groups and their elements as different vertices in the

same embedding, and visualize their associations as

bipartite edges connecting them. The produced node-

link diagram thus has two types of edges: topologi-

cal edges connecting element vertices to each other,

and bipartite edges connecting group and element

edges. This can allow group-level clustering to be

more apparent as the group structure now directly af-

fects the embeddings seen in (Bigelow et al., 2019)’s

Origraph.

Visualizing Group Structure in Compound Graphs: The Current State, Lessons Learned, and Outstanding Opportunities

701

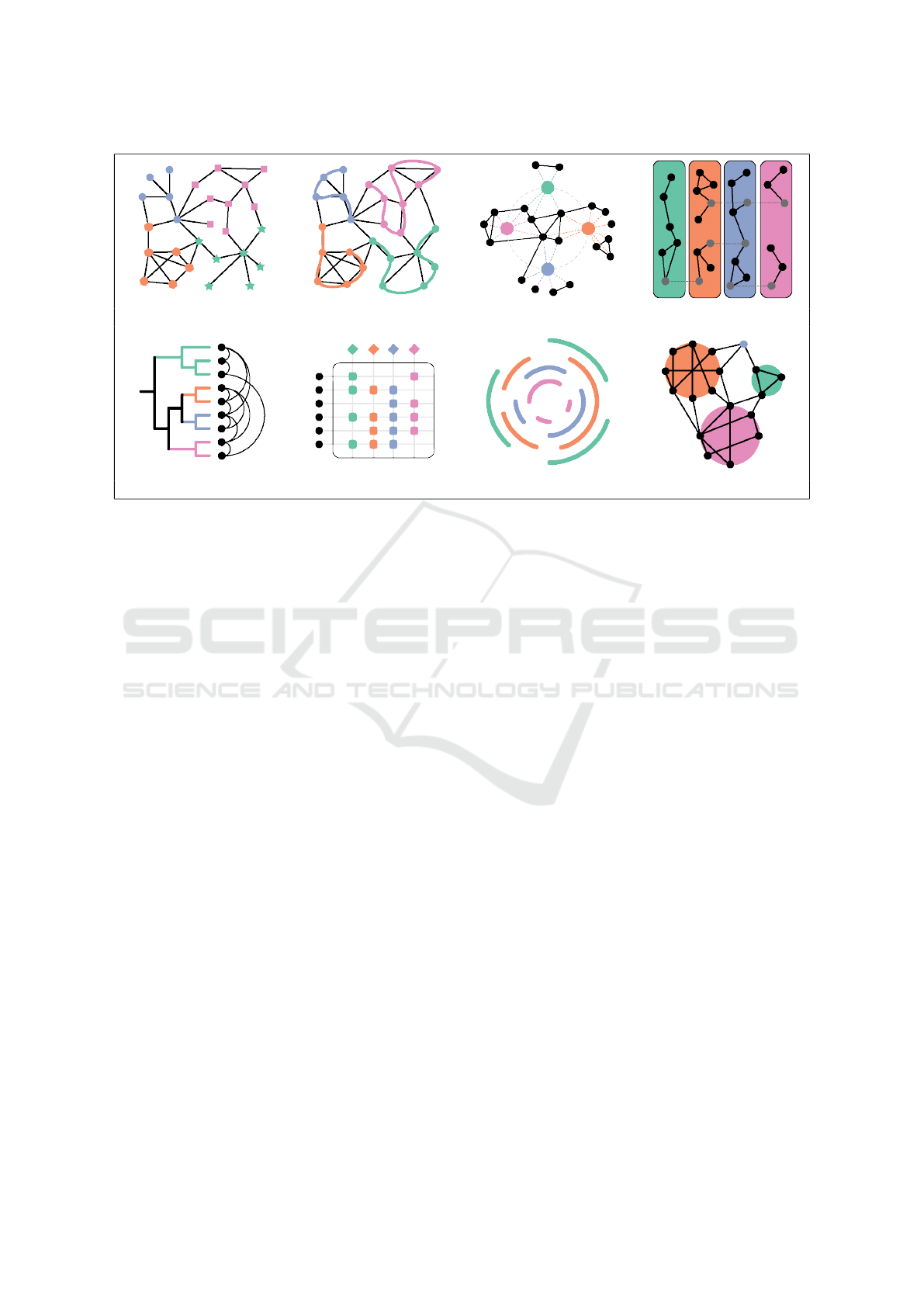
(a) Node Attribute (b) Overlay (c) Bipartite N.L.D. (d) Multiples

(e) Trees (f) Matrix (g) Abstraction (h) Hybrid

Figure 3: Examples of the eight identiﬁed visual encodings of group structure. (a) Node-Attribute encodings simply visualize

nodes’ group memberships using those nodes’ color and/or shape. (b) Overlay encodings visualize group membership as

regions or lines atop the nodes in the graph embedding. (c) Bipartite node-link diagram encodings visualize groups as

additional nodes within the graph’s embedding. Group membership is communicated using bipartite edges connecting group

nodes to topological nodes. (d) Multiples encodings visualize each group’s subgraph separately in its own “tile”. (e) Tree

encodings communicate (hierarchical) group structure between entities, visualized as leaf nodes, as hierarchical nodes whose

edges indicate super/sub-set relationship between them. (f) Identity matrix encodings communicate set membership tabularly

where if a node (row) pertains to a group (column), the respective cell is ﬁlled. (g) Abstraction encodings provide an

overview of groups’ cardinalities and their relationships by abstracting away the individual elements that make up said group.

Intersections are communicated through angular overlap between lines. Finally, (h) hybrid encodings combine any of the

above encoding types, e.g. a combination of multiples with node-link diagrams.

Multiple. Instead of visualizing group information

within, atop, or next to a graph’s embedding, multi-

ples, described as “Partitioning” by (Vehlow et al.,

2015), visualize each group’s topology separately.

Here, each such subgraph is displayed in its own

“tile”, arranged most commonly either in a juxta-

posed or interchangeable manner. Juxtaposed mul-

tiples, such as (Bach et al., 2015)’s Small MultiP-

iles. allow for a straightforward side-by-side com-

parison of subgraphs. Interchangeable multiples re-

quire (animated) transitions from one tile to the next,

as seen in (Bach et al., 2014a)’s Graph Diaries. On

the one hand, multiples allow for a clear visualization

of each group’s subgraph’s topology and its element-

group memberships. On the other, however, the visual

communication of group-level intersections in non-

disjoint graphs is complicated, as vertices that map

to multiple groups must be duplicated; once per tile.

Tree. Trees are prevalent in the visualization of dis-

joint, hierarchical group structures. Elements are rep-

resented as the tree’s leaves and the various levels

of the tree represent the various (hierarchically re-

lated) sets. Edges encode set-element membership

as well as set-set hierarchies. Most commonly, trees

are visualized in separate views, e.g. (Abello et al.,

2006)’s ASK-Graph. as visualizing topological edges

between the tree’s leaf nodes can be visually difﬁ-

cult. For example, (Telea and Auber, 2008)’s Code-

Flows addresses this challenge by visualizing topo-

logical relationships as a bipartite graph and duplicat-

ing the group’s hierarchical tree structure along each

bi-partition.

Matrix. Matrices (Alsallakh et al., 2016) can com-

municate set membership and relationships tabularly

in one of two ways. On the one hand, an iden-

tity matrix arranges elements and sets along its rows

and columns, respectively, and “ﬁlls” a correspond-

ing matrix cell if an element maps to that particu-

lar set. Intersections are communicated by a speciﬁc

row (element) mapping to multiple columns (sets) —

e.g. (Chuang et al., 2012)’s Termite. On the other

hand, a similarity matrix places either sets or elements

along both rows and columns and ﬁlls each cell with

some measure of similarity, thereby communicating

IVAPP 2024 - 15th International Conference on Information Visualization Theory and Applications

702

set or element relationships, but being unable to com-

municate element-set-membership on its own.

Abstraction. Abstraction-based techniques, de-

scribed by (Alsallakh et al., 2016) as “Aggregation”,

opt to visualize not all sets, elements, and their

relationships, but instead provide an overview of one,

at the expense of the others. Here, given the scope of

the paper, we deﬁne abstraction-based techniques as

techniques that abstract away element information in

favor of more clearly communicating group-level in-

formation. Quite naturally, this fairly broad category

can encompass many different approaches; from the

relatively simple Linear Diagram (Rodgers et al.,

2015) to the much more complex Graph Thumbnail

(Yoghourdjian et al., 2018).

Hybrid. Finally, hybrid approaches (Vehlow et al.,

2015) combine the aforenoted representations in

unique ways, exempliﬁed by (Henry et al., 2007)’s fu-

sion of node-link diagrams and matrices - NodeTrix,

or (Angori et al., 2019)’s combination of chord and

node-link diagrams - ChordLink.

4.3 Group Structure

Lastly, continuing the work of (Vehlow et al., 2015),

we categorize collected techniques based on the type

of group structure they are designed to visualize.

While they focused on distinguishing not only hierar-

chical from ﬂat and disjoint from overlapping group

structures, these authors additionally noted crisp from

fuzzy groupings. Given the scope of our work, we

omit the latter from our own categorization of litera-

ture. Thus, for each combination of visual encoding

and visual relationship, we count the total number of

approaches that apply to each considered type of data

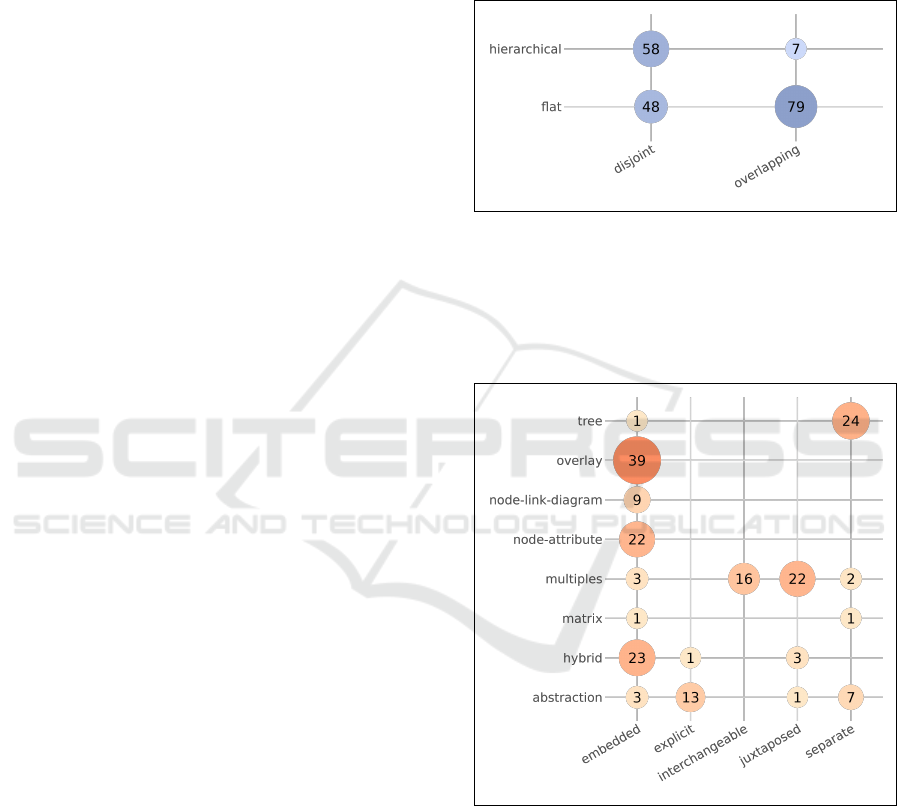
in order to identify potential gaps (Figure 4).

5 LESSONS LEARNED

Following our taxonomy of visual encoding and vi-

sual relationships described in Sections 4.2 and 4.1,

we classify the collected corpus accordingly, the re-

sults of which are presented in Figure 5.

Foregone Conclusions. Somewhat unsurprisingly,

many combinations of visual encodings pair (almost)

exclusively with certain visual relationships (Fig-

ure 5). Most notably, overlays and node attributes, by

deﬁnition, are embedded encodings, visualized within

the graph topological embedding. Thus, the 39 over-

lay and 22 node-attribute techniques map exclusively

to the embedded relationship category. Similarly,

multiples, if presented in 2D, would most commonly

only be visualized either interchangeably or juxta-

posed to each other, or separately from some other

topological representation.

Figure 4: Group structures compatible with the visualiza-

tion approaches collected from the selected papersp. Circle

area and color intensity encode the number of papers and

techniques that map to a particular combination of group

structure and “overlappedness”. The exact number of pa-

pers is displayed at the center of each circle in black. Papers

could map to more than one such combination of categories.

Figure 5: Co-occurence of visual encodings and visual rela-

tionships of the selected papers. Circle area and color inten-

sity encode the number of papers and techniques that map to

a particular combination of encoding and relationship. The

exact number of papers is displayed at the center of each

circle in black. Some papers featured multiple visual en-

codings and/or relationships and were thus mapped to more

than one combination of such categories.

Everyday Embedded. Of the 167 papers collected,

the majority (98 references) featured an embedded re-

lationship between graph topology and group struc-

Visualizing Group Structure in Compound Graphs: The Current State, Lessons Learned, and Outstanding Opportunities

703

ture (Figure 5). Most commonly, these papers rep-

resented their graph’s group structure using overlay,

node-attribute, or hybrid techniques. Overlays and

node-attributes appear to be especially popular when

the graph’s topology is of greater importance than

its group structure, as they do not alter the topol-

ogy representation. For completeness, however, it

should be noted that several region-based overlays

speciﬁcally, such as Polyptychon (Daniel et al., 2014)

and H-BLOB (Sprenger et al., 2000), are algorithmi-

cally incorporated during the (spring-)embedding of

the graph and thus do affect the graph’s visualization.

Their popularity seems to also be connected to their

conceptual simplicity and ease of implementation.

Embedded relationships were used for all group

structures, though primarily for ﬂat ones. 37 papers

were applied to disjoint/ﬂat group structures, such as

the region-based overlay MapSets (Efrat et al., 2014)

or the hybrid technique ChordLink (Angori et al.,

2019), and 36 papers mapped to overlapping/ﬂat

group structures, as seen in (Dinkla et al., 2014)’s

hybrid tool eXamine or (Vehlow et al., 2013)’s node-

attribute approach.

This combination of embedded encoding and ﬂat

groupings is perhaps unsurprising, as the use of node

attributes or overlays —the two most common em-

bedded encoding techniques— do not straightfor-

wardly allow for the encoding of hierarchical rela-

tionships on their own. Additionally, as discussed in

Section 4.2, embedded approaches’ ability to visually

communicate overlap between more complex groups

is also somewhat limited. Thus, most combinations of

embedded encoding and overlapping groupings limit

themselves to fairly simple cases, i.e. either few

groups or few intersections.

However, embedded approaches were also uti-

lized for hierarchical relationships, though pri-

marily disjoint ones, with 24 instances of dis-

joint/hierarchical and 4 overlapping/hierarchical.

Disjoint/Hierarchical relationships mostly focus on

visualizing a single layer of the hierarchy within the

compound graph’s embedding while visualizing the

full hierarchy in a separate (linked) view, as seen in

OntoTrix (Bach et al., 2013), HybridVis (Bach et al.,

2013), or TreeMatrix (Ruﬁange et al., 2012).

Lastly, for the few overlapping-hierchical em-

bedded visualizations, (Wang et al., 2016) and

(Nakazawa et al., 2012) opted to visualize one layer at

a time and communicate overlap using colored glyphs

while the complete hierarchy was visualized sepa-

rately, while (Jusuﬁ et al., 2013) opted to visualize

group-entity associations as a node-link diagram.

Seeing the Forest for the Trees. Tree-style

encodings were applied predominantly to dis-

joint/hierarchical group structures with 21 instances

thereof, while all other group structures featured

2 instances each. Here, tree representations of

group structure are most commonly visualized sep-

arately from the graph’s topology: of these 21 dis-

joint/hierarchical group structures, 20 were visual-

ized separately (Figure 5). This can be attributed

to the visual complexity that such trees introduce on

their own, i.e. a whole set of nodes and edges repre-

senting set relationships between groups in addition

to topological ones between entities. By visualizing

topology and group structure separately, equal weight

can be given to both without one affecting the other

which allows for such complex, hierarchical relation-

ships to be visualized more easily.

Indeed, looking at techniques intended for larger

networks, such as (Abello et al., 2006)’s ASK-

GraphView or (Abello et al., 2005)’s combination of

ﬁsheye views and treemaps, the graph’s hierarchical

group structure becomes complex enough to require

a separate view. For simpler hierarchies and smaller

graphs, a separate tree representation has been com-

bined with abstracted graph embeddings, such as (Ar-

chambault et al., 2007a)’s Grouse framework. Com-

bining topological and group node-link diagrams in

a single integrated view is possible as well (Pretorius

and Van Wijk, 2006). However, even in the examples

given, understanding the graph’s topology and group

structure is challenging.

This Is Getting Out of Hand: Now There Are Mul-

tiples of Them! Multiples are a reasonably pop-

ular approach for representing group structures, as

they allow for each group’s subgraph to be embedded

(partially) independently of other groups’ topologies.

With 37 counts, they are primarily used for the visu-

alization of overlapping/ﬂat group structure, though

they are also applied to 6 disjoint/ﬂat groupings.

Of these 37 overlapping/ﬂat applications, 14 visual-

ized these multiples interchangeably, such as (Erten

et al., 2004)’s GraphAEL, and 19 juxtaposed (Fed-

erico et al., 2011) (Figure 5). Especially for dynamic

graphs, the use of interchangeable multiples, akin to

the mapping of time to time (Beck et al., 2014), is a

popular choice, with 12 of the 14 interchangeable pa-

pers using the visualization of dynamic graphs (Ma

et al., 2015; Ruﬁange and Melanc¸on, 2014).

If the comparison of two or more graphs is of in-

terest, the juxtaposition of subgraphs as multiples al-

lows for a clear and uncluttered view of their differ-

ences, as seen in the works of (Yoghourdjian et al.,

2018), (Bach et al., 2015), and (Behrisch et al., 2014).

IVAPP 2024 - 15th International Conference on Information Visualization Theory and Applications

704

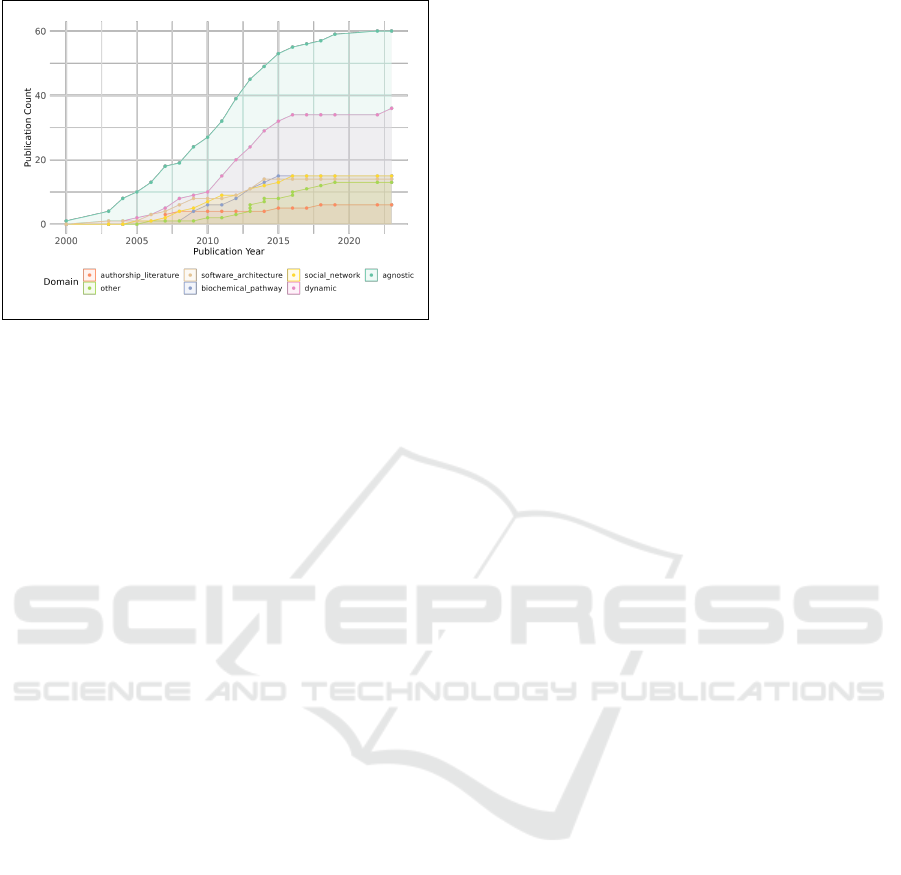
Figure 6: Cumulative number of the selected papers

mapped to application area across time. Papers could map

to multiple such application areas.

However, multiples can also be valuable in provid-

ing users with a small “thumbnail” representation of a

subgraph to aid in exploration (Al-Awami et al., 2014;

Barsky et al., 2008).

Lastly, beyond such 2D arrangements, 3 papers

opted to present multiples in embedded relationships.

Here, multiples are presented in 3D “cubes”, formed

by arranging them independently as seen in Matrix-

Cubes (Bach et al., 2014b), or arranging them in a jux-

taposed manner as seen in Caleydo (Lex et al., 2010).

6 OUTSTANDING

OPPORTUNITIES

Enter the Matrix. Adjacency matrices are used to

visually communicate graph topology, which is ex-

pected given their advantages over common node-link

diagrams (Ghoniem et al., 2004). Surprisingly ma-

trices, despite being a straightforward and scalable

method for the visualization of group structure, are

hardly used (Figure 5). Though, it should also be

mentioned that some hybrid techniques, most notably

NodeTrix (Henry et al., 2007) and Anchord+Matrix

Diagrams (Misue and Zhou, 2011), combine topo-

logical adjacency matrices and node-link diagrams to

communicate topology and structure simultaneously.

This has also been noted by (Nobre et al., 2019)

within the context of multivariate graphs, (Beck et al.,

2014) within the context of dynamic graphs, as well

as (Alsallakh et al., 2016) within the context of set-

typed data visualization. We also see ample opportu-

nity to reap the beneﬁts of (interactive) matrix visu-

alization for the communication of compound graph

group structures, as they are simple to implement and

understand.

Putting Some Node-Link Diagrams in Your Node-

Link Diagrams. Somewhat surprisingly, bipartite

node-link diagrams are infrequently used to commu-

nicate group structure, be it embedded or separately

(Figure 5). Similar to trees (Section 5), it is pos-

sible that the additional complexity introduced by a

second set of nodes for groups and edges, represent-

ing group memberships, simply makes them unsuit-

able for graphs with more complex topologies. In-

deed, as seen in the works of (Bigelow et al., 2019),

(Ahmed et al., 2007) and (Pienta et al., 2018), the

graphs studied are relatively small and simple. More-

over, color and/or shape are necessary to distinguish

between topological and group nodes, further adding

visual complexity. Nonetheless, this particular gap

strikes us as worth investigating with scalable, and

presumably interactive, bipartite node-link diagrams

that combine topology and group structure in a sin-

gle embedding. Speciﬁcally, for more clustered group

structures, this could potentially allow for very clear

visual distinctions between nodes that map to exclu-

sively one group, and those that map to multiple.

Looking for Group. Mirroring the ﬁnding of

(Vehlow et al., 2015) Disjoint/Flat and Dis-

joint/Hierarchical are well represented with 48 and

58 papers, respectively, and the Overlapping/Flat cat-

egory is the most represented with 79 entries. Inter-

estingly, only 7 of the collected papers were applied to

Overlapping/Hierarchical group structure (Figure 4).

Most such papers opted to visualize only two or

three group hierarchies at a time, usually separately,

and link these to the graph’s topology using either

color (Wang et al., 2016) or edges (Daniel et al.,

2014). Since overlapping, hierarchical groupings are

common in ontologies and clusterings (Vehlow et al.,

2015), we see a great opportunity to tackle the chal-

lenges that such group structures present in the con-

text of compound graphs, such as how to concurrently

visualize different levels of the overlapping hierar-

chies, or how to best visualize each node’s mapping

to multiple categories of different hierarchies.

Yeah, It’s a Hybrid. 16 hybrid visualization tech-

niques (deﬁned as any combination of visual encod-

ings) were found in our paper set (Figure 5). Interest-

ingly, however, all collected hybrid techniques com-

bine speciﬁcally node-link diagrams with other visu-

alization encodings, such as i) matrices (Henry et al.,

2007; Misue and Zhou, 2011; Bach et al., 2013), ii)

treemaps (Balzer and Deussen, 2005), iii) bounded

node-link diagram embeddings (Vehlow et al., 2013;

Chaturvedi et al., 2014), and iv) chord diagrams (An-

gori et al., 2022). However, node-link diagrams are

Visualizing Group Structure in Compound Graphs: The Current State, Lessons Learned, and Outstanding Opportunities

705

known to suffer from certain visual aesthetic limita-

tions that can make them difﬁcult to read when ap-

plied naively to larger and complex graphs, such as

node/node occlusions, heterogeneous node density,

edge crossings, or incident edge angles. Here, we

see an opportunity for interesting and novel hybrid vi-

sualization strategies with which to communicate the

group structure of compound graphs that go beyond

node-link diagrams, thereby potentially opening the

door for more visually scalable approaches.

Brave New Worlds. Certain application domains

are notably more represented than others in the paper

set collected (Figure 6). More speciﬁcally, domain-

agnostic techniques and dynamic graphs appear to far

outnumber all others. Application areas, such as au-

thorship and citation networks, appear not to have

been studied as extensively or recently. Often, as seen

in biochemical application areas, a particular applica-

tion area is constrained by the visual conventions of

the domain and/or the (perceived) visual literacy of

its users (Lex et al., 2010; Partl et al., 2013). This

points, at least in our estimation, to an opportunity

to revisit such domains, to identify potentially unan-

swered challenges.

7 CONCLUSION & FUTURE

WORK

We have surveyed literature based on both an in-

dependent collection of references, and the existing

works of (Nobre et al., 2019), (McGee et al., 2019),

(Beck et al., 2014), and (Vehlow et al., 2015). The

collected corpus of application and technique papers

were then categorized within a comprehensive tax-

onomy that, inspired by the works of (Kim et al.,

2017) and (Alsallakh et al., 2016), disentangles the

visual relationship between the graph’s topology and

group structure, as well as the chosen visual encod-

ing of the graph’s group structure, respectively. Based

on this classiﬁcation of literature, several lessons and

outstanding research opportunities were identiﬁed: i)

the under-utilization of identity and similarity ma-

trices, ii) the under-representation of bipartite node-

link diagrams, iii) the under-studied visualization of

Overlapping/Hierarchical data sources, iv) the over-

representation of node-link diagram-based hybrid vi-

sualization approaches, and v) the under-studied of

certain application domains. A future elaboration of

this paper in the shape of a formal state-of-the-art re-

port should aim for a completely independent, large-

scale collection of literature, and/or the collection of

additional authoritative reviews to avoid any possible

bias in the collected corpus of literature to, in turn,

draw potentially broader and more general conclu-

sions.

REFERENCES

Abello, J., Kobourov, S. G., and Yusufov, R. (2005). Visu-

alizing Large Graphs with Compound-Fisheye Views

and Treemaps. In Pach, J., editor, Graph Drawing,

Lecture Notes in Computer Science, pages 431–441,

Berlin, Heidelberg. Springer.

Abello, J., van Ham, F., and Krishnan, N. (2006). ASK-

GraphView: A Large Scale Graph Visualization Sys-

tem. IEEE Transactions on Visualization and Com-

puter Graphics, 12(5):669–676. Conference Name:

IEEE Transactions on Visualization and Computer

Graphics.

Adomavicius, G. and Bockstedt, J. (2008). C-TREND:

Temporal Cluster Graphs for Identifying and Visualiz-

ing Trends in Multiattribute Transactional Data. IEEE

Transactions on Knowledge and Data Engineering,

20(6):721–735. Conference Name: IEEE Transac-

tions on Knowledge and Data Engineering.

Ahmed, A., Batagelj, V., Fu, X., Hong, S.-h., Merrick, D.,

and Mrvar, A. (2007). Visualisation and analysis of

the internet movie database. In 2007 6th International

Asia-Paciﬁc Symposium on Visualization, pages 17–

24.

Al-Awami, A. K., Beyer, J., Strobelt, H., Kasthuri, N.,

Lichtman, J. W., Pﬁster, H., and Hadwiger, M. (2014).

NeuroLines: A Subway Map Metaphor for Visualiz-

ing Nanoscale Neuronal Connectivity. IEEE Trans-

actions on Visualization and Computer Graphics,

20(12):2369–2378.

Alper, B., Riche, N., Ramos, G., and Czerwinski, M.

(2011). Design Study of LineSets, a Novel Set Vi-

sualization Technique. IEEE Transactions on Visual-

ization and Computer Graphics, 17(12):2259–2267.

Alsallakh, B., Micallef, L., Aigner, W., Hauser, H., Miksch,

S., and Rodgers, P. (2016). The State-of-the-Art of Set

Visualization. Computer Graphics Forum, 35(1):234–

260.

Angori, L., Didimo, W., Montecchiani, F., Pagliuca, D.,

and Tappini, A. (2019). ChordLink: A New Hybrid

Visualization Model. In Graph Drawing and Net-

work Visualization: 27th International Symposium,

GD 2019, Prague, Czech Republic, September 17–20,

2019, Proceedings, pages 276–290, Berlin, Heidel-

berg. Springer-Verlag.

Angori, L., Didimo, W., Montecchiani, F., Pagliuca, D., and

Tappini, A. (2022). Hybrid Graph Visualizations With

ChordLink: Algorithms, Experiments, and Applica-

tions. IEEE Transactions on Visualization and Com-

puter Graphics, 28(2):1288–1300.

Archambault, D., Munzner, T., and Auber, D. (2007a).

Grouse: Feature-Based, Steerable Graph Hierarchy

Exploration. In EuroVis, volume 2007, pages 67–74.

Archambault, D., Munzner, T., and Auber, D. (2007b).

TopoLayout: Multilevel Graph Layout by Topologi-

IVAPP 2024 - 15th International Conference on Information Visualization Theory and Applications

706

cal Features. IEEE Transactions on Visualization and

Computer Graphics, 13(2):305–317.

Bach, B., Henry-Riche, N., Dwyer, T., Madhyastha, T.,

Fekete, J.-D., and Grabowski, T. (2015). Small Mul-

tiPiles: Piling Time to Explore Temporal Patterns

in Dynamic Networks. Computer Graphics Forum,

34(3):31–40.

Bach, B., Pietriga, E., and Fekete, J.-D. (2014a). GraphDi-

aries: Animated Transitions andTemporal Navigation

for Dynamic Networks. IEEE Transactions on Visu-

alization and Computer Graphics, 20(5):740–754.

Bach, B., Pietriga, E., and Fekete, J.-D. (2014b). Visualiz-

ing dynamic networks with matrix cubes. In Proceed-

ings of the SIGCHI Conference on Human Factors in

Computing Systems, CHI ’14, pages 877–886, New

York, NY, USA. Association for Computing Machin-

ery.

Bach, B., Pietriga, E., and Liccardi, I. (2013). Visualizing

Populated Ontologies with OntoTrix:. International

Journal on Semantic Web and Information Systems,

9(4):17–40.

Balzer, M. and Deussen, O. (2005). Exploring Relations

within Software Systems Using Treemap Enhanced

Hierarchical Graphs. In 3rd IEEE International Work-

shop on Visualizing Software for Understanding and

Analysis, pages 1–6.

Barsky, A., Munzner, T., Gardy, J., and Kincaid, R. (2008).

Cerebral: Visualizing Multiple Experimental Condi-

tions on a Graph with Biological Context. IEEE

Transactions on Visualization and Computer Graph-

ics, 14(6):1253–1260.

Beck, F., Burch, M., Diehl, S., and Weiskopf, D. (2014).

The State of the Art in Visualizing Dynamic Graphs.

In EuroVis - STARs. The Eurographics Association.

Behrisch, M., Davey, J., Fischer, F., Thonnard, O., Schreck,

T., Keim, D., and Kohlhammer, J. (2014). Visual

Analysis of Sets of Heterogeneous Matrices Using

Projection-Based Distance Functions and Semantic

Zoom. Computer Graphics Forum, 33(3):411–420.

Bigelow, A., Nobre, C., Meyer, M., and Lex, A. (2019). Ori-

graph: Interactive Network Wrangling. In 2019 IEEE

Conference on Visual Analytics Science and Technol-

ogy (VAST), pages 81–92.

Bothorel, G., Serrurier, M., and Hurter, C. (2013). Visu-

alization of Frequent Itemsets with Nested Circular

Layout and Bundling Algorithm. In Bebis, G., Boyle,

R., Parvin, B., Koracin, D., Li, B., Porikli, F., Zordan,

V., Klosowski, J., Coquillart, S., Luo, X., Chen, M.,

and Gotz, D., editors, Advances in Visual Computing,

Lecture Notes in Computer Science, pages 396–405,

Berlin, Heidelberg. Springer.

Burch, M., Schmidt, B., and Weiskopf, D. (2013). A

Matrix-Based Visualization for Exploring Dynamic

Compound Digraphs. In 2013 17th International Con-

ference on Information Visualisation, pages 66–73.

ISSN: 2375-0138.

Chaturvedi, S., Dunne, C., Ashktorab, Z., Zachariah, R.,

and Shneiderman, B. (2014). Group-in-a-Box Meta-

Layouts for Topological Clusters and Attribute-Based

Groups: Space-Efﬁcient Visualizations of Network

Communities and Their Ties. Computer Graphics Fo-

rum, 33(8):52–68.

Chuang, J., Manning, C. D., and Heer, J. (2012). Ter-

mite: visualization techniques for assessing textual

topic models. In Proceedings of the International

Working Conference on Advanced Visual Interfaces,

AVI ’12, pages 74–77, New York, NY, USA. Associ-

ation for Computing Machinery.

Daniel, D. T., Wuchner, E., Sokolov, K., Stal, M.,

and Liggesmeyer, P. (2014). Polyptychon: A

Hierarchically-Constrained Classiﬁed Dependencies

Visualization. In 2014 Second IEEE Working Con-

ference on Software Visualization, pages 83–86.

De Domenico, M., Porter, M. A., and Arenas, A. (2015).

MuxViz: a tool for multilayer analysis and visual-

ization of networks. Journal of Complex Networks,

3(2):159–176.

Dinkla, K., El-Kebir, M., Bucur, C.-I., Siderius, M., Smit,

M. J., Westenberg, M. A., and Klau, G. W. (2014).

eXamine: Exploring annotated modules in networks.

BMC Bioinformatics, 15(1):201.

Dinkla, K., van Kreveld, M. J., Speckmann, B., and West-

enberg, M. A. (2012). Kelp Diagrams: Point Set

Membership Visualization. Computer Graphics Fo-

rum, 31(3pt1):875–884.

Dunne, C. and Shneiderman, B. (2013). Motif simpliﬁ-

cation: improving network visualization readability

with fan, connector, and clique glyphs. In Proceed-

ings of the SIGCHI Conference on Human Factors in

Computing Systems, CHI ’13, pages 3247–3256, New

York, NY, USA. Association for Computing Machin-

ery.

Efrat, A., Hu, Y., Kobourov, S. G., and Pupyrev, S.

(2014). MapSets: Visualizing Embedded and Clus-

tered Graphs. In Duncan, C. and Symvonis, A., edi-

tors, Graph Drawing, Lecture Notes in Computer Sci-

ence, pages 452–463, Berlin, Heidelberg. Springer.

Erten, C., Harding, P. J., Kobourov, S. G., Wampler, K.,

and Yee, G. (2004). GraphAEL: Graph Animations

with Evolving Layouts. In Liotta, G., editor, Graph

Drawing, Lecture Notes in Computer Science, pages

98–110, Berlin, Heidelberg. Springer.

Federico, P., Aigner, W., Miksch, S., Windhager, F., and

Zenk, L. (2011). A visual analytics approach to dy-

namic social networks. In Proceedings of the 11th

International Conference on Knowledge Management

and Knowledge Technologies, i-KNOW ’11, pages 1–

8, New York, NY, USA. Association for Computing

Machinery.

Ghoniem, M., Fekete, J.-D., and Castagliola, P. (2004).

A Comparison of the Readability of Graphs Using

Node-Link and Matrix-Based Representations. In

IEEE Symposium on Information Visualization, pages

17–24. ISSN: 1522-404X.

Henry, N., Fekete, J.-D., and McGufﬁn, M. J. (2007).

NodeTrix: a Hybrid Visualization of Social Networks.

IEEE Transactions on Visualization and Computer

Graphics, 13(6):1302–1309.

Jusuﬁ, I., Kerren, A., and Zimmer, B. (2013). Multivari-

ate Network Exploration with JauntyNets. In 2013

17th International Conference on Information Visual-

isation, pages 19–27. ISSN: 2375-0138.

Kim, K., Carlis, J. V., and Keefe, D. F. (2017). Comparison

techniques utilized in spatial 3D and 4D data visual-

Visualizing Group Structure in Compound Graphs: The Current State, Lessons Learned, and Outstanding Opportunities

707

izations: A survey and future directions. Computers

& Graphics, 67:138–147.

Kivel

a, M., Arenas, A., Barthelemy, M., Gleeson, J. P.,

Moreno, Y., and Porter, M. A. (2014). Multilayer net-

works. Journal of Complex Networks, 2(3):203–271.

Krzywinski, M., Birol, I., Jones, S. J., and Marra, M. A.

(2012). Hive plots—rational approach to visualiz-

ing networks. Brieﬁngs in Bioinformatics, 13(5):627–

644.

Lex, A., Partl, C., Kalkofen, D., Streit, M., Gratzl, S.,

Wassermann, A. M., Schmalstieg, D., and Pﬁster, H.

(2013). Entourage: Visualizing Relationships be-

tween Biological Pathways using Contextual Subsets.

IEEE Transactions on Visualization and Computer

Graphics, 19(12):2536–2545.

Lex, A., Streit, M., Kruijff, E., and Schmalstieg, D. (2010).

Caleydo: Design and evaluation of a visual analysis

framework for gene expression data in its biological

context. In 2010 IEEE Paciﬁc Visualization Sympo-

sium (PaciﬁcVis), pages 57–64. ISSN: 2165-8773.

Ma, C., Kenyon, R. V., Forbes, A. G., Berger-Wolf, T.,

Slater, B. J., and Llano, D. A. (2015). Visualizing

Dynamic Brain Networks Using an Animated Dual-

Representation. In EuroVis Short Papers, pages 73–

77.

McGee, F., Ghoniem, M., Melanc¸on, G., Otjacques, B., and

Pinaud, B. (2019). The State of the Art in Multilayer

Network Visualization. Computer Graphics Forum,

38(6):125–149.

Mesa-Arango, R. and Ukkusuri, S. V. (2015). Demand

clustering in freight logistics networks. Transporta-

tion Research Part E: Logistics and Transportation

Review, 81:36–51.

Meulemans, W., Riche, N. H., Speckmann, B., Alper, B.,

and Dwyer, T. (2013). KelpFusion: A Hybrid Set Vi-

sualization Technique. IEEE Transactions on Visual-

ization and Computer Graphics, 19(11):1846–1858.

Misue, K. and Zhou, Q. (2011). Drawing Semi-bipartite

Graphs in Anchor+Matrix Style. In 2011 15th In-

ternational Conference on Information Visualisation,

pages 26–31. ISSN: 2375-0138.

Nakazawa, R., Itoh, T., Sese, J., and Terada, A. (2012).

Integrated Visualization of Gene Network and On-

tology Applying a Hierarchical Graph Visualization

Technique. In 2012 16th International Conference on

Information Visualisation, pages 81–86. ISSN: 2375-

0138.

Nobre, C., Meyer, M., Streit, M., and Lex, A. (2019). The

State of the Art in Visualizing Multivariate Networks.

Computer Graphics Forum, 38(3):807–832.

Paduano, F. and Forbes, A. G. (2015). Extended LineSets:

a visualization technique for the interactive inspection

of biological pathways. BMC Proceedings, 9(6):S4.

Partl, C., Lex, A., Streit, M., Kalkofen, D., Kashofer, K.,

and Schmalstieg, D. (2013). enRoute: dynamic path

extraction from biological pathway maps for explor-

ing heterogeneous experimental datasets. BMC Bioin-

formatics, 14(19):S3.

Perer, A. and Sun, J. (2012). MatrixFlow: Temporal Net-

work Visual Analytics to Track Symptom Evolution

during Disease Progression. AMIA Annual Sympo-

sium Proceedings, 2012:716–725.

Pienta, R., Hohman, F., Endert, A., Tamersoy, A., Roundy,

K., Gates, C., Navathe, S., and Chau, D. H. (2018).

VIGOR: Interactive Visual Exploration of Graph

Query Results. IEEE Transactions on Visualization

and Computer Graphics, 24(1):215–225.

Pretorius, A. J. and Van Wijk, J. J. (2006). Visual Anal-

ysis of Multivariate State Transition Graphs. IEEE

Transactions on Visualization and Computer Graph-

ics, 12(5):685–692.

Renoust, B., Melanc¸on, G., and Munzner, T. (2015). Detan-

gler: Visual Analytics for Multiplex Networks. Com-

puter Graphics Forum, 34(3):321–330.

Rodgers, P., Stapleton, G., and Chapman, P. (2015). Visual-

izing Sets with Linear Diagrams. ACM Transactions

on Computer-Human Interaction, 22(6):27:1–27:39.

Ruﬁange, S., McGufﬁn, M. J., and Fuhrman, C. P. (2012).

TreeMatrix: A Hybrid Visualization of Compound

Graphs. Computer Graphics Forum, 31(1):89–101.

Ruﬁange, S. and Melanc¸on, G. (2014). AniMatrix: A

Matrix-Based Visualization of Software Evolution. In

2014 Second IEEE Working Conference on Software

Visualization, pages 137–146.

Sallaberry, A., Zaidi, F., Pich, C., and Melanc¸on, G.

(2010). Interactive Visualization and Navigation of

Web Search Results Revealing Community Structures

and Bridges. In Proceedings of Graphics Interface,

pages 105–112.

Sprenger, T., Brunella, R., and Gross, M. (2000). H-BLOB:

a hierarchical visual clustering method using implicit

surfaces. In Proceedings Visualization 2000. VIS 2000

(Cat. No.00CH37145), pages 61–68.

Telea, A. and Auber, D. (2008). Code Flows: Visualiz-

ing Structural Evolution of Source Code. Computer

Graphics Forum, 27(3):831–838.

Vehlow, C., Beck, F., and Weiskopf, D. (2015). The State

of the Art in Visualizing Group Structures in Graphs.

Eurographics Conference on Visualization (EuroVis) -

STARs, page 20 pages.

Vehlow, C., Reinhardt, T., and Weiskopf, D. (2013). Visu-

alizing Fuzzy Overlapping Communities in Networks.

IEEE Transactions on Visualization and Computer

Graphics, 19(12):2486–2495.

Wang, X., Liu, S., Liu, J., Chen, J., Zhu, J., and Guo, B.

(2016). TopicPanorama: A Full Picture of Relevant

Topics. IEEE Transactions on Visualization and Com-

puter Graphics, 22(12):2508–2521.

Xia, J., Gill, E. E., and Hancock, R. E. W. (2015). Net-

workAnalyst for statistical, visual and network-based

meta-analysis of gene expression data. Nature Proto-

cols, 10(6):823–844.

Yoghourdjian, V., Dwyer, T., Klein, K., Marriott, K., and

Wybrow, M. (2018). Graph Thumbnails: Identifying

and Comparing Multiple Graphs at a Glance. IEEE

Transactions on Visualization and Computer Graph-

ics, 24(12):3081–3095.

Zhou, H., Xu, P., and Qu, H. (2015). Visualization of bi-

partite relations between graphs and sets. Journal of

Visualization, 18(2):159–172.

IVAPP 2024 - 15th International Conference on Information Visualization Theory and Applications

708