Applying the Neural Bellman-Ford Model to the Single Source Shortest
Path Problem
Spyridon Drakakis
a
and Constantine Kotropoulos
b
Department of Informatics, Aristotle University of Thessaloniki, Thessaloniki 54124, Greece
Keywords:
Message-Passing Neural Networks, Graph Neural Networks, Bellman-Ford Algorithm,
Single-Source Shortest Paths.
Abstract:
The Single Source Shortest Path problem aims to compute the shortest paths from a source node to all other
nodes on a graph. It is solved using deterministic algorithms such as the Bellman-Ford, Dijkstra’s, and A*
algorithms. This paper addresses the shortest path problem using a Message-Passing Neural Network model,
the Neural Bellman Ford network, which is modified to conduct Predecessor Prediction. It provides a roadmap
for developing models to calculate true optimal paths based on user preferences. Experimental results on real-
world maps produced by the Open S treet Map package show the ability of a Graph Neural Network to imitate
the Bellman-Ford algorithm and solve the Single-Source Shortest Path problem.
1 INTRODUCTION
The Optimal Path problem (Martins et al., 19 99) is
the problem of calculating the optimal path from one
point to another. The vagueness in the definition of
optimality is pu rposeful since its generality allows for
complex and arbitrary criteria to be encompassed in
the definition. Instances of this general problem are
the Single-Source Single-Destination and the Single-
Source Shortest Path (SSSP) problem . In this paper,
the SSSP problem is considered.
The SSSP problem is the problem of calculating
the shortest paths from a source node u ∈ V to all
other nodes, given a graph G = (V , E). There are
plenty of classical algorithms th at solve this prob-
lem, such as Brea dth-First Search (BFS), Dijkstra’s
Algorithm (Dijkstra, 1959), Bellman-Ford Algorithm
(Bellman, 1958), A
∗
(Hart et al., 1968), efficiently.
However, these algorithms cannot model c omplex cri-
teria and, except A
∗
, cannot model any heuristic infor-
mation at all. Thus, they are re stricte d to o ptimizing a
limited amount of criteria, or one criterion, at a time
and cannot solve the general Optimal Path problem .
The prominence of Neu ral Networks and their ca-
pacity to optimize complex cost fu nctions make them
ideal as a vehicle to regain the vagueness and gener-
ality in the definition of optimality caused by solv-
a
https://orcid.org/0009-0001-1253-9498
b
https://orcid.org/0000-0001-9939-7930
ing a particular instance of the Optimal Path problem,
namely the SSSP problem. Specifically, we will con-
sider Message-Passing Neural Networks (MPNNs), a
type of Graph Neural Network (GNN) suited for rea-
soning and making predictions on graphs.
MPNNs require that the ed ges and nodes of the
graph have defined represen ta tions. The classical al-
gorithms use th e weights of the edges as a represen-
tation of the edges and the distance from the source
node as a representation of th e node s, both scalar. In
(Zhu e t al., 2021), a very sound theoretical foundation
was set for path-oriented node representatio n algo-
rithms, encapsulating several classical algorithms. An
analogo us process can be used to define an MPNN.
Also, we will be taking inspiration from the Bellman-
Ford algorithm and, first, show how it can be param-
eterized by a message-passing process and, second,
define the SSSP problem in a way that an MPNN can
solve. The choice of the Bellman-Ford algorithm lies
in its inclination for parallelization and its easy imple-
mentation as a message-passing process.
In this paper, we present a novel appro ach regard-
ing the analysis of MPNNs, according to which we
address failures caused b y restraints (such as a dead
end on a directed graph) and provide proper and ef-
ficient recovery solutions. We outline critical limita-
tions of the model a nd ways to overcome them, pro-
vide visualizations and explanations of instances of
failure, and outline solutions based on the observa-
tions.
386
Drakakis, S. and Kotropoulos, C.
Applying the Neural Bellman-Ford Model to the Single Source Shortest Path Problem.
DOI: 10.5220/0012425800003654
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 13th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2024), pages 386-393
ISBN: 978-989-758-684-2; ISSN: 2184-4313
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

The outline of the paper is as follows. In Sec-
tion 2, some related works on GNNs and their use
in solving the SSSP proble m are presented . In Sec-
tion 3, the model derivation is explained. We descr ibe
the Bellman-Ford a lgorithm and MPNNs and discuss
how they are con nected. Then, we explain how the
Bellman-Ford algorithm can be ge neralized and p a -
rameterized by an MPNN, and we subsequently de-
fine such an MPNN for the SSSP problem. In Section
4, experimental results are presented . We provide an
analysis of the operation of the model on trivial and
real-world maps, outline how to overcome the lim-
itations, and analyze instance s of failure, p roposing
suitable recovery methods from failures. In Section
5, concluding remarks are given.
2 RELATED WORK
This section reviews related works on GNNs and their
use in solving path problems.
(Zhu e t al., 2021) showed that m any classical al-
gorithms can b e encapsula te d by a general path
formu lation and laid the theoretical foundation
behind the Generalized Bellman-Ford algorithm
(Baras and Theodorakopoulos, 2010). They also de-
veloped the Neural Bellman-Ford model to solve
the link predic tion problem, which is essentially the
model used in this pa per, with adjustments to apply
it to the SSSP problem. They used pair representa-
tions of nodes produc ed by examining the local sub-
graph between two nodes to predict links, ac hieving
95% average pre c isio n o n the Cora dataset, 93% on
the Citeseer dataset, and 98% on the Pubmed data set.
(Veliˇckovi´c et al., 2020) developed a neural net-
work model that could execute several classical al-
gorithms on graphs at once. Specifically, using an
MPNN for best results, they solved the neural ex-
ecution task, executing BFS, the Bellman-Ford al-
gorithm, and Prim’s algorithm (Prim, 1957) all at
once. They did this using the encoder-process-
decoder paradigm (Battaglia et al., 2018), according
to which 3 neural networks, an encoder, a process, and
a decoder network are e mployed to transform the in-
termediate inputs and share them with the algorithms
being learned. Also, a termination network is needed
to decide the terminatio n condition of the algorithms.
Related to th is paper is the Predecessor Pre diction
they conducted as part of th eir tests, using the BFS
algorithm for rea chability and the Bellman-Ford algo-
rithm simultaneously to predict predecessors of n odes
of the shor te st paths, achieving accuracies of 97.13%,
94.71%, 9 0.91%, 83.08%, 77.53%, 74.90% for graph
sizes of 20, 50, 100, 500, 1000, 1500 nodes, respec-
tively.
(Wu et al., 202 0) used a mixtur e of GNN mod-
els to learn a hierarchical representatio n of road
networks. The hierarchy is functional zones −→
structural zones −→ road segments, wh e re functional
zones are sets of structural regions, indicating some
kind of traffic functionality, structural regions are sets
of spatially connected road segments and road seg-
ments are uniform sections of road. They constructed
representations of these entities by using embedding s
for road segments, spectral clustering and graph at-
tention networks for structural regions, and another
graph attention network for functional zones. Focus-
ing on the route planning task, which is the most sim-
ilar to our case, given an actual path p and a produced
path p
′
, they achieved F1 scores of 0.329, 0.357,
0.301 and edit distances of 7.851, 7.36 1, 8.138 for
road networks of Beijing, Chengdu, and X i’an, re-
spectively.
In the same vein, (Huang et al., 2 021) used an-
other hierarchical em bedding approach, partition-
ing the road network into subgraphs (trees) with a
minimum-cut approximation, calculating embeddings
for each one. The n, the local em beddings (represen-
tation of the nodes) a re learned by minimizing the L
1
distance. Some nodes are designated as landmarks,
and training samples ar e chosen uniformly from the
sets of closest vertices to each landmark, ensuring that
the training sample is diverse. Then, fine-tu ning is
performed using more training samples from those
vertices that produce the highest appro ximation er-
rors. They achieved mean error r ates (against actual
shortest p a ths) of 0.60%, 0.63 %, and 0.48% for road
networks of Beijing, Florida, and Western-USA re-
gions, respectively.
3 METHODOLOGY
The proce ss by wh ic h the MPNN is derived is ex-
plained in detail. Th e process consists of four steps:
• Understanding the Bellman-Ford algorithm.
• Using a Message-Passing process to simulate the
Bellman-Ford algorithm.
• Incorporating Neural Networks as pa rt of the
message-passing.
• Formulating the SSSP problem as a classification
problem.
3.1 Bellman-Ford Algorithm
The Bellman -Ford algorithm (Bellma n, 1958) is a dy-
namic programming algorithm calculating the sho rt-
Applying the Neural Bellman-Ford Model to the Single Source Shortest Path Problem
387

est paths fro m a source node u to all other nodes v
i
,
for i = 1, 2, ..., |V |. It does so by storing node repre-
sentations h
(t)
(u, v
i
) for each nod e , which is the cur-
rent shortest distance to the source node, and updating
them every time there is a n alternative path from u to v
that is shorter than the known path. That is, for every
node v
i
, and an incoming edge e
xv
i
with edge repre-
sentation its weight w(x, v
i
), the update (also called
relaxation) is (Li et al., 2022):
h
(t)
(u, v
i
) = min

h
(t−1)
(u, x) + w(x, v
i
), h
(t−1)
(u, v
i
)

(1)
This process is do ne for every node, i.e., |V | − 1
times per iteration. Therefo re, relaxation is conducted
|V | − 1 times on the edges. In the beginning, the rep-
resentation of the n odes h
(0)
(u, v
i
) is initialized by:
h
(0)
(u, v
i
) =
(
0 if u = v
i
∞ otherwise.
(2)
The key constituents o f the algorithm are easily de-
tected. Firstly, th ere is an initialization based on equa-
tion (2), also ca lled the boundary condition. Then,
every node receives the previous rep resentation of its
neighbors and updates its rep resentation if it is less
than its own. In other words, it collects the repre-
sentations of its neighbors and its own and keeps the
minimum. This alternative wording of the algorith m’s
inner workings provides the recipe for an equivalent
message-passing operation.
3.2 Message-Passing Neural Networks
MPNNs, as described in (Gilmer et al., 2017), are
a general class of GNNs since many GNN ar-
chitectures, like Graph Convolutional Networks
(Kipf and Welling, 2017), can be described in terms
of an MPNN. Th e basic idea of an MPNN is that in-
formation about the representation of a node is linked
to the node representations of its neighb ors. In other
words, a better represen tation of the node can be
achieved by aggregating information from its neigh-
borhood.
The message-passing operation conducted in an
MPNN consists of three steps:
1. Every node compu te s a message for every one of
its neighbors. This message is a function of its
own representation, that of the neighbor, and the
representation of the edge linking the two.
2. The messages are sent, and every node aggregates
the messages it receives usin g a permutation in-
variant function, meaning the order in which the
messages are rec eived does n ot matter.
3. Every node updates its representation as a fu nc-
tion of its current representation and the aggre-
gated me ssages.
The operations cor respond to three different func-
tions, message, aggregate, update. A key fea-
ture of an MPNN is the type of functions it em-
ploys. Fundamental message functions as relational
operators on graph embeddings are natural summa-
tion as in (Bordes et al., 2013), multiplication as in
(Yang et al., 2015). Some important aggregators are
natural summation, the mean operator, m a ximum, and
minimum.
MPNNs consist of layers, like regular Neural Net-
works. In each layer, a messag e -passing ope ration is
condu c te d, and informatio n flows through the model
in a similar fashion to feed- forward neural networks.
The output of one layer, followed by a non-linear ac-
tivation, is the input of the n ext.
If we focus on a single node v
i
, every time a
message-passing operation is conducted , i.e., the in-
put flows through the layers o f the model, the node
receives information from node s k steps away, where
k is the number of message-passing operations con-
ducted.
The message-passing operation ca n easily be
shown to be equivalent to the Bellman- Ford iteration
(Gallager, 1982). Focusing again on a single nod e v
i
,
we see that the node updates its distance to the source
node by examining the difference in its distance to the
source n ode if it uses a different incoming edge. As
stated before, this pro cess can alternatively be defined
as gathe ring messages from every neighboring node
(covering all incomin g edges) and updating its n ode
representation by taking the minimum of all the mes-
sages. Fina lly, to inc lude the nod e itself in the update
operation, we attach a self-loop to each node, allow-
ing it to send a message to itself to co mpare to the
others. This results in a different but similar update
rule:
h
(t)
(u, v
i
) = min

h
(t−1)
(u, x) + w(x, v
i
), h
(0)
(u, v
i
)

(3)
where w(x, v
i
) = 0 for x = v
i
. By conducting multiple
message-passing operations, we can fully simulate
the Bellman-Ford algorithm using m essage-passing
operations.
3.3 Generalizing the Bellman-Ford
Algorithm
One can observe that the r epresentation o f a node
h
(t)
(u, v
i
) is the r epresentation o f the shor te st path
h(P) from u to v
i
, where P = e
1
e
2
...e
|P|
, i.e.,
h(u, v
i
) = h(P) (4)
h(P) = w(e
1
) + w(e
2
) + . . . + w(e
|P|
) (5)
where || stan ds for set cardinality. Generally, find-
ing the shortest path between two nodes can be for-
mulated as a problem of enumerating all the possible
ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods
388

paths between the two nodes and keeping the one with
the minimum cost. That is (Zhu et al., 2021),
h(P = (e
1
, e
2
, . . . , e
|P|
)) = w(e
1
) + w(e
2
)+
+ w(e
|P|
) (6)
h(u, v
i
) = min

h(P
1
), h(P
2
), . . . , h(P
|P
u,v
i
|
)

(7)
where P
u,v
i
is the set of all possible paths between
u and v
i
. If we allow general node and e dge rep-
resentations that are no longer scalar and general-
ized operations, ⊗, ⊕ replacing natural summation
and the min operator, equations (6) and (7) become
(Zhu e t al., 2021):
h(P = (e
1
, e
2
, . . . , e
|P|
)) = w(e
1
) ⊗ w(e
2
) ⊗ . . .
w(e
|P|
) ,
|P|
O
i=1
w(e
i
) (8)
h(u, v) = h(P
1
) ⊕ h(P
2
) ⊕ . . . ⊕ h(P
|P
u,v
|
)| P
i
∈ P
u,v
,
M
P∈P
u,v
h(P) (9)
This formulation is very co mputationally expen-
sive as it requires that all the possible paths are cal-
culated, yielding exponential complexity. If we now
substitute our new operators, node, and edge repre-
sentations in equatio ns (3) and (2), we ge t the gener-
alized Bellman-Ford algorithm. The generalized op-
erators satisfy a semi-ring system with the neutral el-
ement for summation
0
and the neutral element for
multiplication
1
. Additionally, we consider a ho-
mogene ous graph to be a Knowledge Graph (K G)
G = (V , R , E), where R is the set of relations on the
graph, with one r elation. Thus, we have the following
algorithm (Li et al., 2022):
h
(0)
q
(u, v) ←− 1
q
(u = v) (10)
h
(t)
q
(u, v) ←−


M
(x,r,v)∈E(v)
h
(t−1)
q
(u, x) ⊗ w(x, r, v)


⊕ h
(0)
q
(u, v), t ≥ 1 (11)
where q is the query relation and 1
q
(u = v) is an in-
dicator f unction that outputs
1
q
, if u = v and
0
q
otherwise.
1
q
and
0
q
are now neutral elements
for summation and multiplication with respect to the
query relation q.
3.4 Incorporating Neural Networks
To achieve generalization capacity, neural networks
must be incor porated into the model. For this pur-
pose, we will define three neural function s: message,
aggregate, and indicator.
The ind ic a tor function serves the purpose of
a non-trivial boundary condition. So, instead
of initializing node a nd edge representations ac-
cording to equation (2), we use an embedding
(Yang et al., 2015), (Ka zemi and Poole, 2018) for a
shared representation for the edges w(e) a nd initial-
ize the source node with this representation.
The message func tion serves the purpose of the
⊗ operator. It will be imple mented as a linear com-
bination of the represen ta tion of the node x sending
the message and the ed ge representation of the edge
connecting x and v, wh e re v is the node receiving the
message. T he aggregate function is go ing to be im-
plemented as the min operator. Afte r the aggregation
function, a non-linear activation is applied to the node
representations.
The consequence of these changes is that we
have incorporated learnable parameters and can gen-
eralize and classify nodes. Equation (11) becomes
(Li et al., 2022).
h
(t)
q
(u, v) ←− min
"
min
(x,r,v)∈E(v)

h
t−1
q
(u, x)+
+ w
x,v
w(x, r, v)

, h
(0)
q
(u, v)
#
, t ≥ 1 (12)
where w
x,v
is the weight of the edge e(x, v). A Multi-
layer Perceptron is also in c luded at the e nd to classify
the nodes based on the node re presentations.
3.5 SSSP Problem as a Classification
Problem
The SSSP problem can be mod e le d as a classifica-
tion problem. Instead of c la ssifying nodes or edges
as optimal or non-optimal, we can model the prob-
lem as one of Predecessor Prediction, taking inspira-
tion from the original Bellman-Ford algorithm. Thus,
Predecessor Prediction is a multi-class classification
problem with a number of cla sses C = |V |. We clas-
sify each no de in one o f these classes, co rresponding
to its predecessor node. We have a label for every
node that can be c alculated using one of the classical
algorithm s, Bellman-Ford or Dijkstra. The loss func-
tion of such a problem is the Cross-Entropy loss.
4 EXPERIMENTAL RESULTS
The models were trained with the Stochastic Gradi-
ent Descent (SGD) algorithm using the Adaptive M o-
ment Estimation (ADAM) op timizer. T he learning
Applying the Neural Bellman-Ford Model to the Single Source Shortest Path Problem
389

rate used is 5 ·10
−3
and a batch size 16. The other hy-
perpara meters, such as model architecture, message-
passing iterations, and the number of epochs, vary and
are summarized in Table 1.
Experiments were conducted o n 4 small grap hs
produced by the Ope n Str eet Map package. The
graphs are real-world graphs of 3 locations. The first
two stem from the sam e region, Lagadas
1
, and the
remaining three are d ifferent regions of the city of
Thessaloniki, one of the center of The ssaloniki
2
, o ne
of the region around the Aristotle University of Thes-
saloniki
3
and one of the region of Evangelistria
4
.
Before presenting the re sults, analyzing the m odel
on trivial graphs and understanding its weaknesses is
useful.
x
1
x
2
x
3
Figure 1: A simple graph with three nodes.
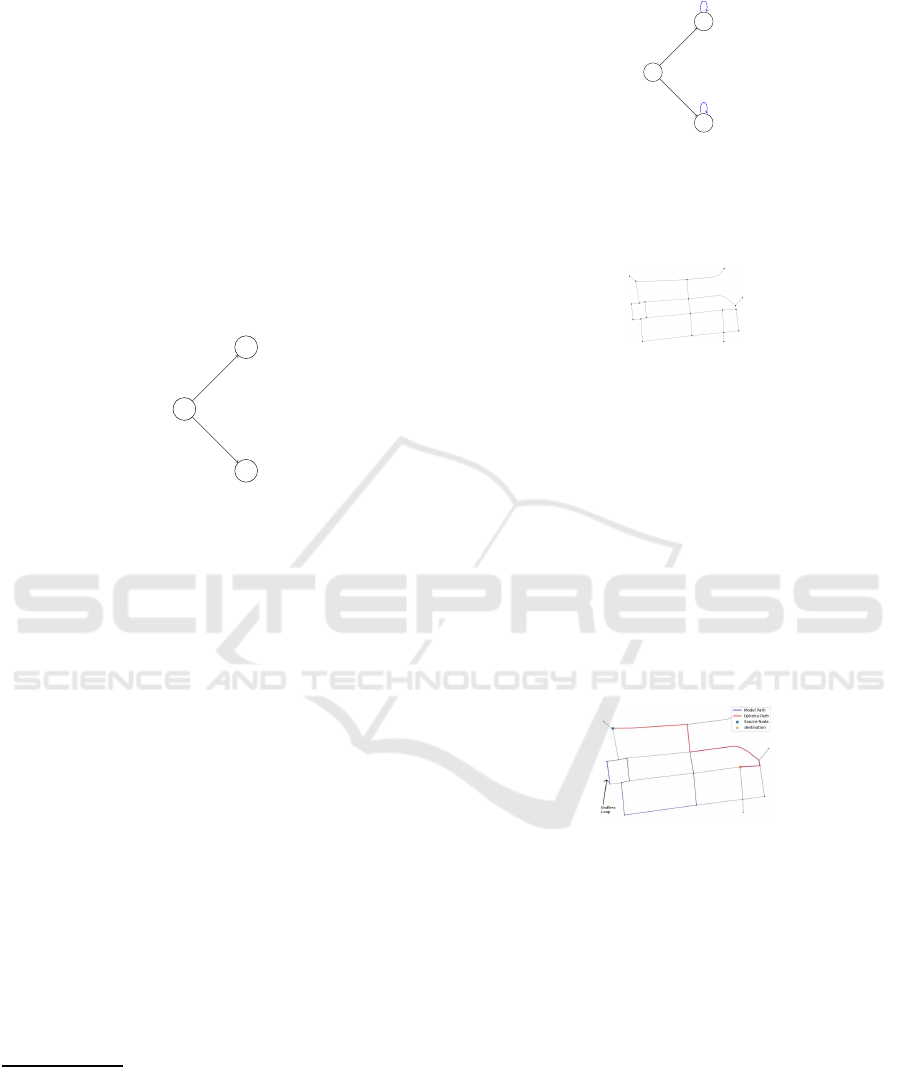
Consider the graph in Fig. 1. In this trivial graph,
there are three nodes an d three edges. If we split the
nodes, as is common practice, in three sets (training,
validation, test), the pr oblem arising is presented in
Fig. 2. Assuming that the training set includes the
nodes x
2
, x
3
and the test set include s the node x
1
,
the model can only learn the trivial rules pred (x
2
)
= x
2
and
pred (x
3
) = x
3
. If it attempts to predict
with source node x
1
, it is bo und to fail since it has
learned that given a source node x
i
, its predecessor is
the no de itself
pred (x
i
) = x
i
. This result indicates that
the choice of the training, validation, and test sets is
crucial for the model’s success. As a proof of con-
cept, if the training set equals the validation and test
sets and is e qual to the whole dataset, then the training
is concluded successfully, and the model can predict
the predecessors for all the nodes correctly. This, of
course, is an instance of overfitting, generally intol-
erable (Hawkins, 2004). However, it provide s useful
insight into the workings of the model.
Moving on to the next graph, presented in Fig. 3,
we have a very small graph of the region of Lagadas
1
https://www.openstreetmap.org/export#map=16/40.
7497/23.0724
2
https://www.openstreetmap.org/export#map=16/40.
6362/22.9477
3
https://www.openstreetmap.org/export#map=16/40.
6338/22.9543
4
https://www.openstreetmap.org/export#map=16/40.
6344/22.9618
x
1
x
2
x
3
pred(x
2
)=x
2
pred(x
3
)=x
3
Figure 2: The rules learned by the model after training.
with 21 nodes. The results in this graph prove that the
model can fully imitate the Bellman-Ford algorithm
and present a problem with gener alization.
Figure 3: Small graph of the region of Lagadas.
First, the model ach ieves 99% accuracy whe n the
training set is equal to the test set. This fact proves
its ability to imitate the Bellman-Ford algorithm de-
terministically. The proble m presented in genera liza -
tion is that th e model can get stuck into infinite loops,
either cycles or constant switching between 2 nodes
without restrictions. This phenome non is explained in
Fig. 4, where the orange line is the true shortest path,
the blue lin e is the walk produced by the m odel (note
that it is not a path since every n ode is not unique), and
the pink line is the intersection of the two. The model
is stuck in an infinite loop betwee n the two nodes in-
dicated b y the black arrow.
Figure 4: An instance of failure on the graph of Lagadas.
To understand th is phenomenon better and to
present a so lution, consider the graph of Fig. 5. It
is a simple graph with a d ead end at the node x
7
. To
be precise, we can observe that the dead end starts at
node x
5
since there is no prospect of recovery after
the model c hooses this node as a pr edecessor node.
The problem is that the following scenario leads to a
failure when reaching node x
4
if the model makes a
wrong prediction, i.e., node x
5
, since the model can-
not escape its predicament without in te rvention.
A recovery algo rithm will be deployed to re con-
struct the shortest path to combat this weakness. The
intuition of the algorithm is presented in Fig.6. When
the reconstruction algorithm reaches node x
7
, the re-
covery algorithm will back-track until it reaches the
nearest node for which there is more than one choice
ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods
390

x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
x
10
Figure 5: A simple graph that contains a dead end.
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
x
10
Figure 6: The intuition behind the recovery algorithm.
for a predecessor nod e. This last point is essential
because taking as few steps as possible is desirab le ,
just enough to steer the algorithm away from the dead
end. However, if we only took one step back to node
x
6
, the recon struction a lgorithm would end up at node
x
7
. If we reach nod e x
4
, the algorithm can recover
if we additionally fo rbid it to choose a node already
in its pa th. Thus, the next choice for a predecessor
node would be node x
2
, escaping the dead end. The
algorithm is presented in Algorithm 1.
Algorithm 1: T he recovery algorithm.
Data: path, list of nodes in c urrent path
Result: Alternative choice v that does not lead
to a dead end
;
while len(pred[v]) = 1 do
path.pop()
v = path[len(path)-1]
end
v = prev[v][k], k is the index of the
second la rgest element of pred[v]
This intervention naturally affects predictions.
During testing, the algorithm will not be deployed to
maintain the integrity of the results with respect to ac-
curacy. This process, however, is useful to guarantee
valid paths when the model fails o n its own. This al-
gorithm has computational complexity O(|V |) since,
worst-case, every node is going to be visited no mo re
than two times, one time when the algorithm reaches
the dead end, plus one time while back-tracking.
Inserting the recovery algorithm into our arsenal,
the analysis proceeds to the graph presented in Fig.
7. This is a graph of the center of Thessaloniki. This
graph pr ovides insight into h ow the model suffers in
the range it can cover. As explained in Section 3.2, an
MPNN model covers the k-neighborhood of a node,
Figure 7: The graph of the center of Thessaloniki.
where k is the number of layers of the network. This
is not a problem with graphs of high node degree (e.g.,
knowledge graphs), but it is a pro blem when dealing
with low nod e degree g raphs, like road networks. To
understand this fact, consider that the paths from one
node to another in a road network can be quite large
so that node s of interest escape the k-neighborhoo d
of a source node. Consequently, a message from the
source node is not guaranteed to reach a node, which
presents a problem when constructing a path of great
length. One solution is to deepen the model by adding
more layers. However, this solution presents more
computational complexity and m ore learnable param-
eters, leadin g to difficulties in training, and is not
guaran teed to work at all (Sun et al., 2015).
The solution is comprised o f two parts. First,
we iteratively conduct the message-passing operation
with the same mod el (i.e., a 6- la yer model) . This
guaran tees that a message from the source node can
reach every other node. The choice of the number of
iterations depends on each graph, and it has to do with
the maximum distance (in steps) to the most remote
node in the graph. In the worst case, the path from the
source node to the most remote node is of length |V |
if all nodes are consequentially sor ted. However, in
practice, the paths that need to be covered are much
shorter. Second, suppose the unaltered distance s be-
tween the node s are u sed for the weights of the graph
edges w(e) (e.g., in meters). In this case, numerical
instability is introduced into the model since the mes-
sages sent and the neural network model weights are
too large, leading to failure in training. To combat this
pheno menon, a regularization of the weights is called
for. The aim is to scale them so that iterative additions
maintain th e messages and the weights of the neu ral
network small. The regularization chosen is the min-
max regularization, g iven by
w
′
=
w − min(A)
max(A) − min(A)
(
new max(A) − new min(A))
+
new min(A)
(13)
where min and max ar e the minimum and maximum
elements of the set A, and new
min, new max are the
desirable new bounds. The result is that the elements
Applying the Neural Bellman-Ford Model to the Single Source Shortest Path Problem
391

of set A are in [ new min , new max ], and the re la tive
distances of the elem e nts are maintained. The pro b-
lem with this regularization is that outliers typically
greatly affect the quality of th e regularization. In our
case, the datasets do not contain noise, so this r egular-
ization is very powerful. We define the new interval as
[0.2, 1] since a weight of 0 has no meaning on a g raph
with no self-loops. After this regularization , the ex-
tension of the range of the message-passing process
is possible, and the result is presented in Fig. 8.
Figure 8: The expansion of the range of the message-
passing operation.
Figure 9: A graph of the region around the Aristotle Uni-
versity of Thessaloniki.
The experimental results are summarized in Table
1. The accuracy refers to the mean accuracy achieved
when p redicting predecessors, given a source node.
Another metric given is the mean distanc e of the path s
produced by the model and the true shortest paths. In
Table 1, the mean distance from the shortest path is
given with the deployment of the rec overy algorithm
and witho ut. As illustrated shortly, the metrics pre-
sented do not give a holistic picture of the model’s
efficiency.
The Evangelistria graph, Fig. 11 is a graph of a re-
gion in Thessalon iki, and its analysis is comparab le to
the sma ll graph of Lagadas presented. The Ar isto tle
University of Thessaloniki (AUTH) and Big Lagadas
graphs are comparable to the graph of the center of
Thessaloniki. They a re shown in Fig. 9 and Fig. 12.
Table 1: Results from experimental results.
Graph # layers # iterations Accuracy Mean Distance (with/
without recovery)
# epochs
Small Lagadas 4 3 90% 3m/218m 160
Big Lag adas 2 4 91% 3m/1370m 180
Evangelistria 2 4 91% 6.8m/1210m 360
Center of Thessaloniki 4 30 75% 2643m/119 82m 20
AUTH 4 20 83% 1652m/156 29m 20
One issue with the metrics given is that they d o not
take into account the damage caused by instan ces of
Figure 10: The rules learned by the model after training.
failure, because the overwhelming number of c orrect
predictions smooths accuracy, and the overwhelming
number of correct paths smooths the mean distance.
The metr ic s give us an idea concerning the general
quality of the model. However, they do not provide
us with insight regardin g instances of failure. Such an
instance is presented in Fig. 10, th e graph of AUTH.
This is an instance of failure, but with the use of the
recovery algorithm, the model can return a valid path
severely longer than the optimal path, 1663m to be ex-
act. Using the recovery algorithm, we can guarantee
valid paths that are n a turally worse than the optimal
ones. This algorithm was a product of analyzing the
model’s inner workings and instances of failure while
trying to find a cure. Many failures can be prevented,
and the results can be improved.
Figure 11: A graph of the region of Evangelistria.
Figure 12: A bigger graph of t he region of Lagadas.
5 CONCLUSIONS
We have used the Neural Bellman-Ford Network to
solve the Single-Source Shortest path problem. The
problem h as been d efined as a Predecessor Prediction
task, taking inspiration from the original Bellman-
Ford algo rithm. The Predecessor Prediction task has
been modeled as a node classification task suited to
be solved by a Message-Passing neural network. We
have examined the weaknesses of a Message-Passing
neural Network model when operating on a road net-
work. We have propo sed a solution. This paper can
ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods
392

be co nsidered a stepping stone to solving the general
Optimal Path problem, which can provide great bene-
fits to professionals and others if efficiently and suffi-
ciently so lved. Another aim of the paper has been to
motivate the integration of classical algorithms with
the latest state-of-the-art methods and the solution of
fundamental problems using those methods.
ACK NOWLEDGEMENTS
This research was carried out as part of the project
“Optimal Path Recommendation with Multi Criteria”
(Project code: KMP6-007899 7) under the framework
of the Action “Investment Plans of Innovation” of
the Operational Program ”Centr al Macedonia 2014-
2020” , that is co-funded by the E uropean Regional
Development Fund and Greece.
REFERENCES
Baras, J. S. and Theodorakopoulos, G. (2010). Path prob-
lems in networks. Synthesis Lectures on Communica-
tion Networks, 3:1–77.
Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-
Gonzalez, A., Zambaldi, V., Malinowski, M., Tac-
chetti, A., R aposo, D., Santoro, A., Faulkner, R ., G ul-
cehre, C., Song, F., Ballard, A., Gilmer, J., Dahl, G.,
Vaswani, A., Allen, K., Nash, C., Langston, V., Dyer,
C., Heess, N., Wierstra, D., Kohli, P., Botvinick, M.,
Vinyals, O., Li, Y., and Pascanu, R. (2018). Relational
inductive biases, deep learning, and graph networks.
arXiv preprint arXiv:1806.01261.
Bellman, R. (1958). On a routing problem. Quarterly of
Applied Mathematics, 16:87–90.
Bordes, A., Usunier, N., Garcia-Duran, A., Weston, J., and
Yakhnenko, O. (2013). Translating embeddings for
modeling multi-relational data. In Burges, C., Bottou,
L., Welling, M., Ghahramani, Z., and Weinberger, K.,
editors, Advances in Neural Information Processing
Systems, volume 26. Curran Associates, Inc.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische mathematik, 1(1):269–
271.
Gallager, R. G. (1982). Distributed minimum hop algo-
rithms. Technical Report LIDS-P 1175, Laboratory
for Information and Decision Systems, Massachusetts
Institute of Technology.
Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., and
Dahl, G. E. (2017). N eural message passing for quan-
tum chemistry. arXiv preprint arXiv:1704.01212.
Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-
mal basis for the heuristic determination of minimum
cost paths. IEEE Transactions on Systems Science and
Cybernetics, 4(2):100–107.
Hawkins, D . M. (2004). The problem of overfitting. Jour-
nal of Chemical Information and Computer Sciences,
44(1):1–12. PMID: 14741005.
Huang, S., Wang, Y., Zhao, T., and Li, G. (2021). A
learning-based method for computing shortest path
distances on road networks. In Proceedings of the
2021 IEEE 37th International Conference on Data
Engineering (ICDE), pages 360–371. IEEE.
Kazemi, S. M. and P oole, D. (2018). Simpl embedding for
link prediction in knowledge graphs. arXiv preprint
arXiv:1802.04868.
Kipf, T. N. and Welling, M. (2017). Semi-supervised clas-
sification with graph convolutional networks. arXiv
preprint arXiv:1609.02907.
Li, J., Zhuo, L., Lian, X., Pan, S., and Xu, L. (2022). DPB -
NBFnet: Using neural Bellman-Ford networks to pre-
dict dna-protein binding. Frontiers in Pharmacology,
13.
Martins, E., Pascoal, M., Rasteiro, D., and Santos, J. ( 1999).
The optimal path problem. Investigacao Operacional,
19:43–60.
Prim, R. C. (1957). Shortest connection networks and some
generalizations. The Bell System Technical Journal,
36(6):1389–1401.
Sun, S ., Chen, W., Wang, L., Liu, X., and Liu, T.-Y. (2015).
On the depth of deep neural networks: A theoretical
view. arXiv preprint arXiv:1506.05232.
Veliˇckovi´c, P., Ying, R., Padovano, M., Hadsell, R., and
Blundell, C. (2020). Neural execution of graph algo-
rithms. arXiv preprint arXiv:1910.10593.
Wu, N., Zhao, X. W., Wang, J., and Pan, D. (2020). Learn-
ing effective road network representation with hier-
archical graph neural networks. In Proceedings of
the 26th ACM SIGKDD international conference on
knowledge discovery & data mining, pages 6–14.
Yang, B., Wen-tau Yih, He, X., Gao, J. , and Deng, L.
(2015). Embedding entities and relations for learn-
ing and inference in knowledge bases. arXiv preprint
arXiv:1412.6575.
Zhu, Z., Zhang, Z., Xhonneux, L .-P., and Tang, J. (2021).
Neural Bellman-Ford networks: A general graph neu-
ral network framework for link prediction. In Ad-
vances in Neural Information Processing Systems,
volume 34. MIT-Press.
Applying the Neural Bellman-Ford Model to the Single Source Shortest Path Problem
393