
Parts-Based Implicit 3D Face Modeling
Yajie Gu
a
and Nick Pears
b
VGL Research Group, Department of Computer Science, University of York, YO10 5GH, U.K.
Keywords:
Face Modeling, Deformation Network, Parts Corresponding Implicit Representations, Signed Distance
Functions.
Abstract:
Previous 3D face analysis has focussed on 3D facial identity, expression and pose disentanglement. However,
the independent control of different facial parts and the ability to learn explainable parts-based latent shape
embeddings for implicit surfaces remain as open problems. We propose a method for 3D face modeling that
learns a continuous parts-based deformation field that maps the various semantic parts of a subject’s face to a
template. By swapping affine-mapped facial features among different individuals from predefined regions we
achieve significant parts-based training data augmentation. Moreover, by sequentially morphing the surface
points of these parts, we learn corresponding latent representations, shape deformation fields, and the signed
distance function of a template shape. This gives improved shape controllability and better interpretability
of the face latent space, while retaining all of the known advantages of implicit surface modelling. Unlike
previous works that generated new faces based on full-identity latent representations, our approach enables
independent control of different facial parts, i.e. nose, mouth, eyes and also the remaining surface and yet
generates new faces with high reconstruction quality. Evaluations demonstrate both facial expression and parts
disentanglement, independent control of those facial parts, as well as state-of-the art facial parts reconstruction,
when evaluated on FaceScape and Headspace datasets.
1 INTRODUCTION
Figure 1: Independent control of two facial regions.
Left: the ‘remainder’ part of the face that excludes the
nose/eyes/mouth is varied. Right: the nose region only is
varied. To achieve this, two (of the four) part-specific la-
tent embeddings are varied (±3σ) over their three principal
components. Other partial shape variations modelled are
the eye region and mouth region (see Appendix).
Three-dimensional shape representation has become
increasingly important over the last 20 years or so.
a
https://orcid.org/0000-0003-0257-0093
b
https://orcid.org/0000-0001-9513-5634
Here we focus on 3D face representation, which is
key to face reconstruction, generation and manipu-
lation. Such representations support many applica-
tions: building avatars, facial biometrics, dentistry,
orthodontics and craniofacial surgery.
Of particular note, the 3D Morphable Model
(3DMM) (Blanz and Vetter, 1999) is a widely-studied
and widely-used shape model expressed in a latent
space, with many interesting works over recent years
(Booth et al., 2016; L
¨
uthi et al., 2017; Booth et al.,
2018; Ghafourzadeh et al., 2019; Li et al., 2020;
Tewari et al., 2021; Feng et al., 2021; Ferrari et al.,
2021). A comprehensive survey on 3DMMs is pro-
vided by (Egger et al., 2020).
Existing 3D facial generative models that employ
a variational auto-encoder (VAE) are able to learn la-
tent embeddings for each face shape. Some recent
works have aimed to disentangle the latent embed-
dings on expressive facial datasets, which makes the
latent representations more explainable. Learning that
decouples identity and expression latent representa-
tions has achieved remarkable results (Gu et al., 2023;
Jiang et al., 2019; Sun et al., 2022). However, learn-
ing both controllable and disentangled latent embed-
dings for distinct facial parts is still a challenging
Gu, Y. and Pears, N.
Parts-Based Implicit 3D Face Modeling.
DOI: 10.5220/0012423200003660
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 2: VISAPP, pages
201-212
ISBN: 978-989-758-679-8; ISSN: 2184-4321
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
201

ground-
truths
predicted
shapes
Nose
Eyes
Mouth
Remainder
Figure 2: Shape reconstruction and parts-based interpolation. The four shapes on the left are two composite heads, each has
the facial features (eyes, nose, mouth) of one subject and the remainder of another subject. Both ground truth shapes and
predicted (inferred) shapes from our network are shown. In the coloured blocks, we gradually warp the first (left) head to
the second (right) by interpolating the latent vectors for each facial feature in sequence. Thus the nose, eyes, mouth and
the remaining parts deform separately. The locally-deformed details are magnified, with the three nose shapes overlaid and
marked by coloring their corresponding nose tips for easier comparison.
task, which is crucial for many applications where lo-
cal controllability is important. Examples include 3D
photofit, craniofacial surgery (e.g. minor adjustments
of the nose) or, in gaming, where small, localised fa-
cial adjustments of game characters is required.
Historically, most 3D face models have been
based on explicit representations such as point clouds,
voxel grids and meshes. However, more recently, im-
plicit representations that use signed distance func-
tions, unsigned distance fields or occupancy func-
tions have become the preferred approach (Park et al.,
2019; Mescheder et al., 2019; Chen and Zhang, 2019;
Liu et al., 2019; Chibane et al., 2020a,b; Zheng et al.,
2021; Chou et al., 2022). The benefit is that such
representations are compact and have the flexibility
to represent complex shapes that are rich in detail,
without being tied to a particular mesh resolution and
topology. Here, we focus on implicit 3D face model-
ing, where a signed distance function and shape defor-
mation fields are employed to represent face shapes,
with the goal of disentangling the encoding of specific
and distinct facial parts.
To achieve this, we propose a new approach for
facial feature swapping for data augmentation and a
parts-based sequential deformation network to learn
separate latent embeddings for separate parts. We pre-
defined three key parts of a human face: nose, eyes
and mouth - with the remainder of the facial structure
(including forehead, chin, cheeks, cranium) grouped
together as a fourth part - although, in principle, this
‘remainder’ part could be further subdivided. To learn
separate part representations, swapped facial features
across pairs of subjects using 3D affine mappings to
enable data augmentation by applying affine trans-
forms to existing facial part shapes. We then trained a
sequence of four sub-modules - one for each part de-
formation. All three part features (nose, eyes, mouth)
belong to one subject, while the ‘remaining’ part is
from a second subject. To the best of our knowledge,
our method is the first to propose latent 3D shape rep-
resentation learning that is both parts-based and im-
plicit. Our approach fits complex head shapes by part-
specific deformation to generate locally-controllable,
high-resolution shapes, see Figure 2.
In summary, the main contributions are: i) in-
troduction of a parts-based face/head representations
that enables separate, localised deformations; ii) the
ability to generate new facial parts/faces/heads; iii)
state-of-the-art performance in face reconstruction (cf
recent non-parts based approaches).
2 RELATED WORK
2.1 Generative Models
Some recent methods have been proposed for 3D face
generative models, with some of them using Varia-
tional AutoEncoders (VAEs) and others using Gen-
erative Adversarial Networks (GANs) to achieve dis-
entanglement of identity and expressions (Bagautdi-
nov et al., 2018; Taherkhani et al., 2023; Aumentado-
Armstrong et al., 2023). Jiang et al. (2019) pro-
posed a nonlinear framework to decompose 3D face
meshes into identity and expression attributes by set-
ting neutral expressions, i.e. identity attributes, as
the origin points, and they observed that different
individuals with the same expressions lie in a simi-
lar high-dimensional manifold. Thus, the expression
on mean face means the same corresponding expres-
sion representation on other faces. Sun et al. (2022)
designed two decoders to learn identity and expres-
sion separately and used an information bottleneck
on the identity reconstruction to enhance the disen-
tangled ability. Foti et al. (2022, 2023) defined a
mesh-convolutional VAE by leveraging known differ-
ences and similarities in the latent space to encour-
age a disentangled representation of identity features.
Aliari et al. (2023) used a set of graph-based varia-
tional encoders to learn representations of different
facial parts and to achieve vertex-based editing by
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
202

optimising the subset of the latent vector that corre-
sponds to the part of the face being modified. Gu et al.
(2023) exploited center points in the expression space
and the invariance of identities from same individu-
als with different expressions to address the identity
and expression disentanglement in scenarios where
neutral faces are unknown. Olivier et al. (2023) pro-
posed a new style-based adversarial autoencoder by
capturing identity and expression features in corre-
sponded low-dimensional space and used a discrim-
inator to enforce the generated shapes to be realistic
and of the correct style class . However, most ex-
isting 3D face generative models concentrate on face
reconstructions and facial identities and expressions
disentanglement, whereas our method learns specific
latent codes for each independently semantic identity
region, which are decoupled from others. Although
Foti et al. (2022, 2023), and Aliari et al. (2023) also
achieved parts disentanglement, they represented 3D
shapes in an explicit manner, which limited the reso-
lution of generated faces and required them to share
the same topology.
2.2 Deep Implicit Functions
As 3D shape representations, deep implicit functions
are attracting more attention. Compared to tradi-
tional explicit representations, such as point clouds,
meshes and voxels, deep implicit functions represent
shapes in a continuous volumetric field. Park, Flo-
rence, Straub, Newcombe and Lovegrove (2019) in-
troduced a learnt continuous signed distance func-
tion (SDF) that enables the representation of complex
shapes (Park et al., 2019). Occupancy probability is
also an option that can be used to achieve flexible res-
olutions and is more robust to complicated topologies
(Mescheder et al., 2019; Chen and Zhang, 2019; Liu
et al., 2019). Some improved works were presented
recently achieving impressive quality in shape recon-
structions, especially in capturing details (Duan et al.,
2020; Takikawa et al., 2021; Chibane et al., 2020a;
Lipman, 2021). The SIREN approach leveraged peri-
odic activation functions with multilayer perceptrons
(MLPs) to fit complicated 3D shapes and addressed
the challenging boundary value problems (Sitzmann
et al., 2020). Yenamandra et al. (2021) proposed
i3DMM, the first deep implicit 3D morphable model
of full heads, and created a new dataset consisting of
64 subjects with different expressions and hairstyles.
PIFu introduced an implicit function that aligns pix-
els of 2D images with the global context of corre-
sponding 3D objects (Saito et al., 2019). Deforma-
tion implicit networks for objects containing compli-
cated geometry variation were also explored (Zheng
et al., 2021; Deng et al., 2021; Zheng et al., 2022;
Sundararaman et al., 2022). Deng et al. (2021) fo-
cused on the template implicit field across the ob-
ject category, and represented 3D shapes by combin-
ing with the template, 3D deformations and correc-
tions. Zheng et al. (2021) learnt a plausible template
and used Long short-term memory (LSTM) as the
spatial warping module to obtain point-wise transfor-
mations in an unsupervised manner. Sundararaman
et al. (2022) and Jung et al. (2022) developed an auto-
decoder based network to recover a 3D deformation
field between a fixed template and a target shape. Re-
cent highly related studies by Zheng et al. (2022) and
Giebenhain et al. (2023) have built separate defor-
mation fields that enable the disentanglement of face
identities and expressions in implicit methods. Zheng
et al. (2022) proposed a data preprocessing method
to generate pseudo watertight shapes, while Gieben-
hain et al. (2023) released a newly-captured dataset
of over 5200 head scans from 255 different identities.
Here, we employ a network architecture inspired by
the work of (Zheng et al., 2022) to deform 3D face
shapes to a template and disentangle identity features
instead of expressions and identities, although in prin-
ciple it is straightforward to prepend an expression de-
formation to our pipeline.
3 METHOD
We now describe the problem setting and explain our
training method, in which the key concept is to swap
facial features across subject pairs to learn disentan-
gled shape part representations by feature morphs.
Our architecture, see Figure 3, is designed as a 3D
face generative model. Within this, we adopt the
‘mini-nets’ structure proposed by Zheng et al. (2022)
for cascaded 3D shape deformations.
3.1 Problem Setting
We utilise an implicit function, specifically a Signed
Distance Function (SDF), as a template shape repre-
sentation, due to its compactness and resolution-free
expressivity, for modeling the fine details of human
faces. Given a 3D query point, p ∈ R
3
, and a set of
latent vectors that represent (global) facial expression,
along with (neutral) facial part shapes, we aim to learn
a conditional SDF:
s = Φ(p|z
exp
,z
nose
,z
eyes
,z
mouth
,z
rem
), (1)
where s ∈ R is the signed distance. Facial features, i.e.
nose, eyes, mouth and the remaining face/head part
(denoted by ‘rem’), are represented by corresponding
Parts-Based Implicit 3D Face Modeling
203
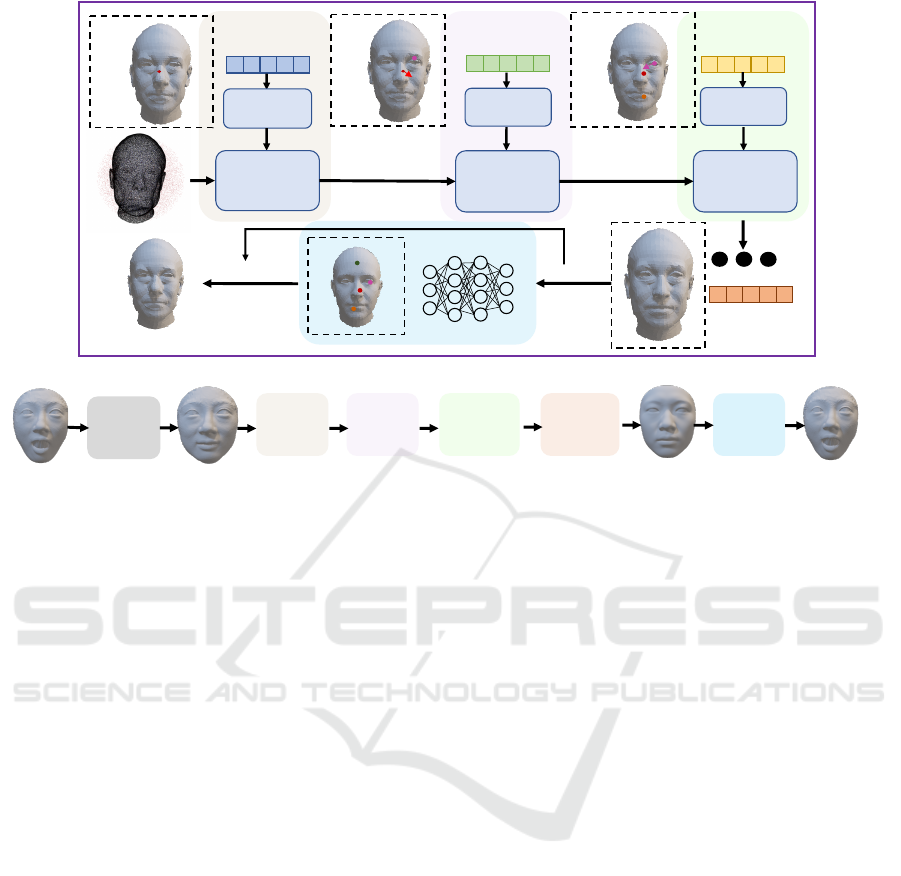
!"
#
$ %
#
&
Hyper-Net
Deform-Net
'
()*+
NoseNet
'
,+-
./
+
0
0
./
(
12
3
!1$ ./
4
&
0
SDFNet
5 6 2
predicted shapes
input point clouds
Deform-Net
'
-)789
MouthNet
!"
:
$ %
:
&
EyesNet
!"
;
$ %
;
&
Deform-Net
'
+<+*
=
>
!?$ @$ '&
N
=
A
=
>
! ?B$ @B$ 'B&
E
=
A
=
>
=
C
M
./
-
0
R
template
=
>
=
A
=
C
T
0
Hyper-Net
Hyper-Net
=
D
ExpNet
NoseNet
EyesNet
MouthNet
SDFNet
RemNet
(a) Detailed
(b) Overall
Figure 3: Architecture of our model. The end-to-end deformation network is composed of six modules (see sub-figure b),
namely ExpNet, NoseNet, EyesNet, MouthNet, RemNet - indicated by ellipsis (...) for compactness (see sub-figure a) -
and SDFNet. The five deformation modules share the same base network and deform the expressive/swapped neutral shape
components back to their corresponding shape components on the template shape. The SDFNet employs a similar network
and initialisations to SIREN (Sitzmann et al., 2020) to learn the signed distance function of the template. As noted in sub-
figure b, the input to the overall network is an expressive face. After ExpNet, a neutral face is obtained, and the part-based
deformations are processed sequentially on the neutral face.
latent vectors denoted as z
nose
, z
eyes
, z
mouth
and z
rem
,
respectively. Then the surface, Ω
0
, of a facial shape
is represented by the zero-level set of the SDF:
Ω
0
(Φ) = {p ∈ R
3
| Φ (p|z
exp
,...,z
rem
) = 0}, (2)
To learn independent latent vectors for expression and
for facial parts - and a conditional signed distance
function, we propose a sequential deformation neu-
ral network that leverages augmented face shape data
for training, by using affine maps to swap facial parts
between different subjects.
3.2 SIREN-Based Architecture
The SIREN approach (Sitzmann et al., 2020) is able
to fit highly-detailed shapes based on signed distance
functions by enforcing the Eikonal constraints for
points and supervising the gradients of sampled ori-
ented points to remain consistent with surface nor-
mals. Inspired by their work, we employ similar loss
functions for our signed distance function network as:
L
SDF
= λ
Eik
∑
p∈Ω
|
∥∇Φ(p)∥
2
− 1
|
+ λ
normal
∑
p∈Ω
(1 −
⟨
∇Φ (p),n(p)
⟩
), (3)
where ∇Φ(p) represents points gradients and n (p)
represents the surface normal. A hyper-network was
also proposed to predict the parameters of SIREN,
which can be modeled in a latent space. We adopt
this design in our model to map part-based latent rep-
resentations of each facial region to weights of our
deformation network.
3.3 Part-Based Deformation Networks
To implement the shape representation described by
Eqn. 2, our network is divided into two functional
parts: one for deformation to a template shape and the
other for the SDF of the template shape. The defor-
mation part is then constructed as a cascade of five de-
formations. As shown in Figure 3, each network com-
ponent is tailored to learn the latent representations
and deformations for either global expression or the
shape of a specific local face region relative to the cor-
responding local shape of the learnt template. There-
fore, a hyper-parameters network, denoted as Hyper-
Net, and a deformation network, denoted as Deform-
Net, are combined. As one of the key parameters to
be learnt, part-based latent codes z
part
∈ {R
d
,R
d
′
},
following a zero-mean multivariate Gaussian distri-
bution, are fed into an auto-decoder-based network
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
204

to be mapped to weights (e.g. R
d
→ R
k
) of our
Deform-Net. Ideally, the on-surface point clouds of
each predefined facial region in Deform-Net should
morph within the corresponding scope when passing
through each part-based deformation module, with
the corresponding swapped features being removed
and aligned with the template shape, which is defined
as:
ˆ
p = D
W,B
(p) + p = D (H
z
,p) + p, (4)
where D represents the Deform-Net and H represents
the Hyper-Net. D (H
z
,p) =⃗v ∈ R
3
is used for posi-
tion translation based on the given on-surface point p.
The predicted translated point, denoted by
ˆ
p, should
be located in a position according to its correspond-
ing point on the template face. Since we swap three
semantic features, i.e. nose, eyes and mouth for each
individual with those of others randomly selected (see
Section 3.4), the full deformation networks are se-
quentially connected, and after each part-based defor-
mation, its corresponding feature will be removed and
aligned with that part on the template.
For the final deformation module, RemNet, which
transforms point coordinates from specific individu-
als to the template, a displacement ε ∈ R is used to
control the shape variation of faces and improve the
shape reconstruction. Due to the variety in details
among human faces, point positional transformations
are not sufficient to fit complex deformations. There-
fore, displacements applied on signed distance fields
are essential and the form of the final Deform-Net is
D
rem
: p ∈ R
3
→
ε ∈ R,⃗v ∈ R
3
(5)
In addition to deformation networks, a fully-
connected network SDFNet is employed at the end of
the architecture to compute a signed distance for the
template face. The final signed distance for the input
face is represented as follows:
Φ (p) = S
∑
i
(p +⃗v
i
)
!
+ ε, (6)
where S represents SDFNet and i corresponds to the
index of one of the four predefined facial region, i.e.
nose, eyes, mouth and the remaining part (‘rem’).
Inspired by the work (Zheng et al., 2022) and
(Peng et al., 2021), a landmarks-generative model G
z
and a neural blend skinning algorithm (Lewis et al.,
2000) are incorporated into our network to enable bet-
ter facial detail reconstruction. In Figure 4 we show
the predefined semantic part-based landmarks marked
by different colors.
Additionally, a supervised MLP network is de-
signed to predict these landmarks for each region,
which helps to improve the effectiveness of the learnt
part-based latent representations. The predicted land-
marks are also used to to further subdivide each pre-
defined region into finer details. Deformations for in-
put point clouds are computed based on these land-
marks in a local semantic field. Following the work
(Zheng et al., 2022), we use a lightweight module to
blend local fields into a global field. Thus, our final
signed distance function Φ (p) is an extension of Eqn.
6, as follows:
Φ (p) = S
∑
i
L
∑
l=1
ω
l
p,p
i
l
p +
⃗v
i
,p
i
l
!
+
L
∑
l=1
ω
l
ε
l
,
(7)
where L is the number of landmarks and ω represents
the blend coefficients.
3.4 Dataset Augmentation by Facial
Part Swapping
In order to augment our training datasets, we swap
facial features (nose, eyes, and mouth) across pairs
of subjects, using the affine transformation that op-
timally (least squares) matches the facial feature pe-
ripheral vertices into the graft site vertices of the
face/head. We predefined surface regions for the nose,
eyes and mouth on the FaceScape dataset from (Yang
et al., 2020) and (Zhu et al., 2023), and used the
parts division scheme provided by the FLAME fitting
of the Headspace dataset (Dai et al., 2019; Zielonka
et al., 2022). Figure 4 shows the region definitions
for FaceScape and Headspace in a color coding. To
train our network, we create composite faces from a
pairs of subjects (a,b) in the training dataset partition,
where a composite face is composed from the surface
parts set as: P = {nose
a
,eyes
a
,mouth
a
,rem
b
}. Figure
4 shows a 3 × 3 array of face shapes, where each col-
umn represents a different subject (a
1...3
), while sub-
ject b, which supplies the remainder part, is kept con-
stant. Then, as we progress through the rows - the
nose, then the eyes are deformed towards the learnt
template shape. The shape shown under the Figure
4 color coding additionally has the mouth deformed
and so has the nose, eyes and mouth of the template
and the remainder part is that of subject b. This final
surface part is deformed by RemNet to generate the
full template shape.
Thus, each parts-based hyper-parameter network
outputs its corresponding factors based on the part-
based latent embeddings. This allows the model to
learn the deformation weights separately as well as in
an end-to-end manner. It is possible to further divide
the remainder surface into smaller parts (e.g. chin,
forehead, cheeks), but the difference among these
parts is harder to observe, the network training time
Parts-Based Implicit 3D Face Modeling
205

Nose
Eyes
Mouth
Colored Landmarks
Predefined Regions
Face with three
template features
Nose
Eyes
Mouth
Colored Landmarks
Predefined regions
Face with three
template features
Figure 4: Pre-defined facial regions and semantic part-based landmarks on both FaceScape (left) and Headspace dataset
(right). The nose, eyes, and mouth parts are marked in green, orange, and blue, respectively. In the 3 × 3 block, the first row
shows composite faces with subject pairings: (a
1
,b), (a
2
,b), (a
3
,b). The second row shows the nose feature being replaced
by that of the template, and the third row additionally shows the eyes being replaced by that of the template. The bottom left
shape in each block has all template features except the remainder part, which is that of subject b. On the right, five feature-
salient landmarks are selected for each region, i.e., nose, eyes, mouth, and remainder, and are marked in green, orange, blue,
and purple colors.
is higher and focussing on three key parts is sufficient
for us to demonstrate the power of our approach.
3.5 Loss Functions
To learn signed distance fields, given that the ground-
truth signed distance values of on-surface and near-
surface points can be obtained, the loss function L
rec
used to constrain the final signed distance functions
for 3D face reconstruction is formed as:
L
rec
= L
SDF
+ λ
gt
∑
p
i
∈Ω
L (Φ (p
i
),s
i
), (8)
where we use l
1
-norm as the loss for p
i
(defined in
Eqn. 6) and the ground-truth signed distance s
i
, as
well as to constrain displacements for faces.
For part-based latent representations learning, a
regularisation loss L
reg
is used for all latent embed-
dings as:
L
reg
=
∑
k∈{exp,n,m,e,r}
∥
z
k
∥
2
, (9)
where exp, n, m, e, r denote expression, nose, mouth,
eyes, remainder parts.
The loss for landmarks L
lmk
is defined as:
L
lmk
= λ
dl
L
D (p
lmk
),p
T
lmk
+ λ
gl
∑
i
L
G
z
k
,p
i
lmk
,
(10)
where l
1
-norm is used to enforce the alignment be-
tween deformed original facial landmarks D (p
lmk
)
and the template landmarks p
T
lmk
, and is also the loss
function for the landmarks-generative model G
z
.
Therefore, our network is trained in an end-to-end
manner by minimising the final loss function, denoted
as:
L = L
rec
+ L
lmk
+ λ
reg
L
reg
. (11)
During inference, the network’s weights are fixed,
and optimal latent representations z
k
are determined
as:
ˆ
z
k
= arg min
z
k
∑
(z
k
,p
i
)
L
rec
(z
k
,p
i
) +
∑
z
k
L
reg
(z
k
). (12)
4 EVALUATION
4.1 Datasets
FaceScape Dataset. (Yang et al., 2020; Zhu et al.,
2023) is a large-scale detailed face dataset consisting
of 847 subjects, each performing 20 expressions. To
ensure a fair comparison, we adopt the same scheme
as proposed in Zheng et al. (2022) to split our training
and test set. We use 365 publicly available individ-
uals, with 355 subjects’ face scans for training and
the remaining 10 for test. For each subject, we use
17 expressions to train the expression identity disen-
tanglement and randomly select 16 different subjects
and swap in their three features to train the parts-
based branch. Therefore, the training set consists of
12,070 scans (6035 for each branch), and there are
170 unseen scans in the test set. The same data pre-
processing method is also applied to crop the defined
unit sphere and generate pseudo watertight shapes.
Headspace Dataset. (Dai et al., 2019) is a set of
3D images of the human head, consisting of 1519 sub-
jects. Due to the time-consuming nature of generating
watertight shapes from the raw face data, we utilise
the FLAME (Li et al., 2017) fitting of the Headspace
dataset, as provided by Zielonka et al. (2022). During
the data pre-processing, we remove the inner struc-
ture, including the eyeballs and part of the mouth, and
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
206

also crop the neck regions. For the sake of time and
memory efficiency, we randomly select 300 subjects
from the original dataset. Following a 9:1 ratio, 270
subjects are used for training and the remaining 30
subjects are used for test.
4.2 Implementation Details
We take one part-based deformation module as an ex-
ample since all modules share same architecture. The
Hyper-Net is a ReLU MLP with one hidden layer.
The Deform-Nets and SDFNet both consist of five
fully connected layers followed by the sine activation
function. Dimensions of Latent codes are set to 48
for the nose, eyes and mouth modules, 112 for the
remainder, and 128 for expression latent codes. Dif-
ferent hyperparameters are explored to balance each
loss, including λ
Eik
being set as 50, λ
{normal,dl}
as
100, λ
gt
as 3e3, λ
reg
as 1e6 and λ
gl
as 1e3. The input
of our network are point clouds, normals and signed
distance functions pre-computed using the python li-
brary (Marian Kleineberg, 2021).
We implement the network using PyTorch and run
on two NVIDIA A40 GPUs. We train our model
using a batch size of 120 and 36, and 800 and 850
epochs for the Headspace and FaceScape dataset, re-
spectively, and 1000 epochs to fit latent representa-
tions on both datasets. The Adam Optimiser (Kingma
and Ba, 2014) is employed with the learning rate at
1×10
−4
, and a learning rate decay is set as 0.95 every
10 epochs starting from 200 epochs. We ran training
process for approximately 47 hours on the Headspace
dataset and 124 hours on the FaceScape dataset.
4.3 Reconstruction Evaluation
In our experiments, we evaluate the ability of our
model for 3D face reconstruction with Symmetric
Chamfer Distance (SCD) and F-Score at a threshold
of 0.01. We estimate SCD using 150,000 sampled sur-
face points on generated shapes and ground-truths. To
demonstrate the effectiveness of our part latent repre-
sentation, we present the results not only on full face
reconstruction but also for separate part (nose, eyes
and mouth) reconstruction. 6000 points are sampled
for each part for evaluation on FaceScape and 10,000
points are sampled on the Headspace dataset.
We compare our methods with DeepSDF (Park
et al., 2019), i3DMM (Yenamandra et al., 2021)
and ImFace (Zheng et al., 2022) on both datasets.
We also compare with FLAME (Li et al., 2017)
on the FaceScape dataset, while no comparison on
Headspace due to our use of FLAME fitting data as
ground-truths. We present the results for FaceScape
ground-
truth
DeepSDF
FLAME
Ours
ImFace
i3DMM
neutral
expressions
Figure 5: Face reconstruction for unseen face shapes on
the FaceScape dataset. Improved qualitative performance
is most clearly seen on the mouth part. No generated ex-
pressive face shapes from DeepSDF (Park et al., 2019) due
to the weak performance on detailed learning, especially the
variation on the expressive mouth.
ground-
truths
DeepSDF
i3DMM
Ours
ImFace
Figure 6: Face reconstruction for unseen face shapes on the
Headspace dataset. Note our qualitatively superior recon-
struction around the semantic facial parts, particularly evi-
dent on the mouth.
in Table 2 and Figure 5. For Headspace, the results
are shown in Table 1 and Figure 6. Since DeepSDF
learns the latent code for each face shape and has
weak performance in capturing fine details, we only
re-train DeepSDF on 355 neutral rather than all ex-
pressive face shapes.
Observed from Table 1 and Table 2, our results
demonstrate state-of-the-art performance on local de-
tail part reconstruction in both dataset. Although our
results perform slightly worse than ImFace for the full
face reconstruction, this can be attributed to the fea-
ture swapping in the predefined regions, which af-
Parts-Based Implicit 3D Face Modeling
207

Table 1: Results of shape reconstruction on the Headspace dataset (Dai et al., 2019). Compared with DeepSDF (Park et al.,
2019), i3DMM (Yenamandra et al., 2021) and ImFace (Zheng et al., 2022).
Methods
SCD (mm) ↓ F-Score ↑
Full Face Nose Eyes Mouth Rem Full Face Nose Eyes Mouth Rem
DeepSDF 0.9809 1.1972 1.0740 0.9027 0.8612 70.41 49.23 55.00 63.95 73.47
i3DMM 0.9009 0.7126 0.5623 0.6710 0.8810 69.61 79.67 89.17 81.73 70.51
ImFace 0.6992 0.7173 0.6966 0.7077 0.7357 84.22 75.71 79.92 78.07 80.93
Ours 0.7184 0.7093 0.6496 0.5910 0.7207 82.03 81.75 84.57 87.26 82.13
Table 2: Results of shape reconstruction on the FaceScape dataset (Yang et al., 2020; Zhu et al., 2023). Compared with
DeepSDF (Park et al., 2019), FLAME (Li et al., 2017), i3DMM (Yenamandra et al., 2021) and ImFace (Zheng et al., 2022).
Methods
SCD (mm) ↓ F-Score ↑
Full Face Nose Eyes Mouth Rem Full Face Nose Eyes Mouth Rem
DeepSDF 1.9393 2.0287 1.5491 1.462 1.982 25.69 27.28 35.21 37.56 27.39
FLAME 1.483 0.623 0.803 0.717 0.695 75.78 87.23 72.08 76.78 84.00
i3DMM 0.875 0.622 0.564 0.652 0.693 74.91 86.56 89.40 81.74 84.19
ImFace 0.567 0.578 0.582 0.607 0.570 94.81 90.15 88.75 84.85 96.40
Ours 0.598 0.558 0.579 0.585 0.519 92.86 91.41 89.40 86.67 96.52
fects the smoothness of the boundary between dif-
ferent parts. In Figure 5, the first three columns de-
pict face shapes with neutral expressions, and the re-
maining five columns shows faces with different ex-
pressions. It can be proven that our method facili-
tates both neutral and expressive face reconstruction
through our ExpNet and parts-based nets. We do not
train expressive faces with DeepSDF, which helps to
save time and memory.
From Figure 6, we can observe our strong per-
formance in both full and part facial reconstruction,
particularly in the mouth region. While i3DMM per-
forms slightly better in some details, e.g. the eyes re-
gion, as it samples larger ratio vertices near the nose,
eyes and mouth region. The Headspace dataset con-
sists of 3D shapes of the full head, which includes less
semantic regions such as the back of the head. There-
fore, sampling more points in specific regions benefits
to learn small local features on full heads. This could
be an improvement for our method to achieve bet-
ter results on part reconstruction when pre-processing
data.
4.4 Parts-Based Disentanglement
Our proposed method aims to disentangle latent em-
beddings from each predefined facial region. We con-
duct comprehensive experiments to evaluate the dis-
entanglement ability of our method. As presented in
Figure 2 and 8, we perform part-based latent codes in-
terpolation from two unseen reconstructed shapes in
the test set in order to observe the gradual deforma-
tion of each individual part. We also randomly gen-
Nose
Eyes Mouth Rem
Original
Figure 7: Examples of randomly generated faces/parts.
The left columns are original, unseen face shapes from the
FaceScape dataset. Parts are generated through random
Gaussian sampling applied to their corresponding part la-
tent vectors, as illustrated in the ‘Nose’, ‘Eyes’, ‘Mouth’
and ‘Rem’ columns.
erate new part features from N (0, 1) based on their
corresponding latent representations in the FaceScape
dataset, as shown in Figure 7. We conduct Princi-
pal Component Analysis (PCA) on each part’s latent
space and show their first three components along the
directions of the training set in Figure 1.
In Figure 2 and Figure 8, we interpolate learnt
part-based representations from the subject A to sub-
ject B (from the face on the left to the right in Figure
2). It is worth noting that the deformation order is not
strictly from the nose to the remaining parts. It also
can be achieved, e.g. from eyes, remainder, nose to
mouth, due to the independence of corresponding part
latent representations. The deformed local details are
visualised in Figure 2, and the error map of the per-
vertex distance between two shapes are visualised in
Figure 8. In the second row of Figure 8, the results
show the distance between the current mesh and the
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
208
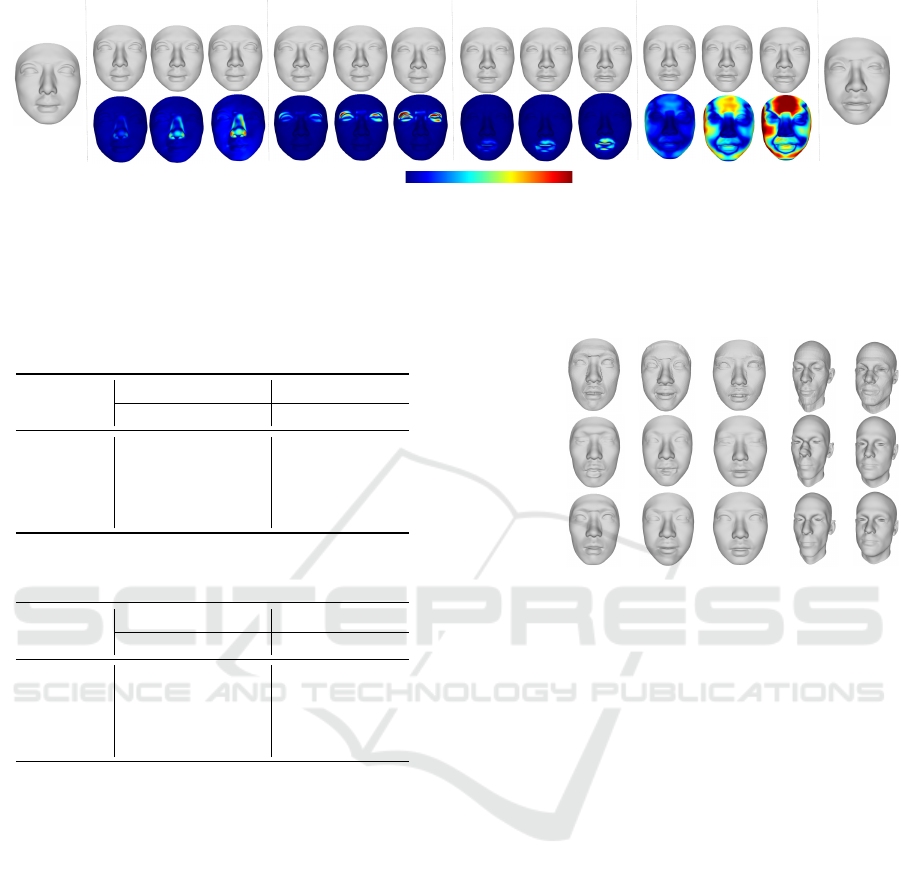
B
A
Nose
Eyes
Mouth
Remainder
0 mm
> 4 mm
Figure 8: Interpolation of parts-based latent representations for two individuals (A and B) in the FaceScape dataset. We
independently interpolate the latent representations for the nose, eyes, mouth, and remaining parts from subjects A (left) to B
(right), which are presented in four groups using the vertical dividing line. For each group, i.e. part, the error map represents
the per-vertex distance between the current shape and the first shape of the corresponding part. Meanwhile, for each first
shape within each group, it is compared with the previous one.
Table 3: Results of shape reconstruction with different land-
marks on the FaceScape dataset (Yang et al., 2020; Zhu
et al., 2023).
Parts
SCD (mm) ↓ F-Score ↑
Ours Five Ours Five
Full Face 0.5639 0.5731 95.09 94.21
Nose 0.5919 0.6133 89.25 87.71
Eyes 0.6093 0.6608 87.20 82.99
Mouth 0.5887 0.6525 86.59 82.10
Table 4: Results of shape reconstruction with different land-
marks on the Headspace dataset (Dai et al., 2019).
Parts
SCD (mm) ↓ F-Score ↑
Ours Five Ours Five
Full Face 0.7218 0.7778 81.66 79.91
Nose 0.6884 0.7251 82.89 79.84
Eyes 0.6395 0.6538 84.72 83.64
Mouth 0.5772 0.5810 88.73 88.94
first shape of the corresponding part, while for each
first shape, it is compared with the previous one. This
demonstrates that only the vertices corresponding to
the specific part deform, while the vertices of other
parts remain unchanged. It is also shown in Figure 7.
For example, in the second row of the ‘Nose’ column,
the nose becomes wider, and in the first row of the
‘Eyes’ column, the eyelids thicken. In both cases, the
other parts remain the same as the original one.
4.5 Ablation Study
We conduct experiments on landmarks selection,
comparing the five original landmarks: the nose tip,
outer eye corners and mouth corners with those used
in our method, as pre-defined in Figure 4. The re-
constructed results for full faces and nose, eyes, and
mouth part are presented in Table 3 for FaceScape and
Table 4 for the Headspace dataset, and the qualitative
results are shown in Figure 9. We can observe that the
ground-
truths
five lmks
our lmks
FaceScape
Headspace
Figure 9: Results of shape reconstruction with different
landmarks, where ’lmks’ denotes landmarks.
results based on the landmarks we used, which are de-
fined for each facial part, outperform the results based
on five landmarks of full face. Our pre-defined land-
marks help the method better learn fine details of each
part. In Figure 9, it is evident that the eyes and mouth
are disappearing when using only five landmarks.
4.6 Limitations
While our proposed method is capable of learn-
ing both global expression and separate part-based
latent representations and this enables independent
deformation on each pre-defined region, human-
understandable shape editing and further explanabil-
ity of the latent spaces requires further work.
Additionally, the quality of our generated 3D
face/head shapes is affected by region seams, result-
ing in less than ideal reconstructed surface smooth-
ness at these locations. This suggests improvements
should be achieved in the preprocessing for feature
swapping. Laplacian ICP (Iterative Closest Points)
(Pears et al., 2023) and blending (Sorkine et al., 2004)
are potential solutions to reduce curvature discontinu-
ities at the swapped junctions.
Our method focuses on 3D parts-based facial gen-
erative modeling, which has the potential to gener-
Parts-Based Implicit 3D Face Modeling
209

ate new expressions and parts and enables individ-
ual modification of each facial part independently to
subtly alter identities. We acknowledge that utilising
our method may have the potential to maliciously al-
ter digital biometric identities. Secure deployment of
systems such as ours is necessary to mitigate these
concerns.
5 CONCLUSIONS
We have demonstrated a system that can model and
generate 3D expressive face/head shapes, whereby
various semantic facial features are disentangled in
the model’s latent space, thus allowing independent
control of those parts. Use of facial feature swap-
ping allowed significant data augmentation for net-
work training and we demonstrated state-of-the-art
reconstruction results on the FaceScape dataset, with
particularly good performance on the facial parts. Ad-
ditionally we have extended evaluations by utilising
the Headspace dataset of full head shapes.
REFERENCES
Aliari, M. A., Beauchamp, A., Popa, T., and Paquette, E.
(2023). Face editing using part-based optimization of
the latent space. In Computer Graphics Forum, vol-
ume 42, pages 269–279. Wiley Online Library.
Aumentado-Armstrong, T., Tsogkas, S., Dickinson, S., and
Jepson, A. (2023). Disentangling geometric deforma-
tion spaces in generative latent shape models. Inter-
national Journal of Computer Vision, pages 1–31.
Bagautdinov, T., Wu, C., Saragih, J., Fua, P., and Sheikh,
Y. (2018). Modeling facial geometry using compo-
sitional vaes. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition,
pages 3877–3886.
Blanz, V. and Vetter, T. (1999). A morphable model for
the synthesis of 3d faces. In Proceedings of the 26th
annual conference on Computer graphics and inter-
active techniques, pages 187–194.
Booth, J., Roussos, A., Ponniah, A., Dunaway, D., and
Zafeiriou, S. (2018). Large scale 3d morphable
models. International Journal of Computer Vision,
126(2):233–254.
Booth, J., Roussos, A., Zafeiriou, S., Ponniah, A., and Dun-
away, D. (2016). A 3d morphable model learnt from
10,000 faces. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition,
pages 5543–5552.
Chen, Z. and Zhang, H. (2019). Learning implicit fields
for generative shape modeling. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition, pages 5939–5948.
Chibane, J., Alldieck, T., and Pons-Moll, G. (2020a). Im-
plicit functions in feature space for 3d shape recon-
struction and completion. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition. IEEE.
Chibane, J., Pons-Moll, G., et al. (2020b). Neural un-
signed distance fields for implicit function learning.
Advances in Neural Information Processing Systems,
33:21638–21652.
Chou, G., Chugunov, I., and Heide, F. (2022). Gensdf: Two-
stage learning of generalizable signed distance func-
tions. arXiv preprint arXiv:2206.02780.
Dai, H., Pears, N., Smith, W., and Duncan, C. (2019). Sta-
tistical modeling of craniofacial shape and texture. In-
ternational Journal of Computer Vision, 128(2):547–
571.
Deng, Y., Yang, J., and Tong, X. (2021). Deformed implicit
field: Modeling 3d shapes with learned dense corre-
spondence. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition,
pages 10286–10296.
Duan, Y., Zhu, H., Wang, H., Yi, L., Nevatia, R., and
Guibas, L. J. (2020). Curriculum deepsdf. In Euro-
pean Conference on Computer Vision, pages 51–67.
Springer.
Egger, B., Smith, W. A., Tewari, A., Wuhrer, S., Zollhoefer,
M., Beeler, T., Bernard, F., Bolkart, T., Kortylewski,
A., Romdhani, S., et al. (2020). 3d morphable face
models—past, present, and future. ACM Transactions
on Graphics, 39(5):1–38.
Feng, Y., Feng, H., Black, M. J., and Bolkart, T. (2021).
Learning an animatable detailed 3d face model from
in-the-wild images. ACM Transactions on Graphics,
40(4):1–13.
Ferrari, C., Berretti, S., Pala, P., and Del Bimbo, A. (2021).
A sparse and locally coherent morphable face model
for dense semantic correspondence across heteroge-
neous 3d faces. IEEE transactions on pattern analysis
and machine intelligence, 44(10):6667–6682.
Foti, S., Koo, B., Stoyanov, D., and Clarkson, M. J. (2022).
3d shape variational autoencoder latent disentangle-
ment via mini-batch feature swapping for bodies and
faces. In Proceedings of the IEEE/CVF Conference
on Computer Vision and Pattern Recognition, pages
18730–18739.
Foti, S., Koo, B., Stoyanov, D., and Clarkson, M. J. (2023).
3d generative model latent disentanglement via local
eigenprojection. In Computer Graphics Forum. Wiley
Online Library.
Ghafourzadeh, D., Rahgoshay, C., Fallahdoust, S.,
Aubame, A., Beauchamp, A., Popa, T., and Paquette,
E. (2019). Part-based 3d face morphable model with
anthropometric local control. In Graphics Interface
2020.
Giebenhain, S., Kirschstein, T., Georgopoulos, M., R
¨
unz,
M., Agapito, L., and Nießner, M. (2023). Learning
neural parametric head models. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition, pages 21003–21012.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
210

Gu, Y., Pears, N., and Sun, H. (2023). Adversarial 3d
face disentanglement of identity and expression. In
2023 IEEE 17th International Conference on Auto-
matic Face and Gesture Recognition (FG), pages 1–7.
IEEE.
Jiang, Z.-H., Wu, Q., Chen, K., and Zhang, J. (2019). Dis-
entangled representation learning for 3d face shape.
In Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 11957–
11966.
Jung, Y., Jang, W., Kim, S., Yang, J., Tong, X., and Lee, S.
(2022). Deep deformable 3d caricatures with learned
shape control. In ACM SIGGRAPH 2022 Conference
Proceedings, pages 1–9.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Lewis, J. P., Cordner, M., and Fong, N. (2000). Pose space
deformation: a unified approach to shape interpolation
and skeleton-driven deformation. In Proceedings of
the 27th annual conference on Computer graphics and
interactive techniques, pages 165–172.
Li, R., Bladin, K., Zhao, Y., Chinara, C., Ingraham, O.,
Xiang, P., Ren, X., Prasad, P., Kishore, B., Xing, J.,
et al. (2020). Learning formation of physically-based
face attributes. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition,
pages 3410–3419.
Li, T., Bolkart, T., Black, M. J., Li, H., and Romero, J.
(2017). Learning a model of facial shape and expres-
sion from 4D scans. ACM Transactions on Graphics,
(Proc. SIGGRAPH Asia), 36(6):194:1–194:17.
Lipman, Y. (2021). Phase transitions, distance functions,
and implicit neural representations. arXiv preprint
arXiv:2106.07689.
Liu, S., Saito, S., Chen, W., and Li, H. (2019). Learning
to infer implicit surfaces without 3d supervision. Ad-
vances in Neural Information Processing Systems, 32.
L
¨
uthi, M., Gerig, T., Jud, C., and Vetter, T. (2017). Gaussian
process morphable models. IEEE transactions on pat-
tern analysis and machine intelligence, 40(8):1860–
1873.
Marian Kleineberg (2021). mesh-to-sdf. https://github.com/
marian42/mesh
to sdf.
Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S.,
and Geiger, A. (2019). Occupancy networks: Learn-
ing 3d reconstruction in function space. In Proceed-
ings of the IEEE/CVF Conference on Computer Vision
and Pattern Recognition, pages 4460–4470.
Olivier, N., Baert, K., Danieau, F., Multon, F., and Avril, Q.
(2023). Facetunegan: Face autoencoder for convolu-
tional expression transfer using neural generative ad-
versarial networks. Computers & Graphics, 110:69–
85.
Park, J. J., Florence, P., Straub, J., Newcombe, R., and
Lovegrove, S. (2019). Deepsdf: Learning continuous
signed distance functions for shape representation. In
Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 165–174.
Pears, N., Dai, H., Smith, W., and Sun, H. (2023). Lapla-
cian icp for progressive registration of 3d human head
meshes. In 2023 IEEE 17th International Conference
on Automatic Face and Gesture Recognition (FG),
pages 1–7. IEEE.
Peng, S., Dong, J., Wang, Q., Zhang, S., Shuai, Q., Zhou,
X., and Bao, H. (2021). Animatable neural radiance
fields for modeling dynamic human bodies. In Pro-
ceedings of the IEEE/CVF international conference
on computer vision, pages 14314–14323.
Saito, S., Huang, Z., Natsume, R., Morishima, S.,
Kanazawa, A., and Li, H. (2019). Pifu: Pixel-aligned
implicit function for high-resolution clothed human
digitization. In Proceedings of the IEEE/CVF inter-
national conference on computer vision, pages 2304–
2314.
Sitzmann, V., Martel, J. N., Bergman, A. W., Lindell, D. B.,
and Wetzstein, G. (2020). Implicit neural representa-
tions with periodic activation functions. In arXiv.
Sorkine, O., Cohen-Or, D., Lipman, Y., Alexa, M., R
¨
ossl,
C., and Seidel, H.-P. (2004). Laplacian surface
editing. In Proceedings of the 2004 Eurograph-
ics/ACM SIGGRAPH symposium on Geometry pro-
cessing, pages 175–184.
Sun, H., Pears, N., and Gu, Y. (2022). Information
bottlenecked variational autoencoder for disentangled
3d facial expression modelling. In Proceedings of
the IEEE/CVF Winter Conference on Applications of
Computer Vision, pages 157–166.
Sundararaman, R., Pai, G., and Ovsjanikov, M. (2022).
Implicit field supervision for robust non-rigid shape
matching.
Taherkhani, F., Rai, A., Gao, Q., Srivastava, S., Chen, X.,
de la Torre, F., Song, S., Prakash, A., and Kim, D.
(2023). Controllable 3d generative adversarial face
model via disentangling shape and appearance. In
Proceedings of the IEEE/CVF Winter Conference on
Applications of Computer Vision, pages 826–836.
Takikawa, T., Litalien, J., Yin, K., Kreis, K., Loop, C.,
Nowrouzezahrai, D., Jacobson, A., McGuire, M., and
Fidler, S. (2021). Neural geometric level of detail:
Real-time rendering with implicit 3d shapes. In Pro-
ceedings of the IEEE/CVF Conference on Computer
Vision and Pattern Recognition, pages 11358–11367.
Tewari, A., Seidel, H.-P., Elgharib, M., Theobalt, C., et al.
(2021). Learning complete 3d morphable face mod-
els from images and videos. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition, pages 3361–3371.
Yang, H., Zhu, H., Wang, Y., Huang, M., Shen, Q., Yang,
R., and Cao, X. (2020). Facescape: a large-scale high
quality 3d face dataset and detailed riggable 3d face
prediction. In Proceedings of the IEEE/CVF Confer-
ence on Computer Vision and Pattern Recognition.
Yenamandra, T., Tewari, A., Bernard, F., Seidel, H.-P., El-
gharib, M., Cremers, D., and Theobalt, C. (2021).
i3dmm: Deep implicit 3d morphable model of human
heads. In Proceedings of the IEEE/CVF Conference
on Computer Vision and Pattern Recognition, pages
12803–12813.
Parts-Based Implicit 3D Face Modeling
211

Zheng, M., Yang, H., Huang, D., and Chen, L. (2022). Im-
face: A nonlinear 3d morphable face model with im-
plicit neural representations. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition, pages 20343–20352.
Zheng, Z., Yu, T., Dai, Q., and Liu, Y. (2021). Deep implicit
templates for 3d shape representation. In Proceedings
of the IEEE/CVF Conference on Computer Vision and
Pattern Recognition, pages 1429–1439.
Zhu, H., Yang, H., Guo, L., Zhang, Y., Wang, Y., Huang,
M., Wu, M., Shen, Q., Yang, R., and Cao, X.
(2023). Facescape: 3d facial dataset and benchmark
for single-view 3d face reconstruction. IEEE transac-
tions on pattern analysis and machine intelligence.
Zielonka, W., Bolkart, T., and Thies, J. (2022). Towards
metrical reconstruction of human faces. European
Conference on Computer Vision.
VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications
212
