Identification of Bistability in Enzymatic Reaction Networks Using

Hysteresis Response

Takashi Naka

Faculty of Science and Engineering, Kyushu Sangyo University, Fukuoka, Japan

Keywords: Enzymatic Reaction Network, Regulatory Network, Hysteresis Response, Bistability, Mathematical Model.

Abstract: Intracellular signaling systems can be viewed as enzymatic reaction networks in which enzymes regulate each

other through activation and inactivation, and exhibit various properties such as bistability depending on their

regulatory structure and parameter values. In this study, we formulate the intracellular signaling systems as

regulatory networks whose nodes are cyclic reaction systems of enzyme activation and inactivation, and

propose an evaluation function that can identify bistability with low computational cost. For the purpose of

demonstrating its effectiveness, we identified 4- and 5-node regulatory networks that exhibit bistability.

Furthermore, the effect of parameter values on bistability was analyzed, suggesting that the regulatory

structure is more dominant than parameter values for the emergence of bistability.

1 INTRODUCTION

Intracellular signaling systems can be viewed as

enzymatic reaction networks in which enzymes

regulate each other through activation and

inactivation, and are known to exhibit various

characteristics depending on their regulatory

relationships and parameter values (Ferrell, 1998;

Jeschke et al., 2013; Kholodenko, 2006; Mai & Liu,

2013; Qiao et al., 2007; Volinsky & Kholodenko,

2013). For example, the MAPK cascade, one of the

most representative and well analyzed enzymatic

reaction network, has been reported to have

ultrasensitive properties that can function as an

analog-to-digital conversion in the cell. It has also

been shown that it can be bistable as an extreme case.

Multistability, represented by bistability,

corresponds to a stable group of states in the cell and

is thought to provide robust control over intra- and

extracellular disturbances (Gedeon et al., 2018; Ma et

al., 2009; Yao et al., 2011). Bistability is also an

important property from the standpoint of synthetic

biology, as it may function as a memory element

(Doncic et al., 2015). Therefore, it is interesting to

know what kind of regulatory structures and

parameter values of enzymatic reaction networks

show bistability, and studies have been conducted to

analyze the properties of enzymatic reaction networks

http://www.is.kyusan-u.ac.jp/~naka/

by changing the structure and parameter values of the

networks in an exhaustive manner (Kuwahara & Gao,

2013; Ramakrishnan & Bhalla, 2008; Shah & Sarkar,

2011; Siegal-Gaskins et al., 2011; Sueyoshi & Naka,

2017).

In order to identify enzymatic reaction networks

with specific properties, such as bistability, an

evaluation function is needed to quantify the degree

of the property. It is also necessary to select an

appropriate mathematical model to describe the

enzymatic reaction networks. With respect to the

number of enzyme species that comprise the

enzymatic reaction network, several efforts have been

made to address the combinatorial increase in

computational cost of their identification.

One innovation is the simplification of the

mathematical model of enzymatic reactions.

Enzymatic reactions can be described by a system of

differential equations by applying the law of mass

action, but to reduce computational cost, the

Michaelis-Menten or linear approximation is

sometimes used (Adler et al., 2017; Kuwahara & Gao,

2013; Ma et al., 2009; Shah & Sarkar, 2011; Sueyoshi

& Naka, 2017; Yao et al., 2011). However, if

possible, the analysis would be more accurate without

those approximations. In fact, with respect to

bistability, it has been suggested that the Michaelis-

Menten approximation overstates the evaluation

Naka, T.

Identiﬁcation of Bistability in Enzymatic Reaction Networks Using Hysteresis Response.

DOI: 10.5220/0012416000003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 1, pages 479-486

ISBN: 978-989-758-688-0; ISSN: 2184-4305

479

(Kim & Tyson, 2020; Naka, 2020). Therefore, in this

study, we use a mathematical model that does not

make any approximations, only applying the law of

mass action.

There are also several methods for the evaluation

function of bistability. An enzymatic reaction

network has two kinds of parameters: the total

concentration of each enzyme that makes it up and the

reaction rate constants for each enzyme. For a

particular set of parameter values of a system, there

are possible ways to transition from a random initial

value group to a steady state (Naka, 2022). If the

system is bistable and a sufficient number of initial

value groups are used, bistability can be detected due

to the system transitions to two values of steady

states. However, the computational cost is higher

because steady-state values must be obtained for a

number of initial value groups.

Another possible method is to fix one value of a

certain reaction rate constant, etc. as an input to the

system, and then gradually change the value to obtain

a steady state sequentially. If the system is bistable, it

takes advantage of the property that different steady-

state values are reached when its input values are

increased or decreased. This is less computationally

expensive than the aforementioned method. This

method will be referred to as the sequential steady-

state tracking method in this study. Figure 1 shows an

example of a regulatory network consisting of 4

nodes. In this study, we propose an evaluation

function using hysteresis response that extends the

sequential steady-state tracking method and verify its

effectiveness.

The MAPK cascade, a representative signaling

system that relays between the plasma membrane and

cell nucleus with respect to cell growth factor (EGF)

signaling, is thought to be the cause of cell cancer,

and much has been learned about its abnormalities

(Ferrell, 1998; Jeschke et al., 2013; Kholodenko,

2006; Mai & Liu, 2013; Qiao et al., 2007; Volinsky

& Kholodenko, 2013). A major component of the

signaling system represented by the MAPK cascade

is the enzymatic activation/inactivation cyclic

reaction system through phosphorylation and

dephosphorylation of enzymes. The cyclic reaction

system is a combination of two post-translational

modification reactions. Therefore, we model and

analyze the intracelluler signaling system as a

regulatory network consisting of enzymatic

activation/inactivation cyclic reaction systems, which

mutually regulate each other.

Figure 1: Regulatory network consisting of 4 nodes. The

number is the node number. Node 1 is an input node. Node

4 is the output node. Blue and red arrows represent positive

and negative regulations, respectively.

2 REGULATORY NETWORKS TO

BE ANALYZED

The regulatory network is a representation of the

regulatory relationships between enzymes, where

each node included corresponds to a cyclic reaction

system of enzymatic activation and inactivation. The

cyclic reaction system is an enzymatic reaction

system that combines two post-translational

modification reactions represented by

phosphorylation. It is represented by the following

reaction scheme.

is the inactive form of the enzyme, S

is the

activating enzyme that catalyzes the activation of U

is the enzyme-substrate complex to which U

and

are bound, P

is the active form of the enzyme, V

is the inactivating enzyme that catalyzes the

inactivation of P

, R

is the enzyme-substrate complex

to which P

and V

are bound. a

, d

, k

, b

, e

, and l

are

the reaction rate constants for each reaction. The

subscript i is the node number in the regulatory

network.

By applying the law of mass action to the reaction

scheme, we obtain a system of differential equations

describing the behavior of the system shown below.

The activated enzyme P

catalyzes the activation or

inactivation reaction of the enzyme at the other node.

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

480

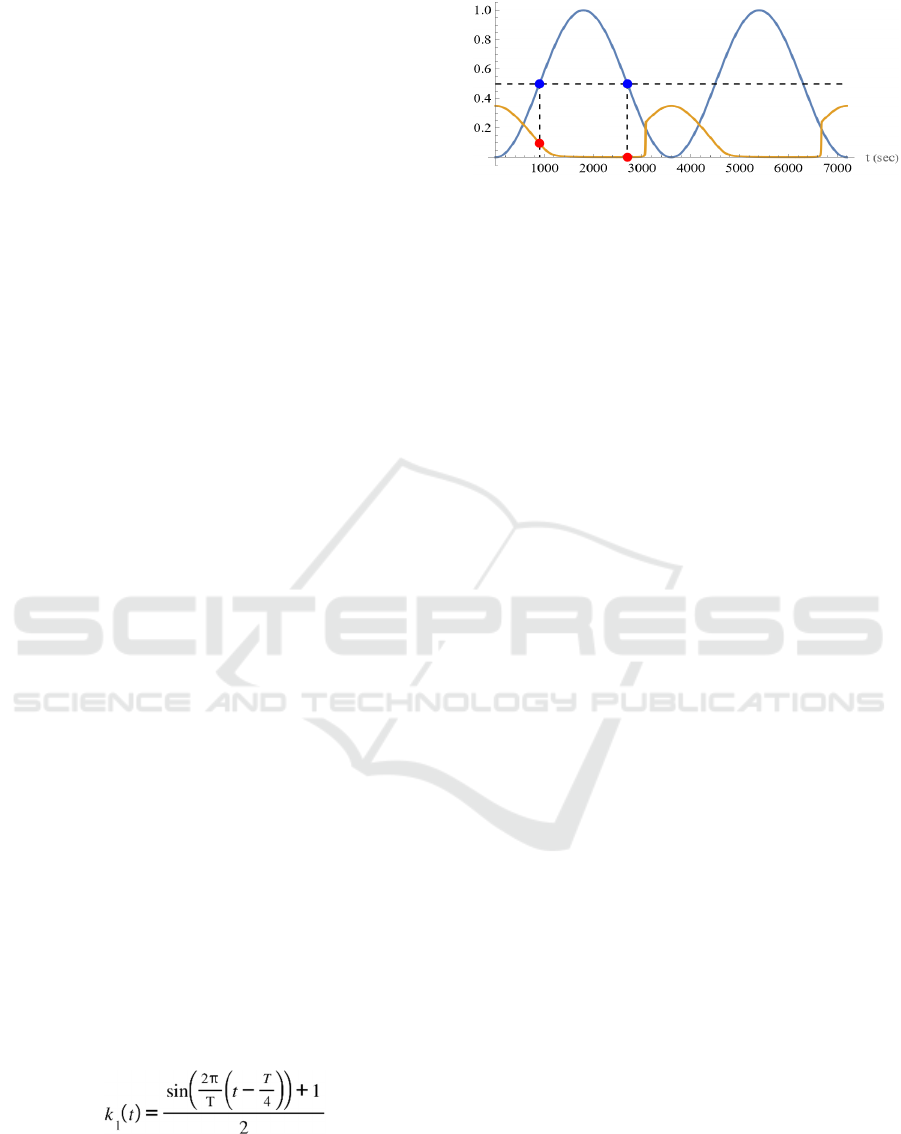
Figure 1 shows an example of a regulatory

network consisting of 4 nodes. The blue arc from

node j to node i means that the activated enzyme P

node j is catalyzing the activation reaction of the

enzyme at node i as the activated enzyme S

. This is

called node j positively regulating node i. The red arc

from node j to node i means that the activated enzyme

at node j is catalyzing the inactivation reaction of

the enzyme at node i as the inactivating enzyme V

This is called node j negatively regulating node i.

In this study, assuming a typical signaling system

such as a MAPK cascade, we will analyze regulatory

networks with 4 and 5 nodes that satisfy the following

constraints.

• It has one input node and one output node, and

is connected from the input node to the output

node with positive or negative regulations

through intermediate nodes.

• Each node receives at most two regulations,

positive and negative, from the other nodes.

• Each node regulates at most two other nodes.

• There is no auto-regulaton.

• The input node is node 1 and is not regulated by

any other node.

• The output node is node N if the number of

nodes is N. Since a regulation of the outside of

the regulatory network is assumed for the output

node, the output node regulates at most one

other node in the regulatory network.

There are 80 regulatory networks of 4 nodes and 912

regulatory networks of 5 nodes that satisfy the above

conditions.

3 IDENTIFICATION OF

BISTABILITY USING THE

HYSTERESIS RESPONSE

The value of the reaction rate constant k

of the cyclic

reaction system corresponding to the input node is the

external input to the regulatory network, which is the

oscillatory stimulus in the following equation.

T is the period of oscillation. In this study, the period

was set to 3600 seconds, i.e. 1 hour. This is large

enough to allow time for the intracellular signaling

system to reach a steady state.The system is intended

Figure 2: Oscillatory input and the response. Response of

the output enzyme activity to the oscillatory input stimulus

for the regulatory network of Fig. 1. The blue curve is the

time course of k

, the input to the system. Two periods are

displayed. The ochre curve is the time course of the relative

concentration of P

, the output of the system. The red circle

corresponds to the value of the output when the value of the

input is 0.5, indicated by the blue circle.

to maintain an approximate steady state in its

response to the oscillatory input. The output of the

regulatory network is the relative concentration P

the activated enzyme at node N if the number of nodes

is N.

Figure 2 shows an example of the response of the

4-node regulatory network shown in Fig. 1 to a

oscillatory input. The total concentration of each

enzyme and the reaction rate constant are all set to 1,

except for k

, the input to be varied. The unit system

is the μM-sec system. The blue curve is the time

course of k

, the input to the system. Two periods are

displayed. The ochre curve is the time course of the

relative concentration of P

, the output of the system.

The time course of the output differs when the input

is increasing and when it is decreasing, indicating the

appearance of hysteresis. When the input is

increasing, the output gradually decreases as the input

increases, but when the input is decreasing, the output

is almost zero until the value of the input is around

0.25, at which point it rapidly increases. The red

circle in the figure corresponds to the value of the

output when the input value is 0.5, indicated by the

blue circle. It can be seen that the values are different

when the input is increasing and when it is

decreasing.

The phase diagram between input k

and output P

in Fig. 2 is shown in Fig. 3. The blue and red circles

correspond to those in Fig. 2. The upper right-

descending line corresponds to the output when the

input is rising, and the lower curve corresponds to the

output when the input is decreasing. It can be seen

that a typical hysteresis appears, where the response

differs between rising and falling inputs. From the

figure, it can be read that the input is bistable in the

range of 0.2 to around 0.8.

Identiﬁcation of Bistability in Enzymatic Reaction Networks Using Hysteresis Response

481

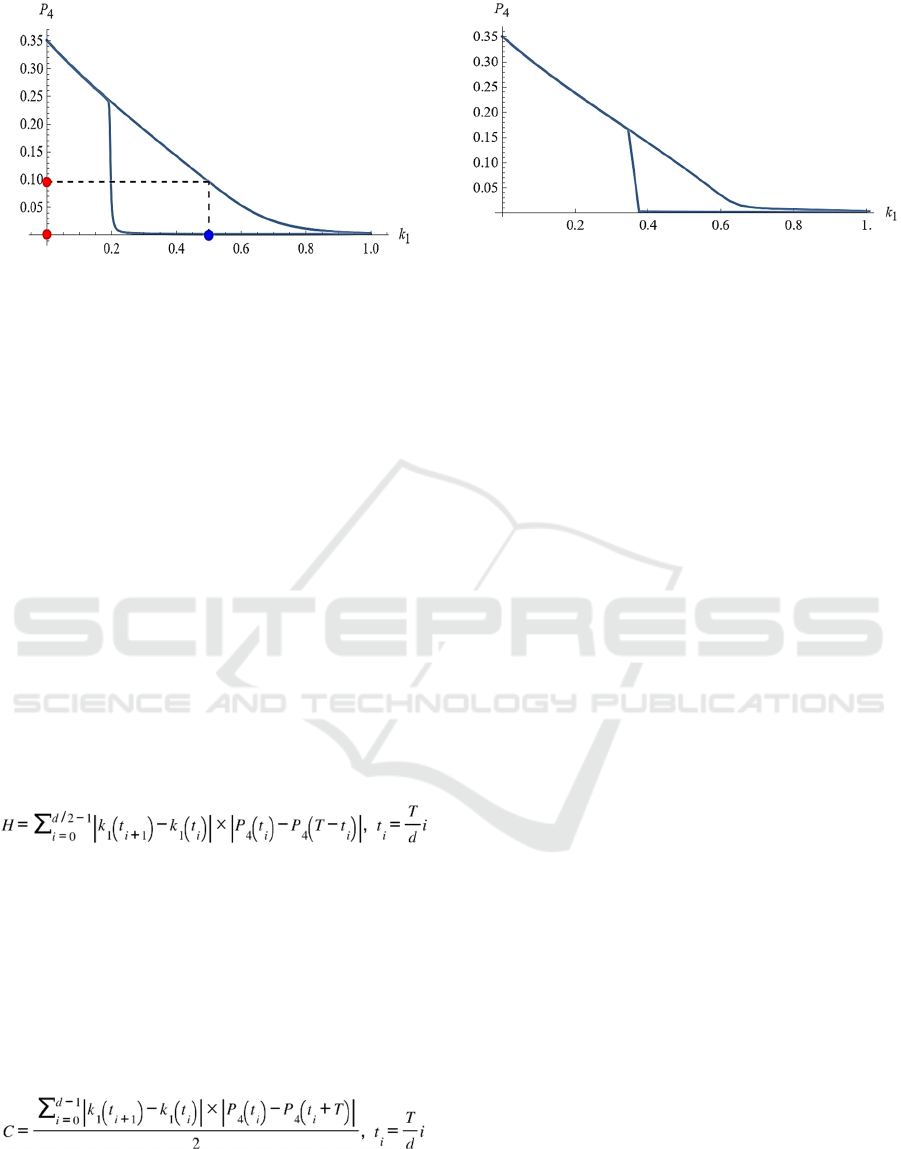
Figure 3: Hysteresis on the oscillatory response. Phase

diagram of the input k

and output P

in Fig. 2. The blue and

red circles correspond to those in Fig. 2.

The hysteresis loss H is used as a quantitative

measure of the bistability of the system, which is

formulated as bellow.

The hysteresis loss is the area of the closed region

appearing in the phase diagram. The area is

approximated by a finite sum of T/d time intervals,

where T is the period of the input and d is the number

of divisions. Since both input and output are

normalized to a maximum value of 1, the maximum

hysteresis loss is 1. In this study, the value of the

number of divisions d is set to 50. The convergence

rate C is used to quantify the degree of convergence

of the hysteresis loss, which is formulated as bellow.

This is the difference between the hysteresis loss in

the first period and the hysteresis loss in the

subsequent period.

Figure 4 shows the hysteresis loss using the

sequential steady-state tracking method mentioned

above. This is a method in which the steady-state

value of the system is first obtained with zero input,

and the value at that time is used as the initial value,

and the steady-state value is obtained sequentially as

the input is gradually increased. Therefore, the

accuracy is considered to be higher than the method

using hysteresis response proposed here. However, if

this method is executed in a form corresponding to

the number of divisions mentioned above, a

convergence calculation of the system is performed

for the number of divisions, and the computational

cost is at least the number of division times. The

curves in Fig. 4 is similar to that in Fig. 3 using

hysteresis, indicating that the hysteresis-based

method proposed here is effective. Mathematica

Figure 4: Hysteresis on the steady state. Hysteresis loss by

sequential steady-state tracking method.

v13.0 was used to derive a system of differential

equations describing the behavior of the system from

the enzymatic reaction network and to numerically

solve the derived system of differential equations to

calculate hysteresis loss H and convergence rate C,

and to analyze bistability (Wolfram Research, 2021).

4 IDENTIFICATION OF

BISTABLE REGULATORY

NETWORKS

The results of the analysis for 80 regulatory networks

of 4 nodes that satisfy the constraints are shown in

Fig. 5. The horizontal axis is the hysteresis loss H and

the vertical axis is the convergence rate C. The total

concentration of each enzyme and the reaction rate

constants, all set to 1, are circled in red. The unit

system is μM-sec.

To further investigate the effect of reaction rate

constants on hysteresis loss, the reaction rate

constants of the nodes other than the input node were

varied. However, to prevent the combination of

parameters from becoming too large, the six values

included in the cyclic reaction system comprising

each node were kept the same value. The range of

change was set to 11 values of 2

(p is an integer from

-5 to 5) to approximately include the values used in

the literature as reaction rate constants for the

enzymes comprising the MAPK cascade (Brightman

& Fell, 2000; Hatakeyama et al., 2003; Huang &

Ferrell, 1996; Levchenko et al., 2000; Schoeberl et

al., 2002). On the other hand, with respect to the input

node, k

among the reaction rate constants of that

cyclic reaction system was assumed to be the

oscillatory input and all other reaction rate constants

were fixed at 1, since it is intended to change the

concentration of P

, which is the input to node 2.

Thus, the total number of combinations of parameters

is 11

=1331. In practice, however, the values of all

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

482

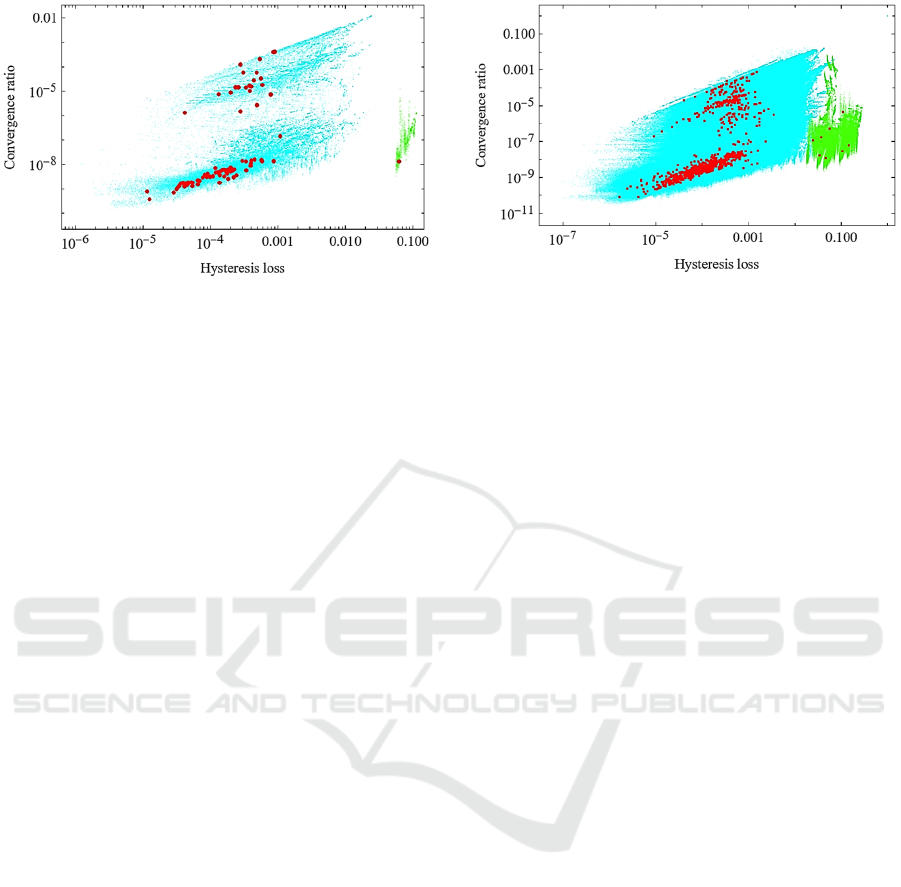
Figure 5: Aspect of hysteresis on 4 nodes networks. Results

for 80 4-node regulatory networks. The horizontal axis is

the hysteresis loss H and the vertical axis is the convergence

rate C. The red circles are the results when the total

concentration of each enzyme and the reaction rate

constants are all set to 1. The other set of fine dots

correspond to the case where the reaction rate constants of

the nodes other than the input node are varied.

reaction rate constants are multiplied by a factor of 10

for the purpose of increasing the rate of convergence.

This is the same as multiplying the period of the

oscillatory input by a factor of 10, which means that

the velocity of the oscillation is slowed down to 1/10.

The results are shown as a set of blue and green

fine dots in Fig. 5. Only one regulatory network had

a hysteresis loss value of about 0.1. The hysteresis

loss of 0.1 is a fairly prominent value for the

hysteresis loss region in the phase diagram. This

regulatory network corresponds to the red circle and

the fine green points isolated on the right side of the

figure. This is the regulatory network used as an

example in Fig. 1 through Fig. 4. Compared to the

distribution of the red circles, the variation due to the

parameter values indicated by the fine colored dots is

distributed over a limited small area. This suggests

that the network structure is dominant with respect to

the property of bistability and robust with respect to

parameter values, despite the limitation that the

reaction rate constants within each node are identical.

There are 912 regulatory networks of 5 nodes that

satisfy the constraints. Figure 6 shows the results of

the analysis. As in Fig. 5, the horizontal axis is the

hysteresis loss H and the vertical axis is the

convergence rate C.

The meaning of the red circles and colored fine

point groups is the same as in Fig. 5. In the 6-node

regulatory network, eight had hysteresis loss values

greater than 0.01. These correspond to the eight red

circles and green fine dots scattered on the right side

of the fig. 6. As in the 5-node regulatory network, the

variation due to the values of the parameters indicated

Figure 6: Aspect of hysteresis on 5 nodes networks. Results

for 912 5-node regulatory networks. The horizontal axis is

the hysteresis loss H and the vertical axis is the convergence

rate C. The red circles are the results when the total

concentration of each enzyme and the reaction rate

constants are all set to 1. The other set of fine dots

correspond to the case where the reaction rate constants of

the nodes other than the input node are varied.

by the fine blue and green dots is distributed in a

limited area, compared to the distribution of the red

circles. This suggests again that the network structure

is dominant with respect to the bistability property

and robust with respect to the parameter values,

although there is still the restriction that the reaction

rate constants within each node are identical.

Figure 7 shows 5-node regulatory networks with

hysteresis loss greater than 0.01. The regulatory

structure of the network and the phase diagram of

input k

and output P

are laid out. It can be seen that

the regulatory structure of the 4-node regulatory

network, which exhibits the bistability shown in Fig.

1, is contained in the third from the top of the left

column and the second from the top of the right

column. It is a structure of mutual negative regulation

between node 2 and node 3 and positive regulation

between node 3 and node 4. The regulatory structures

of the remaining three regulatory networks are also

found to have similar structures, although there is

intervening positive regulation in between.

5 CONCLUSIONS

For 4- and 5-node regulatory networks, where the

cyclic reaction system is the node and the regulatory

relationship between them is the arc, the method

using hysteresis response for identifying bistability

was found to be effective. This method has errors

compared to the sequential steady-state tracking

method, but the computational cost is much lower.

Identiﬁcation of Bistability in Enzymatic Reaction Networks Using Hysteresis Response

483

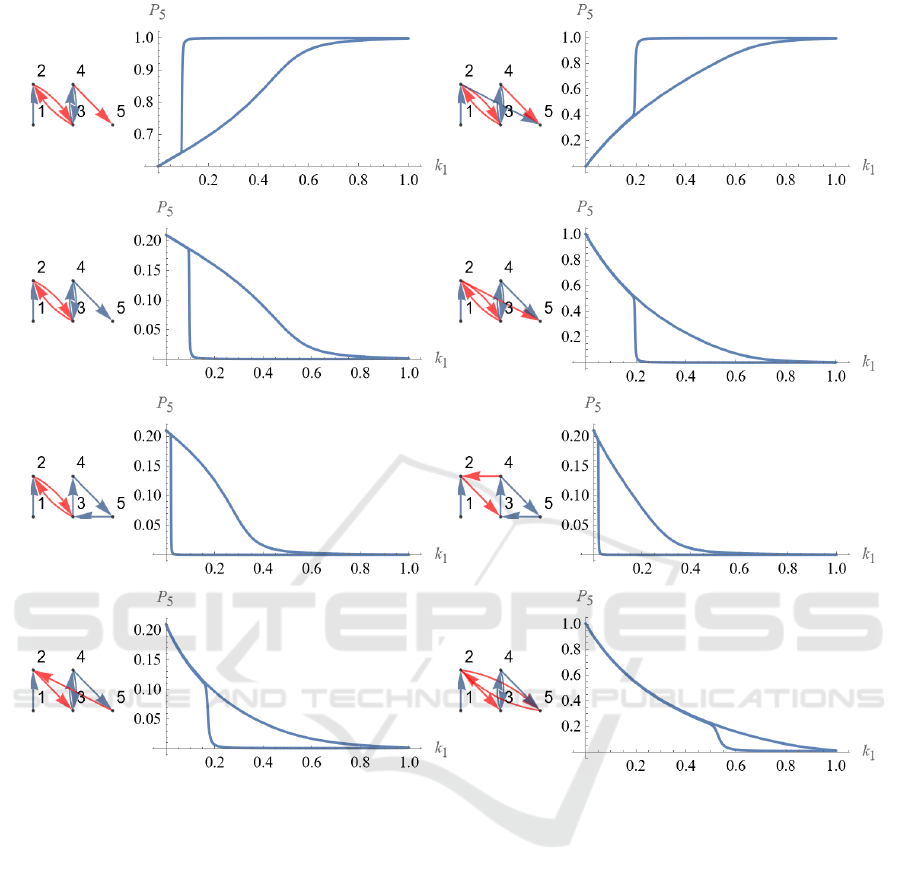
Figure 7: Bistable regulatory 5 nodes networks. 5-node regulatory networks with hysteresis loss greater than 0.01. The

regulatory structure of the network and the phase diagram of input k

and output P

are laid out.

This error is not particularly problematic when it

comes to primary screening of the regulatory

networks.

The authors have proposed a representation of

enzymatic reaction networks using set partitioning

and a search algorithm based on the representation, in

which a method with random initial value group is

used as the evaluation function for bistability (Naka,

2022). The computational cost was therefore

enormous, requiring time on the order of several days

to complete the search. The evaluation function using

hysteresis response proposed here is expected to have

an application to search as well, since its cost is

expected to be about 1/100 of that estimated from its

computational complexity. In fact, most of the

computational cost is the convergence calculation

performed to find the steady state of the system. In

the sequential steady state tracking method used to

validate the proposed method, the convergence

calculation must be performed as many times as the

number of divisions of the parameter values to be

analyzed, which in this study is set at 50, resulting in

a computational cost approximately 50 times higher.

Furthermore, the method using a random initial value

group described above requires a sufficient number of

initial values to separate two transition destinations in

a bistable system. Even if the value is set to about 10,

the convergence calculation must be performed about

500 times, i.e., the number of initial values multiplied

by the number of divisions. In the evaluation function

using the hysteresis response proposed here, the

convergence calculation to find the steady state of the

system only needs to be performed once to find the

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

484

initial values, and as a result, the computational cost

is about 1/100 of the original cost.

The results also suggest that the regulatory

structure of the network is dominant with respect to

the bistability compared to the parameter values. This

indicates that, when searching for regulatory

networks with bistability, it may be effective, for

example, to fix all parameter values to 1 and search

for variations in structure only.

By the way, the enzymatic reaction networks

analyzed here were cyclic reaction systems as nodes.

The MAPK cascade, a typical signal transduction

system, includes the process of double

phosphorylation. To extend the mathematical model

of this study to include the process of double

phosphorylation in the analysis, the set of differential

equations derived from a single node can be modified.

In the future, we intend to extend it as such and apply

it to a more realistic analysis of bistability in

intracellular signaling systems.

REFERENCES

Adler, M., Szekely, P., Mayo, A., & Alon, U. (2017).

Optimal Regulatory Circuit Topologies for Fold-

Change Detection. Cell Syst, 4(2), 171-181 e178.

https://doi.org/S2405-4712(16)30419-7 [pii],

10.1016/j.cels.2016.12.009

Brightman, F. A., & Fell, D. A. (2000). Differential

feedback regulation of the MAPK cascade underlies the

quantitative differences in EGF and NGF signalling in

PC12 cells. FEBS Letters, 482, 169-174.

Doncic, A., Atay, O., Valk, E., Grande, A., Bush, A.,

Vasen, G., Colman-Lerner, A., Loog, M., & Skotheim,

J. M. (2015). Compartmentalization of a bistable switch

enables memory to cross a feedback-driven transition.

Cell, 160(6), 1182-1195. https://doi.org/10.1016/

j.cell.2015.02.032, S0092-8674(15)00198-1 [pii]

Ferrell, J. E., Jr. (1998). How regulated protein

translocation can produce switch-like responses.

Trends in Biochemical Science, 23, 461-465.

Gedeon, T., Cummins, B., Harker, S., & Mischaikow, K.

(2018). Identifying robust hysteresis in networks. PLoS

Comput Biol, 14(4), e1006121. https://doi.org/10.1371/

journal.pcbi.1006121 PCOMPBIOL-D-17-01583 [pii]

Hatakeyama, M., Kimura, S., Naka, T., Kawasaki, T.,

Yumoto, N., Ichikawa, M., Kim, J. H., Saito, K., Saeki,

M., Shirouzu, M., Yokoyama, S., & Konagaya, A.

(2003). A computational model on the modulation of

mitogen-activated protein kinase (MAPK) and Akt

pathways in heregulin-induced ErbB signalling.

Biochemical Journal, 373(Pt 2), 451-463.

Huang, C. F., & Ferrell, J. E., Jr. (1996). Ultrasensitivity in

the mitogen-activated protein kinase cascade.

Proceedings of the National Academy of Science of the

United States of America, 93, 10078-10083.

Jeschke, M., Baumgartner, S., & Legewie, S. (2013).

Determinants of cell-to-cell variability in protein kinase

signaling. PLoS Comput Biol, 9(12), e1003357.

https://doi.org/10.1371/journal.pcbi.1003357

PCOMPBIOL-D-13-00825 [pii]

Kholodenko, B. N. (2006). Cell-signalling dynamics in

time and space. Nat Rev Mol Cell Biol, 7(3), 165-176.

http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=

Retrieve&db=PubMed&dopt=Citation&list_uids=164

82094

Kim, J. K., & Tyson, J. J. (2020). Misuse of the Michaelis-

Menten rate law for protein interaction networks and its

remedy. PLoS Comput Biol, 16(10), e1008258.

https://doi.org/10.1371/journal.pc bi.1008258

Kuwahara, H., & Gao, X. (2013). Stochastic effects as a

force to increase the complexity of signaling networks.

Sci Rep, 3, 2297. https://doi.org/10.1038/srep02297

srep02297 [pii]

Levchenko, A., Bruck, J., & Sternberg, P. W. (2000).

Scaffold proteins may biphasically affect the levels of

mitogen-activated protein kinase signaling and reduce

its threshold properties. Proceedings of the National

Academy of Science of the United States of America,

97(11), 5818-5823.

Ma, W., Trusina, A., El-Samad, H., Lim, W. A., & Tang,

C. (2009). Defining network topologies that can

achieve biochemical adaptation. Cell, 138(4),

760-773. https://doi.org/10.1016/j.cell.2009.06.013

S0092-8674(09)00712-0 [pii]

Mai, Z., & Liu, H. (2013). Random parameter sampling of

a generic three-tier MAPK cascade model reveals major

factors affecting its versatile dynamics. PLoS One, 8(1),

e54441. https://doi.org/10.1371/journal.pone.0054441

PONE-D-12-24261 [pii]

Naka, T. (2020). Validity of the Michaelis-Menten

Approximation for the Stability Analysis in Regulatory

Reaction Networks. BIOSTEC 2020 (13th International

Joint Conference on Biomedical Engineering Systems

and Technologies), Valletta, Malta.

Naka, T. (2022). The partition representation of enzymatic

reaction networks and its application for searching bi-

stable reaction systems. PLoS One, 17(1), e0263111.

https://doi.org/10.1371/journal.pone.0263111

Qiao, L., Nachbar, R. B., Kevrekidis, I. G., & Shvartsman,

S. Y. (2007). Bistability and oscillations in the Huang-

Ferrell model of MAPK signaling. PLoS Comput Biol,

3(9), 1819-1826. https://doi.org/07-PLCB-RA-0294

[pii] 10.1371/journal.pcbi.0030184

Ramakrishnan, N., & Bhalla, U. S. (2008). Memory

switches in chemical reaction space. PLoS Comput

Biol, 4(7), e1000122. https://doi.org/10.1371/

journal.pcbi.1000122

Schoeberl, B., Eichler-Jonsson, C., Gilles, E. D., & Muller,

G. (2002). Computational modeling of the dynamics of

the MAP kinase cascade activated by surface and

internalized EGF receptors. Nature Biotechnology, 20,

370-375.

Shah, N. A., & Sarkar, C. A. (2011). Robust network

topologies for generating switch-like cellular

responses. PLoS Comput Biol, 7(6), e1002085.

Identiﬁcation of Bistability in Enzymatic Reaction Networks Using Hysteresis Response

485

https://doi.org/10.1371/journal.pcbi.1002085 10-

PLCB-RA-2608 [pii]

Siegal-Gaskins, D., Mejia-Guerra, M. K., Smith, G. D., &

Grotewold, E. (2011). Emergence of switch-like

behavior in a large family of simple biochemical

networks. PLoS Comput Biol, 7(5), e1002039.

https://doi.org/10.1371/journal.pcbi.1002039

PCOMPBIOL-D-10-00298 [pii]

Sueyoshi, C., & Naka, T. (2017). Stability Analysis for the

Cellular Signaling Systems Composed of Two

Phosphorylation-Dephosphorylation Cyclic Reactions.

Computational Molecular Bioscience, 7, 33-45.

Volinsky, N., & Kholodenko, B. N. (2013). Complexity of

receptor tyrosine kinase signal processing. Cold Spring

Harb Perspect Biol, 5(8), a009043. https://doi.org/

10.1101/cshperspect.a009043a009043 [pii] 5/8/a009

043 [pii]

Wolfram Research, I. (2021). Mathematica. In (Version

13.0)

Yao, G., Tan, C., West, M., Nevins, J. R., & You, L. (2011).

Origin of bistability underlying mammalian cell cycle

entry. Mol Syst Biol, 7, 485. https://doi.org/10.1038/

msb.2011.19msb201119 [pii]

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

486