FEAT: A Fast, Effective, and Feasible Model for Molecular Property

Prediction Based on Graph Neural Network

Mukesh Kumar Rohil

and Ishan Sharma

Department of Computer Science and Information Systems, Birla Institute of Technology and Science,

Pilani, Rajasthan 333 031, India

Keywords: Artificial Intelligence, Machine Learning, Graph Neural Networks, QSAR, Molecular Property Prediction.

Abstract: Artificial Intelligence based methods and algorithms are being increasingly used by chemists to perform

various tasks that would be rather difficult to perform using conventional methods. Whenever scientists design

a new set of molecules for certain application, they need to experimentally validate if it possesses the desirable

properties. Such (iterative) methods are often expensive and time-consuming. In the realm of Artificial

Intelligence and Machine Learning, the molecules can themselves be viewed as graphs present in nature with

bonds as edges and nodes as atoms. Therefore, it is worthwhile to exploit Graph Neural Networks for

extracting the structural properties of these atoms and bonds, so as to further leverage these to predict the

properties of these molecules (represented as graphs) as a whole. We propose a Graph Neural Network based

model, FEAT, for this purpose. FEAT’s performance has been evaluated on multiple publicly available

datasets and the results obtained are promising.

1 INTRODUCTION

In recent times various Artificial Intelligence (AI)

methods and algorithms are being used more and more

by chemists to perform various tasks that would be

rather difficult to perform using traditional methods.

Latest applications of AI in chemistry are targeted

towards designing new molecules for drug discovery,

attaining knowledge of universe etc. Whenever

researchers design a new molecule, its properties have

to be experimentally identified and analysis is to be

performed whether they are the desired ones or not.

Many a times the process of experimentally identifying

the properties becomes rather expensive and time-

consuming as we may have hundreds or even

thousands of new molecules designed and waiting to

test for properties. These experimentations can be

iteratively done with the help of artificial intelligence.

1.1 Quantitative Structure, Activity

Relationship

Quantitative Structure-Activity Relationship (QSAR)

models have been used in the past to predict

https://orcid.org/0000-0002-2597-5096

molecular properties using physical laws or empirical

relationships relating the structure of the molecule to

their properties.

The physiological activity Φ was expressed as a

function of chemical structure C.

Φ = f(C) (1)

One of the first historical QSAR applications was

to predict boiling points for different molecules

(Dearden, 2003). A general trend was observed

between number of carbons in alkanes and their

boiling points. The boiling points for alkanes

increases as the number of carbons increased in the

molecules (Dearden, 2003).

But generally, the patterns within structure and

properties are not usually very straightforward and

are very complex in nature. Hence, we try to

implement the same idea using Artificial Intelligence

and Machine Learning so that complex structural-

property relations could be extracted from molecules

to predict some property (e.g. solubility) accurately.

1.2 Graph Neural Networks

Graphs are a type of data structures having two

878

Rohil, M. and Sharma, I.

FEAT: A Fast, Effective, and Feasible Model for Molecular Property Prediction Based on Graph Neural Network.

DOI: 10.5220/0012410700003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 878-881

ISBN: 978-989-758-680-4; ISSN: 2184-433X

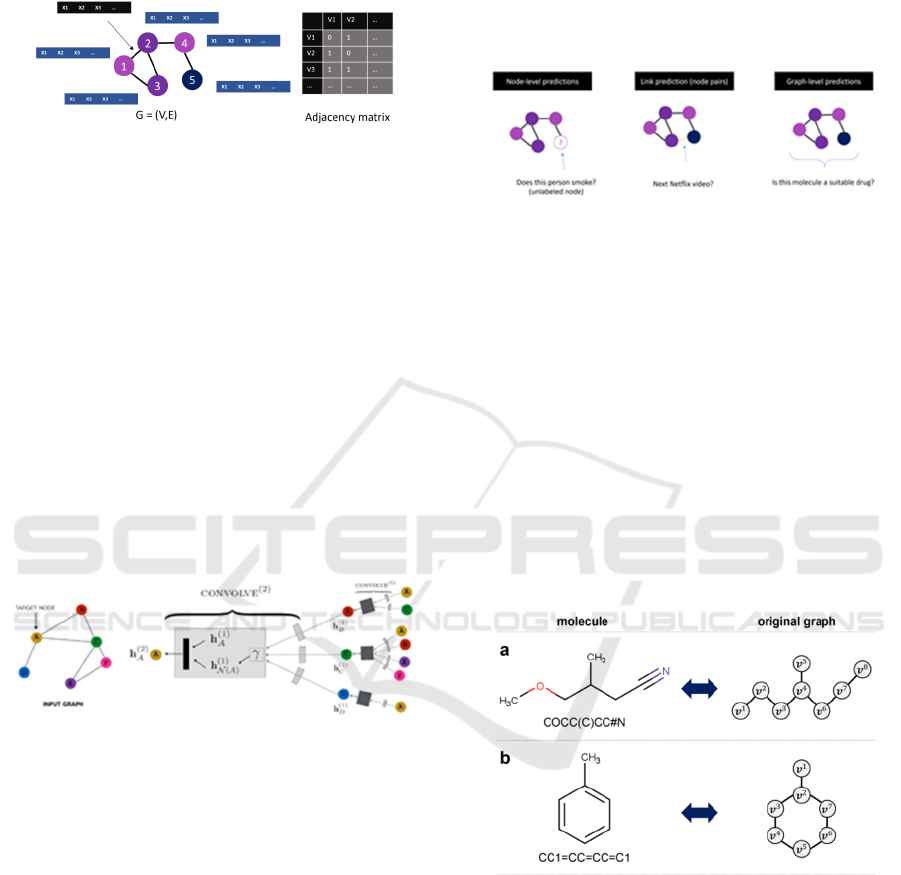
components: Vertices (or Nodes) and edges. An edge

connects two nodes as shown in Figure 1. A graph can

be represented by an adjacency matrix.

Figure 1: Graph Representation: Nodes and edges both can

have a set of features that are unique for that node or edge.

Graph neural networks (GNN) refer to the neural

network architectures that operate on graph data.

Each node has some set of features that defines it. For

example, in case of a social network these features

could be gender, age, country, friends etc. Similarly,

edges may also contain some set of features e.g.

friendship between two people, distance between two

persons’ locations etc.

The GNNs, as shown in Figure 2, work by

gathering and passing information between nodes and

its neighbours. Nodes receive information from

neighbours via edges. Data from these edges are

aggregated (using many different techniques like max

pooling, averaging etc.) and are passed to an

activation function to get new set of embeddings for

the node.

Figure 2: Working of GNN, current node embeddings h

are

calculated with the help if neighbouring node embeddings,

neighbouring edge features and current node features.

Every node in the initial state has features X

. The

embeddings for a node after message passing can be

defined as:

= f(X

co[v]

, h

ne[v]

, X

ne[v]

)

(2)

Where,

f is a local transition function,

ne[v]

denotes the features of the neighbours of v,

co[v]

denotes the edge features connected to v,

ne[v]

denotes the embeddings of the neighbours of v.

In the Figure 2 above, h

(1)

is the initial embedding

of the node, h

N(A)

(1)

is the aggregated embeddings of

its neighbours. Combining these and passing to the

node’s activation function will provide the new

embeddings for the node A. In different steps, as

shown in Figure 3, each node gets a new set of

embeddings for itself. After various iterations or K

layers of message passing, a node learns more and

more about its neighbourhood and its distant

neighbours as well.

Figure 3: GNN-produced node level, edge level and graph

level predictions.

QSAR relations can be utilised and built upon to

extract information from structural composition of a

molecule. We could input a molecule to a simple

feed-forward recurrent neural network; the predicted

molecular properties would be as a result of the model

learning the sequential grammar of molecular

structure (SMILES strings) rather than extracting

information from structural properties of it.

A molecule itself could be viewed as a graph as

depicted in Figure 4. The atoms correspond to the

vertices and edges corresponds to the bonds between

those vertices / atoms. Vertices can contain features as

electronic configuration, formal charge, etc. Edges

may contain features like bond type, bond distance, etc.

Figure 4: Molecules represented as graphs with individual

atoms representing the nodes of the graph and bonds

representing the edges of the graph.

2 DATASETS AND

ARCHITECTURE

2.1 Datasets and Pre-Processing

Three MoleculeNet datasets have been used to train

and test the model (Wu et al., 2018).

FEAT: A Fast, Effective, and Feasible Model for Molecular Property Prediction Based on Graph Neural Network

879

a) ESOL: (1128 molecules) Water solubility for

common organic molecules (Wu et al., 2018).

b) Free Solv: (642 molecules) Experimental and

calculated hydration free energy of molecules in

water (Wu et al., 2018).

c) Lipophilicity: (4200 molecules) Octanol/water

distribution coefficient (Wu et al., 2018).

Using rdkit library molecules are pre-processed to

attach the following atomic properties to the

individual atoms in the molecule: Atomic Number,

Chirality, Degree, Formal Charge, Number of

Hydrogens, Number of Radical Electrons,

Hybridization, Aromatic or not, Atom inside the ring

or not. Bond type, stereo configuration and

conjugation were the three properties chosen as the

bond properties that the edges of the graph will hold.

2.2 Model Architecture

The model, which we call as FEAT, consists of five

message passing layers as listed in Table 1. The

number of layers itself is a hyper parameters hence

can be changed accordingly whether the data under fit

or over fit the model. The first message passing layer

has an input dimension of which refers to the 9 atomic

properties that we shortlisted for the data. These

message passing layers constitute of Graph

Convolution Network layer (Kipf and Welling, 2017)

with tanh activation function (Wang et al., 2020). The

dimensions of hidden message passing layers are

hyper-parameters too, here 64 has been chosen as the

dimension of hidden message passing layers.

A concatenation of global mean and max pooling

layer was added to aggregate the features together.

The final layer consists of a linear layer which takes

in the output of global pooling layer as input and

outputs the value of the predicted property.

The tanh activation function was chosen over

ReLu or Sigmoid due to its higher performance for

convolutional systems (Wang et al., 2020), (Wieder

et al., 2020).

3 RESULTS AND DISCUSSION

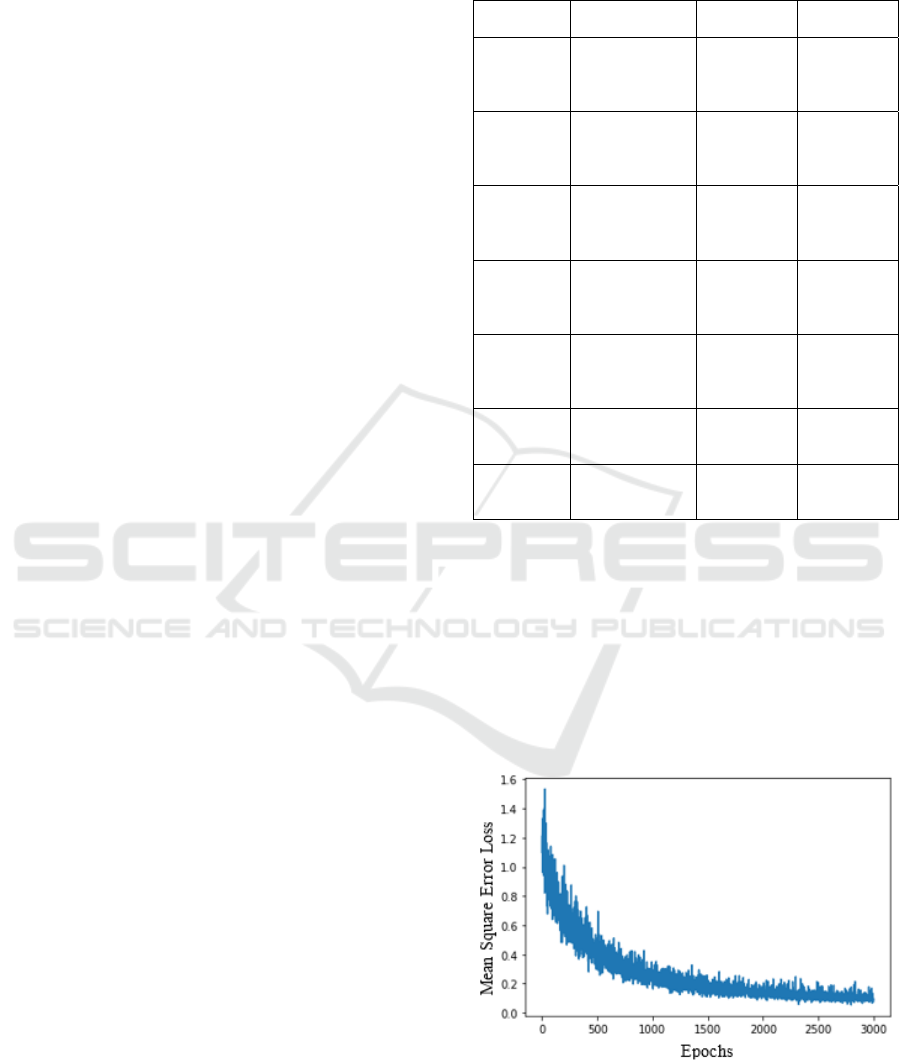
The model FEAT was run on Dataset-1 (ESOL) and

the plot shown in Figure 5 is obtained, it contains a

graph that has been plotted between Mean Square

Error and Number of Epochs for the ESOL dataset,

we can see a steep loss in the mean squared error

value which indicated the training going in the right

direction with a good learning rate.

Table 1: GNN Model Architecture consisting of Five

Message Passing Layers, a Global Pooling Layer and Final

Linear Layer for Property Prediction.

Layer Components

Input

Dimensions

Output

Dimensions

First

Message

Passing

Graph

Convolution

with tanh

Activation

9 64

Second

Message

Passing

Graph

Convolution

with tanh

Activation

64 64

Third

Message

Passing

Graph

Convolution

with tanh

Activation

64 64

Fourth

Message

Passing

Graph

Convolution

with tanh

Activation

64 64

Fifth

Message

Passing

Graph

Convolution

with tanh

Activation

64 64

Global

Pooling

Global Mean

and Max

Pooling

64 128

Linear

Layer

Linear

Regression

Laye

128 1

To evaluate the predictions, 128 data points (1

batch) from the test dataset (20% of the whole

dataset) were plotted against the actual

experimentally determined values. The Figure 6

presents the graph between the experimentally

determined solubility values vs the solubility values

predicted by the model. The line y = x has been added

to visualize the accuracy of the predicted property

values by FEAT as compared to experimentally

determined values.

Figure 5: MSE vs Epoch for ESOL dataset, good descent

for loss observed for the MSE function as epochs increase.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

880

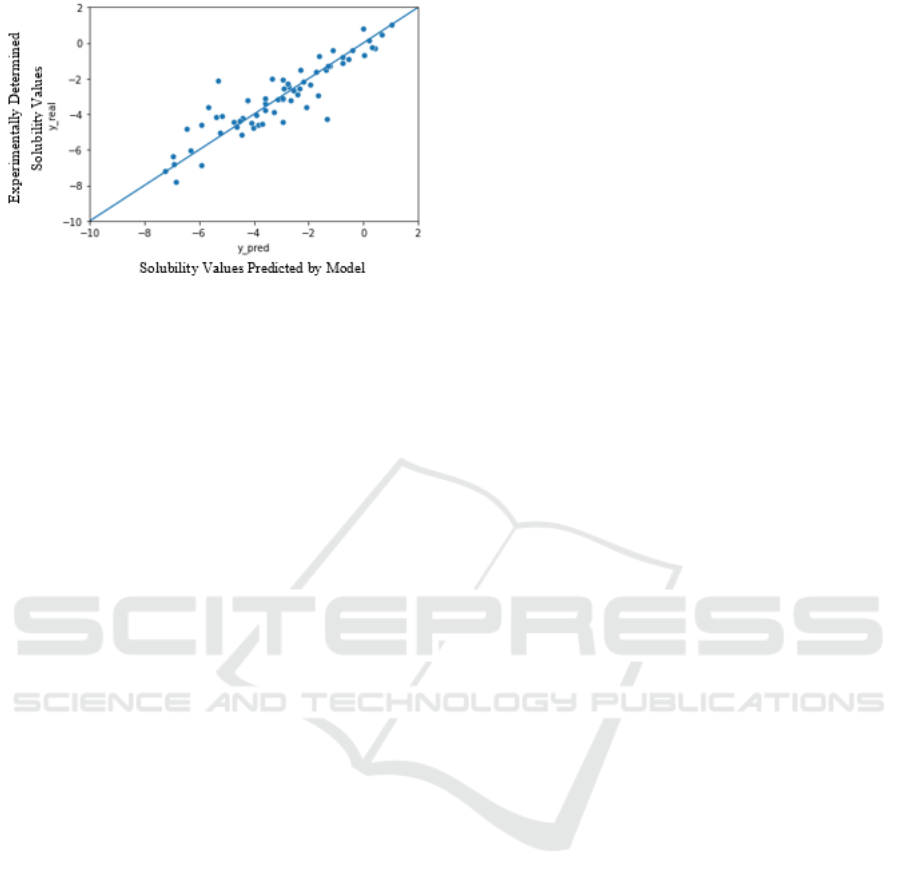
Figure 6: Experimentally determined solubility values

plotted against solubility values predicted by model.

Similar graphs were obtained for model run on

Dataset-2 (Free Solv) and Dataset-3 (Lipophilicity).

In both the cases, the model FEAT seems to underfit

the data. Nevertheless, various hyper-parameters can

be tweaked and experimented with to generate more

accurate results.

4 CONCLUSIONS AND SCOPE

FOR FUTURE RESEARCH

It is known that physiological properties of the

chemicals can be related to structural properties of the

chemicals by some functions as we call these

relations as QSAR relations. QSAR relations are not

usually linear in nature, they might be very complex

in higher order polynomials, hence we try to take help

of artificial neural networks in achieving this task. As

molecules can be views as graphs present in nature,

the bonds correspond to the edges and atoms

correspond to the nodes in the graph. It makes sense

to use Graph Neural Network to extract structural

information from the molecular graphs and use this

information to predict various properties from it.

The graph neural network based model FEAT was

Convolutional Network Layers with a catenated

Global Mean and Max pooling layer with a final

linear layer to predict the property. The presented

model FEAT gave nearly accurate results. In addition,

it promises to be a fast and feasible means to predict

molecular properties in comparison to conventional

methods based off manual experimentation by

chemists. Considering the present state of this

research, it definitely cannot be taken as an alternative

to conventional experimentation; however, it could

potentially serve as a means for the required

predictions in environments or situations that are

resource- and time-constrained. As a scope for future

research in this relatively less researched domain, the

model can be further improved by adding more

message passing layers, experimenting with different

learning rates, changing atomic properties chosen for

atoms, etc.

REFERENCES

Dearden, J.C. (2003). Quantitative structure-property

relationships for prediction of boiling point, vapor

pressure, and melting point. Environmental Toxicology

and Chemistry, vol. 22, no. 8, pp. 1696–1709. Wiley-

Blackwell.

Kipf, T.N., Welling, M. (2017). Semi-Supervised

Classification with Graph Convolutional Networks. In

Proceedings of the 2017 International Conference on

Learning Representations, pp. 1–14. ICLR.

Wang, Y., Li, Y., Song, Y., Rong, X. (2020). The Influence

of the Activation Function in a Convolution Neural

Network Model of Facial Expression Recognition.

Applied Sciences, vol. 10, no. 5, pp. 1897. MDPI.

Wieder, O., Kohlbacher, S., Kuenemann, M., Garon, A.,

Ducrot, P., Seidel, T., Langer, T. (2020). A compact

review of molecular property prediction with graph

neural networks. Drug Discovery Today: Technologies,

vol. 37, pp. 1-12. Elsevier.

Wu, Z., Ramsundar, B., Feinberg, E.N., Gomes, J.

Geniesse, C., Pappu, A.S., Leswing, K., Pande, V.

(2018). MoleculeNet: A Benchmark for Molecular

Machine Learning. Chemical Science, vol. 9, pp. 513–

530. Royal Society of Chemistry.

FEAT: A Fast, Effective, and Feasible Model for Molecular Property Prediction Based on Graph Neural Network

881