Conic Linear Units: Improved Model Fusion and Rotational-Symmetric

Generative Model

Changqing Fu

and Laurent D. Cohen

CEREMADE, University Paris Dauphine, PSL Research University, UMR CNRS 7534, Paris, 75016, France

Keywords:

Generative AI, Deep Learning for Visual Understanding, Machine Learning Technologies for Vision.

Abstract:

We introduce Conic Linear Unit (CoLU), a natural generalization of commonly used activation functions in

neural networks. The common pointwise ReLU activation is a projection onto the positive cone and is per-

mutation symmetric. We propose a nonlinearity that goes beyond this symmetry: CoLU is a skew projection

onto a hypercone towards the cone’s axis. Due to the nature of this projection, CoLU enforces symmetry in a

neural network with width C from the ﬁnite-order permutation group S (C) to the inﬁnite-order rotation/reﬂec-

tion group O(C −1), thus producing deep features that are motivated by the HSV color representation. Recent

results on merging independent neural networks via permutation modulus can be relaxed and generalized to

soft alignment modulo an optimal transport plan (Singh and Jaggi, 2020), which is useful in aligning models

of different widths. CoLU aims to further alleviate the apparent deﬁciency of soft alignment. Our simula-

tion indicates that CoLU outperforms existing generative models including Autoencoder and Latent Diffusion

Model on small or large-scale image datasets. Additionally, CoLU does not increase the number of parame-

ters and requires negligible additional computation overhead. The CoLU concept is quite general and can be

plugged into various neural network architectures. Ablation studies on extensions to soft projections, general

cones, and the non-convex double-cone cases are brieﬂy discussed.

1 INTRODUCTION

Scaling up neural networks is one thing, while reduc-

ing their redundancies is quite another. Aligning/Fus-

ing different models into a canonical form (Ashmore

and Gashler, 2015) is a useful way to simplify the

model structure and reduce its redundancy. In the

mean time, practically speaking, alignment enables

different models to collaborate with each other. The

term alignment in this context refers to ﬁxing a base

model and transforming any alternative ones so that

the alternative model is very similar, if not equivalent,

to the base model. This similarity, in our setting, is

deﬁned as the fact that both models can be linearly

interpolated without losing much performance. In the

generative model case, the effect of alignment is illus-

trated in ﬁgure 1, showing that the weights of aligned

models can be linearly interpolated to obtain a model

which performs well. In other words, the symmetry of

the model’s function space (visualized by the symme-

try of the triangle in ﬁgure 1) is represented by sym-

metry group P (permutations), and we aim to let the

https://orcid.org/0000-0002-4485-9824

https://orcid.org/0000-0002-3940-645X

GM0

GM1

GM2

GM0

Modulo

Input Input

Group Quotient

GM0, GM1’, GM2’

GM0

GM2

GM1

GM1’ GM2’

Outputs Outputs

Loss

Landscape

Before

After

−

Align

Figure 1: Model Fusion. Fixing a base generative

model GM0, alternative models GM1, GM2 at differ-

ent local minima on the loss landscape are aligned as

GM1’=Align(GM1), GM2’=Align(GM2). Before the

alignment, the linear interpolation between GM0 and

GM1/GM2 has increased loss, whereas after the alignment,

this increase is reduced.

quotient space (deﬁned in section 2) modulo P be reg-

ular, in the sense that we hope the aligned models to

be close to the base model, so that they can be merged

via linear interpolation.

686

Fu, C. and Cohen, L.

Conic Linear Units: Improved Model Fusion and Rotational-Symmetric Generative Model.

DOI: 10.5220/0012406500003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 2: VISAPP, pages

686-693

ISBN: 978-989-758-679-8; ISSN: 2184-4321

However, existing alignment methods are often

rough due to the fact that the function space of the

network is speciﬁc. For example, for the widely-

used pointwise activation functions, the equivariance

is limited to permutations. We propose a better de-

sign which enables smoother fusion. Meanwhile, it

is intriguing that the new structure outperforms exist-

ing ones under certain validation criteria for various

generative tasks.

1.1 Model Fusion

First of all, why do we need model fusion? We list

several aspects from both applied and theoretical per-

spectives.

Practical Uses. First, in the federated learning set-

ting when the training task is distributed to local

agents each having access to a subset of the data, fu-

sion is a way to aggregate the parallelized training

subtasks and synchronize the local models to obtain

a global result (Wang et al., 2020a). Second, in the

knowledge distillation setting when there is no ac-

cess to training data such as for safety reasons, fusion

makes it possible to directly ensemble models from

multiple teacher models as an alternative to aggregat-

ing the training data. Third, in the transfer learn-

ing setting, the expensive computation overhead of

re-training from scratch is saved by utilizing the in-

formation in multiple pre-trained models.

Theoretical Beneﬁts. First, geometry. Associated

with the correspondence between the aligned models

is the symmetry of the network architecture’s func-

tion space: the intuitive exchangeability of the hid-

den feature maps is algebraically characterized by the

permutation modulus. In other words, CNN is equiv-

ariant under channel permutation group. Different

forms of group equivariance has led to network de-

signs with better efﬁciency and generalization ability.

Second, optimization. Learning the parameters of a

neural network is a non-convex optimization problem.

Alignment reshapes the loss landscape and largely

convexiﬁes it (Garipov et al., 2018). Consequently,

the training process largely converges to a minimum

which is unique up to a transformation group. Third,

probability. A fully-connected (or convolutional)

layer is a linear ensembling among neurons (or fea-

ture maps) of previous layers. Fixing a certain set of

trained neurons as the key’s dictionary, alignment is

used to de-anonymize an arbitrary set of neurons so

that the activating behavior of an individual neuron at

the same index follows the same pattern. Each neuron

is assigned deterministically with an unrepeated key.

1.2 Probabilistic Fusion

Then a natural question arises: what if the widths of

the models to be aligned differ from each other? It’s

evident that deterministic assignment is not feasible

when fusing models of varying width. In this un-

balanced case, the assignment constraint can be re-

laxed by optimal transport. In a probabilistic sense,

each key (channel index) is not deterministically as-

signed to a neuron, but instead a fuzzy mixture of neu-

rons, whose probability values sum up to 1 (Singh and

Jaggi, 2020). However, the model formed by the new

set of neurons, each as a multi-identity mixture, does

not behave the same way as in the unaligned model,

since activating each individual neuron is no longer

feasible. To resolve this apparent deﬁciency naturally

caused by the relaxation, re-designing a more sym-

metric function is a must.

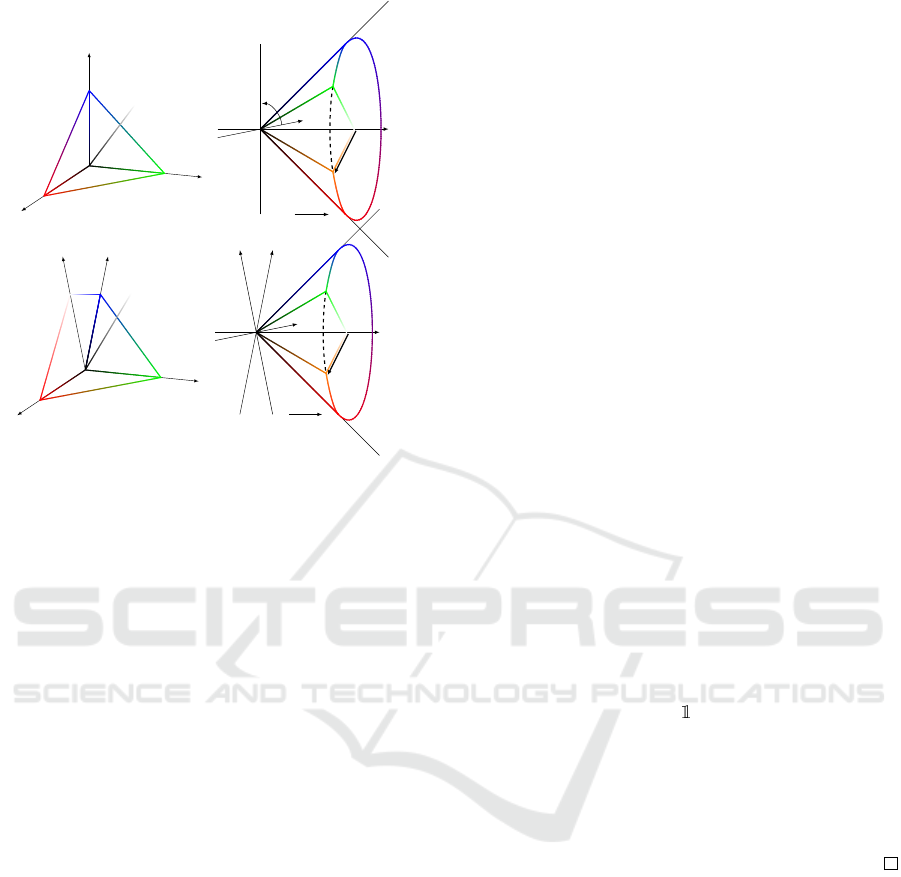
Figure 2: Conic Linear Unit (three-channel case). Left:

ReLU. Middle: equivalent projective illustration of ReLU.

Right: projective illustration of CoLU. With axes denoted

as R,G,B, a 3D vector inside the positive cone represents a

RGB color, and is visualized in the 3D space. Any points

outside the cone is not visualized since the vector does not

represent a color. The arrows point from the input to the

output of the activation function.

Conic Linear Unit: From RGB to HSV. The pro-

posed activation is termed as Conic Rectiﬁed Linear

Unit (abbreviated as CoReLU or CoLU for short),

named after Rectiﬁed Linear Unit (ReLU). The point-

wise ReLU is generalized to pixel-wise CoLU in the

following way.

In the special case of three channels, CoLU is

naturally motivated by switching from Red-Green-

Blue (RGB) to the Hue-Saturation-Value (HSV) color

representation, visualized in ﬁgure 2. ReLU is at-

tending to perceptible color deﬁned by the posi-

tive octant, where color components which are too

dark (negative-valued) are not perceivable (mapped to

zero). Instead of ReLU which preserves positive val-

ues, CoLU preserves low values on saturation, which

means saturation values larger than a threshold value

(proportional to the luminosity value) are mapped to

the maximal threshold.

In high dimensions as is shown in ﬁgure 3, where

the token space does not represent a color, migration

Conic Linear Units: Improved Model Fusion and Rotational-Symmetric Generative Model

687

(1, 0, 0)

(0, 1, 0)

(0, 0, 1)

1 =(1, 1, 1)

Hue

=(1, 0, 0)

Chroma

Value

3· · ·

1 = (1, 1, . . .)

3···

C≠1

=(1, 0,...)

Îx

≠1

Figure 3: Conic Linear Units, from 3 channels to many

channels. Top: cartesian axes of positive cones of ReLU

and CoLU in three dimensions. Bottom: generalizations to

high-dimensional space.

from the positive hypercone to the round hypercone

motivates CoLU in hidden layers. Closed-form for-

mula of CoLU is detailed in section 3.

Contributions. We propose CoLU, a class of acti-

vation functions which present convolutional neural

networks with rotational symmetry in the channel di-

mension. In principle, CoLU achieves improved soft

alignment using optimal transport which is useful in

federated learning. Intriguingly, CoLU outperforms

baseline generative models on several tasks.

Organization of Sections. After introducing pre-

liminaries in section 2, we deﬁne CoLU in section 3,

and describe the fusion algorithm in section 4. Quan-

titative improvements of conic activation and high-

resolution generation results are presented in section

5.1. Then, weight alignment for both recognition and

generative models are experimented in section 5.2.

Related works are discussed in section 6 and the paper

is concluded in section 7.

2 PRELIMINARIES

Consider a neural network learned on paired data

,y), where the input and output are sampled from

random variables following some data distribution

,y) ∼ µ. The network is parameterized with weight

W = {W

ℓ

}

ℓ=1

trained from initialization W ∼ π, and

the layer outputs are a sequence of hidden states

{x(ℓ)}

ℓ=0

, with terminal layers being the input x(0) =

and output x(T ) = y respectively.

Deﬁnition 1 (Equivariance). A group P’s action on

a space M is deﬁned by P × M → M, (P,x) 7→ Px,

∀P ∈ P,x ∈ M. A function f : M → M is said to admit

the group P, or being equivariant under group ac-

tion P if and only if the function commutes with the

left multiplication as f ◦ P = P ◦ f ,∀P ∈ P. Here P is

called an alignment.

Deﬁnition 2 (Hidden State Alignment). Two hidden

states x

(0)

(ℓ) and x

(1)

(ℓ) are equivalent up to an

alignment if and only if there exists an alignment P

such that x

(1)

(ℓ) = Px

(0)

(ℓ), denoted as a relation

(0)

(ℓ) ∼

(1)

(ℓ). Two neural networks are equiv-

alent if and only if all hidden states are equivalent,

that is ∀ℓ = 1,. .., T − 1, x

(0)

(ℓ) ∼

(1)

(ℓ), denoted

as x

(0)

∼

(1)

Example 1 (CNN with Pointwise Activation). The

CNN’s symmetry group P is channel permutations. A

CNN (without skip connections) is deﬁned by

x(ℓ + 1) = W

ℓ

⋆ λ(x(ℓ)) (1)

where λ is a pointwise activation such as

ReLU, and the convolution is deﬁned as

(w ⋆ x)(σ,ω

,ω

) =

∑

′

∑

(ω

′

,ω

′

)∈Ω

′

x(σ

′

,ω

′

,ω

+ ω

′

)w(σ,σ

′

,ω

′

,ω

′

) where Ω

′

is a small

convolution window. The channel permutation

group is deﬁned as P = S (C) := {P

ℓ

∈ R

C×C

∃ permutation σ,(P

ℓ

)

i j

{ j=σ(i)}

∀i = 1,...,C}.

Proof. Pointwise activation function commutes with

permutation as Pλ(x) = λ(Px), and since the align-

ment is along the channel axis, by exchanging the or-

der of multiplication and sum in the deﬁnition of con-

volution, we obtain (PW) ⋆ x = W ⋆ (Px). Therefore

x 7→ W

ℓ

⋆ λ(x) and P commutes.

Theorem 1 (Weight Alignment). The CNN’s hid-

den state alignment is equivalent to weight align-

ment. The weight alignment is deﬁned as W

(1)

ℓ

(0)

ℓ

−1

ℓ−1

,∀ℓ = 1,...,T − 1, and denoted as

(0)

ℓ

∼

(1)

ℓ

Proof. Fix a base neural network with states x

(0)

(ℓ)

and parameters W

(0)

ℓ

. By deﬁnition of hidden state

alignment, equation 1 is written as P

−1

ℓ

(1)

(ℓ) =

(0)

ℓ

⋆ λ(P

−1

ℓ−1

(0)

(ℓ − 1)) where P is a group element

and hence invertible. Since pointwise activation is

equivariant under permutation, this is equivalent to

(1)

(ℓ) = P

ℓ−1

(0)

ℓ

⋆



−1

ℓ−1

λ(x

(0)

(ℓ − 1))



Finally by

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

688

equivariance of convolution under channel permuta-

tion we obtain x

(1)

(ℓ) =



ℓ

(0)

ℓ

−1

ℓ−1



⋆ λ(x

(0)

(ℓ −

1)).

Deﬁnition 3 (Quotient Space). The set of equivalent

classes is deﬁned as [x] = {y ∈ M : x ∼ y} where x ∈ M

is called a representative. Given a relation ∼

on a

space M, the quotient space denoted by M/ ∼

simply M/P is deﬁned as the set of equivalent classes

M/ ∼

:= {[x] : x ∈ M} ⊂ 2

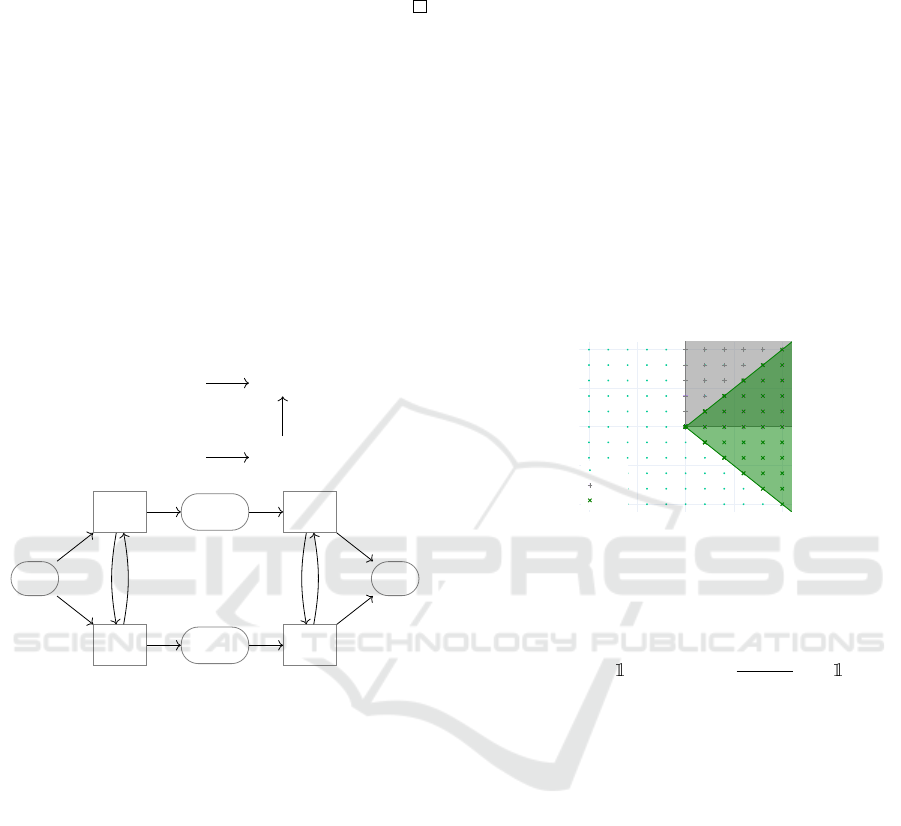
Conjecture 1 (Fusion by Linear Interpolation). Two

neural network weights W

(0)

ℓ

and W

(1)

ℓ

with the same

structure (probably with different channel sizes),

which are obtained by different data and initializa-

tion (π

(0)

,µ

(0)

) and (π

(1)

,µ

(1)

) respectively, have rep-

resentatives which can be interpolated so that the loss

function remains low on the interpolated weight.

(π

(0)

,µ

(0)

) W

(0)

(π

(1)

,µ

(1)

) W

(1)

Optim

Align

x(0)

(0)

(1)

(0)

(1)

(0)

(1)

x(2)

−1

Figure 4: Model Fusion. Top: different models (indepen-

dently trained on different datasets or initializations) coin-

cides in the same loss basin by means of weight alignment.

Bottom: diagram of the per-layer channel alignment P

ℓ

The alignment is illustrated in ﬁgure 4. To fa-

cilitate our conjecture of model fusion, a new class

of activation functions is designed so that it admits a

larger (inﬁnite-order) alignment group namely (C −

1)-channel rotations around the ﬁrst axis P := {P

ℓ

∈

C×C

: P

ℓ

[2,.. .,C;2,. ..,C] ∈ O(C −1)}, where O(C)

is the set of C-dimensional orthogonal matrices.

3 CONIC LINEAR UNITS

Projective Form. Let x = (x

,.. .,x

) be the in-

put of the activation function where C is the network

width. Inspired by ReLU

ReLU(x) = Proj

(x) = x

(2)

whose projected cone V

= R

= {x ∈ R

: x

≥ 0,i =

1,.. .,C} is the positive cone, CoLU is deﬁned as

CoLU(x) = Proj

V ∩H(x)

(x) = argmin

y∈V

(y−x)⊥e

∥y − x∥

, (3)

where the hypercone is V = {x ∈ R

: ∥x

⊥

∥

≤ tx · e}

with e being the unit vector in the axis direction, x =

x · e+x

⊥

, meaning x

is parallel to e and x

⊥

is perpen-

dicular to e, and the cone’s cross-section hyperplane

is H(x) = {y ∈ R

: y · e = x · e} whose normal vector

is e. t > 0 is the tangent value of the opening angle

of the cone. We set t = 1 and e = e

= (1,0, ... ,0)

without loss of generality.

In comparison of pointwise activations, CoLU is

attending to the round hypercone instead. The two

dimensional case is illustrated in ﬁgure 5.

input

ReLU

CoLU

Figure 5: ReLU and CoLU’s projective cone in 2D.

Closed Form. CoLU is a closed-form and auto-

differentiable activation as a drop-in replacement of

pointwise activations.

CoLU(x)

= x

+ (x

∥x

−1

∥

−1

)

(

clamp(x



∥x

−1

∥

,0,1)x

, i = 2, ... ,C

max{x

,0}, i = 1

(4)

where x

−1

= (0,x

,.. .,x

), clamp(x,a,b) =

min{max{x,a}, b}, V

is the complement set of

V ⊆ R

. In practice, ∥x

−1

∥ is replaced with

(∥x

−1

∥+ ε) where ε is a small constant, for numerical

stability.

Extensions of Conic Linear Unit

Soft Projection. Inspired by Sigmoid-Weighted

Linear Units (SiLU) SiLU(x) = x sigmoid(x), CoLU

can be relaxed as a soft projection.

CoSiLU(x)

(

sigmoid(x



∥x

−1

∥ − 0.5)x

, i ≥ 2

max{x

,0}, i = 1

(5)

-Cones. CoLU can also be extended to the case

of L

cones where p ∈ R

∪ {∞}.

Conic Linear Units: Improved Model Fusion and Rotational-Symmetric Generative Model

689

CoReLU

(x)

(

clamp(x



∥x

−1

∥

,0,1)x

, i ≥ 2

max{x

,0}, i = 1

(6)

Non-convex Double-Cones. Replacing the cone

with a signed cone,

CoReLU

(x)

(

clamp(x



∥x

−1

∥,−1,1)x

, i ≥ 2

, i = 1

(7)

4 MODEL FUSION

4.1 Model Alignment

With proper permutations, the aligned weights

ℓ

(1)

ℓ

⊤

ℓ−1

live in the same basin with the reference

model relatively. More precisely, deﬁne interpolated

weight as

(λ)

ℓ

= (1 − λ)W

(0)

ℓ

+ λP

ℓ

(1)

ℓ

⊤

ℓ−1

,λ ∈ [0,1], (8)

then the loss barrier L(W

(λ)

) as a function over λ is

a concave function for P

ℓ

= I, ∀ℓ = 1, ... ,T , and this

barrier is largely ﬂattened after the alignment, illus-

trated in ﬁgure 8 in the experiment session.

Algorithm 1: Soft Alignment via Optimal Transport.

Data: W

(0)

(1)

; // Pre-Trained

Reference and Alternative Models

Data: P

ℓ

← I

ℓ

; // Initialization

Data: ε ; // Small Constant

Result: P = argmax

ℓ

∈Π(1,1)

∑

ℓ=1

⟨W

(0)

ℓ

(1)

ℓ

⊤

ℓ−1

⟩

ℓ

← I

ℓ

; // Initialization

ε ; // Small Constant

S,S

← −∞ ;

repeat

← S ;

for ℓ ← RandPerm({1,..., T − 1}) do

ℓ

← argmax

ℓ

1=1,P

ℓ

⊤

1=1

⟨W

(0)

ℓ

(1)

ℓ

⊤

ℓ−1

⟩

⟨W

(0)

ℓ+1

(1)

ℓ+1

⊤

ℓ

⟩

;

end

S ←

∑

ℓ=1

⟨W

(0)

ℓ

(1)

ℓ

⊤

ℓ−1

⟩

;

until S ≤ S

+ ε;

4.2 Optimal Alignment

The algorithm to ﬁnd the optimal permutation is max-

imizing the Frobenius product between the reference

model and the aligned model, by using either the

weights or activations. Both cases are referred to as

Figure 6: Geometry of point-wise activations ℓ

(left) ver-

sus that of CoLU ℓ

(right) and their comparisons to OT

space.

weight matching and activation matching respec-

tively, and we focus on the ﬁrst method which doesn’t

require training data. It reduces to a Sum of Bilinear

Assignment Problem (SOBAP), and is approximated

by solving the Linear Assignment Problem sequen-

tially in a greedy manner, whose convergence is ana-

lyzed in (Ainsworth et al., 2023).

Each permutation P

ℓ

for ℓ = 1, ... ,T − 1 takes

the form of a permutation matrix P ∈ S (C

ℓ

). Fixing

ℓ−1

ℓ+1

obtained in the outer loop, the linear as-

signment problem is stated as

max

ℓ

∈S (C

ℓ

)

⟨W

(0)

ℓ

(1)

ℓ

⊤

ℓ−1

⟩

+ ⟨W

(0)

ℓ+1

(1)

ℓ+1

⊤

ℓ

⟩

(9)

where the input and output channel spaces are ﬁxed

and not aligned, meaning P

= I

. Equiv-

alently, the linear optimization objective in equation 9

can be written as

∑

i, j=1

i j

4.3 Algorithm: Optimal Transport

The constraint of permutation matrices P

ℓ

∈ S(C

ℓ

) can

be relaxed to probabilistic assignment matrices whose

marginals are ones in both dimensions Π(1, 1) = {P ∈

C×C

∑

i j

∑

i j

= 1,∀i, j}, also known as bi-

stochastic matrices. This is useful especially in the

more general case when the layer width C

ℓ

differs

between the two models, and it’s an instance of op-

timal transport. Using entropic regularization and

the Sinkhorn’s algorithm, the time complexity can be

accelerated from O(C

) by Linear Programming to

O(C) by ﬁxed-point method. The Kantorovich relax-

ation of optimal transport problem is stated as:

min

P1=1,P

⊤

1=1

∑

i, j=1

i j

+ εH(P) (10)

where the cost matrix C is given in equation 9, and

H(P) = −P

i j

(logP

i j

− 1) is an entropic regulariza-

tion term scaled by ε > 0. However, the relaxation

of Optimal Transport breaks the model, since a neural

network is permutation equivariant, but not channel-

wise interpolation equivariant. Figure 6 explains the

reason why CoLU is a better choice for fusion.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

690

5 EXPERIMENTS

5.1 Generative Performance of CoLU

Table 1: Performance of point-wise activation (SiLU) ver-

sus CoSiLU (Ours).

Performance SiLU CoSiLU

Symmetry Group S (C) O(C −1)

# Symmetries C

∞

Time Complexity O(C) O(C)

PSNR / dB (↑) 24.53 ± 2.54 25.83 ± 2.52

IS (↑) 7.23 ± 0.08 8.04 ± 0.94

KID / ×10

−3

(↓) 6.35 ± 0.77 2.71 ± 0.50

SSIM / ×10

−1

(↑) 8.61 ± 0.55 8.93 ± 0.44

Figure 7: Generation results of CoLU-LDM on FFHQ.

Two tasks are experimented: image reconstruction

task with autoencoder with regularization of Genera-

tive Adversarial Networks (GAN), and in image gen-

eration with Diffusion Models (DM).

Image Reconstruction. We follow the autoencoder

architecture in (Rombach et al., 2022) to build a vari-

ational autoencoders enhanced with GAN and per-

ceptual loss regularizations, and replace the Sigmoid

Linear Unit activation, SiLU(x) = x softmax(x), with

CoSiLU in equation 5. The model is trained on

the CIFAR10 dataset (Krizhevsky and Hinton, ).The

models are trained using 8×NVIDIA A100 GPUs un-

til convergence, which typically occurs around 200 ∼

300 epochs. The hyperparameters involve a base

learning rate of 10

−7

, a batch size of 64, and other

parameters as stated in LDM. We validate multiple

evaluation measures including peak signal-to-noise

ratio (PSNR), Inception Score (IS) (Salimans et al.,

2016), Kernel Inception Distance (KID) (Bi

nkowski

et al., 2018), and Structural Similarity Index Measure

(SSIM) (Wang et al., 2004). Results are shown in

table 1. The generated samples and loss curves are

shown in the appendix.

High-resolusion Image Generation. Then we val-

idate CoSiLU on FFHQ (Karras et al., 2019) and

AFHQ (Choi et al., 2018) datasets. It is shown that on

both datasets, CoSiLU-based diffusion models pro-

duces sharp results and work on par with SiLU ac-

tivation. Generated high-resolution images trained on

FFHQ are shown in ﬁgure 7.

5.2 Model Fusion

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

1.2

before alignment

after alignment

ReLU+Perm

0 0.2 0.4 0.6 0.8 1

0.5

1.5

before alignment

after alignment

CoLU+OT

Figure 8: Seamless Model Fusion. Loss function along

the linear interpolation between two models independently

trained from different initializations of fully-connected

models on MNIST dataset. The blue line is na

ıve interpola-

tion, and the red line is interpolation after alignment. Left:

ReLU network with permutation alignment. Right: CoLU

network with soft alignment. Both alignments successfully

align alternative models towards the base one.

Fusing Recognition Models. Alignment of

MNIST recognition models are performed on the

same network as above with three fully-connected

layers and two nonlinearities. As is shown in ﬁgure

8, both CoLU and ReLU aligns models with permu-

tation modulus or optimal transport, which applies to

networks with varying width.

Fusing Generative Models. CoLU was designed

aiming at a goal of merging generative models. Figure

9 shows partial milestone towards this goal, namely

it’s possible to align two super-resolution model so

that their interpolation path is closer to the ground-

truth of the output. Here it shows a lightening of the

output. The super resolution model follows ESPCN

(Shi et al., 2016), where all settings follow the origi-

nal work. We observe an alleviation of the darkening

effect after alignment. The base model and the al-

ternative model are initialized with independent and

identically distributed weights.

Conic Linear Units: Improved Model Fusion and Rotational-Symmetric Generative Model

691

Before

After

Figure 9: Fusing generative models. Outputs of models whose parameters are interpolated between two super-resolution

models trained from different initializations. Top row: no alignment. Bottom row: the second model is aligned towards the

ﬁrst model, where intermediate outputs are brighter.

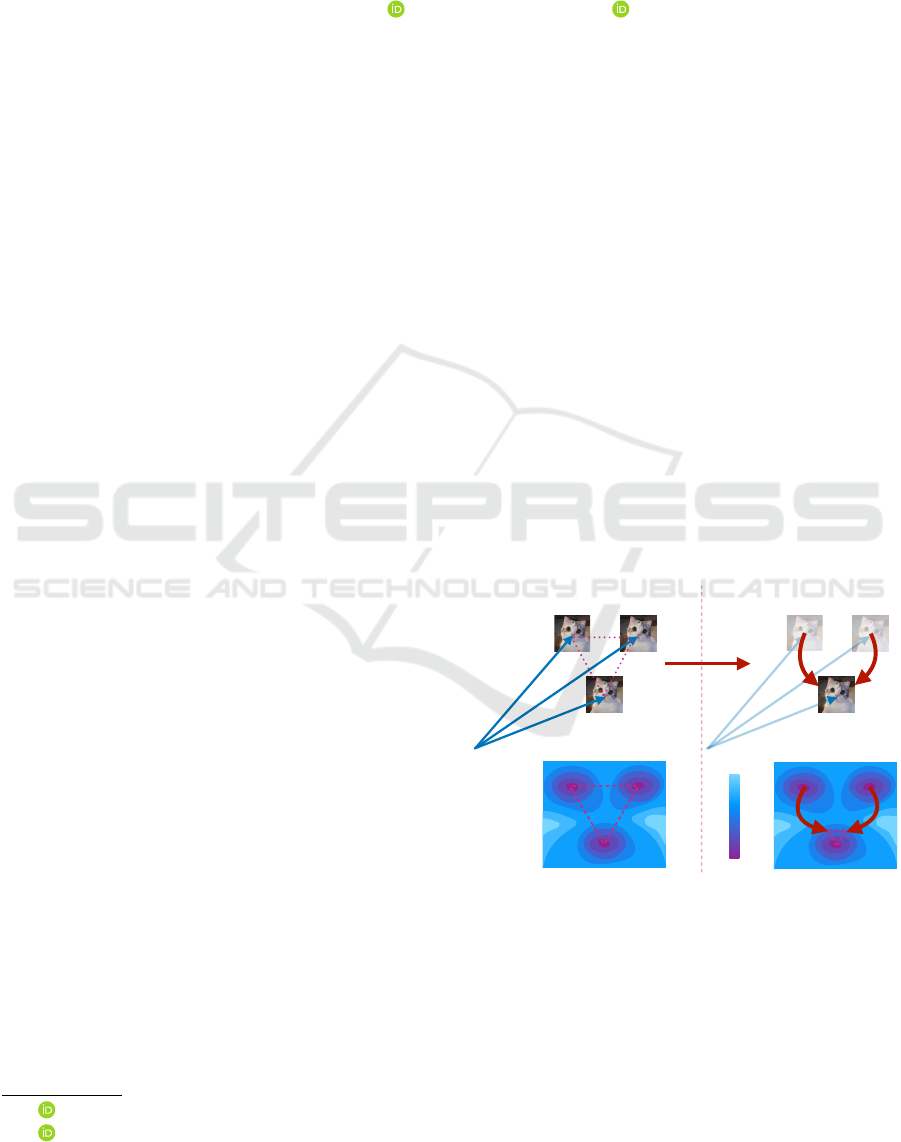
Figure 10: Fusing ﬁne-tuned models. Outputs of interpolated models between a Diffusion Model with parameters W

and a

Diffusion Model with parameters W

ﬁne-tuned from the previous model on the dataset of three cat images on the right. More

precisely, the 6 left images represent the outputs from a diffusion model whose parameters are W = (1 − λ)W

+ λW

where

λ = 0,

,1. λ = 0 corresponds to no ﬁne-tuning and λ = 1 corresponds to the ﬁne-tuned model.

Figure 10 is another result showing that diffusion

model might be a more suitable choice than single-

pass generative models for fusion via interpolation.

The interpolating effect between two dependent dif-

fusion models. Instead of aligning, the right image

is output by a model ﬁne-tuned (continually trained)

using the three images shown on the right following

(Ruiz et al., 2022). The generated images present no

perceptible degradation of quality. The smooth inter-

polation and sharp outcome presents the feasibility of

merging dependent models by linear interpolation.

6 RELATED WORKS

Equivariant Network. Convolutional weight shar-

ing (LeCun et al., 1989) is a successful example of

imposing spatial homogeneity on the 2D image can-

vas as a successful a priori assumption upon the net-

work architecture. The introduction of CoLU con-

siders new homogeneity on the channel dimension.

More generally, (Weiler and Cesa, 2019) conducts

a review on equivariant nonlinearities in neural net-

works and studies certain special forms of nonlinear

functions, such as point-wise activations, individual

subspace (pixel-wise) activations, norm nonlineari-

ties, etc., which do not cover the case of CoLU.

Disentangling the Channel Dimension. Related to

the permutation equivariance is the homogeneity of

the channel indice’s space. It is a crucial subject

in convolutional neural networks since it has been

proven that local spatial correlation can be sufﬁ-

ciently characterized with deterministic wavelet ﬁl-

ters (Bruna and Mallat, 2013). Combined with

learned pixel-wise linear transform, or 1-by-1 convo-

lution, invariant scattering networks are sufﬁcient to

achieve high performance in recognition tasks. There-

fore, disentangling the channel dimension is the miss-

ing ingredient in simplifying neural networks, where

various assumptions can be imposed. For instance,

sparsity as strong as block-diagonal in the channel di-

mension results in group convolution. Orthogonal-

ity results in spectrum-preserving weights. In the

case of convolutional neural networks, the authors

of (Wang et al., 2020b) propose an orthogonality-

inducing regularization term to ensure that the con-

volutional weights are empirically orthogonal. The

link to CoLU is close since the symmetric property of

CoLU is exactly pixel-wise rotation/reﬂection equiv-

ariance, which bridges the gap of the symmetry bot-

tleneck caused by the permutation-restrictive point-

wise activations.

Model Alignment. Merging trained models by ex-

ploiting permutation symmetry of pointwise activa-

tions has led to a fruitful line of research (Ashmore

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

692

and Gashler, 2015; Wang et al., 2020a). Recently

in (Ainsworth et al., 2023), deep recognition mod-

els like ResNet-50 are also align-able by deterministi-

cally matching weights. We continue on this path and

further explore the merit of a more symmetric activa-

tion function to improve the merging effect, on both

recognition and generative models.

7 CONCLUSION

We have introduced a new class of activation func-

tions called Conic Linear Units. Our contribu-

tion allows neural networks to possess inﬁnite-order

group symmetry beyond channel permutations, which

was previously unattainable. This novel design ad-

dresses the apparent deﬁciency by incorporating soft-

alignment through optimal transport. Moreover, it

outperforms baseline results in terms of image gen-

eration quality.

ACKNOWLEDGEMENT

This work was funded in part by the French govern-

ment under management of Agence Nationale de la

Recherche as part of the ”Investissements d’avenir”

program, reference ANR-19-P3IA-0001 (PRAIRIE

3IA Institute). This work was granted access to

the HPC resources of IDRIS under the allocation

2022-AD011013178 made by GENCI, and supported

by cloud TPU from Google’s TPU Research Cloud

(TRC). We thank Ir

ene Waldspurger, Jalal Fadili,

Gabriel Peyr

e and Gr

egoire Szymanski for insightful

suggestions on the draft of the paper.

REFERENCES

Ainsworth, S., Hayase, J., and Srinivasa, S. (2023). Git

re-basin: Merging models modulo permutation sym-

metries. In The Eleventh International Conference on

Learning Representations.

Ashmore, S. and Gashler, M. (2015). A method for ﬁnd-

ing similarity between multi-layer perceptrons by for-

ward bipartite alignment. In 2015 International Joint

Conference on Neural Networks (IJCNN), pages 1–7.

IEEE.

nkowski, M., Sutherland, D. J., Arbel, M., and Gretton,

A. (2018). Demystifying MMD GANs. In Interna-

tional Conference on Learning Representations.

Bruna, J. and Mallat, S. (2013). Invariant scattering convo-

lution networks. IEEE transactions on pattern analy-

sis and machine intelligence, 35(8):1872–1886.

Choi, Y., Choi, M., Kim, M., Ha, J.-W., Kim, S., and Choo,

J. (2018). Stargan: Uniﬁed generative adversarial net-

works for multi-domain image-to-image translation.

In Proceedings of the IEEE conference on computer

vision and pattern recognition, pages 8789–8797.

Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D. P., and

Wilson, A. G. (2018). Loss surfaces, mode connectiv-

ity, and fast ensembling of dnns. Advances in neural

information processing systems, 31.

Karras, T., Laine, S., and Aila, T. (2019). A style-based

generator architecture for generative adversarial net-

works. In Proceedings of the IEEE/CVF conference

on computer vision and pattern recognition, pages

4401–4410.

Krizhevsky, A. and Hinton, G. Technical report.

LeCun, Y., Boser, B., Denker, J., Henderson, D., Howard,

R., Hubbard, W., and Jackel, L. (1989). Handwrit-

ten digit recognition with a back-propagation network.

Advances in neural information processing systems, 2.

Rombach, R., Blattmann, A., Lorenz, D., Esser, P., and

Ommer, B. (2022). High-resolution image synthesis

with latent diffusion models. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 10684–10695.

Ruiz, N., Li, Y., Jampani, V., Pritch, Y., Rubinstein, M., and

Aberman, K. (2022). Dreambooth: Fine tuning text-

to-image diffusion models for subject-driven genera-

tion.

Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V.,

Radford, A., Chen, X., and Chen, X. (2016). Im-

proved techniques for training gans. In Lee, D.,

Sugiyama, M., Luxburg, U., Guyon, I., and Garnett,

R., editors, Advances in Neural Information Process-

ing Systems, volume 29. Curran Associates, Inc.

Shi, W., Caballero, J., Huszar, F., Totz, J., Aitken, A. P.,

Bishop, R., Rueckert, D., and Wang, Z. (2016). Real-

time single image and video super-resolution using

an efﬁcient sub-pixel convolutional neural network.

In 2016 IEEE Conference on Computer Vision and

Pattern Recognition (CVPR), pages 1874–1883. IEEE

Computer Society.

Singh, S. P. and Jaggi, M. (2020). Model fusion via optimal

transport. Advances in Neural Information Processing

Systems, 33:22045–22055.

Wang, H., Yurochkin, M., Sun, Y., Papailiopoulos, D.,

and Khazaeni, Y. (2020a). Federated learning with

matched averaging. In International Conference on

Learning Representations.

Wang, J., Chen, Y., Chakraborty, R., and Yu, S. X. (2020b).

Orthogonal convolutional neural networks. In Pro-

ceedings of the IEEE/CVF conference on computer vi-

sion and pattern recognition, pages 11505–11515.

Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004).

Image quality assessment: from error visibility to

structural similarity. IEEE Transactions on Image

Processing, 13(4):600–612.

Weiler, M. and Cesa, G. (2019). General e (2)-equivariant

steerable cnns. Advances in Neural Information Pro-

cessing Systems, 32.

Conic Linear Units: Improved Model Fusion and Rotational-Symmetric Generative Model

693