A Toolset for Constraint Programming

Thibault Falque

1,2 a

and Romain Wallon

2 b

Exakis Nelite, France

CRIL, Univ Artois & CNRS, France

Keywords:

Tools, Constraint Programming, Solver Interface, Remote Control.

Abstract:

Constraint Programming (CP) allows solving combinatorial problems across various domains. Numerous

solvers and tools have been developed in this area. However, their interoperability is often limited. This

paper presents a suite of tools for constraint programming, consisting of a solver interface and a remote

control application. The solver interface offers a uniﬁed API for interacting with different solvers of various

programming languages. Based on this API, we present a remote control system enabling to conﬁgure the

solver and to observe and analyze its behaviour while it is running.

1 INTRODUCTION

Constraint Programming (CP) is a powerful paradigm

to solve complex combinatorial problems across var-

ious domains. In this paper, we consider CP in

a broad sense, including the Boolean satisﬁability

problem (SAT) (Biere et al., 2021), its generaliza-

tion to pseudo-Boolean (PB) problems (Roussel and

Manquinho, 2021), and general constraint program-

ming as deﬁned for instance in (Rossi et al., 2006)

(Lecoutre, 2009).

For these different paradigms, numerous solvers

have been proposed such as Kissat (Biere and

Fleury, 2022), Glucose (Audemard and Simon, 2018),

RoundingSat (Elffers and Nordstr

om, 2018), Sat4j

(Le Berre and Parrain, 2010), ACE (Lecoutre, 2023),

Choco (Narendra Jussien, 2008), or Picat (Zhou et al.,

2015). These solvers often have very different pro-

gramming interfaces. Choosing one solver or an-

other thus imposes to follow this particular interface

when using the solver as a library. To face this is-

sue, generic interfaces like IPASIR or IPAMIR have

been developed to provide a simple common inter-

face for incremental SAT and MaxSAT solvers, espe-

cially in the context of the SAT Competition and the

MaxSAT Evaluation. Moreover, different formats and

tools have been developed to represent the problems

to solve, such as DIMACS (DIMACS, 1993) for SAT,

OPB for PB problems and OPL (van Hentenryck,

https://orcid.org/0000-0003-2803-1530

https://orcid.org/0000-0001-7200-4279

1999), MiniZinc (Nethercote et al., 2007) (Stuckey

et al., 2010), Essence (Frisch et al., 2007) and PyCSP

(Lecoutre and Szczepanski, 2020) (which can be

used to generate XCSP

instances (Boussemart et al.,

2020)) for CP instances. Not all solvers support all

these representation languages, preventing the inter-

operability of these tools.

To ease the development and deployment of CP

solutions, this paper presents a suite of synergistic

tools that facilitate the integration of constraint pro-

gramming solutions across diverse software applica-

tions. The core component of our toolset is a solver

interface called Universe, which provides a uniﬁed

API for interacting with different constraint solvers

directly from the code. By offering a consistent and

intuitive interface, it is possible to seamlessly switch

between various solvers without the need for exten-

sive modiﬁcations, enabling greater ﬂexibility and the

exploration of different solver capabilities, without

relying on a particular modelization format. This is a

very different philosophy compared to that of MiniZ-

inc or PyCSP

, for instance, which require to en-

code the problem in their own formats before ask-

ing a solver to read this modelization and solve it.

Universe is deﬁned in two different popular program-

ming languages, namely C++ and Java, enabling the

use of solvers almost independently of the language in

which they have been implemented, which is not the

case of tools like, for instance, CPMpy (Guns, 2019).

The second component is a graphical remote control

system inspired by (Le Berre and Roussel, 2014) that

allows one to ﬁnely conﬁgure a chosen solver before

854

Falque, T. and Wallon, R.

A Toolset for Constraint Programming.

DOI: 10.5220/0012403700003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 854-861

ISBN: 978-989-758-680-4; ISSN: 2184-433X

running it on a particular instance, and even to change

its conﬁguration on the ﬂy for solvers that support

such updates. During the solver’s execution, the be-

haviour of the solver may be observed live, by show-

ing statistics about the decision it makes and the con-

ﬂicts it encounters. Additionally, the search tree can

also be displayed as the solver explores it.

The rest of this paper is organized as follows. In

Section 2, we give some preliminaries regarding con-

straint programming and solving. In Section 3, we

present the Universe solver interface. In Section 4,

we give examples of the capabilities offered by our

remote control application, and in Section 5, we con-

clude and give some perspectives for future works.

2 PRELIMINARIES

In this section, we brieﬂy describe how the dif-

ferent solvers implementing the different considered

paradigms (SAT, PB, and CP) work.

2.1 SAT Solving

A Boolean variable x is a variable that can either take

the value 0 (false) or 1 (true). We call a literal ℓ a

Boolean variable x or its negation ¯x = 1 − x. A literal

ℓ is satisﬁed when ℓ is assigned to 1, and falsiﬁed oth-

erwise. A clause is a disjunction of literals, requiring

at least one of its literals to be satisﬁed. A problem is

in Conjunctive Normal Form (CNF) when it is a con-

junction of clauses. The SATisﬁability problem (SAT)

is to determine whether such a conjunction is consis-

tent. It is the ﬁrst problem that has been proven to be

NP-complete (Cook, 1971).

2.2 Pseudo-Boolean (PB) Constraints

A pseudo-Boolean (PB) constraint is a constraint of

the form

∑

i=1

ℓ

△ δ, where n is a positive integer,

the weights (or coefﬁcients) α

and the degree δ are

integers, ℓ

are literals and △∈ {<, ≤,=,≥,>}. A PB

constraint is said to be normalized when all the coef-

ﬁcients and the degree of this constraint are positive,

and △ is ≥. Any PB constraint may be rewritten as a

conjunction of normalized PB constraints. A PB car-

dinality constraint is a normalized PB constraint in

which all the coefﬁcients are equal to 1, and a clause

is a PB cardinality constraint with its degree equal to

1. This deﬁnition is equivalent to the deﬁnition of

clauses as disjunctions of literals, and shows that PB

solvers generalize SAT solvers.

2.3 Constraint Programming

A constraint network (CN) is composed of a set of

discrete variables and a set of constraints. Each vari-

able X takes its value in a ﬁnite set called domain of

X, denoted dom(X ). Each constraint deﬁnes a relation

on a set of variables. A solution of a CN is an as-

signment of values to all its variables such that all the

constraints of the CN are satisﬁed. A CN is said to be

consistent if it has at least one solution, and the cor-

responding decision problem, called Constraint Satis-

faction Problem (CSP), is to determine whether a CN

is consistent.

2.4 Solving Techniques

Let us now give a brief overview of how the solvers

of these different paradigms work. Most of them fol-

low a similar approach, which interleaves variable as-

signments (or refutations), and a constraint propaga-

tion mechanism to ﬁlter the search space. Typically,

a search tree T is built: at each internal node of T ,

(i) a pair (x,v) is selected where x is an unﬁxed vari-

able and v is a value in dom(x), and (ii) several cases

(branches) are considered, corresponding to either an

assignment x = v or a refutation x ̸= v. The solver

chooses the variable to assign by using a variable

selection heuristic (e.g., VSIDS (Moskewicz et al.,

2001), its PB variants (Le Berre and Wallon, 2021) or

dom/wdeg (Boussemart et al., 2004) for CP solvers).

A value selection heuristic then decides the order in

which the values are chosen when assigning variables

(this heuristic is often called phase selection in SAT or

PB solvers). After each assignment, constraint prop-

agation is applied to ﬁlter out values from the do-

main of the variables, such as unit propagation (Zhang

and Stickel, 1996) for SAT solvers, its extension to

PB constraints (Dixon and Ginsberg, 2002) or MAC

(Sabin and Freuder, 1994) for maintaining arc consis-

tency in CP solvers. Each time the solver encounters

a conﬂict, it can learn a new constraint, called a no-

good. This is particularly true for SAT solvers imple-

menting the CDCL architecture (Silva and Sakallah,

1996) (E

en and S

orensson, 2004). When a conﬂict is

detected, it is analyzed by repeatedly applying the res-

olution proof system to infer a new clause explaining

the reason of the conﬂict. PB solvers also implement

a similar conﬂict analysis (Dixon, 2004), based on

the cutting-planes proof system (Gomory, 1958). CP

solvers also learn nogoods, but to a lesser extent than

SAT and PB solvers (Lecoutre et al., 2007). Because

there may be a huge amount of recorded nogoods,

solvers may delete them regularly, both to preserve

memory space and to avoid slowing down constraint

A Toolset for Constraint Programming

855

propagation. To this end, the solver applies a so-

called learned constraint deletion strategy to decide

which constraints to remove and when. Restart poli-

cies ﬁnally play an essential role in modern constraint

solvers, as they permit addressing the heavy-tailed

runtime distributions of SAT, PB and CSP instances

(Gomes et al., 2000). In essence, a restart policy cor-

responds to a function restart : N

→ N

, that in-

dicates the maximum number of steps allowed for the

search algorithm per attempt, called run. It means that

a backtrack search piloted by a restart policy builds a

sequence of binary search trees ⟨T

,. . .⟩, where T

is the search tree explored at run j. Note that the cut-

off, which is the maximum number of allowed steps

during a run, may correspond to the number of back-

tracks, the number of wrong decisions (Bessiere et al.,

2004), or any other relevant measure.

3 UNIVERSE: A UNIVERSAL

SOLVER INTERFACE

There exists a large number of solvers implementing

the different paradigms presented in the previous sec-

tion. These solvers are often very efﬁcient in practice,

but they are also somehow complementary. Indeed,

some solvers may have very good performance on

some kinds of problems, while they may be very slow

on some other problems. For instance, SAT solvers

are able to solve very efﬁciently a wide variety of in-

stances, but it is well-known that they perform poorly

on instances requiring the ability to “count”. This

is illustrated by the pigeonhole principle problem,

which states that it is not possible to put n pigeons

in n − 1 holes. Proving the unsatisﬁability of such

problems requires an exponential number of resolu-

tion steps for SAT solvers (Haken, 1985). However,

PB solvers based on the cutting-planes proof sys-

tem (Gomory, 1958) can prove it with a linear number

of derivation steps (Hooker, 1988). Such a comple-

mentarity can also be observed between solvers im-

plementing the same paradigm while using different

strategies, see, e.g., (Le Berre et al., 2020). Identi-

fying the best solver for a particular problem may be

critical in some applications, such as those involving

human interactions: end-users may ﬁnd it inaccept-

able to wait for a long time for the solution to their

problem. In order to select the best solver, one may

want to try out different ones, and thus to be able

to plug any solver in one’s application, and evaluate

its performance. However, changing the solver in-

tegrated in an application often requires a lot of ef-

fort, as solvers most of the time deﬁne their own in-

terface (when they provide one). Choosing another

solver thus implies rewriting the part of the applica-

tion invoking the functions of the solver’s API. In this

section, we present the C++ Universe interface, which

provides a common interface for the solvers of the dif-

ferent paradigms, allowing one to seamlessly switch

between different solvers. This interface may either

be natively implemented by existing solvers, or be

used in solver adapters that forward method invoca-

tions to the adapted solver’s API. We already provide

adapters for the solvers Sat4j (Le Berre and Parrain,

2010) and ACE (Lecoutre, 2023), and other ones will

be available in the near future.

3.1 An Overview of Universe

Figure 1 gives an overview of the interfaces deﬁned

in Universe. In the following, we give a detailed de-

scription of the features they provide.

The main interface of Universe is

IUniverseSolver. It allows any solver to be invoked

to check whether a problem is consistent, and to get

a solution when it is. This interface does not depend

on the paradigm implemented by the underlying

solver: the solver is expected to read the problem

itself from the ﬁle given to loadInstance() when

this method is invoked. This interface is extended

by the IUniverseSatSolver interface to allow one

to programmatically add clauses to the solver, which

is extended by IUniversePseudoBooleanSolver

for adding PB constraints, which is itself extended

by IUniverseCspSolver for adding general CP

constraints (e.g., sum, count, etc.). These methods

allow one to dynamically build the problem to solve,

and to incrementally solve it. Note that the interface

hierarchy we described follows an is-a principle: for

instance, a CSP solver is-a SAT solver in the sense

that it is able to solve a SAT problem, while a SAT

solver is-not-a CP solver, as it does not natively

recognize CP constraints (it can only deal with

clauses). Universe also deﬁnes the abstract factory

IUniverseSolverFactory, which provides meth-

ods to create SAT, PB, and CP solvers. This factory

allows implementing solvers to be easily instantiated,

and also to provide various default conﬁgurations

that can be used as-is in user applications.

3.2 Conﬁguring a Solver

Optionnally, the IUniverseConfigurableSolver

interface may be implemented by solvers to allow

the users to ﬁnely conﬁgure the solver according to

their needs. In particular, users can choose the vari-

able and value selection heuristics, the restart pol-

icy and the learned constraint deletion strategies the

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

856

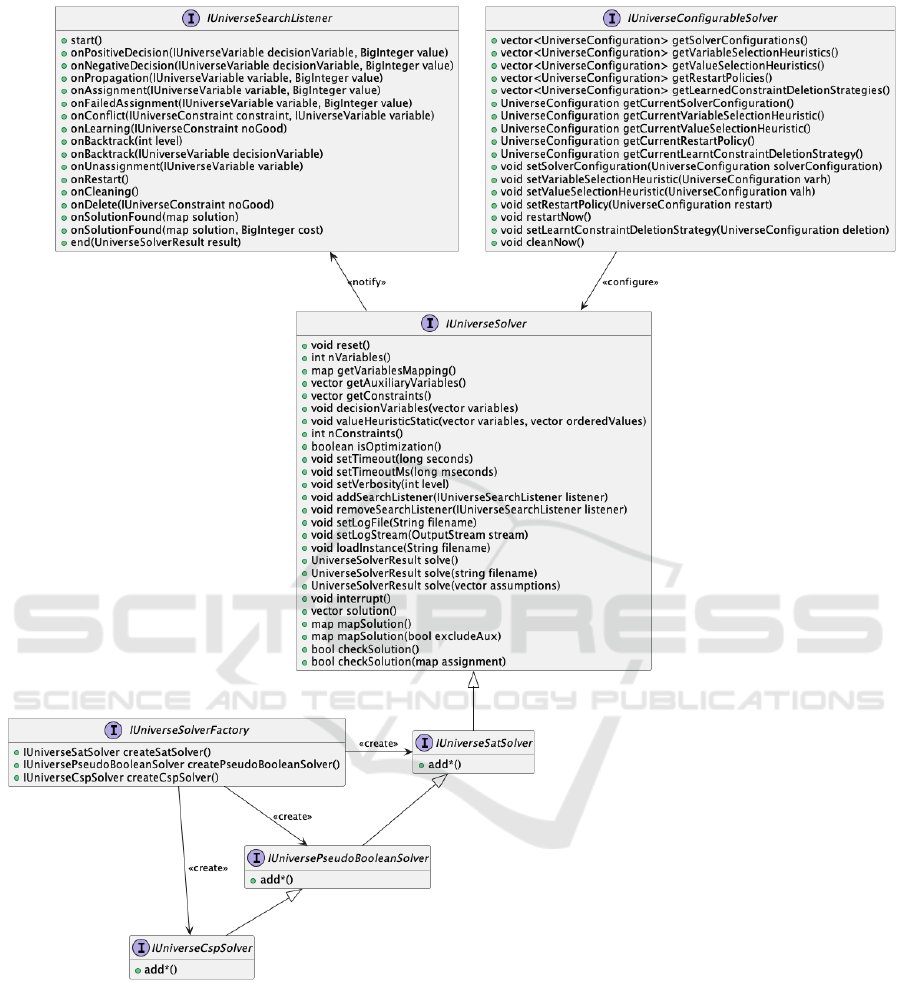
Figure 1: Class diagram of Universe.

solver will apply during its execution. To be as

generic as possible, these strategies are identiﬁed by

their names, and not by their types. Solvers im-

plementing the IUniverseConfigurableSolver are

expected to provide the list of the names of the strate-

gies they support, and to switch to the desired strategy

when asked to. Optional parameters may be speci-

ﬁed to conﬁgure the strategies (for instance, the num-

ber of conﬂicts before performing the ﬁrst restart).

The IUniverseConfigurableSolver also provides

method for manually performing a restart or deleting

learned constraints.

3.3 Listening to Search Events

Solvers implementing Universe may notify instances

of IUniverseSearchListener during the search, for

instance when a decision is made, a conﬂict is en-

A Toolset for Constraint Programming

857

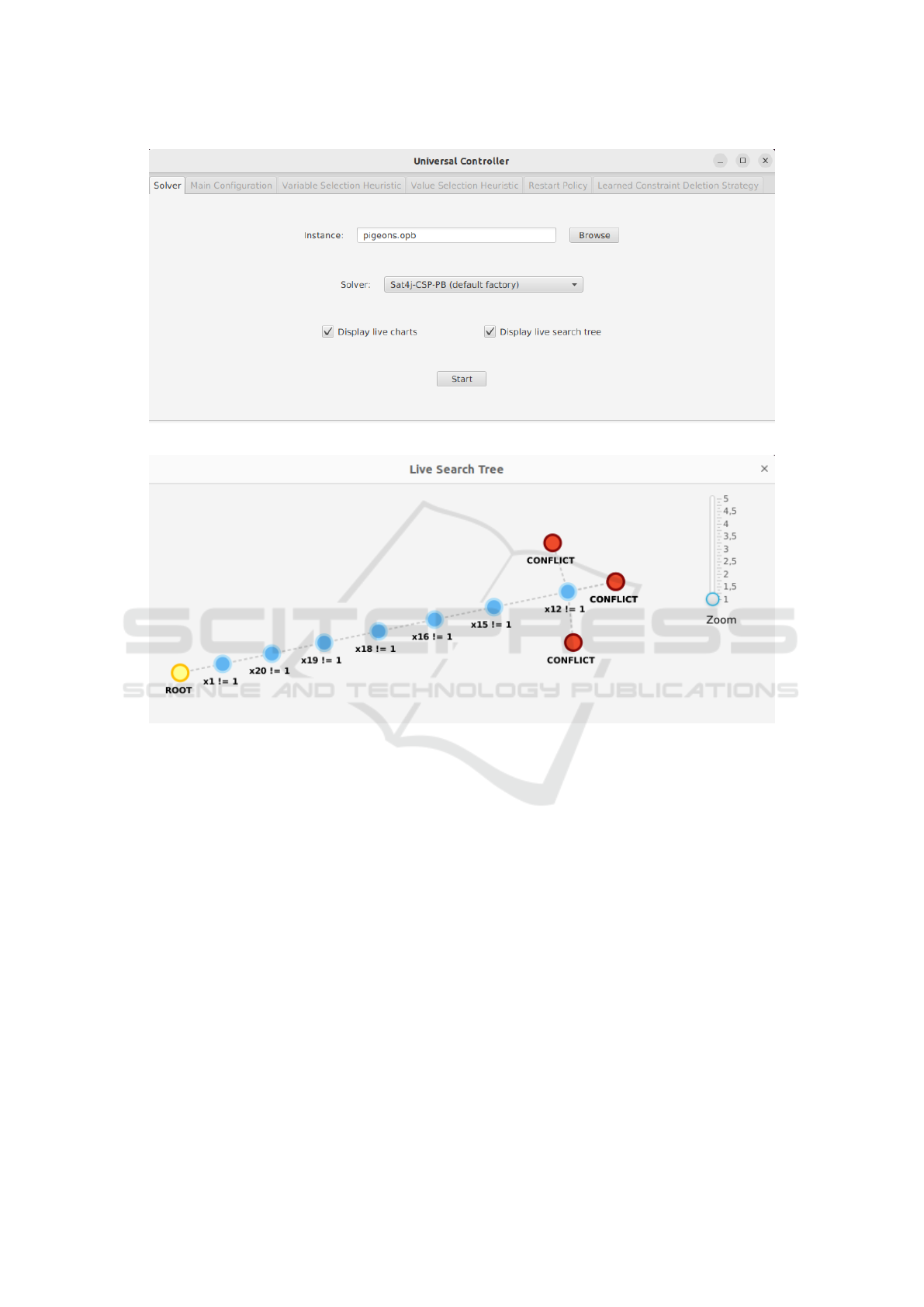
Figure 2: Main menu of the Remote Control.

Figure 3: The search tree displayed in the remote control.

countered, a constraint is learned, a restart is per-

formed, constraints are deleted or a solution is found.

Listeners may be very useful to allow one to trace the

solver execution, as well as monitor it. This interface

is for instance the basis of the remote control applica-

tion we present in Section 4.

3.4 JUniverse: Universe in Java

All the interfaces deﬁned in Universe are also deﬁned

in JUniverse, the Java equivalent to the Universe li-

brary. The signatures of the methods they deﬁne are

similar: they have the same name, and similar param-

eters (common classes from the Java standard library

replace those of C++, such as List which is used in-

stead of std::vector). Thanks to an integration with

Java Native Interface (JNI) in Universe, any Java

solver implementing an interface from JUniverse can

be used as a Universe solver. Said differently, devel-

opers of Java solvers do not need to provide a C++

port to their solvers: they only need to implement JU-

niverse in Java, and Universe does the rest.

4 A REMOTE CONTROL FOR

SOLVERS

SAT, PB, or CP solvers may be considered as black-

boxes for laypeople. They often provide many pa-

rameters, and understanding the impact of changing

one of them is not straightforward. On the contrary,

solver developers often know well how to interpret

the behaviour of their solver, and how to tune it to

get the best performance on a hard instance. In both

cases, monitoring the behaviour of the solver is cru-

cial. The most common approach is to regularly out-

put the solvers statistics in the console in which the

solver is run. Another approach is that implemented

in Sat4j (Le Berre and Roussel, 2014), which pro-

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

858

vides a remote control to modify its conﬁguration and

to graphically visualize the statistics of the search.

Based on the Universe interface, we present a uni-

versal remote control inspired by that of Sat4j, that

can be used to control and monitor any solver imple-

menting the Universe interface. This tool may be use-

ful for both solver developers and end-users, as it can

be used either for debugging purposes and for ﬁnd-

ing the most appropriate conﬁguration for solving a

particular problem. This tool is publicly available on

GitHub. In the following, we describe the different

features it provides.

4.1 Solver Conﬁguration

The remote control provides a graphical interface for

conﬁguring the solver by exploiting the methods pro-

vided by the IUniverseConfigurableSolver. The

user interface is dynamically built based on the strate-

gies that are recognized by the solver for variable and

value selection heuristics, restart policies and learned

constraint deletions (a different tab is provided for

each of these features, see Figure 2). Users can

choose the strategy they want to apply by selecting

it in a combobox, and they can then set the (optional)

parameters of the selected strategy to ﬁnely conﬁg-

ure it. The critical feature of the remote control is

that this conﬁguration can be applied before running

the solvers, but also while it is running (of course, if

the underlying solver supports such an update). This

allows one to immediately see the impact of a strat-

egy compared to another, and thus to guide users to-

wards ﬁnding the most appropriate one to solve their

problem. In the same spirit, the remote control al-

lows one to manually trigger a restart or a learned

constraint deletion. For solvers that do not imple-

ment IUniverseConfigurableSolver, the remote

control can still be used, but the conﬁguration tabs

are disabled. Only the solver execution and its moni-

toring are available for such solvers.

4.2 Live Statistics

As for the remote control provided by Sat4j, the

solver’s statistics are displayed live during its execu-

tion. In addition to the solver’s logs that are redirected

to the remote control window, six plots are updated at

each conﬂict encountered by the solver, as shown in

Figure 4:

• the size of the constraint learned by the solver af-

ter this conﬂict,

• the quality of the learned constraints,

• the number of negative (resp. positive) decisions

made before the conﬂict,

Figure 4: Dynamic plots of the Remote Control.

• the decision level at which the conﬂict occurred,

and

• the total number of assigned variables when the

conﬂict occurred.

Together, these plots provide a representation of

the solver behaviour that is more visual and inter-

pretable than their textual counterpart printed in the

logs.

4.3 Live Search Tree

The remote control also offers to display the search

tree while it is being explored by the solver. Each time

a new decision is made by the solver, a node is added

to the tree, with a label displaying the corresponding

decision. Conﬂicts and solutions are the leaves of the

tree, and are displayed in red and green, respectively.

An example of such a tree is given on Figure 3. This

feature should however be used with caution, and on

rather small inputs. Indeed, the search tree that is built

by the solver may be very large, and displaying it may

not be possible in the window of the remote control.

Additionally, showing the search tree live may have

an impact on the solver performance, which may be-

come very slow.

A Toolset for Constraint Programming

859

5 CONCLUSION

In this paper, we introduced the Universe interface,

which provides a universal interface for SAT, PB and

CP solvers. Universe allows one to conﬁgure a solver,

ﬁll it with constraints, solve the associated problem

and follow its trace while it is being executed, mak-

ing it possible to seamlessly integrate various solvers

in different applications. Based on this interface,

this paper also introduced a universal remote control

for solvers, providing a graphical user interface for

performing the operations described above while the

solver is running. As perspective for future works,

we plan to develop more adapters for other popular

solvers developed by the community. We also would

like to complete the Universe ecosystem by designing

new tools, such as, e.g., a modeling system that can be

integrated into any application.

ACKNOWLEDGEMENTS

The authors would like to thank Micha

el Valet, who

did a signiﬁcant contribution to the remote control

presented in this paper during its internship at CRIL.

REFERENCES

Audemard, G. and Simon, L. (2018). On the glucose SAT

solver. Int. J. Artif. Intell. Tools, 27(1):1840001:1–

1840001:25.

Bessiere, C., Zanuttini, B., and Fernandez, C. (2004). Mea-

suring search trees. In Proceedings of ECAI’04 work-

shop on Modelling and Solving Problems with Con-

straints, pages 31–40.

Biere, A. and Fleury, M. (2022). Gimsatul, IsaSAT and

Kissat entering the SAT Competition 2022. In Proc. of

SAT Competition 2022 – Solver and Benchmark De-

scriptions, volume B-2022-1, pages 10–11. University

of Helsinki.

Biere, A., Heule, M., van Maaren, H., and Walsh, T., editors

(2021). Handbook of Satisﬁability - Second Edition,

volume 336 of Frontiers in Artiﬁcial Intelligence and

Applications. IOS Press.

Boussemart, F., Hemery, F., Lecoutre, C., and Sais, L.

(2004). Boosting systematic search by weighting con-

straints. In Proceedings of ECAI’04, pages 146–150.

Boussemart, F., Lecoutre, C., Audemard, G., and Piette,

C. (2020). Xcsp3-core: A format for representing

constraint satisfaction/optimization problems. CoRR,

abs/2009.00514.

Cook, S. A. (1971). The Complexity of Theorem-proving

Procedures. In Proceedings of the Third Annual

ACM Symposium on Theory of Computing, STOC ’71,

pages 151–158, New York, NY, USA. ACM.

DIMACS (1993). Satisﬁability: Suggested Format. DI-

MACS Challenge. DIMACS.

Dixon, H. (2004). Automating Pseudo-boolean Inference

Within a DPLL Framework. PhD thesis, Eugene, OR,

USA. AAI3153782.

Dixon, H. E. and Ginsberg, M. L. (2002). Inference meth-

ods for a pseudo-boolean satisﬁability solver. In

AAAI’02, pages 635–640.

en, N. and S

orensson, N. (2004). An extensible sat-solver.

In Theory and Applications of Satisﬁability Testing,

pages 502–518.

Elffers, J. and Nordstr

om, J. (2018). Divide and conquer:

Towards faster pseudo-boolean solving. In Proceed-

ings of IJCAI 2018, pages 1291–1299.

Frisch, A., Grum, M., Jefferson, C., Hernandez, B. M., and

Miguel, I. (2007). The design of ESSENCE: A con-

straint language for specifying combinatorial prob-

lems. In Proceedings of IJCAI’07, pages 80–87.

Gomes, C., Selman, B., Crato, N., and Kautz, H. (2000).

Heavy-tailed phenomena in satisﬁability and con-

straint satisfaction problems. Journal of Automated

Reasoning, 24(1):67–100.

Gomory, R. E. (1958). Outline of an algorithm for integer

solutions to linear programs. Bulletin of the American

Mathematical Society, pages 275–278.

Guns, T. (2019). Increasing modeling language conve-

nience with a universal n-dimensional array, cppy as

python-embedded example. In Proceedings of the

18th workshop on Constraint Modelling and Reformu-

lation at CP (Modref 2019), volume 19.

Haken, A. (1985). The intractability of resolution. Theo-

retical Computer Science, 39:297 – 308. Third Con-

ference on Foundations of Software Technology and

Theoretical Computer Science.

Hooker, J. N. (1988). Generalized resolution and cutting

planes. Annals of Operations Research, 12(1):217–

239.

Le Berre, D., Marquis, P., and Wallon, R. (2020). On weak-

ening strategies for PB solvers. In Pulina, L. and Seidl,

M., editors, SAT 2020, pages 322–331. Springer.

Le Berre, D. and Parrain, A. (2010). The SAT4J library,

Release 2.2, System Description. Journal on Satisﬁa-

bility, Boolean Modeling and Computation, 7:59–64.

Le Berre, D. and Roussel, S. (2014). Sat4j 2.3.2: on the

ﬂy solver conﬁguration, System Description. Journal

on Satisﬁability, Boolean Modeling and Computation

(JSAT), 8:197–202.

Le Berre, D. and Wallon, R. (2021). On dedicated cdcl

strategies for pb solvers. In Proceedings of SAT 2021,

pages 315–331.

Lecoutre, C. (2009). Constraint Networks: Techniques and

Algorithms. ISTE/Wiley.

Lecoutre, C. (2023). Ace, a generic constraint solver.

CoRR, abs/2302.05405.

Lecoutre, C., Sais, L., Tabary, S., and Vidal, V. (2007).

Recording and minimizing nogoods from restarts. J.

Satisf. Boolean Model. Comput., 1(3-4):147–167.

Lecoutre, C. and Szczepanski, N. (2020). PYCSP3: mod-

eling combinatorial constrained problems in python.

CoRR, abs/2009.00326.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

860

Moskewicz, M. W., Madigan, C. F., Zhao, Y., Zhang, L.,

and Malik, S. (2001). Chaff: Engineering an Efﬁcient

SAT Solver. In Proceedings of the 38th Annual De-

sign Automation Conference, DAC ’01, pages 530–

535, New York, NY, USA. ACM.

Narendra Jussien, Guillaume Rochart, X. L. (2008). Choco:

an open source java constraint programming library.

In Conference on the Integration of Constraint Pro-

gramming, Artiﬁcial Intelligence, and Operations Re-

search.

Nethercote, N., Stuckey, P., Becket, R., Brand, S., Duck, G.,

and Tack, G. (2007). MiniZinc: Towards a Standard

CP Modelling Language. In Proceedings of CP’07,

pages 529–543.

Rossi, F., Beek, P. V., and Walsh, T. (2006). Handbook of

Constraint Programming. Elsevier.

Roussel, O. and Manquinho, V. M. (2021). Pseudo-boolean

and cardinality constraints. In Biere, A., Heule, M.,

van Maaren, H., and Walsh, T., editors, Handbook of

Satisﬁability - Second Edition, volume 336 of Fron-

tiers in Artiﬁcial Intelligence and Applications, pages

1087–1129. IOS Press.

Sabin, D. and Freuder, E. (1994). Contradicting conven-

tional wisdom in constraint satisfaction. In Proceed-

ings of CP’94, pages 10–20.

Silva, J. a. P. M. and Sakallah, K. A. (1996). GRASP – New

Search Algorithm for Satisﬁability. In Proceedings

of the 1996 IEEE/ACM International Conference on

Computer-aided Design, ICCAD ’96, pages 220–227,

Washington, DC, USA. IEEE Computer Society.

Stuckey, P., Becket, R., and Fischer, J. (2010). Philosophy

of the MiniZinc challenge. Constraints, 15(3):307–

316.

van Hentenryck, P. (1999). The OPL Optimization Pro-

gramming Language. The MIT Press.

Zhang, H. and Stickel, M. E. (1996). An efﬁcient algo-

rithm for unit propagation. In In Proceedings of the

Fourth International Symposium on Artiﬁcial Intelli-

gence and Mathematics (AI-MATH’96), Fort Laud-

erdale (Florida USA, pages 166–169.

Zhou, N., Kjellerstrand, H., and Fruhman, J. (2015). Con-

straint Solving and Planning with Picat. Springer

Briefs in Intelligent Systems. Springer.

A Toolset for Constraint Programming

861