Scheduling Single AGV in Blocking Flow-Shop with Identical Jobs
Erik Boom
1,2
, Mat
´
u
ˇ
s Mihal
´
ak
1 a
, Frank Thuijsman
1 b
and Mark H. M. Winands
1 c
1
Department of Advanced Computing Sciences, Maastricht University, Maastricht, The Netherlands
2
VDL Nedcar, Born, The Netherlands
Keywords:
Scheduling, Flow-Shop, Makespan, AGV, Manufacturing, Integer Linear Programming (ILP), Heuristics.
Abstract:
We consider a flow-shop with m stations (machines) and n identical jobs that need to be processed on each
station. The processing time of every job on station i is p
i
. After a job is processed on a station i, it needs to
be transported by an automated guided vehicle (AGV) to the next station i + 1. There is only one AGV. We
assume no buffers, i.e., when the AGV transports a job to a station, the station needs to be empty. Furthermore,
an AGV can transport at most one job at a time, non-preemptively, i.e., it cannot leave the job in the middle
of transportation. The transportation times between the stations are given and are independent of whether the
AGV carries a job or not. We study the problem of scheduling the single AGV such that all jobs are processed
and the makespan is minimized. We provide a characterization of feasible schedules, and use it to derive an
integer linear program (ILP) for the problem. We observe that solving the ILP requires a rather large amount of
computation time even for very small instances. We use the ILP-formulation to design a rolling-window based
heuristic that scales up and provides close-to-optimum schedules, as demonstrated by experimental evaluation
that also involves comparison to two natural greedy algorithms.
1 INTRODUCTION
Transportation robots such as automated guided vehi-
cles (AGVs), autonomous mobile robots (AMRs), or
autonomous intelligent vehicles (AIVs) are being in-
creasingly used in manufacturing plants to accommo-
date the so-called high-mix low-volume manufactur-
ing, in which many different product types are man-
ufactured in small quantities. In a manufacturing
plant with several workstations, the variety of prod-
ucts often manifest itself in different production paths
through the workstations. AGVs, AMRs, and AIVs
are unconstrained in their movements between the
workstations, compared to transportation by conveyor
belts, and thus are an ideal mean to transport jobs
along their individual production paths. Manufactur-
ing environments that offer flexibility in production
routes between stations are often called flexible as-
sembly lines. This paper discusses only AGVs, but all
the results apply to AMRs and AIVs as well.
The inherent flexibility of AGVs in movement
poses scheduling challenges that are not present in
the classic conveyor-belt based manufacturing: at any
a
https://orcid.org/0000-0002-1898-607X
b
https://orcid.org/0000-0001-8139-8003
c
https://orcid.org/0000-0002-0125-0824
time, the AGV has to decide which of the possible
transportation tasks it executes as next. Here, a trans-
portation task is a transportation of a product from one
station to the next station along the product’s produc-
tion path. Such decisions can quickly chain and lead
to a combinatorial explosion of possible outcomes.
In this paper, we study a conceptually straightfor-
ward setting for scheduling AGVs in flexible manu-
facturing systems: use a single AGV for all trans-
portation tasks in a manufacturing that processes n
identical jobs (products) on m workstations, where
every job j ∈ {1, ...,n} has the same production path
(1,2, . .. , m) through the m workstations, and the time
every job j needs at workstation i is pr(i), i.e., the jobs
are identical and each operation of a job has a specific
processing time. The single AGV can at any moment
transport at most one product, can drop-off or pick-up
a product only at the workstations, the workstations
have no buffer (to store products before they are pro-
cessed or after they are processed on the station) and
thus a product on station i blocks this station from be-
ing used until the AGV picks-up the product at the
station and moves it to the next station i + 1. In par-
ticular, if the AGV carries a product and arrives at a
station which has a finished product on it, there is no
mean for the AGV to swap the two products (between
Boom, E., Mihalák, M., Thuijsman, F. and Winands, M.
Scheduling Single AGV in Blocking Flow-Shop with Identical Jobs.
DOI: 10.5220/0012398200003639
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 325-332
ISBN: 978-989-758-681-1; ISSN: 2184-4372
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
325

the AGV and the station).
We study the problem of minimizing the
makespan – the completion time of the last job on the
last workstation. Motivated by solving the problem
to optimality, we first develop a non-trivial integer-
linear-programming (ILP) formulation of the prob-
lem. The formulation heavily uses a simple character-
ization of a feasible schedule that we provide in this
paper. The experiments demonstrate that even state-
of-the-art commercial ILP-solvers do not scale up to
solve even modestly sized instances of 25 jobs and 6
stations. To mitigate this computational hurdle, we
design a heuristic that uses a moving-time-window
and solves iteratively smaller sub-instances corre-
sponding to the time-windows using the ILP formula-
tion, obeying decisions about jobs that were made in
previous iterations of the heuristic. For comparison,
we also implement two straightforward greedy algo-
rithms, and experimentally compare the algorithms.
2 RELATED WORK
There are many papers dealing with scheduling and/or
routing of AGVs in manufacturing environments (Vis,
2006; Hosseini et al., 2023). The published results
deal with different scheduling or routing aspects of
operating manufacturing processes where transporta-
tion happens by AGVs. For example, the schedul-
ing environment, as coined by the scheduling litera-
ture, may be parallel machines, flow shops, job shops,
or open shops; the machines may have input/output
buffers or not (where jobs may be queuing to be pro-
cessed by a machine); one or more AGVs may be
used; collisions of AGVs are/are-not taken into ac-
count; the capacity of AGVs is one or more jobs. Fi-
nally, the optimization goal can be the makespan, total
completion time, latency, or tardiness.
Our scheduling problem is to minimize the
makespan in a flow-shop setting with m machines and
n identical jobs, without buffers, and where the jobs
are transported between the stations (machines) by a
single AGV, with given transportation times between
any two stations. Our problem is a special case of the
so-called robotic cell problem (RCP) (Carlier et al.,
2010; Kharbeche et al., 2011). RCP is a flow-shop
with no buffers and with one AGV of capacity one for
the transportation tasks. Our problem is specific in
that all the jobs are identical, and thus we do not need
to schedule the order (permutation) of the jobs on the
machines. The main results are two heuristics based
on a decomposition of the problem and genetic pro-
gramming (Carlier et al., 2010) and an exact branch-
and-bound algorithm (Kharbeche et al., 2011). We
provide an ILP formulation, and use it to derive a
heuristic that scales with the number of jobs.
While the complexity of our problem is not
known, it is worth noting that the makespan mini-
mization in a flow shop with two machines, one AGV,
and unlimited buffers is NP-hard (Kise, 1991; Hurink
and Knust, 2001). For the case of zero travel times,
the problem reduces to the flow-shop with blocking
constraints, which was proved to be NP-hard for m ≥
3 by Hall and Sriskandarajah (Hall and Sriskandara-
jah, 1996). For the case of no buffers, three stations,
and arbitrary processing times (and travel times), Hall
et al. show that given a fixed periodic schedule of
period 6 for a robotic arm (that can be seen as a
transportation robot), the problem of sequencing the
jobs such that the used fixed periodic schedule of the
AGV minimizes the makespan is NP-hard (Hall et al.,
1998). Obviously, this is not directly related to our
problem, since do not consider sequencing of jobs (we
have identical jobs), nor periodic schedules, nor con-
stant number of stations.
In this paper, besides others, we develop an
ILP formulation of the problem. There are sev-
eral papers that deal with different variants of the
scheduling problem with AGVs that also provide ILP-
formulations. None of the ILP-formulations cov-
ers our problem. It is noteworthy to mention that
the literature often reports non-scalability of using
ILP-formulations to solve instances beyond tiny ones.
There is one exception, and that is the work of (Fontes
and Homayouni, 2019), who consider a scheduling
problem with equivalent machines (any job-task can
be processed on any machine) and infinite buffers and
demonstrate reasonable runtimes for modestly large
ILPs (4 stations, 8 jobs, 23 operations in total).
3 PROBLEM DEFINITION
We consider the makespan minimization problem in
the following flow-shop setting. There are n identical
jobs and m workstations. Every job needs to be pro-
cessed on each workstation in the order 1, 2, . . . , m. In
the beginning, all jobs are at a pick-up station (also
called the loading station), which we refer to as sta-
tion 0. Before a job can be processed at workstation i,
i ∈ {1, . .. , m}, it needs to be transported from station
i−1 to station i. Transportation is performed by a sin-
gle AGV. When the AGV arrives at station i, the job is
moved from the AGV to the station only if the station
has no other job. Upon arriving, the processing of the
job starts immediately and takes pr(i) time units (i.e.,
the moving of a job from the AGV to the station hap-
pens in no time). The processing is non-preemptive.
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
326

Figure 1: All jobs are at pick-up station 0, and need to be
processed on the workstations 1, 2, .. . , m in the order indi-
cated by the arrows. All jobs finish in delivery station m +1.
Every workstation can only handle one job at a time,
and there are no buffers at any workstation (where the
jobs could be stored to wait for being processed by
the workstation). This implies that whenever there is
a job at a workstation, the workstation is blocked un-
til the job is transported to the next workstation. A
job that has been processed on the last workstation m
needs to be eventually transported to the delivery sta-
tion (also called an unloading station), which we refer
to as station m+1. We stress that stations 0 and m + 1
are no real workstations as no processing happens at
these stations. When a job arrives at station m + 1, the
job is treated as finished and away from the overall
system. See Figure 1 for a schematic overview of the
flow of the jobs throughout the flow-shop.
The jobs are transported between the stations by a
single AGV. The time it takes for the AGV to move
from station i
1
to station i
2
is d(i
1
,i
2
), and is indepen-
dent of whether the AGV carries a job, or not. Thus,
transporting a job from station i to station i + 1 takes
d(i, i + 1) time. Because there can be at most one job
at any station, because the AGV can carry at most one
job, and because we are minimizing the makespan,
the only meaningful operations of the AGV are “go
from current location (a station) to a station i, pick-
up the job at this station, and transport it to station
i + 1”, for i ∈ {0, 1,. . ., m}. We call such an operation
a transportation task i.
Observe that because of the blocking nature of the
flow-shop, the jobs are processed on each of the sta-
tions in the same order given by the order in which
the jobs enter station 1. Furthermore, because the
jobs are identical, the order in which they are picked-
up from station 0 has no influence on the makespan.
Thus, only the order in which the jobs are transported
between the stations influences the overall makespan.
The time it takes to complete a transportation task i is
a sum of three values: the time d(c,i) that is needed to
travel from the current station c to station i, the wait-
ing time w at station i from the arrival until the job on
station i is processed (it can be zero, when the pro-
cessing of the job on machine i has been completed
before the arrival of the AGV), and the time d(i,i+ 1)
that is needed to travel from station i to station i+1. It
is obvious that c depends on the previous transporta-
tion task of the AGV, and w also depends on the previ-
ous transportation task(s). Thus, we want to schedule
the transportation tasks for the single AGV so that the
resulting makespan is minimum.
3
0
1
2
1
2
1
2
1
2
1
2
1
2
1
2
0
0
0
0
0
0
3
3
3
3
3
3
Figure 2: Execution of schedule S = (0, 1, 0, 2, 1, 2) for n =
2 jobs and m = 2 stations. Every row k corresponds to a
state before execution of the k-th transportation task. A dot
depicts a job and its position at a workstation. For example,
the third row corresponds to the state (1,0,1,0).
Since all jobs are identical, they can be picked
from station 0 in any order, say in the order 1,2, . .. , n,
and a transportation task ”transport job from station i
to station i + 1 is uniquely defined by the origin sta-
tion i (the identity of a job is simply the job currently
present at station i, if i ≥ 1, or it is simply the next job
in the order if i = 0). Hence, a schedule of transporta-
tion tasks can be represented as a sequence (ordering)
S = (s
1
,s
2
,. . ., s
k
) of all transportation tasks, where
s
p
∈ {0, 1,. . ., m}, p = 1,. . ., k, stands for the trans-
portation task “transport the (next) job from station s
p
to station s
p
+ 1”. Naturally, the AGV executes the
transportation tasks in this order, as soon as possible,
thus inducing completion times of jobs at the stations
and thus also the overall makespan. Figure 2 gives
an example of a schedule and its execution. Here, we
define a state to reflect the position of all jobs just be-
fore an execution of a transportation task. Formally,
for a schedule S = (s
1
,s
2
,. . ., s
k
), a state at sched-
ule position p ∈ {1, 2, . . . , k} is a vector state(p) =
(n
0
,n
1
,. . ., n
m+1
), where n
a
is the number of jobs at
station a, a = 0, . . . , m + 1, after the completion of
the first p−1 transportation tasks s
1
,s
2
,. . ., s
p−1
from
schedule S. Clearly, 0 ≤ n
0
,n
m+1
≤ n, 0 ≤ n
a
≤ 1, for
a = 1 . . . , m, and n
0
+n
1
+· ··+n
m+1
= n. We will also
use the notation state(p, i) := n
i
to denote the number
of jobs at station i in state(p).
Finally, we denote the completion time
of the transportation task s
p
in schedule
S = (s
1
,. . ., s
p
,. . ., s
k
) by c
p
(S), or simply c
p
if
the schedule S is clear from the context.
3.1 Characterization of Schedules
Recall that every job needs to be processed on ev-
ery machine i, i = 1,. . ., m. Thus, the transportation
task i = 0, . . . , m appears exactly n times in S. Hence,
the length of every schedule S is k = n · (m + 1),
and every feasible schedule S is a permutation of
Scheduling Single AGV in Blocking Flow-Shop with Identical Jobs
327

(0,. . ., 0
| {z }
n times
,1, . .. , 1
| {z }
n times
,. . ., m, .. . ,m
| {z }
n times
). Not every permuta-
tion is a feasible schedule. For example, S always
needs to start with the transportation task 0. In gen-
eral, schedule S = (s
1
,. . ., s
k
) is feasible, if and only
if, for every p = 1, . . . , k,
1. there is a job at station s
p
in state(p), i.e.,
state(p, s
p
) ≥ 1, and
2. if s
p
̸= m, there is no job at station s
p
+ 1 in
state(p), i.e., state(p, s
p
+ 1) = 0.
The claim follows, because we can transport a job
from station s
p
to station s
p
+ 1 only if there is a job
at station s
p
and the station s
p
+ 1 is empty (unless
station s
p
+ 1 is the delivery station).
We provide an equivalent characterization of fea-
sible schedules. For this, we denote by #
p
(i) the num-
ber of occurrences of transportation task i in S until
and including position p.
Theorem 1. Let S = (s
1
,. . ., s
k
) be a permutation of
(0,. . ., 0
| {z }
n times
,1, . .. , 1
| {z }
n times
,. . ., m, .. . ,m
| {z }
n times
). S is feasible, if and
only for every p = 1,. . . , k, and for every i = 1, . . . , m,
#
p
(i + 1) + 1 ≥ #
p
(i) ≥ #
p
(i + 1). (1)
Proof. Let S be a feasible schedule. Let p ∈ {1, .. . ,k}
and i ∈ {1, . . . , m}. Clearly, a transportation task i +
1 can only be made if there is a job at station i + 1.
This requires that for every transportation task s
j
=
i + 1 in S there needs to be in S before position j a
unique transportation task i (which brings job from
station i to station i + 1), and thus #
p
(i) ≥ #
p
(i + 1).
To show that #
p
(i + 1) + 1 ≥ #
p
(i), observe first that
in state(p + 1), state(p + 1, i + 1) = #
p
(i) − #
p
(i + 1)
(the number of jobs on station i + 1 is the number of
times we bring a job to i + 1 minus the number of
times we take a job from i+ 1). Since state(p + 1,i +
1) ≤ 1, the inequality follows.
To prove the second implication, assume that the
necessary condition is true. We will show that S is
a feasible schedule. We want to show that whenever
s
p
= i, there is a job at station i and there is no job at
station i + 1 in state(p). First, recall that the number
of jobs at station i in state(p) is #
p−1
(i−1)−#
p−1
(i).
We show that this quantity is at least one. Since s
p
= i,
we get that #
p
(i) = #
p−1
(i) + 1. For the same reason,
#
p−1
(i −1) = #
p
(i). Using these equalities, we derive
#
p−1
(i − 1) = #
p
(i − 1) ≥ #
p
(i) = #
p−1
(i) + 1,
where the inner inequality follows from Eq. (1). Thus,
the number of jobs at station i in state state(p) is at
least one.
Second, recall that the number of jobs at sta-
tion i + 1 in state(p) is #
p−1
(i) − #
p−1
(i + 1). We
show that this quantity is zero, or, equivalently, that
#
p−1
(i) ≤ #
p−1
(i + 1) and #
p−1
(i) ≥ #
p−1
(i + 1). The
first inequality follows directly from Eq. (1). We ob-
tain the second inequality as follows. Since s
p
= i, we
get that #
p−1
(i) = #
p
(i) − 1 and #
p
(i + 1) = #
p−1
(i +
1). Then, using Eq. (1) again, we get
#
p−1
(i) = #
p
(i)− 1 ≤ #
p
(i + 1) + 1 − 1 = #
p−1
(i + 1).
This concludes the proof.
3.2 Challenges
We want to formulate the problem as an ILP. The-
orem 1 gives a way to check whether a schedule
S = (s
1
,. . ., s
k
) is feasible. The characterization can
be easily translated to linear inequalities in an ILP,
as we will see in the next sections. The challenge
is to encode in the ILP the completion time c
p
(S)
of a transportation task s
p
, p = 1,. . . , k. Recall that
c
p
(S) = d(c, i) + w + d(i, i + 1), where c is the cur-
rent position of the AGV when the transportation task
s
p
is to be executed, and w is the waiting time of the
AGV at station s
p
for the station to finish processing
its job. Expressing w as a linear function of previous
decisions s
1
,s
2
,. . ., s
p−1
for the AGV is a challenge
as it needs to compare the arrival time of the AGV
at station s
p
with the processing time pr(s
p
) plus the
time when the current job at station s
p
arrived.
4 ALGORITHMS
4.1 ILP Formulation
In this section, we provide an ILP for our problem.
We first define the variables and the objective func-
tion. We then continue with the constraints regard-
ing the feasibility of the schedule. We finish with
constraints that concern completion times and arrival
times.
4.1.1 Decision Variables & Objective Function
We view the problem of computing an optimal sched-
ule S = (s
1
,. . ., s
k
) as an assignment problem that as-
signs to every of the k positions of schedule S one of
the n(m + 1) transportation tasks. We model such an
assignment by binary decision variables. We define
for every i = 0, 1, .. . ,m and p = 1, 2,. . ., n(m + 1) a
binary variable x
i,p
with the obvious meaning
x
i,p
=
(
1 if s
p
= i,
0 otherwise.
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
328

We define c
p
to be a variable that equals the com-
pletion time (in schedule encoded by variables x
i,p
)
of the task that has been assigned in S to position p.
The objective is to minimize the makespan. Thus, the
objective of the ILP is to minimize c
n(m+1)
.
4.1.2 Validity Constraints
We need to ensure that variables x
i,p
encode an
assignment and that it encodes a permutation of
(0,. . ., 0
| {z }
n times
,1, . .. , 1
| {z }
n times
,. . ., m, .. . ,m
| {z }
n times
). First, we make sure
that for every position p, exactly one of transportation
tasks is assigned to position p by constraints:
∀p :
m
∑
i=0
x
i,p
= 1. (2)
Furthermore, to make sure that variables x
i,p
, i =
0,. . ., m, p = 1, . . . , n(m + 1), encode the desired per-
mutation, we make sure that every transportation task
i = 0,1, . . . , m is assigned exactly n times (this is
equivalent to saying that all n jobs were transported
from each of the m + 1 stations 0,1, . .. , m):
∀i :
n(m+1)
∑
p=1
x
i,p
= n. (3)
Until now, the constraints assure that the
decision variables encode a permutation of
(0,. . ., 0
| {z }
n times
,1, . .. , 1
| {z }
n times
,. . ., m, .. . ,m
| {z }
n times
). We define a variable
s
p
that expresses the transportation task that is
assigned to position p by the decision variables. We
can assure this by the following linear constraints:
∀p : s
p
=
m
∑
i=0
i · x
i,p
. (4)
We now provide linear constraints that ensure that the
decision variables encode a feasible schedule. We use
the characterization of feasible schedules from Theo-
rem 1, which requires that for every position p and ev-
ery station i, #
p
(i + 1) + 1 ≥ #
p
(i) ≥ #
p
(i + 1). Thus,
we define variables c(i, p) for i = 0, . . . , m and for
p = 1, . . . , n(m + 1) that we want to be equal to #
p
(i).
We can assure this by the following linear constraints:
∀i∀p : c(i, p) =
p
∑
q=1
x
i,q
. (5)
Assuring the feasibility of the computed schedule
according to Theorem 1 is now straightforward:
∀p∀i < m : c(i + 1, p) + 1 ≥ c(i, p) (6)
∀p∀i < m : c(i, p) ≥ c(i + 1, p) (7)
4.1.3 Time-Related Constraints
Recall that the completion time c
p
of the transporta-
tion task s
p
that is assigned to position p depends on
the pick-up station i that is assigned to s
p
, but it also
depends on the completion time and delivery location
of the preceding transportation task s
p−1
, and on the
time when the job that is going to be transported from
station s
p
has been processed. Following this obser-
vation, we define two new variables. We define for
every position p the variable l(p) that equals the sta-
tion (location) at which the AGV is present when it
starts executing the transportation task s
p
. Obviously,
l(p) is the delivery station of the previous transporta-
tion task s
p−1
, i.e., l(p) should equal to s
p−1
+ 1. We
can ensure this with the following constraints:
∀p : l(p) = s
p−1
+ 1, (8)
where s
−1
:= 0 is the initial position of the AGV be-
fore we start any transportation.
The AGV can start the transportation task s
p
as
soon as possible, but not earlier than (i) the arrival
time of the AGV at station s
p
, i.e., time c
p−1
+
d (l(p),s
p
), and not earlier than (ii) the time when
the job at station s
p
has been processed, i.e., time
c
pred(p)
+ pr(s
p
), where pred(p) is the last previous
transportation task s
q
that delivers a job to station s
p
.
We define a pred(p) for every p > 1 as follows:
pred(p) =
(
max
q<p
q : s
q
= s
p
− 1 if s
p
̸= 0
p − 1 if s
p
= 0
(9)
We can now express the completion time c
p
of the
task s
p
at position p. Since the first task s
1
is always
to take a job from station 0 to station 1, we set
c
1
= d(0, 1). (10)
For p > 1, we define
∀p > 1 : c
p
= max{c
p−1
+ d(l(p),s
p
),
c
pred(p)
+ pr(s
p
)} + d(s
p
,s
p
+ 1). (11)
In this equation, d(s
p
,s
p
+ 1) is the time it takes to
do the actual transportation. The max operator gives
the earliest time when the task can be started. The job
arrives at station s
p
at time c
pred(p)
and takes pr(s
p
)
time to be processed. Thus, the transportation task
cannot start before the processing is finished at time
c
pred(p)
+ pr(s
p
). Expression c
p−1
+ d(l(p), s
p
) is the
earliest time when the AGV is able to start the task,
since the AGV is required to finish the preceding task
(which occurs at time c
p−1
), and then travel to sta-
tion s
p
. Since c
p
is the maximum of linear func-
tions, the above constraints can be expressed by lin-
ear inequalities in a standard way, if we can express
Scheduling Single AGV in Blocking Flow-Shop with Identical Jobs
329

c
pred(p)
, d(s
p
,s
p
+1), and d(l(p), s
p
), respectively, by
linear constraints. To do so, we introduce new vari-
ables c
pred
p
, d
p
and d
ℓ
p
that get the values, respectively,
of the just mentioned expressions. We can set these
variables to the right values by non-trivial yet stan-
dard modeling techniques. Due to space constraints,
we defer the details to the full version of the paper.
These constraints now fully describe the ILP-
formulation of the scheduling problem.
4.2 Time-Window Heuristic
It turns out that state-of-the-art ILP-solvers such as
Gurobi (Gurobi Optimization, LLC, 2023) do not
solve the ILP for instances of 25 jobs and 6 stations
within few hours. Since ILP can be solved relatively
quickly for smaller instances, we use this to design a
heuristic that decomposes the problem of computing
schedule S = (s
1
,. . ., s
n(m+1)
) at once into several sub-
problems of computing a contiguous part of S of size
w; here, we call w the time-window of the heuristic.
Formally, the time-window heuristic, parameter-
ized by a positive integer w < n(m + 1), is an iterative
algorithm that in iteration i = 0, 1, 2, . . . computes the
sub-schedule (s
1+w·i
,. . ., s
w·(i+1)
) of schedule S using
the ILP formulation that only takes into account the
decisions (variables) relevant to the considered sub-
schedule. Naturally, we modify the ILP so that the
state from previous decisions (s
1
,. . ., s
i·w
) are taken
into account (basically, we turn the respective vari-
ables from previous iterations into constants in the
current iteration). We set the objective of the ILP for
the subproblem to be the time it takes to execute the
transportation tasks of the considered time-window,
i.e., the makespan of that sub-problem.
The size of the time-window influences the run-
time and the quality of the computed schedule. We
will experimentally evaluate this later in the paper.
4.3 Greedy Algorithms
To get an insight into the performance of the time-
window heuristic for larger instances, we com-
pare it to two straightforward greedy algorithms.
Both greedy algorithms compute the schedule s =
(s
1
,. . ., s
n(m+1)
) iteratively task-by-task, starting with
task s
1
. Both greedy algorithms choose the task s
i
in
iteration i to be the task among all tasks that keeps
the schedule feasible (according to Theorem 1) that
minimizes one of the following greedy scores:
• Time it takes for the AGV to start task s
i
. It is the
travel time of the AGV from current location to
station s
i
plus the waiting time for the job at s
i
to
be finished.
Table 1: Runtime of the ILP on the randomized instances.
The mean of the runtime T is measured in seconds.
n m + 1 r T[mean] T[var]
6 5 0.1 81 1381
6 5 0.4 107 4570
6 5 0.8 205 48786
6 5 1.1 173 29053
7 4 0.1 7.92 11.00
7 4 0.4 4.15 1.70
7 4 0.8 4.97 7.03
7 4 1.1 5.96 8.42
7 5 0.1 884 313628
7 5 0.4 319 59471
7 5 0.8 366 62302
7 5 1.1 348 34389
• The completion time of task s
i
. It is the time to
start task s
i
plus the travel time d(s
i
,s
i
+ 1).
We denote by Greedy-start and Greedy-finish the
greedy algorithm that uses the first and the second
greedy score, respectively.
5 EXPERIMENTS
Set-up. We experimentally evaluate the exact ILP-
based algorithm, the ILP-based heuristic, and the two
greedy algorithms. First, we measure the run-time
of the ILP for small instances of varying values of
n and m. To investigate the influence of processing
times and travel times on the runtime, we create, for
each combination of n and m, random instances where
the average of the generated processing times is a r-
fraction of the average of the generated travel times;
here, r is a parameter. Concretely, we draw travel
times from a uniform distribution taking integer val-
ues between 15 and 25 such that the mean is 20. For
given parameter r, we draw processing times from a
uniform distribution taking integer values between 0
and r · 40 such that the mean is r · 20. For each com-
bination of n, m, and r we draw ten instances, and
we report the average of the observed values. We
note that the generated travel times are truly random,
and in particular may not satisfy the triangle inequal-
ity. Second, we run the time-window heuristic and the
greedy algorithms on the generated instances. Third,
we also generate random instances as described above
for larger values of n and m, and run the heuristic and
the greedy-algorithms on these instances.
We run the experiments on a laptop with 8GB of
RAM, and with a quad-core Intel i5 CPU of the 11th
generation. We use the Gurobi solver and its Python
interface for ILP-related experiments.
Results. The results of the experiments are presented
in Tables 1, 2, and 3. Table 1 shows that increasing
m has larger effect on the run-time than increasing n.
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
330

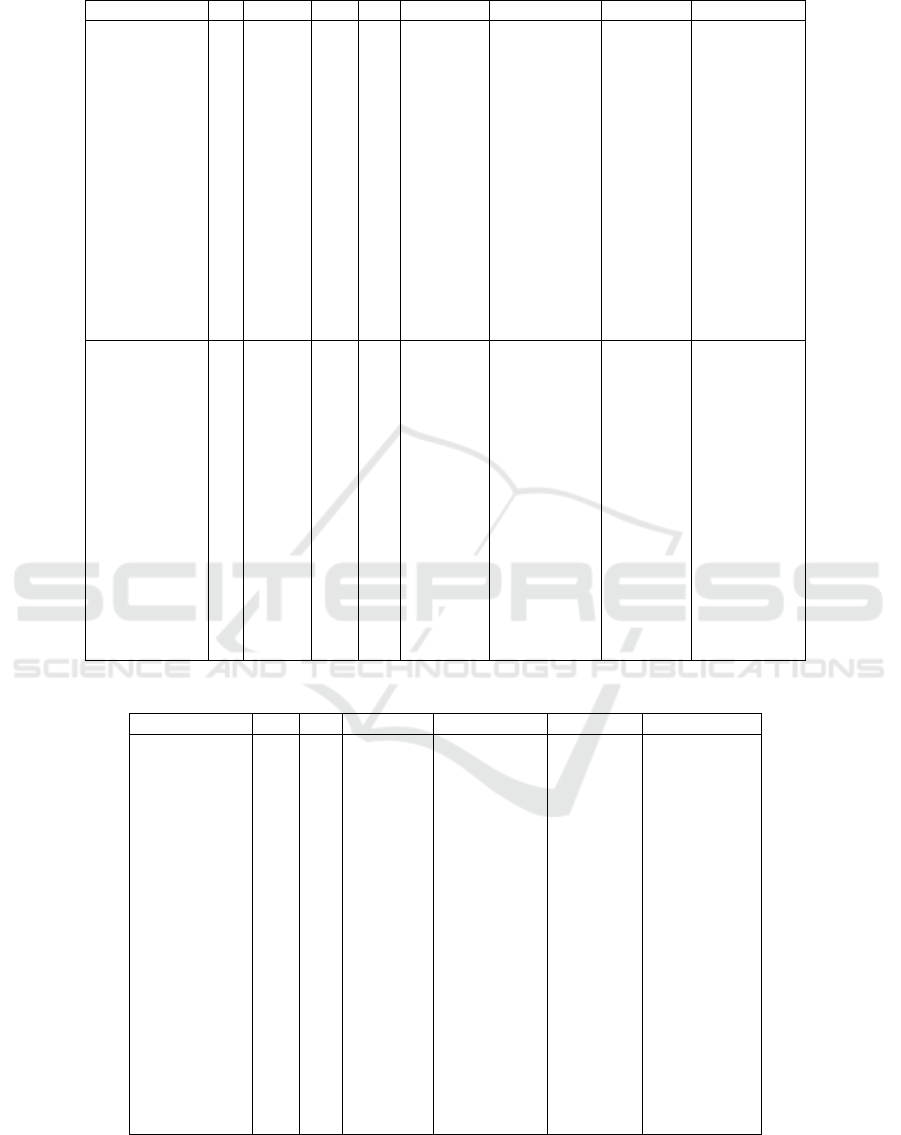
Table 2: Experiments for smaller instances. ρ is the ratio between the makespan of the algorithm and the optimum makespan.
Algorithm n m + 1 r w ρ[mean] ρ[variance] T[mean] T[variance]
TW 6 5 0.1 1k 0.99 0.000 0.18 0.001
TW 6 5 0.1 3k 1.00 0.000 1.96 0.235
Greedy-start 6 5 0.1 0.99 0.000 0.00 0.000
Greedy-finish 6 5 0.1 0.99 0.000 0.000 0.000
TW 6 5 0.4 1k 0.94 0.003 0.17 0.002
TW 6 5 0.4 3k 0.98 0.000 2.19 0.186
Greedy-start 6 5 0.4 0.92 0.002 0.00 0.000
Greedy-finish 6 5 0.4 0.87 0.003 0.00 0.000
TW 6 5 0.8 1k 0.98 0.002 0.138 0.001
TW 6 5 0.8 3k 0.99 0.000 3.82 1.071
Greedy-start 6 5 0.8 0.90 0.006 0.00 0.000
Greedy-finish 6 5 0.8 0.87 0.008 0.00 0.000
TW 6 5 1.1 1k 0.95 0.004 0.12 0.001
TW 6 5 1.1 3k 0.99 0.000 2.70 1.010
Greedy-start 6 5 1.1 0.90 0.002 0.00 0.000
Greedy-finish 6 5 1.1 0.87 0.007 0.00 0.000
TW 7 5 0.1 1k 0.99 0.001 0.23 0.002
TW 7 5 0.1 3k 0.99 0.000 8.48 9.184
Greedy-start 7 5 0.1 0.99 0.000 0.00 0.000
Greedy-finish 7 5 0.1 0.99 0.000 0.00 0.000
TW 7 5 0.4 1k 0.93 0.004 0.23 0.004
TW 7 5 0.4 3k 0.97 0.001 5.12 7.173
Greedy-start 7 5 0.4 0.91 0.003 0.00 0.000
Greedy-finish 7 5 0.4 0.87 0.004 0.00 0.000
TW 7 5 0.8 1k 0.98 0.002 0.18 0.001
TW 7 5 0.8 3k 0.99 0.000 6.64 12.161
Greedy-start 7 5 0.8 0.90 0.007 0.00 0.000
Greedy-finish 7 5 0.8 0.86 0.009 0.00 0.000
TW 7 5 1.1 1k 0.95 0.004 0.16 0.001
TW 7 5 1.1 3k 0.98 0.001 5.40 4.238
Greedy-start 7 5 1.1 0.90 0.002 0.00 0.000
Greedy-finish 7 5 1.1 0.87 0.007 0.00 0.000
Table 3: Experiments for larger instances (n = 25, m + 1 = 6). M is the makespan of the computed schedule.
Algorithm r w T[mean] T[variance] M[mean] M[variance]
TW 0.1 1k 11.72 1.567 903.11 11221.111
TW 0.1 2k 45.23 1099.14 885.44 10802.28
TW 0.1 3k 1075.13 908646.03 885.33 10853.25
Greedy-start 0.1 0.00 0.00 896.44 11133.03
Greedy-finish 0.1 0.00 0.00 913.44 13209.03
TW 0.4 1k 11.75 0.82 2461.70 433514.90
TW 0.4 2k 35.85 283.70 2375.90 267671.21
TW 0.4 3k 819.37 146320.90 2347.90 247904.32
Greedy-start 0.4 0.00 0.00 2579.30 305117.57
Greedy-finish 0.4 0.00 0.00 2708.70 199664.90
TW 0.8 1k 11.33 0.66 4176.30 345108.01
TW 0.8 2k 39.67 487.16 3912.30 291342.90
TW 0.8 3k 662.17 238831.36 3846.50 276170.28
Greedy-start 0.8 0.00 0.00 4288.00 433658.22
Greedy-finish 0.8 0.00 0.00 4596.70 725442.23
TW 1.1 1k 10.84 0.46 5646.30 1468051.12
TW 1.1 2k 28.19 131.33 5359.20 1314365.96
TW 1.1 3k 378.68 11430.71 5280.70 1198168.01
Greedy-start 1.1 0.00 0.00 5872.50 858943.17
Greedy-finish 1.1 0.00 0.00 6499.00 1427400.67
In any case, experiments (not reported in the table)
show that scheduling around 25 jobs requires, typi-
cally, several hours. The experiments do not reveal
any monotonous effect of r on runtime.
Tables 2 and 3 show the performance of the time-
window heuristic and the two greedy algorithms.
Scheduling Single AGV in Blocking Flow-Shop with Identical Jobs
331

Overall, for small instances, the time-window heuris-
tic gets close to the optimal makespan, not dropping
below 93% with a window size of 1k, and not drop-
ping below 97% with a window size of 3k. It is not
surprising to see that increasing the time-window w
leads to better schedules. The running times on the
larger instances are reasonable, even when taking a
larger window size.
The greedy algorithms do not perform well,
specifically for larger ratios r of travel/processing
time. It is interesting to note that for larger instances,
the algorithm taking the earliest time to start a task
(Greedy-start) is consistently giving a better solution
on average than the other algorithm (Greedy-finish).
It would be interesting to investigate whether it holds
up for other cases as well.
6 CONCLUSION
In this paper, we considered a flow-shop setting with
identical jobs and no buffers operated by a single
AGV, and studied the makespan minimization prob-
lem of scheduling the transportation tasks of the sin-
gle AGV. Surprisingly, this problem has not been
studied in the literature before. We provided a char-
acterization of feasible schedules, and used it to de-
sign an ILP formulation of the problem. We ob-
served that even state-of-the-art ILP solvers cannot
solve more than few stations and jobs within hours of
computation time, and resorted to heuristics. We used
the ILP-formulation as a subroutine and developed
a time-window based heuristic that decomposes the
scheduling problem into several subproblems defined
by time-windows of fixed size, and solve the subprob-
lems using our ILP formulation. We experimentally
evaluated this approach with two simple greedy al-
gorithms and, for small instances, also with optimum
algorithms (based on the ILP formulation). We ob-
served that the time-window heuristic performs well
both in the run-time as well as in the quality of com-
puted schedules.
We have done few more experiments that due to
space constraints were not presented in this paper. We
plan to do more experiments and report on these in a
full version of the paper. Furthermore, we note that
all our algorithms can be applied to the setting where
the travel time depends on whether the AGV carries a
job or not.
For future research, we would like to settle the
complexity question of deciding whether the schedul-
ing problem is NP-hard. Furthermore, we aim to test
the developed heuristic in real-world scenario in one
of the demo manufacturing lines of VDL Nedcar.
ACKNOWLEDGEMENTS
This research has received financial support from the
Ministry of Economic Affairs and Climate, under the
grant “R&D Mobility Sectors” carried out by the
Netherlands Enterprise Agency. We also want to
thank VDL Nedcar for fruitful discussions and for the
research question based on their real-world use-case.
REFERENCES
Carlier, J., Haouari, M., Kharbeche, M., and Moukrim,
A. (2010). An optimization-based heuristic for the
robotic cell problem. European Journal of Opera-
tional Research, 202(3):636–645.
Fontes, D. B. M. M. and Homayouni, S. M. (2019). Joint
production and transportation scheduling in flexible
manufacturing systems. Journal of Global Optimiza-
tion, 74:879—-908.
Gurobi Optimization, LLC (2023). Gurobi Optimizer Ref-
erence Manual.
Hall, N. G., Kamoun, H., and Sriskandarajah, C. (1998).
Scheduling in robotic cells: Complexity and steady
state analysis. European Journal of Operational Re-
search, 109(1):43–65.
Hall, N. G. and Sriskandarajah, C. (1996). A survey of ma-
chine scheduling problems with blocking and no-wait
in process. Operations Research, 44(3):510–525.
Hosseini, A., Otto, A., and Pesch, E. (2023). Scheduling in
manufacturing with transportation: Classification and
solution techniques. European Journal of Operational
Research.
Hurink, J. and Knust, S. (2001). Makespan minimiza-
tion for flow-shop problems with transportation times
and a single robot. Discrete Applied Mathematics,
112(1):199–216. Combinatorial Optimization Sym-
posium, Selected Papers.
Kharbeche, M., Carlier, J., Haouari, M., and Moukrim,
A. (2011). Exact methods for the robotic cell prob-
lem. Flexible Services and Manufacturing Journal,
23:242–261.
Kise, H. (1991). On an automated two-machine flowshop
scheduling problem with infinite buffer. Journal of
the Operations Research Society of Japan, 34(3):354–
361.
Vis, I. F. (2006). Survey of research in the design and con-
trol of automated guided vehicle systems. European
Journal of Operational Research, 170(3):677–709.
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
332