Feasibility of Random Forest with Fully Homomorphic Encryption

Applied to Network Data

Shusaku Uemura and Kazuhide Fukushima

KDDI Research, Inc., Saitama, Japan

Keywords:

Fully Homomorphic Encryption, Privacy-Preserving Machine Learning, Random Forest, TFHE,

Network Data.

Abstract:

Random forests are powerful and interpretable machine learning models. Such models are used for analyzing

data in various ﬁelds. To protect privacy, many methods have been proposed to evaluate random forests with

fully homomorphic encryption (FHE), which enables operations such as addition and multiplication under the

encryption. In this paper, we focus on the feasibility of random forests with FHE applied to network data. We

conducted experiments with random forests with FHE on IoT device classiﬁcation for three types of bits and

nine types of depths. By exponential regressions on the results, we obtained the relations between computation

time and depths. This result enables us to estimate the computation time for deeper models.

1 INTRODUCTION

In the era of big data, analyzing data has become

more important than ever in the ﬁeld of industries and

research. In such circumstances, data analysis has

been applied to various data including network analy-

sis (Pashamokhtari et al., 2023).

Machine learning has been playing a signiﬁcantly

important role in data analysis. In recent decades,

many machine learning models have been developed

and studied to make predictions more accurate. Due

to the development of machine learning and artiﬁcial

intelligence technologies, they are becoming more

important and are being used in many domains.

Decision trees and random forests (Breiman,

2001) are widely used machine learning models. De-

cision trees classify data by partitioning the feature

space. Partition is performed by comparing the input

data to the thresholds that are learned in the training

phase. By traversing from the root node to a leaf node

according to the comparison results, a decision tree

outputs the classiﬁcation result. A random forest con-

sists of many decision trees and it classiﬁes input data

by aggregating the classiﬁcation results of the com-

ponent decision trees. As a decision tree uses only

comparisons to classify, the results of decision trees

can be interpreted well. The reasons for speciﬁc re-

sults can be explained by tracking the traversal from

https://orcid.org/0000-0003-2571-0116

the root to the leaf. This explainability of a decision

tree has helped decision trees and random forests to

be used in various ﬁelds.

With the rise of data analysis over these years, the

importance of privacy has been growing. To analyze

data, they must be available to data analysts. There-

fore, analyses of highly conﬁdential data are generally

restricted. Conﬁdential machine learning models are

not shared, and the analysis of sensitive data is less

likely to be outsourced even though it sometimes pro-

vides deeper insights.

Fully homomorphic encryption (FHE) is one of

the solutions to the above problem. Encryption has

been used for decades to protect data against leak-

age. However, as encryption hides data information,

operations on encrypted data are impossible to per-

form correctly without decryption. Fully homomor-

phic encryption is a kind of encryption scheme that

overcomes this difﬁculty; that is, operations such as

addition and multiplication on encrypted data can be

performed correctly without decryption. Thus, it is

useful for analysis of conﬁdential data.

Since machine learning basically consists of many

basic computations, it works well with FHE. The ap-

plication of FHE to machine learning is not straight-

forward due to the risk of data leakage. To apply

privacy-preserving technologies to machine learning,

research has been done such as SVM (Park et al.,

2020), (Bajard et al., 2020) and neural networks

(Dowlin et al., 2016), (Lee et al., 2022). Among such

534

Uemura, S. and Fukushima, K.

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data.

DOI: 10.5220/0012394600003648

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Information Systems Security and Privacy (ICISSP 2024), pages 534-545

ISBN: 978-989-758-683-5; ISSN: 2184-4356

research, several researches have focused on privacy-

preserving decision trees and random forests. As

random forests are easily used due to their simplic-

ity, these researches are valuable. Although privacy-

preserving decision trees and random forests have

been broadly studied, the number of studies on their

applicability to real data is limited because in several

papers, popular datasets such as UCI datasets (Kelly

et al., 2023) are used. Such datasets are standard for

evaluating machine learning models, but these are ex-

ample data and sometimes less complicated than real

data. To the best of our knowledge, there is no study

on the feasibility of random forests with FHE to the

analysis of network data. Therefore, there is a neces-

sity to study it.

Our Contribution. We implemented random forest

models with FHE in order to assess their applicability

to network data of IoT devices. We conducted exper-

iments on random forests with nine depths for three

types of bits. The computation time and the accuracy

of random forests with FHE were measured. With our

results, exponential regressions are performed on the

computation time with respect to depth. By using the

coefﬁcients and intercepts we obtained, we can esti-

mate the computation time for larger bits or depths.

This paper consists of 5 sections including this

section. This section includes descriptions of related

works. The following section is for preliminaries

where FHE and random forests are reviewed brieﬂy.

in the third section, we explain the details of our im-

plementation especially the differences between nor-

mal random forests and privacy-preserving ones. In

Section 4, we describe our experiments, results and

discussion. Finally, in Section 5, we conclude this pa-

per.

1.1 Related Works

Akavia et al. (Akavia et al., 2022) proposed an FHE-

friendly decision tree algorithm using polynomial ap-

proximation. They implemented privacy-preserving

decision trees with Cheon-Kim-Kim-Song (CKKS)

FHE scheme (Cheon et al., 2017), and evaluated them

with UCI datasets.

Azogagh et al. (Azogagh et al., 2022) proposed a

privacy-preserving decision tree that can make predic-

tions without interactive processes, which is beneﬁ-

cial in circumstances where communication resources

are limited. Their algorithms were based on fully ho-

momorphic encryption over the torus (TFHE) scheme

(Chillotti et al., 2016; Chillotti et al., 2020), mak-

ing use of an outstanding property of the scheme

called functional bootstrapping. They compared their

proposed algorithm with previous works in terms of

rounds, communication and computational complex-

ity, not implementations.

Alouﬁ et al. (Alouﬁ et al., 2021) explored a

method to evaluate random forests with multikey ho-

momorphic encryption. In their setting, there existed

several random forest model owners and they col-

laboratively aggregated the outputs in a blindfolded

manner. They implemented the algorithms with

Brakerski-Gentry-Vaikuntanathan (BGV) somewhat

homomorphic encryption scheme (Brakerski et al.,

2012). Their research evaluated their random forests

on UCI datasets.

The research of Kjamilji (Kjamilji, 2023) was

dedicated to a constant time algorithm of a privacy-

preserving decision tree. The implementation of the

research was based on Microsoft SEAL 3.7 (SEAL,

2021), which allows to use BGV and Brakerski-Fan-

Vercauteren (BFV) scheme (Brakerski, 2012; Fan and

Vercauteren, 2012). The algorithm was evaluated

with UCI datasets.

Paul et al.(Paul et al., 2022) made use of pro-

grammable bootstrapping to evaluate nonlinear func-

tions emerging in evaluation of decision trees. Thier

research is based on TFHE scheme and assessed the

algorithms with UCI datasets.

2 PRELIMINARIES

In this section, we introduce notations that we use

throughout this paper. Then, we quickly review ho-

momorphic encryption and random forests.

2.1 Notations

Z,R denotes the set of integers and real numbers, re-

spectively. For a positive integer q, we deﬁne Z

Z/qZ. T denotes a torus, R/Z, and we deﬁne a dis-

cretized torus as T

= q

−1

Z/Z, the representatives

of which are {0,1/q,...,(q − 1)/q}. The sets of

n-dimensional vectors and n × m-matrix are R

and

n×m

, respectively. For a vector v, we use v

to de-

note the i-th entry. For positive integers N,q, where

N is a power of two, we set R

= Z[x]/(x

+ 1) and

= R/qR. We use ⌊·⌉ for a rounding function.

2.2 Fully Homomorphic Encryption

Fully homomorphic encryption (FHE) is an encryp-

tion scheme under which encrypted values can be

operated without decryption. Since Gentry devel-

oped the ﬁrst FHE scheme (Gentry, 2009), several

FHE schemes have been proposed such as Brakerski-

Gentry-Vaikuntanathan (BGV) (Brakerski et al.,

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data

535

2012), Brakerski-Fan-Vercauteren (BFV) (Brakerski,

2012; Fan and Vercauteren, 2012), Cheon-Kim-Kim-

Song (CKKS) (Cheon et al., 2017), and a torus fully

homomorphic encryption (TFHE) (Chillotti et al.,

2016; Chillotti et al., 2020). Each FHE scheme has

its pros and cons. Among them, TFHE has an out-

standing property called programmable bootstrapping

(PBS), which enables the evaluation of an arbitrary

discrete function. We explain this later in Section

2.2.4.

Since PBS goes well with machine learning which

sometimes requires evaluations of nonlinear func-

tions, we employed TFHE to conduct experiments.

2.2.1 LWE Chiphertext

As all of the FHE schemes developed so far are

based on the Learning with Errors (LWE) encryption

scheme(Regev, 2005), we quickly review the LWE

encryption and TFHE scheme.

Deﬁnition 2.1 (LWE Ciphertext). Let n,q, p be pos-

itive integers, and p divides q. Let N be a discrete

Gaussian distribution with a mean 0 and a small vari-

ance σ

and s be a vector whose elements are sampled

uniformly over {0,1}. An LWE ciphertext of m ∈ Z

is a pair (a,b) ∈ Z

n+1

where each elements of a ∈ Z

is uniformly sampled over Z

, ∆

, and

= ⟨a,s⟩ + ∆m + e mod q, (1)

where e is sampled from N and ⟨·,·⟩ is an inner prod-

uct.

In this deﬁnition, we call a vector s a secret vec-

tor or secret key, e a noise and m a message. We use

LWE(∆m) to denote an LWE ciphertext (a, b) of a

message m. We deﬁne a general LWE (GLWE) ci-

phertext almost the same as LWE, except that it is de-

ﬁned over R

instead of Z

. We use GLWE (∆m) to

represent a GLWE ciphertext of m.

By identifying Z

with a discrete torus T

via mul-

tiplying q to the elements of the torus, we can redeﬁne

the above deﬁnition on T

. Thus, the TFHE scheme is

called fully homomorphic encryption over the torus.

The addition of two LWE ciphertexts can be per-

formed by simply adding them entrywise. The mul-

tiplication of two encrypted numbers is not straight-

forward. It requires another way such as an external

product. We explain the details in the next subsection.

2.2.2 External Product

As mentioned above, an external product is a way to

multiply two ciphertexts. An external product is a

product of a Gentry-Sahai-Waters (GSW) ciphertext

(Gentry et al., 2013) and an LWE ciphertext. Thus we

deﬁne a GSW ciphertext at ﬁrst.

Deﬁnition 2.2 (GSW Ciphertext). Let n, l be posi-

tive integers and q, p,B be powers of two. Let s =

,...,s

n−1

) be a vector whose elements are sam-

pled uniformly over {0,1}. A GSW ciphertext of

m ∈ Z

is a vector of (n + 1)l LWE ciphertexts. For

1 ≤ j < l, 0 ≤ k ≤ n − 1, the ( j + kl − 1)-th row is

an LWE ciphertext of −

, i.e. LWE



−



. The

( j + nl − 1)-th row is an LWE ciphertext of

, i.e.

LWE





We use GSW (m) to denote a GSW ciphertext of

a message m. As an LWE ciphertext is a vector of

the length n + 1, a GSW ciphertext is a matrix in

(n+1)l×(n+1)

. In the above deﬁnition, the parame-

ters B,l are called the base and the level, respectively.

We deﬁne a GGSW ciphertext over R

, represented

by GGSW (m), similar to a GLWE ciphertext. Note

that the above deﬁnition is different from the original

deﬁnition that uses a certain matrix called a gadget

matrix, but the both are equivalent.

An external product is an operator that maps a pair

of a GGSW ciphertext and a GLWE ciphertext to a

GLWE ciphertext of the product of messages that the

two ciphertexts encrypt.

Deﬁnition 2.3 (External Product). We deﬁne an ex-

ternal product  as

 : (GGSW (m

),GLWE(∆m

)) 7→ GLWE(∆m

(2)

There exists an algorithm that realizes the external

product deﬁned above. See (Chillotti et al., 2020),

etc., for details.

External products can be performed on GSW and

LWE ciphertexts but we deﬁned it as above because

TFHE-rs (Zama, 2022), the Rust library we used in

the experiments, currently supports the external prod-

ucts of only GGSW and GLWE ciphertexts.

2.2.3 Key Switching

Key switching of an LWE ciphertext is an operation to

change the secret keys of an LWE ciphertext without

decryption. We can also change the parameters of an

LWE ciphertext by key switching. In order to execute

key switching, a special key called a key switching

key is needed.

As details of key switching are not signiﬁcant for

the analysis of the applicability of FHE to machine

learning, we skip the explanation of them. Refer to

(Chillotti et al., 2020) for details of key switching in

TFHE.

2.2.4 Programmable Bootstrapping

In the context of FHE, bootstrapping is an operation

of reducing the noise of an LWE ciphertext without

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

536

decryption. In TFHE, the evaluation of an arbitrary

function on an LWE ciphertext can be performed dur-

ing bootstrapping. This is called programmable boot-

strapping (PBS). As PBS changes the parameter of an

LWE ciphertext, key switching to the previous param-

eters is needed before the next PBS.

2.3 Random Forest

A random forest is a popular machine learning model

that can perform classiﬁcation and regression tasks.

This paper focuses only on classiﬁcation tasks.

A random forest consists of many decision trees,

thus we ﬁrst review the structure of a decision tree.

A decision tree is a binary tree-based model,

which can be viewed as a function mapping input data

to a class. A decision tree consists of two kinds of

nodes, internal nodes and leaf nodes. Each internal

node represents a partition of the input feature space,

while each leaf node corresponds to the determination

of an output class. Every internal node has its feature

index and threshold value and every leaf node have

probability of predicted classes.

Prediction with a decision tree is associated with

a traversal from the root node to a leaf node. Speciﬁ-

cally, the root node compares its threshold value with

input data at its feature index. If the threshold is larger

than or equal to the data, then do the same process is

performed at its left child node; otherwise, it is per-

formed at the right child node. Until the traversal

reaches a leaf node, the tree repeats this procedure.

Once it reaches a leaf node, a decision tree outputs

the class index of the selected leaf node as a predic-

tion result.

A random forest is a machine learning model that

consists of many decision trees. Random forests clas-

sify data by aggregating the classiﬁcation results of

their component decision trees.

3 IMPLEMENTATION OF

RANDOM FOREST WITH TFHE

In this section, we describe how we evaluated a ran-

dom forest with homomorphic encryption. We im-

plemented random forests with FHE with TFHE-

rs (Zama, 2022), which is a Rust library of TFHE

(Chillotti et al., 2020). As a random forest is com-

posed of many decision trees, we ﬁrst implemented a

decision tree with TFHE.

Our implementation is basically similar to that

of (Paul et al., 2022) in the sense that we imple-

ment decision trees with TFHE and make use of pro-

grammable bootstrapping as they do. Although the

developer of TFHE-rs, Zama, also supports a library

for machine learning with FHE, concrete ML (Meyre

et al., 2022), we did not use it because we investigated

details of the evaluation of a random forest with FHE.

An overview of implementation follows below. In

order to evaluate a decision tree homomorphically,

there are three differences from evaluation with plain-

text. One is how to evaluate comparisons at each in-

ternal node, and the others are related to how to eval-

uate tree predictions.

On the one hand, the former can be easily solved

with programmable bootstrapping. On the other hand,

the latter is not straightforward. First, the selection of

leaf nodes requires new ideas that are not necessary

for plaintext because the results of comparison are en-

crypted; hence, they cannot be directly used to select

a leaf node. After selecting a leaf node, the decision

tree needs to output what class the leaf node repre-

sents. This also cannot be done easily as the result of

selection cannot be known without decryption.

Several ideas to overcome the difﬁculty in the se-

lection of leaf nodes have been proposed such as path

costs (Tai et al., 2017) and polynomial form (Bost

et al., 2015). As the idea of path costs requires ad-

dition and checking whether the path cost is zero, it

goes well with TFHE. Therefore, we employed the

path costs to evaluate decision trees.

Before explaining the implementation of decision

trees, we ﬁrst explain quantization of data.

3.1 Quantizing Data

As fully homomorphic encryption computes fast with

small bit values, it is efﬁcient to quantize data into

small bits. Among several ways to quantize data such

as (Jacob et al., 2018), the simplest way is to quantize

uniformly, as done in (Frery et al., 2023). Uniform

quantization into n bits divides the interval between

the max value and the minimum value into 2

parts of

the same size, and then rounds a value into the clos-

est value of the quantized interval. In other words, for

ﬁxed maximum M and minimum m, uniform quanti-

zation into n bits is

(x) :=

⌊

− 1)(x − m)/(M − m)

⌉

. (3)

To adapt to a value larger than the maximum or

smaller than the minimum, we slightly modify this

function as

(x) :=











− 1 if x > M

−3)(x−m)

(M−m)

+ 1 if m ≤ x ≤ M

0 if x < m

. (4)

With this quantization, we can convert data into de-

sired bits. As this includes rounding, quantization has

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data

537

a slight inﬂuence on accuracy, which we will discuss

in Section 4.3.1.

3.2 Implementation Details of Decision

Tree

As we mentioned above, the implementation of a

decision tree with homomorphic encryption differs

from that in plaintext. We describe the three afore-

mentioned differences; comparison, selection of leaf

nodes and outputting a class as prediction.

3.2.1 Comparison

Comparing two encrypted data is not easy in general.

However, if one value is known by the encrypter pre-

viously, it can be done with programmable bootstrap-

ping.

A comparison of a value x with a ﬁxed value y can

be regarded as a step function such as

Comp

(x) =



0 if x ≤ y

1 if x > y

. (5)

By evaluating encrypted data via programmable boot-

strapping with this comparison function, compari-

son can be performed homomorphically. We used

(message bit−4)

instead of one as we switch the mes-

sage bits after comparison for efﬁciency of computa-

tion.

3.2.2 Selection of Leaf Nodes

In order to determine which leaf node should be out-

put, we employed path costs (Tai et al., 2017). Path

costs are nonnegative integers assigned to each node

of a decision tree. For leaf nodes, the path cost is

equal to zero if and only if a leaf node corresponds to

the selected node.

Path costs can easily be computed with compari-

son results at all internal nodes. To illustrate how to

compute path costs, we deﬁne two types of variables,

path cost pc

and comparison result c

at the i-th node.

The numbering of nodes begins with the root node as

zero, and increases as the depth becomes deeper. For

nodes at the same depth, numbers are assigned from

left to right. Therefore, if a tree is a complete binary

tree, the number of left child nodes of the i-th node is

2i + 1 for the right child node 2i + 2.

With the notations above, path costs are computed

recursively as



2i+1

= pc

+ c

2i+2

= pc

+ (1 − c

)

(6)

where i = 0,...,2

− 1 and c

is the comparison result

at the i-th node. As this computation requires only ad-

dition, it is perform homomorphically with encrypted

Algorithm 1: How to select a leaf node. Note that all the

computations below are performed under encryption.

Input: Array of comparison results of the size 2

−1:

Output: Array of 0/1s where only index of selected

leaf is 1

1: PathCosts ← [0,...,0] of length 2

d+1

− 1

2: for i ← 0 To 2

− 2 do

3: PathCosts[2i + 1] ← PathCosts[i] + C[i]

4: PathCosts[2i + 2] ← PathCosts[i] + (1−C[i])

5: end for

6: LeafPathCosts ← PathCosts[2

...2

d+1

− 2]

7: SelectedLeaf ← [0,...,0] of length 2

d+1

− 1

8: for i ← 0 To 2

− 2 do

9: SelectedLeaf[i] ← PBS(LeafPathCosts[i],

is zero)

10: end for

11: return SelectedLeaf

values. After computing the path costs above, we ex-

ecute programmable bootstrapping with a function to

determine whether the input is zero or not, that is

is zero(x) =



1 if x = 0

0 if x ̸= 0

(7)

With the procedure above, we obtain encrypted val-

ues corresponding to leaf nodes, one of which is an

encrypted one and the rest are encrypted zeros. This

algorithm is shown in Algorithm 1.

3.2.3 Output Class

Through the above process described in Section 3.2.2,

we obtain a one-or-zero value corresponding to which

leaf is selected. Outputting the predicted class is,

however, not straightforward because the result is en-

crypted. To output the predicted class without decryp-

tion, we use homomorphic multiplication. For each

leaf node, we ﬁrst prepare for a one-hot vector of the

number of classes. The i-th entry of the vector is set

to one if the leaf node is associated with the i-th class,

and the rest are set to zero. Then encrypt each entry

of the vectors. Finally, after multiplying the result-

ing values of selection of leaf node to the correspond-

ing encrypted one-hot vectors, we take the entrywise

summation of the vectors. This completes the homo-

morphic evaluation of a privacy-preserving decision

tree.

Note that in order to evaluate one decision tree, it

is more efﬁcient to multiply a class index instead of

one-hot vector. We used it for extensibility to random

forests at the expense of the computational cost.

Multiplication on encrypted values in TFHE-rs is

executed by an external product of the GGSW value

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

538

Algorithm 2: Output class one-hot vector. All the com-

putations are performed under encryption. KStoGLWE is

a function that switches the keys of LWE to GLWE. Exter-

nalProd is an external product. PBS(x, f ) is a programmable

bootstrapping on x with a function f . id is the identity func-

tion.

Input: GGSW encrypted one-hot vectors of class as-

sociated to leaf nodes: C, LWE encrypted one-hot

vectors of selection of leaf nodes: S

Output: one-hot vector of tree result where only in-

dex of selected class is 1

1: GlweS ← KStoGLWE(S)

2: TreeOnehot ← [0,...,0] of length

NumberO fClasses

3: for i ← 0 To 2

− 1 do

4: for j ← 0 To NumberO fClasses − 1 do

5: TreeOnehot[j] ← TreeOnehot[j] + External-

Prod(C[i][j],GlweS[i])

6: if i mod 8 = 7 then

7: TreeOnehot[j] ← PBS(TreeOnehot[j],

id)

8: end if

9: end for

10: end for

11: return TreeOnehot

and GLWE. We can convert an LWE ciphertext into

GLWE ciphertext via key switching. We obtain a

GLWE ciphertext of the multiplication of GGSW and

GLWE. Sample extraction enables the conversion of

a GLWE ciphertext into an LWE ciphertext.

Since an external product increases the noise of

an encrypted message, it is necessary to refresh the

noise. To do so, we executed programmable boot-

strapping with the identity function every eight addi-

tions.

3.2.4 Expansion of Decision Tree

A complete binary tree is a tree where all internal

nodes have two child nodes. In general, a decision

tree is not complete. When a decision tree is not com-

plete, partial information of the tree might be leaked

from the evaluation time. As random forests with

FHE take more time to predict than those without

FHE, the risk of this increases.

Expanding incomplete decision trees into com-

plete ones can prevent this. The expansion of a de-

cision tree appends dummy nodes until the tree be-

comes complete. Descendant dummy nodes of an

internal node have random thresholds and the same

class as the internal node previously had as a leaf

node. Thus this expansion process does not affect the

classiﬁcation result. Such expansion is performed in

(Alouﬁ et al., 2021; Kjamilji, 2023), for instance.

Algorithm 3: Overview the Complete Algorithm. All the

computations below are performed under encryption.

Input: Data, Model

Output: Encrypted summation of one-hot vector of

all component decision trees

1: Generate keys

2: EncModel ← Encrypt(Model)

3: QuanData ← Quantize(Data)

4: EncData ← Encrypt(QuanData)

5: for i ← 0 To NumberO f Models − 1 do

6: CompRes ← CompWithPBS(EncData, Enc-

Model)

7: KsCompRes ← KeySwitch(CompRes)

8: SelectedLeafOnehot ← LeafSelec-

tion(KsCompRes)

9: ClassOnehots[i] ← Output-

Class(SelectedLeafOnehots)

10: end for

11: RandomForestResult ← Sum(ClassOnehot)

12: return RandomForestResults

3.3 Implementation of Random Forests

Our implementation of a random forest with FHE is

a natural expansion of decision trees with FHE. As a

random forest is a aggregation of many decision trees,

entrywise summation of the one-hot vectors output by

component decision trees can compute the prediction

of a random forest. By taking the index of the max-

imum value of the summation of the one-hot vector,

we obtain the index of the predicted class.

3.4 Algorithm

We summarize our implementation here. The

overview of the algorithm we executed is depicted in

Algorithm 3.

As we mentioned in Section 3.2.1 after comparing

thresholds and data, the required message space is at

most the depth of the tree or the number of trees be-

cause the encrypted values are 0/1, the path cost, or

the summation of tree results. Thus, we can switch

the message modulus into a smaller one. In this pa-

per, as we used 15 trees and depth of at most 9, we

selected a four-bit massage space. As it needs PBS

after this switching, we used a ﬁve-bit message space.

4 EXPERIMENTS

In this section, we describe the details of the experi-

ments we conducted.

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data

539

4.1 Data Used in Experiments

The original data we used are IoT device network

data, KDDI-IoT-2019 (available at https://github.c

om/nokuik/KDDI-IoT- 2019) (Okui et al., 2022).

These data are composed of IP Flow Information Ex-

port (IPFIX) (Trammell and Boschi, 2008) data col-

lected from 25 IoT devices, such as smart speakers,

network cameras or door locks. The task we focused

on was to classify which device the IPFIX data were

collected from. Thus, the number of target classes

was 25.

We processed the raw data into feature data so

that the models can predict the labels more accurately.

This process was the same as that performed in (Okui

et al., 2022). Details of this are as follows. We used

eight types of packet data. They were tcp, udp, smb,

ntp, ssdp, dns, http and https . For these types of

data, we aggregate them in the range of 1800 sec-

onds according to four criteria: outward packet, in-

ward packet, bytes of outward packet and bytes of in-

ward packet. After aggregating them, we calculated

four statistics: maximum, minimum, mean and me-

dian. Thus, we made 128(= 8 × 4 × 4) features. In

addition, we used the total number of records for all

eight types of protocols as features. In total, we used

136 features for our experiments.

Table 1: Description of Feature Data.

number of feature data 109870

number of features 136

number of classes 25

4.2 Models Used in Experiments

The random forest models we used are trained with

scikit-learn (Pedregosa et al., 2011), a machine learn-

ing library in Python. We performed experiments on

9 different random forest models. Every model has

15 component decision trees of the same depth. The

depths of a tree are integers between one and nine.

The procedure to make the models follows below.

We split the feature data into training and test data,

90% for training and 10% for testing. We trained each

random forest with the training data and expanded ev-

ery component tree into a complete tree. After train-

ing, we picked the information of the models such as

thresholds and feature indices of internal nodes and

classes that each leaf node is associated with, and

saved them into ﬁles. This is the preparation for the

experiments.

The parameters of TFHE we used are the

prepared parameter settings of TFHE-rs. For

experiments of B bits, we used parameters of

PARAM MESSAGE {B + 1} CARRY 0 KS PBS due to

PBS, which requires one more bit than the desired

message bit. Some values of the parameter settings,

which are important for discussion later, are shown

in Table 2. Refer to the implementation of TFHE-rs

(Zama, 2022) for other values.

Table 2: Parameter settings of

PARAM MESSAGE {B + 1} CARRY 0 KS PBS.

Bits: B 5 6 7

Ciphertext bit size 64 64 64

LWE dimension 915 930 1017

GLWE dimension 1 1 1

Polynomial size 8192 16384 32768

PBS level 1 2 2

4.3 Difference Between Plaintext and

Ciphertext

There are three main differences between plaintext

and ciphertext that affect the prediction of models.

They are quantization, noise and aggregation of the

results of decision trees. The details of them follows

below.

4.3.1 Quantizaion

As mentioned in Section 3.1, the data are quantized.

For values close to a threshold, the result of compari-

son may be wrong.

Concretely, let n be the number of bits into which

the value is quantized, and let {t

,...,t

−1

} be a se-

quence of the values at which the quantized value is

switched. In other words, for a number x, it holds that

(x) = i if and only if t

i−1

≤ x < t

for i ∈ {1,...,2

−

3}. For other i ∈ {0,2

− 3,2

− 2}, the following

holds. If x < t

then q

(x) = 0, if t

−3

≤ x ≤ t

−2

then q

(x) = 2

− 2 and if t

−2

< x then q

(x) =

− 1. Let T be a threshold of comparison at an in-

ternal node, which satisﬁes t

l−1

≤ T < t

for a certain

l. Then, the tree comparison result after quantization

for a value x satisfying T < x < t

is wrong. As T < x

holds, Comp

(x) = 1. However, the comparison after

quantization is that Comp

(T )

(x)) = 0.

When the comparison result is wrong, the selected

leaf node is different, and eventually, the result of the

tree is wrong. However this may not be a signiﬁcant

problem because the range where the comparison re-

sult is wrong is not broad. Even if one tree result is

wrong, the result of the random forest might not be

affected because it is a majority vote of all the com-

ponent trees.

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

540

Table 3: Mean time [s] to evaluate with a random forest of 15 component decision trees under fully homomorphic encryption.

1 2 3 4 5 6 7 8 9

5 bits 2.5 8.5 41.0 59.5 120.8 245.6 473.3 957.4 2602.2

6 bits 4.7 13.5 43.6 94.0 192.4 391.7 754.2 1529.8 3722.9

7 bits 9.4 27.6 77.4 165.3 396.2 930.1 1857.6 3736.3 8495.3

Table 4: Standard deviation of time [s] to evaluate with a random forest of 15 component decision trees under fully homo-

morphic encryption.

1 2 3 4 5 6 7 8 9

5 bits 0.49 4.85 22.93 2.59 4.55 8.99 15.50 30.78 1113.06

6 bits 0.48 0.53 1.44 3.26 6.75 12.15 19.67 30.85 1426.03

7 bits 0.33 0.97 2.50 2.44 136.23 420.69 804.14 1538.64 3176.40

4.3.2 Noise

As explained in Section 2.2.1, an LWE ciphertext has

a noise. As noise is small compared to the message

(∆m in Deﬁnition 2.1), it does not affect the decryp-

tion. However, many operations on a ciphertext such

as multiplication increase the noise. Once the noise

increases so much that it becomes comparable to the

message, it has an inﬂuence on the decryption result.

In order to prevent this, programmable bootstrap-

ping is executed to reduce the noise, but the compu-

tational cost of PBS is higher than other simple op-

erations. Thus the more PBS are executed the longer

it takes to ﬁnish the whole procedure of evaluating a

random forest. Therefore, we executed PBS as few

times as possible.

We executed PBS for comparisons at each internal

node and determined whether path costs are zero. We

also executed PBS with the identity function just to

reduce the noise while computing one-hot vectors of

tree results as illustrated in Algorithm 2. These PBS

were not enough to evaluate a random forest without

noise affecting the results. However, the errors caused

by the increase in noise seldom occurred in our exper-

iments and, for the same reason as that of quantiza-

tion, it did not have a signiﬁcant impact on the result

of a random forest.

4.3.3 Aggregation of Tree Results

The most signiﬁcant difference between plaintext and

ciphertext is aggregation of the results of the compo-

nent decision tree. On the one hand, in scikit-learn,

the result of each tree is weighted by their probabil-

ity estimates. On the other hand, our random forests

with FHE aggregate the results by simple summation.

Therefore, the result might be different even though

the all the computations are performed without any

other error. This error occurs especially when the

probability estimates of each tree is close to uniform,

that is, each tree generates less conﬁdence in the re-

sults. If a tree result is output a probability estimate

where the probability of one class is close to one and

those of the others are almost zero, it is virtually one-

hot vector, which is the output of a decision tree with

FHE.

4.4 Results

Here, we show the results of the experiments.

In this paper, a message bit means the number

of bits to express features and thresholds of internal

nodes. The message bits we used are ﬁve, six and

seven.

As we mentioned in Section 4.2, we made 9 ran-

dom forest models. We conducted experiments with

ﬁve to seven message bits on 9 models. Therefore, we

conducted 27 types of experiments.

For each model and bit, we computed the predic-

tions with the random forest on 40 test data.

The computer we used has 3.00 GHz CPU (13th

Gen Intel(R) Core(TM) i9-13900K) and 128 GB

RAM. The Rust version is 1.72.0, and the TFHE-rs

version is 0.3.1. We did not compute in parallel to

assess the total time of computation.

4.4.1 Time of Computation

The mean times to evaluate with a random forest of

each model and bit are illustrated in Table 3. The box

plots of each bit are depicted in Figures 1, 2 and 3.

These ﬁgures have regression curves of the mean time

of each depth. Linear regressions were performed on

the logarithm of mean time with respect to depths one

to nine. As the linear regressions were performed

on logarithm of the time, they are exponential regres-

sions on the time.

We conducted linear regressions on logarithm of

time as it requires 2

− 1 comparisons, 2

PBS at leaf

nodes and so on to evaluate a random forest and thus

the number of computations is expected to be the or-

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data

541

Table 5: Accuracy of a random forest composed of 15 component decision trees under fully homomorphic encryption and

plaintext.

1 2 3 4 5 6 7 8 9

Plaintext 0.300 0.525 0.650 0.825 0.925 0.925 0.975 1.000 0.950

5 bits 0.175 0.350 0.450 0.600 0.650 0.600 0.850 0.850 0.850

6 bits 0.175 0.300 0.400 0.600 0.650 0.650 0.875 0.900 0.925

7 bits 0.175 0.325 0.450 0.600 0.675 0.650 0.875 0.900 0.875

Table 6: Coefﬁcients and intercepts of regression on the log-

arithm of time with respect to depth.

coefﬁcient intercept

5 bits 0.805 0.664

6 bits 0.800 1.097

7 bits 0.834 1.679

der of two to the power of d.

Figure 4 shows how the computation time in-

creases as the depth of the decision trees increases

for each bit. Note that the scale of the vertical axis

is logarithmic.

4.4.2 Accuracy

The accuracy of random forests is shown in Table 5.

In the table, the row of ”Plaintext” shows the accu-

racy of prediction that the original models in plaintext

output. As the number of samples we had the exper-

iments with were limited to 40, the accuracy is not

necessarily higher as the depth becomes larger.

If the encrypted models work without errors, the

predictions are supposed to be as accurate as those of

models in plaintext.

4.5 Discussion

In this subsection, we discuss the results shown in the

previous section with respect to time and accuracy.

4.5.1 Time

As shown in Figure 1, 2 and 3, the computation time

increases exponentially as the depth increases. This

is explainable because there are some computations

almost proportional to two to the power of the depth.

One of them is the comparisons at each internal

node. As a complete binary tree of depth d has 2

− 1

internal nodes, it requires the same number of com-

parisons with PBS to obtain the results of comparison.

Computation of the path costs of all the leaf nodes

is expected to have less inﬂuence on the time than

that of comparisons because the homomorphic addi-

tion is much faster than that of PBS. When selecting

the leaf node corresponding to the tree result, it also

requires 2

times of PBS to evaluate whether the path

cost is zero, and also C · 2

multiplication to output

the prediction where C is the number of classes. This

also affects the resulting computation time. There are

several computation that requires O(2

) operations.

Therefore, our results do not contradict this.

We performed an exponential regression on the

computation time and obtained the coefﬁcients and

intercepts as shown in Table 6. With these coefﬁ-

cients, we can estimate computation time of deeper

random forests assuming that this trend continues in

the range of larger depths.

Additionally, with these regressions, we can esti-

mate computation time of more bits. The reason the

time varies among the bits is basically the differences

in the parameter set. As shown in Table 2, the LWE

dimension increases as the bit increases, and the poly-

nomial size, which affects the PBS, doubles as the bit

increases. It is necessary to take the inﬂuence of the

parameter set into account when estimating the time

of more bits.

4.5.2 Accuracy

As shown in Table 5, the accuracy of the random

forests with FHE is less than that of the random for-

est without FHE. The reasons for this are discussed

in Section 4.3. The differences in accuracy between

plaintext and FHE random forests seem to decrease

as the depth increases. This may be because the accu-

racy of decision trees increases as the depth increases,

and thus even if a few component trees predict incor-

rectly, the inﬂuence on the prediction of random forest

is not signiﬁcant since many trees predict accurately.

As discussed in Section 4.3.3, the difference in ag-

gregation can be a signiﬁcant error. Increasing the

depth of component trees of a random forest is ex-

pected to be one of the solutions to this because mak-

ing component trees more accurate by increasing the

depth leads to increasing the probability of plaintext

tree prediction to 1.

5 CONCLUSION

We conducted experiments on random forests with

TFHE to evaluate their feasibility on network data of

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

542

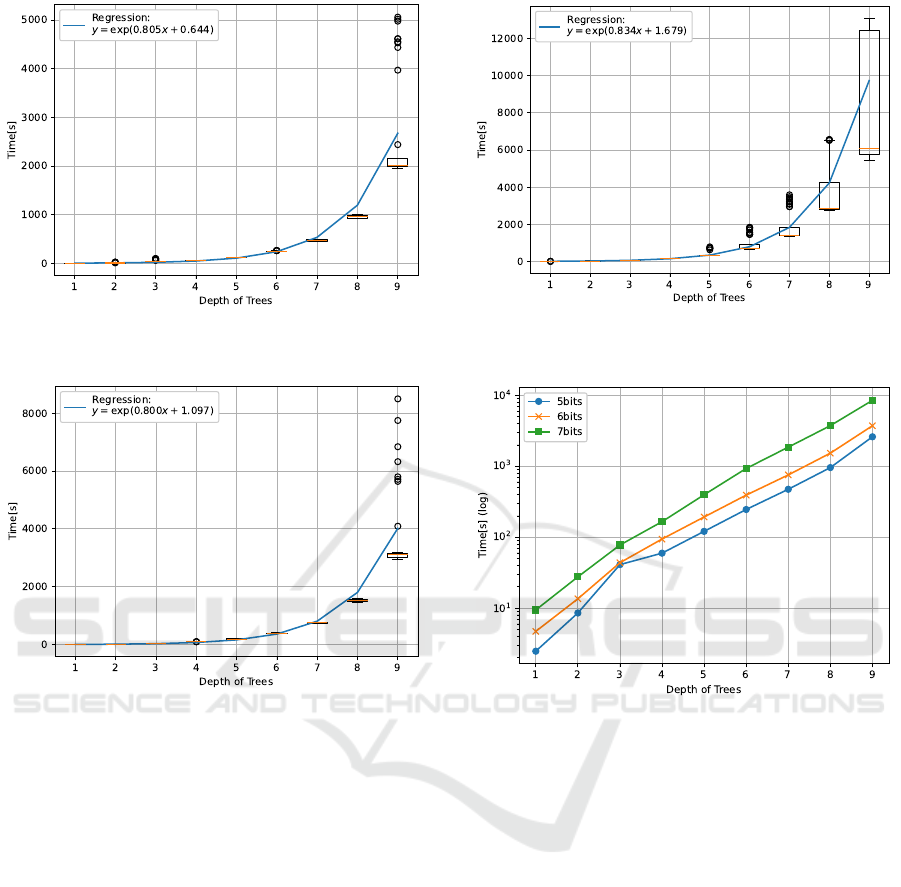
Figure 1: Box plot of time to evaluate a random forest for 5

message bits and their regression curve.

Figure 2: Box plot of time to evaluate a random forest for 6

message bits and their regression curve.

IoT devices. Through our experiments, we revealed

the computation time and accuracy of random forest

with FHE applied to real network data. We obtained

the time to compute random forests with fully homo-

morphic encryption and their accuracy. With these

results, we conducted an exponential regression on

the time with respect to the depths of the component

trees and obtained coefﬁcients and intercepts of the

regression, which allows us to estimate the computa-

tion time for larger depths.

Although the current time we obtained does not

seem feasible for real data as it takes a few hours to

evaluate a random forest, our results are beneﬁcial for

estimating the cost of introducing random forests with

FHE.

5.1 Future Work

As we implemented random forests with FHE in a

simple way without parallel computation, there is

room for improvement. Our future work is to improve

Figure 3: Box plot of time to evaluate a random forest for 7

message bits and their regression curve.

Figure 4: Comparison of the logarithm of mean time to eval-

uate a random forest.

the implementation and accelerate processing.

Using other real data in ﬁelds such as network and

cyber security to assess the feasibility of a random

forest is also our future work.

REFERENCES

Akavia, A., Leibovich, M., Resheff, Y. S., Ron, R., Shahar,

M., and Vald, M. (2022). Privacy-preserving decision

trees training and prediction. ACM Trans. Priv. Secur.,

25(3).

Alouﬁ, A., Hu, P., Wong, H. W. H., and Chow, S. S. M.

(2021). Blindfolded evaluation of random forests

with multi-key homomorphic encryption. IEEE

Transactions on Dependable and Secure Computing,

18(4):1821–1835.

Azogagh, S., Delfour, V., Gambs, S., and Killijian, M.-

O. (2022). PROBONITE: PRivate One-Branch-

Only Non-Interactive Decision Tree Evaluation. In

Proceedings of the 10th Workshop on Encrypted

Computing & Applied Homomorphic Cryptography,

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data

543

WAHC’22, page 23–33, New York, NY, USA. Asso-

ciation for Computing Machinery.

Bajard, J.-C., Martins, P., Sousa, L., and Zucca, V. (2020).

Improving the efﬁciency of SVM classiﬁcation with

FHE. IEEE Transactions on Information Forensics

and Security, 15:1709–1722.

Bost, R., Popa, R. A., Tu, S., and Goldwasser, S. (2015).

Machine learning classiﬁcation over encrypted data.

In Proceedings 2015 Network and Distributed System

Security Symposium. Internet Society.

Brakerski, Z. (2012). Fully homomorphic encryption with-

out modulus switching from classical GapSVP. In

Safavi-Naini, R. and Canetti, R., editors, Advances in

Cryptology – CRYPTO 2012, pages 868–886, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2012).

(leveled) fully homomorphic encryption without boot-

strapping. In Proceedings of the 3rd Innovations in

Theoretical Computer Science Conference, ITCS ’12,

page 309–325, New York, NY, USA. Association for

Computing Machinery.

Breiman, L. (2001). Random forests. Machine Learning,

45(1):5–32.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-

momorphic encryption for arithmetic of approximate

numbers. In Takagi, T. and Peyrin, T., editors, Ad-

vances in Cryptology – ASIACRYPT 2017, pages 409–

437, Cham. Springer International Publishing.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(2016). Faster fully homomorphic encryption: Boot-

strapping in less than 0.1 seconds. In Cheon, J. H.

and Takagi, T., editors, Advances in Cryptology –

ASIACRYPT 2016, pages 3–33, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(2020). TFHE: Fast fully homomorphic encryption

over the torus. Journal of Cryptology, 33:34–91.

Dowlin, N., Gilad-Bachrach, R., Laine, K., Lauter, K.,

Naehrig, M., and Wernsing, J. (2016). Cryptonets:

Applying neural networks to encrypted data with high

throughput and accuracy. In Proceedings of the 33rd

International Conference on International Conference

on Machine Learning - Volume 48, ICML’16, page

201–210. JMLR.org.

Fan, J. and Vercauteren, F. (2012). Somewhat practical fully

homomorphic encryption. Cryptology ePrint Archive,

Paper 2012/144. https://eprint.iacr.org/2012/144.

Frery, J., Stoian, A., Bredehoft, R., Montero, L., Kherfal-

lah, C., Chevallier-Mames, B., and Meyre, A. (2023).

Privacy-preserving tree-based inference with fully ho-

momorphic encryption. Cryptology ePrint Archive,

Paper 2023/258. https://eprint.iacr.org/2023/258.

Gentry, C. (2009). Fully homomorphic encryption using

ideal lattices. In Proceedings of the Forty-First Annual

ACM Symposium on Theory of Computing, STOC ’09,

page 169–178, New York, NY, USA. Association for

Computing Machinery.

Gentry, C., Sahai, A., and Waters, B. (2013). Homomorphic

encryption from learning with errors: Conceptually-

simpler, asymptotically-faster, attribute-based. In

Canetti, R. and Garay, J. A., editors, Advances in

Cryptology – CRYPTO 2013, pages 75–92, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Jacob, B., Kligys, S., Chen, B., Zhu, M., Tang, M., Howard,

A., Adam, H., and Kalenichenko, D. (2018). Quan-

tization and training of neural networks for efﬁcient

integer-arithmetic-only inference. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition (CVPR).

Kelly, M., Longjohn, R., and Nottingham, K.

(2023). The UCI machine learning repository.

https://archive.ics.uci.edu.

Kjamilji, A. (2023). A constant time secure and private

evaluation of decision trees in smart cities enabled by

mobile IoT. In 2023 IEEE International Conference

on Smart Mobility (SM), pages 51–58.

Lee, J.-W., Kang, H., Lee, Y., Choi, W., Eom, J., Deryabin,

M., Lee, E., Lee, J., Yoo, D., Kim, Y.-S., and No, J.-

S. (2022). Privacy-preserving machine learning with

fully homomorphic encryption for deep neural net-

work. IEEE Access, 10:30039–30054.

Meyre, A., Chevallier-Mames, B., Frery, J., Stoian, A., Bre-

dehoft, R., Montero, L., and Kherfallah, C. (2022).

Concrete ML: a privacy-preserving machine learning

library using fully homomorphic encryption for data

scientists. https://github.com/zama-ai/concrete-ml.

Okui, N., Nakahara, M., Miyake, Y., and Kubota, A. (2022).

Identiﬁcation of an IoT device model in the home do-

main using IPFIX records. In 2022 IEEE 46th An-

nual Computers, Software, and Applications Confer-

ence (COMPSAC), pages 583–592.

Park, S., Byun, J., Lee, J., Cheon, J. H., and Lee, J. (2020).

HE-friendly algorithm for privacy-preserving SVM

training. IEEE Access, 8:57414–57425.

Pashamokhtari, A., Okui, N., Nakahara, M., Kubota, A.,

Batista, G., and Habibi Gharakheili, H. (2023). Dy-

namic inference from IoT trafﬁc ﬂows under concept

drifts in residential ISP networks. IEEE Internet of

Things Journal, 10(17):15761–15773.

Paul, J., Tan, B. H. M., Veeravalli, B., and Aung, K. M. M.

(2022). Non-interactive decision trees and applica-

tions with multi-bit TFHE. Algorithms, 15(9).

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Regev, O. (2005). On lattices, learning with errors, random

linear codes, and cryptography. In Proceedings of the

Thirty-Seventh Annual ACM Symposium on Theory of

Computing, STOC ’05, page 84–93, New York, NY,

USA. Association for Computing Machinery.

SEAL (2021). Microsoft SEAL (release 3.7). https:

//github.com/Microsoft/SEAL. Microsoft Research,

Redmond, WA.

Tai, R. K. H., Ma, J. P. K., Zhao, Y., and Chow, S. S. M.

(2017). Privacy-preserving decision trees evaluation

via linear functions. In Foley, S. N., Gollmann, D.,

ICISSP 2024 - 10th International Conference on Information Systems Security and Privacy

544

and Snekkenes, E., editors, Computer Security – ES-

ORICS 2017, pages 494–512, Cham. Springer Inter-

national Publishing.

Trammell, B. and Boschi, E. (2008). Bidirectional Flow Ex-

port Using IP Flow Information Export (IPFIX). RFC

5103.

Zama (2022). TFHE-rs: A Pure Rust Implementation of the

TFHE Scheme for Boolean and Integer Arithmetics

Over Encrypted Data. https://github.com/zama-ai/tf

he-rs.

Feasibility of Random Forest with Fully Homomorphic Encryption Applied to Network Data

545