Efﬁcient and Accurate Hyperspectral Image Demosaicing with Neural

Network Architectures

Eric L. Wisotzky

1,2 a

, Lara Wallburg

, Anna Hilsmann

1 b

, Peter Eisert

1,2 c

Thomas Wittenberg

3,4

and Stephan G

3,4 d

Computer Vision & Graphics, Fraunhofer HHI, Einsteinufer 37, 10587 Berlin, Germany

Department of Informatics, Humboldt University, Berlin, Germany

Fraunhofer IIS, Erlangen, Germany

Chair of Visual Computing, Friedrich-Alexander-Universit

at Erlangen-N

urnberg, Erlangen, Germany

Keywords:

Sensor Array and Multichannel Signal Processing, Deep Learning, Biomedical Imaging Techniques, Image

Analysis, Image Upsamling.

Abstract:

Neural network architectures for image demosaicing have been become more and more complex. This results

in long training periods of such deep networks and the size of the networks is huge. These two factors prevent

practical implementation and usage of the networks in real-time platforms, which generally only have limited

resources. This study investigates the effectiveness of neural network architectures in hyperspectral image

demosaicing. We introduce a range of network models and modiﬁcations, and compare them with classical

interpolation methods and existing reference network approaches. The aim is to identify robust and efﬁcient

performing network architectures. Our evaluation is conducted on two datasets, ”SimpleData” and ”SimReal-

Data,” representing different degrees of realism in multispectral ﬁlter array (MSFA) data. The results indicate

that our networks outperform or match reference models in both datasets demonstrating exceptional perfor-

mance. Notably, our approach focuses on achieving correct spectral reconstruction rather than just visual

appeal, and this emphasis is supported by quantitative and qualitative assessments. Furthermore, our ﬁndings

suggest that efﬁcient demosaicing solutions, which require fewer parameters, are essential for practical appli-

cations. This research contributes valuable insights into hyperspectral imaging and its potential applications

in various ﬁelds, including medical imaging.

1 INTRODUCTION

The use of multispectral images (MSIs) or hyperspec-

tral images (HSIs), which encompass a wide range

of different spectral channels across various wave-

lengths both within and beyond the visible spectrum,

has gained increasing prominence in recent years.

These types of images ﬁnd broad applications in var-

ious ﬁelds such as healthcare (Calin et al., 2014; Lu

and Fei, 2014; Zhang et al., 2017), industrial appli-

cations (Shafri et al., 2012), and agriculture (Jung

et al., 2006; Moghadam et al., 2017). However, con-

ventional acquisition methods and devices are associ-

ated with signiﬁcant drawbacks, including high costs

https://orcid.org/0000-0001-5731-7058

https://orcid.org/0000-0002-2086-0951

https://orcid.org/0000-0001-8378-4805

https://orcid.org/0000-0002-1206-7478

and lengthy acquisition times (Wisotzky et al., 2018;

uhle et al., 2021).

In recent times, alternative approaches have been

developed to address these challenges. One promis-

ing technique is based on the use of spectral mask-

ing at the pixel level, utilizing only a single sensor

plane. This concept is known as Multi-Spectral Fil-

ter Arrays (MSFAs). Unlike RGB images, which are

composed of three color values (red, green and blue),

MSFAs map the spectrum in more than three spec-

tral bands, e.g., nine, 16 or 25 bands (Hershey and

Zhang, 2008). A data cube is formed from the deter-

mined data. Its edges represent the image dimensions

in x- and y-direction and the determined wavelengths

in λ-direction. In contrast to MSIs, HSIs use several

hundred spectral bands to capture the spectrum of a

source.

When image data is acquired by a multispectral

camera using the principle of MSFA, not all image

Wisotzky, E., Wallburg, L., Hilsmann, A., Eisert, P., Wittenberg, T. and Göb, S.

Efﬁcient and Accurate Hyperspectral Image Demosaicing with Neural Network Architectures.

DOI: 10.5220/0012392300003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

541-550

ISBN: 978-989-758-679-8; ISSN: 2184-4321

541

information of a data cube can be acquired. An in-

crease in spectral resolution is accompanied by a loss

of spatial resolution. This missing information needs

a successive interpolation using image processing or

image analysis techniques. Common image process-

ing techniques for spectral reconstruction include bi-

linear and nonlinear ﬁlters, referred to as debayering

or demosaicing.

While MSFAs offer the advantage of real-time im-

plementation and general applicability, accurate in-

terpolation of missing spectral or spatial information

is challenging. This, however, is crucial for precise

spatial localization of entities such as cancer cells in

healthcare, damage in plants in agriculture, or objects

in industrial applications. To enhance existing meth-

ods, neural networks have recently been proposed as

promising approaches.

Figure 1: Description of the processing pipeline and demo-

saicing of multispectral cameras.

The contribution of this work is as follows. We

present a pipeline to achieve real-world MSFA data

from different hyperspectral datasets. Further, we

propose different new and extended demosaicing net-

works and compare these using classical public avail-

able datasets and a dataset processed with our intro-

duced pipeline.

The analysis is performed from the perspective

that the networks should provide good reconstruction

quality and be able to compute it quickly, i.e., con-

tain as few parameters as possible for potential near-

sensor processing.

The remainder of this paper is as follows. The next

chapter gives an overview on related publications rel-

evant for this work. Chapter 3 describes the proposed

network architectures, before chapter 4 explains data

processing and presents training and evaluation pa-

rameters. Chapter 5 describes experiments and re-

sults, followed by a thorough discussion and conclu-

sion.

2 RELATED WORK

The most commonly used algorithms for demosaicing

in imaging are analytical ones such as nearest neigh-

bor, bilinear interpolation or cubic interpolation. The

multispectral debayering relies on these existing al-

gorithms used in RGB imaging. The basic approach

involves classic interpolation techniques. However,

more complex methods take into account not only the

information from the nearest pixel of the same chan-

nel but also the next of other channels or even fur-

ther away pixels. There are many different variations

of demosaicing algorithms available for RGB imag-

ing (Malvar et al., 2004). However, implementing

these algorithms for multispectral ﬁlter structures is

challenging due to the different number of channels.

An approach based on the weighted bilinear interpo-

lation (Brauers and Aach, 2006) is the advancement

of linear interpolation using MSFAs, called Intensity

Difference (ID interpolation) (Mihoubi et al., 2015).

Further, interpolation methods based on image fu-

sion have been proposed (Eismann and Hardie, 2005;

Bendoumi et al., 2014; Zhang, 2014). Fusion based

methods usually require the availability of a guiding

image with higher spatial resolution, which is difﬁcult

to obtain in many scenarios.

Demosaicing by interpolation based techniques,

both traditional as well as fusion-based, is easy to

achieve, however, these methods suffer from color ar-

tifacts and lead to lower spatial resolution. Especially

at edges, they do not take into account the spectral

correlations between adjacent bands as well as due to

crosstalk. This results in spectral distortions in the

demosaiced image, especially for increasing mosaic

ﬁlter size.

Alternatively, deep neural networks can be trained

to account for scene information as well as correla-

tions between individual spectral bands.

2.1 Network-Based Demosaicing

Demosaicing using convolutional neural networks

(CNN) was ﬁrst proposed for images with 2×2 Bayer

pattern (Wang, 2014; Gharbi et al., 2016). In recent

years, CNN based color image super resolution (SR)

has gained popularity. Examples of such networks

include SRCNN (Dong et al., 2014), DCSCN (Ya-

manaka et al., 2017) and EDSR (Lim et al., 2017).

Due to their success, these networks have been ex-

tended to HSI super resolution (Li et al., 2018). The

underlining aspect of all CNN based HSI demosaic-

ing networks is the utilization of spatial and spectral

context from the data during training.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

542

Nevertheless there is only a small number of pub-

lications where CNNs are used for patterns > 2 × 2.

In the NTIRE 2022 Spectral Demosaicing Challange

several deep learning-based demosaicing algorithms

were introduced (Arad et al., 2022b). The leading

methods all involved very large and complex net-

work structures, such as an enhanced HAN (Niu et al.,

2020), NLRAN and a Res2-Unet (Song et al., 2022)

based method. An interesting approach for the recon-

struction of MSI uses leaner network structures of ﬁve

residual blocks (Shinoda et al., 2018). Bilinear inter-

polated data are used as input for this reﬁnement ap-

proach. Furthermore, there are already approaches to

replace the bilinear interpolation by the ID interpo-

lation (G

ob et al., 2021). Dijkstra et al. (2019) pro-

posed a similarity maximization network for HSI de-

mosaicing, inspired by single image SR. This network

learns to reconstruct a downsampled HSI by upscal-

ing via deconvolutional layers. The network results

are presented for a 4 × 4 mosaic pattern and the de-

mosaiced HSI showed high spatial and spectral reso-

lution. Habtegebrial et al. (2019) used residual blocks

to learn the mapping between low and high resolu-

tion HSI, inspired by the HCNN+ architecture (Shi

et al., 2018). These two networks use 2D convolu-

tions in order to learn the spectral-spatial correlations.

An important characteristic of HSI is the correlation

between adjacent spectral bands which are not taken

into account when using 2D convolutional based net-

works. These correlations can be incorporated by us-

ing 3D convolutional networks. Mei et al. (2017) pro-

posed one of the ﬁrst 3D CNNs for hyperspectral im-

age SR addressing both the spatial context between

neighboring pixels as well as the spectral correlation

between adjacent bands of the image. A more effec-

tive way to learn the spatial and spectral correlations

is through a mixed 2D/3D convolutional network (Li

et al., 2020).

Further, deep learning (DL) have been employed

in order to predict HSI data from MSI or even classic

RGB image data (Arad et al., 2022a, 2020). However,

the main problem here is the lack of training data and

the large dependence of the method on the application

and training data. This means that the spectral behav-

ior of individual scenes is learned by the DL model for

interpolation and thus there is a dependency between

the planned application and training data, which can

lead to poor results and incorrect hyperspectral data if

the training data is improperly selected, of poor qual-

ity, or too small in scope (Wang et al., 2021). Thus,

the need of high quality ground truth data is essential.

In such a dataset, each pixel should contain the entire

spectral information, which is difﬁcult to acquire in a

natural environment.

2.2 Datasets

In order to be able to train and evaluate networks, both

fully completed data cubes and the corresponding raw

data are required. For this purpose, a number of dif-

ferent databases containing are available. One major

challenge for the task of snapshot mosaic HSI demo-

saicing using neural networks is the lack of real world

ground truth data.

The only databases available are those that use

either the pushbroom method or spatio-spectral-line

scans, usually realized by a liquid crystal. Hence, the

data has different characteristics than snapshot mosaic

data (e.g., missing cross-talk) and therefore a trained

network cannot adequately represent reality. How-

ever, we are not aware of any data sets that include

MSFAs. All HSI databases used in this work are pre-

sented in Tab. 1 and include a large number of differ-

ent colored objects.

One alternative to include real MSFA data into

training is to downsample captured snapshot mosaic

data as presented in Dijkstra et al. (2019). How-

ever, simple downsampling leads to differences in dis-

tances of adjacent pixels, which affects the network

results in an unknown manner. Therefore, this ap-

proach is not been followed in this work.

3 NETWORK ARCHITECTURE

In the following, three different architecture types are

presented. All are based on different works recently

published and have been modiﬁed in order to achieve

improved demosaicing results.

3.1 ResNet-Based Architecture

In the initial phase, we aimed to enhance the network

proposed by Shinoda et al. (2018). The modiﬁcations

can be classiﬁed into two components: the prepro-

cessing of input data and the CNN itself. Due to its

superior effectiveness, we use ID interpolation as in-

put of the network.

The alterations made to the CNN were intended

to reduce the number of parameters without compro-

mising the quality and are visualized in Fig. 2. Ini-

tially, the network comprised of ﬁve residual blocks.

The ﬁrst two blocks contained two conv-blocks in the

main-path and one conv-block in the skip-connection,

while the next three residual blocks consisted of three

conv-blocks in the main-path and one conv-block

in the skip-connection. The number of ﬁlters in-

creased from the ﬁrst to the ﬁfth residual block with

8/16/32/64/64, and were formed by a 3D kernel-size

Efﬁcient and Accurate Hyperspectral Image Demosaicing with Neural Network Architectures

543

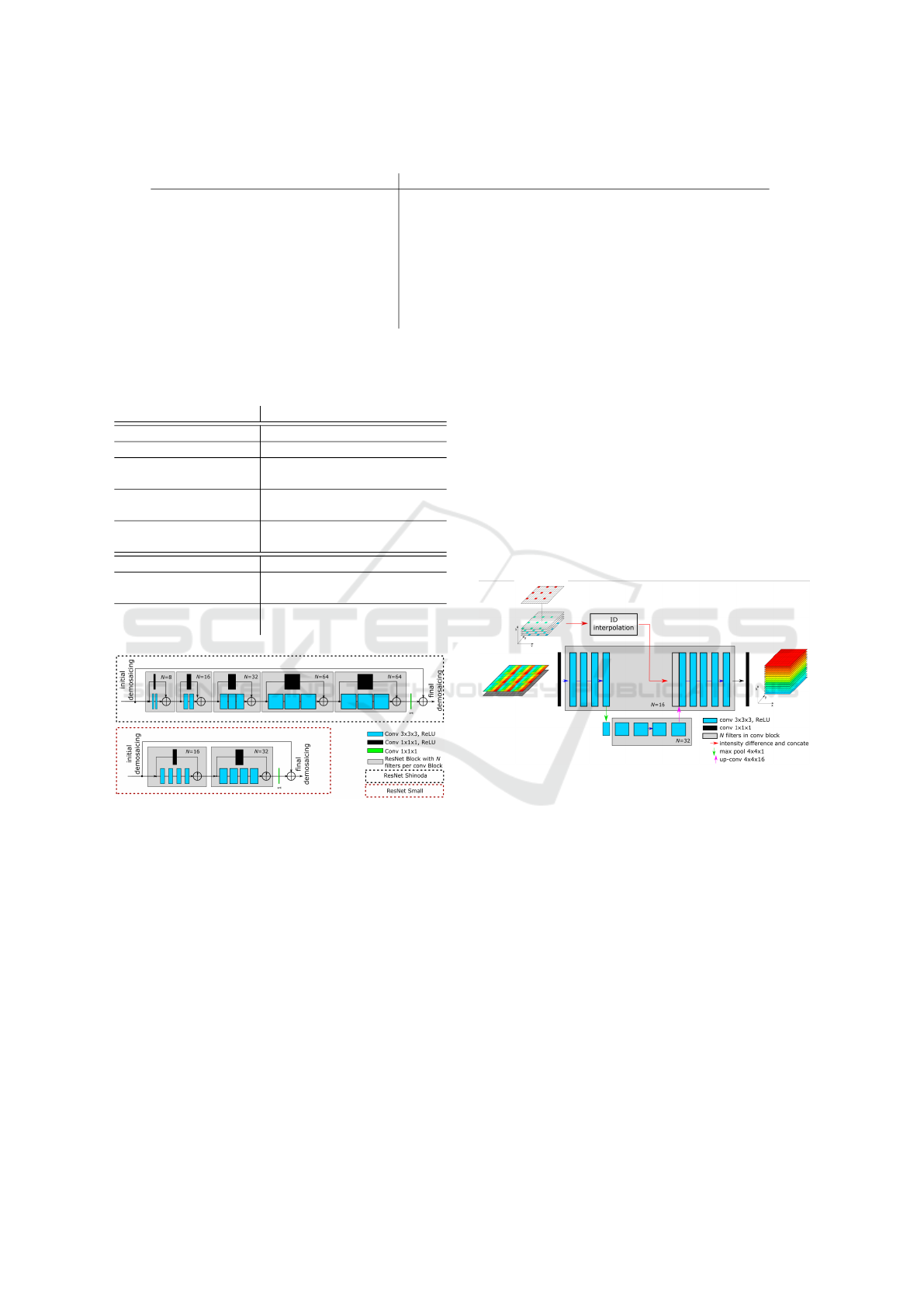
Table 1: The used hyperspectral data collections.

Dataset # Images Size [px] Spectrum [nm] Bands Range

CAVE (Yasuma et al., 2010) 32 512x512 400-700 31 1:65536

HyTexiLa (Khan et al., 2018) 112 1024x1024 405-996 186 0:1

TokyoTech31 (Monno et al., 2015) 30 500x500 420-720 31 0:1

TokyoTech59 (Monno et al., 2018) 16 512x512 420-1000 59 0:1

SIDRI-v10 (Mirhashemi, 2019) 5 640x480 400-1000 121 0:1

SIDRI-vis (Mirhashemi, 2019) 1 640x480 400-720 31 0:1

ODSI-DB Nuance (Hyttinen et al., 2020) 139 1392x1040 450-950 51 1:65536

ODSI-DB Specim (Hyttinen et al., 2020) 171 Various 400-1000 204 1:65536

Google 670 480x1312 400-1000 396 1:4096

Table 2: The number of parameters and sizes of the input

images of the different networks. If two input sizes are

stated, the network structure needs different input.

Network Parameter Input Size

ID-ResNet-L 697k [16 × 100 × 100]

ID-ResNet-S 118k [16 × 100 × 100]

ID-UNet 128k

[16 × 100 × 100]

[1 × 100 × 100]

Parallel-S 331k

[16 × 100 × 100]

[1 × 100 × 100]

Parallel-L 382k

[16 × 25 × 25]

[1 × 100 × 100]

UNet 227k [1 × 100 × 100]

ResNet

697k [16 × 100 × 100]

(Shinoda et al., 2018)

Parallel

281k

[16 × 25 × 25]

(Wisotzky et al., 2022) [1 × 100 × 100]

Figure 2: The ResNet-based architectures. Top: ResNet

according to Shinoda et al. (2018). Bottom: our modiﬁed

version.

of 3 × 3 × 3. Since our data input shows improved

quality, we optimize the architecture by reducing the

number of residual blocks to two. To achieve the de-

sired quality of the CNN, we modiﬁed the number of

conv-blocks to four in the main-path and one in the

skip-connection, with 16 ﬁlters in the ﬁrst residual

block and 32 in the second. These modiﬁcations re-

duced the overall number of parameters presented in

Tab. 2.

3.2 U-Net-Based Architecture

Originally introduced for medical image segmenta-

tion, the U-Net is a classical approach to reconstruct

images (Ronneberger et al., 2015). Speciﬁcally, the

downsampling path of the U-Net captures the con-

text of the image, while the upsampling path performs

the complete reconstruction. To transfer information

from the downsampling path to the upsampling path,

skip connections are used. In this work, we modiﬁed

the skip connections to insert external information for

reconstruction improvements. We utilize a fully re-

constructed image obtained by classical demosaicing,

i.e., ID interpolation, which is then inserted into the

upsampling path via the skip connection. A detailed

schematic of this approach is provided in Fig. 3.

Figure 3: The U-Net-based architecture. A small U-Net

structure is used, while instead of the skip connection, we

insert the results from ID interpolation in the network.

The input to the U-Net is the 2D MSFA. To en-

sure a small, simple, and effective network architec-

ture, we limit the downsampling layer to a max-pool

4 ×4× 1 operation and reconstruct the image in its 16

spectral regions using a 4 × 4 × 16 kernel in the up-

sampling path. The conv-blocks in the network con-

sist of 16 ﬁlters in the upper layers and 32 ﬁlters in the

lower layers and are provided with 3 × 3 × 3 kernels.

3.3 Parallel Architecture

As third, we use a CNN architecture with paral-

lel building blocks to reconstruct the correct spatial-

spectral distribution in the image. We elaborated

two general types based on literature (Dijkstra et al.,

2019; Shinoda et al., 2018; Habtegebrial et al., 2019;

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

544

Wisotzky et al., 2022). First, two parallel feature

extracting layers using a mosaic to cube converter

(M2C) on one side and ResNet blocks on the other

side are used followed by a feature adding and two

deconvolution (deconv) layers to upsample the spatial

dimensions of the image. The second implementation

combines two effective approaches introduced by Di-

jkstra et al. (2019) and Shinoda et al. (2018)/Habtege-

brial et al. (2019), which are added and reﬁned to

form the demosaiced output. Both implementations

use 3D kernels and are presented in Fig. 4.

Figure 4: The parallel CNN architectures. Top: network

Parallel-L is an extension of Wisotzky et al. (2022) using

the small ResNet-structure (cf. Fig. 2). Bottom: network

Parallel-S is a combination of two effective approaches.

4 DATA AND TRAINING

During training, we used image patches of size [1 ×

100 × 100] (representing the mosaic sensor output) as

input for the network. The output and ground truth

data had a size of [16 × 100 × 100]. Depending on

the model, the input is either left unchanged or was

transformed in the following way:

• Transformation to a sparse 3D cube where empty

values are ﬁlled with mean; size: [16 ×100× 100]

• Transformation to a 3D cube with low resolution

and smaller spatial size; size: [16 × 25 × 25]

• Transformation to a 3D cube by ID interpolation;

size: [16 × 100 × 100].

On each side of the images, we removed four pixels

resulting in a shape of 92×92 px, because ID interpo-

lation distorts those outermost pixels making it more

difﬁcult for the models to predict the correct interpo-

lation.

In order to train and validate the networks pro-

posed in this work, a large HSI data set was built

from different data collections introduced earlier. To

allow comparability between the individual data col-

lections, the value range of all HSI data are normal-

ized to [0, 1]. The data set was split into 75% training,

15% validation and 10% test data. As described, the

data does not represent real snapshot mosaic behavior

including cross-talk and characteristic ﬁlter responses

for each mosaic pixel. Therefore, an MSFA had to be

simulated. First, we just selected 16 wavelengths in

the range of 450 − 630 nm, interpolated these bands

from the HSI data and built an MSFA as widely been

done in literature (Arad et al., 2020, 2022a; G

ob et al.,

2021; Habtegebrial et al., 2019). We refer to this data

set as SimpleData.

In addition, we built a data set better represent-

ing real captured MSFAs by transforming the stated

reﬂectances of the data r(λ) into real MSI snapshot

camera measurements r

at band b according to

max

min

T (λ)I(λ) f

(λ)r(λ)dλ

max

min

T (λ)I(λ) f

(λ)dλ

, (1)

where T is the optical transmission proﬁle of the op-

tical components of our used hardware setup, f

char-

acterize the optical ﬁlter responses of each of the b

spectral bands of the used camera (M

uhle et al., 2021;

Wisotzky et al., 2020), and I is the relative irradiance

of the light source. All proﬁles are well known and

allow to transform HSI data into real MSI snapshot

camera outputs. We refer to this data set as SimReal-

Data.

For training, we used the ADAM optimizer with

an adaptive learning rate strategy and an initial learn-

ing rate of 0.0002. At every 10th epoch, the learn-

ing rate is reduced by the factor 0.9. We trained each

model for 100 epochs. The batch size was 20. The

loss function for calculating the difference between

the ground truth and the predicted full-spectrum hy-

perspectral cube is deﬁned by the mean squared error

(MSE)

MSE(o, p) =

∑

i=0

− p

, (2)

where o is the ground truth and p is the predicted

value. To evaluate model performance, we calculated

the structural similarity index (SSIM), peak signal-to-

noise ratio (PSNR) and spectral angle mapper (SAM).

5 RESULTS AND DISCUSSION

In the following, we present the evaluation results

of the predictions of our presented network archi-

tectures. For this purpose, they are examined and

compared in a quantitative and qualitative manner.

Efﬁcient and Accurate Hyperspectral Image Demosaicing with Neural Network Architectures

545

We compare our proposed networks with classical

interpolation approaches, bilinear and ID interpola-

tion, as well as with different reference network ap-

proaches introduced in Sec. 2: ResNet (Shinoda et al.,

2018), HSUp (Dijkstra et al., 2019), U-Net and Paral-

lel (Wisotzky et al., 2022).

Further, we analyze the resulting images visually

and, to show the usability of our work, we visually an-

alyze intraoperative snapshot images acquired during

a surgery of parotidectomy.

5.1 Quantitative Results

All networks, our proposed networks as well as the

different references, were trained on the two cre-

ated datasets SimpleData and SimRealData. For both

dataset modiﬁcations, the networks learned to predict

a full spectral cube of dimension [16 × 100 × 100]

from the given input images. Our networks outper-

formed or were in the same range as the reference

networks for both datasets.

5.1.1 SimpleData

For the SimpleData without cross-talk all modiﬁed

and newly introduced networks perform better that

the state-of-the-art methods, see Tab. 3. The large

modiﬁed ResNet-based model using ID interpolation

as input performed signiﬁcantly best. The larger the

network in terms of trainable parameter the better the

results for all three evaluation measures, but also the

slower the network performance. In comparison with

the reference ResNet model (Shinoda et al., 2018),

the quality of the input image, i.e., the quality of the

initial demosaicing, is of high relevance. Using bet-

ter input quality (ID instead of bilinear interpolation),

the ResNet is able to achieve an relatively higher in-

creases in reconstruction accuracy. It can be assumed

that with even better initial demosaiced data by us-

ing network-based demosaicing methods, the perfor-

Table 3: Demosaicing results on SimpleData patches. Best

result is bold, second best is bold-italic and third rank is

italic.

Network SSIM PSNR [dB] SAM

ID-ResNet-L 0.9891 52.3846 3.48e-02

ID-ResNet-S 0.9856 51.1377 3.90e-02

ID-UNet 0.9868 51.3331 3.85e-02

Parallel-S 0.9865 51.4654 3.78e-02

Parallel-L 0.9857 51.1386 3.93e-02

UNet 0.9839 50.5408 4.25e-02

ResNet 0.9792 48.9982 4.07e-02

Parallel 0.9863 51.1316 3.96e-02

HSUp 0.9846 50.8835 4.05e-02

Bilinear 0.9235 37.5282 5.90e-02

ID 0.9671 39.7182 5.27e-02

mance is further improved. However, this would also

increase the number of parameters and thus reduce

performance.

The network Parallel-S follows the ID-ResNet-L

model in reconstruction accuracy. It performed as

second best in PSNR and SAM metrics and third in

SSIM. The performance order is switched with the

ID-UNet, which is third in PSNR and SAM, and sec-

ond in SSIM. The Parallel-L network, which includes

the smaller ID-ResNet-S, shows an improvement in

comparision to ID-ResNet-S. Both methods are fourth

and ﬁfth in terms of the analyzed metrics. Thus, all

proposed methods and modiﬁded networks perform-

ing better than the compared modalities from litera-

ture. This also shows that it is possible to greatly

reduce the network complexity (by up to six times:

118k network parameters for ID-ResNet-S instead

of 697k parameters for ID-ResNet-L) with only mi-

nor loss of quality compared to the best performing

model.

Interestingly, also with respect to other recent

work (Arad et al., 2022b), it appears that the complex-

ity of the models, i.e., the number of model paramter,

has a great impact on the quality of the demosaicing

results on simple, rather unrealistic, data sets. Be-

cause after all, the best results in this study are also

achieved with the most complex models.

5.1.2 SimRealData

For the SimRealData, which much better represent

real captured data, the results of all networks, pro-

posed as well as reference networks, are very much

improved in comparison to SimpleData, see Tab. 4.

Further, the difference between the reconstruction re-

sults of all networks is reduced. Again the largest net-

work ID-ResNet-L performed best, but closely fol-

lowed by the parallel networks. Interestingly, the

state-of-the-art parallel model is performing second

best, closely followed by Parallel-S. The other net-

works, expect for the standard U-Net, are following

closely. Thus, networks with only 40% or 50% of

the parameters (Parallel or Parallel-S, respectively)

Table 4: Demosaicing results on SimRealData. Best result

is bold, second best is bold-italic and third rank is italic.

Network SSIM PSNR SAM

ID-ResNet-L 0.9989 62.0690 1.29e-02

ID-ResNet-S 0.9984 60.6000 1.55e-02

ID-UNet 0.9985 60.7327 1.58e-02

Parallel-S 0.9983 60.9021 1.44e-02

Parallel-L 0.9982 60.5968 1.52e-02

UNet 0.9973 58.3865 2.28e-02

Parallel 0.9986 61.2197 1.41e-02

HSUp 0.9983 60.6398 1.50e-02

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

546

Figure 5: Visual results and error images. Spectral data are represented in RGB and error images of two region of interest

(ROI) are build using l

-Norm. The maximum errors in the top ROI are 0.0598, 0.0994, 0.1001, 0.0805, 0.0667 and in the

bottom ROI are 0.0401, 0.0597, 0.0614, 0.0520, 0.0366 in order of appearance of the models from left to right.

achieve similarly good reconstruction results.

Obviously, the complexity of the networks is not

decisive for the reconstruction results, but rather the

quality of the input data and the general structure.

The networks can draw information about all spectral

bands from the complex spectral behavior of the in-

dividual pixels on an MSFA. The effect of cross-talk

contains essential data, which are useful to all net-

works for a more precise spectral interpolation. This

allows using simpler network structures while main-

taining similar high reconstruction quality.

5.2 Qualitative Results

An analysis of the individual spectral channels did not

reveal any discernible deviations in the quality char-

acteristics between the spectral channels. Thus, no

channel stands out as particularly defective during the

demosaicing process. Therefore, the qualitative anal-

ysis of the results is made on RGB-calculated images.

As can be seen in Fig. 5, all reconstruction results

appear in similar quality at ﬁrst glance. On closer in-

spection, minor differences are evident at strong im-

age edges, e.g., at the bottom right wing. These small

differences can be quantitatively represented in a dif-

ference image (Fig. 5) or in a spectral plot, Fig. 6.

In addition, we have demosaiced intraoperative

images, see Fig. 7. In terms of quality, these im-

460 470 480 490 500 510 520 530 540 550 560 570 580 590 600 610 620 630 640

0.2

0.4

0.6

0.8

Ground Truth Data

Parallel-S

Parallel-L

ID-ResNet-L

ID-ResNet-S

Unet

Figure 6: Spectral plot of a central left point in the left top

wing of the butterﬂy in Fig. 5. The SAM of the spectra in

comparison to the ground truth are 0.0133, 0.0157, 0.0158,

0.0265, 0.0276 for the models ID-Resnet-L, Parallel-S,

Parallel-L, ID-UNet and ID-Resnet-S, respectively.

ages show a high resolution as small details as well

as edges are clearly visible. It is also noticeable that

artifacts such as color fringes are reduced.

6 CONCLUSION

In conclusion, our results clearly show that signif-

icant improvements in demosaicing algorithms can

be achieved by using well-designed neural network

architectures. The networks and modiﬁcations we

have introduced feature excellent reconstruction of

the ground truth data while reducing or at least hold-

Efﬁcient and Accurate Hyperspectral Image Demosaicing with Neural Network Architectures

547

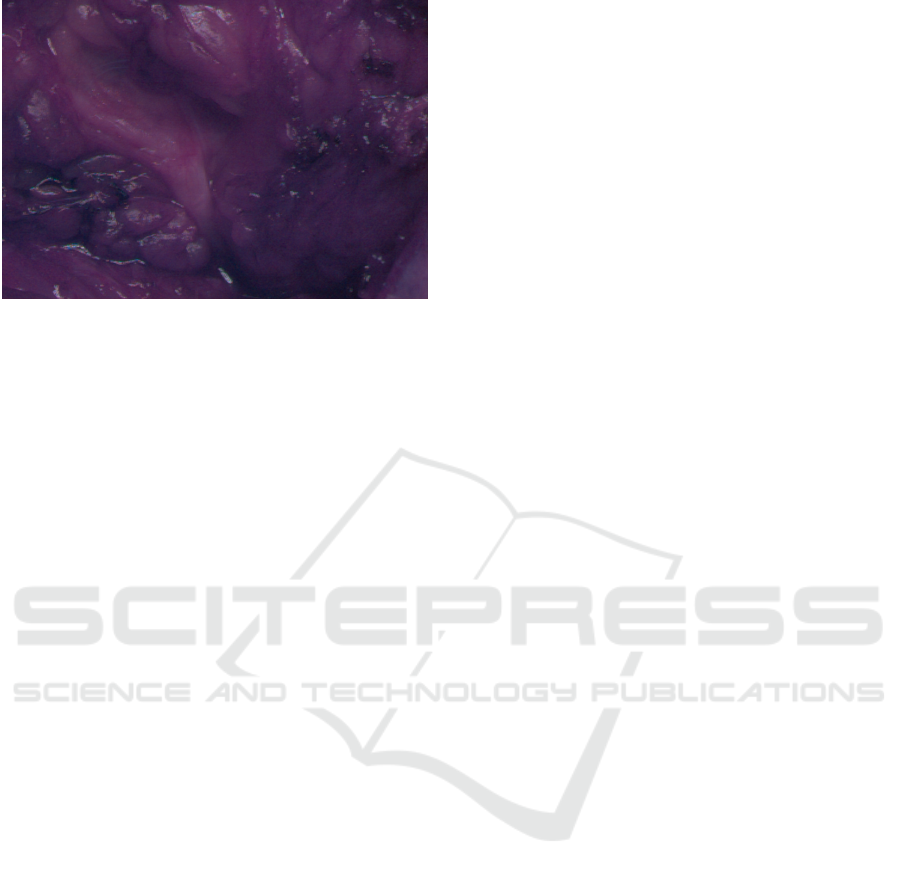
Figure 7: Demosaiced medical image showing qualitatively

high image quality.

ing the model parameters constant. The results were

tested both quantitatively and qualitatively, showing

convincing results over traditional as well as CNN-

based demosaicing methods.

Due to comparatively fewer network parame-

ter, our networks result in more efﬁcient computa-

tion proving the capability for real-time application,

e.g., for intraoperative hyperspectral image applica-

tion. Especially in comparison to current work (Arad

et al., 2022b), which uses very complex networks and

achieves similar results, this is a gain. Importantly,

our focus is on correct spectral reconstruction rather

than visual attractiveness, which is of high importance

for the mentioned applications and supported by the

quantitative results conﬁrmed by our qualitative eval-

uation.

Moreover, the differences between the results of

different datasets, in agreement with the existing liter-

ature Dijkstra et al. (2019), provide valuable insights

for the demosaicing of real camera data. This un-

derscores the importance of developing demosaicing

solutions that train on data being as close as possi-

ble to real MSFA data. Our results demonstrated that

the use of synthetic representatives of real MSFA data

are suitable for training and networks trained on these

data perform well despite fewer training parameters,

thereby enabling fast processing. This pursuit of ef-

ﬁcient solutions is critical for practical applications

in various ﬁelds, including medical imaging and re-

mote sensing, allowing to integrate compact acquisi-

tion concepts like snapshot mosaic imaging into such

processes.

ACKNOWLEDGMENT

This work was funded by the German Federal

Ministry for Economic Affairs and Climate Action

(BMWK) under Grant No. 01MK21003 (NaLamKI).

Only tissue that has been exposed during normal sur-

gical treatment has been scanned additionally with

our described camera. This procedure has been ap-

proved by Charit

e–Universit

atsmedizin Berlin, Ger-

many.

REFERENCES

Arad, B., Timofte, R., Ben-Shahar, O., Lin, Y.-T., and Fin-

layson, G. D. (2020). Ntire 2020 challenge on spectral

reconstruction from an rgb image. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR) Workshops.

Arad, B., Timofte, R., Yahel, R., Morag, N., Bernat, A.,

Cai, Y., Lin, J., Lin, Z., Wang, H., Zhang, Y., Pﬁs-

ter, H., Van Gool, L., Liu, S., Li, Y., Feng, C., Lei,

L., Li, J., Du, S., Wu, C., Leng, Y., Song, R., Zhang,

M., Song, C., Zhao, S., Lang, Z., Wei, W., Zhang, L.,

Dian, R., Shan, T., Guo, A., Feng, C., Liu, J., Agarla,

M., Bianco, S., Buzzelli, M., Celona, L., Schettini,

R., He, J., Xiao, Y., Xiao, J., Yuan, Q., Li, J., Zhang,

L., Kwon, T., Ryu, D., Bae, H., Yang, H.-H., Chang,

H.-E., Huang, Z.-K., Chen, W.-T., Kuo, S.-Y., Chen,

J., Li, H., Liu, S., Sabarinathan, S., Uma, K., Bama,

B. S., and Roomi, S. M. M. (2022a). Ntire 2022

spectral recovery challenge and data set. In 2022

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition Workshops (CVPRW), pages 862–

880.

Arad, B., Timofte, R., Yahel, R., Morag, N., Bernat, A.,

Wu, Y., Wu, X., Fan, Z., Xia, C., Zhang, F., Liu, S.,

Li, Y., Feng, C., Lei, L., Zhang, M., Feng, K., Zhang,

X., Yao, J., Zhao, Y., Ma, S., He, F., Dong, Y., Yu,

S., Qiu, D., Liu, J., Bi, M., Song, B., Sun, W., Zheng,

J., Zhao, B., Cao, Y., Yang, J., Cao, Y., Kong, X., Yu,

J., Xue, Y., and Xie, Z. (2022b). Ntire 2022 spectral

demosaicing challenge and data set. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 882–896.

Bendoumi, M. A., He, M., and Mei, S. (2014). Hyper-

spectral image resolution enhancement using high-

resolution multispectral image based on spectral un-

mixing. IEEE Transactions on Geoscience and Re-

mote Sensing, 52(10):6574–6583.

Brauers, J. and Aach, T. (2006). A color ﬁlter array based

multispectral camera. In 12. Workshop Farbbildverar-

beitung, pages 5–6. Ilmenau.

Calin, M. A., Parasca, S. V., Savastru, D., and Manea, D.

(2014). Hyperspectral imaging in the medical ﬁeld:

present and future. Applied Spectroscopy Reviews,

49(6):435–447.

Dijkstra, K., van de Loosdrecht, J., Schomaker, L., and

Wiering, M. A. (2019). Hyperspectral demosaicking

and crosstalk correction using deep learning. Machine

Vision and Applications, 30(1):1–21.

Dong, C., Loy, C. C., He, K., and Tang, X. (2014). Learn-

ing a deep convolutional network for image super-

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

548

resolution. In European conference on computer vi-

sion, pages 184–199. Springer.

Eismann, M. T. and Hardie, R. C. (2005). Hyperspectral

resolution enhancement using high-resolution multi-

spectral imagery with arbitrary response functions.

IEEE Transactions on Geoscience and Remote Sens-

ing, 43(3):455–465.

Gharbi, M., Chaurasia, G., Paris, S., and Durand, F. (2016).

Deep joint demosaicking and denoising. ACM Trans-

actions on Graphics (TOG), 35(6):1–12.

ob, S., G

otz, T. I., and Wittenberg, T. (2021). Multispec-

tral single chip reconstruction using dnns with appli-

cation to open neurosurgery. Current Directions in

Biomedical Engineering, 7(2):37–40.

Habtegebrial, T. A., Reis, G., and Stricker, D. (2019). Deep

convolutional networks for snapshot hypercpectral de-

mosaicking. In 2019 10th Workshop on Hyperspectral

Imaging and Signal Processing: Evolution in Remote

Sensing (WHISPERS), pages 1–5. IEEE.

Hershey, J. and Zhang, Z. (2008). Multispectral digital

camera employing both visible light and non-visible

light sensing on a single image sensor. US Patent

7,460,160.

Hyttinen, J., F

alt, P., J

asberg, H., Kullaa, A., and Hauta-

Kasari, M. (2020). Oral and dental spectral image

database—odsi-db. Applied Sciences, 10(20):7246.

Jung, A., Kardev

an, P., and T

okei, L. (2006). Hyperspectral

technology in vegetation analysis. Progress in Agri-

cultural Engineering Sciences, 2(1):95–117.

Khan, H. A., Mihoubi, S., Mathon, B., Thomas, J.-B., and

Hardeberg, J. Y. (2018). Hytexila: High resolution

visible and near infrared hyperspectral texture images.

Sensors, 18(7):2045.

Li, Q., Wang, Q., and Li, X. (2020). Mixed 2d/3d con-

volutional network for hyperspectral image super-

resolution. Remote Sensing, 12(10):1660.

Li, Y., Zhang, L., Dingl, C., Wei, W., and Zhang, Y.

(2018). Single hyperspectral image super-resolution

with grouped deep recursive residual network. In 2018

IEEE Fourth International Conference on Multimedia

Big Data (BigMM), pages 1–4. IEEE.

Lim, B., Son, S., Kim, H., Nah, S., and Mu Lee, K. (2017).

Enhanced deep residual networks for single image

super-resolution. In Proceedings of the IEEE con-

ference on computer vision and pattern recognition

workshops, pages 136–144.

Lu, G. and Fei, B. (2014). Medical hyperspectral imaging:

a review. Journal of Biomedical Optics, 19(1):10901.

Malvar, H. S., He, L.-w., and Cutler, R. (2004). High-

quality linear interpolation for demosaicing of bayer-

patterned color images. In 2004 IEEE International

Conference on Acoustics, Speech, and Signal Process-

ing, volume 3, pages iii–485. IEEE.

Mei, S., Yuan, X., Ji, J., Zhang, Y., Wan, S., and Du, Q.

(2017). Hyperspectral image spatial super-resolution

via 3d full convolutional neural network. Remote

Sensing, 9(11):1139.

Mihoubi, S., Losson, O., Mathon, B., and Macaire, L.

(2015). Multispectral demosaicing using intensity-

based spectral correlation. In International Confer-

ence on Image Processing Theory, Tools and Applica-

tions (IPTA), volume 5, pages 461–466. IEEE.

Mirhashemi, A. (2019). Conﬁguration and registration of

multi-camera spectral image database of icon paint-

ings. Computation, 7(3):47.

Moghadam, P., Ward, D., Goan, E., Jayawardena, S., Sikka,

P., and Hernandez, E. (2017). Plant disease detection

using hyperspectral imaging. In 2017 International

Conference on Digital Image Computing: Techniques

and Applications (DICTA), pages 1–8. IEEE.

Monno, Y., Kikuchi, S., Tanaka, M., and Okutomi, M.

(2015). A practical one-shot multispectral imaging

system using a single image sensor. IEEE Transac-

tions on Image Processing, 24(10):3048–3059.

Monno, Y., Teranaka, H., Yoshizaki, K., Tanaka, M., and

Okutomi, M. (2018). Single-sensor rgb-nir imaging:

High-quality system design and prototype implemen-

tation. IEEE Sensors Journal, 19(2):497–507.

uhle, R., Markgraf, W., Hilsmann, A., Malberg, H., Eis-

ert, P., and Wisotzky, E. L. (2021). Comparison

of different spectral cameras for image-guided or-

gan transplantation. Journal of Biomedical Optics,

26(7):076007.

Niu, B., Wen, W., Ren, W., Zhang, X., Yang, L., Wang,

S., Zhang, K., Cao, X., and Shen, H. (2020). Sin-

gle image super-resolution via a holistic attention net-

work. In Computer Vision–ECCV 2020: 16th Euro-

pean Conference, Glasgow, UK, August 23–28, 2020,

Proceedings, Part XII 16, pages 191–207. Springer.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-

net: Convolutional networks for biomedical image

segmentation. In Medical Image Computing and

Computer-Assisted Intervention–MICCAI 2015: 18th

International Conference, Munich, Germany, October

5-9, 2015, Proceedings, Part III 18, pages 234–241.

Springer.

Shafri, H. Z., Taherzadeh, E., Mansor, S., and Ashurov, R.

(2012). Hyperspectral remote sensing of urban areas:

an overview of techniques and applications. Research

Journal of Applied Sciences, Engineering and Tech-

nology, 4(11):1557–1565.

Shi, Z., Chen, C., Xiong, Z., Liu, D., and Wu, F. (2018).

Hscnn+: Advanced cnn-based hyperspectral recovery

from rgb images. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition

Workshops, pages 939–947.

Shinoda, K., Yoshiba, S., and Hasegawa, M. (2018). Deep

demosaicking for multispectral ﬁlter arrays. arXiv

preprint arXiv:1808.08021.

Song, B., Ma, S., He, F., and Sun, W. (2022). Hyperspec-

tral reconstruction from rgb images based on res2-unet

deep learning network. Opt Precis Eng, 30(13):1606.

Wang, Y., Cao, R., Guan, Y., Liu, T., and Yu, Z. (2021).

A deep survey in the applications of demosaick-

ing. In 2021 3rd International Academic Exchange

Conference on Science and Technology Innovation

(IAECST), pages 596–602. IEEE.

Wang, Y.-Q. (2014). A multilayer neural network for image

demosaicking. In 2014 IEEE International Confer-

Efﬁcient and Accurate Hyperspectral Image Demosaicing with Neural Network Architectures

549

ence on Image Processing (ICIP), pages 1852–1856.

IEEE.

Wisotzky, E. L., Daudkane, C., Hilsmann, A., and Eisert, P.

(2022). Hyperspectral demosaicing of snapshot cam-

era images using deep learning. In DAGM German

Conference on Pattern Recognition, pages 198–212.

Springer.

Wisotzky, E. L., Kossack, B., Uecker, F. C., Arens, P., Hils-

mann, A., and Eisert, P. (2020). Validation of two

techniques for intraoperative hyperspectral human tis-

sue determination. Journal of Medical Imaging, 7(6).

Wisotzky, E. L., Uecker, F. C., Arens, P., Dommerich, S.,

Hilsmann, A., and Eisert, P. (2018). Intraoperative hy-

perspectral determination of human tissue properties.

Journal of Biomedical Optics, 23(9):1–8.

Yamanaka, J., Kuwashima, S., and Kurita, T. (2017). Fast

and accurate image super resolution by deep cnn with

skip connection and network in network. In Interna-

tional Conference on Neural Information Processing,

pages 217–225. Springer.

Yasuma, F., Mitsunaga, T., Iso, D., and Nayar, S. K. (2010).

Generalized assorted pixel camera: postcapture con-

trol of resolution, dynamic range, and spectrum. IEEE

transactions on image processing, 19(9):2241–2253.

Zhang, Y. (2014). Spatial resolution enhancement of hy-

perspectral image based on the combination of spec-

tral mixing model and observation model. In Image

and Signal Processing for Remote Sensing XX, vol-

ume 9244, page 924405. International Society for Op-

tics and Photonics.

Zhang, Y., Wirkert, S. J., Iszatt, J., Kenngott, H., Wag-

ner, M., Mayer, B., Stock, C., Clancy, N. T., Elson,

D. S., and Maier-Hein, L. (2017). Tissue classiﬁcation

for laparoscopic image understanding based on multi-

spectral texture analysis. Journal of Medical Imaging,

4(1):015001–015001.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

550