Action Duration Generalization for Exact Multi-Agent Collective
Construction
Martin Rame
ˇ
s
a
and Pavel Surynek
b
Faculty of Information Technology, Czech Technical University, Th
´
akurova 9, 160 00 Prague 6, Czech Republic
fi
Keywords:
Multi-Agent Construction, Multi-Agent Planning, Mixed Integer Linear Programming.
Abstract:
This paper addresses exact approaches to multi-agent collective construction problem which tasks a group
of cooperative agents to build a given structure in a blocksworld under the gravity constraint. We propose
a generalization of the existing exact model based on mixed integer linear programming by accommodating
varying agent action durations. We refer to the model as a fraction-time model. The introduction of action
durations enables one to create a more realistic model for various domains. It provides a significant reduction
of plan execution duration at the cost of increased computational time, which rises steeply the closer the model
gets to the exact real-world action duration. We also propose a makespan estimation function for the fraction-
time model. This can be used to estimate the construction time reduction size for cost-benefit analysis. The
fraction-time model and the makespan estimation function have been evaluated in a series of experiments
using a set of benchmark structures. The results show a significant reduction of plan execution duration for
non-constant duration actions due to decreasing synchronization overhead at the end of each action. According
to the results, the makespan estimation function provides a reasonably accurate estimate of the makespan.
1 INTRODUCTION
The multi-agent collective construction (MACC)
problem tasks a group of cooperative agents to build
a given structure in a blocksworld. Agents can pick
up, move, and place blocks, which are used as the
only building material for a three-dimensional struc-
ture. Both blocks and agents are moving under the
condition of gravity. The problem aims to determine
a collision-free plan for the agent movement, which
would perform the construction task while minimiz-
ing the execution time (makespan) and the sum of du-
rations the agents spend on the grid (sum-of-costs).
Previously, such problems were solved heuristi-
cally with no proof of optimality. Recently, a new
branch of research emerged, aiming to study optimal
MACC problem solutions. This paper aims to fur-
ther this research by generalizing the currently best
optimal model – MILP model by (Lam et al., 2020)
– further referred to as the constant-time model. The
generalization, further referred to as the fraction-time
model, allows agent actions to differ in duration to
better map real-world multi-agent systems.
a
https://orcid.org/0009-0000-3301-6269
b
https://orcid.org/0000-0001-7200-0542
(a) ”Termes robot 01” by Forgemind ArchiMedia is licensed
under CC BY 2.0 (Forgemind ArchiMedia, 2014).
(b) Visualization of the world state in the MACC problem.
Figure 1: Example of the TERMES system and its MACC
representation. Three robotic agents are building a long
stair structure. The middle agent is performing a deliver-
block action.
718
Rameš, M. and Surynek, P.
Action Duration Generalization for Exact Multi-Agent Collective Construction.
DOI: 10.5220/0012385600003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 3, pages 718-725
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

The constant-time model (Lam et al., 2020) ex-
actly optimizes the MACC plan to achieve minimum
makespan and sum-of-costs as primary and secondary
optimization criteria, respectively, assuming all ac-
tions to have the same duration. This is not the case in
real life and the robots are forced to wait for the end of
the longest action. This includes the TERMES robots
(Petersen et al., 2011), which inspired the constant-
time model. Notably, the difference between average
block pick-up time (15s) and placement time (24s),
measured in (Petersen et al., 2011), is 46%. The paper
also shows that agents carrying a block or moving on
unstructured terrain (i.e. gravel, grass) move slower.
To better utilize the information about mean ac-
tion durations, we propose the fraction-time model.
The model will accept a structure height map along
with action durations as input and provide a MACC
plan as output. We modify the constant-time model
to include the action durations. The modification is
non-trivial, as the generalized model needs to prevent
mid-action agent collisions and maintain the network
flow substructure of the base model to remain compu-
tationally viable. We demonstrate the improvement of
plan execution duration on three instances with three
non-constant action durations, including TERMES
durations. We provide two makespan lower bounds,
one based on fraction-time model relaxation and one
based on the fraction-time model with a less detailed
action duration assignment, which can also be used to
get the makespan upper bound. To solve the fraction-
time MILP model, we use the state-of-the-art solver
Gurobi (Gurobi Optimization, LLC, 2023).
2 RELATED WORK
The MACC problem is part of a wider research
branch, which studies various forms of collaborative
construction. These forms include, for instance, self-
assembly, where the agents themselves act as build-
ing blocks, once they reach their destination (Piranda
and Bourgeois, 2018; Romanishin et al., 2013). An-
other uses quadrotors to assemble the structure from
beams and columns (Barros dos Santos et al., 2018).
Robotic arms with connectors on both sides are pro-
posed by (Jenett and Cheung, 2017) to build and move
atop lightweight lattice structures like an inchworm.
All these approaches focus on robots with unique
capabilities and limitations, requiring dedicated algo-
rithms. We focus on the TERMES, a termite-inspired
multi-agent system by (Petersen et al., 2011). The
TERMES robots can pick up, carry, and place similar-
sized blocks. Each robot can carry at most one block,
and climb the difference of one block. The robots
can build complex structures based on simple sen-
sor feedback and high-level instructions – move for-
ward by one block, turn 90° left, turn 90° right, pick
up the block in front of the robot, and deliver a car-
ried block at a position in front of the robot (Petersen
et al., 2011). The MACC discretizes the movement
of the TERMES robot and makes the problem par-
tially hardware-independent by limiting the robots to
the above high-level actions. Image 1 shows the TER-
MES robots and their MACC representation.
Currently, there are only two models that can solve
the MACC makespan-optimally (Lam et al., 2020) – a
mixed integer linear programming (MILP) model and
a constraint programming model. The results of both
models in the paper match on finished instances, with
the MILP model being much faster to compute. Both
models assume a constant action duration.
There are also multiple heuristic/sub-optimal ap-
proaches to the MACC problem. The Compiler for
Scalable Construction by the TERMES Robot Col-
lective heuristically minimizes the number of agents,
who pass through the construction site (Deng et al.,
2019). Another approach presents an algorithm mini-
mizing the number of pick-up and deliver actions, per-
forming dynamic programming on a spanning tree to
find paths for a TERMES robot (Cai et al., 2016).
There are also two approaches, which utilize a
solver/planner but sacrifice the optimal solution to
gain order-of-magnitude better computation speed
(Srinivasan et al., 2023; Singh et al., 2023). Both
compare their solution to the constant-time model.
3 THE FRACTION-TIME MODEL
To allow more precise modeling of non-constant ac-
tion durations of real-world robots, we propose the
fraction-time model. The model replaces the timestep
t of each action by t
s
and t
e
, which denote the timestep
of action start (inclusive) and action end (exclusive),
respectively. This notation mirrors non-preemptive
scheduling notation, where the action is executed
within a time interval [t
s
,t
e
).
We use the non-standard notation of (Lam et al.,
2020). For set U of tuples (u
1
,u
2
,. .. , u
n
) with length
n ∈ Z
+
notation U
u
1
,u
2
,...,u
n
is short for {(u
′
1
,u
′
2
,. .. ,
u
′
n
) : u
′
1
= u
1
∧ u
′
2
= u
2
∧ ··· ∧ u
′
n
= u
n
}. Let ∗ be a
wildcard symbol matching any value at its position in
the tuple (i.e. U
∗,u
2
,...,u
n
is short for {(u
′
1
,u
′
2
,. .. , u
′
n
) :
u
′
2
= u
2
∧ ··· ∧ u
′
n
= u
n
} and U
u
1
,u
2
,∗,...,∗
is short for
{(u
′
1
,u
′
2
,. .. , u
′
n
) : u
′
1
= u
1
∧ u
′
2
= u
2
}).
Let
b
a be shorthand for {0,. . . , a − 1},a ∈ Z
+
. Let
(X,Y) be the size of the building area and (Z − 1)
be the height of the target structure in blocks, the ex-
Action Duration Generalization for Exact Multi-Agent Collective Construction
719

tra layer allows travel on top of the structure. Let
C =
b
X ×
b
Y ×
b
Z be the set of all positions within the
grid, P =
b
X ×
b
Y is the projection of C into the first two
dimensions, B = {(x,0,0) : x ∈
b
X} ∪ {(x,Y − 1,0) :
x ∈
b
X} ∪ {(0,y, 0) : y ∈
b
Y } ∪ {(X − 1,y, 0) : y ∈
b
Y } is
the set of border cells at the perimeter of the building
area. Let z
(x,y)
be the target height of the block column
at position (x,y). Let C
′
= C ∪ {(S, S, S),(E,E,E)}
be a set of all agent-accessible positions – including
two special positions (S,S,S),(E, E, E), which sym-
bolize the start and the end position outside the grid.
Let K = {M, P, D} be a set of agent action type dis-
tinguishers – M for move action (used for “entry”,
“leave”, “move block”, “move empty” and “wait” ac-
tion types), P for “pick up” action type and D for
“deliver” action type. Let N
(x,y)
= {(x − 1,y),(x +
1,y), (x,y − 1),(x,y + 1)} ∩ P be the set of neigh-
bor positions of (x,y) and T =
b
T be the planning
horizon of T timesteps. The actions are tuples i =
(t
s
,t
e
,x,y,z,c,k, x
′
,y
′
,z
′
), which consist of values:
• start time t
s
∈ Z
+
(inclusive)
• end time t
e
= t
s
+ d,d ∈ Z
+
(exclusive), where d
is the action duration
• start position (x, y,z) ∈ C ∪{(S,S,S)}
• indicator c ∈ {0,1} if agent carries a block
• action type distinguisher k ∈ K
• end position (x
′
,y
′
,z
′
) ∈ C ∪ {(E,E,E)}
– position of affected block for pick up and de-
liver actions (agent stays at the same position)
– marks agent position at the end of the action for
other action types
Let duration d
i
of action i = (t
s
,t
e
,. .. ) be d
i
= t
e
−t
s
.
Let f
d
: Z
+
×C
′
×{0,1} ×K × C
′
−→ Z
+
be a func-
tion of action duration, based on the rest of action tu-
ple – that is t
s
, (x,y,z), c, k and (x
′
,y
′
,z
′
) respectively.
Let A = {entry, leave,move block, move empty,
deliver,pick up, wait} be the set of all action types.
• Q
entry
= {(t
s
,S,S, S, c, M, x,y,z) : t
s
∈
[
T − 3 ∧ c ∈
{0,1} ∧ (x,y, z) ∈ B}
• Q
move empty
= {(t
s
,x,y,z,0,M,x
′
,y
′
,z
′
) : t
s
∈
{1,. .. , T − 3} ∧ (x,y, z) ∈ C ∧ (x
′
,y
′
) ∈
N
(x,y)
∧ |z
′
− z| ≤ 1}
• Q
move block
= {(t
s
,x,y,z,1,M,x
′
,y
′
,z
′
) : t
s
∈
{1,. .. , T − 3} ∧ (x,y, z) ∈ C ∧ (x
′
,y
′
) ∈
N
(x,y)
∧ |z
′
− z| ≤ 1}
• Q
wait
= {(t
s
,x,y,z,c,M,x,y, z) : t
s
∈ {1,. . . , T −
3} ∧ c ∈ {0,1} ∧ (x,y, z) ∈ C }
• Q
leave
= {(t
s
,x,y, z, c, M, E, E, E) : t
s
∈ {2,...,T −
2} ∧ c ∈ {0,1} ∧ (x,y, z) ∈ B}
• Q
pick up
= {(t
s
,x,y,z,0,P,x
′
,y
′
,z) : t
s
∈ {1,...,T −
3} ∧ (x,y) ∈ P ∧ (x
′
,y
′
) ∈ N
(x,y)
∧ z ∈
[
Z − 1}
• Q
deliver
= {(t
s
,x,y, z, 1, D, x
′
,y
′
,z) : t
s
∈ {1, . . . , T −
3} ∧ (x,y) ∈ P ∧ (x
′
,y
′
) ∈ N
(x,y)
∧ z ∈
[
Z − 1}
Let Q =
S
a∈A
Q
a
. Let f
q
: Z
+
×C
′
×{0,1}×K ×
C
′
−→ Q
+
be a function, which assigns each action a
duration f
q
(t
s
,. .. , z
′
),(t
s
,. .. , z
′
) ∈ Q . If not specified
otherwise, the f
q
function must be part of the model
input. Let m be the least common multiple of de-
nominators in { f
q
(t
s
,. .. , z
′
) : ∀(t
s
,. .. , z
′
) ∈ Q }. Then,
unless otherwise specified, the f
d
function is de-
fined as f
d
(t
s
,. .. , z
′
) = m f
q
(t
s
,. .. , z
′
),∀(t
s
,. .. , z
′
) ∈
Q . Let us introduce the following simplifying nota-
tion – let f
d
(v) = f
d
(t
s
,. .. , z
′
),∀v = (t
s
,. .. , z
′
) ∈ Q .
Let us define a set of all actions for each action
type a ∈ A as R
a
= {(t
s
,t
e
,x,y,z,c,k, x
′
,y
′
,z
′
) : v =
(t
s
,x,y,z,c,k, x
′
,y
′
,z
′
) ∈ Q
a
∧t
e
= t
s
+ f
d
(v)}.
The proposed model has seven disjoint sets of
agent action types, which in union give the new set
of agent actions. Agent action types are derived from
six different action subsets in the original model:
Set R
entry
of “entry” type actions features all ac-
tions, where the agent enters from the starting posi-
tion outside the grid to a border cell. The agent might
carry a block when it enters. This action type is the
only source of new blocks for the construction site.
The set of agent actions, where the agent moves to
the neighbor grid position is divided into two action
types – “move block” and “move empty” for moving
to the neighbor position while carrying / not carry-
ing a block, respectively. This distinction is made for
cases where the carried block requires the agent to
move slower. Set R
move empty
is for “move empty”,
set R
move
block
is for “move block” action type. Both
action types can be implemented on TERMES robots
as a combination of turn and move-forward actions.
Action type “wait” with action set R
wait
has a du-
ration of T
wait
= 1 timestep, chosen because the mini-
mum wait-time of agents is generally not limited. Ac-
tion type “leave” is for agents leaving the grid from a
border cell (going to the end position (E,E, E)). The
associated action set is R
leave
. The agents can carry
a block when leaving the grid, the only way to re-
move blocks from the construction site. Set R
pick up
of “pick up” type actions features all actions, where
the agent picks up a block from a neighbor position.
Set of “deliver” type actions R
deliver
features all ac-
tions, where the agent delivers a block to a neighbor
position. Let the set of all actions be R =
S
a∈A
R
a
.
Let H be a set of block-actions. Block-action is
a tuple (t, x,y,z,z
′
) ∈ H , where (x, y,z) ∈ C ∧ z
′
∈
{z − 1, z, z + 1} ∩
b
Z ∧ t ∈
b
T . All block-actions last
one timestep, meaning that only action start time t
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
720

is required. Indicators r
i
∈ {0,1},i ∈ R and h
i
∈
{0,1}, i ∈ H decide, which action is part of the plan.
For instance, r
j
= 1, j = (5,7,1,2,0,1,D,2,2,0) ∈ R
in the solution indicates that an agent at timestep 5
delivers block to position (2,2,0) ∈ C while standing
at (1,2, 0) ∈ C . The action is finished by timestep 7.
The objective function 1 minimizes the sum-of-
costs (the sum of timesteps each robot spends on the
grid). The proposed model counts the “entry”-type
action timesteps into the objective function, because
the agent is considered to partially be on the grid,
when the action starts (blocking the border cell as part
of the action exclusion zone).
The exclusion zones are proposed as a measure to
avoid agent collisions. Each exclusion zone is cre-
ated at the start of an action, removed at the end
of the same action and grants the agent performing
the action exclusive access to start- and end-position
columns, if the position is within grid. The exclusive
access does not allow the remaining agents to perform
actions, which start or end within the exclusion zone.
min(
∑
i∈R
r
i
d
i
) (1)
h
t,x,y,z,z
= 1,∀t ∈
b
T , (x, y,z) ∈ B (2)
h
0,x,y,0,0
= 1,∀(x, y) ∈ P (3)
h
T −1,x,y,z
(x,y)
,z
(x,y)
= 1,∀(x, y) ∈ P (4)
∑
i∈H
t,x,y,∗,z
h
i
=
∑
i∈H
t+1,x,y,z,∗
h
i
, ∀t ∈
[
T − 1, (x, y,z) ∈ C (5)
∑
i∈H
t,x,y,∗,∗
h
i
= 1,∀t ∈
b
T , (x, y) ∈ P (6)
Constraints 2 – 6 are the same as in the origi-
nal MILP model. Constraint 2 forbids placement of
blocks at border cells, constraint 3 starts the world
devoid of blocks, constraint 4 ensures that the target
structure is finished at the end of construction, con-
straint 5 flows the column height from one timestep
to the next and constraint 6 forces every position to
have one height.
∑
i∈R
∗,t,
∗,∗,∗,
0,M,
x,y,z
r
i
+
∑
i∈R
∗,t,
x,y,z,
1,D,
∗,∗,∗
r
i
=
∑
i∈R
t,∗,
x,y,z,
0,M,
∗,∗,∗
r
i
+
∑
i∈R
t,∗,
x,y,z,
0,P,
∗,∗,∗
r
i
,∀t ∈
b
T , (x, y,z) ∈ C (7)
∑
i∈R
∗,t,
∗,∗,∗,
1,M,
x,y,z
r
i
+
∑
i∈R
∗,t,
x,y,z,
0,P,
∗,∗,∗
r
i
=
∑
i∈R
t,∗,
x,y,z,
1,M,
∗,∗,∗
r
i
+
∑
i∈R
t,∗,
x,y,z,
1,D,
∗,∗,∗
r
i
,∀t ∈
b
T , (x, y,z) ∈ C (8)
Constraints 7 and 8 flow the agents from one ac-
tion to the next. Semi-closed interval of action exe-
cution [t
s
,t
e
) is exploited for a seamless transition be-
tween actions. Similarly to the base model, constraint
7 flows agents without block and ensures that the
number of agents ending their action without block at
position (x,y,z) at timestep t is the same as the num-
ber of agents without block starting their action at the
same position and in the same timestep. Constraint 8
does the equivalent for agents carrying a block.
∑
i∈R
t
s
,t
e
,
x,y,∗,
∗,∗,
∗,∗,∗
t
s
≤t<t
e
r
i
+
∑
i∈R
t
s
,t
e
,
∗,∗,∗,
∗,∗,
x,y,∗
t
s
≤t<t
e
r
i
−
∑
i∈R
t
s
,t
e
,
x,y,∗,
∗,∗,
x,y,∗
t
s
≤t<t
e
r
i
≤ 1,∀t ∈
b
T , (x, y) ∈ P (9)
Constraint 9 addresses vertex collision of agents
during action execution. Since the only requirement
for the agent is to perform the action a between t
s
and t
e
, the exact position of the agent is unknown and
both start and end position are made into the exclu-
sion zone, where no other action can take place (for
timesteps within interval [t
s
,t
e
)). To avoid agents re-
moving blocks under moving agents, the constraint
makes the whole block column at position (x, y) of
both the start and end of the action an exclusion zone.
Separate constraint to prevent edge collisions (like in
the base model) is no longer necessary, as two actions
can no longer share vertices while executing simulta-
neously, due to the exclusion zones.
∑
i∈R
t
s
,t
e
,∗,∗,∗,∗,∗,∗,∗,∗
:t
s
≤t<t
e
r
i
≤ A,∀t ∈ T (10)
Constraint 10 limits the number of agents on the
grid to at most A ∈ Z
+
, given as part of model input.
∑
i∈H
t,x,y,z,∗
h
i
≥
∑
i∈R
t
s
,t
e
,x,y,z,∗,∗,∗,∗,∗
:t
s
≤t<t
e
r
i
, ∀t ∈
b
T , (x, y,z) ∈ C (11)
h
t,x,y,z+1,z
=
∑
i∈R
∗,t+1,∗,∗,∗,0,P,x,y,z
r
i
,
∀t ∈
[
T − 1, (x, y) ∈ P ,z ∈
[
Z − 1 (12)
h
t,x,y,z,z+1
=
∑
i∈R
∗,t+1,∗,∗,∗,1,D,x,y,z
r
i
,
∀t ∈
[
T − 1, (x, y) ∈ P ,z ∈
[
Z − 1 (13)
h
i
∈ {0,1}, ∀i ∈ H (14)
r
i
∈ {0,1}, ∀i ∈ R (15)
Constraint 11 forces agents to always stand on
the highest block in the column. Constraints 12 and
13 govern decreases and increases in block column
height, respectively. Constraint 12 ties every decrease
by one block to pick up action. Constraint 13 ties in-
crease by one block to deliver action. Constraints 14
and 15 specify the variable domains.
Action Duration Generalization for Exact Multi-Agent Collective Construction
721

The model is used to exactly optimize makespan
and sum-of-costs, the primary and secondary opti-
mization criteria, respectively. Optimization of the
makespan is done by starting at the minimum possible
value (estimated by a lower bound function described
below) and sequentially increasing the makespan by
one timestep until a solution is found.
We expect that the most often used f
d
assignment
will give each action-type a fixed duration (i.e. all
actions in Q
deliver
will have the duration T
deliver
, the
“pick up” actions will have the duration T
pick up
etc. –
see equation 16). Namely, in the case of the TERMES
robots, the first two action type durations would be
T
deliver
= 3 and T
pick up
= 2. The times assume one
timestep is 10 s and are from (Petersen et al., 2011),
where the block pick-up time is measured to be 15± 5
s and the block delivery time 24 ± 5 s. The rest of the
action type durations are derived similarly, the full list
is in table 1 in column “TERMES”.
f
d
(v) =
(
T
a
if v ∈ Q
a
,a ∈ A
1 otherwise.
(16)
4 MAKESPAN ESTIMATION,
UPPER AND LOWER BOUND
Due to the generalization, the fraction-time model is
expected to be more computationally demanding than
the base model, when the action durations are not con-
stant. To allow for an informed decision, whether
the use of a fraction-time model is required, a lower
bound, heuristic estimate, and upper bound of the
fraction-time model makespan are presented.
A lower bound is computed using the relaxed
problem MACC
r
. MACC
r
relaxes the requirement
for the maximum number of agents (allowing an un-
limited number of agents), the constraint of agent
collisions (allowing multiple agents to stand on one
block), exclusion zone constraint (allowing agents
to place blocks under other agents) and constraints
limiting changes of agent vertical position (allowing
agents to stay on top of a column, while it is be-
ing built and place blocks to the neighbor column
at the same time). The only optimization criterion
for MACC
r
is makespan. MACC
r
has a trivial so-
lution – for each column in the building area add the
number of agents equal to the column height and as-
sign them to the column, starting at the border po-
sition closest to the column. For all agents – enter
at the assigned starting position with a block, move
to the assigned column (simultaneously), and one by
one place the held block at the top of the assigned
column. Once all agents assigned to a column place
their blocks, move all those agents to the starting bor-
der cell and leave the building area. The makespan of
MACC
r
is the lower bound of fraction-time MACC
(because MACC
r
is the relaxation of MACC). Let
T
r
be the optimum makespan of MACC
r
. Let s
(x,y)
be the minimum L
1
distance from a border cell to
N
(x,y)
(a neighbor of (x, y)). Let d
min
a
= min
i∈R
a
d
i
,a ∈
A be the minimum duration of action type a. Let
d
min
move
= min{d
min
move block
,d
min
move empty
}. Let T
(x,y)
=
d
min
entry
+ s
(x,y)
d
min
move
+ z
(x,y)
d
min
deliver
+ s
(x,y)
d
min
move
+ d
min
leave
be the duration of the described action sequence for
building the column at (x,y) (z
(x,y)
is the desired
height of the column). Then l
r
= max{T
(x,y)
| ∀(x, y) ∈
P ∧z
(x,y)
> 0} ≤ T
r
is a MACC lower bound (building
of each column is independent in MACC
r
, due to the
relaxations, l
r
is equal to the longest duration T
(x,y)
).
A simple mission duration improvement func-
tion is proposed to assist in cost-benefit analysis and
makespan estimation for more precise action dura-
tion mapping of the fraction-time model. Let d
avg
a
=
(
∑
i∈R
a
d
i
)/|R
a
|,a ∈ A. Let α =
∑
a∈A
d
avg
a
/|A| be
the estimation of the relative makespan increase. Let
T
b
be the makespan computed by the fraction-time
model where all actions last one timestep. The es-
timated makespan of the fraction-time model with a
more detailed action duration mapping is defined as
T
h
= max(l
r
,min(u
f
,⌈αT
b
⌉)), where u
f
is an upper
bound defined later in the chapter.
Finally, the fraction-time model can be used for
its own makespan estimation. Let r
i
, R , T and d
i
for the fraction-time model with less precise action
duration mapping be marked as r
′
i
, R
′
, T
′
and d
′
i
, re-
spectively. Since the more precise mapping of action
durations makes the model more computationally de-
manding, a model with less precise mapping – defined
as max
i∈R
′
a
d
′
i
≤ min
i∈R
a
d
i
,∀a ∈ A – can be used for
estimating the makespan of the more computation-
ally demanding task. In this regard, the model with
d
′
i
= 1,∀i ∈ R
′
is especially interesting, as constant
action durations should provide the smallest runtime
of the fraction-time model for given height-map. Let
l
f
= T
′
be a lower bound gained using fraction-time
model with less precise action duration mapping.
Let u
f
be an upper bound, defined as the execution
duration of a plan by the fraction-time model with
less precise action duration mapping, where the ac-
tions use durations of the more precise mapping and
the agents wait at the beginning of each timestep until
all actions that were supposed to end at that timestep
are performed. This waiting strategy can also be used
when executing the plan on real hardware. When
d
′
i
= 1,∀i ∈ R
′
, u
f
is defined by equation 17.
Let u
c
= T
′
∗ max
v∈Q
f
d
(v) be a naive upper
bound, where T
′
is the makespan of fraction-time
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
722

Figure 2: Instance used for makespan estimation precision
measurement.
Figure 3: Three different instances used in experiments.
model with d
′
i
= 1, ∀i ∈ R
′
. In practice, we mul-
tiply the makespan of unit-action-duration fraction-
time model with the duration of the longest action.
u
f
0
= 0
u
f
n
= u
f
n−1
+ max
(t
s
,t
e
,x,...,z
′
)
∈R
′
n−1,∗,...,∗
f
d
(u
f
n−1
,x,...,z
′
),
(17)
5 EXPERIMENTS
The first experiment aims to demonstrate construction
time reduction for non-constant action durations. It
is performed with the Gurobi 10.0.3 solver (Gurobi
Optimization, LLC, 2023), limited to 32 threads on a
3 GHz Intel Skylake processor with 16 physical cores
and hyper-threading, along with 132 GB of RAM.
For evaluation, we translate the fraction-time
model to Python Gurobi API, which we use to de-
scribe the objective function 1 and all the constraints
(2 – 15). The resulting translation requires a known
makespan and optimizes only the sum-of-costs. To
optimize makespan, we add an outer loop, iterating
over makespans starting at lower bound l
r
and in-
creasing by 1 until a solution (construction plan) is
found. The input for the Python program is speci-
fied as a 2-dimensional height-map of the structure,
durations for enter, leave, move block, move empty,
deliver and pick up action types. The output of the
model is a set of indicators r
i
and h
i
, which action tu-
ples were used. Each action tuple contains a start and
an end position, which is used to assign the actions to
agents and compile an action sequence for each agent.
We experiment with three structures shown in fig-
ure 3. These instances represent a subset of instances
from (Lam et al., 2020) that have the lowest solver
computation time, with part of the area without blocks
around the third structure removed to reduce access
time for the agents. The fraction-time model is used
to compute plans for the construction of each struc-
ture instance. Four action duration sets (i.e. sets of ac-
tion durations) are used for each structure – the action
durations can be seen in table 1. The maximum num-
ber of agents is 50 for instances 1 and 2; 20 for the
third instance (due to the smaller construction area).
The table 2 shows the results of the first experi-
ment, measuring solver runtime, solution makespan,
and sum-of-costs for each instance–action-type-set
duo. The construction plans are saved as well, the 1-
timestep plan is used for u
f
and u
c
upper bound com-
putation (result in parentheses next to makespan). The
u
f
and u
c
values are very similar, showing that in most
cases, the more easily computed u
c
value is sufficient.
The makespan values show a decrease in construction
duration in comparison with the wait-action padded
plan by u
f
. The construction duration decreases on
average by approximately 19% for 1-2 timestep, 6%
for 1-2-3 timestep, and 9% for TERMES timestep.
The table also contains the average value and sam-
pling variance of the runtime, showing a steep growth
in computational complexity. The results suggest an
exponential increase of computation time in regards
to makespan, which was also observed in a similar
model by (Srinivasan et al., 2023). This is likely
caused by linear dependency between the number of
MILP variables (r
i
and h
i
) and model makespan (also
noted by (Srinivasan et al., 2023)) and a general MILP
problem being NP-hard (Bulut and Ralphs, 2021).
Table 1: Action type durations for used action duration sets.
Action duration sets
Action 1 1-2 1-2-3 TERMES
enter 1 2 3 3
leave 1 1 2 3
move block 1 1 3 3
move empty 1 1 1 2
pick up 1 2 3 2
deliver 1 2 3 3
The second experiment aims to evaluate the ef-
fects of varying action durations on the makespan es-
timation accuracy of T
h
. For this purpose, all action
types, but T
wait
, are assigned durations T
a
∈ {1,2,3} =
β,∀a ∈ A \ {wait} and all combinations of those du-
rations are measured (requiring |β|
|A|−1
= 729 con-
struction plans to be computed). T
wait
is left as 1, as
the minimum robot wait time is not limited. We select
a 2 × 2 × 2 cube target structure (figure 2) due to the
high number of required measurements.
The results in figure 4 show that T
h
both can
Action Duration Generalization for Exact Multi-Agent Collective Construction
723

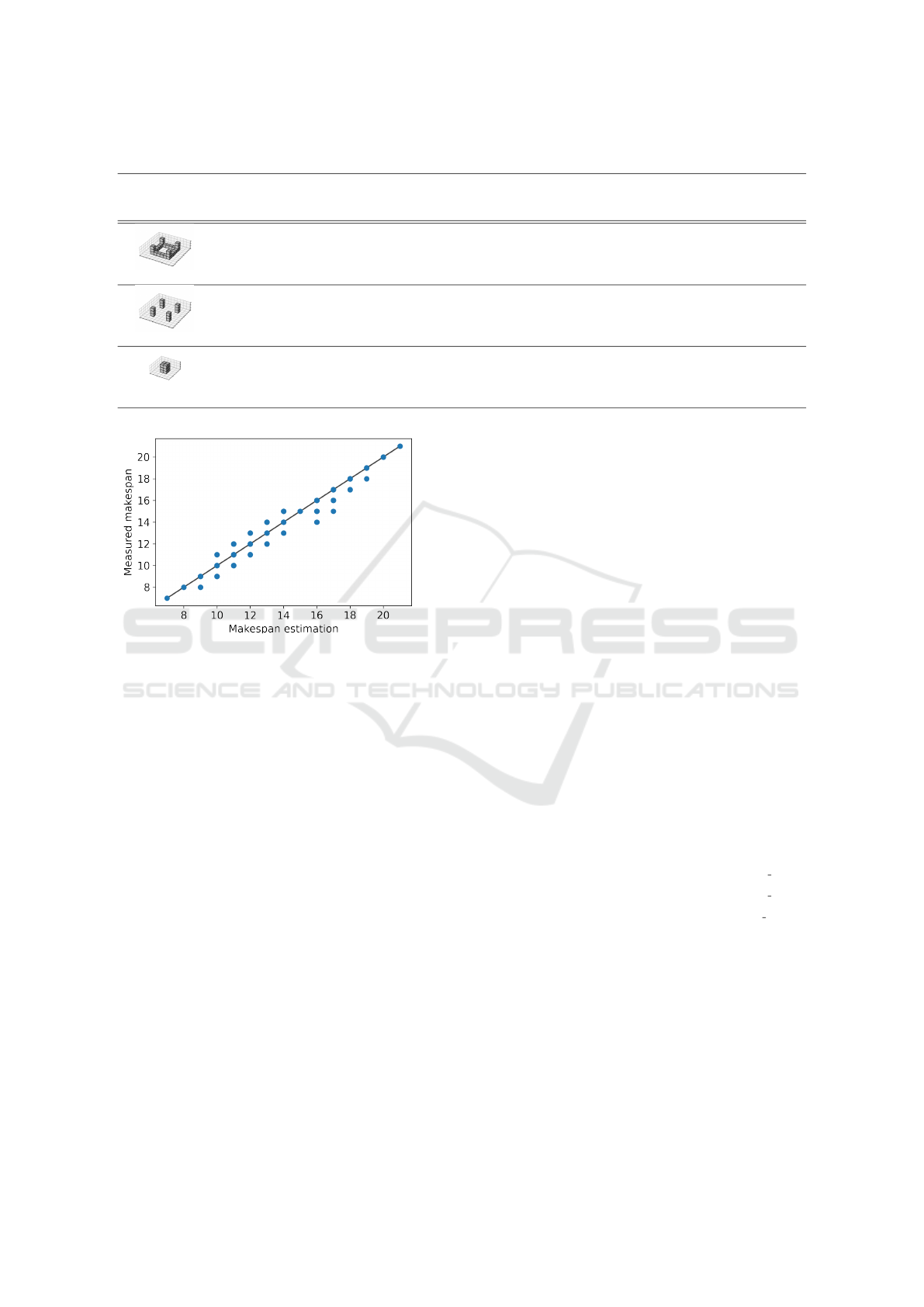
Table 2: Experimental results.
Instance Action duration set Run-time Run-time Makespan Makespan Sum-of-costs Robots
mean [s] sampling lower with (u
f
;u
c
variance [s
2
] bound upper bound)
1
1-timestep 26.75 1.41 6 11 (11; 11) 232 32, 33, 34, 37
1-2-timestep 355.33 95.16 10 17 (21; 22) 316 32, 33
1-2-3-timestep 426.32 28.48 15 30 (32; 33) 576 32
TERMES-timestep 322.73 9.19 18 30 (33; 33) 648 32, 33, 34
2
1-timestep 24.10 1.05 6 11 (11; 11) 196 32
1-2-timestep 58.88 0.93 10 17 (21; 22) 284 32
1-2-3-timestep 287.24 15.76 15 30 (32; 33) 508 32
TERMES-timestep 264.28 2.83 18 30 (33; 33) 548 32
3
1-timestep 239.21 47.98 6 14 (14; 14) 142 16, 17
1-2-timestep 303.92 43.62 10 21 (27; 28) 213 17
1-2-3-timestep 3807.62 414.87 15 37 (41; 42) 352 17
TERMES-timestep 6152.27 1132.99 18 38 (41; 42) 398 16, 17
Figure 4: Scatter plot of makespanheuristic relation.
under- and over-estimate the actual makespan value.
The root mean square error (RMSE) of T
h
is 0.655,
with minimum estimation error absolute value, rela-
tive to makespan, being 0 and maximum 0.143. The
error stems from the simplicity of T
h
– it depends only
on the action type duration mean and makespan of the
generalized model with unit action durations. It does
not take into account the usage of the action types.
The last test aims to show another beneficial ac-
tion duration set for the fraction-time model. The
real TERMES use marine foam blocks with indenta-
tions/protrusions and neodymium magnets to ensure
block alignment and stability (Petersen et al., 2011).
The resulting block columns are stable enough that
the agents do not need to adapt their movement speed
to their height on the structure – at least at the scales
used in the paper. For TERMES-like multiagent sys-
tems with less stability, the fraction-time model al-
lows to adjust the agent movement speed according
to the vertical position of the agent. This is shown on
a task with action durations given by the equation 18,
ensuring that the action durations grow linearly with
the vertical position of the robot at the action’s end
(except the wait action, where the robot stays still).
The experiment measures 10 run-times with ac-
tion durations f
d
h
(referred to as “Unstable columns”
in the results) on the instance 1. Makespan, sum-
of-costs and run-time are compared with results for
“TERMES-timestep” action duration set of instance
1. The “TERMES-timestep” results are called “Base”
in the results table 3. The makespan of unstable
columns task has increased by 40%, the sum-of-
costs by 7.4%, relative to the base. The increase
of makespan was expected, due to f
d
h
consisting of
TERMES-timestep f
d
with an added positive linear
component. The interesting result is the small 7.4%
increase in sum-of-costs in relation to the 40% rel-
ative increase in makespan. This indicates a lower
agent utilization in case of the unstable columns task.
The run-time increased with the makespan. How-
ever, it is still notably lower than runtime of in-
stance 3 with TERMES-timestep in table 2, which has
makespan 38. This indicates, that while run-time is
greatly dependent on makespan, the remaining task-
dependent constraints, such as the structure height
map and the agent count, also affect the computa-
tional complexity to a relatively large degree.
f
d
h
(v) =

















3 if v ∈ Q
entry
∪ Q
leave
2 + z
′
if v = (.. . , z
′
) ∈ Q
move empty
3 + z
′
if v = (.. . , z
′
) ∈ Q
move block
2 + 2z
′
if v = (.. . , z
′
) ∈ Q
pick up
3 + 2z
′
if v = (.. . , z
′
) ∈ Q
deliver
1 otherwise.
(18)
6 CONCLUSION
A new branch of the multi-agent construction has re-
cently emerged – exact optimization of the problem.
The current state-of-the-art exact approach provides
solutions with optimal makespan and sum-of-costs
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
724

Table 3: Comparison of TERMES task solution where
movement and block manipulation speed depends on agent
height (unstable columns) with task solution, where move-
ment speed is independent of the agent height (base).
TERMES Base Unstable columns
Makespan 30 42
Sum-of-costs 648 696
Mean run-time [s] 322.73 3837.64
but assumes all agent high-level actions to have the
same duration. This is not the case in the real world.
For instance, the mean duration of block manipulation
actions of the TERMES robot differs by 46%.
This has motivated us to generalize the current
state-of-the-art exact MILP model (Lam et al., 2020)
into the fraction-time model with action durations
specified as part of the model input. The generaliza-
tion is non-trivial – upholding the agent collision con-
straint has necessitated the redefinition of agent colli-
sion using exclusion zones while keeping the model
computationally viable required the preservation of
the two network flow structures within the model. We
test the generalized model on various action durations
(including TERMES), studying its behavior. The ex-
periment shows a 9% decrease in construction dura-
tion (makespan vs u
f
upper bound, which can provide
a non-optimal plan) for the TERMES robots. Other
action duration sets also show similar results.
The second experiment analyses the heuristic
makespan estimation function T
h
and its behavior
with different action duration sets. The experiment
uses toy instance – 2 × 2 × 2 cube and showcases the
spread of estimated makespan values in comparison
with the real ones. The RMSE of the T
h
is 0.665, mak-
ing it a viable source of information for cost-benefit
analysis when considering a more computationally
demanding action duration mapping. The last exper-
iment showcases the ability of the model to adjust to
agents moving slower at greater heights. The opti-
mal solutions show a notably lower relative utiliza-
tion of the agents in comparison with a non-height-
dependent action duration assignment.
While the model is computationally demanding,
it can provide reference solutions for both existing
and future heuristic models. These solutions can be
used to estimate the heuristic model efficiency and
as long-term targets for models optimizing makespan
(i.e. construction duration).
ACKNOWLEDGEMENTS
This work has been supported by the project number
22-31346S of the Czech Science Foundation GA
ˇ
CR
and by the CTU project SGS23/210/OHK3/3T/18.
An extended version of this paper is available at
(Rame
ˇ
s and Surynek, 2023).
REFERENCES
Barros dos Santos, S. R., Givigi, S., Nascimento, C. L., Fer-
nandes, J. M., Buonocore, L., and de Almeida Neto,
A. (2018). Iterative decentralized planning for col-
lective construction tasks with quadrotors. Journal of
Intelligent & Robotic Systems, 90(1):217–234.
Bulut, A. and Ralphs, T. K. (2021). On the complexity of
inverse mixed integer linear optimization. SIAM Jour-
nal on Optimization, 31(4):3014–3043.
Cai, T., Zhang, D. Y., Kumar, T. S., Koenig, S., and Aya-
nian, N. (2016). Local search on trees and a frame-
work for automated construction using multiple iden-
tical robots. In Proceedings of the 2016 International
Conference on Autonomous Agents & Multiagent Sys-
tems, pages 1301–1302.
Deng, Y., Hua, Y., Napp, N., and Petersen, K. (2019).
A compiler for scalable construction by the termes
robot collective. Robotics and Autonomous Systems,
121:103240.
Forgemind ArchiMedia (2014). Termes robot 01.
Gurobi Optimization, LLC (2023). Gurobi Optimizer Ref-
erence Manual.
Jenett, B. and Cheung, K. (2017). Bill-e: Robotic plat-
form for locomotion and manipulation of lightweight
space structures. In 25th AIAA/AHS Adaptive Struc-
tures Conference, page 1876.
Lam, E., Stuckey, P., Koenig, S., and Kumar, T. (2020). Ex-
act approaches to the multi-agent collective construc-
tion problem. In Simonis, H., editor, Principles and
Practice of Constraint Programming, Lecture Notes
in Computer Science, pages 743–758. Springer. In-
ternational Conference on Principles and Practice of
Constraint Programming 2020, CP2020 ; Conference
date: 07-09-2020 Through 11-09-2020.
Petersen, K. H., Nagpal, R., and Werfel, J. K. (2011).
Termes: An autonomous robotic system for three-
dimensional collective construction. Robotics: sci-
ence and systems VII.
Piranda, B. and Bourgeois, J. (2018). Geometrical
Study of a Quasi-spherical Module for Building Pro-
grammable Matter, pages 387–400. Springer Interna-
tional Publishing, Cham.
Rame
ˇ
s, M. and Surynek, P. (2023). Action duration gener-
alization for exact multi-agent collective construction.
arXiv.org. https://arxiv.org/abs/2312.13485.
Romanishin, J. W., Gilpin, K., and Rus, D. (2013). M-
blocks: Momentum-driven, magnetic modular robots.
In 2013 IEEE/RSJ International Conference on Intel-
ligent Robots and Systems, pages 4288–4295.
Singh, S., Gutow, G., Srinivasan, A. K., Vundurthy, B., and
Choset, H. (2023). Hierarchical propositional logic
planning for multi-agent collective construction. In
Construction Robotics Workshop.
Srinivasan, A. K., Singh, S., Gutow, G., Choset, H., and
Vundurthy, B. (2023). Multi-agent collective con-
struction using 3d decomposition.
Action Duration Generalization for Exact Multi-Agent Collective Construction
725