Quantum Advantage Actor-Critic for Reinforcement Learning

Michael K

olle

∗

, Mohamad Hgog

∗

, Fabian Ritz, Philipp Altmann, Maximilian Zorn, Jonas Stein

and Claudia Linnhoff-Popien

Institute of Informatics, LMU Munich, Munich, Germany

ﬁ

Keywords:

Quantum Computing, Quantum Reinforcement Learning, Advantage Actor-Critic.

Abstract:

Quantum computing offers efﬁcient encapsulation of high-dimensional states. In this work, we propose a

novel quantum reinforcement learning approach that combines the Advantage Actor-Critic algorithm with

variational quantum circuits by substituting parts of the classical components. This approach addresses rein-

forcement learning’s scalability concerns while maintaining high performance. We empirically test multiple

quantum Advantage Actor-Critic conﬁgurations with the well known Cart Pole environment to evaluate our

approach in control tasks with continuous state spaces. Our results indicate that the hybrid strategy of using ei-

ther a quantum actor or quantum critic with classical post-processing yields a substantial performance increase

compared to pure classical and pure quantum variants with similar parameter counts. They further reveal the

limits of current quantum approaches due to the hardware constraints of noisy intermediate-scale quantum

computers, suggesting further research to scale hybrid approaches for larger and more complex control tasks.

1 INTRODUCTION

Quantum computing (QC) promises to revolutionize

problem-solving by exploiting quantum mechanics’

unique properties, potentially outperforming classical

computers in complex tasks such as quantum cryptog-

raphy, quantum chemistry, and quantum optimization

(Nielsen and Chuang, 2010; Preskill, 2018; Pirandola

et al., 2020; Shor, 1997; Cao et al., 2019; Bauer et al.,

2020; Dral, 2020; Farhi and Harrow, 2016; Cerezo

et al., 2020; Farhi et al., 2014). This has spurred in-

terest in quantum machine learning (QML), particu-

larly in leveraging quantum interference for acceler-

ated training and inference in machine learning mod-

els (Biamonte et al., 2017).

Reinforcement learning (RL) is a machine learn-

ing subﬁeld focused on training agents to interact with

an environment and learn from their experiences. RL

has achieved remarkable success in applications such

as game playing (e.g., AlphaGo (Silver et al., 2017)),

robotics (Kober et al., 2013), and autonomous driv-

ing (You et al., 2017). However, the performance of

classical RL algorithms is often limited by their sam-

ple inefﬁciency. This leads to slow convergence and

requires a large number of interactions with the en-

vironment. Since quantum computing offers the efﬁ-

cient encapsulation of high-dimensional states as one

Authors contributed equally to this work.

of its signiﬁcant beneﬁts, recent research interest in

quantum reinforcement learning (QRL) has emerged

(Meyer et al., 2022b).

This work concentrates on the Advantage Actor-

Critic (A2C) method, a well-established RL algo-

rithm, in the context of QRL (Konda and Tsitsiklis,

1999; Mnih et al., 2016; Andrychowicz et al., 2021).

We explore the application of variational quantum cir-

cuits (VQCs) in policy gradient methods like A2C,

suitable for current noisy intermediate scale quantum

(NISQ) computers (Preskill, 2018). We introduce two

A2C conﬁgurations: a pure quantum and a hybrid

quantum classical conﬁguration. We employ VQCs

for both the actor and critic components, and evalu-

ate our experiments on the Cart Pole control problem

from OpenAI gymnasium (Brockman et al., 2016).

First, we compare the performance of our quantum

A2C conﬁgurations with the classical A2C algorithm,

ensuring a similar number of parameters. Further-

more, we investigate the effectiveness of a VQC with

a classical post-processing layer. Finally, we compare

the performance of this hybrid approach with a clas-

sical A2C algorithm, maintaining a similar parame-

ter count. This study aims to demonstrate the en-

hanced learning efﬁciency and accuracy of quantum

A2C algorithms in control tasks with continuous state

spaces.

Kölle, M., Hgog, M., Ritz, F., Altmann, P., Zorn, M., Stein, J. and Linnhoff-Popien, C.

Quantum Advantage Actor-Critic for Reinforcement Learning.

DOI: 10.5220/0012383900003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 1, pages 297-304

ISBN: 978-989-758-680-4; ISSN: 2184-433X

297

2 RELATED WORK

Research in QRL has progressed signiﬁcantly, with

studies exploring quantum algorithms and circuits for

both policy-based and value-based methods, compar-

ing QRL to classical RL, and applying QRL to real-

world problems (Kwak et al., 2021).

Early research introduced VQC for RL, speciﬁ-

cally in approximating Q-value functions in Deep Q-

Learning (DQN) for discrete and continuous environ-

ments (Chen et al., 2019; Skolik et al., 2022). En-

hancements like Double DQN were also adapted into

VQC architecture, showing efﬁcacy in tasks like robot

navigation and in various OpenAI Gym environments

(Heimann et al., 2022; Lockwood and Si, 2020).

Signiﬁcant advancements in policy-based QRL

methods have been made, with studies using VQC for

algorithms like REINFORCE (Jerbi et al., 2022; Jerbi

et al., 2021; Sequeira et al., 2022). In actor-critic

methods, VQCs have been effectively used as actor

and critic networks. Examples include a policy-VQC

for Proximal Policy Optimization and a soft actor-

critic algorithm with VQCs outperforming classical

models (Kwak et al., 2021; Lan, 2021). Addition-

ally, a quantum version of the A3C algorithm demon-

strated superior convergence speed and sample efﬁ-

ciency (Chen, 2023).

Addressing the NISQ era’s qubit limitations, stud-

ies have combined VQC with neural networks for efﬁ-

cient data processing. Pre-processing neural networks

and tensor networks have been employed for dimen-

sionality reduction, while post-processing layers have

enhanced VQC’s expressive power (Mari et al., 2020;

Chen et al., 2021; Chen et al., 2022; Chen, 2023; Se-

queira et al., 2022; Hsiao et al., 2022; Meyer et al.,

2022a).

3 QUANTUM ADVANTAGE

ACTOR-CRITIC

The ﬁrst step in the A2C algorithm (Line 1) involves

initializing both the actor-network π

(s) and the critic

network V

(s) with random parameters θ and ω. The

actor-network maps the current state of the environ-

ment to an appropriate action, while the critic net-

work maps the current state to its corresponding state

value. Then, initialize the stochastic gradient descent

optimizer Adam (Kingma and Ba, 2014) to update the

parameters θ and ω throughout the optimization pro-

cess.

Once the networks have been initialized, the algo-

rithm enters a loop that iterates for each episode. In

each iteration t, the algorithm selects an action a

Initialize the environment;

Initialize the actor-network π

(s);

Initialize the critic-network V

(s);

Initialize Adam optimizer for θ and ω;

for each episode do

Initialize next observation state s

env.reset();

Initialize done d = False;

for each iteration t do

Select an action a

based on π

);

Execute action a

in the environment;

Observe reward r

, new state s

t+1

, and

done d;

if d = True then

break;

end

Calculate TD target value

y = r

+ γV

t+1

);

Calculate advantage A = y −V

);

Update the actor-network by

minimizing the loss

actor

(θ) = −A logπ

);

Update the critic-network by

minimizing the loss

critic

(ω) = (y −V

))

;

Update the state s

= s

t+1

;

end

Algorithm 1: Advantage Actor-Critic Algorithm (Mnih

et al., 2016).

based on the current state s of the environment, as de-

termined by the actor-network π

(s). This action is

executed in the environment, and the algorithm ob-

serves the resulting reward r

, the new state s

t+1

, and

the done status d, which indicates whether the episode

has ended.

The next step is calculating the TD target value y.

The advantage A is estimated from the TD error (dif-

ference between the TD target value y and the pre-

dicted state value). The advantage is then used to up-

date the actor-network by minimizing the loss func-

tion L

actor

(θ). and the critic-network V

(s) by mini-

mizing the loss function L

critic

(ω).

Finally, the state s

of the environment is up-

dated to the new state s

t+1

, and the algorithm repeats

the loop for the next iteration. This process contin-

ues until the maximum number of episodes has been

reached, or d is set to True, at which point the A2C

algorithm terminates.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

298

3.1 Baselines

In our study, we compared quantum A2C algorithms

with classical A2C implementations using neural net-

works of varying sizes, ensuring comparable model

sizes for a fair analysis. Speciﬁcally, we contrasted

a classical A2C with four hidden neurons against our

quantum A2C, and another with ﬁve hidden neurons

against our hybrid A2C (Sections 3.2 and 3.3). The

neural network architectures, consist of an input layer

with four input neurons to encode the 4-dimensional

state, a single hidden layer, and an output layer with

two neurons for the actor-network and one for the

critic network.

The choice of four and ﬁve neurons in the hid-

den layer for the classical A2C models was deliber-

ate, aligning the number of trainable parameters with

those in the quantum and hybrid A2C models. This

alignment ensures that performance differences are

attributable to the inherent characteristics of the mod-

els rather than parameter count discrepancies.

For the neural networks’ activation functions, we

employed the Rectiﬁed Linear Unit (ReLU) function

(Agarap, 2018) in both actor and critic networks to

address the vanishing gradient problem. In the actor-

network’s output layer, a softmax activation function

(Bridle, 1990) was used to generate a probability dis-

tribution.

3.2 Quantum Advantage Actor-Critic

Algorithm

In this work, we employ a speciﬁc VQC architecture,

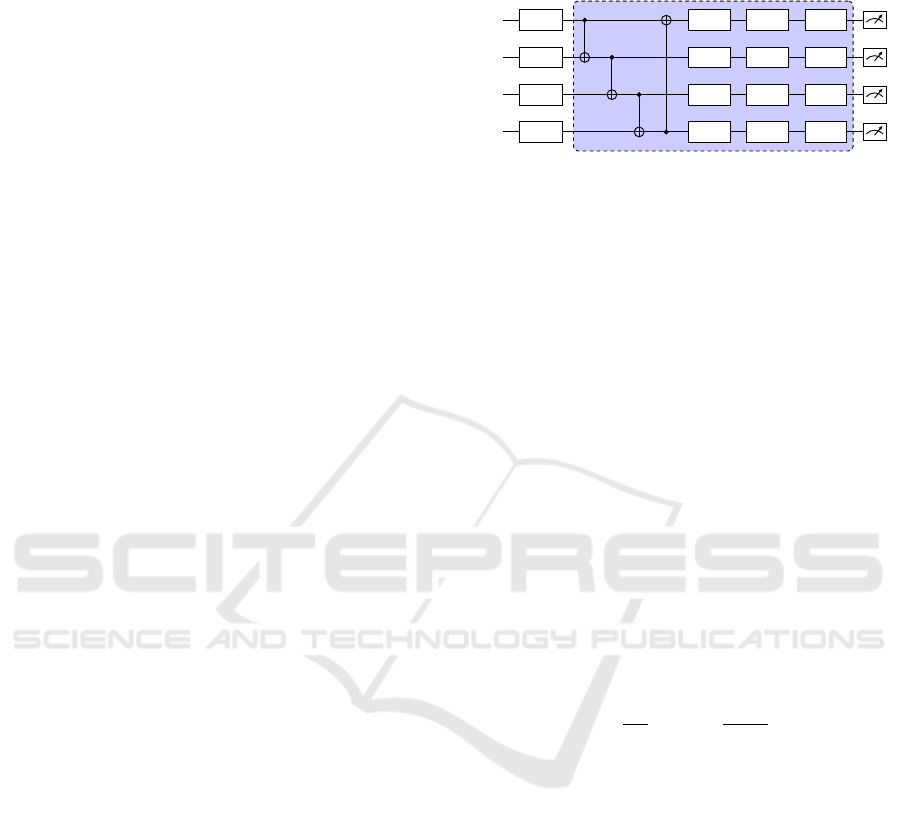
shown in Fig. 1, for both actor and critic quantum cir-

cuits in the QA2C and HA2C algorithms. A VQC

comprises three main components: an encoding layer,

repeated variational layers, and measurements.

The proposed VQC utilizes RX quantum gates to

encode the observed state of the environment into a

quantum state. For the Cart Pole problem, the ob-

served state is four-dimensional, necessitating four

qubits in both the actor and critic circuits to represent

the state information.

Following the encoding process, a variational

layer is applied, repeated a speciﬁc number of times

n. In this particular implementation, we use n = 2

repetitions. Each variational layer consists of four

CNOT gates to entangle all qubits and three single-

qubit gates, R

(θ

), R

(φ

), and R

(δ

), applied to

each qubit i (Kwak et al., 2021). The parameters θ, φ,

and δ are iteratively optimized using the classical op-

timization algorithm Adam (Kingma and Ba, 2014).

Lastly, each qubit’s state is measured, and the

measurement outcomes are utilized to determine the

action for the actor and the state value for the critic in

the following steps of the A2C algorithm.

VARIATIONAL LAYER

⟩

(λ

) R

(θ

) R

(φ

) R

(δ

)

⟩

(λ

) R

(θ

) R

(φ

) R

(δ

)

⟩

(λ

) R

(θ

) R

(φ

) R

(δ

)

⟩

(λ

) R

(θ

) R

(φ

) R

(δ

)

Figure 1: VQC architecture utilized by QA2C and HA2C

algorithms.

3.2.1 State Encoding

In this work, the RX gate is employed for encoding,

which acts on a single qubit and performs a rotation

around the x-axis of the Bloch sphere (Nielsen and

Chuang, 2010). Given that RX rotations are periodic

with a period of 2π, different values might map to

the same quantum state, leading to inaccurate predic-

tions. To mitigate this issue, additional operations are

applied to the observed state variables to ensure the

parameters fall within the range of [−π,π].

The ﬁrst two variables o

and o

have ﬁnite

ranges, whereas the last two variables o

and o

have

inﬁnite ranges. Consequently, we establish separate

normalization and transformation rules for these two

groups of variables.

For the cart’s position o

and the pole’s angle o

which have ﬁnite ranges, the normalization procedure

consists of simple scaling using their respective mini-

mum and maximum values:

4.8

,λ

0.418

, (1)

where λ

and λ

denote the transformed variables that

are input into the quantum circuit.

The normalization process is more intricate than

simple scaling for the cart’s velocity o

and the pole’s

angular velocity o

, which have inﬁnite ranges. To

normalize these values, we ﬁrst use the arctan func-

tion to map the inﬁnite range to the ﬁnite interval

[−π/2,π/2] and then apply simple scaling to stretch

the interval to the desired range. The process can be

expressed as follows:

= 2arctan o

,λ

= 2arctan o

(2)

where λ

and λ

represent the transformed variables

used in the quantum circuit.

3.2.2 Measurement and Action Selection of the

Quantum Actor

The actor’s VQC in the QA2C algorithm is designed

to convert the observed state into a quantum state and

Quantum Advantage Actor-Critic for Reinforcement Learning

299

predict the optimal action to take. We use a VQC

comprising four qubits and two variational layers. At

the end of the circuit, the qubits are measured, and the

probability of measuring 0 is employed to determine

the actor’s action. Given that the action space in the

Cart Pole environment is two-dimensional, only the

measurement values of the ﬁrst two qubits are consid-

ered.

To convert these values into a probability distribu-

tion, we apply the softmax function, which maps the

input vector (in this case, the probabilities of the ﬁrst

two qubits) to a probability distribution that sums to 1

(Bridle, 1990). The softmax function is deﬁned as:

softmax(x

) =

∑

(3)

where x

represents the i-th element of the input vec-

tor, e denotes Euler’s number, and the sum is taken

over all elements in the input vector. After obtaining

the probability distribution, the actor selects its action

stochastically by randomly choosing an action from

the probability distribution, based on the probabilities

assigned to each action.

3.2.3 Measurement in Quantum Critic

In the QA2C algorithm, the quantum critic employs a

VQC to estimate the value function, which serves as

a measure of the quality of a given state for the agent.

As only a single value is needed for the estimation,

the quantum critic measures just the ﬁrst qubit and uti-

lizes the probability of measuring 0 as the estimated

state value.

3.3 Hybrid Quantum Advantage

Actor-Critic Algorithm

In this section, we explore the potential of integrating

VQCs and neural networks within the A2C algorithm.

Neural networks can be employed in conjunction with

VQCs as pre-processing and post-processing layers

(Chen, 2023).

In the VQC architecture depicted in Fig. 1, we

measured at most two qubits for the actor and one

qubit for the critic. With the proposed hybrid archi-

tecture, we expand the VQC by incorporating a post-

processing neural network layer. This modiﬁcation

allows us to measure all four qubits and scale the

VQC output to the desired measurement size. For the

actor, we reduce the output from four values to two,

corresponding to the action space of the environment.

In the case of the critic, we reduce the output from

four values to a single value needed for the state value

function.

We refer to the proposed architecture as the Hy-

brid Advantage Actor-Critic (HA2C), which will be

applied to the QA2C algorithm in three different ap-

proaches. The ﬁrst approach entails replacing the

critic network with a hybrid VQC while retaining the

neural network for the actor. The second approach

involves substituting the actor-network with a hybrid

VQC while keeping the critic as a neural network. Fi-

nally, we replace both the actor and critic neural net-

works with hybrid VQCs.

3.3.1 Hybrid Quantum Actor

The hybrid actor in the HA2C algorithm combines a

VQC with a post-processing single-layer neural net-

work, as illustrated in Fig. 2a. The measurements ob-

tained from the VQC are used as inputs for the post-

processing layer. The neural network has four inputs

and two outputs, enabling the use of measurements

from all the qubits, rather than just two, as in the quan-

tum actor in QA2C. The softmax activation function

is employed at the neural network output to generate

the probability distribution for the actor.

3.3.2 Hybrid Quantum Critic

Similarly, the hybrid critic model comprises a combi-

nation of a VQC and a post-processing neural network

layer, as depicted in Fig. 2b. The quantum circuit pro-

duces measurements that are subsequently used as in-

put for the neural network. The critic’s output is a sin-

gle value, the state function, which means the neural

network also has only one output. This setup allows

the use of measurements from all four qubits in the

VQC to estimate the state value, providing the neural

network with a comprehensive set of information to

process.

4 EXPERIMENTAL SETUP

This paper investigates the classical A2C algorithm

with two distinct implementations, each utilizing two

neural networks, as described in Section 3.1 on the

CartPole environment. The ﬁrst implementation em-

ploys four neurons in its hidden layer, while the sec-

ond uses ﬁve neurons. Additionally, we examine the

quantum versions of A2C, which includes two main

architectures: QA2C and HA2C, as explained in Sec-

tion 3.2 and Section 3.3, respectively. Finally, for

both architectures, we present three different actor-

critic implementations.

In the ﬁrst implementation, we replaced the neu-

ral network for the critic with a VQC in QA2C and a

VQC with post-processing in HA2C, while the actor

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

300

(a) Hybrid VQC used as hybrid actor (b) Hybrid VQC used as hybrid critic

Figure 2: Hybrid VQC-based hybrid actor and critic models.

remained a neural network. We refer to this as the Ad-

vantage Actor-Quantum-Critic (A2Q) algorithm. The

second implementation involved using a VQC for the

actor in QA2C and a VQC with post-processing in

HA2C, while the critic remained a neural network.

We refer to this as the Advantage Quantum-Actor-

Critic (Q2C) algorithm.

Finally, in the third implementation, we replaced

both the actor and critic neural networks with a VQC

in QA2C and a VQC with post-processing in HA2C.

We refer to this as the Advantage Quantum-Actor-

Quantum-Critic (Q2Q) algorithm.

The classical actor and critic in QA2C and HA2C

used a neural network with four and ﬁve neurons in

the hidden layer, respectively. Furthermore, in all

experiments, the QA2C and HA2C algorithms were

benchmarked against a classical A2C algorithm with

four and ﬁve neurons in its hidden layer, respectively.

Classical neural networks for actor and critic were

implemented using the popular deep learning library

PyTorch (Paszke et al., 2019), and we used Penny-

Lane, a widely-used quantum machine learning li-

brary, to implement VQCs. The experiments were

conducted on the compute cloud provided by Leibniz-

Rechenzentrum der Bayerischen Akademie der Wis-

senschaften (LRZ), which consists of one Intel(R)

Xeon(R) Platinum 8160 CPU.

4.1 Cart Pole

The OpenAI-provided Cart Pole environment is a

standard benchmark for RL algorithm performance

evaluation (Brockman et al., 2016). This environment

features a cart moving on a track with a hinged pole.

The agent’s goal is to prevent the pole from falling by

controlling the cart’s movement.

The Cart Pole environment is well-suited for test-

ing QRL algorithms due to its simplicity, the chal-

lenge of balancing the pole through a series of actions,

and a clear reward signal for easy algorithm evalua-

tion and comparison. It involves four state variables

representing the cart’s position and velocity, and the

pole’s angle and angular velocity (Gymlibrary, 2022).

The continuous nature of these state variables, which

can take any real value within a range, adds complex-

ity to the learning process.

In this RL setting, the agent aims to keep the pole

upright by moving the cart left or right. Rewards are

based on the duration the pole is balanced: positive re-

wards accumulate each timestep the pole remains up-

right. Failure occurs if the pole falls (exceeds ±12°) or

the cart strays too far from the center (beyond ±2.4),

ending the episode (Gymlibrary, 2022). Success is

achieved if the pole stays upright for 500 steps, mo-

tivating the RL agent to maximize pole balancing du-

ration.

4.2 Hyperparameters and Model Size

Hyperparameters, such as learning rates and discount

factors, play a crucial role in determining the per-

formance of RL algorithms (Henderson et al., 2017).

Therefore, we conducted a small-scale hyperparame-

ter tuning study to ﬁnd a suitable learning rate α and

discount factor γ for the classical A2C, QA2C, and

HA2C algorithms. Based on the results, we selected

a learning rate α = 1 × 10

−4

to be used in the Adam

optimizer and a discount factor γ = 0.99 for all algo-

rithms. All runs were executed on nodes with Intel(R)

Core(TM) i5-4570 CPU @ 3.20GHz.

Our proposed VQC for the QA2C and HA2C al-

gorithms is visualized in Fig. 1. The VQC employs

four qubits and two variational layers, with each layer

consisting of three single-qubit rotations, resulting in

a total of 24 quantum parameters to be optimized. To

ensure fair comparisons between the classical A2C

and the quantum algorithms, we implemented the

A2C algorithm with four and ﬁve neurons in the hid-

den layer.

5 RESULTS

The ﬁrst experiment aimed to compare the perfor-

mance of three versions of the QA2C algorithm with

the classical A2C algorithm, which had four neurons

in the hidden layer. All algorithms were trained on 10

runs, each consisting of 450,000 and 1,000,000 steps

Quantum Advantage Actor-Critic for Reinforcement Learning

301

in Fig. 3, respectively. The x-axis denotes the steps,

the y-axis shows the average reward obtained for all

runs in each step, and the shaded region represents

the standard deviation of the results.

The results revealed that none of the proposed

quantum architectures, namely A2Q, Q2C, and Q2Q,

could learn the Cart Pole environment across all

runs. In contrast, classical A2C demonstrated a stable

learning curve until a sudden drop at around 400,000

steps reaching a reward of 73. However, the reward

threshold for the Cart Pole environment is 475, which

the classical A2C’s average reward did not attain, in-

dicating its inability to solve the environment across

all runs.

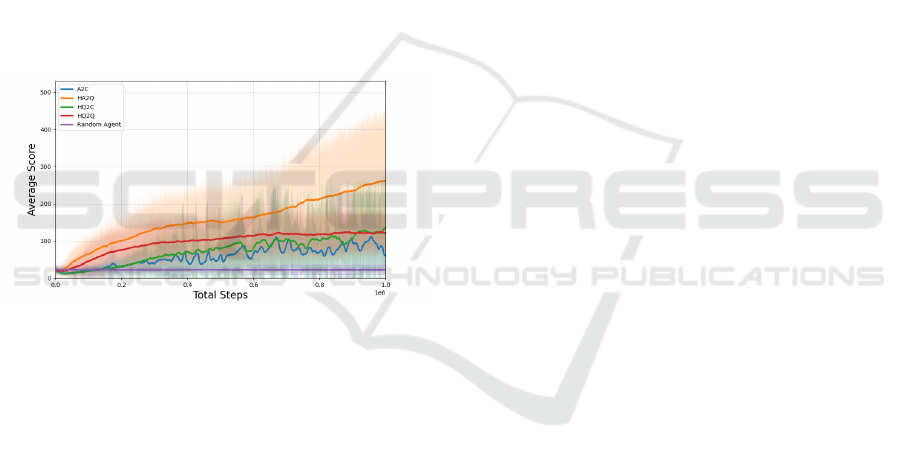
The goal of the second experiment was to improve

the architecture of the VQC by combining it with a

post-processing neural network in order to achieve

better results. Fig. 3 shows the performance of the

classical A2C with 5 neurons in the hidden layer and

the three versions of the HA2C algorithm: HA2Q,

HQ2C, and HQ2Q.

Figure 3: HA2C and classical A2C performance in Cart

Pole.

The aim was to train both algorithms on 10 runs,

each with 1,000,000 steps in the Cart Pole environ-

ment. In Fig. 3, we can see an evident success for

the HA2C algorithms over classical A2C, especially

in HA2Q and HQ2Q. The proposed hybrid architec-

ture learned the task in almost every run, while the

classical A2C succeeded in only 5 of the 10 runs.

Two additional VQCs with different single-qubit ro-

tations were also tested in a pre-study for the QA2C

and HA2C algorithms. However, the other QA2C al-

gorithms also failed to learn.

In conclusion, the experiments demonstrated that

the hybrid quantum-classical approach could achieve

better results than the classical A2C algorithm with

5 neurons in the hidden layer. Speciﬁcally, the HA2C

algorithms, HA2Q and HQ2Q, showed signiﬁcant im-

provement over the classical A2C algorithm, learning

the Cart Pole environment in almost every run. This

highlights the potential of combining quantum and

classical architectures to enhance the performance of

reinforcement learning algorithms.

However, it is essential to consider the signif-

icantly longer training time for the quantum algo-

rithms compared to the classical A2C algorithm. This

performance gap emphasizes the need for further re-

search and optimization of quantum algorithms to re-

duce training time and improve their applicability in

real-world scenarios.

Future work could involve exploring alternative

quantum architectures or optimization methods to en-

hance performance and reduce training time. Addi-

tionally, more complex environments and tasks could

be considered to further investigate the potential of

quantum-classical hybrid approaches in reinforce-

ment learning.

5.1 Discussion

After conducting experiments on the Cart Pole en-

vironment, it became evident that the pure quantum

A2C algorithm did not effectively learn the task. Af-

ter looking at the average gradients (−0.000056), we

concluded that this was caused by vanishing gradi-

ents. Both hybrid approaches, A2Q and Q2C suffer

from the same problem using the quantum actor and

quantum critic. Additionally, like with any machine

learning algorithm, the performance of VQCs can be

inﬂuenced by several factors, including hyperparame-

ter settings, circuit structure, and task complexity. To

improve the performance of the quantum algorithm,

future work could explore techniques such as circuit

ansatz design or gradient-free optimization to miti-

gate this issue (McClean et al., 2018; Chen et al.,

2022). In summary, the quantum approach did not

provide any signiﬁcant advantage over classical meth-

ods.

Building upon that, we employ VQCs with clas-

sical post-processing to circumvent barren plateaus.

This proved to be more effective in addressing the

challenges of the Cart Pole environment than the clas-

sical A2C algorithm, as the hybrid quantum A2C sub-

stantially outperforms the classical A2C in learning

the environment. The VQC uses a post-processing

neural network, which may be crucial for enabling

the VQC to learn. Notably, both HA2Q and HQ2C

started to learn the task immediately, while HQ2Q

learned at a slower rate.

These experiments were conducted on a quan-

tum simulator since current quantum hardware is not

widely available at the time of writing. This circum-

stance leads to signiﬁcantly higher training times for

all tested quantum approaches than the classical base-

line. Thus, without access to an actual quantum de-

vice, there is currently no real beneﬁt to the quantum

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

302

approaches. Even with exclusive access to real quan-

tum hardware, we can not say for certain if a quantum

parameter trains as fast as a classical one. It is es-

sential to recognize that the ﬁeld of quantum comput-

ing and quantum machine learning is still in its early

stages, with much research needed to gain a deeper

understanding of the capabilities and limitations of

VQCs in machine learning. As such, further explo-

ration is necessary to unlock the full potential of this

emerging technology.

6 CONCLUSION

We investigated how quantum computing techniques

could enhance the performance of the A2C algorithm.

To achieve this goal, we conducted experiments and

compared the performance of three variations of the

A2C algorithm: classical, quantum, and hybrid A2C.

In each variation, we replaced either the actor, critic,

or both with a quantum circuit, leading to a total of

three different conﬁgurations. By testing these con-

ﬁgurations, we aimed to understand the impact of

each variation on the algorithm’s overall performance.

Furthermore, ensuring a fair comparison between the

algorithms was a signiﬁcant challenge in this study.

Therefore, to maintain fairness, we kept the number

of parameters in the algorithms roughly equal.

Our results show that the classical A2C outper-

forms the pure quantum A2C. To improve the quan-

tum A2C performance, we introduced a hybrid ap-

proach integrating a VQC with a post-processing neu-

ral network layer. We tested three conﬁgurations of

the hybrid algorithm and found that it substantially

outperformed both the quantum and classical coun-

terparts. This paper contributes to the growing body

of evidence highlighting the potential of combining

quantum computing and classical machine learning

algorithms to improve reinforcement learning tasks’

performance.

Future research in RL and QRL is essential, par-

ticularly in hyperparameter tuning, which is vital for

optimizing performance. Exploring various VQC

architectures, including data re-uploading, not used

in our current models, could enhance performance

erez-Salinas et al., 2020). Investigating different

encoding strategies like amplitude encoding (Schuld

and Petruccione, 2018), and employing techniques

like weight re-mapping (K

olle et al., 2023) could im-

prove convergence.

ACKNOWLEDGEMENTS

This research is part of the Munich Quantum Valley,

which is supported by the Bavarian state government

with funds from the Hightech Agenda Bayern Plus.

REFERENCES

Agarap, A. F. (2018). Deep learning using rectiﬁed linear

units (relu). arXiv preprint arXiv:1803.08375.

Andrychowicz, M., Raichuk, A., Sta

nczyk, P., Orsini, M.,

Girgin, S., Marinier, R., Hussenot, L., Geist, M.,

Pietquin, O., Michalski, M., et al. (2021). What mat-

ters for on-policy deep actor-critic methods? a large-

scale study. In International conference on learning

representations.

Bauer, B., Bravyi, S., Motta, M., and Chan, G. K.-L.

(2020). Quantum Algorithms for Quantum Chemistry

and Quantum Materials Science. Chemical Reviews,

120(22):12685–12717. Publisher: American Chemi-

cal Society.

Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe,

N., and Lloyd, S. (2017). Quantum machine learning.

Nature, 549(7671):195–202.

Bridle, J. S. (1990). Probabilistic interpretation of feed-

forward classiﬁcation network outputs, with relation-

ships to statistical pattern recognition. In Souli

e, F. F.

and H

erault, J., editors, Neurocomputing, pages 227–

236, Berlin, Heidelberg. Springer Berlin Heidelberg.

Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,

Schulman, J., Tang, J., and Zaremba, W. (2016). Ope-

nai gym. arXiv preprint arXiv:1606.01540.

Cao, Y., Romero, J., Olson, J. P., Degroote, M., Johnson,

P. D., Kieferov

a, M., Kivlichan, I. D., Menke, T.,

Peropadre, B., Sawaya, N. P. D., Sim, S., Veis, L.,

and Aspuru-Guzik, A. (2019). Quantum chemistry in

the age of quantum computing. Chemical Reviews,

119(19):10856–10915.

Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C.,

Endo, S., Fujii, K., McClean, J. R., Mitarai, K., Yuan,

X., Cincio, L., and Coles, P. J. (2020). Variational

quantum algorithms. Nature Reviews Physics, 3:625

– 644.

Chen, S. Y.-C. (2023). Asynchronous training of quantum

reinforcement learning.

Chen, S. Y.-C., Huang, C.-M., Hsing, C.-W., Goan, H.-S.,

and Kao, Y.-J. (2022). Variational quantum reinforce-

ment learning via evolutionary optimization. Machine

Learning: Science and Technology, 3(1):015025.

Chen, S. Y.-C., Huang, C.-M., Hsing, C.-W., and Kao, Y.-

J. (2021). An end-to-end trainable hybrid classical-

quantum classiﬁer. Machine Learning: Science and

Technology, 2(4):045021.

Chen, S. Y.-C., Yang, C.-H. H., Qi, J., Chen, P.-Y., Ma, X.,

and Goan, H.-S. (2019). Variational quantum circuits

for deep reinforcement learning.

Quantum Advantage Actor-Critic for Reinforcement Learning

303

Dral, P. O. (2020). Quantum Chemistry in the Age of

Machine Learning. The Journal of Physical Chem-

istry Letters, 11(6):2336–2347. Publisher: American

Chemical Society.

Farhi, E., Goldstone, J., and Gutmann, S. (2014).

A Quantum Approximate Optimization Algorithm.

arXiv:1411.4028 [quant-ph]. arXiv: 1411.4028.

Farhi, E. and Harrow, A. W. (2016). Quantum supremacy

through the quantum approximate optimization algo-

rithm.

Gymlibrary, F. F. (2022). Cart pole - gym documentation.

Heimann, D., Hohenfeld, H., Wiebe, F., and Kirchner, F.

(2022). Quantum deep reinforcement learning for

robot navigation tasks.

Henderson, P., Islam, R., Bachman, P., Pineau, J., Precup,

D., and Meger, D. (2017). Deep reinforcement learn-

ing that matters.

Hsiao, J.-Y., Du, Y., Chiang, W.-Y., Hsieh, M.-H., and

Goan, H.-S. (2022). Unentangled quantum reinforce-

ment learning agents in the openai gym.

Jerbi, S., Cornelissen, A., Ozols, M., and Dunjko, V. (2022).

Quantum policy gradient algorithms.

Jerbi, S., Gyurik, C., Marshall, S. C., Briegel, H. J., and

Dunjko, V. (2021). Parametrized quantum policies for

reinforcement learning.

Kingma, D. P. and Ba, J. (2014). Adam: A method for

stochastic optimization.

Kober, J., Bagnell, J. A., and Peters, J. (2013). Reinforce-

ment learning in robotics: A survey. The International

Journal of Robotics Research, 32(11):1238–1274.

Konda, V. and Tsitsiklis, J. (1999). Actor-critic algo-

rithms. In Solla, S., Leen, T., and M

uller, K., editors,

Advances in Neural Information Processing Systems,

volume 12. MIT Press.

Kwak, Y., Yun, W. J., Jung, S., Kim, J.-K., and Kim, J.

(2021). Introduction to quantum reinforcement learn-

ing: Theory and pennylane-based implementation.

olle, M., Giovagnoli, A., Stein, J., Mansky, M. B., Hager,

J., and Linnhoff-Popien, C. (2023). Improving conver-

gence for quantum variational classiﬁers using weight

re-mapping.

Lan, Q. (2021). Variational quantum soft actor-critic.

Lockwood, O. and Si, M. (2020). Reinforcement learning

with quantum variational circuits.

Mari, A., Bromley, T. R., Izaac, J., Schuld, M., and Killo-

ran, N. (2020). Transfer learning in hybrid classical-

quantum neural networks. Quantum, 4:340.

McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush,

R., and Neven, H. (2018). Barren plateaus in quantum

neural network training landscapes. Nature Commu-

nications, 9(1).

Meyer, N., Scherer, D. D., Plinge, A., Mutschler, C., and

Hartmann, M. J. (2022a). Quantum policy gradient

algorithm with optimized action decoding.

Meyer, N., Ufrecht, C., Periyasamy, M., Scherer, D. D.,

Plinge, A., and Mutschler, C. (2022b). A survey on

quantum reinforcement learning.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Harley,

T., Lillicrap, T. P., Silver, D., and Kavukcuoglu,

K. (2016). Asynchronous methods for deep rein-

forcement learning. In Proceedings of the 33rd In-

ternational Conference on International Conference

on Machine Learning - Volume 48, ICML’16, page

1928–1937. JMLR.org.

Nielsen, M. and Chuang, I. (2010). Quantum Computation

and Quantum Information: 10th Anniversary Edition.

Cambridge University Press.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).

Pytorch: An imperative style, high-performance deep

learning library. In Advances in Neural Information

Processing Systems 32, pages 8024–8035. Curran As-

sociates, Inc.

erez-Salinas, A., Cervera-Lierta, A., Gil-Fuster, E., and

Latorre, J. I. (2020). Data re-uploading for a universal

quantum classiﬁer. Quantum, 4:226.

Pirandola, S., Andersen, U. L., Banchi, L., Berta, M.,

Bunandar, D., Colbeck, R., Englund, D., Gehring, T.,

Lupo, C., Ottaviani, C., Pereira, J. L., Razavi, M.,

Shaari, J. S., Tomamichel, M., Usenko, V. C., Vallone,

G., Villoresi, P., and Wallden, P. (2020). Advances in

quantum cryptography. Advances in Optics and Pho-

tonics, 12(4):1012.

Preskill, J. (2018). Quantum computing in the NISQ era

and beyond. Quantum, 2:79.

Schuld, M. and Petruccione, F. (2018). Supervised Learn-

ing with Quantum Computers. Springer Publishing

Company, Incorporated, 1st edition.

Sequeira, A., Santos, L. P., and Barbosa, L. S. (2022). Pol-

icy gradients using variational quantum circuits.

Shor, P. W. (1997). Polynomial-time algorithms for prime

factorization and discrete logarithms on a quantum

computer. SIAM Journal on Computing, 26(5):1484–

1509.

Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou,

I., Huang, A., Guez, A., Hubert, T., Baker,

L., Lai, M., Bolton, A., Chen, Y., Lillicrap,

T., Hui, F., Sifre, L., van den Driessche, G.,

Graepel, T., and Hassabis, D. (2017). Mas-

tering the game of Go without human knowl-

edge. Nature, 550(7676):354–359. Bandiera abtest:

a Cg type: Nature Research Journals Number:

7676 Primary atype: Research Publisher: Na-

ture Publishing Group Subject term: Computational

science;Computer science;Reward Subject term id:

computational-science;computer-science;reward.

Skolik, A., Jerbi, S., and Dunjko, V. (2022). Quantum

agents in the gym: a variational quantum algorithm

for deep q-learning. Quantum, 6:720.

You, Y., Pan, X., Wang, Z., and Lu, C. (2017). Virtual to

real reinforcement learning for autonomous driving.

CoRR, abs/1704.03952.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

304