Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using

Variable Subsampling and Randomized Measurements

Michael K

olle

, Afrae Ahouzi

1,2

, Pascal Debus

, Robert M

uller

, Dani

elle Schuman

and Claudia Linnhoff-Popien

Institute of Informatics, LMU Munich, Munich, Germany

Fraunhofer AISEC, Garching, Germany

ﬁ

Keywords:

Quantum Machine Learning, Anomaly Detection, OC-SVM.

Abstract:

Quantum computing, with its potential to enhance various machine learning tasks, allows signiﬁcant advance-

ments in kernel calculation and model precision. Utilizing the one-class Support Vector Machine alongside a

quantum kernel, known for its classically challenging representational capacity, notable improvements in aver-

age precision compared to classical counterparts were observed in previous studies. Conventional calculations

of these kernels, however, present a quadratic time complexity concerning data size, posing challenges in prac-

tical applications. To mitigate this, we explore two distinct approaches: utilizing randomized measurements to

evaluate the quantum kernel and implementing the variable subsampling ensemble method, both targeting lin-

ear time complexity. Experimental results demonstrate a substantial reduction in training and inference times

by up to 95% and 25% respectively, employing these methods. Although unstable, the average precision of

randomized measurements discernibly surpasses that of the classical Radial Basis Function kernel, suggesting

a promising direction for further research in scalable, efﬁcient quantum computing applications in machine

learning.

1 INTRODUCTION

In the prevailing digital landscape, anomaly detection

algorithms safeguard numerous systems by identify-

ing irregularities, such as unauthorized intrusion into

a network, unexpected machinery behavior, or abnor-

mal medical readings (Fernando et al., 2021; Boloka

et al., 2021). In e-commerce, these algorithms are

pivotal in protecting both customers and companies

from fraudulent transactions, which could precipitate

substantial ﬁnancial losses (ECB, 2023). Anomaly

detection faces challenges, including the diverse and

rarely similar nature of anomalies, and often encoun-

ters high-dimensional, correlated, and sometimes un-

labeled data sets.

Quantum Machine Learning (QML), a synthe-

sis of machine learning and quantum computing,

promises potential solutions to some of these chal-

lenges by leveraging the capability of quantum al-

gorithms to compute classically challenging kernels

(Havl

cek et al., 2019). Some initiatives have aimed

at ameliorating existing anomaly detection methods

with quantum methods. A notable attempt (Kyriienko

and Magnusson, 2022) achieved a 20% elevation in

average precision using one-class support vector ma-

chine models with a quantum kernel, though con-

fronted quadratic scaling challenges with data size,

impacting both training and testing times.

Addressing the aforementioned time complexity

challenge, this work replicates the results from (Kyri-

ienko and Magnusson, 2022) and employs them as

benchmarks to explore the efﬁcacy of two linear time

complexity methods based on data size: randomized

measurements for quantum kernel measurement and

an ensemble method termed variable subsampling.

The focus rests on two pivotal questions:

1. Can the quantum kernel extract superior informa-

tion from the data compared to the classical Ra-

dial Basis Function kernel, and thereby offer over-

all enhanced results?

2. Do randomized measurements and variable sub-

sampling models maintain the performance of the

quantum kernel derived through the inversion test,

while diminishing the time complexity related to

data size?

The evaluation engages synthetic data and the Credit

Card Fraud data set, inspecting performance and time

324

Kölle, M., Ahouzi, A., Debus, P., Müller, R., Schuman, D. and Linnhoff-Popien, C.

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements.

DOI: 10.5220/0012381200003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 2, pages 324-335

ISBN: 978-989-758-680-4; ISSN: 2184-433X

Input space

b −w ·Φ(x

)b −w ·Φ(x

)

Separating hyperplaneSeparating hyperplane

AnomalousAnomalous

NormalNormal

Feature space

′

Feature Map

Figure 1: The linearly inseparable points on the input space

are mapped using a quantum feature Φ into a feature space

where they are linearly separable (Aggarwal, 2017).

complexities contingent on data size and qubit num-

ber. Our ﬁndings, diverging from (Kyriienko and

Magnusson, 2022), reveal that while attainable im-

provements in average precision and F1 score over

the classical kernel are discernible, they are min-

imally signiﬁcant. Models utilizing variable sub-

sampling with the inversion test exhibited stability,

whereas those employing the randomized measure-

ment method presented high variance. Nevertheless,

variable subsampling did manifest considerable en-

hancements in training and testing times, indicating

potential performance elevation opportunities through

alternate hyperparameters. All Code and Experiments

can be found here

2 PRELIMINARIES

2.1 One-Class Support Vector Machines

The One-Class Support Vector Machine (OC-SVM),

originally presented by (Sch

olkopf et al., 1999), of-

fers an unsupervised variant of the SVM for anomaly

and novelty detection. Differing from the conven-

tional SVM, which ﬁnds a maximum margin hyper-

plane to distinguish normal from anomalous data, the

OC-SVM presupposes that the origin represents the

anomalous class when labels are absent. It seeks to

maximize the margin b between origin and the input

data, penalizing points below the hyperplane (Fig. 1).

These are governed by a hyperparameter ν ∈ (0, 1]

which dictates the portion of points categorized as

anomalous.

min

w,b

νN

∑

i=1

max{b −w ·Φ(x

), 0}−b (1)

https://github.com/AfraeA/q-anomaly

To address non-linearly separable data, feature

maps Φ : X → F elevate data from input space X to

a higher dimensional feature space F . Since direct

calculations of feature maps are computationally in-

tensive, a kernel function k : X ×X → R is used to

ascertain data point similarity in the embedded fea-

ture space.

k(x

, x

) = ⟨Φ(x

), Φ(x

)⟩ (2)

The use of the kernel function, which can be

summed up in matrix form by the kernel matrix

G = [k(x

, x

)], facilitates a dual problem formulation.

Solving this dual problem leads to an implicit parame-

terization of the hyperplane based on the support vec-

tors α

Relying on this parameterization, scoring new

data depends on its relation to the separating hyper-

plane:

Score(x

new

) =

∑

i=1

·k(x

new

, x

) (3)

The label is determined by the score’s sign: neg-

ative connoting an anomaly and positive signifying

normalcy.

2.2 Quantum Kernel Embedding

Quantum feature maps allow for the embedding of

classical data into quantum states within Hilbert space

H through the use of data-dependent quantum unitary

gates U

(x), mathematically expressed as

Φ(x)

⟩

(x)

⟩

. The IQP-like (Instantaneous Quantum

Polynomial) feature map, recognized for being hard

to simulate classically (Havl

cek et al., 2019), en-

codes a d-dimensional input x

into d qubits as fol-

lows:

Φ(x

)

⟩

= U

⊗d



) = exp

∑

j=1

λx

i j

∑

j=1

∑

′

i j

′

(4)

where λ, inﬂuenced by data reuploading counts, im-

pacts the kernel bandwidth analogously to γ (Shay-

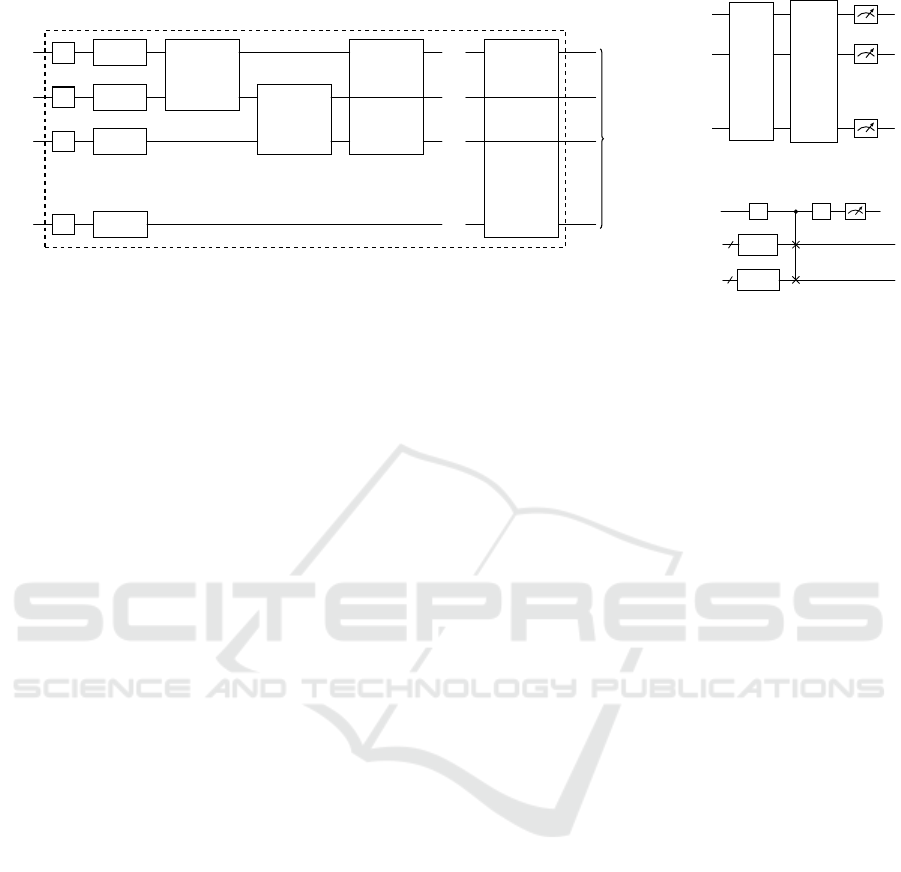
dulin and Wild, 2022). We refer to FigureFig. 2a for a

visual representation. Upon data encoding, ﬁdelity,

distilled to the overlap of states for pure quantum

states as F(x, x

′

) = |

⟨

Φ(x

′

)

Φ(x)

⟩

, quantiﬁes data

similarity.

Two prominent methods for measuring ﬁdelity are

the inversion and swap tests. The inversion test, de-

tailed in FigureFig. 2b, calculates the overlap of two

data points’ pure quantum states with O(n

) kernel

evaluations, but necessitates unitary feature maps and

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements

325

yields deeper circuits. Conversely, the swap test, de-

picted in FigureFig. 2c, is applicable to both pure and

mixed states but necessitates wider circuits. It is based

on the swap trick (Hubregtsen et al., 2022), which de-

duces the inner product from the tensor product of

density matrices ρ

and ρ

utilizing a swap gate S,

expressed in Eq. 5:

Tr(ρ

) = Tr(Sρ

⊗ρ

). (5)

2.3 Time Complexity for Quantum

Kernels

Quantum one-class Support Vector Machines provide

a nuanced method for detection but are hindered by

formidable time complexity, particularly given the ex-

isting operational frequencies of quantum hardware.

The intrinsic quadratic time complexity of one-class

SVMs is signiﬁcantly ampliﬁed in a quantum com-

puting context, requiring a substantial number of rep-

etitions (shots) to accurately measure ﬁdelity between

points due to its probabilistic nature; typically, at

least 1000 shots per circuit measurement are neces-

sary to obtain replicable results. Training a quantum

one-class SVM on a large dataset, exempliﬁed by the

284,000 instances from the Credit Card dataset in our

experiments, would theoretically necessitate approxi-

mately 4 ×10

kernel function value calculations to

construct the symmetrical kernel matrix. This implies

a staggering requirement of 4 × 10

shots, which,

with a measurement rate of 5kHz (Haug et al., 2021),

equates to a minimum training time of 255 years us-

ing a swap or inversion test kernel.

Reducing the dataset may abbreviate training time

but risks degrading algorithmic performance and sta-

bility due to decreased representativity of training

samples. This diminution can result in less depend-

able support vectors and decision functions, jeopar-

dizing the reliability and consistency of the one-class

SVM, especially when training data substantially de-

viates from the overall distribution. The challenge

also permeates inference times, as predicting a new

point demands evaluating the kernel function against

all training points, elongating detection times and hin-

dering real-time applications like patient monitoring

and fraud prevention.

To surmount these obstacles, optimization of ker-

nel calculation algorithms and investigation into in-

novative quantum measurement techniques, which

could minimize the requisite shots, are pivotal. Viable

approaches may encompass adapting classical meth-

ods to minimize data needed for kernel matrix com-

putations while preserving performance, employing

clustering, and applying matrix decomposition and

approximation methods to avoid evaluating the kernel

across the entire training set.

3 RELATED WORK

3.1 Quantum Anomaly Detection

This work augments the methodology propounded in

(Kyriienko and Magnusson, 2022), amalgamating the

one-class SVM with a computationally intricate ker-

nel based on the IQP feature map (FigureFig. 2a) to

secure a 20% enhancement in average precision vis-

a-vis their classical benchmark. Subsequent exper-

iments herein adhere to this protocol as a quantum

yardstick, exploring two strategies to diminish the

time complexity relative to data size.

Hybrid quantum-classical models manifest as a

prominent archetype in anomaly detection research.

For instance, (Sakhnenko et al., 2022) innovatively

reﬁnes the auto-encoder (AE) hidden representation

by interfacing a parameterized quantum circuit (PQC)

with its bottleneck, segueing into an unsupervised

model post-training by substituting the decoder with

an isolation forest, and vetting performance across

multifarious data sets and PQC architectures. Concur-

rently, (Herr et al., 2021) pioneers an adaptation of the

classical AnoGAN (Schlegl et al., 2017) by deploying

a Wasserstein GAN, wherein the generator is substi-

tuted with a hybrid quantum-classical neural network,

and subsequently trained via a variational algorithm.

Contrastingly, quantum annealing approaches,

such as the QUBO-SVM presented in (Wang

et al., 2022), reformulate the conventional SVM

optimization predicament into a quadratic uncon-

strained binary optimization problem (QUBO) which

is amenable to resolution via quantum annealing

solvers. Although retaining the conventional SVM

optimization problem, this methodology expedites

accurate predictions through adept kernel function

identiﬁcation, thereby facilitating plausible real-time

anomaly detection.

(Ray et al., 2022) explores hybrid ensembles, con-

structing an amalgamation of bagging and stacking

ensembles from assorted quantum and classical com-

ponents, each playing a pivotal role in the anomaly

detection framework. The amalgamated quantum

components encapsulate disparate variable quan-

tum circuit architectures, kernel-based, and quan-

tum annealing-based SVMs, while the classical con-

stituents encompass logistic regression, graph convo-

lutional neural networks, and light gradient boosting

models. Despite superﬁcial similarity to the variable

subsampling utilized herein, it’s noteworthy that the

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

326

⟩

. . .

⟩

. . .

⟩

. . .

⟩

. . .

)

(x)

⟩

)

×2λ

(a) IQP-like feature map

⟩

(x)

†

′

)

(b) Inversion test circuit

⟩

⊗d

⟩

⊗d

H H

(x)

′

)

Figure 2: Quantum circuits for IQP-like feature map, inversion test and swap test.

latter method’s adoption of varying sub-sample sizes

uniquely addresses the OC-SVM’s parameterization

dependence.

3.2 Efﬁcient Gram Matrix Evaluation

Quantum kernel methods, pivotal for various quan-

tum machine learning applications, grapple with no-

table computational demands in matrix evaluations.

Approaches to mitigate this complexity are: (i)

Quantum-Friendly Classical Methods, reducing ker-

nel matrix elements to evaluate, and (ii) Quantum Na-

tive Methods, minimizing the shot requirements yet

necessitating classical post-processing, albeit feasibly

parallelizable or vectorizable.

Randomized measurement kernels, pioneered by

(Haug et al., 2021) and utilized with hardware-

efﬁcient feature maps, achieved an expedited ker-

nel measurement while approximating Radial Basis

Function (RBF) kernels, demonstrated via both syn-

thetic and MNIST data. Conversely, the classical

shadow method, proposed by (Huang et al., 2020),

employs a similar quantum protocol but diverges in

classical post-processing to provide classical state

snapshots via the inversion of a quantum channel, of-

ten attaining reduced error in predicting second R

enyi

Entropy.

Variable subsampling, introduced by (Aggarwal

and Sathe, 2015), and its sophisticated counterpart,

variable subsampling with rotated bagging, offer an

efﬁcient ensemble training approach, leveraging var-

ied sample sizes and rotational orthogonal axis system

projections respectively. These methods not only con-

fer computational efﬁciency but also harness an adap-

tive ensemble model training strategy, tested efﬁca-

ciously with algorithms like local outlier factor (LOF)

models and the k-Nearest Neighbors algorithm.

The Distance-based Importance Sampling and

Clustering (DISC) approach, by (Hajibabaee et al.,

2021), and Block Basis Factorization, by (Wang

et al., 2019), represent variants of matrix decomposi-

tion based methods for kernel approximation. While

DISC employs cluster centroids as landmarks to for-

mulate approximation matrices and assumes kernel

matrix symmetry, block basis factorization avails ran-

domized spectral value decomposition on cluster sam-

ples and creates a smaller, computationally tractable

inner similarity matrix, demonstrating superior per-

formance relative to the k-means Nystr

om method.

4 APPROACHES

In the preceding review of related work, several

methodologies of efﬁcient gram matrix evaluation

were highlighted. However, moving forward, we will

focus on two speciﬁc approaches which can be ap-

plied to both symmetric training kernel matrices and

asymmetric ones used during prediction. Although

the classical shadows and block basis factorization

methods satisfy this criterion, we have decided to

explore randomized measurements and variable sub-

sampling methods because of their intuitive concep-

tual frameworks.

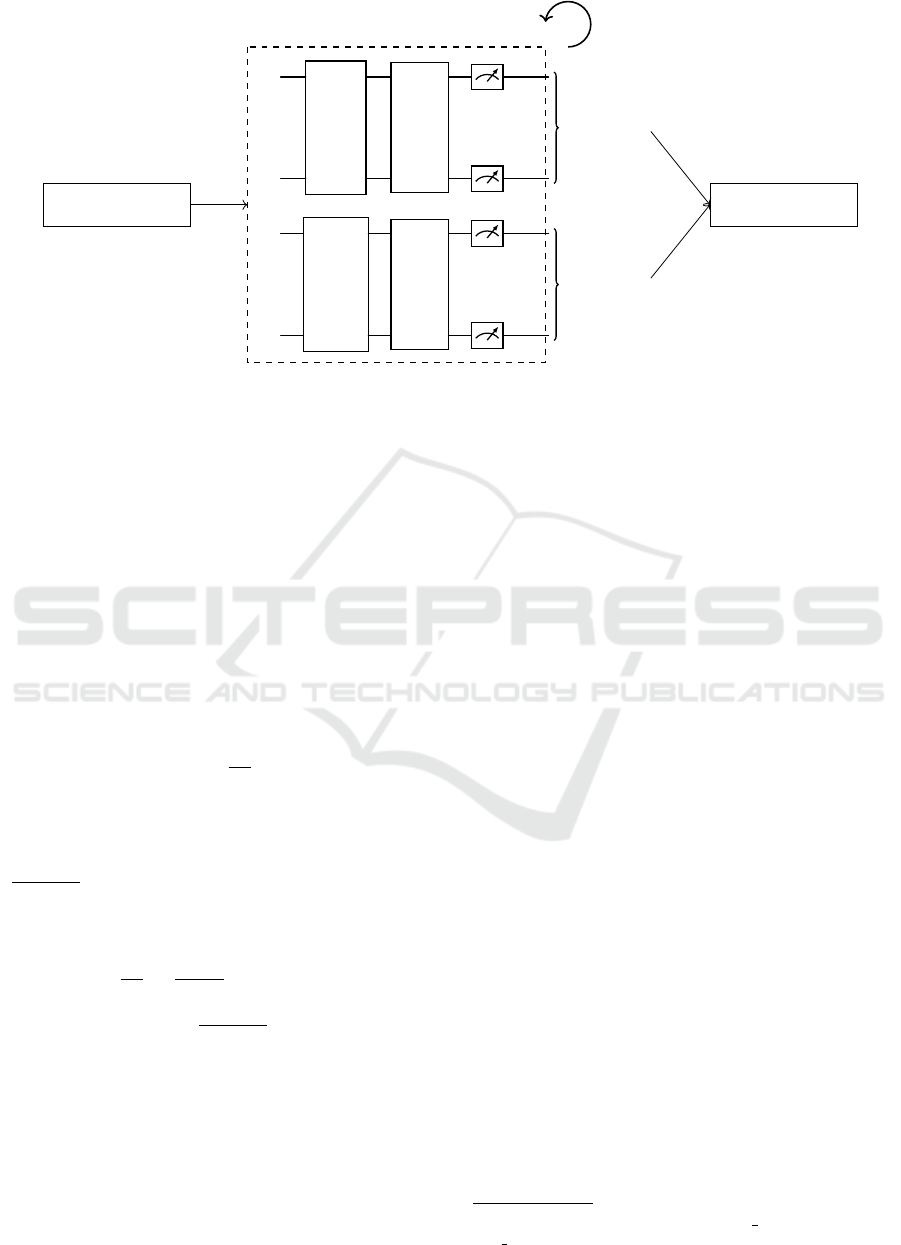
4.1 Randomized Measurements Kernel

Expanding upon the method of randomized measure-

ments, suggested for future exploration in (Kyriienko

and Magnusson, 2022), and practically employed in

kernel calculation for classiﬁcation by (Haug et al.,

2021), this method endeavors to adeptly meld linear

and quadratic complexities concerning data size. This

is achieved respectively through acquiring measure-

ments of feature maps and subsequent classical post-

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements

327

processing. The method notably diminishes the req-

uisite quantum shots, thereby alleviating the overall

computational burden.

The inception of the ﬁdelity calculation was mo-

tivated by the possibility of conceiving the swap op-

erator S as a quantum twirling channel Φ

(2)

(Elben

et al., 2019). Quantum twirling channels are opera-

tions commonly used in error correction. A 2-fold lo-

cal quantum twirling channel applied to an arbitrary

operator O is articulated by

(2)

(O) = (U

⊗2

)

†

⊗2

, (6)

with . . . denoting the average over the unitaries U =

and U

sampled from a unitary 2-design. A

unitary t-design approximates property averages over

all possible unitaries using a ﬁnite set, while the

Haar measure provides a uniform sampling mecha-

nism across unitary matrices. (Elben et al., 2019)

demonstrate that the expectation value of applying

such a twirling channel on an operator O acting on

two copies of a quantum state ρ is obtainable from

the probability products P

resulting from the mea-

surements:

∑

s,s

′

s,s

′

(s)P

′

) = Tr



(2)

(O) ρ ⊗ρ



(7)

The coefﬁcients O

s,s

′

speciﬁc to the swap operator are

derived by employing Weingarten calculus of Haar

random unitaries and Schur-Weyl duality (Roberts

and Yoshida, 2017) to calculate the purity of the state

ρ, yielding:

s,s

′

= d

(−d)

(

s,s

′

)

. (8)

A formula for quantum ﬁdelities in terms of random-

ized measurement probabilities is obtained by utiliz-

ing the swap trick, then employing Eq. 6 with the co-

efﬁcients from Eq. 7.

Local Haar random unitaries U

Haar

are constructed

by tensoring sampled unitary U

∈ SU (2) for each

qubit. As illustrated in Fig. 3, each quantum circuit

leverages a unitary U

, corresponding to the quantum

feature map, and one of the r different local Haar ran-

dom unitaries U

Haar

. Every circuit requires s different

shots. This yields r sets of strings s

and their mea-

surement probabilities P

(i)

) for the different ran-

dom basis rotations U

Haar

. Post-processing harnesses

the formula:

K(x

, x

) = Tr(ρ

)

= 2

∑

′

(−2)

−D(s

′

)

(i)

( j)

′

)

(9)

The statistical error in ﬁdelity measurement, quan-

tiﬁed as ∆G ≈

√

, necessitates error mitigation, par-

ticularly pertinent in noisy hardware scenarios. A fa-

cilitative aspect of the randomized measurements ap-

proach is its provision for straightforward error mit-

igation, involving purities calculated and recorded in

the diagonal of the training kernel matrix and exploit-

ing a minor computational overhead in the testing

phase for the asymmetrical kernel matrix.

The quantum kernel calculation segment, employ-

ing randomized measurements, presents a time com-

plexity of nrs (n: data size, r: basis rotation unitaries,

s: shots per rotation), while classical post-processing

demands n

complexity, albeit with an unfavorable

exponential time complexity concerning the number

of qubits (features). Implementation aligning with

(Haug et al., 2021) is accessible via the Large Scale

QML

GitHub repository, whereas randomized mea-

surement processing and combination utilize func-

tionalities from the qc optim

repository. Accommo-

dating the IQP-like feature map and enabling interim

kernel copy retention and calculation time-keeping

mandated the development of a novel implementa-

tion.

4.2 Variable Subsampling

Introduced by (Aggarwal, 2017), variable subsam-

pling addresses sensitivities in the one-class SVM to

kernel choice and hyperparameter ν values by exploit-

ing ensemble methods. Unlike bagging ensembles,

variable sampling ensembles, while utilizing random

subset selection for model training, employ varying

sub-sample sizes, permitting sampling over parame-

ter spaces, particularly those related to data size, like

the expected anomaly ratio ν in the one-class SVM.

Supposing a variable subsampling ensemble com-

prises 3 OC-SVMs trained with ν = 0.1 and sample

sizes of 53, 104, and 230, differing support vector

lower bounds among components yield varied deci-

sion boundaries. These can subsequently be com-

bined in a manner that diminishes the bias or variance

in predictions.

Ensemble construction commences with uni-

formly sampling c different subsample sizes between

50 and 1000. Data subsets, corresponding to sam-

pled sizes, are randomly selected from the dataset

and employed to train base model versions, here,

the quantum one-class SVM with inversion test. Al-

though subsamples may contain identical elements,

each avoids reusing data points to better reduce vari-

ance. Predictions are calculated by combining nor-

malized (to zero mean and unit standard deviation)

decision functions of all components, considering

https://github.com/chris-n-self/large-scale-qml

https://github.com/chris-n-self/qc optim

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

328

Sample r random

Haar unitaries U

Haar

⟩

(x)

Haar

, P

)

′

)

Haar

′

, P

′

)

Classical Postpro-

cessing using Eq. 9

Repeat measurement for r Haar

random unitaries, each for s shots

Figure 3: The protocol and the circuit architecture for calculating quantum kernel functions using randomized measurement.

each is trained with distinct data sizes, thus possessing

varied decision function value ranges (Aggarwal and

Sathe, 2015). Simple averaging of outlier scores is ad-

vantageous for reducing variance and superior perfor-

mance with smaller datasets. Applying the maximum

score, conversely, curtails bias but elevates variance.

Post decision function value extraction, the threshold

function sgn(.) derives the class label.

More components and a higher maximum sub-

sample size facilitate optimal variance reduction, at

the expense of increased computational resource and

time demands. However, this trade-off can be man-

aged through wise hyperparameter selection. For ex-

ample, we choose a maximum subsample size of 100,

instead of the recommended 1000 points from the

original research, and use ⌊

100

⌋ components instead

of 100. While this may negatively affect performance,

it provides insight into the ensemble’s behavior when

scalability takes precedence.

The training phase exhibits approximately c ·

(

min

max

)

time complexity, where c is the number

of ensemble components, and n

min

= 50 and n

max

100 are the minimum and maximum subsample sizes

respectively. Incorporating scalability modiﬁcations,

this becomes ⌊

100

⌋·



50+100



, indicating linear com-

plexity. Testing similarly maintains linear time com-

plexity, formulated as c·

min

max

·n

test

, with n

test

rep-

resenting test samples.

5 EXPERIMENTAL SETUP

Ensuring the reproducibility of our experiments, this

section meticulously delineates implementation as-

pects, encompassing pre-processing, various kernel

calculation methodologies, and hyperparameter se-

lection. Two distinct experiment sets facilitate the

comparative analysis of our approaches:

1. The ﬁrst set aspires to examine performance,

training, and testing durations with respect to data

size. Primarily, it endeavors to contrast the com-

putational efﬁciencies afforded by our methodolo-

gies, delineated in Section 4, and to comprehend

model responses to elevated data volumes.

2. Focusing on the relationship between perfor-

mance, computational time, and the number of

features (or qubits), the second experiment set

seeks not only to discern whether the methods im-

pose detrimental effects on performance but also

to elucidate the time feature/qubit relationship.

Experiments are conducted using 15 distinct

seeds, ranging from 0 to 14.

5.1 Datasets

Our experiments utilize two datasets, distinguished by

their synthetic or real-world origin, to investigate vari-

ous methodologies. The synthetic dataset is employed

exclusively in the ﬁrst experiment set, given its two-

dimensional nature and the associated limitations in

exploring numerous features.

5.1.1 Synthetic Data

Our synthetic dataset is a bi-dimensional, non-

linearly separable dataset, derived by modifying an

SKlearn OC-SVM demonstration

to yield training

samples of diverse sizes. Testing samples consistently

https://scikit-learn.org/stable/auto examples/svm/

plot oneclass.html

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements

329

comprise 125 points, incorporating a 0.3 anomaly ra-

tio.

5.1.2 Credit Card Fraud Data

The credit card fraud data

encompasses approxi-

mately 284,000 datapoints, with 492 classiﬁed as

anomalous (class 1), across 31 features. Omitting

’time’ and ’amount’, 28 PCA-applied, anonymized

numerical features are retained. Each seed corre-

sponds to a unique data split. The size varies for

the set of experiments exploring the effects of data

size, while it is kept at a constant 500 data samples

for the set of experiments exploring the effects of

the qubit/feature number. Training data only contains

non-anomaly samples while the test set always con-

tains 125 points, which include 6 anomalies, achiev-

ing a 0.05 anomaly ratio.

5.2 Data Pre-Processing

Distinctive pre-processing methodologies were ne-

cessitated based on the quantum kernel measurement

technique applied and the data type (synthetic or real).

Radial Basis Function (RBF) Kernel. For imple-

mentations utilizing the RBF kernel, standard scaling

was executed post data partitioning into training and

test subsets, ensuring zero mean and unit standard de-

viation across all features. Subsequently, Principal

Component Analysis (PCA) was employed to consol-

idate the data into the requisite number of features.

Inversion Test Kernels. The application of inver-

sion test kernels warranted an additional step follow-

ing the pre-processing used for the RBF kernel. Given

that data was utilized as rotation angles within the

quantum circuit, a scaling by a factor of 0.1 was an

imperative post-PCA application.

Randomized Measurements Kernels. Adhering

to guidelines by (Haug et al., 2021), the randomized

measurements kernels necessitated a unique rescaling

approach. Post-PCA, a second round of standard

scaling was administered, succeeded by an additional

rescaling using factor

√

, with M representing the

post-PCA data dimensionality.

Note that while real data pre-processing was

adapted in accordance with the speciﬁc quantum ker-

nel measurement technique deployed, synthetic data

https://www.kaggle.com/datasets/mlg-ulb/

creditcardfraud

was subjected to pre-processing solely when imple-

menting the randomized measurement kernel, only re-

quiring a step of standard scaling with an additional

rescaling by factor

√

5.3 Baselines

For the real dataset, we aim to replicate the one-class

SVM results from (Kyriienko and Magnusson, 2022),

adopting them as quantum and classical benchmarks.

Lacking detailed insight into their sampling method

and explicit test set sizes, we employ random sam-

pling to generate data sets comprising 500 training

and 125 test data points, training the OC-SVM solely

on non-anomalous data, like the original authors. An

anomaly ratio of 0.05 is maintained in the test set.

The experiments concerning model responses to

various data sizes retain these architectures, holding

the number of PCA features steady while manipulat-

ing data sizes. Speciﬁcally, we utilize 2 features for

synthetic and 6 for real data sets, exploring data sizes

n ∈ {250, 500, 750, 1000, 1250, 1500}.

5.4 Models and Parameter Selection

Employing both classical and quantum versions of

the OC-SVM, we utilize OneClassSVM from the

SKlearn

library. All classical models adopt the RBF

kernel with γ =

N·Var(M)

and a consistent ν = 0.1.

Quantum circuits, pivotal for kernel calculations,

are crafted with the qiskit

library, simulated via

qiskit aer.QasmSimulator. Employing λ = 3 data

reuploadings for all quantum methods’ feature maps,

inversion test kernel elements are determined using

1000 shots each.

Randomized measurement circuits, realized with

r = 30 measurement settings and subjected to s =

9000 shots each, leverage crucial classical post-

processing, which emphasizes minimal embedded

loops and prioritizes efﬁcient matrix operations. The

variable subsampling method, utilizing c = ⌊

100

⌋

components (n representing the training set size) and

a subsample size n

∈ [50, 100] to ensure scalable

model performance, invokes the inversion test for ker-

nel calculations with 1000 shots per element. Em-

ploying a consistent ν value, the desired kernel matrix

calculation function is passed as a callable kernel pa-

rameter, designed to accept two data sets and method-

speciﬁc hyper-parameters, subsequently returning the

computed kernel matrix.

https://scikit-learn.org/stable/modules/generated/

sklearn.svm.OneClassSVM.html

https://qiskit.org/

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

330

5.5 Performance Metrics for

Imbalanced Data Sets

Analyzing highly imbalanced data sets, prevalent in

anomaly detection, necessitates alternative metrics to

accuracy due to its incapability to reﬂect model per-

formance accurately across classes (Aggarwal, 2017).

Hence, derivatives of precision and recall like the F1

score and average precision gain prominence.

F1 Score: represents the harmonic mean of preci-

sion and recall, providing a balanced perspective on

model performance regarding false positives and neg-

atives. It is deﬁned as

F1 score = 2 ·

Precision ·Recall

Precision + Recall

. (10)

Average Precision: quantiﬁes the model’s capabil-

ity to discern anomalies, irrespective of threshold, by

measuring the area under the precision-recall curve.

Speciﬁcally,

AP =

∑

[Recall(k) −Recall(k + 1)] ·Precision(k).

(11)

An average precision equal to the data’s anomaly ratio

signiﬁes a model with no anomaly detection capabil-

ity, while a score of 1 indicates a ﬂawless detector.

Consequently, our analysis prioritizes average preci-

sion, complemented by precision, recall, and F1 score

insights.

6 RESULTS

6.1 Performance Analysis Synthetic

Dataset

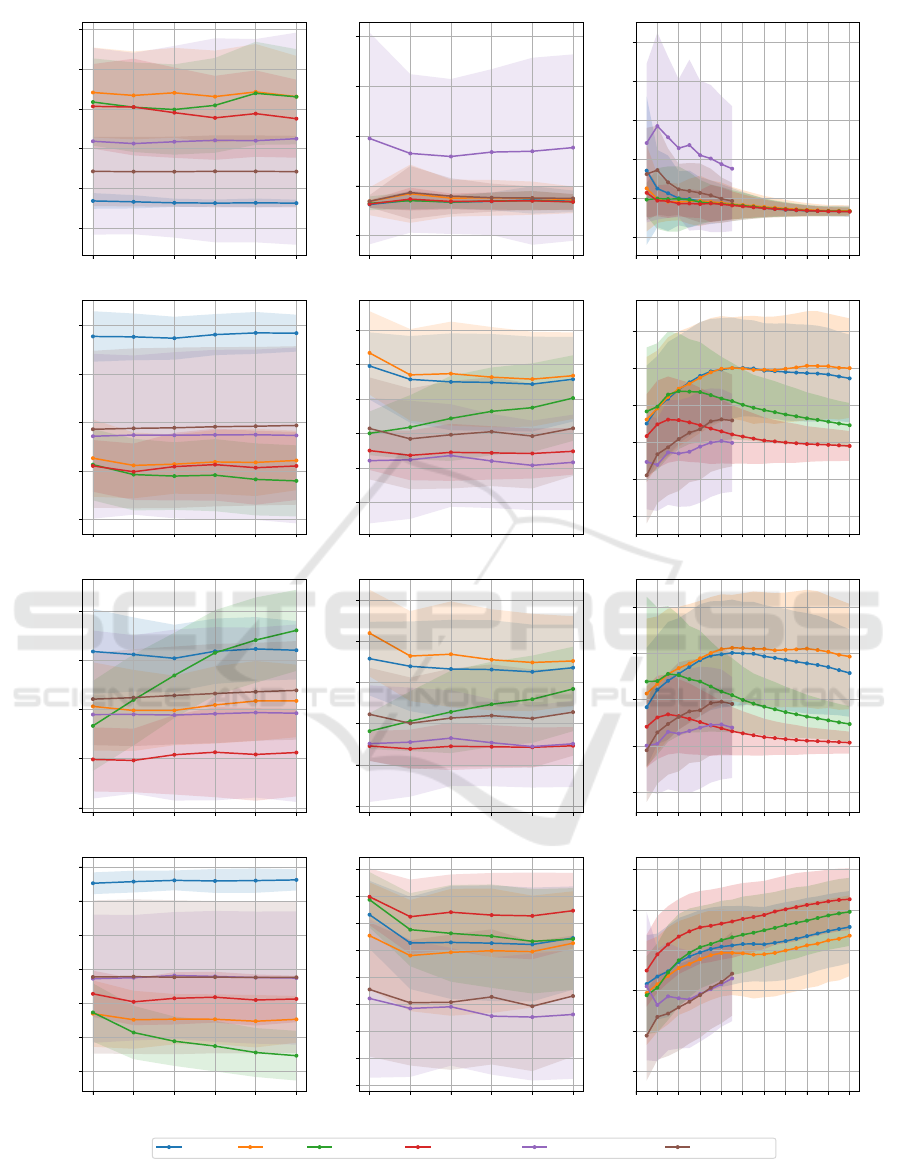
The performance results utilizing synthetic data are

presented in the ﬁrst column of Fig. 4a. Quantum

methods demonstrate superior average precision com-

pared to classical Radial Basis Function (RBF) mod-

els with the synthetic data. Despite this, given the

anomaly ratio of 0.3, most methods underperform rel-

ative to a random detector, with inversion test and

variable subsampling (using the maximum score) as

exceptions. Variable subsampling not only surpasses

randomized measurements in average precision but

also exhibits comparable variance in ensemble results

across different combination functions. Notably, it

presents augmented results with the maximum over

the average function for data sizes exceeding 750

points.

Upon applying the sign as a threshold, classical

models outperform quantum models with the RBF

kernel models securing an approximate F1 score of

0.88 and demonstrating lower variance. The random-

ized measurements and inversion test models follow

in performance, with versions of the variable subsam-

pling ensemble trailing. Despite the mitigated version

of randomized measurements models achieving supe-

rior precision, F1 scores, and recall values were alike

between mitigated and unmitigated versions. Contrar-

ily, variable subsampling employing the maximum

score delivers superior precision but inferior recall

compared to its average score counterpart, suggest-

ing its unsuitability for anomaly detection using the

current threshold.

Although results might appear conﬂicting, dispar-

ities may stem from suboptimal threshold selection

for quantum methods. Given that average precision

operates independently of a threshold, ﬁndings might

imply an optimal threshold where quantum methods

supersede classical RBF.

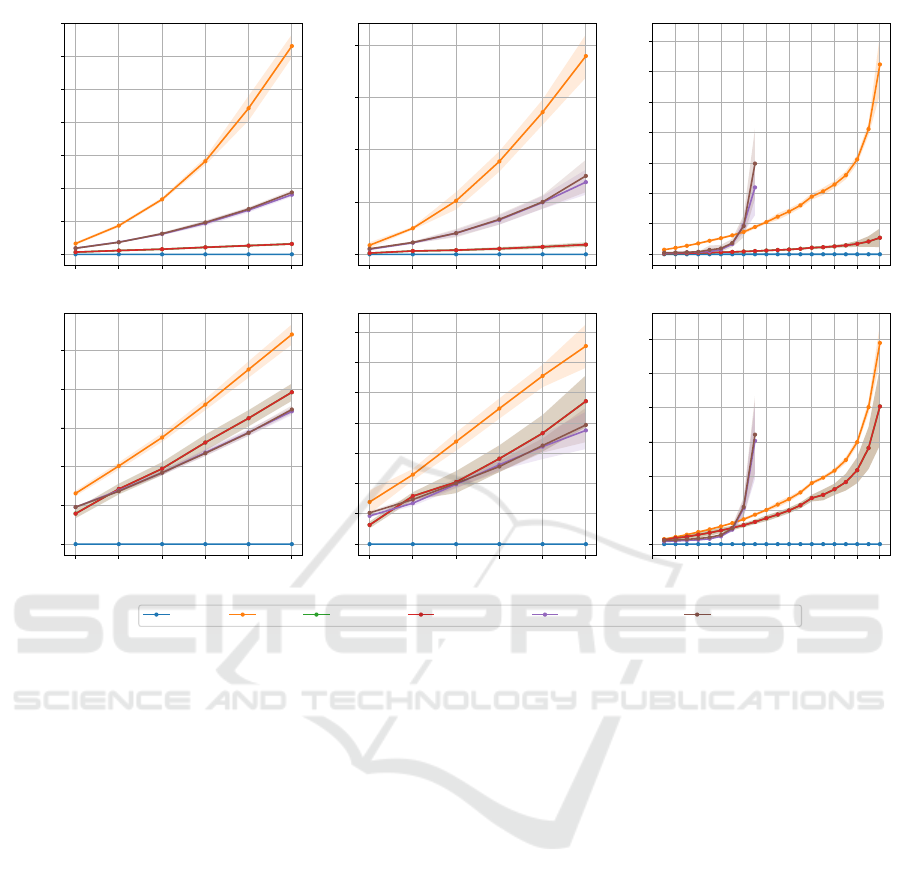
6.2 Training and Testing Durations

Synthetic Dataset

Fig. 5a depicts the notable efﬁciency of the variable

subsampling method in reducing training durations,

achieving the lowest among all employed quantum

methods for both VS Max and VS Average. Interest-

ingly, varied score functions do not impact the time

consumption. Variable subsampling not only realizes

linear time but also accomplishes a ∼ 95% reduction

in training time with 1500 data points, suggesting po-

tential similar results in signiﬁcantly less time given

their average precision closely mirroring that of an

individual one-class SVM utilizing the inversion test

(Section 2). Furthermore, a ∼ 25% enhancement in

testing time is observed at 1500 training data points.

Mitigated and unmitigated randomized measure-

ments methods yielded analogous times, corroborat-

ing that error mitigation imposes minimal overhead.

While randomized measurements facilitate substan-

tial training time reduction, complexity is non-linear

relative to data size, attributed to the inclusion of clas-

sical post-processing in training time, which demands

quadratic time complexity. Albeit the training time

reduction from the randomized measurement method

falls below that of variable subsampling, it yet pro-

vides ∼ 35% and ∼ 12% reduced testing times com-

pared to the inversion test and variable subsampling

respectively at 1500 training data points.

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements

331

250 500 750 1000 1250 1500

Training data size

0.15

0.20

0.25

0.30

0.35

0.40

Average precision

(a) Synthetic Data by Size

250 500 750 1000 1250 1500

Training data size

0.00

0.05

0.10

0.15

0.20

(b) Credit Card Fraud Data by Size

0 2 4 6 8 10 12 14 16 18 20

Number of qubits/features

0.00

0.05

0.10

0.15

0.20

0.25

250 500 750 1000 1250 1500

Training data size

0.5

0.6

0.7

0.8

0.9

F1 score

250 500 750 1000 1250 1500

Training data size

0.1

0.2

0.3

0.4

0.5

0.6

0 2 4 6 8 10 12 14 16 18 20

Number of qubits/features

0.0

0.1

0.2

0.3

0.4

0.5

250 500 750 1000 1250 1500

Training data size

0.5

0.6

0.7

0.8

0.9

Precision

250 500 750 1000 1250 1500

Training data size

0.0

0.1

0.2

0.3

0.4

0.5

0 2 4 6 8 10 12 14 16 18 20

Number of qubits/features

0.0

0.1

0.2

0.3

0.4

250 500 750 1000 1250 1500

Training data size

0.4

0.5

0.6

0.7

0.8

0.9

1.0

Recall

250 500 750 1000 1250 1500

Training data size

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0 2 4 6 8 10 12 14 16 18 20

Number of qubits/features

0.0

0.2

0.4

0.6

0.8

1.0

RBF IT VS Max VS Average Unmitigated RM Mitigated RM

Figure 4: The performance of the models trained using the different methods. The ﬁrst column of the ﬁgure corresponds to

the synthetic dataset, used with 2 features and various data sizes. The second and third columns correspond to the Credit Card

dataset, with 6 as the number of features using various data sizes, then used with various numbers of features and a constant

data size of 500.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

332

250 500 750 1000 1250 1500

Training data size

2000

4000

6000

8000

10000

12000

14000

Training Time [s]

(a) Synthetic Data by Size

250 500 750 1000 1250 1500

Training data size

20000

40000

60000

80000

(b) Credit Card Fraud Data by Size

0 2 4 6 8 10 12 14 16 18 20

Number of qubits/features

20000

40000

60000

80000

100000

120000

140000

250 500 750 1000 1250 1500

Training data size

500

1000

1500

2000

2500

Testing Time [s]

250 500 750 1000 1250 1500

Training data size

2500

5000

7500

10000

12500

15000

17500

0 2 4 6 8 10 12 14 16 18 20

Number of qubits/features

10000

20000

30000

40000

50000

60000

RBF IT VS Max VS Average Unmitigated RM Mitigated RM

Figure 5: Training and testing durations in seconds, based on the data size.

6.3 Performance Analysis Relative to

Data Size Credit Card Data

Fig. 4b reveals a predominant equivalence to a ran-

dom detector across most models, with the unmiti-

gated randomized measurements kernel being a no-

table exception. Despite this hinting at a potential

performance threshold, the model’s notable variance

signiﬁes an inherent instability.

At the utilized threshold, the inversion test and

classical RBF exhibit comparable F1 scores in

Fig. 4b, succeeded by variable subsampling models

employing maximum scoring, which seem to exhibit

an enhancement with increased data usage. Despite

affording the highest recall, both variable subsam-

pling variations grapple with suboptimal precision.

Meanwhile, both randomized measurement ker-

nels, under the current threshold, struggle with no-

tably low recall, undermining their utility for anomaly

detection.

6.4 Time Complexity Relative to Data

Size Credit Card Data

In Fig. 5b, we demonstrate that, analogous to syn-

thetic data outcomes, employing variable subsam-

pling assures linear time complexity and substantially

curtails training time. Furthermore, randomized mea-

surements realize up to a 50% reduction in training

time, even while tripling data utilization. Both vari-

able sampling and randomized measurements main-

tain comparable, and notably reduced, inference times

relative to the inversion test method.

6.5 Performance Analysis Concerning

Qubit Number - Credit Card Fraud

Dataset

In our endeavor to replicate the results from (Kyri-

ienko and Magnusson, 2022), we also explore ad-

ditional metrics including precision, recall, and

F1 score, employing thresholds in model evalua-

tion. The original study lacks explicit data selection

methodology for training and testing, along with ab-

sent details on the number of runs, prompting us to

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements

333

opt for a uniformly random data selection.

Our ﬁndings, notably divergent from (Kyriienko

and Magnusson, 2022), are presented in Fig. 4c.

Average Precision reveals considerably less favor-

able outcomes for classical RBF and quantum inver-

sion test than the aforementioned study, particularly

over 15 different runs, underperforming even a ran-

dom detector. Increasing feature/qubit usage evens

the average precision of the inversion test kernel, uti-

lizing the IQP-like kernel, to that of the classical

RBF, suggesting the original paper’s results might

hinge more on beneﬁcial sample selection for the

quantum IQP-like kernel rather than demonstrating a

clear quantum advantage. Notably, models exhibit en-

hanced stability—diminishing average precision vari-

ance—with augmented feature/qubit use.

Thresholded metrics indicate marginal improve-

ment with inversion tests over classical methods, yet

a similar F1 score is attainable via the classical ker-

nel with fewer qubits. Variable subsampling, while

offering the highest recall and consistent results, un-

derachieves in F1 score due to suboptimal preci-

sion—potentially attributable to conservative hyper-

parameter selections. An exploration into its perfor-

mance with increased components and a larger maxi-

mum subsample could be interesting.

6.6 Time Complexity Concerning Qubit

Number - Credit Card Fraud

Dataset

Fig. 5c illustrates a quadratic relationship between the

training time and the number of qubits for the inver-

sion test. Despite a similar relationship, variable sub-

sampling effectively diminishes training time, poten-

tially attributed to its ensemble components utilizing

the inversion test independently of qubit number, con-

strained by limited and non-correlated component and

data sizes. Conversely, the randomized measurements

method sees escalated training times with 8 or more

qubits, hindering its utility for high-dimensional data

sets. A rise in testing times is also observed with in-

creasing qubit numbers.

7 CONCLUSION

This work explores two methodologies aimed at en-

hancing the scalability of the quantum one-class SVM

in a semi-supervised framework: (1) the randomized

measurements and (2) variable subsampling ensem-

ble methods. The former, inherently quantum, re-

alizes linear quantum time complexity but demands

a quadratically complex classical post-processing

based on data size. It generates kernel matrices by

combining measurements from quantum feature maps

of the data, executed through a randomized scheme.

The latter adopts an ensemble approach, training mul-

tiple base model instances on varied-sized data sub-

sets.

Two experimental datasets, synthetic and Credit

Card, were deployed, revealing a marginal average

precision improvement over the classical RBF for

all methods in the synthetic data. Discrepancies

emerged between outcomes from the Credit Card

Fraud dataset and those in (Kyriienko and Magnus-

son, 2022). While models utilizing the inversion

test and variable subsampling approximated the RBF

and were relatively stable, those yielding higher aver-

age precision, like unmitigated randomized measure-

ments, exhibited instability.

Future research trajectories include exploring the

integration of variable subsampling with random-

ized measurements kernels and employing random-

ized measurements or variable subsampling alongside

alternative kernels, such as learnable ones. Incorpo-

rating importance sampling in selecting the Haar ran-

dom unitaries (Rath et al., 2021), as suggested by

(Haug et al., 2021), could reﬁne the randomized mea-

surements method. The classical shadow method, due

to its lower average error compared to randomized

measurements, and the examination of Nystr

om and

block basis factorization approximations of a quan-

tum kernel, warrant further exploration. Finally, en-

hancing the quantum SVM’s performance through

the proposed variable sampling method, by utilizing

more components and enlarging maximum subsam-

ple sizes, remains a viable avenue, given the resultant

training and testing time reductions.

ACKNOWLEDGEMENTS

This research is part of the Munich Quantum Valley,

which is supported by the Bavarian state government

with funds from the Hightech Agenda Bayern Plus.

REFERENCES

Aggarwal, C. C. (2017). An introduction to outlier analysis.

Springer.

Aggarwal, C. C. and Sathe, S. (2015). Theoretical foun-

dations and algorithms for outlier ensembles. ACM

SIGKDD explorations newsletter, 17(1):24–47.

Boloka, T., Crafford, G., Mokuwe, W., and Eden,

B. V. (2021). Anomaly detection monitoring sys-

tem for healthcare. In 2021 Southern African

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

334

Universities Power Engineering Conference/Robotics

and Mechatronics/Pattern Recognition Association of

South Africa (SAUPEC/RobMech/PRASA), pages 1–6.

ECB (2023). Report on card fraud in 2020 and 2021.

Elben, A., Vermersch, B., Roos, C. F., and Zoller, P. (2019).

Statistical correlations between locally randomized

measurements: A toolbox for probing entanglement

in many-body quantum states. Physical Review A,

99(5):052323.

Fernando, T., Gammulle, H., Denman, S., Sridharan, S.,

and Fookes, C. (2021). Deep learning for medical

anomaly detection – a survey.

Hajibabaee, P., Pourkamali-Anaraki, F., and Hariri-

Ardebili, M. A. (2021). Kernel matrix approximation

on class-imbalanced data with an application to scien-

tiﬁc simulation. IEEE Access, 9:83579–83591.

Haug, T., Self, C. N., and Kim, M. (2021). Large-scale

quantum machine learning. arXiv e-prints, pages

arXiv–2108.

Havl

cek, V., C

orcoles, A. D., Temme, K., Harrow, A. W.,

Kandala, A., Chow, J. M., and Gambetta, J. M. (2019).

Supervised learning with quantum-enhanced feature

spaces. Nature, 567(7747):209–212.

Herr, D., Obert, B., and Rosenkranz, M. (2021). Anomaly

detection with variational quantum generative adver-

sarial networks. Quantum Science and Technology,

6(4):045004.

Huang, H.-Y., Kueng, R., and Preskill, J. (2020). Predicting

many properties of a quantum system from very few

measurements. Nature Physics, 16(10):1050–1057.

Hubregtsen, T., Wierichs, D., Gil-Fuster, E., Derks, P.-J. H.,

Faehrmann, P. K., and Meyer, J. J. (2022). Train-

ing quantum embedding kernels on near-term quan-

tum computers. Physical Review A, 106(4):042431.

Kyriienko, O. and Magnusson, E. B. (2022). Unsupervised

quantum machine learning for fraud detection. arXiv

preprint arXiv:2208.01203.

Rath, A., van Bijnen, R., Elben, A., Zoller, P., and Verm-

ersch, B. (2021). Importance sampling of randomized

measurements for probing entanglement. Physical Re-

view Letters, 127(20).

Ray, A., Guddanti, S. S., Ajith, V., and Vinayagamurthy, D.

(2022). Classical ensemble of quantum-classical ml

algorithms for phishing detection in ethereum trans-

action networks. arXiv preprint arXiv:2211.00004.

Roberts, D. A. and Yoshida, B. (2017). Chaos and com-

plexity by design. Journal of High Energy Physics,

2017(4).

Sakhnenko, A., O’Meara, C., Ghosh, K. J., Mendl, C. B.,

Cortiana, G., and Bernab

e-Moreno, J. (2022). Hybrid

classical-quantum autoencoder for anomaly detection.

Quantum Machine Intelligence, 4(2):1–17.

Schlegl, T., Seeb

ock, P., Waldstein, S. M., Schmidt-Erfurth,

U., and Langs, G. (2017). Unsupervised anomaly de-

tection with generative adversarial networks to guide

marker discovery.

Sch

olkopf, B., Williamson, R. C., Smola, A., Shawe-Taylor,

J., and Platt, J. (1999). Support vector method for nov-

elty detection. Advances in neural information pro-

cessing systems, 12.

Shaydulin, R. and Wild, S. M. (2022). Importance of ker-

nel bandwidth in quantum machine learning. Physical

Review A, 106(4).

Wang, H., Wang, W., Liu, Y., and Alidaee, B. (2022). In-

tegrating machine learning algorithms with quantum

annealing solvers for online fraud detection. IEEE Ac-

cess, 10:75908–75917.

Wang, R., Li, Y., Mahoney, M. W., and Darve, E. (2019).

Block basis factorization for scalable kernel evalua-

tion. SIAM Journal on Matrix Analysis and Applica-

tions, 40(4):1497–1526.

Towards Efﬁcient Quantum Anomaly Detection: One-Class SVMs Using Variable Subsampling and Randomized Measurements

335