Efﬁcient Posterior Sampling for Diverse Super-Resolution with

Hierarchical VAE Prior

Jean Prost

, Antoine Houdard

, Andr

es Almansa

and Nicolas Papadakis

Univ. Bordeaux, Bordeaux IMB, INP, CNRS, UMR 5251, F-33400 Talence, France

Ubisoft La Forge, F-33000 Bordeaux, France

Universit

e Paris Cit

e, CNRS, MAP5, F-75006 Paris, France

Univ. Bordeaux, CNRS, INRIA, Bordeaux INP, IMB, UMR 5251, F-33400 Talence, France

Keywords:

Diverse Image Super-Resolution, Hierarchical Variational Autoencoder, Conditional Generative Model.

Abstract:

We investigate the problem of producing diverse solutions to an image super-resolution problem. From a

probabilistic perspective, this can be done by sampling from the posterior distribution of an inverse problem,

which requires the deﬁnition of a prior distribution on the high-resolution images. In this work, we propose to

use a pretrained hierarchical variational autoencoder (HVAE) as a prior. We train a lightweight stochastic en-

coder to encode low-resolution images in the latent space of a pretrained HVAE. At inference, we combine the

low-resolution encoder and the pretrained generative model to super-resolve an image. We demonstrate on the

task of face super-resolution that our method provides an advantageous trade-off between the computational

efﬁciency of conditional normalizing ﬂows techniques and the sample quality of diffusion based methods.

1 INTRODUCTION

Image super-resolution is the task of generating a

high-resolution (HR) image x

x corresponding to a low-

resolution (LR) observation y

y. A typical approach

for image super-resolution is to train a deep neural

network in a supervised fashion to map a LR im-

age to its HR counterpart (see (Lepcha et al., 2022)

for an extensive review). Despite impressive perfor-

mances, those regression based methods are funda-

mentally limited by their lack of diversity. Indeed,

there might exist many plausible HR solutions asso-

ciated with one LR observation, but regression based

methods only provide one of those solutions.

An alternative approach for image super-

resolution is to sample from the posterior distribution

p(x

x|y

y). Speciﬁcally, we can train conditional deep

generative models to ﬁt the posterior p(x

x|y

y). With

the recent advances in deep generative modeling, it

is possible to generate realistic and diverse samples

from the posterior distribution.

Starting from the seminal work of (Lugmayr

et al., 2020), many approaches proposed to train con-

ditional generative models such as conditional nor-

malizing ﬂow or conditional variational autoencoders

in order to model the posterior distribution of the

super-resolution problem. We refer to those methods

as direct methods, as they only require one network

function evaluation (NFE) to generate one sample.

With the recent development of score-based gen-

erative models (also known as denoising diffusion

models) (Ho et al., 2020; Song et al., 2021), poste-

rior sampling methods based on conditional denoising

diffusion models are now able to produce high-quality

samples outperforming previous direct methods (Choi

et al., 2021; Chung et al., 2022; Kawar et al., 2022).

However, denoising diffusion methods are limited by

their computationally expensive sampling process, as

they require numerous network function evaluations

to generate one super-resolved sample. In the follow-

ing, we classify those methods as iterative methods.

In this work, we address the question: Can we get

the best of both worlds between the sampling qual-

ity of iterative methods, and the computationnal efﬁ-

ciency of direct methods? We show that it is indeed

possible to reach this goal with our diverse super-

resolution method CVDVAE (Conditional VDVAE).

Our approach is based on reusing a pretrained hi-

erarchical variational autoencoder (HVAE) (Sønderby

et al., 2016; Kingma et al., 2016). HVAE models are

able to generate high-quality images by relying on an

expressive sequential generative model (Vahdat and

Kautz, 2020; Child, 2021; Hazami et al., 2022). By

associating one latent variable subgroup to each resid-

ual block of a generative network, HVAE models are

able to learn compact high-level representations of the

data, and they can generate new samples efﬁciently,

with only one evaluation of the generative network.

Prost, J., Houdard, A., Almansa, A. and Papadakis, N.

Efﬁcient Posterior Sampling for Diverse Super-Resolution with Hierarchical VAE Prior.

DOI: 10.5220/0012352800003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

393-400

ISBN: 978-989-758-679-8; ISSN: 2184-4321

393

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Samples

×4

×8

Figure 1: Diverse super-resolved samples at different upscaling factors. Our method can generate realistic samples with

diverse attributes (hairs, mouth, eyes. . . ).

The fast sampling time and the expressivity of

HVAE models make them suitable candidates for ef-

ﬁcient posterior sampling. In this work, we exploit

a pretrained VD-VAE model (Child, 2021). In or-

der to repurpose VD-VAE generative model for image

super-resolution, we train a low-resolution encoder

to encode LR images in the latent space of the VD-

VAE model. By combining the LR encoder with the

VD-VAE generative model, we can produce a sample

with only one (autoencoder) network evaluation. By

adopting a stochastic model for the LR encoder, our

method can generate diverse samples from the poste-

rior distribution, as illustrated in Figure 1. We show

that the LR encoder can be trained with reasonable

computational resources by exploiting the VD-VAE

original (HR) encoder to generate labels for training

the LR-encoder, and by sharing weights between the

LR encoder and VD-VAE generative model. We eval-

uate our method on super-resolution of face images,

with upscaling factor ×4 and ×8 and demonstrate that

it reaches sample quality on par with sequential meth-

ods, while being signiﬁcantly faster (> ×500).

The paper is organised as follows. In section 2,

we provide the necessary background on HVAE mod-

els. Then we present in section 3 our super-resolution

method. Experimental results are given in section 4

and we discuss related works in section 5.

2 HIERARCHICAL VAE

Variational Autoencoder. We propose to use a hier-

archical variational autoencoder as a prior model over

high-resolution images. A variational autoencoder is

a deep latent variable model of the form:

x) =

z)p

x|z

z)dz

z. (1)

where p

z) deﬁnes the prior distribution of the latent

variable z

z and p

x|z

z) is the decoding distribution.

A VAE also provides an inference model (en-

coder) q

z|x

x), trained to match the intractable model

posterior p

z|x

x) (Kingma and Welling, 2013). In

order to deﬁne expressive models, both the gener-

ative model p

z, x

x) and the encoder q

z|x

x) are

parameterized by neural networks, whose weights are

respectively parameterized with θ and φ.

Hierarchical Generative Model. A hierarchical

VAE is a speciﬁc class of VAE where the la-

tent variable z

z is partitioned into L subgroups z

z =

, z

, ·· · , z

L−1

), and the prior is set to have a hier-

archical structure:

z) = p

, z

, ·· · , z

L−1

) (2)

= p

)

L−1

∏

l=1

). (3)

In practice, each latent supgroup is a 3-dimensional

tensor z

∈ R

×h

×w

, with increasing resolution h

≤

≤ · ≤ h

L−1

. Each conditional model in the hierar-

chical prior is set as a Gaussian:

(

) = N (z

;µ

θ,0

, Σ

θ,0

)

) = N (z

;µ

θ,l

),Σ

θ,l

)).

(4)

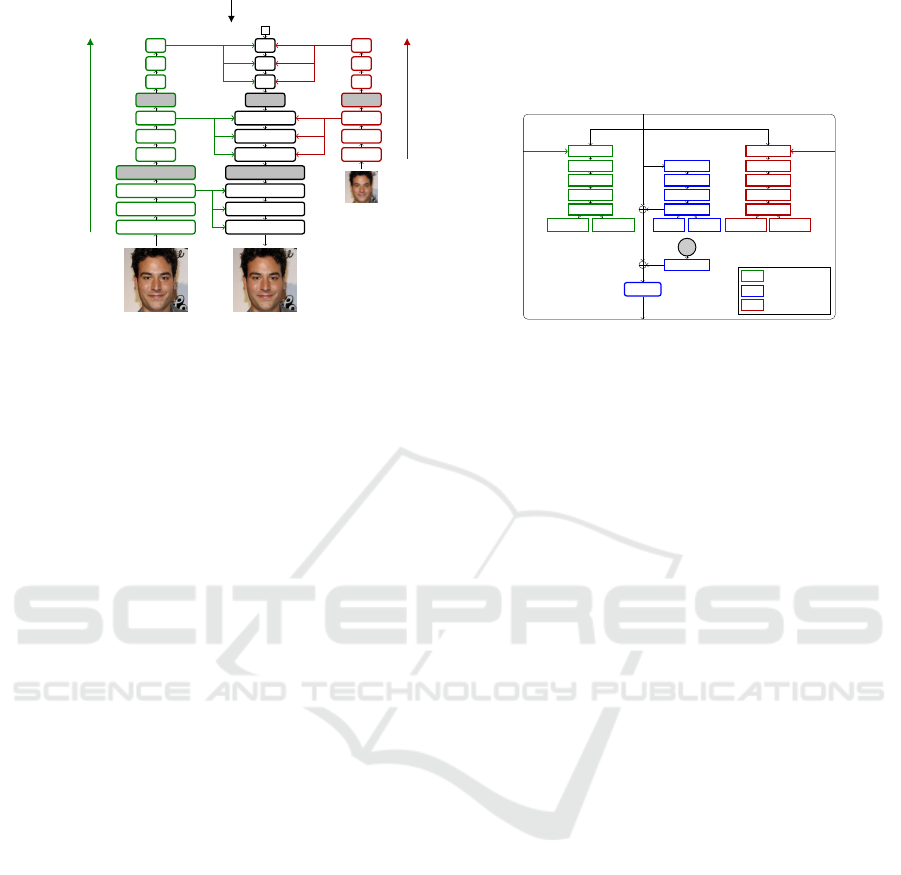
As illustrated in Figure 2, the generative model is

embedded within a ”top-down” generative network.

To generate an image, a low-resolution constant input

tensor is sequentially processed by a serie of top-

down blocks and upsampling layers (Figure 2a). In

each top-down block l (Figure 2b), a latent subgroup

is sampled according to the statistics µ

θ,l

) and

θ,l

) computed within the top-down block.

Hierarchical Encoder. The HVAE encoder has the

same hierarchical structure as the generative model:

z|x

x) = q

∏

l=1

, x

x), (5)

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

394

with Gaussian parameterization of the conditional

distributions:

(

x) = N



;µ

φ,0

x), Σ

φ,0



, x

x) = N



;µ

φ,l

, x

x), Σ

φ,l

, x



(6)

The HVAE encoder is merged with the generative top-

down network. In each top-down block l, a branch as-

sociated with the encoder uses features from the input

x along with features from the previous levels to infer

the encoder statistics at level l (in green in Figure 2b).

The image features are extracted by a ”bottom-up”

network (in green in Figure 2a).

3 SUPER-RESOLUTION HVAE

Problem Formulation. In this section we describe

our super-resolution method based on a pretrained

HVAE model. We assume that the LR image y

y ∈

3×

, and its associated HR image x

x ∈ R

3×H×W

are related by a linear degradation model:

y = (k ∗ x

x) ↓

, (7)

where k is a low-pass ﬁlter and (u) ↓

is deﬁned as the

subsampling operation with downsampling factor s.

Our goal is to sample from the posterior distribution

of the inverse problem:

p(x

x|y

y) ∝ p(y

y|x

x)p(x

x). (8)

In (8), the likelihood p(y

y|x

x) can be deduced from

the degradation model (7). On the other hand, the

prior model p(x

x) needs to be speciﬁed by the user.

Deep generative models such as GANs, VAE or dif-

fusion models can be used to model the prior on high-

resolution images. In the following, we propose to

parameterize p(x

x) with a hierarchical variational au-

toencoder. Given a pretrained HVAE prior p

x), the

ideal super-resolution model is:

x|y

y) =

x|y

y, z

z)p

z|y

y)dz

z, (9)

where probability laws correspond to the con-

ditional of the augmented model p

z, x

x, y

y) :=

z)p

x|z

z)p(y

y|x

x). Since we do not have acces to

x|y

y, z

z) and p

z|y

y), we can not directly sample

from (9). However, we will see in the following part

that we can efﬁciently approximate this model by

making use of the structure of the HVAE hierarchical

latent representation and of the its pretrained encoder.

Super-resolution Model. It has been observed in

several works that the low-frequency information of

images generated by HVAE model where mostly con-

trolled by the low-resolution latent variable, at the be-

ginning of the hierarchy (Vahdat and Kautz, 2020;

Child, 2021; Havtorn et al., 2021). Hence, for a

large enough number of latent groups k, samples from

x|x

) share the same low-frequency information.

As a consequence, all the samples from p

x|x

) are

consistent to a LR image y

y (up to a small error).

This motivates us to deﬁne the following super-

resolution model:

x|y

y) =

x|z

y)dz

z, (10)

where q

z|y

y) is a stochastic low-resolution encoder,

trained to encode the low-resolution latent groups.

By deﬁnition of the super-resolution model (10), we

can sample from p

x|y

y) by sequentially sampling

∼ q

y) and x

x ∼ p

x|z

Hierarchical Low-Resolution Encoder. We set the

LR encoder to have a hierarchical structure:

y) = q

∏

l=1

, y

y), (11)

with Gaussian conditional distributions:

(

y) = N



;µ

ψ,0

y), Σ

ψ,0



, y

y) = N



;µ

ψ,l

, y

y), Σ

ψ,l

, y



(12)

We implement the LR encoder with the same archi-

tecture as VD-VAE original (HR) encoder, but with

a limited number of blocks due to reduced number

of latent variable to be predicted (Figure 2). Only

the parameters of the low-resolution encoder (in red

in Figure 2) are trained, while the shared parameters

(in blue in Figure 2) are set to the value of the

corresponding parameters in the pretrained VD-VAE

generative model, and remain frozen during training.

Training. We keep the weights of the HVAE decoder

x|z

z), so that the only trainable weights of our

super-resolution model (10) are the weights of the LR

encoder ψ. Given a joint training distribution of HR-

LR image pairs p

x, y

y), the LR encoder is trained to

match the available ”high-resolution” HVAE encoder

x) on the associated HR images, by minimiz-

ing the Kullback-Leibler (KL) divergence:

L(ψ) = E

x,y





x)||q



. (13)

The criterion (13) was introduced by (Harvey et al.,

2022), who demonstrated that minimizing (13) is

equivalent to maximizing a lower-bound of the super-

resolution conditional log-likelihood on the training

dataset, and that under additional assumptions on the

pretrained HVAE model, one can reach optimal per-

formance by only training the low-resolution encoder

y). In practice, the KL divergence within the

Efﬁcient Posterior Sampling for Diverse Super-Resolution with Hierarchical VAE Prior

395

ResBlock

Pooling

Top-down block

Unpool

Top-down block

ResBlock

x x

HR encoder bottom-up path

LR encoder bottom-up path

Top-down path

(a) CVDVAE architecture

conv 1 × 1

conv 3 × 3

conv 1 × 1

) Σ

)

concat

conv 1 × 1

conv 3 × 3

conv 1 × 1

, x) Σ

, x)

HR features

concat

conv 1 × 1

conv 3 × 3

conv 1 × 1

, y) Σ

, y)

LR features

conv 1 × 1

ResBlock

encoder

generative model

LR-encoder

(b) Top-down block

Figure 2: Super-resolution model based on a pretrained VD-VAE model. (a) Given a pretrained VD-VAE network, composed

of an encoder bottom-up network (in green), and a top-down network (in black), we train a LR encoder (in red) to encode

low-resolution images in the latent space of VD-VAE. The LR-encoder has the same structure than VD-VAE encoder, with a

bottom-up path that extracts multiscale features, and a top-down path merged with VD-VAE top-down path. (b) In each block

of the top-down path, we add branch for the LR encoder (in red) to infer the statistics of q

, y

y).

training criterion (13) can be decomposed into a sum

of KL divergence on each latent subgroup:



x)||q



= KL



x)||q



+ E

∑

l=1



, x

x)||q

, y



(14)

Since each conditional law involved in (14) is Gaus-

sian, each KL term can be computed in closed-form.

In practice the covariance matrices Σ

φ,l

, x

x) and

ψ,l

, y

y) are constrained to be diagonal, so that the

KL can be computed efﬁciently.

4 EXPERIMENTS

4.1 Experimental Settings

Dataset and Upscaling Factors. We test our

super-resolution method CVDVAE on the FFHQ

dataset (Karras et al., 2019), with images of

resolution 256 × 256. We experiment on 2 upscal-

ing factors: ×4 (64 × 64 → 256 × 256) and ×8

(32 × 32 → 256 × 256). The low resolution images

are initially downscaled by applying an antialiasing

kernel followed by a bicubic interpolation.

Compared Methods. We compare CVDVAE with a

conditional normalizing ﬂow (HCFlow) (Liang et al.,

2021), a conditional diffusion model (SR3) (Saharia

et al., 2021), and a method that add guidance to

a non-conditional diffusion model at inference

(DPS) (Chung et al., 2022). We retrain HCFlow on

FFHQ256 using the ofﬁcial implementation. For

DPS, we also reuse the ofﬁcial implementation with

the available pretrained model, which was trained

on FFHQ. For SR3, since no ofﬁcial implementation

is available, we used an open-source (non-ofﬁcial)

implementation (Jiang, 2022), and we trained a

model on FFHQ. When training SR3, we found that a

color shift (Deck and Bischoff, 2023) was responsible

for important reconstruction errors. To compensate

this weakness of the method, we project the super-

resolved image on the space of consistent solutions at

inference as proposed in (Bahat and Michaeli, 2020).

For fair comparison, we retrained both HCFlow and

SR3 with the same computational budget as for our

low-resolution encoder. For HCFlow and CVDVAE,

we set the temperature of the latent variables at

τ = 0.8 during sampling.

Evaluating a Diverse SR Method. Due to the

ill-posedness of the problem, evaluating a diverse

super-resolution model based solely on the distortion

to the ground truth is not satisfactory. Indeed, there

exist many solutions that are both realistic and

consistent with the LR input while being far from the

ground truth. Thus, in order to evaluate the super-

resolution model, we provide a series of metrics that

evaluate different expected characteristics of a diverse

super-resolution model, such as the consistency of the

solution, the diversity of the samples and the general

visual quality. It should be noted that those metrics

are not necessarily correlated: a model could generate

diverse solutions, that are not consistent or realistic,

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

396

or, on the opposite, it could provide solutions that

are realistic and consistent but with a low diversity.

Thus, to evaluate a diverse super-resolution model, it

is necessary to consider these three different aspects

together: diversity, consistency and visual quality.

Evaluation Metrics. The general quality of the

super-resolved images is evaluated using the blind

Image quality metric BRISQUE (Mittal et al., 2012).

Consistency with the LR input is measured via peak

Signal-to-Noise Ratio (PSNR, denoted as LR-PSNR

in Tables 1 and 2). Furthermore, to evaluate the di-

versity of the super-resolution, we compute the Aver-

age Pairwise distance between different samples com-

ing from the same LR input (denoted as APD in

Tables 1 and 2), both at the pixel level, using the

mean square error (MSE) between samples (consid-

ering pixel intensity value between 0 and 1), and at

a perceptual level using the LPIPS similarity crite-

ria (Zhang et al., 2018). For one LR input, the av-

erage pairwise distance is computed as the average

distance between all the possible pairs of images in a

set of 5 super-resolved samples. The reported APD

in Tables 1 and 2 corresponds to the mean value of

the single image APD over 500 LR inputs in the test

set. We measure the distortion of the super-resolved

samples with respect to the ground truth HR image in

terms of PSNR, structural similarity (SSIM) (Wang

et al., 2004) and LPIPS, as it is common in the super-

resolution literature. All numbers reported corre-

spond to the metric mean value on a subset of 1000

images from FFHQ256 test set.

4.2 Results

Quantitative Evaluation. The quantitative results

presented in Table 1 indicate that CVDVAE provides

a good trade-off between the different evaluated met-

rics. Indeed, it obtains the second best results in terms

of distortion and visual quality, and the second or

third best results in terms of diversity. CVDVAE is

also one of the fastest methods, along with HCFlow.

HCFlow provides the best results for distortion met-

rics as it explicitly penalizes bad reconstruction in its

training loss. Similar to CVDVAE, its application

is fast, as it requires only one network evaluation to

produce a super-resolved image. However, HCFlow

lacks high-level diversity (as measured by the LPIPS

average pairwise distance), compared with the con-

current methods. We postulate that this lack of diver-

sity is due to the relative lack of expressiveness of nor-

malizing ﬂows architecture compared to the convolu-

tional architectures used by diffusion and HVAE mod-

els. Our method, along with DPS, produces the best

LR Ours

HCFlow

DPS

SR3

Figure 3: Samples from different diverse SR methods (×4).

results in terms of visual quality as measured by the

BRISQUE metric, illustrating the beneﬁt of using a

pretrained unconditional generative model. The com-

putational cost of DPS is nevertheless signiﬁcantly

higher than the ones of CVDVAE and HCFlow, as

DPS requires 1000 steps of network evaluations (and

backpropagation through the denoiser) to produce one

super-resolved sample. Finally, SR3 performances

are inferior to the compared methods. We used the

same computational budget (48 hours on 4 GPUs)

for training the SR3 models than our CVDVAE and

HCFlow. This computational budget is signiﬁcantly

lower than the one reported in the SR3 paper (Saharia

et al., 2021) (≈ 4 days on 64 TPUv3 chip), and we

expect that training the SR3 model for more epochs

would improve its performance. Like DPS, SR3 is

slower than our method as it requires 2000 network

evaluations to produce one super-resolved image; al-

though, unlike DPS, SR3 does not require to back-

propagate through the score-network.

Qualitative Evaluation. Visual comparisons of

super-resolved samples from the different evaluated

methods are provided in Figures 3 and 4. CVDVAE is

able to produce diverse textures as illustrated by the

facial hair variation in Figure 3 or the hair variation

in 4. CVDVAE appears to produce super-resolved

samples with higher semantic diversity, in terms of

textures (hairs, skin), in line with the higher percep-

tual diversity measured in the quantitative evaluation.

Temperature Control. As for the unconditionnal

HVAE models, CVDVAE offers the possibility to

control the conditional generation via the tempera-

Efﬁcient Posterior Sampling for Diverse Super-Resolution with Hierarchical VAE Prior

397

Table 1: Comparison of diverse SR methods face super-resolution. Best result is in bold, second best is underlined.

Distortion Visual Quality Consistency Diversity (APD)

model PSNR↑ SSIM↑ LPIPS ↓ BRISQUE↓ LR-PSNR ↑ MSE (×10

) ↑ LPIPS (×10

) ↑ time (s)

×4

Bicubic 27.49 0.84 0.29 61.79 36.99 0 0

HCFlow 31.74 0.89 0.13 37.21 52.81 161.8 62.6 0.11

CVDVAE (ours) 30.24 0.85 0.16 32.30 75.20 88.8 123.0 0.14

SR3 28.87 0.73 0.25 37.17 63.47 20.06 209.2 46

DPS 28.50 0.81 0.20 32.21 38.96 10.4 150.0 103

×8

Bicubic 23.50 0.70 0.45 78.42 33.61 0 0

HCFlow 26.72 0.76 0.24 36.25 51.13 575.5 155.3 0.17

Ours 25.47 0.71 0.27 32.26 70.15 248.2 236.4 0.13

SR3 26.26 0.70 0.29 34.78 68.6 19.95 234.3 62

DPS 24.38 0.68 0.28 30.09 36.97 35.68 247.4 103

ture of the latent variable distributions (Vahdat and

Kautz, 2020; Child, 2021). The temperature parame-

ter τ controls the variance of the Gaussian latent dis-

tributions. In order to assess the behavior of the model

on both low and high temperature regime, we evaluate

our method on 2 temperatures (τ ∈ {0.1, 0.8}). Quan-

titative results in Table 2 show that reducing the tem-

perature leads to a solution closer to the ground truth

in terms of low-levels distortion metrics (PSNR and

the SSIM), while using a higher temperature helps

to improve the perceptual similarity (LPIPS) with the

ground-truth, as well as the general perceptual quality

of the generated HR images and the diversity of the

samples. On Figure 5, we display CVDVAE’s sam-

ples at different temperatures τ. The sampling tem-

perature correlates with the perceptual smoothness of

the super-resolved sample, a higher sampling temper-

ature inducing images with sharper details.

5 RELATED WORKS

Super-Resolution with Pre-Trained Generative

Models A large number of methods were designed

to solve imaging inverse problems such as im-

age super-resolution by using pretrained deep gen-

erative models (DGM) as a prior. This includes

methods relying on generative adversarial networks

(GAN) (Menon et al., 2020; Marinescu et al., 2020;

Pan et al., 2021; Daras et al., 2021; Daras et al.,

2022; Poirier-Ginter and Lalonde, 2023), variational

autoencoders (Mattei and Frellsen, 2018; Gonz

alez

et al., 2022; Prost et al., 2023) and denoising diffu-

sion models (Choi et al., 2021; Chung et al., 2022;

Kawar et al., 2022; Song et al., 2023). However,

those approaches are computationally expensive as

they require an iterative sampling or optimization pro-

cedure which require many network evaluation. On

the other hand, our approach enables fast inference

(one network evaluation), at the cost of reduced ﬂex-

ibility (due to the need of training a task-speciﬁc en-

coder). The idea of training an encoder to map a de-

graded image in the latent space of a generative net-

LR Ours

HCFlow

DPS

SR3

Figure 4: Samples from different diverse SR methods (×8.)

work was previously exploited in the context of im-

age inpainting with HVAE (Harvey et al., 2022), and

super-resolution with a GAN prior (Chan et al., 2021;

Richardson et al., 2021).

Diverse Super-Resolution with Conditional Gen-

erative Models. Although it is possible to sample

from the posterior p(x

x|y

y) by using an unconditionnal

deep generative models, those methods are restricted

to speciﬁc dataset for which pretrained models are

available. On generic natural images, the state of the

art methods rely on conditional generative models, di-

rectly trained to model the posterior p(x

x|y

y) (Lugmayr

et al., 2021; Lugmayr et al., 2022). Those methods in-

clude conditional normalizing ﬂows (Lugmayr et al.,

2020; Liang et al., 2021), conditional GAN (Bahat

and Michaeli, 2020), conditional VAE (Gatopoulos

et al., 2020; Zhou et al., 2021; Chira et al., 2022)

and conditional denoising diffusion models (Li et al.,

2022; Saharia et al., 2021).

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

398

Table 2: Effect of the sampling temperature τ on CVDVAE super-resolution results.

Distortion Visual Quality Consistency Diversity (APD)

τ PSNR↑ SSIM↑ LPIPS ↓ BRISQUE↓ LR-PSNR ↑ MSE (×10

) ↑ LPIPS (×10

) ↑

×4

0.1 30.75 0.86 0.15 36.47 75.70 64.6 104.5

0.8 30.24 0.85 0.16 32.3 75.20 88.8 123.0

×8

0.1 26.27 0.75 0.30 50.34 71.63 140.4 179.0

0.8 25.47 0.708 0.28 32.26 70.15 248.2 236.4

LR τ = 0 τ = 0.25 τ = 0.5 τ = 0.75 τ = 1

Figure 5: Effect of the sampling temperature τ on the super-resolved result. Increasing the temperature yields image with

more high-frequency details.

6 CONCLUSIONS

In this work we presented CVDVAE, a method that

realizes an efﬁcient sampling from the posterior of

a super-resolution problem, by combining a low-

resolution image encoder with a pretrained VD-VAE

generative model. CVDVAE showed promising re-

sults on face super-resolution, on par with state-of-

the-art diverse SR methods, providing semantically

diverse and high-quality samples. Our results illus-

trate the ability of conditional hierarchical generative

models to perform complex image-to-image tasks.

Our results are in line with many works that illus-

trates the beneﬁts of using HVAE models for down-

stream applications (Havtorn et al., 2021; Agarwal

et al., 2023; Prost et al., 2023). One drawback of

our approach is its limitation to dataset for which pre-

trained HVAE models are available, such as human

faces or low-resolution ImageNet. However, we pos-

tulate that HVAE models have not yet reached their

limits, and, by adapting design features from current

SOTA deep generative models (Rombach et al., 2022;

Kang et al., 2023) (architectural improvement, longer

training, larger dataset), HVAE models could signif-

icantly improve their performance and expreessive-

ness, and generalize on much diverse datasets.

ACKNOWLEDGEMENTS

This study has been carried out with ﬁnancial support

from the French Research Agency through the Post-

ProdLEAP project (ANR-19-CE23-0027-01). Com-

puter experiments for this work ran on several plat-

forms including HPC resources from GENCI-IDRIS

(Grant 2021-AD011011641R1), and the PlaFRIM

experimental testbed, supported by Inria, CNRS

(LABRI and IMB), Universit

e de Bordeaux, Bor-

deaux INP and Conseil R

egional d’Aquitaine (see

https://www.plafrim.fr).

REFERENCES

Agarwal, S., Hope, G., Younis, A., and Sudderth, E. B.

(2023). A decoder sufﬁces for query-adaptive vari-

ational inference. In The 39th Conference on Uncer-

tainty in Artiﬁcial Intelligence.

Bahat, Y. and Michaeli, T. (2020). Explorable super resolu-

tion. In the IEEE/CVF CVPR, pages 2716–2725.

Chan, K. C., Wang, X., Xu, X., Gu, J., and Loy, C. C.

(2021). Glean: Generative latent bank for large-factor

image super-resolution. In IEEE/CVF CVPR, pages

14245–14254.

Child, R. (2021). Very deep vaes generalize autoregressive

models and can outperform them on images. arXiv

preprint arXiv:12011.10650.

Chira, D., Haralampiev, I., Winther, O., Dittadi, A., and

evin, V. (2022). Image super-resolution with deep

variational autoencoders.

Choi, J., Kim, S., Jeong, Y., Gwon, Y., and Yoon,

S. (2021). Ilvr: Conditioning method for denois-

ing diffusion probabilistic models. arXiv preprint

arXiv:2108.02938.

Chung, H., Kim, J., Mccann, M. T., Klasky, M. L., and Ye,

J. C. (2022). Diffusion posterior sampling for general

noisy inverse problems. In The Eleventh ICLR.

Daras, G., Dagan, Y., Dimakis, A., and Daskalakis, C.

(2022). Score-guided intermediate level optimization:

Fast langevin mixing for inverse problems. In ICML,

pages 4722–4753. PMLR.

Daras, G., Dean, J., Jalal, A., and Dimakis, A. (2021). Inter-

mediate layer optimization for inverse problems using

deep generative models. In ICML, pages 2421–2432.

PMLR.

Deck, K. and Bischoff, T. (2023). Easing color shifts

in score-based diffusion models. arXiv preprint

arXiv:2306.15832.

Gatopoulos, I., Stol, M., and Tomczak, J. M. (2020). Super-

resolution variational auto-encoders. arXiv preprint

arXiv:2006.05218.

Efﬁcient Posterior Sampling for Diverse Super-Resolution with Hierarchical VAE Prior

399

Gonz

alez, M., Almansa, A., and Tan, P. (2022). Solving in-

verse problems by joint posterior maximization with

autoencoding prior. SIAM Journal on Imaging Sci-

ences, 15(2):822–859.

Harvey, W., Naderiparizi, S., and Wood, F. (2022). Con-

ditional image generation by conditioning variational

auto-encoders. In ICLR.

Havtorn, J. D., Frellsen, J., Hauberg, S., and Maaløe, L.

(2021). Hierarchical vaes know what they don’t know.

In ICML, pages 4117–4128. PMLR.

Hazami, L., Mama, R., and Thurairatnam, R. (2022).

Efﬁcient-vdvae: Less is more.

Ho, J., Jain, A., and Abbeel, P. (2020). Denoising diffusion

probabilistic models. NeurIPS, 33:6840–6851.

Jiang, L. (2022). Image super-resolution via it-

erative reﬁnement. https://github.com/Janspiry/

Image-Super-Resolution-via-Iterative-Reﬁnement.

Kang, M., Zhu, J.-Y., Zhang, R., Park, J., Shechtman, E.,

Paris, S., and Park, T. (2023). Scaling up gans for

text-to-image synthesis. In IEEE/CVF CVPR, pages

10124–10134.

Karras, T., Laine, S., and Aila, T. (2019). A style-based

generator architecture for generative adversarial net-

works. In IEEE/CVF CVPR, pages 4401–4410.

Kawar, B., Elad, M., Ermon, S., and Song, J. (2022). De-

noising diffusion restoration models. arXiv preprint

arXiv:2201.11793.

Kingma, D. P., Salimans, T., Jozefowicz, R., Chen, X.,

Sutskever, I., and Welling, M. (2016). Improved vari-

ational inference with inverse autoregressive ﬂow. Ad-

vances in neural information processing systems, 29.

Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-

ational bayes. arXiv preprint arXiv:1312.6114.

Lepcha, D. C., Goyal, B., Dogra, A., and Goyal, V. (2022).

Image super-resolution: A comprehensive review, re-

cent trends, challenges and applications. Information

Fusion.

Li, H., Yang, Y., Chang, M., Chen, S., Feng, H., Xu, Z.,

Li, Q., and Chen, Y. (2022). Srdiff: Single image

super-resolution with diffusion probabilistic models.

Neurocomputing, 479:47–59.

Liang, J., Lugmayr, A., Zhang, K., Danelljan, M.,

Van Gool, L., and Timofte, R. (2021). Hierarchi-

cal conditional ﬂow: A uniﬁed framework for image

super-resolution and image rescaling. In IEEE/CVF

ICCV, pages 4076–4085.

Lugmayr, A., Danelljan, M., Gool, L. V., and Timofte, R.

(2020). Srﬂow: Learning the super-resolution space

with normalizing ﬂow. In European conference on

computer vision, pages 715–732. Springer.

Lugmayr, A., Danelljan, M., and Timofte, R. (2021). Ntire

2021 learning the super-resolution space challenge. In

IEEE/CVF CVPR, pages 596–612.

Lugmayr, A., Danelljan, M., Timofte, R., Kim, K.-w., Kim,

Y., Lee, J.-y., Li, Z., Pan, J., Shim, D., Song, K.-U.,

et al. (2022). Ntire 2022 challenge on learning the

super-resolution space. In IEEE/CVF CVPR, pages

786–797.

Marinescu, R. V., Moyer, D., and Golland, P. (2020).

Bayesian image reconstruction using deep generative

models. arXiv preprint arXiv:2012.04567.

Mattei, P.-A. and Frellsen, J. (2018). Leveraging the exact

likelihood of deep latent variable models. NeurIPS,

31.

Menon, S., Damian, A., Hu, S., Ravi, N., and Rudin, C.

(2020). Pulse: Self-supervised photo upsampling via

latent space exploration of generative models. In

IEEE/CVF CVPR, pages 2437–2445.

Mittal, A., Moorthy, A. K., and Bovik, A. C. (2012).

No-reference image quality assessment in the spa-

tial domain. IEEE Trans. on Image Processing,

21(12):4695–4708.

Pan, X., Zhan, X., Dai, B., Lin, D., Loy, C. C., and

Luo, P. (2021). Exploiting deep generative prior for

versatile image restoration and manipulation. IEEE

Trans. on Pattern Analysis and Machine Intelligence,

44(11):7474–7489.

Poirier-Ginter, Y. and Lalonde, J.-F. (2023). Robust un-

supervised stylegan image restoration. In IEEE/CVF

CVPR, pages 22292–22301.

Prost, J., Houdard, A., Almansa, A., and Papadakis, N.

(2023). Inverse problem regularization with hierar-

chical variational autoencoders. In IEEE/CVF ICCV,

pages 22894–22905.

Richardson, E., Alaluf, Y., Patashnik, O., Nitzan, Y., Azar,

Y., Shapiro, S., and Cohen-Or, D. (2021). Encoding

in style: a stylegan encoder for image-to-image trans-

lation. In IEEE/CVF CVPR, pages 2287–2296.

Rombach, R., Blattmann, A., Lorenz, D., Esser, P., and Om-

mer, B. (2022). High-resolution image synthesis with

latent diffusion models. In IEEE/CVF CVPR, pages

10684–10695.

Saharia, C., Ho, J., Chan, W., Salimans, T., Fleet, D. J., and

Norouzi, M. (2021). Image super-resolution via itera-

tive reﬁnement. arXiv preprint arXiv:2104.07636.

Sønderby, C. K., Raiko, T., Maalø e, L., Sø nderby, S. r. K.,

and Winther, O. (2016). How to train deep variational

autoencoders and probabilistic ladder networks. In

NeurIPS, volume 29.

Song, J., Vahdat, A., Mardani, M., and Kautz, J. (2023).

Pseudoinverse-Guided Diffusion Models for Inverse

Problems. In (ICLR) ICLR.

Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Er-

mon, S., and Poole, B. (2021). Score-based generative

modeling through stochastic differential equations. In

ICLR.

Vahdat, A. and Kautz, J. (2020). Nvae: A deep hi-

erarchical variational autoencoder. arXiv preprint

arXiv:2007.03898.

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.

(2004). Image quality assessment: from error visi-

bility to structural similarity. IEEE transactions on

image processing, 13(4):600–612.

Zhang, R., Isola, P., Efros, A. A., Shechtman, E., and Wang,

O. (2018). The unreasonable effectiveness of deep

features as a perceptual metric. In IEEE CVPR, pages

586–595.

Zhou, H., Huang, C., Gao, S., and Zhuang, X. (2021).

Vspsr: Explorable super-resolution via variational

sparse representation. In IEEE/CVF CVPR, pages

373–381.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

400