A Sequential Heuristic for the Efﬁcient Management of a Work Center’s

Stocking Area

Fabrizio Marinelli

and Andrea Pizzuti

Dipartimento di Ingegneria dell’Informazione, Universit

a Politecnica delle Marche, Ancona I-60131, Italy

Keywords:

Packing Problem, Heuristic, Buffers Management, Manufacturing.

Abstract:

In our partnership with a leading company specializing in automatic cutting machines for reinforcement pro-

cesses, we address the management of a work center whose optimization calls for the solution of four distinct

subproblems. Focusing on the third one, the subproblem asks for the effective packing of items on the identical

buffers of a stocking area. The items arrive divided into subgroups (i.e., patterns), are associated with orders,

and have time windows. We devise an SVC heuristic that efﬁciently determines feasible packing solutions

while simultaneously minimizing the number of used buffers, lowering operations and fragmented orders.

The SVC incorporates the idea of reachable points to restrict the location sets on the buffers.

The experimental campaign highlights the SVC’s effectiveness in achieving optimality for small realistic in-

stances, with a speciﬁc emphasis on reducing fragmented orders. Additionally, the approach showcased its

ability to explore the multi-objective space and demonstrated scalability in solving practical instances.

1 INTRODUCTION

In today’s rapidly evolving manufacturing landscape,

efﬁciency, precision, and ﬂexibility are paramount for

companies striving to remain competitive. Cutting

processes are employed by a large variety of com-

panies to realize products and semi-ﬁnished prod-

ucts, distinguishing the treated materials and shapes

and depending on the subsequent destinations and

uses. The assortment of raw materials, the variety

of the parts to cut and their distribution of demands

typically affect the practical difﬁculty of identify-

ing effective patterns with small fractions of waste

ascher et al., 2007). The uses of parts cut, such

as further manufacturing, assembly, or handling op-

erations, call for a wider perspective in which cutting

processes are tightly interlaced with the whole ﬁrm

environment, and their effective management must

go beyond the simplistic material saving. Aspects

that cannot be neglected are, for instance, the num-

ber of setups (i.e., changes among cutting patterns)

(Umetani et al., 2003), the schedule of the operations

(Arbib and Marinelli, 2014) and the collection of parts

into temporary stacks (Belov and Scheithauer, 2007).

One signiﬁcant development in this pursuit of op-

https://orcid.org/0000-0003-0405-3110

https://orcid.org/0000-0003-3255-8378

erational excellence is the utilization of work cen-

ters designed for cutting material and seamlessly

handling it through integrated stock areas. These

advanced work centers represent a convergence of

cutting-edge technologies, automation, and intelligent

logistics management. They have modiﬁed traditional

manufacturing paradigms by offering a holistic solu-

tion that addresses the challenges of material process-

ing.

Based on the model of a prominent partner com-

pany (see the diagram in Figure 1), known for its lead-

ership in designing and assembling automatic man-

ufacturing machines, we illustrate the characteristics

and the operations of a sophisticated work center em-

ployed for both cutting and handling iron bars in the

reinforcement processes.

Figure 1: Block diagram of the manufacturing work center.

Arrows represent tracks for material handling.

Marinelli, F. and Pizzuti, A.

A Sequential Heuristic for the Efﬁcient Management of a Work Center’s Stocking Area.

DOI: 10.5220/0012352000003639

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 253-260

ISBN: 978-989-758-681-1; ISSN: 2184-4372

253

The work center includes a material loading ma-

chine for bar provision, capable of storing up to three

assortments of materials. Each material has its spe-

ciﬁc length and diameter and includes a certain quan-

tity of bars. Operators also can manually introduce

additional materials into the loading machine.

A conveyor belt serves as the conduit for trans-

ferring batches of uniform iron bars to an automatic

hydraulic cutter. This cutting system carries out se-

quential cuts according to cutting stock solutions pre-

calculated by the company’s optimizing software.

Following each cutting operation, the resulting

parts are released onto a transfer track. These are sub-

sequently moved to speciﬁc coordinates, a process fa-

cilitated by mechanical dividers.

The transfer track is positioned between two sym-

metrical and identical unloading stations. Here, the

parts are overturned among the stations and grouped

into homogeneous lots; i.e., lots that share the same

order code and have identical geometric attributes.

Two portals equipped with grippers are stationed at

the unloading stations. A portal empties its related

station by collecting all the available lots and allo-

cating the lots through lowering operations in a dedi-

cated stocking area. This area hosts identical parallel

buffers designed for lot collection. Importantly, ho-

mogeneous lots may be efﬁciently stacked together.

The portals offer ﬂexibility by translating over the

stocking areas, while lots are transferred exclusively

lengthwise without altering their horizontal coordi-

nates. Furthermore, the grippers on each portal oper-

ate independently, allowing for the separate allocation

or retrieval of individual lots.

Once an order is consolidated, requests may ar-

rive from downstream departments. The portals are

then tasked with transporting the consolidated orders

to releasing depots, positioned on both sides of the

system. From these depots, the ﬁnalized orders leave

the work center for further processing or distribution.

In the work center, the automatic cutter plays a

critical role and acts as a bottleneck. It must halt

its operation if the produced parts cannot ﬁnd an al-

location on the unloading stations, resulting in ma-

chine idle time. To maximize system efﬁciency, it

is needed to effectively utilize the unloading stations,

the buffers in stocking areas, and the portals. Given

the challenging nature of the problem at hand, we di-

vide the process into four distinct subproblems:

i) PATTERN SEQUENCING OPTIMIZATION: This

entails determining the optimal sequence of pat-

terns to minimize the spread of orders.

ii) PART PARTITIONING ON THE UNLOADING STA-

TIONS: Subsets of parts are allocated between the

two unloading stations to compose homogeneous

lots, limiting the number of ofﬂoading operations.

iii) OPTIMAL MANAGEMENT OF THE STOCKING

AREA: The lots on an unloading station are trans-

ferred through a portal on the buffers of the stock-

ing area, optimizing the occupied space and the

stacking of lots.

iv) SCHEDULE OF THE RELEASES OF CONSOLI-

DATED ORDERS: The timing and scheduling of

consolidated orders’ release are decided to mini-

mize the portal’s busy time.

Because of the limited space, in this paper we fo-

cus on addressing subproblem iii). We introduce a

sequential value correction heuristic (SVC) designed

to optimize the packing of lots onto parallel buffers

within a stocking area in a multi-objective fashion,

generating a pool of non-dominated solutions. Op-

timization criteria are the minimization of the occu-

pied space, the reduction of portal lowering opera-

tions, and the mitigation of order fragmentation. The

SVC embeds the concept of reachable points to effec-

tively describe the set of feasible destinations for lots

on the buffers.

2 PROBLEM DEFINITION

In this section, we formalize the problem by describ-

ing the problem features and details while introducing

some convenient notation.

The stocking area is modeled as a discretized grid

of locations (b, s) ∈ B × S, where the m buffers in B

correspond to rows and slots in S are the columns.

Each row has a width W given by the total width of

the |S| identical slots of size w.

We indicate with L the bill of orders and with I

the set of items (lots) to allocate, such that |I| = n.

Each order l is a subset of homogeneous items with

the same width w

= w

(assumed as multiple of w),

a release date r

, and a due date d

= d

. A subset of

items S

⊂ S can be trivially identiﬁed for each item i,

limited to eligible items s ∈ S such that s ≤ W − w

1. An order is considered fragmented if at least two

items i, j ∈ l are packed in different locations. We use

to refer to the order comprising item i.

Items arrive partitioned into unloading groups

(patterns) according to an ordered list P =<

, . . . , p

>. Each pattern is a subset of items ﬁtting

within the capacity of the station W . Items must be

packed without overlapping on the buffer slots and a

safety slack (i.e., a minimum number of empty slots

between any two items) can be requested for applica-

tion extent. The only exception holds for items shar-

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

254

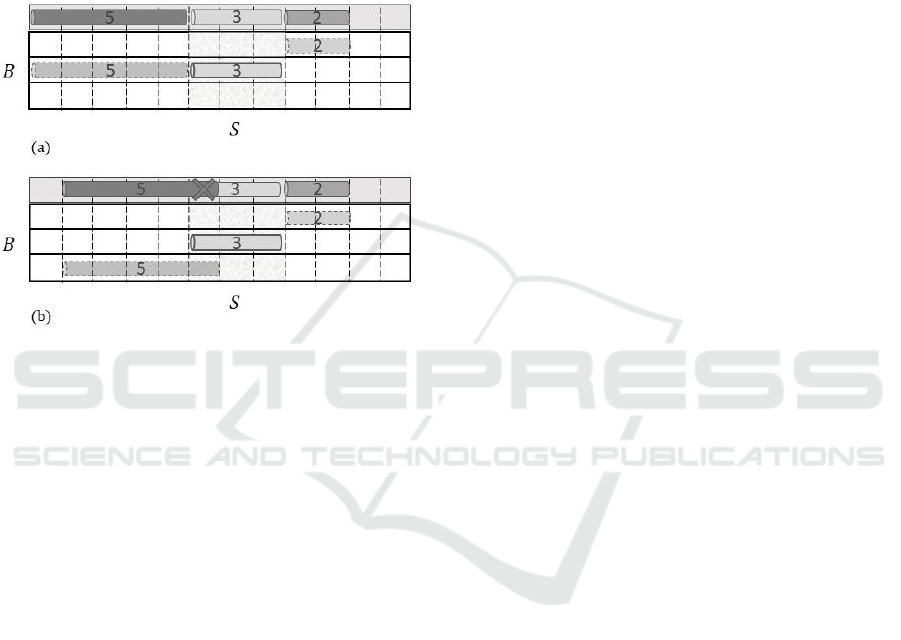
ing an order, which can be stacked on the same buffer

locations.

Each item in a pattern requires the selection of an

absolute position s (i.e., left-side slot coordinate) to

be occupied both on the station, before being packed,

and on the destination buffer b, after the lengthwise

transport and the portal lowering. Note that, due to

the independent grippers of the portal, two items in a

pattern can be packed on different buffers using two

distinct lowering operations (see Figure 2).

Figure 2: A pattern made by three items 5, 3 and 2 on the

unloading station (light grey area). Item 3 is stacked on the

homogeneous item (bolded), the shaded area is the overlap-

ping area. Dashed bars indicate the selected locations of 2

and 5. (a) is a feasible selection of locations, (b) is unfeasi-

ble due to the overlap on the unloading station.

We express for brevity with i ∈ p if item i belongs

to the pattern p, with p

∈ P the pattern containing i.

Concerning the item dates, r

and d

are set as mul-

tiples of the unloading cycle (i.e., input patterns); e.g.,

= 2 and d

= 7 indicate respectively p

= p

and p

as the instant for the release of l

. In our setting, d

coincides with the last pattern containing an item in

order l. Thus, an item i ∈ l persists in the stocking

area within the time window [r

, d

]. At time d

, all

the items in l are collected and moved toward down-

stream departments through the release depot. Hence,

two items i and h such that l

6= l

cannot share buffer

locations only if their time windows overlap; that is,

, d

] ∩ [r

, d

] 6=

As evaluation criteria for the problem, three mea-

sures are optimized in a multi-objective framework:

the number of buffers employed during the whole

packing procedure (D), the total number of lowering

operations performed by the portal (L), and the num-

ber of fragmented orders (F). While D is an estima-

tion of the required stocking area’s size m, L evaluates

the portal workload and F gives a measure of the po-

tential saving in terms of space (and time, if looking

at the ﬁnalized order release) that one may reach by

relying on the stacking. To avoid trivial fragmenta-

tion, we assume that in any pattern p each item i ∈ p

belongs to a distinct order l.

2.1 Related Problems

The problem at hand is an extended one-dimensional

bin packing problem (BPP) (Martello and Toth, 1990)

that incorporates four additional peculiarities: the in-

put consists of item groups (patterns), packing is done

through lengthwise movements, items can be oppor-

tunely stacked and have time windows. To the best of

our knowledge, no literature has addressed all these

aspects simultaneously.

Regarding the input, the concept can be related to

the bin packing with fragmentation problem (Casazza

and Ceselli, 2016). In this problem, objects (our pat-

terns) can be fragmented into multiple parts, and the

goal is to minimize the number of bins used while

limiting fragmentation or vice versa. However, in our

scenario, fragments are restricted to the items within

a pattern. Additionally, it can be easily seen that the

cost associated with the item fragmentation does not

directly correspond to the number of required lower-

ing operations.

The constraint imposed by portal lengthwise

movements must be considered alongside the ﬁrst

aspect; otherwise, singleton patterns (single items)

wouldn’t be affected. The use of portals suggests

a connection with storage yard operations in con-

tainer terminals (Carlo et al., 2014) where rail-

mounted gantry cranes are employed for container

storage/retrieval and are limited by rails. In con-

tainer yard operations, containers arrive separately by

trucks, and the options for concurrent storage oper-

ations depend on the yard layout and crane type, but

these operations follow different allocation rules from

our packing problem.

The opportunity to stack homogeneous items has

also been explored in virtual machine packing or pag-

ination problems (Grange et al., 2018). Virtual ma-

chine packing involves allocating virtual machines

(tiles) to a minimum number of servers (pages) to save

resources between VMs sharing memory pages (sym-

bols). In our context, virtual machines can be seen

as patterns, servers as buffers, and symbols as items.

However, there are differences: item sizes are not uni-

tary as the symbols, and items within the same pattern

may be placed in different locations.

This last point mismatches the assumptions set

in the hypergraph partitioning problem (C¸ ataly

urek

et al., 2023). In this problem, hypergraph vertices

represent our patterns, hyperedges represent orders

A Sequential Heuristic for the Efﬁcient Management of a Work Center’s Stocking Area

255

shared by connected vertices, and hyperedge weights

are order widths. Hypergraph partitioning typically

asks a ﬁxed number of partitions (used buffers) and

focuses on balancing the partition sizes, in place of

observing a capacity constraint.

Lastly, time windows recall the recent temporal

bin packing problem (Dell’Amico et al., 2020). Re-

lease and due dates are associated with items and the

number of used bins must be reduced while consid-

ering the renewable resources. Although relatively

new, several contributions have already been made to

this problem; for a detailed literature review, refer to

(Martinovic et al., 2023).

In conclusion, the SVC heuristic warrants some

attention. Instead of opting for a rigorous yet time-

consuming approach involving exact dual prices for

pricing problems, algorithms of this kind use pseudo-

prices to gradually construct individual patterns. This

approach has proven to efﬁciently compute good pri-

mal bounds in various packing scenarios, including

the classical BPP (Cui et al., 2015) and CSP (Belov

and Scheithauer, 2007), as well as their extended (Ar-

bib et al., 2021) and enriched (Arbib. et al., 2018)

versions.

2.2 Reachable Points

Any solution to the problem provides a packing

of items on the buffer locations. The set of slots

amenable for placing the left side of item i are the

ones that geometrically allow to respect buffer bound-

aries, and the ones that, once selected, admit a feasi-

ble position of the other items in p

at the unloading

station. While the former was naturally embedded in

the deﬁnition of each S

, the latter can be exploited to

reduce the set of feasible locations.

We call reachable points, namely r-points, the set

of the slots in which the left-side of item i can

be located and there still exists a way to pack each

h ∈ p

\ {i}. Clearly, R

⊆ S

holds. Similarly to the

procedure described in (Arbib et al., 2023), for all

i ∈ p the sets R

can be computed through dynamic

programming for the enumeration of the items left-

side coordinates where p gives rise to a normal pat-

tern (Christoﬁdes and Whitlock, 1977). A standard

dynamic programming algorithm requires O(|p|

W )

operations per pattern.

An additional step can be further implemented to

reduce the number of potential locations in each R

Given an order l, each i ∈ l has a restricted

given

only by the r-points common to all items in l. For-

mally, we are imposing:

= ∩

h∈l

for each item i ∈ I. Experiments on small instances

showed that such construction can reduce the total

number of r-points up to 27.0% compared to the r-

points counted in

∑

i∈I

|. The major drawback lies

in pruning some of the solutions with fragmented or-

ders, which can end up with an unfeasible instance if

any

0 holds.

3 A SEQUENTIAL VALUE

CORRECTION HEURISTIC

Preliminary experiments carried out on real-world in-

stances by using the mixed integer linear program M

presented in (Pizzuti et al., 2022), showed the non-

viability of the formulation. More in general, the

company’s requirements demand a sufﬁciently efﬁ-

cient (and effective) solution method able to quickly

identify packing strategies from scratch, and possibly

re-optimizing for replying to the modiﬁcations of op-

erations planning and work center status. For these

reasons, we designed an SVC heuristic.

Given an ordered list P of unloading patterns, the

SVC is used to build a tentative packing of items on

the buffers of the stocking area. The algorithm initial-

izes a pseudo-price λ

to each order l ∈ L according

to formula

− min

i∈l

}

|P|

The initialization promotes orders (items) with higher

widths and longer time windows, which are critical to

ﬁnding initial feasible (and possibly good) solutions.

The SVC runs by packing orders’ items following

non-increasing values of λ

and the sequence of the

patterns in P; i.e., given i, h ∈ l, i is packed before h

if i ∈ p

, h ∈ p

and k < j. A packing decision must

select a location (b, s) for the left side of the item i.

Only its r-points, R

depending on the search-

ing strategy, are considered feasible slots. Thus, each

couple (b, s) is tested and a location can be chosen if

all (b, s), . . . , (b, s+w

−1) are available within [r

, d

or are occupied by h ∈ l

The best location (

b, ˜s) is selected according to hi-

erarchically ordered local criteria:

1. the smallest number of r-points forbidden to the

remaining items of p

after packing i;

2. the smallest number of locations used by items i ∈

3. the largest number of simultaneous packing on

buffer

4. the largest number of simultaneous collections

from buffers;

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

256

5. the smallest number of available slots to the right

of ˜s in

b, divided by the length of [r

, d

6. the largest number of unused periods (i.e., pat-

terns) of the selected location.

Whenever an item is packed, locations

(

b, ˜s), . . . , (

b, ˜s + w

− 1) are ﬂagged as occupied

for each time step [r

, d

]. The r-points of each h ∈ p

are coherently updated to prevent overlapping.

Once all orders’ items are processed, a new fea-

sible solution is stored in the pool if non-dominated

with respect to D, L, and F criteria.

The pseudo-prices are then conveniently enlarged

by accounting for two terms: ﬁrstly, the ratio between

the number of the used different locations by items

i ∈ l and the number of patterns including any such

i; secondly, only for the orders with an item packed

in the D-th buffer, the ratio between the current D

and m. While the former contributes to prioritizing

currently fragmented orders, the latter advantages the

orders packed after long persisting ones.

The SVC heuristic is repeated up to N

SVC

times

and the pool of non-dominated solutions is ﬁnally re-

turned.

Using the sets

as r-points may lead to unfeasi-

ble partial solutions due to the over-reduction induced

by the intersection step. To avoid this, in our imple-

mentation the algorithm ﬁrstly tries the packing with

, then looks for alternative feasible locations in R

once an unfeasibility occurs. Only if this second at-

tempt fails, the current iteration is interrupted without

a valid solution.

By using this scheme, in our experiments the SVC

was able to converge to high-quality packing, in par-

ticular with low values of F and D, while avoiding

unfeasible states.

To provide a concise overview of the SVC heuris-

tic, its pseudocode is provided in Algorithm 1. The

initialization steps are performed by using dynamic

programming (Line 1, see Section 2.2) and in lin-

ear time (Line 2), respectively. Sorting is done in

O(|L| · log|L|) (Line 3) and r-points matrices are re-

freshed in O(|I| · W ) (Line 4). Finding the best lo-

cations (Lines 9 and 11) demands testing at most

O(m · |S|) positions, packing item i (Line 16) requires

O(|P| · W) locations modiﬁcations, and updating the

r-points matrices (Line 17) is done in O(|L| · W ) as

|p| ≤ |L| for any p ∈ P. These three steps are per-

formed for each item i ∈ I, thus asking O(|I|·(m·|S|+

|P| · W + |L| · W )). To compute the objective crite-

ria (Line 20), one needs to ﬁnd the largest employed

buffer b in the process lasting |P| time frames, and

to count the number of lowering operations and frag-

mented orders; i.e., O(

∑

p∈P

|p|

) and O(

∑

l∈L

|l|

respectively. Updating the pseudo-prices is done in

linear time. Finally, the core (Lines 4-24) is repeated

SVC

times.

Algorithm 1: SVC heuristic.

Data: Sets L, I and P, parameters B and S

Result: Pool Sol of non-dominated solutions.

1 Initialize R

and

for each i ∈ I;

2 Initialize λ

for each l ∈ L;

3 for N

SVC

times do

4 Sort orders by non-increasing λ

;

5 Reset R

and

for each i ∈ I;

6 sol =

7 (

b, ˜s) = ∅;

8 for l ∈ L, i ∈ l do

9 Find best location (

b, ˜s) ∈ B×

;

10 if ¬(

b, ˜s) then

11 Find best location (

b, ˜s) ∈ B×R

;

12 if ¬(

b, ˜s) then

13 go to 21;

14 end

15 end

16 Pack i to (

b, ˜s) within [r

, d

];

17 Update R

and

for each h ∈ p

;

18 end

19 Update sol;

20 Compute criteria values D, L and F;

21 if ¬dominated(sol) then

22 Add sol to pool Sol;

23 end

24 Update λ

for each l ∈ L;

25 end

26 return Sol;

4 COMPUTATIONAL RESULTS

Computational experiments were carried out on an

Intel

Core(TM) i7-7500U 2.70 GHz with 16Gb

RAM. The SVC algorithm was coded in C++ and runs

with N

SVC

= 1000. For the sake of comparison on

small cases, the mixed integer linear program M pre-

sented in (Pizzuti et al., 2022) was employed by using

IBM

CPLEX

12.8.0.0 with a time limit of 3600

seconds.

The experimental campaign counted two test

beds: ten small realistic instances S = {I

, . . . , I

}

with 15 orders, whose features were generated sim-

ilarly to the real ones; ﬁve real-world instances R =

, . . . , J

} provided by the industrial partner with up

to 105 orders. The grid sizes were set to |S| = 33

and m = 12, although the model M employed only

5 buffers. This allowed to optimally solve some of

A Sequential Heuristic for the Efﬁcient Management of a Work Center’s Stocking Area

257

Table 1: Basic features of instances S , analysis on the r-points, results achieved by M and SVC.

r-points M SVC

S |P| n R R

T T

tot

B L F T |Sol| T

tot

12 32 426 56.5 311 41.2 7.1 415.2 4 14 1 0.2 1 0.8

16 36 505 62.2 409 50.4 34.3 3600.0 5 21 2 0.4 5 1.3

11 27 468 73.1 388 60.6 10.2 68.1 4 13 0 0.1 4 1.0

15 32 601 81.7 496 67.4 17.0 3600.0 4 18 2 0.4 1 1.3

12 26 502 82.7 458 75.5 0.0 35.1 3 12 0 0.0 1 1.0

15 28 503 81.5 410 66.5 7.4 320.4 4 16 1 0.2 2 1.3

11 27 471 74.5 407 64.4 0.0 18.2 3 13 0 0.6 3 0.9

13 33 599 76.4 491 62.6 8.7 3600.0 4 18 2 0.9 2 1.3

11 27 459 72.2 367 57.7 1.2 13.6 3 14 0 0.1 3 1.0

15 35 592 72.3 462 56.4 11.8 3600.0 5 19 1 0.2 3 1.3

avg. 13.1 30.3 512.6 73.3 419.9 60.3 9.8 1527.1 3.9 15.8 0.9 0.3 2.5 1.1

the instances in S by using M within the time limit,

whereas on R this never occurred. Given the poor

performance of M on the second test bed, we do not

explicitly report the results.

In the ﬁrst set of experiments, the objective func-

tion was assumed to be D + L + |I| · F compliantly

with the hypothesis set in M . Furthermore, the model

made use of the tighter sets of r-points

Starting from the left, Table 1 reports the details

of the instances in S within the ﬁrst three columns.

Then, statistics are given about the employed r-points:

R (

R) counts the total number of r-points in the sets

(

), whereas R

(

) gives the percentage used

points with respect to the initial

∑

i∈I

. Columns

8 and 9 provide the CPU times of the MILP, where

T generally indicates the time required to compute

the best primal solution and T

tot

refers to the total

approach running time. For M , when T

tot

= 3600

means that the time limit was reached without prov-

ing the solution optimality. Finally, the remaining six

columns show, the objective function components of

the minimum cost solutions, the CPU times, and the

number of non-dominated solutions |Sol| found by the

SVC for the multi-objective problem.

By using the sets R

, the r-points diminished on

the mean by 26.3%, lasting 512.6 per instance on the

average. The further intersection step cut an addi-

tional 18.1% of the remaining r-points, leaving on the

mean 419.9 per instance (the 60.3% of the original

ones).

Moving to the SVC performance, the algorithm

was always able to ﬁnd the best primal solution com-

puted by M . The objective function prioritized the

reduction of the fragmented orders, which were 0.9

on the mean. Expect for I

and I

, the CPU time de-

manded by the SVC was always smaller at least by

one order of magnitude. Looking at T

tot

, the SVC al-

ways terminated in 1.3 seconds and took 11.2 seconds

in total to run on the whole test bed. To certify the op-

timality on closed instances (6 out of 10) M needed

870.6 seconds in total.

Finally, the SVC identiﬁed 2.5 solutions on the

mean per instance, only in 20% of the cases with

B > 5 (in instances I

and I

For the group R , Table 2 reports the instance fea-

tures and the analysis of the r-points. Without recur-

ring to the intersect step, the r-points in R

are 89.0%

on the average of the initial points, which is signif-

icantly more than the 73.3% achieved in S . On the

other hand, the intersection cut widely more points

on this set, up to 75.1% in J

and 48.8% on the mean.

Overall, the 53.3% of the original points were pruned

by the procedure.

Table 2: Basic features of instances R and analysis on the

r-points.

r-points

R |L| |P| n R R

24 25 89 1724 72.3 430 18.0

25 26 30 580 98.8 447 76.1

80 60 156 3723 93.3 1723 43.2

84 90 138 3219 91.6 1841 52.4

105 74 186 4072 89.0 2063 45.1

avg. 63.6 55.0 119.8 2663.6 89.0 1300.8 47.0

Table 3 shows the full pool of non-dominated so-

lutions per instance, ordered by the required running

time T. The SVC identiﬁed 5.8 solutions on the mean

per instance, demonstrating its capability of diversify-

ing the search. The values of L and F showed a more

pronounced variability (with standard deviations up to

4.5 and 3.9 in J

) than D (at most 1.2 of standard devi-

ation in J

). This is understandable since an excessive

increment in the number of the employed buffers typ-

ically compromises the performance on L and F, both

asking for compact packing (the former among a pat-

tern’s items, the latter among order’s items).

The algorithm required 13.7 seconds on average

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

258

Table 3: Results obtained by SVC on instances R .

SVC

R |Sol| T

tot

D L F T

5 3.3 4 53 7 1.2

6 52 5 1.5

4 47 9 1.7

5 43 6 1.9

5 42 16 2.5

1 12.9 2 10 0 11.7

8 18.2 3 75 11 7.7

3 74 13 8.5

3 71 16 8.6

4 68 9 8.7

6 67 9 8.7

6 68 8 12.2

4 66 10 16.8

4 69 5 18.1

4 14.9 4 61 2 3.9

3 62 2 5.2

4 63 1 6.0

3 64 1 11.1

11 19.2 4 77 14 6.9

6 69 11 7.4

6 73 10 7.5

5 78 10 7.6

5 70 15 12.7

6 67 13 15.1

5 71 11 15.4

6 75 9 15.4

4 73 15 15.9

6 77 8 16.7

4 82 11 17.8

avg. 5.8 13.7 - - - -

to terminate and at most 19.2 seconds for the largest

instance with 105 orders. The computational burden

scaled reasonably along with the input size.

Overall, the solutions provided by the SVC ful-

ﬁlled the prescribed requirements and the algorithm is

currently exploited in the partner company’s system.

5 CONCLUSIONS AND

PERSPECTIVES

In the context of a partnership with a leading company

in the design and assembly of automatic cutting ma-

chines for the reinforcement processes, we described

the process performed by a work center model whose

efﬁcient management asks for the challenging solu-

tion of four distinct subproblems.

We focused on a peculiar packing subproblem for

the optimal management of the identical buffers in the

stocking area. In our problem items belong to orders,

can be stacked in the same location if homogeneous

and each has a relevant time window. Moreover, items

arrive according to a prescribed list of patterns and,

for each pattern, the items included cannot occupy co-

ordinates that overlap even on different buffers.

We implemented an SVC heuristic to efﬁciently

compute feasible packing minimizing the number of

employed buffers, the total number of lowering opera-

tions, and the number of fragmented orders in a multi-

objective fashion. The performance of the procedure

was enhanced by embedding the concept of r-points

as restricted sets of feasible destinations.

The experimental campaign highlighted the efﬁ-

cacy and efﬁciency of the SVC in optimally solving

small realistic instances while prioritizing the reduc-

tion of fragmented orders. Moreover, on real-world

instances results assessed the capability of exploring

the multi-objective space by diversifying the search,

and the scalability of the approach.

As future work we aim at handling subproblem

iv), concerning the schedule of ﬁnalized orders’ re-

lease with arbitrary due dates, in the solution algo-

rithm to reduce the portal workload for the evacua-

tions of the buffers. Furthermore, the design of an

algorithmic scheme that embeds the SVC and can ef-

ﬁciently solve the work center management problem

as a whole is currently under investigation.

REFERENCES

Arbib, C. and Marinelli, F. (2014). On cutting stock with

due dates. Omega, 46:11–20.

Arbib, C., Marinelli, F., Pferschy, U., and Ranjbar, F. K.

(2023). One-dimensional stock cutting resilient

against singular random defects. Computers & Op-

erations Research, 157:106280.

Arbib, C., Marinelli, F., and Pizzuti, A. (2021). Number

of bins and maximum lateness minimization in two-

dimensional bin packing. European Journal of Oper-

ational Research, 291(1):101–113.

Arbib., C., Marinelli., F., Pizzuti., A., and Rosetti., R.

(2018). A heuristic for a rich and real two-dimensional

woodboard cutting problem. In Proceedings of the

7th International Conference on Operations Research

and Enterprise Systems - ICORES, pages 31–37. IN-

STICC, SciTePress.

Belov, G. and Scheithauer, G. (2007). Setup and open-

stacks minimization in one-dimensional stock cutting.

INFORMS J. on Computing, 19(1):27–35.

Carlo, H. J., Vis, I. F., and Roodbergen, K. J. (2014). Stor-

age yard operations in container terminals: Litera-

ture overview, trends, and research directions. Euro-

pean Journal of Operational Research, 235(2):412–

430. Maritime Logistics.

Casazza, M. and Ceselli, A. (2016). Exactly solving pack-

A Sequential Heuristic for the Efﬁcient Management of a Work Center’s Stocking Area

259

ing problems with fragmentation. Computers & Op-

erations Research, 75:202–213.

C¸ ataly

urek, U., Devine, K., Faraj, M., Gottesb

uren, L.,

Heuer, T., Meyerhenke, H., Sanders, P., Schlag, S.,

Schulz, C., Seemaier, D., and Wagner, D. (2023).

More recent advances in (hyper)graph partitioning.

ACM Comput. Surv., 55(12).

Christoﬁdes, N. and Whitlock, C. (1977). An algorithm for

two-dimensional cutting problems. Operations Re-

search, 25(1):30–44.

Cui, Y.-P., Cui, Y., and Tang, T. (2015). Sequential heuris-

tic for the two-dimensional bin-packing problem. Eu-

ropean Journal of Operational Research, 240(1):43 –

53.

Dell’Amico, M., Furini, F., and Iori, M. (2020). A

branch-and-price algorithm for the temporal bin pack-

ing problem. Computers & Operations Research,

114:104825.

Grange, A., Kacem, I., and Martin, S. (2018). Algorithms

for the bin packing problem with overlapping items.

Computers & Industrial Engineering, 115:331–341.

Martello, S. and Toth, P. (1990). Knapsack Problems: Al-

gorithms and Computer Implementations. John Wiley

& Sons, Inc., USA.

Martinovic, J., Strasdat, N., Val

erio de Carvalho, J., and

Furini, F. (2023). A combinatorial ﬂow-based formu-

lation for temporal bin packing problems. European

Journal of Operational Research, 307(2):554–574.

Pizzuti, A., Lausdei, P., and Marinelli, F. (2022). Optimal

allocation of the unloading buffers of a cutting ma-

chine in iron manufacturing. In Euro 2022 - 32st Eu-

ropean Conference on Operational Research - Espoo.

Book of Abstracts.

Umetani, S., Yagiura, M., and Ibaraki, T. (2003). One-

dimensional cutting stock problem to minimize the

number of different patterns. European Journal of Op-

erational Research, 146(2):388 – 402.

ascher, G., Haußner, H., and Schumann, H. (2007). An

improved typology of cutting and packing problems.

Eur. J. Oper. Res., 183:1109–1130.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

260