Exploring Unsupervised Anomaly Detection with Quantum Boltzmann

Machines in Fraud Detection

Jonas Stein

, Dani

elle Schuman

, Magdalena Benkard

, Thomas Holger

, Wanja Sajko

Michael K

olle

, Jonas N

ußlein

, Leo S

unkel

, Olivier Salomon

and Claudia Linnhoff-Popien

LMU Munich, Germany

Allianz, France

ﬁ

Keywords:

Quantum Boltzmann Machine, Quantum Annealing, Anomaly Detection.

Abstract:

Anomaly detection in Endpoint Detection and Response (EDR) is a critical task in cybersecurity programs

of large companies. With rapidly growing amounts of data and the omnipresence of zero-day attacks, man-

ual and rule-based detection techniques are no longer eligible in practice. While classical machine learning

approaches to this problem exist, they frequently show unsatisfactory performance in differentiating mali-

cious from benign anomalies. A promising approach to attain superior generalization compard to currently

employed machine learning techniques is using quantum generative models. Allowing for the largest represen-

tation of data on available quantum hardware, we investigate Quantum-Annealing-based Quantum Boltzmann

Machines (QBMs) for the given problem. We contribute the ﬁrst fully unsupervised approach for the prob-

lem of anomaly detection using QBMs and evaluate its performance on an EDR-inspired synthetic dataset.

Our results indicate that QBMs can outperform their classical analog (i.e., Restricted Boltzmann Machines) in

terms of result quality and training steps in special cases. When employing Quantum Annealers from D-Wave

Systems, we conclude that either more accurate classical simulators or substantially more QPU time is needed

to conduct the necessary hyperparameter optimization allowing to replicate our simulation results on quantum

hardware.

1 INTRODUCTION

Anomaly detection is the identiﬁcation of abnormal

behavior in data, which manifests in individual data

points that differ signiﬁcantly from the majority of

the data (Chandola et al., 2009). This task fre-

quently appears in many domains including ﬁnance,

medicine and telecommunications (Aleskerov et al.,

1997; Spence et al., 2001; Kumar, 2005). A particu-

larly challenging application of Anomaly Detection

can be found in Endpoint Detection and Response

(EDR), which aims at detecting and investigating sus-

picious activities on endpoints such as mobile phones

or workstations in cybersecurity (Chuvakin, 2023). In

practice, the respective networks can be comprised of

billions of nodes, generating an immense amount of

data, in which the search for extremely scarce, mali-

cious anomalies can be very tedious.

This vast number of typically high-dimensional

data points and additional impediments such as zero-

day attacks raise a demand for suitable anomaly de-

tection techniques deviating from the still widely-

used manual and rule-based approaches. While many

classical machine learning approaches to this mostly

unsupervised learning problem exist, (e.g., cluster-

ing (Muniyandi et al., 2012), autoencoders (Finke

et al., 2021) or Bayesian networks (Mascaro et al.,

2014)), the distinction between malicious and benign

anomalies frequently remains intractable due to insuf-

ﬁcient generalization (Karami, 2018). This problem

substantiates in a trade-off between detecting an un-

acceptably high number of false positives (i.e., benign

data) and failing to reliably detect all true positives

(i.e., the malicious anomalies).

In search for alternative approaches that can cope

with the encountered real world data better, we inves-

tigate the application of Quantum Computing (QC)

to this problem, as QC has shown promising perfor-

mance in generative data modelling, which is a pop-

ular technique used in unsupervised anomaly detec-

tion (Zhu et al., 2022). The three most prominent

prospects of using QC-based approaches in this con-

text are likely (1) that they need less data points dur-

ing training (Caro et al., 2022), (2) that they can per-

Stein, J., Schuman, D., Benkard, M., Holger, T., Sajko, W., Kölle, M., Nüßlein, J., Sünkel, L., Salomon, O. and Linnhoff-Popien, C.

Exploring Unsupervised Anomaly Detection with Quantum Boltzmann Machines in Fraud Detection.

DOI: 10.5220/0012326100003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 2, pages 177-185

ISBN: 978-989-758-680-4; ISSN: 2184-433X

177

form the central step of sampling from the model

distribution signiﬁcantly more efﬁciently than their

classical analogs (Amin et al., 2018) and (3), that

they have shown the ability to efﬁciently sample

from some speciﬁc classically intractable data distri-

butions (Hangleiter and Eisert, 2023). The general

motivation behind using generative models speciﬁ-

cally for unsupervised anomaly detection is that their

core functionality of replicating a given data distri-

bution yields a data model that closely represents the

input dataset with the exclusion of all anomalies, as

they are too scarce to be learned reliably. Therefore,

anomalies can be detected by verifying their absence

in the generated data distribution.

A particularly powerful type of quantum gen-

erative models are Quantum Boltzmann Machines

(QBMs) (Amin et al., 2018), which have been shown

to be universal approximators for probability distri-

butions (Sussmann, 1988; Younes, 1996; Amin et al.,

2018; Wiebe and Wossnig, 2019). QBMs can be un-

derstood as a quantum analog to classical Boltzmann

Machines. The core difference is displayed in the

sampling procedure, in which the QBM represents

an approximate Boltzmann distribution in a quantum

state, which generally allows for efﬁcient sampling

via measurements. Curious to investigate the scal-

ing performance of such quantum approaches in terms

of, i.a., the dimensionality of the dataset, we select

a Quantum-Annealing-based implementation of this

sampling step, as its physical implementations have a

key advantage over the usage of gate based quantum

computers: They currently offer the highest number

of qubits, which is the central factor for the repre-

sentable dimensionality of the dataset.

Framed by related concepts in literature, we con-

tribute the ﬁrst fully unsupervised anomaly detection

based on QBMs and evaluate its performance on suit-

ably generated synthetic datasets. Our core contribu-

tions to the investigation of the applicability of Quan-

tum Boltzmann Machines for unsupervised anomaly

detection amount to the following:

• We introduce the ﬁrst fully unsupervised anomaly

detection approach using QBMs.

• We conduct a case study evaluating the presented

approach on two D-Wave Quantum Annealers

while using a similarly sized classical Restriced

Boltzmann Machine (RBM) as baseline.

The subsequent contents of this paper are struc-

tured as follows. In section 2, we explain the func-

tionality of Boltzmann Machines and their variants.

In section 3, we give an overview of related work.

In section 4, we present our methodology on how

Quantum Boltzmann Machines can be used to detect

anomalies in a fully unsupervised manner. In sec-

tion 5, we show how suitable hyperparameters can be

chosen and evaluate the results achieved, comparing

classical and quantum hardware. Finally, section 6

concludes our ﬁndings and demonstrates possible fu-

ture work.

2 BACKGROUND

2.1 Boltzmann Machines

A classical Boltzmann Machine (BM) is an undi-

rected, stochastic neuronal network, which typically

consists of two or more separate layers and is not

restricted in its nodes’ connections. For the sake of

simplicity, we assume a very basic BM consisting of

two layers in the following explanation. BMs contain

exactly one input layer which simultaneously acts as

the output layer and is also referred to as visible layer

v = (v

,...,v

) ∈ {0, 1}

, consisting of visible units

. The other layers are referred to as hidden lay-

ers h = (h

,...,h

) ∈ {0,1}

and likewise consist of

hidden units h

. Both hidden and visible units are re-

stricted to assume the values zero or one. The proba-

bility of a speciﬁc conﬁguration of (v,h) occurring in

practice is determined by a stochastic distribution –

the Boltzmann distribution p (Fischer and Igel, 2012)

in which T > 0 denotes a speciﬁc parameter called

temperature, which we can assume as a given con-

stant for now:

p(v,h,θ) =

exp



−

E(v,h,θ)



with Z =

∑

(v,h)∈{0,1}

N×M

exp



−

E(v,h,θ)



where θ ≡ {W

i j

(0)

(1)

} denotes the weights W

i j

be-

tween units as well as the biases and acting on all vis-

ible and hidden units b

(0)

and b

(1)

. The Boltzmann

distribution is determined by the energy function E,

which is generally expressed as an Ising Hamiltonian:

E(v,h,θ) = −

∑

i=1

∑

j=1

i j

−

∑

i=1

∑

k<i

−

∑

j=1

∑

l< j

−

∑

i=1

(0)

−

∑

j=1

(1)

Choosing the Kullback-Leibler divergence (KL diver-

gence) as the corresponding loss function and com-

bining it with training methods such as stochastic gra-

dient descent, BMs can be trained so that their Boltz-

mann distributions match the distribution of a given

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

178

dataset in a straightforward manner. The KL diver-

gence is a measure of similarity between two prob-

ability distributions, which becomes zero when the

two distributions are identical and yields higher val-

ues the more dissimilar the distributions are. Its gra-

dient, which is calculated repeatedly throughout the

BM’s training process, conveniently takes the follow-

ing simple form (Ackley et al., 1985):

∂D

data

|| P

model

)

∂W

i j

=⟨s

⟩

data

− ⟨s

⟩

model

(2)

∂D

data

|| P

model

)

∂b

(·)

=⟨s

⟩

data

− ⟨s

⟩

model

(3)

Here W

i j

is the weight associated with the connection

between the neurons s

∈ {v

,...,v

,...,h

⟨s

⟩ denotes the expectation value of the product of

the neuron values s

and s

, i.e., the probability that

both neurons assume the value one. Analogously, ⟨s

⟩

denotes the probability of s

assuming the value one.

Computing the exact values for all partial deriva-

tives generally demands calculating the energy of ev-

ery possible combination of states v ∈ {0,1}

, h ∈

{0,1}

, making this approach intractable in prac-

tice as there are exponentially many in terms of the

input domain {0, 1}

. Fortunately, sufﬁciently well

approximating heuristic methods often exist that al-

low for a shorter runtime. The core idea for these

approaches is repeated sampling from the respective

distributions, represented by the BM, and averaging

the results. Sampling is generally performed in two

phases: First, in the clamped phase, the values of

the visible neurons are ﬁxed to the bits of a ran-

domly selected data point. In this phase, only the

values s

of the hidden units, which now depend on

the data point’s value, are subsequently sampled from

the BM’s Boltzmann distribution. Together with the

input data point, these values can be viewed as a sam-

ple from the data’s probability distribution P

data

and

used to calculate ⟨s

⟩

data

and ⟨s

⟩

data

. The expec-

tation values ⟨s

⟩

model

and ⟨s

⟩

model

for the model

are then determined in the unclamped phase, by sam-

pling from the Boltzmann distribution associated with

the BM using techniques like Markov chain Monte

Carlo. These samples are subsequently used to cal-

culate ⟨s

⟩

model

and ⟨s

⟩

model

. In practice, sampling

from BMs is hence typically performed by iteratively

computing the values of each neuron, depending on

the values of its neighboring neurons, until an equi-

librium is reached. As this has to be done for each

sample, while multiple samples have to be calculated

for each data point in each training epoch, the train-

ing time quickly takes intractably long. (Amin et al.,

2018; Ackley et al., 1985; Adachi and Henderson,

2015)

2.2 Restricted Boltzmann Machines

When using Restricted Boltzmann Machines

(RBMs), considerably shorter training compared to

the standard BMs can be achieved. Analog to our

course of action for the standard BM, we also restrict

the content of this section to networks of a single

hidden and visible layer. RBMs restrict all possible

neuron connections so that only interlayer weights

can be non-zero, making it possible to sample from

the entire visible respectively hidden layer at once.

As hidden and visible units only depend on the

neuron values in the opposing layer, which are

known in the clamped phases, this allows for faster

sampling. For RBMs, the energy function is thus

reduced to (Fischer and Igel, 2012):

E(v,h,θ) =

∑

i=1

∑

j=1

i j

−

∑

i=1

(0)

−

∑

j=1

(1)

(4)

As it remains intractable to calculate the gradient of

the weights and biases directly, sampling from the

given Boltzmann distribution is mandatory. How-

ever, even for the RBM, drawing independent sam-

ples from the model in order to approximate the gra-

dient is computationally expensive. Even though ap-

proximate sampling techniques like Contrastive Di-

vergence can often be used effectively, their trade-

off in runtime against accuracy is frequently worse

than state-of-the-art classical generative models be-

sides BMs for big datasets. (Gabri

e et al., 2015)

2.3 Quantum Boltzmann Machines

A very promising approach towards speeding up the

time consuming sampling process in classical (re-

stricted) BMs are Quantum Boltzmann Machines

(QBMs), which use quantum algorithms to prepare a

quantum state that resembles the desired probability

distribution and allows for sampling from it via mea-

surements. One such quantum algorithm is Quantum

Annealing, which has been shown to be capable of ap-

proximating Boltzmann distributions when executed

on analog quantum hardware natively implementing

this algorithm, i.e., Quantum Annealers (Amin et al.,

2018). Quantum Annealing conducts a time evolu-

tion starting in the ground state of a known Hamilto-

nian that gradually evolves into an Ising Hamiltonian

that is often used to model the cost landscape of

an optimization problem. When this time evolution

is done adiabatically (i.e., not too fast) and without

any hardware errors, the ﬁnal state is guaranteed to

be the ground state of the Hamiltonian

, i.e., the

global minimum of the cost function (Kadowaki and

Nishimori, 1998). When conducting this process on a

Exploring Unsupervised Anomaly Detection with Quantum Boltzmann Machines in Fraud Detection

179

physical Quantum Annealer however, the system nat-

urally interacts with the environment, which interest-

ingly perturbs the ﬁnal state to approximate a classi-

cal Boltzmann distribution over the energy function

described by the Hamiltonian

. The temperature

of the resulting approximate Boltzmann distribution

is determined by device speciﬁc properties in corre-

lation with the speciﬁc Ising Hamiltonian and can be

tuned by rescaling the weights and biases by the in-

verse of the so-called effective temperature, which

can be calculated efﬁciently as shown in (Benedetti

et al., 2016). (Adachi and Henderson, 2015; Yarkoni

et al., 2021; Benedetti et al., 2016)

As Quantum Annealing drastically reduces the

amount of steps needed to create a sample, a quantum

advantage in the form of a speedup can be expected

here. Experiments of (Amin et al., 2018) show that

QBMs can achieve better KL divergences than the

BMs employed in their study when given the same

runtime capabilities, suggesting that QBMs can also

outperform their classical analogs in terms of result

quality. Another advantage of QBMs is that they do

not require restricting the connectivity of the BMs ar-

chitecture, allowing for more complex models with a

higher number of connections (Hinton, 2012; Adachi

and Henderson, 2015).

3 RELATED WORK

Our contribution to existing literature is constituted

by the ﬁrst successful application of QBMs for fully

unsupervised anomaly detection. This represents a

novel use case for QBMs trained using unsuper-

vised techniques, extending the portfolio of known

productive QBM applications like image reconstruc-

tion (Benedetti et al., 2017) or image generation (Sato

et al., 2021).

In regards to supervised learning, QBMs have

shown promising performance for anomaly detec-

tion in applications like the classiﬁcation of cyber-

security data, for which (Dixit et al., 2021) showed

that their Quantum-Annealing-based RBM can pro-

vide similar results to comparable classical RBMs.

(Vyas et al., 2022) proposed a semi-supervised ap-

proach to anomaly detection for credit card trans-

action data that employs an ensemble of quantum-

inspired RBMs. For sampling, they use a set of

solvers from the “Azure Quantum-Inspired Optimiza-

tion (QIO)” suite instead of real quantum algorithms,

while excluding the anomalies from the training data.

They subsequently calculate the energy values of all

data points (i.e., including anomalies) for all RBMs of

the ensemble analytically and then identify an energy

threshold separating normal data from the anomalies.

Beyond QBMs, other quantum generative models

have been shown to perform well on similar tasks:

(Bermot et al., 2023) haven shown the effective ap-

plicability of Quantum Generative Adversarial Net-

works for anomaly detection in high energy physics,

(Ngairangbam et al., 2022) used a Quantum Autoen-

coder for a very similar use case, and (Schuhmacher

et al., 2023) applied a Quantum Support Vector Clas-

siﬁer to ﬁnd beyond standard model physics in data

recorded at the LHC.

4 METHODOLOGY

In line with known techniques to use generative mod-

els for anomaly detection, we utilize a QBM as a gen-

erative model and subsequently identify anomalies by

their infrequence in the generated model (Hoh et al.,

2022; Luo et al., 2022; Dietrichstein et al., 2022;

Amin et al., 2018). More speciﬁcally, we classify a

given data point as anomalous if its energy value in

the QBM exceeds a speciﬁc limit. To implement the

presented approach, we now ﬁrst specify the QBM

model architecture and then choose an energy thresh-

old separating normal from anomalous data.

4.1 QBM Model Architecture

To perform anomaly detection in a fully unsupervised

manner using a QBM, a suitable model architecture

must be selected. Inspired by the work of (Amin et al.,

2018), we also choose to employ a semi-restricted

QBM for unsupervised learning (i.e., a QBM with one

hidden layer, having lateral connection only between

the visible neurons). A general overview of this archi-

tecture can be found in ﬁgure 1b. More speciﬁcally,

we allow all neuron connections possible in this ar-

chitecture and treat the number of hidden neurons as

a hyperparameter, while the number of visible neu-

rons is completely dependent on the dimensionality

of the dataset.

4.2 Choosing an Energy Threshold

As stated previously, the identiﬁcation of anomalies is

done by verifying their absence (or at least signiﬁcant

infrequence) in the model distribution. For Energy

Based Models (EBMs) like the QBM, the probability

of a point in our model is fully dependent on its en-

ergy value by deﬁnition (Lecun et al., 2006). Thus,

the classiﬁcation of data points as anomalous or nor-

mal can be achieved by drawing an energy thresh-

old between the two categories (Zhai et al., 2016;

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

180

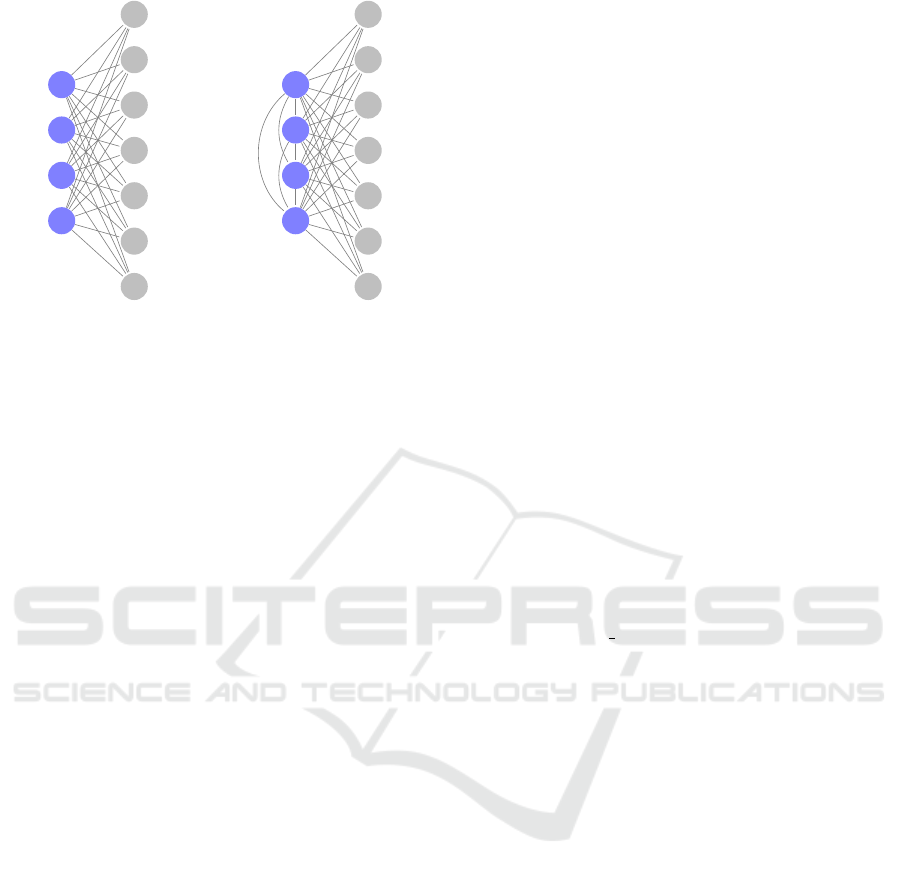
Hidden

layer

Visible

layer

(a) RBM

Hidden

layer

Visible

layer

(b) QBM

Figure 1: Schematic visualization of the architecture of the

BMs used in this paper.

Do et al., 2018). This causes our model to classify

all points with energy values higher than the thresh-

old as anomalous and all points with lower energies

as normal. While related work in the quantum do-

main speciﬁed this threshold for anomaly detection

using (semi-) supervised learning (Vyas et al., 2022),

we draw the threshold in an unsupervised manner, by

having the Quantum Annealer return the energy val-

ues of all data points in the training dataset and sub-

sequently calculating the threshold as the p-th per-

centile, analog to (Zhai et al., 2016) and (Do et al.,

2018). For our evaluation in section 5, we chose

p = 95, analog to (Do et al., 2018), assuming that

no more than 5% of the training data is anomalous.

While this amount is unrealistically high for the data

employed in our use case, we choose it to increase the

likelihood of ﬁnding all anomalies in the test dataset.

If any kind of ad-hoc testing for the validity of an

anomaly is available, e.g., through human inspection

as is typically the case for EDR, this percentile can

be tuned accordingly (see, e.g., (Do et al., 2018; Zhai

et al., 2016)).

5 EVALUATION

To give an indication whether our proposed method

might provide a quantum advantage over purely clas-

sical EBM-based approaches, we compare our ap-

proach to a RBM with a similarly simple architec-

ture to our semi-restricted QBM: The chosen RBM

is described in section 2.2 and displayed in ﬁgure 1a.

As we treat the size of the hidden layer as a hyperpa-

rameter and as one hidden layer already sufﬁces for

the RBM to be an arbitrary distribution approximator,

this choice yields a potent, practical, classical base-

line. Preparing for our experiments, we now select a

suitable dataset and conduct an in-depth hyperparam-

eter optimization. Note that we use a 50/50 train/test

split in this evaluation and only show the results from

test data.

5.1 Dataset

In lack of suitably small real world EDR datasets that

ﬁt on current quantum hardware, we generate a syn-

thetic data set, aimed at matching the following prop-

erties found in real world data: (1) a high dimension-

ality to assess scaling performance, (2) scarce anoma-

lies and (3) a substantial number of data points. While

satisfying (2) and (3) is straightforward, (1) is directly

proportional to the number of visible units and thus

the space complexity. Compromising on (1) to fa-

cilitate a visual evaluation and retain enough space

for exploring a large space of hidden units for this

ﬁrst case study on fully unsupervised anomaly detec-

tion using a QBM, we restrict the data set to three

dimensions. To satisfy (2) and (3) within the limita-

tions of current hardware capabilities, we thus gen-

erate 1007 3D data points x ∈ [0,...,127]

clustered

in ﬁve clusters and containing seven anomalies using

the method make blobs from scikit-learn (Pedregosa

et al., 2011). Therefore, seven bits are required per

dimension, which means that 21 visible neurons are

needed to represent the QBM’s input, i.e., a single

data point. Due to the 50/50 train/test split, the ra-

tio of anomalies is ≤ 7/500 ≈ 1%, satisfying (2). A

pairplot of the generated data set is displayed in ﬁg-

ure 2.

5.2 Hyperparameter Optimization

Being generative models, the BMs have several hy-

perparameters which need to be optimized to achieve

decent results. Choosing a greedy optimization strat-

egy due to heavy computation time demands, we

tuned the following hyperparameters descending in

their typical relevance: (1) The number of hidden

neurons, (2) the number of epochs and ﬁnally (3)

the batchsize, while choosing standard values for the

latter ones inspired by (Hinton, 2012). Notably, the

learning rate was determined independent of all other

hyperparameters in an empirical pre-study to the eval-

uation. For details on our implementation, see https:

//github.com/jonas-stein/QBM-Anomaly-Detection.

As we estimate that the here conducted hyper-

parameter search would take roughly two days of

QPU time, our limited access to D-Wave’s Anneal-

Exploring Unsupervised Anomaly Detection with Quantum Boltzmann Machines in Fraud Detection

181

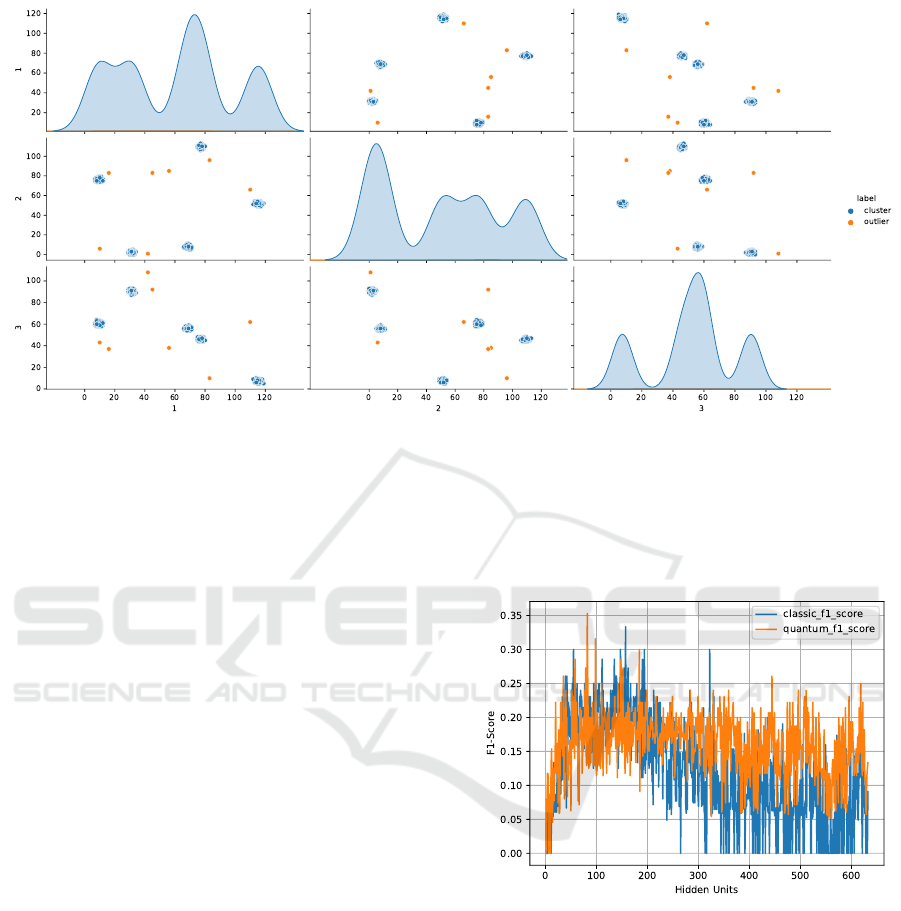
Figure 2: Visualization of the constructed 3D dataset comprised of 5 clusters and 7 anomalies. The diagonal shows the

distribution of the data in each dimension. The off-diagonal plots, show a 2D ﬂattened version of the dataset for all dimension-

combinations.

ers (∼3 hours) necessitates a hyperparameter search

using classical simulators for sampling. As also prac-

tically employed in (Schuman et al., 2023), Simulated

Annealing (SA) can be a suitable choice for this, as it

(like a quantum annealer (Nishimori et al., 2015)) in-

trinsically approximates a Boltzmann distribution for

a given temperature when using a suitable annealing

schedule and neighbor generation (for details, see the

articles of (Crosson and Harrow, 2016; Denchev et al.,

2016)). Note that for other QUBO solvers such as

the D-Wave hybrid, it is a priori not clear if they also

possess this property. We strongly encourage future

work on this topic, as long as QPU availability does

not meet the needed requirements.

Starting our hyperparameter optimization with the

number of hidden neurons, we respect the physically

possible qubit embeddings on the employed D-Wave

QPUs, which empirically restricts us to a maximum

of 94 and respectively 632 hidden neurons for the D-

Wave 2000Q and the Advantage 4.1. Figure 3 illus-

trates that the QBM requires signiﬁcantly fewer hid-

den neurons to reach its optimal F1 score compared to

the RBM: While the QBMs optimum is at 82 hidden

neurons with an F1 score of 0.35, the RBM reaches

its optimal F1 score of 0.33 at 157 hidden neurons.

Thus, the QBM achieves a better result with fewer re-

sources. This is most likely the case, as the QBM can

generally model complex dependencies better com-

pared to a similarly sized RBM, since it allows for

lateral connections. However, as the F1 scores show

a large variance for small changes in the number of

hidden units, caution has to be taken when conclud-

ing from these results, as it appears that the number

of employed seeds might be too low for undeniable

statistical relevance.

Figure 3: F1 score for increasing number of hidden neurons.

The blue line shows the classical RBM and the orange line

shows the QBM using the Simulated-Annealing-based sam-

pler.

Subsequently, the number of epochs was opti-

mized, while each approach was ﬁtted with the pre-

viously determined optimal number of hidden neu-

rons. Figure 4 displays the results which clearly show

that the QBM again outperforms the RBM. While the

RBM reaches its optimum at 13 epochs, with an F1

score of 0.33, the optimum of the QBM is at 14 and 16

epochs, respectively, with an F1 score of 0.375. In ad-

dition, the QBM consistently yields better results than

the RBM approach at fewer epochs. At seven epochs,

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

182

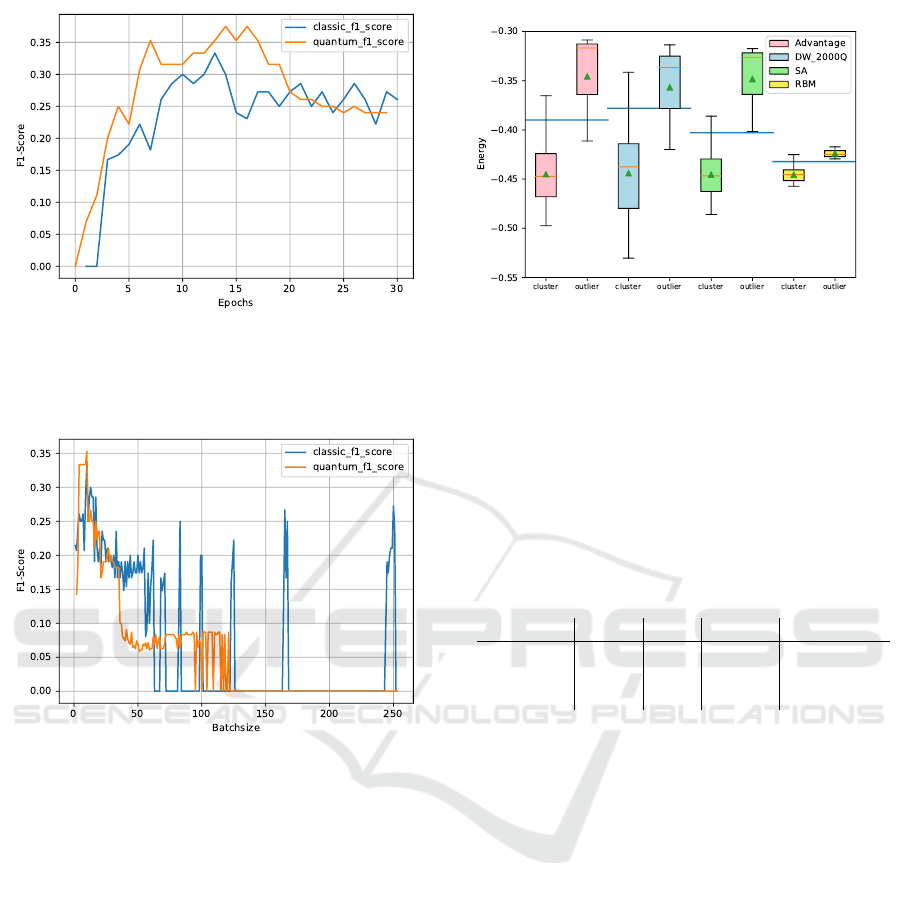
Figure 4: F1 score for increasing number of epochs. The

blue line shows the classical RBM and the orange line

shows the QBM using the Simulated-Annealing-based sam-

pler.

Figure 5: F1 score for increasing batch sizes. The blue

line shows the classical RBM and the orange line shows

the QBM using the Simulated Annealing based sampler.

the F1 score of the QBM already reaches 0.35, which

exceeds the global optimum of the RBM which is ob-

tained at 13 epochs. Thus, the QBM only needs about

half the number of epochs to reach an even better per-

formance than the RBM. Due to the limited available

computing time on quantum hardware, seven epochs

are chosen for further optimization steps, and 13 for

the RBM.

Concluding the hyperparameter optimization, Fig-

ure 5 shows that both the RBM and the QBM reach

their optimum at a batch size of ten. The RBM re-

mains at an F1 score of 0.33, while the QBM achieves

0.35.

5.3 QPU Results

Using the optimized hyperparameters, we now ex-

plore the result quality of the D-Wave 2000Q and the

Advantage 4.1 in comparison with the SA sampler

Figure 6: Normalized energies of anomalies and cluster

points for different approaches. The blue line represents the

chosen energy threshold separating normal from anomalous

data.

and the RBM baseline. Table 1 depicts the obtained

results, which show that the Quantum Annealers are

(still) outperformed by the classical approaches. Both

quantum annealers missed one anomaly and thus

achieved an identical recall. The Advantage 4.1 how-

ever identiﬁed less false positives according to its

62% higher precision.

Table 1: Result quality of all examined approaches.

RBM SA 2000Q Advantage

F1-Score 0.33 0.35 0.14 0.21

Recall 1 1 0.67 0.67

Precision 0.20 0.21 0.08 0.13

Fig. 6 shows a compact overview for comparing

the energy levels in form of a box plot. Interestingly,

the variance in the purely classical RBM approach is

signiﬁcantly lower than for all QBM variants, which

might be caused by the less complex model, as it does

not have any lateral neuron connections. Compar-

ing the three QBM results, we clearly see that SA

achieved the best performance, which makes sense,

as the hyperparameters were trained for it. For the

D-Wave QPUs a clear improvement can be observed

for the newer Advantage 4.1 system compared to the

older 2000Q model, which gives the promising out-

look of outperforming purely classical approaches

with future hardware generations if this trend contin-

ues. We expect the main reasons for this to be the

higher error rate of the 2000Q and the larger num-

ber of employed qubits, as its weaker connectivity de-

mands for more ancillary qubits for the same number

of hidden units.

Exploring Unsupervised Anomaly Detection with Quantum Boltzmann Machines in Fraud Detection

183

6 CONCLUSION

Our results indicate that QBMs can outperform their

classically employed analog (RBMs) for unsuper-

vised anomaly detection in terms of (1) training steps

and (2) result quality. With limited access to quan-

tum hardware however, we were unable to yield evi-

dence for this claim when using Quantum Annealers

as samplers, most probably because the hyperparame-

ter tuning was conducted using a simulated annealing

sampler that merely approximates the QPU results.

Furthermore, the results show that the more recent D-

Wave Advantage 4.1 QPU achieves signiﬁcantly bet-

ter performance than its predecessor D-Wave 2000Q,

even suggesting a possible quantum advantage in case

that the hardware performance continues to improve

similarly in the future.

To improve the results of the quantum approach

for future work, we suggest to implement a clas-

sical sampler that more closely matches the results

of the utilized quantum hardware in a high perfor-

mance computing oriented programming language to

improve the accuracy and statistical relevance of the

hyperparameter search. If successful, this should al-

low an upscaling to a more realistic dataset dimen-

sionality to gradually approach the limitations of clas-

sical approaches for this task. This should also facili-

tate the usage of a dataset containing benign and ma-

licious anomalies, to allow for comparing the results

of the QBM with classical baselines in this regard.

Furthermore, a closer evaluation in terms of training

steps for a higher number of data points would be very

interesting, as we expect our approach to be more efﬁ-

cient than the classical baselines in this regard, based

on our experimental results.

ACKNOWLEDGEMENTS

This paper was partially funded by the German Fed-

eral Ministry for Economic Affairs and Climate Ac-

tion through the funding program ”Quantum Comput-

ing – Applications for the industry” based on the al-

lowance ”Development of digital technologies” (con-

tract number: 01MQ22008A).

REFERENCES

Ackley, D. H., Hinton, G. E., and Sejnowski, T. J. (1985). A

learning algorithm for boltzmann machines. Cognitive

science, 9(1):147–169.

Adachi, S. and Henderson, M. (2015). Application of quan-

tum annealing to training of deep neural networks.

arXiv preprint arXiv:1510.06356, page 3.

Aleskerov, E., Freisleben, B., and Rao, B. (1997). Card-

watch: a neural network based database mining sys-

tem for credit card fraud detection. In Proceedings of

the IEEE/IAFE 1997 Computational Intelligence for

Financial Engineering (CIFEr), pages 220–226.

Amin, M. H., Andriyash, E., Rolfe, J., Kulchytskyy, B.,

and Melko, R. (2018). Quantum boltzmann machine.

Physical Review X, 8(2):021050.

Benedetti, M., Realpe-G

omez, J., Biswas, R., and Perdomo-

Ortiz, A. (2016). Estimation of effective temperatures

in quantum annealers for sampling applications: A

case study with possible applications in deep learning.

Physical Review A, 94(2):022308.

Benedetti, M., Realpe-G

omez, J., Biswas, R., and Perdomo-

Ortiz, A. (2017). Quantum-assisted learning of

hardware-embedded probabilistic graphical models.

Physical Review X, 7(4):041052.

Bermot, E., Zoufal, C., Grossi, M., Schuhmacher, J.,

Tacchino, F., Vallecorsa, S., and Tavernelli, I. (2023).

Quantum generative adversarial networks for anomaly

detection in high energy physics. arXiv preprint

arXiv:2304.14439.

Caro, M. C., Huang, H.-Y., Cerezo, M., Sharma, K., Sorn-

borger, A., Cincio, L., and Coles, P. J. (2022). Gener-

alization in quantum machine learning from few train-

ing data. Nat. Commun., 13(1):4919.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly detection: A survey. ACM Comput. Surv.,

41(3).

Chuvakin, A. (2023). Named: Endpoint threat detection &

response.

Crosson, E. and Harrow, A. W. (2016). Simulated quantum

annealing can be exponentially faster than classical

simulated annealing. In 2016 IEEE 57th Annual Sym-

posium on Foundations of Computer Science (FOCS),

pages 714–723.

Denchev, V. S., Boixo, S., Isakov, S. V., Ding, N., Bab-

bush, R., Smelyanskiy, V., Martinis, J., and Neven,

H. (2016). What is the computational value of ﬁnite-

range tunneling? Phys. Rev. X, 6:031015.

Dietrichstein, M., Major, D., Trapp, M., Wimmer, M.,

Lenis, D., Winter, P., Berg, A., Neubauer, T., and

uhler, K. (2022). Anomaly detection using gener-

ative models and sum-product networks in mammog-

raphy scans. In Mukhopadhyay, A., Oksuz, I., Engel-

hardt, S., Zhu, D., and Yuan, Y., editors, Deep Gen-

erative Models, pages 77–86, Cham. Springer Nature

Switzerland.

Dixit, V., Selvarajan, R., Aldwairi, T., Koshka, Y., Novotny,

M. A., Humble, T. S., Alam, M. A., and Kais, S.

(2021). Training a quantum annealing based restricted

boltzmann machine on cybersecurity data. IEEE

Transactions on Emerging Topics in Computational

Intelligence, 6(3):417–428.

Do, K., Tran, T., and Venkatesh, S. (2018). Energy-based

anomaly detection for mixed data. Knowledge and

Information Systems, 57(2):413–435.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

184

Finke, T., Kr

amer, M., Morandini, A., M

uck, A., and

Oleksiyuk, I. (2021). Autoencoders for unsupervised

anomaly detection in high energy physics. J. High En-

ergy Phys., 2021(6):161.

Fischer, A. and Igel, C. (2012). An introduction to restricted

boltzmann machines. In Iberoamerican congress on

pattern recognition, pages 14–36. Springer.

Gabri

e, M., Tramel, E. W., and Krzakala, F. (2015). Train-

ing restricted boltzmann machine via the thouless-

anderson-palmer free energy. Advances in neural in-

formation processing systems, 28.

Hangleiter, D. and Eisert, J. (2023). Computational advan-

tage of quantum random sampling.

Hinton, G. E. (2012). A practical guide to training restricted

boltzmann machines. In Neural networks: Tricks of

the trade, pages 599–619. Springer.

Hoh, M., Sch

ottl, A., Schaub, H., and Wenninger, F. (2022).

A generative model for anomaly detection in time

series data. Procedia Computer Science, 200:629–

637. 3rd International Conference on Industry 4.0 and

Smart Manufacturing.

Kadowaki, T. and Nishimori, H. (1998). Quantum an-

nealing in the transverse ising model. Phys. Rev. E,

58:5355–5363.

Karami, A. (2018). An anomaly-based intrusion detection

system in presence of benign outliers with visualiza-

tion capabilities. Expert Systems with Applications,

108:36–60.

Kumar, V. (2005). Parallel and distributed computing

for cybersecurity. IEEE Distributed Systems Online,

6(10).

Lecun, Y., Chopra, S., Hadsell, R., Ranzato, M., and Huang,

F. (2006). A tutorial on energy-based learning. MIT

Press.

Luo, X., Jiang, Y., Wang, E., and Men, X. (2022). Anomaly

detection by using a combination of generative ad-

versarial networks and convolutional autoencoders.

EURASIP J. Adv. Signal Process., 2022(1):112.

Mascaro, S., Nicholso, A. E., and Korb, K. B. (2014).

Anomaly detection in vessel tracks using bayesian

networks. International Journal of Approximate Rea-

soning, 55(1, Part 1):84–98. Applications of Bayesian

Networks.

Muniyandi, A. P., Rajeswari, R., and Rajaram, R. (2012).

Network anomaly detection by cascading k-means

clustering and c4.5 decision tree algorithm. Proce-

dia Engineering, 30:174–182. International Confer-

ence on Communication Technology and System De-

sign 2011.

Ngairangbam, V. S., Spannowsky, M., and Takeuchi,

M. (2022). Anomaly detection in high-energy

physics using a quantum autoencoder. Phys. Rev. D,

105:095004.

Nishimori, H., Tsuda, J., and Knysh, S. (2015). Compar-

ative study of the performance of quantum annealing

and simulated annealing. Phys. Rev. E, 91:012104.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Sato, T., Ohzeki, M., and Tanaka, K. (2021). Assessment

of image generation by quantum annealer. Scientiﬁc

reports, 11(1):1–10.

Schuhmacher, J., Boggia, L., Belis, V., Puljak, E., Grossi,

M., Pierini, M., Vallecorsa, S., Tacchino, F., Barkout-

sos, P., and Tavernelli, I. (2023). Unravelling physics

beyond the standard model with classical and quantum

anomaly detection. arXiv preprint arXiv:2301.10787.

Schuman, D., S

unkel, L., Altmann, P., Stein, J., Roch, C.,

Gabor, T., and Linnhoff-Popien, C. (2023). Towards

transfer learning for large-scale image classiﬁcation

using annealing-based quantum boltzmann machines.

In 2023 IEEE International Conference on Quantum

Computing and Engineering (QCE), volume 02, pages

42–47.

Spence, C., Parra, L., and Sajda, P. (2001). Detection, syn-

thesis and compression in mammographic image anal-

ysis with a hierarchical image probability model. In

Proceedings IEEE Workshop on Mathematical Meth-

ods in Biomedical Image Analysis (MMBIA 2001),

pages 3–10.

Sussmann, H. (1988). Learning algorithms for boltzmann

machines. In Proceedings of the 27th IEEE Confer-

ence on Decision and Control, pages 786–791 vol.1.

Vyas, A., Roberts, L., Gupta, S., and Patel, R. (2022).

Anomaly detection using azure quantum qio (quan-

tum inspired optimization) platform. Technical re-

port, Mphasis Corporation, New York, NY, USA. Ac-

cessed: 2022-08-21.

Wiebe, N. and Wossnig, L. (2019). Generative training

of quantum boltzmann machines with hidden units.

arXiv preprint arXiv:1905.09902.

Yarkoni, S., Raponi, E., Schmitt, S., and B

ack, T. (2021).

Quantum annealing for industry applications: Intro-

duction and review. arXiv preprint arXiv:2112.07491,

page 31.

Younes, L. (1996). Synchronous boltzmann machines can

be universal approximators. Applied Mathematics Let-

ters, 9(3):109–113.

Zhai, S., Cheng, Y., Lu, W., and Zhang, Z. (2016). Deep

structured energy based models for anomaly detec-

tion. In International conference on machine learning,

pages 1100–1109. PMLR.

Zhu, E. Y., Johri, S., Bacon, D., Esencan, M., Kim, J., Muir,

M., Murgai, N., Nguyen, J., Pisenti, N., Schouela,

A., Sosnova, K., and Wright, K. (2022). Genera-

tive quantum learning of joint probability distribution

functions. Phys. Rev. Res., 4:043092.

Exploring Unsupervised Anomaly Detection with Quantum Boltzmann Machines in Fraud Detection

185