A Methodology Based on Subgroup Discovery to Generate Reduced

Subgroup Sets for Patient Phenotyping

Antonio Lopez-Martinez-Carrasco

1 a

, Jose M. Juarez

1 b

, Manuel Campos

1,2 c

and Bernardo Canovas-Segura

1 d

Med AI Lab, University of Murcia, Spain

Murcian Bio-Health Institute (IMIB-Arrixaca), Spain

Keywords:

Methodology, Patient Phenotyping, Subgroup Discovery, Reduced Subgroup Set.

Abstract:

Subgroup Discovery (SD) is a supervised machine learning technique that mines a set of easily readable

features of patients with a medical condition in the form of a subgroup set (called patient phenotype). However,

using only the output obtained by a single execution of an SD algorithm hinders the discovery of the best

phenotypes since it is difﬁcult for clinicians to choose the most suitable algorithm, its best hyperparameters

and the quality measure. Therefore, we propose a new phenotyping approach based on SD that evaluates

the outcomes of different SD algorithms to obtain a ﬁnal patient phenotype with a reduced dependency on

the initial conditions of these executions and to ensure diversity in terms of coverage of the subgroups from

this phenotype. For that, we ﬁrst deﬁne the problem of mining a patient phenotype in the form of a reduced

subgroup set and, after that, we propose a new 6-step methodology to tackle this problem. Moreover, we carry

out experiments driven by this methodology and focused on the antibiotic resistance problem by using the

MIMIC-III public database and the patients infected by an Enteroccous Sp. bacterium resistant to Vancomycin

as a target. Finally, we obtain a phenotype formed of 7 subgroups.

1 INTRODUCTION

Finding a set of observable features of patients with a

medical condition has become a core issue in the clin-

ical research ﬁeld. This task is denominated as patient

phenotyping and these patient features are denomi-

nated as patient phenotypes (Wojczynski and Tiwari,

2008). Patient phenotyping is useful for discover-

ing novel and possibly unexpected relations between

patient attributes, generating clinical hypotheses, or

supporting medical experts decision-making, among

others. Therefore, the development of new machine

learning (ML) methods to ﬁnd patient phenotypes is a

key area in the health informatics research ﬁeld.

A relevant application of the patient phenotyping

is the antibiotic resistance problem, which, according

to main healthcare organizations, is one of the grow-

ing and most alarming problems in the clinical ﬁeld.

This problem takes place when microorganisms be-

https://orcid.org/0000-0002-2990-886X

https://orcid.org/0000-0003-1776-1992

https://orcid.org/0000-0002-5233-3769

https://orcid.org/0000-0002-0777-0441

come resistant to antimicrobials, causing antimicro-

bials to lose their effectiveness in combating microor-

ganism infections. In this context, ML-guided patient

phenotyping can be applied to automatically discover

patient phenotypes related to the antibiotic resistance

problem.

Subgroup Discovery (SD) (Atzmueller, 2015) is

a suitable approach by which to tackle patient phe-

notyping. SD is a supervised machine learning tech-

nique whose main objective is to extract a simple and

legible set of relations among attributes from a dataset

regarding a target attribute of interest. These indi-

vidual relations are denominated as subgroups. This

technique is used to model a subgroup set for de-

scriptive and exploratory data analysis, generating hy-

potheses, or extracting patterns, among others. An es-

sential aspect of this technique is to compute the qual-

ity of the individual subgroups obtained. For that, a

quality measure is used, which is a function that as-

signs a numerical value to a subgroup according to

different properties from the dataset.

Although the SD technique is useful and gener-

ates easily readable phenotypes in the form of sub-

group sets, using only the output obtained by a sin-

346

Lopez-Martinez-Carrasco, A., Juarez, J., Campos, M. and Canovas-Segura, B.

A Methodology Based on Subgroup Discovery to Generate Reduced Subgroup Sets for Patient Phenotyping.

DOI: 10.5220/0012321200003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 2, pages 346-353

ISBN: 978-989-758-688-0; ISSN: 2184-4305

gle execution of a speciﬁc SD algorithm could involve

certain disadvantages. One of them concerns the SD

algorithm itself and its initial hyperparameters. In

this sense, an SD algorithm could implement either

an exhaustive or heuristic exploration strategy, return

either all subgroups explored or the top-k subgroups

explored, implement different pruning, and accept the

use of different quality measures. Besides, different

implementations of the same algorithm could incor-

porate other hyperparameters further than the origi-

nally deﬁned ones (e.g., exploration depth). All the

aforementioned characteristics make the subgroup set

obtained by an SD algorithm highly variable and de-

pendent on the initial conditions of the algorithm, thus

causing the subgroups mined by different SD algo-

rithms or by different hyperparameters can be notably

different. Another disadvantage is the large number of

subgroups that could be mined by a certain SD algo-

rithm execution (pattern explosion problem), increas-

ing the subgroup set size and making the result hardly

readable and interpretable by experts in these cases.

Taking all this into account, we propose and de-

velop a new approach based on the evaluation of the

overlap between the subgroup sets mined by differ-

ent SD algorithm executions to obtain a reduced sub-

group set. More precisely, the main contributions of

this research are (1) the deﬁnition of the problem of

mining a patient phenotype in the form of a reduced

subgroup set and (2) a new 6-step methodology that

tackles this problem and allows the involvement of

clinical experts in the process. The idea behind this

methodology supported by the SD technique is based

on a previously developed work (Lopez-Martinez-

Carrasco et al., 2021), which consisted of ﬁnding pa-

tient cohorts by evaluating the overlap between differ-

ent executions of a certain clustering algorithm.

The experiments carried out in this research are

driven by the 6-step methodology proposed and the

results obtained are compared with another descrip-

tive SD method.

2 PROBLEM STATEMENT

This section provides the formal deﬁnitions related to

the problem of mining a patient phenotype in the form

of a reduced subgroup set.

An attribute a is a unique characteristic of an ob-

ject, which has an associated value. An example of

an attribute is a = headache : yes. Moreover, the

domain of a, denoted as dom(a), is the set of all

unique values that a can take. Note that an attribute

can be nominal or numeric depending on its domain.

An instance i is a tuple of attributes of the form

i = (a

, . . . , a

). Given the attributes a

= f ever :

no and a

= headache : yes, an example of an in-

stance is i = ( f ever : no, headache : yes). A dataset

d is a tuple of instances of the form d = (i

, . . . , i

Given the instances i

= (headache : yes, f ever :

no) and i

= (headache : yes, f ever : yes), an ex-

ample of a dataset is d = ((headache : yes, f ever :

no), (headache : yes, f ever : yes)). Moreover, the no-

tation v

x,y

is used to indicate the value of the x-th in-

stance i

and its y-th attribute a

from a dataset d.

Given an attribute a

from a dataset d, a bi-

nary operator ∈ {=, ̸=, <, >, ≤, ≥} and a value w ∈

dom(a

), then a selector e is deﬁned as a 3-tuple of the

form (a

.characteristic, operator,w). Informally, a

selector is a binary relation between an attribute from

a dataset and a possible value of its domain. An ex-

ample of a selector is e = (headache, =, yes).

Given an instance i and a selector e, then i is cov-

ered by e if the binary expression “v

x,y

operator w”

holds true. Otherwise, i is not covered by e.

Given a dataset d, a pattern p is a list of selectors

of the form < e

, . . . , e

> in which all attributes of the

selectors are different. It is interpreted as a conjunc-

tion of selectors that represents a list of properties of a

subset from d. Additionally, the pattern size is deﬁned

as the number of selectors that it contains.

Given an instance i and a pattern p, then i is cov-

ered by p if i is covered by all selectors e ∈ p. Other-

wise, i is not covered by p.

Given a pattern p and a selector e, a subgroup

s is a pair (p, e) in which the pattern is denomi-

nated as ‘description’ and the selector is denomi-

nated as ‘target’. Additionally, the subgroup size is

deﬁned as the number of selectors that its descrip-

tion contains. An example of subgroup is s = (<

(headache, =, yes), ( f ever, =, no) >, ( f lu, =, no)).

Given two subgroups s and s

′

, s

′

is a reﬁnement

of s (denoted as s ≺ s

′

) if s

′

has the same target as s,

i.e., s

′

.target = s.target, and has an extended descrip-

tion, i.e., s

′

.description = concat(s.description, <

, . . . , e

>).

Given a subgroup s and a dataset d, a quality mea-

sure q is a function that computes one numeric value

according to s and certain metrics from d (Atzmueller,

2015).

Focusing on a speciﬁc subgroup s and a speciﬁc

dataset d, different metrics with which to compute

quality measures can be deﬁned: (1) true positives

(t p), deﬁned as the number of instances i from the

dataset d that are covered by the subgroup descrip-

tion s.description and by the subgroup target s.target;

(2) false positives ( f p), deﬁned as the number of in-

stances i from d that are covered by s.description, but

not by s.target; (3) true population (T P), deﬁned as

A Methodology Based on Subgroup Discovery to Generate Reduced Subgroup Sets for Patient Phenotyping

347

subgroup

: IF description

THEN distribution

(target)

subgroup

: IF description

THEN distribution

(target)

subgroup

: IF description

THEN distribution

(target)

Figure 1: Example of a subgroup set with k subgroups in the form of a decision set.

the number of instances i from d that are covered by

s.target, and (4) false population (FP), deﬁned as the

number of instances i from d that are not covered by

s.target.

Some examples of quality measures are Piatet-

sky Shapiro (PS = (t p + f p) · (

t p

t p+ f p

−

T P

T P+FP

)),

Weighted Relative Accuracy (W RAcc =

t p+ f p

T P+FP

(

t p

t p+ f p

−

T P

T P+FP

)) or Incremental Response Rate

(IRR =

t p

t p+ f p

− 1 +

FP− f p

A subgroup set ss is an unordered collection of

subgroups of the form ss = {s

, s

, . . . , s

}. It can be

interpreted as a decision set of the form “if”, meaning

that all subgroups from the set apply independently

from the rest (Lakkaraju et al., 2016). An example is

depicted in Figure 1.

The SD problem consists of exploring the search

space of a dataset d to mine a subgroup set ss in which

the quality value, computed with a quality measure

q, for each individual subgroup s ∈ ss is greater or

equal to a given threshold. Some examples of SD al-

gorithms are SD-Map (Atzmueller and Puppe, 2006),

VLSD (Lopez-Martinez-Carrasco et al., 2023a) or

BSD (Lemmerich et al., 2010), among others.

Two different subgroups generated by any SD al-

gorithm are redundant when both cover the same por-

tion of instances from a speciﬁc dataset. In this con-

text and according to their coverage, one of them is

called the dominant subgroup and the other is called

the dominated subgroup, allowing the latter to be

deleted. Therefore, two types of dominance rela-

tions can be stated: (1) close (Garriga et al., 2006),

and (2) closed-on-the-positives (Lemmerich et al.,

2010). Considering both dominance relations, other

examples of SD algorithms are CBSD (BSD with the

close dominance relation) and CPBSD (BSD with the

closed-on-the-positives dominance relation).

Given a collection of subgroup sets

{ss

, ss

, . . . , ss

}, the overlap function o f is a

function that evaluates the overlap between these

subgroup sets by computing their intersections

and returns another subgroup set. Formally:

o f ({ss

, ss

, . . . , ss

}) =

i=1

Finally, the subgroup set returned by an overlap

function o f is denominated as a reduced subgroup set

and is denoted as rss. In this context, we use a reduced

subgroup set rss to represent a phenotype.

3 METHODOLOGY

This section describes the proposed 6-step methodol-

ogy with which to tackle the problem deﬁned in Sec-

tion 2, allowing the involvement of clinical experts in

the process. This methodology is shown in Figure 2

and consists of the following steps:

Step 1 consists of extracting the data from the

clinical source(s) to later preprocess it. This prepro-

cessing comprises different tasks such as data clean-

ing or data transformation, among others, which are

necessary to obtain the ﬁnal dataset (denominates as

the mining view). Note that different SD algorithms

accept different data formats (e.g., only nominal at-

tributes, only numerical attributes, both nominal and

numerical attributes, etc.). Therefore, it is necessary

to ensure that the mining view has the correct format

according to the SD techniques that will be used in

the following steps. Step 1 also includes the selection

of the pair attribute-value that will be used as a target

in all SD algorithm executions.

Step 2 is formed of two phases: (1) splitting the

mining view as many times as different algorithms

and hyperparameters will be applied, and (2) for each

split, selecting the speciﬁc SD algorithm and its hy-

perparameters that will be applied over this split. In

this step, the greater the number of splits and different

algorithms and hyperparameters, the lower the depen-

dency between the algorithms, the hyperparameters

and the ﬁnal subgroup set mined and, therefore, the

more reduced the ﬁnal subgroup set will be. How-

ever, using an excessive number of splits, algorithms,

and hyperparameters may imply that the intermedi-

ate subgroup sets obtained do not overlap each other

and, therefore, that the rss is either of poor quality or

even empty. In Step 2, it is also possible to duplicate

a certain split to apply different algorithms and/or hy-

perparameters to the same data. Concerning this step,

remember that the target established in the ﬁrst step

must be used in all the SD algorithm executions.

Step 3 consists of executing all SD algorithms

with their hyperparameters over the corresponding

splits to obtain the subgroup sets, one per algo-

rithm. These intermediate subgroup sets are denoted

as ss

, ss

, . . . , ss

. Note that these subgroup sets

are intermediate phenotypes that are highly dependent

on the speciﬁc SD algorithms and hyperparameters

HEALTHINF 2024 - 17th International Conference on Health Informatics

348

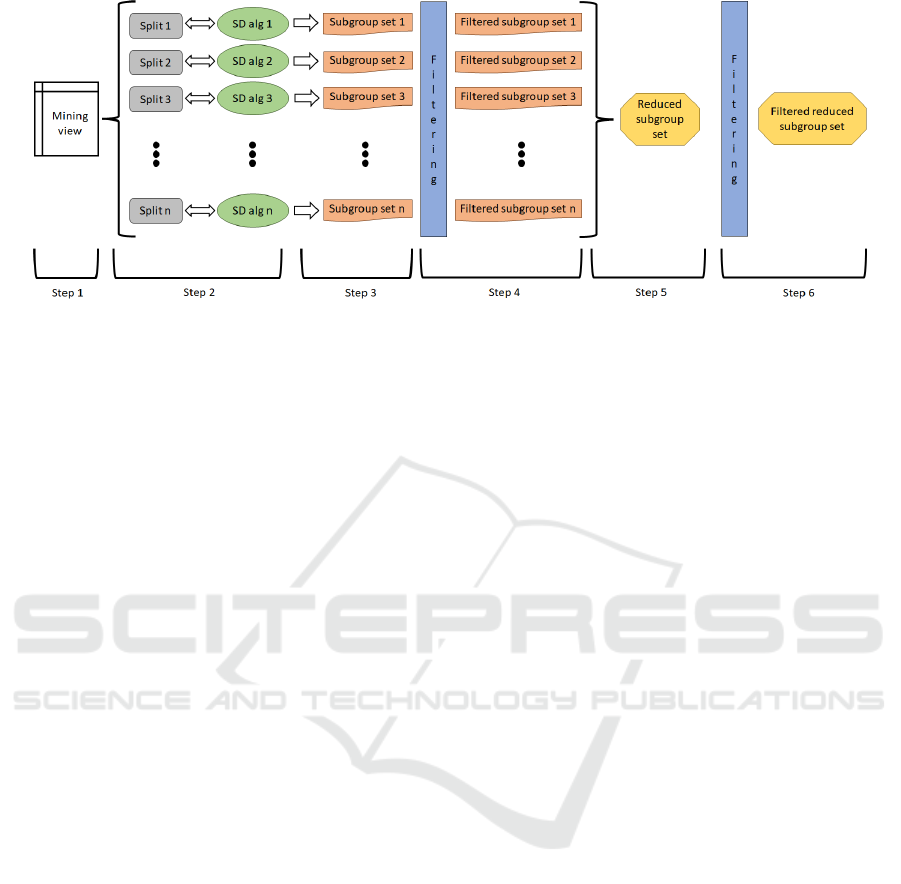
Figure 2: 6-Step methodology proposed.

used to generate them. Therefore, they will be com-

bined later to generate the rss, i.e., the ﬁnal pheno-

type with a reduced dependency concerning each of

the multiple SD algorithms executed.

Step 4 consists of ﬁltering each subgroup set gen-

erated by the SD algorithms in the previous step, ob-

taining a new collection of subgroup sets denoted as

f ss

, f ss

, . . . , f ss

. The applied ﬁlters can be of

two types: (1) automatic ﬁlters, based on certain com-

putable criteria, for example, the quality measure of

the subgroups contained in the subgroup set or rules

ﬁlters, applied directly by experts and based on their

knowledge and experience.

Step 5 is based on the execution of the over-

lap function to combine all ﬁltered subgroup sets

obtained previously to generate the rss. This

means that, given the collection of subgroup

sets { f ss

, f ss

, . . . , f ss

}, then the function

o f ({ f ss

, f ss

, . . . , f ss

}) is executed. Once the

rss is generated, it is also possible to reorder its sub-

groups by using another different quality measure.

Finally, Step 6 consists of ﬁltering the rss from the

previous step to obtain the phenotype f rss. In both

Steps 4 and 6, either automatic or manual ﬁlters can

be applied and domain experts actively participate in

the confection of the phenotypes. These ﬁltering pro-

cesses could be supported by visualization tools for

clinicians’ decision-making.

4 EXPERIMENTS AND RESULTS

The objective of the experiments carried out in this

work was to test our methodology regarding the de-

ﬁned problem as well as its suitability to identify

patient phenotypes in the context of antibiotic resis-

tance. For that purpose, we used real clinical data

obtained from MIMIC-III, which is a public dataset

that contains health data related to more than 45,000

patients treated in ICUs (intensive care units) and

around 60,000 admissions between the years 2001

and 2012. This database contains data related to de-

mography, laboratory tests, vital sign measurements

or administered medications, among others. In addi-

tion, the experiments presented and described in this

section are driven by our 6-step methodology.

4.1 Step 1

First, we extracted data from the MIMIC-III public

database to compose a mining view in which each

instance was a strain of a population of a microor-

ganism obtained in a culture (laboratory test) of a

patient during one of their admissions. During this

process, we applied a preprocessing phase to delete

duplicate instances and attributes, delete empty at-

tributes or those with only one value, and discretize

numerical attributes since SD algorithms used only

accept this type of attributes. The mining view had

9,240 instances and 12 attributes, which are described

in Table 1. Finally, we used as a target the patients in-

fected by an Enteroccous Sp. bacterium resistant to

Vancomycin, i.e. Class = Yes, having therefore 2,126

positive instances and 7,114 negative instances.

4.2 Step 2

The next step was to split this mining view. In this

case, we generated 5 different stratiﬁed splits (with

no duplicates). For each split, we assigned the fol-

lowing algorithms and hyperparameters: for the split

1 (1,849 rows), the SD-Map algorithm with the Pi-

atetsky Shapiro quality measure and with no mini-

mum quality thresholds; for the split 2 (1,848 rows),

the VLSD algorithm with the WRAcc quality mea-

sure (deﬁned between -1 and 1, both included) and a

minimum quality threshold of 0; for the split 3 (1,848

A Methodology Based on Subgroup Discovery to Generate Reduced Subgroup Sets for Patient Phenotyping

349

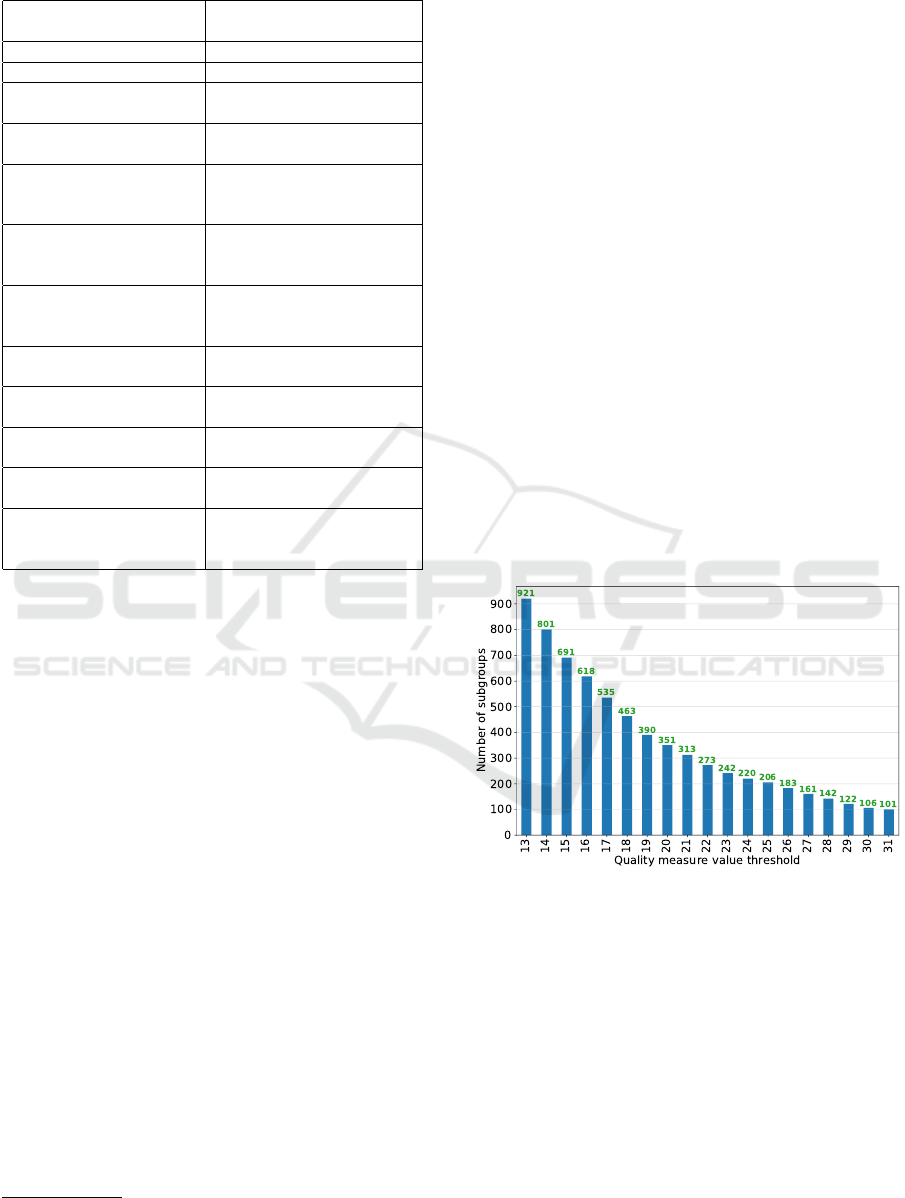
Table 1: Mining view details.

Attribute

name

Attribute

description

Patient gender Male or Female

Patient age Child, Adult or Elderly

Admission location

Patient’s location

before arriving

Dischage location

Patient’s location

after discharging

Culture

specimen type

Specimen which

was tested in the culture

for bacterial growth

Service when

culture

Service where the patient

resided when the culture

was done

ICU when

culture

ICU where the patient

resided when the culture

was done

Readmission

If the patient was in the

hospital in the past

Days between admission

and ﬁrst ICU

Zero, or One or more

Previous Vancomycin

treatments

If the patient was treated

with vancomycon before

Culture month

Month when the culture

was done

Class

Enteroccous Sp. bacterium

resistant to Vancomycin

(Yes / No)

rows), the BSD algorithm with Piatetsky Shapiro

quality measure, with no minimum quality thresholds

and with a maximum of 1,000 subgroups (i.e., the best

1,000 subgroups); for the split 4 (1,848 rows), the

CBSD algorithm with WRAcc quality measure, with

no minimum quality thresholds and with a maximum

of 1,000 subgroups (i.e., the best 1,000 subgroups),

and for the split 5 (1,847 rows), the CPBSD algorithm

with Piatetsky Shapiro quality measure, with no mini-

mum quality thresholds and with a maximum of 1,000

subgroups (i.e., the best 1,000 subgroups). All these

algorithms and quality measures are implemented in

the subgroups python library, which is available on

PyPI or

4.3 Step 3

The next step was to actually run the algorithms.

After executing the SD-Map algorithm over split 1,

we obtained a subgroup set ss

with 1,315,110 sub-

groups. After running the VLSD algorithm over split

2, we generated a subgroup set ss

with 374,817 sub-

groups. After executing the BSD algorithm over split

3, we mined a subgroup set ss

with 1,000 subgroups.

After running the CBSD algorithm over split 4, we

obtained a subgroup set ss

with 1,000 subgroups. Fi-

https://github.com/antoniolopezmc/subgroups

nally, after executing the CPBSD algorithm over split

5, we mined a subgroup set ss

with 1,000 subgroups.

In this point, remember that we used different

algorithms with different quality measures and hy-

perparameters over different datasets (obtained after

splitting the initial mining view). The ﬁve subgroup

sets obtained are intermediate phenotypes that are

highly dependent on the ﬁve SD algorithms and hy-

perparameters used to generate them.

4.4 Step 4

After executing all the SD algorithms, we mined a to-

tal number of 1,692,927 subgroups, which would be

relatively high for direct human intervention in case

these were the ﬁnal phenotypes to analyse. There-

fore, we applied an automatic ﬁltering process based

on the quality measure of the subgroups from each

subgroup set obtained. For that, for each subgroup

set, we only selected those subgroups whose quality

measure value was greater than or equal to a certain

threshold. Figures 3, 4, 5, 6, and 7 shows the num-

ber of subgroups that we ﬁnally obtain in each SD

model when varying the quality measure threshold.

Note that these ﬁgures serve as visual support for the

clinical experts’ decision-making.

Figure 3: Step 4 - Subgroup set 1 (ss

For the subgroup set 1 (i.e., ss

), we established

a threshold value of 23, obtaining therefore a ﬁltered

subgroup set f ss

with 242 subgroups. For the sub-

group set 2 (i.e., ss

), we set a threshold value of 0.02,

obtaining therefore a ﬁltered subgroup set f ss

with

104 subgroups. For the subgroup set 3 (i.e., ss

), we

established a threshold value of 23, obtaining there-

fore a ﬁltered subgroup set f ss

with 247 subgroups.

For the subgroup set 4 (i.e., ss

), we set a threshold

value of 0.01, obtaining therefore a ﬁltered subgroup

set f ss

with 234 subgroups. Note that, in this case,

there is a higher concentration of subgroups at val-

ues close to 0. Finally, for the subgroup set 5 (i.e.,

HEALTHINF 2024 - 17th International Conference on Health Informatics

350

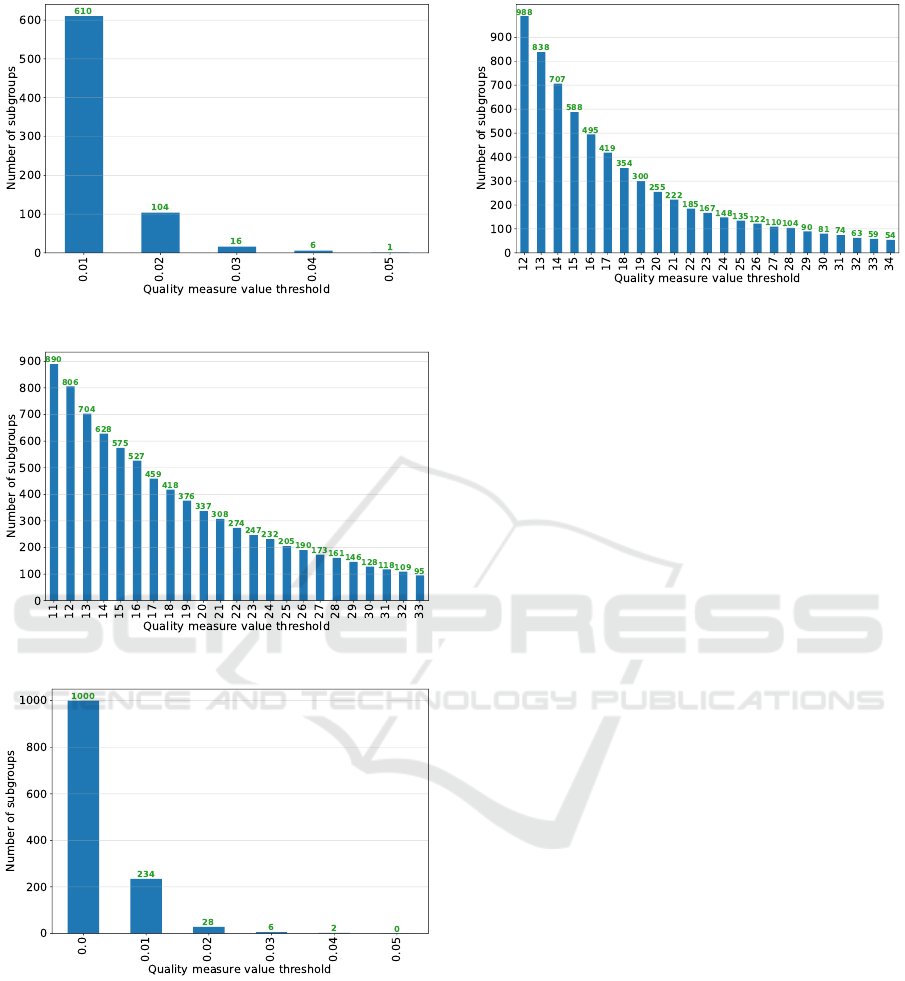
Figure 4: Step 4 - Subgroup set 2 (ss

Figure 5: Step 4 - Subgroup set 3 (ss

Figure 6: Step 4 - Subgroup set 4 (ss

), we established a threshold value of 20, obtaining

therefore a ﬁltered subgroup set f ss

with 255 sub-

groups.

After applying this ﬁltering process, we had a to-

tal number of 1,082 subgroups, which would also be

relatively high for direct human intervention in case

these were the ﬁnal phenotypes to analyse. For this

reason, these ﬁltered phenotypes were combined in

Step 5.

Figure 7: Step 4 - Subgroup set 5 (ss

4.5 Step 5

This step consisted of applying the overlap function

in order to combine f ss

, f ss

and f ss

obtain rss. In these experiments, we used the over-

lap function o f deﬁned in Section 2. Once apply-

ing the overlap function over all previous ﬁltered sub-

group sets, i.e. o f ({ f ss

, f ss

}), we

obtained a rss with 14 subgroups. After that, we re-

ordered the subgroups contained in the rss by using

the IRR quality measure, considering the mining view

completely.

4.6 Step 6

Finally, the last step of our methodology consisted of

ﬁltering the rss to obtain the f rss, which was the ﬁ-

nal phenotype generated by our methodology. In this

case, we applied an automatic ﬁltering process based

on the deletion of subgroup reﬁnements. For that pur-

pose, for each pair of distinct subgroups s

and s

from rss, we deleted the subgroup with lower qual-

ity if s

is a reﬁnement of s

or s

is a reﬁnement of

. An advantage of this ﬁlter is that it allows for a

reduction of the number of instances simultaneously

covered by different subgroups from f rss. After ap-

plying this ﬁltering process, we ﬁnally obtained a f rss

with 7 subgroups, which are shown in Table 2.

At this point, it is necessary to remember that both

rss and f rss are two phenotypes with a reduced de-

pendency on the previous SD algorithms and hyper-

parameters used.

The obtained phenotype (Table 2) describes adult

male patients admitted to the surgical service (SURG)

and in the surgical ICU (SICU) who were readmitted

in the hospital and spent one day or more between

the hospital admission and the admission in the ﬁrst

ICU, and in which the cultures were swab. Addition-

ally, the subgroup descriptions from f rss have either

two or three selectors. With respect to the phenotype

A Methodology Based on Subgroup Discovery to Generate Reduced Subgroup Sets for Patient Phenotyping

351

Table 2: Step 6 - Filtered reduced subgroup set f rss.

Subgroup

description

Positive

instances

(tp)

Negative

instances

(fp)

IRR

icu when culture = ’SICU’,

patient age = ’ADULT’,

service when culture = ’SURG’

250

(12%)

178

(3%)

0.559

readmission = ’yes’,

service when culture = ’SURG’

370

(17%)

384

(5%)

0.437

culture specimen type

description = ’SWAB’,

readmission = ’yes’

322

(15%)

372

(5%)

0.412

culture specimen type

description = ’SWAB’,

patient age = ’ADULT’

416

(20%)

481

(7%)

0.396

days between admission

and ﬁrst ICU = ’OneDayOrMore’,

service when culture = ’SURG’

354

(17%)

460

(6%)

0.370

culture specimen type

description = ’SWAB’,

patient gender = ’M’

454

(21%)

600

(8%)

0.346

days between admission

and ﬁrst ICU = ’OneDayOrMore’,

patient age = ’ADULT’

487

(23%)

673

(9%)

0.325

coverage, Table 2 also shows that the subgroups in-

dividually considered always cover less than 25% of

the positive instances and less than 10% of the nega-

tive instances.

4.7 Comparison of the Results

This section compares the f rss obtained by our

methodology with the model obtained by another

descriptive SD method in terms of coverage by

analysing the overlap between the dataset instances

covered by both models. More precisely, we fo-

cus on previous research (Lopez-Martinez-Carrasco

et al., 2023b) in which the DSLM algorithm along

with the mining view presented in Section 4.1 were

used to mine two patient phenotypes in the form of di-

verse top-2 subgroup lists. This comparison process

showed, according to the Dice coefﬁcient, an over-

lap of 50% between f rss and the ﬁrst subgroup list

and 62% between f rss and the second subgroup list.

This means that our methodology was able to mine

a patient phenotype in which, at least, half of the in-

stances were the same as the ones generated by a phe-

notyping SD method based on the Minimum Descrip-

tion Length (MDL) principle (Gr

unwald, 2007) and a

compression gain metric.

5 DISCUSSION

In this section, we discuss our proposed 6-step

methodology and its application to the MIMIC-III

database in the context of patient phenotyping applied

to the antibiotic resistance problem.

With respect to Step 1, it is highly dependent on

the data that we have, the speciﬁc problem that we

are handling and the concrete clinical target to study.

In this work, we present a clinical database with real

data and, after a preprocessing, we obtain a mining

view with 9,240 instances and 12 attributes.

Concerning Step 2, there are two aspects to con-

sider. The ﬁrst one is the number of splits, which de-

termines the quality of the ﬁnal output of the method-

ology. If we have a lower number of splits, algorithms

and hyperparameters, then the rss will remain highly

dependent on those few splits, algorithms and hyper-

parameters used. However, if we have a higher num-

ber of splits, algorithms and hyperparameters, then

the reduced phenotype may be of poor quality since

there is no overlapping between the intermediate sub-

group sets. The second one is the quality measure

used in each SD algorithm. Each quality measure

is designed to focus on different dataset characteris-

tics and, therefore, obtain subgroups with these char-

acteristics (e.g., more general subgroups, more spe-

ciﬁc subgroups, etc.). For this reason, the utilization

of different quality measures allows us to mine a re-

duced phenotype containing subgroups that share all

these characteristics at the same time. Additionally,

this methodology offers the possibility of duplicating

the same split to apply different algorithms and/or hy-

perparameters to the same data. However, it is advis-

able not to abuse this duplication in certain cases since

we can produce that some instances and/or subgroups

have a greater weight than others.

Regarding Step 3, SD is a highly parallelisable

technique since, in general, all subgroups obtained by

a certain SD algorithm can be represented as a tree or

as a lattice. For this reason, each algorithm could be

executed in parallel to improve the methodology per-

formance. Focusing on the WRAcc quality measure,

it prioritises those subgroups that cover more positive

instances than negative ones. This means that all sub-

groups obtained with the mining view or the splits and

this quality measure had values close to 0 because the

number of negative instances is always higher than

the number of positive instances.

Concerning Step 4, this is a step in which the do-

main experts can participate. For this reason, different

visualization methods, apart from those used in this

work, can be deﬁned and provided to help experts’

decision-making.

Regarding Step 5, this work deﬁnes and uses a

speciﬁc overlap function (see Section 2), although

other functions to obtain reduced subgroup sets could

be also explored and deﬁned.

HEALTHINF 2024 - 17th International Conference on Health Informatics

352

With respect to Step 6, it is especially useful in

case the rss has such a large number of subgroups that

it is hardly readable and interpretable by experts. In

this work, we applied a ﬁlter based on the deletion of

subgroup reﬁnements, obtaining therefore a f rss with

7 subgroups in which the shared instances between

different subgroups have been reduced. This is use-

ful to increase the diversity in terms of coverage, i.e.,

to have subgroups that explain as different dataset re-

gions as possible.

Finally, not only the third step can be executed in

parallel. It is also possible to parallelize steps 2 and 4

to enhance the methodology performance.

6 CONCLUSIONS

This research was developed to provide clinicians

with a new approach for obtaining patient phenotypes

with a reduced dependency on the speciﬁc SD algo-

rithm(s) and hyperparameters used. For that, we ﬁrst

deﬁned the problem of mining a patient phenotype in

the form of a reduced subgroup set and, after that,

we proposed a new 6-step methodology based on the

evaluation of the overlap between the output of differ-

ent SD algorithm executions.

The experiments carried out in this work were fo-

cused on the antibiotic resistance problem and were

driven by our methodology. Besides, we used the

MIMIC-III public database as a data source and we

established the patients infected by an Enteroccous

Sp. bacterium resistant to Vancomycin as a target. We

obtained a phenotype f rss with 7 subgroups which

described adult male patients admitted to the surgi-

cal service (SURG) and in the surgical ICU (SICU)

who were readmitted in the hospital and spent one

day or more between the hospital admission and the

admission in the ﬁrst ICU, and in which the cultures

were swab. Moreover, each subgroup from the ﬁnal

phenotype covered 25% of the positive instances and

10% of the negative instances as maximum. Addition-

ally, this phenotype was compared in terms of cover-

age with the diverse top-2 subgroup lists obtained by

the DSLM algorithm. We used the Dice coefﬁcient

for this comparison, obtaining an overlap of 50% be-

tween f rss and the ﬁrst subgroup list and 62% be-

tween f rss and the second subgroup list.

Finally, future work can focus, for example, on us-

ing other visual support techniques in the methodol-

ogy (apart from the already used in this work), explore

other overlap functions, or integrate other techniques

such as the MDL principle in the phenotype genera-

tion process.

ACKNOWLEDGEMENTS

This work was partially funded by the CON-

FAINCE project (Ref: PID2021-122194OB-I00) by

MCIN/AEI/10.13039/501100011033 and by “ERDF

A way of making Europe”, by the “European

Union”, and by the GRALENIA project (Ref:

2021/C005/00150055) supported by the Spanish Min-

istry of Economic Affairs and Digital Transformation,

the Spanish Secretariat of State for Digitization and

Artiﬁcial Intelligence, Red.es and by the NextGen-

erationEU funding. This research was also partially

funded by a national grant (Ref: FPU18/02220), of

the Spanish Ministry of Science, Innovation and Uni-

versities (MCIU).

REFERENCES

Atzmueller, M. (2015). Subgroup Discovery - Advanced

Review. WIREs: Data Mining and Knowledge Dis-

covery, 5(1):35–49.

Atzmueller, M. and Puppe, F. (2006). SD-Map - A Fast

Algorithm for Exhaustive Subgroup Discovery. In

Knowledge Discovery in Databases (PKDD 2006),

pages 6–17.

Garriga, G., Kralj Novak, P., and Lavrac, N. (2006). Closed

Sets for Labeled Data. volume 9, pages 163–174.

unwald, P. D. (2007). The Minimum Description Length

Principle, volume 1. The MIT Press.

Lakkaraju, H., Bach, S. H., and Leskovec, J. (2016). In-

terpretable Decision Sets: A Joint Framework for De-

scription and Prediction. In Proceedings of the 22nd

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining, page 1675–1684.

Lemmerich, F., Rohlfs, M., and Atzm

uller, M. (2010). Fast

Discovery of Relevant Subgroup Patterns. In The

Florida AI Research Society.

Lopez-Martinez-Carrasco, A., Juarez, J. M., Campos, M.,

and Canovas-Segura, B. (2021). A methodology

based on Trace-based clustering for patient phenotyp-

ing. Knowledge-Based Systems, 232:107469.

Lopez-Martinez-Carrasco, A., Juarez, J. M., Campos, M.,

and Canovas-Segura, B. (2023a). VLSD - An Efﬁcient

Subgroup Discovery Algorithm Based on Equivalence

Classes and Optimistic Estimate. Algorithms, 16(6).

Lopez-Martinez-Carrasco, A., Proenc¸a, H. M., Juarez,

J. M., Leeuwen, M. v., and Campos, M. (2023b).

Novel approach for phenotyping based on diverse top-

k subgroup lists. In Artiﬁcial Intelligence in Medicine,

pages 45–50.

Wojczynski, M. K. and Tiwari, H. K. (2008). Deﬁnition of

Phenotype. In Genetic Dissection of Complex Traits,

volume 60, pages 75–105.

A Methodology Based on Subgroup Discovery to Generate Reduced Subgroup Sets for Patient Phenotyping

353