Two-Stage Adaptable Robust Optimization for Glass Production

Anton Medvedev

2 a

, Saﬁa Kedad-Sidhoum

1 b

and Fr

eric Meunier

3 c

CEDRIC - CNAM, France

CEDRIC - CNAM & SGR, France

CERMICS -

Ecole des Ponts ParisTech, France

ﬁ

Keywords:

Robust Optimization, Finite Adaptability, Two-Stage Optimization, Glass Production.

Abstract:

In the glass industry, visual and thermal properties of the glass sheets are obtained via the deposit of thin layers

of different materials. A standard way to perform this step is the use of a “magnetron,” in which the materials

are transferred from cathodes to the sheets using a magnetic ﬁeld. Since the cathodes are very expensive,

activation and replacement decisions have to be carefully decided to keep the cost of the wasted materials low.

The production is organized in campaigns and the activation and replacement decisions of the cathodes have

to be taken before each campaign. Yet, the exact orders to process during a campaign are only revealed after

the decisions have been taken. We focus here on the case of two campaigns, which we model as a two-stage

robust optimization problem. We propose a method based on the ﬁnite adaptability approach of Bertsimas and

Caramanis (2010) combined with the branch-and-bound of Subramanyam et al. (2020). Experiments on real

instances show that our method leads to clear diminutions of the cost of wasted material in the worst cases,

and—even more interesting—allow to ﬁnd solutions for cases that are unfeasible with the heuristic used by

the practitioners.

1 INTRODUCTION

Within the glass industry, the visual and thermal prop-

erties of glass sheets are achieved by applying thin

layers of different materials. A common method

for accomplishing this is the utilization of a “ mag-

netron,” which employs a magnetic ﬁeld to transfer

materials from cathodes to the glass sheets. As cath-

odes are a costly component, it is crucial to care-

fully determine how to reﬁll, to replace, and to ac-

tivate them in order to minimize the wasted material

costs. Due to possible changes of the initial produc-

tion plan, the consumption of cathodes is somewhat

uncertain, making the task of ﬁnding the best reﬁll, re-

placement, and activation decisions highly challeng-

ing. In this procedure, production is structured into

campaigns that include numerous orders. During the

intervals between these campaigns, maintenance for

the magnetron is carried out and decisions regarding

reﬁlling, replacing, and activating the equipment have

to be taken.

https://orcid.org/0009-0003-7726-7168

https://orcid.org/0000-0002-2184-2261

https://orcid.org/0000-0002-5331-2863

This magnetron problem is encountered by Saint-

Gobain, a French multinational company producing

a variety of construction high-performance materials

such as coated glass. The magnetron has already been

the subject of an academic work, by Gicquel et al.

(2010). But the focus of this latter paper is different:

while we assume in the present work that the location

of the cathodes is ﬁxed, the cited paper addresses the

problem of ﬁnding the optimal locations of the cath-

odes in the magnetron.

Uncertainty of the parameters may have crucial

impact on the feasibility and optimality of an opti-

mization problem (Ben-Tal and Nemirovski, 2000).

The two main viewpoints on uncertainty in optimiza-

tion are the stochastic viewpoint and the robust one.

The assumptions and goals of these two viewpoints

are different. Stochastic optimization relies on the

probability distribution of the uncertain parameters

and in general aims at optimizing the expectation

of an objective function. Ruszczy

nski and Shapiro

(2003) provide details on stochastic optimization.

Feasibility of all uncertainty realizations is not neces-

sary required. On the other hand, robust optimization

relies on a set-based uncertainty model, the solutions

are required to be feasible for all uncertainty realiza-

Medvedev, A., Kedad-Sidhoum, S. and Meunier, F.

Two-Stage Adaptable Robust Optimization for Glass Production.

DOI: 10.5220/0012316900003639

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 229-235

ISBN: 978-989-758-681-1; ISSN: 2184-4372

229

tions, and in general the aim is to optimize the worst

case. Gabrel et al. (2014) provide a comprehensive

review of developments of robust optimization and its

application areas.

In this paper, we address the uncertainty of the

magnetron problem from the robust viewpoint. Ac-

cording to the engineers operating the magnetron, fea-

sibility must be ensured in all cases. Indeed, a lack

of material on a cathode might lead to a very costly

interruption of the campaign, and, moreover, expos-

ing such a cathode with the magnetic ﬁeld can even

lead to serious damages to the magnetron itself. This

already brings the problem in the realm of robust op-

timization. A second reason comes from the main ob-

jective function behind the decisions of the engineers:

not to have to perform too many tasks on the cathodes

between the campaigns. Once a reasonable number of

tasks ensuring feasibility has been identiﬁed, the cost

of wasted material has to be kept acceptable, even in

the worst scenario.

We focus on the two-campaign case, which we

model as a “two-stage” robust optimization problem.

In such a problem, there is a ﬁrst series of decisions

to be taken (the “here-and-now” decisions), then un-

certainty is revealed, and then there is a second series

of decisions to be taken (the “wait-and-see” recourse

decisions). It is worth noting that even though in

the magnetron problem the uncertain data is revealed

in two steps—with recourse decisions between these

two steps—we manage to get a two-stage problem,

with only one step of uncertainty to take into account.

We propose then an efﬁcient method to solve this

problem. We follow the ﬁnite adaptability approach

by Bertsimas and Caramanis (2010), combined with

the exact branch-and-bound by Subramanyam et al.

(2020). Experiments show that our method outper-

forms the standard one by two aspects: the cost of

wasted material is always smaller in our solutions

than in the ones computed with the heuristic used by

the practitioners; we show that there exists situations

where this latter method concludes to unfeasibility,

while our method does ﬁnd solutions.

In Section 2, a formal description of the prob-

lem is given. This description is done in two steps:

ﬁrst, the deterministic version, where all parameters

are known when the decisions have to be taken: sec-

ond, the robust version, where the uncertain parame-

ters are progressively revealed, and where some de-

cisions depend on the uncertainty. This problem is

then modeled as a mathematical program in Section 3.

Section 4 presents the method proposed to solve the

problem after a brief introduction to ﬁnite adaptability

and to the branch-and-bound approach. In Section 5,

numerical results are provided and commented, prov-

ing the efﬁciency of the method.

2 PROBLEM FORMULATION

In this section we present the formulation of the mag-

netron problem in its two versions, deterministic and

robust.

2.1 Deterministic Version

On the magnetron, there are n possible locations for

the cathodes. A campaign C is a multiset of orders.

An order o corresponds to a triple (G

, p

), with

⊆ [n] and p

∈ R

. The number p

is the total

power that must be distributed among the cathodes at

locations in G

. The number t

is the processing time

of the order o.

Moreover, the cathodes’ locations are partitioned

into m subsets denoted by A

,. ..,A

. Each of these

subsets corresponds to locations assigned to a certain

material.

As we focus on a two-campaign setting, an in-

stance of the problem is a pair of campaigns C

The orders in C

are processed before those in C

The following decisions have to be taken for each

campaign C

• Reﬁll: choose a subset R

⊆ [n] of locations for

which the cathodes will be reﬁlled at the full level

just before C

. The full level at location j is de-

noted by Q

• Replacement: choose a permutation σ

of [n] such

that σ

) = A

for all i ∈ [m]: for j ∈ A

, the cath-

ode at j will be placed at σ

( j) ∈ A

just before the

reﬁlls R

• Activation: distribute the power p

of order o ∈ C

among the cathodes at locations in G

, as p

∑

j∈G

o, j

The number of cathode’s reﬁlls before C

cannot ex-

ceed a given limit r

. The number of replacements

between cathodes before C

cannot exceed a given

threshold s

. Given o ∈ C

, the quantities p

o, j

of an

activation decision p

∑

j∈G

o, j

have to belong to

{0} ∪ [p

, p

], where p

and p

are parameters. In

words, this last constraint means that when a cathode

is activated, the power of the activation has to lie in a

given interval.

For the cathode located at j, we denote by q

the

initial quantity of material, by q

the quantity of ma-

terial just after C

, and by q

the quantity of material

just after C

. While q

is a parameter, the quantities

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

230

and q

are auxiliary variables. For c ∈ {1,2}, the

quantity q

c+1

can be expressed as

c+1

= −

∑

o∈C

o, j

(

if j ∈ R

( j)

otherwise.

The ﬁrst term in the expression of q

c+1

stands for the

material consumption implied by campaign C

and

activation decisions on the cathode at j. For c ∈ {2, 3}

the quantity q

has to be non-negative: q

⩾ 0.

The only cost implied by the reﬁll, the replace-

ment, and the activation decisions is the materials

waste cost. For a cathode at location j just before

, the latter is c

, where c

is the unit cost of the

material located at j. In words, this means that when

a cathode at j is reﬁlled, all the current quantity on

it is lost. With the notation F(q

)

∑

j∈R

the total resulting cost can be written as F(q

) +

F(q

2.2 Robust Version

We present now the robust version to handle the un-

certain parameters.

For C

there is a polyhedral uncertainty set Ω

The only parameters that depend on the uncertainty

are the production times t

, which we write from now

on t

(ω

), where ω

∈ Ω

if o ∈ C

. We assume that

this dependence is afﬁne.

The uncertainty realizations ω

∈ Ω

and ω

∈ Ω

are revealed in two steps: ω

is revealed after C

has

been processed, and ω

is revealed after C

has been

processed. This implies that the decisions taken be-

tween C

and C

may depend on ω

. In particular,

the reﬁll decisions of C

becomes R

(ω

). No deci-

sions are taken after C

has been processed. Yet some

auxiliary variables depend on ω

The last changes the robust version implies with

respect to the deterministic version are the expression

of q

and q

, the non-negativity of the available quan-

tity of material on the cathodes, and the expression of

the objective function.

For all j ∈ [n] the quantity q

becomes

(ω

) = −

∑

o∈C

(ω

o, j

(

if j ∈ R

( j)

otherwise,

and the quantity q

becomes

(ω

,ω

) = −

∑

o∈C

(ω

o, j

(ω

)

(

if j ∈ R

(ω

)( j)

(ω

) otherwise,

for all ω

∈ Ω

,ω

∈ Ω

The non-negativity constraints translate into

(ω

) ⩾ 0 and q

(ω

,ω

) ⩾ 0 for all ω

∈ Ω

,ω

∈

Ω

The objective function becomes F(q

) +

max

∈Ω

F(q

(ω

),R

(ω

)). Robustness refers to

the requirement to be feasible for every realization

of the uncertainty and to be minimal for the maximal

possible cost.

3 MODELING

In this section we model the magnetron problem in its

robust version as a mathematical program.

The constraints related to the number of reﬁlls are:

∑

j=1

⩽ r

∑

j=1

(ω

) ⩽ r

∀ω

∈ Ω

(1)

The variable r

is binary and takes the value 1 if

the cathode located at j is reﬁlled, i.e., if j ∈ R

. Sim-

ilarly, the variable r

(ω

) is binary and takes the value

1 if the cathode located at j is reﬁlled in the realiza-

tion ω

, i.e., if j ∈ R

(ω

The constraints related to the number of replace-

ments are:

∑

j=1

∑

k=1

k̸= j

j,k

⩽ s

∑

k=1

j̸=k

k, j

∑

k=1

j̸=k

j,k

∀ j ∈ [n]

∑

k=1

j,k

= 1 ∀ j ∈ [n]

∑

j=1

∑

k=1

k̸= j

j,k

(ω

) ⩽ s

∀ω

∈ Ω

∑

k=1

j̸=k

k, j

(ω

) =

∑

k=1

j̸=k

j,k

(ω

) ∀ j ∈ [n], ω

∈ Ω

∑

k=1

j,k

(ω

) = 1 ∀ j ∈ [n], ω

∈ Ω

(2)

The variable y

j,k

is binary and takes the value 1

if the cathode at j is replaced by the cathode at k,

i.e., if σ

( j) = k. Similarly, the variable y

j,k

(ω

) is

binary and takes the value 1 if the cathode at j is re-

placed by the cathode at k in the realization ω

, i.e.,

Two-Stage Adaptable Robust Optimization for Glass Production

231

if σ

(ω

)( j) = k. Constraints (2) models the permu-

tation in a standard way, as done for instance for the

directed TSP; see, e.g., Korte et al. (2011).

The constraints on the activation decisions are:

∑

j∈G

o, j

= p

∀o ∈ C

∑

j∈G

o, j

(ω

) = p

∀o ∈ C

, ω

∈ Ω

(3)

The constraints on the quantities of material on

cathodes at any location before both campaigns are:

(ω

) = −

∑

o∈C

(ω

o, j

+ r

+(1 − r

)

∑

k=1

j,k

∀ j ∈ [n] ,ω

∈ Ω

(ω

,ω

) = −

∑

o∈C

(ω

o, j

(ω

) + r

(ω

+(1 − r

(ω

))

∑

k=1

j,k

(ω

)

∀ j ∈ [n] ,ω

∈ Ω

,ω

∈ Ω

(4)

The robust magnetron problem is formulated as

follows:

min

∑

j=1

+ max

∈Ω

∑

j=1

(ω

)

s.t. (1), (2), (3), (4)

∈ {0,1} ∀ j ∈ [n]

(ω

),r

(ω

) ∈ {0,1} ∀ j ∈ [n], ω

∈ Ω

o, j

∈ {0} ∪ [p

, p

] ∀o ∈ C

, j ∈ [n]

o, j

(ω

) ∈ {0} ∪ [p

, p

]

∀o ∈ C

, j ∈ [n],ω

∈ Ω

(ω

) ∈ [0,Q

] ∀ j ∈ [n], ω

∈ Ω

(ω

,ω

) ∈ [0,Q

]

∀ j ∈ [n], ω

∈ Ω

,ω

∈ Ω

(P)

The problem (P) has non-linear constraints. We

are able to linearize all of these constraints and

write (P) in the following form without loss of gen-

erality:

min

˜x, ˜y(·)

˜c

⊤

˜x + max

∈Ω

⊤

˜y(ω

)

s.t.

A(ω

,ω

) ˜x +

B(ω

,ω

) ˜y(ω

) ⩽

∀ω

∈ Ω

,ω

∈ Ω

(5)

with

A and

B two matrices afﬁnely depending on

(ω

,ω

) ∈ Ω

× Ω

, and

b, ˜c, and

d are determinis-

tic vectors. The variables are ˜x and ˜y(·): the variable

˜x is the “here-and-now” variable, whose value has to

be determined without knowing the exact ω

∈ Ω

that will be selected, contrary to ˜y(·)—the “wait-and-

see” recourse variable—whose value can arbitrarily

depend on ω

The problem (5) does not ﬁt in the standard form

of two-stage robust optimization problems because of

the presence of a second uncertainty ω

, which is re-

vealed after all decisions have been taken. We use

a standard duality technique of the robust optimiza-

tion (Gorissen et al., 2015), which allows to transform

the for all quantiﬁer for ω

∈ Ω

into an exists quan-

tiﬁer. The obtained problem form is the following:

min

x,y(·)

⊤

x + max

ω∈Ω

⊤

y(ω)

s.t. A(ω)x + B(ω)y(ω) ⩽ b ∀ω ∈ Ω

(6)

with A and B two matrices afﬁnely depending on ω ∈

Ω, and b, c, and d are deterministic vectors. Note that

in (6) the indices for uncertainty realization and for

uncertainty set are dropped, as there is only one uncer-

tainty set. The variables are x and y(·): the variable x

is the “here-and-now” variable, whose value has to be

determined without knowing the exact ω ∈ Ω that will

be selected, contrary to y(·)—the “wait-and-see” re-

course variable—whose value can arbitrarily depend

on ω. The problem (6) is a complete adaptability ver-

sion of a two-stage robust optimization problem, as

the recourse is an arbitrary function of uncertainty.

4 METHOD

Solving exactly problem (6) is referred as complete

adaptability, but this is in general considered as not

tractable since it implies in particular computing an

optimal recourse function y(·) that may be arbitrar-

ily complicated. Bertsimas and Caramanis (2010)

introduced the notion of ﬁnite adaptability (or k-

adaptability). This approach bridges the gap between

complete adaptability and a “myopic” approach—the

static variant—taking a ﬁxed recourse decision inde-

pendently of the uncertainty. We address the mag-

netron problem via ﬁnite adaptability, and rewrite ac-

cordingly the magnetron problem as

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

232

min

Ω

∪···∪Ω

x,y

,...,y

⊤

x + max

i∈[k]

⊤

s.t. A(ω)x + B(ω)y

⩽ b ∀i ∈ [k] ∀ω ∈ Ω

)

The idea behind the k-adaptability is to split the

uncertainty set Ω into k parts and to assign to each

part a constant recourse decision. The advantage of

such a method compared to the myopic one is that it

allows to separate extreme scenarios and cover them

with different recourse decisions. Multiple heuristics

appeared in the last decade, allowing to solve (P

such as Bertsimas and Dunning (2016) or Postek and

Hertog (2016). Subramanyam et al. (2020) proposed

a branch-and-bound method solving (P

) efﬁciently,

with proven lower and upper bounds. It is this algo-

rithm which we use to solve the problem.

This branch-and-bound takes as a parameter k, the

number of parts in which the uncertainty set will be

split. Each node of the branch-and-bound tree cor-

responds to a collection of k pairwise disjoint subsets

Ω

′

,. ..,Ω

′

⊆ Ω (a “partial partition”). Branching cor-

responds to adding an element ω from Ω that is not

yet covered by the Ω

′

, to each of the Ω

′

. This way, k

branches stems from each node that is not a leaf. A

“separation” subroutine tests whether an optimal so-

lution to the partial partition is also valid for a full

partition completing it. If this is the case, then we

have reached a leaf. If not, the subroutine has actu-

ally found an ω to be added to the Ω

′

5 NUMERICAL EXPERIMENTS

Before describing brieﬂy the instances and the results,

we explain how the uncertainty is modeled in the ex-

periments. We claim that this modeling is quite accu-

rate.

5.1 Modeling Uncertainty

The only parameters that depend on the uncertainty

are the production times, which we assume to be of

the following form for campaign C

. Given ω

∈ Ω

we have t

(ω

) =

(1+ pω

), where p is a coefﬁcient

in [0,1] and

is a coefﬁcient in R depending on the

order o. The uncertainty set Ω

is deﬁned as

Ω

(

(ω

)

o∈C

: ω

∈ [−1,1] and

∑

o∈C

= 0

)

This is the most elementary way to model the uncer-

tainty so that

• the production times of every order o can take

any value in an interval centered at some value

which corresponds to the predicted value of t

• the total duration of a campaign is ﬁxed (does not

depend on the uncertainty).

5.2 Instances and Setting

To assess the performance of the method proposed in

Section 4, a real dataset corresponding to seven cam-

paigns has been used to derive three two-campaign in-

stances of the magnetron problem. The dataset corre-

sponds to a magnetron of thirty cathodes of ten differ-

ent materials. Each instance is of size n = 30, m = 10

with |C

| ∈ [10,12] and |C

| ∈ [10,12].

For these experiments, we have chosen to forbid

replacements (i.e., the parameters s

and s

are set to

zero). We have r

= 8 and r

= 14 for data1 and data2.

For data3, we have r

= 14 and r

= 8.

Parameter c

ranges from 200 to 1000 for j =

1,. ..,n, j /∈ {9,10,24}, c

= c

= 35 and c

= 45.

Regarding uncertainty, the experiments have been

conducted with p ∈ {0.1,0.2,0.5}.

We used the open-source implementation of the

algorithm of Subramanyam et al. (2020), based on the

C callable library of CPLEX. All experiments were

conducted on 32 cores of an Intel Xeon 2.30GHz

computer, with a gap limit of 0.1%, a time limit of

3600 seconds and a memory limit of 10Gb.

5.3 Results

The three available instances have been solved us-

ing the branch-and-bound algorithm of Subramanyam

et al. (2020) for all the values of k ∈ [10]. The solu-

tion obtained for k is used as a warm-start for k + 1.

Table 1 gives the numerical results for problem (P

The ﬁrst column refers to the dataset. The next two

columns give the parameters p and k respectively.

Columns four and ﬁve provide the value of the ob-

jective function and the CPU time in seconds. The

second-to-last column gives the average relative gap

between the global lower bound for (P

) (for the given

k) and the achieved objective value (either optimal

or provided by the incumbent branch-and-bound tree

when the time limit is reached). The last column

of the table displays the relative gain brought by k-

adaptability for the associated value of k, compared

to the 1-adaptability.

5.4 Comments

For the static version a nearly-optimal solution is

found most of the time very quickly, but in some set-

tings as for the instance data1 with p = 0.5, it is more

time consuming. For k > 1 the gap signiﬁcantly grows

in most of cases, but for instances data1 and data2

Two-Stage Adaptable Robust Optimization for Glass Production

233

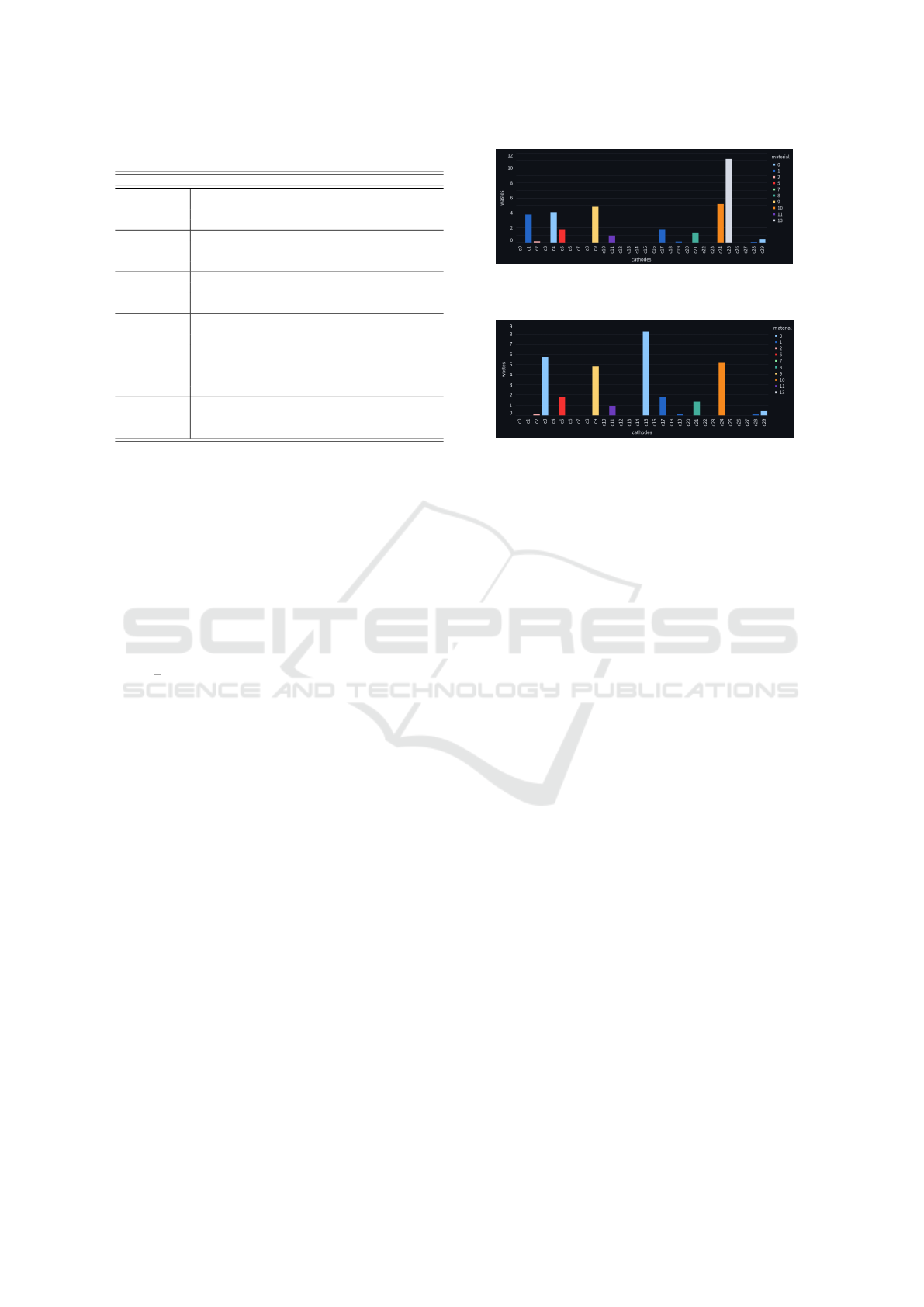
Table 1: Numerical results for problem (P

dataset p k value time (s) gap (%) gain vs k = 1 (%)

data1 0.20 1 10,514.60 144.12 0.10 0.00

data1 0.20 2 10,507.20 3,606.84 56.48 0.07

data1 0.20 5 10,498.10 3,606.50 56.45 0.16

data1 0.20 10 10,351.30 359.64 0.09 1.55

data2 0.20 1 4,983.26 1.93 0.10 0.00

data2 0.20 2 4,865.31 3,603.19 7.45 2.37

data2 0.20 5 4,865.31 3,604.79 7.30 2.37

data2 0.20 10 4,865.31 1,126.59 0.10 2.37

data3 0.20 1 8,215.78 1.82 0.04 0.00

data3 0.20 2 8,190.85 3,607.50 27.09 0.30

data3 0.20 5 7,634.37 3,603.38 26.79 7.08

data3 0.20 10 7,634.37 3,605.04 26.79 7.08

data1 0.50 1 25,275.90 957.35 0.10 0.00

data1 0.50 2 22,403.90 3,602.72 39.31 11.36

data1 0.50 5 22,282.40 3,605.31 49.60 11.84

data1 0.50 10 22,282.40 2,252.41 50.33 11.84

data2 0.50 1 5,433.87 2.71 0.00 0.00

data2 0.50 2 5,433.87 3,600.27 6.95 0.00

data2 0.50 5 5,433.87 3,605.70 7.66 0.00

data2 0.50 10 5,433.87 3,613.37 21.93 0.00

data3 0.50 1 11,700.30 1.36 0.04 0.00

data3 0.50 2 11,680.10 3,600.62 7.13 0.17

data3 0.50 5 11,627.40 3,602.26 13.05 0.62

data3 0.50 10 11,627.40 3,602.55 13.05 0.62

with p = 0.2 and k = 10 a nearly optimal solution is

also found with an optimality gap close to zero.

The k-adaptability framework has a great impact

on the quality of the obtained solutions. For some

instances the gap for k = 1 is smaller than the relative

gain brought by larger values of k. This means that it

is guaranteed that increasing k in these cases leads to

better decisions.

We do not know the exact description of the

heuristic used by the practitioners but since it uses a

ﬁxed recourse, it is dominated by our results for k = 1.

Complementary experiments have shown that

when r

= 12, data1 with p = 0.5 has no feasible

solution for k = 1, while there are feasible solutions

for k > 1. It means that for some instances the k-

adaptability may not only bring better solutions in

terms of the objective function, but also and more im-

portantly may bring feasibility.

6 CONCLUDING REMARKS

We formulated and modeled an industrial problem in

the framework of ﬁnite adaptability and solved it with

a branch-and-bound algorithm developed by Subra-

manyam et al. (2020). The experimental results show

that for some instances ﬁnite adaptability brings more

optimal solutions and even feasibility.

Two research directions can be further explored.

The ﬁrst one aims at comparing the long term effects

of the ﬁnite adaptability and the static method. This

study is interesting because a good short-term opti-

mization may have bad impact on the long-term re-

sults. The second one seeks to adapt the problem for-

mulation in the case of a heavy production planning.

In that case the objective would be to minimize the

number of reﬁlls, leading to the maintenance duration

Figure 1: Wasted quantities of material (mm) before the ﬁrst

campaign for the static solution for data1 with p = 0.50.

Figure 2: Wasted quantities of material (mm) before the

ﬁrst campaign for the 10-adaptable solution for data1 with

p = 0.50.

minimization.

ACKNOWLEDGEMENTS

This research was supported by Saint Gobain Re-

search Paris as part of a CIFRE collaboration with the

CEDRIC laboratory of the CNAM Paris. We thank

our colleagues Amaury Civrac and S

ebastien De-

schamps from who provided insight and expertise that

greatly assisted the research. We also thank Bastien

Rolland and his supervisor Tristan Barbe, who started

working of this subject as part of an internship.

REFERENCES

Ben-Tal, A. and Nemirovski, A. (2000). Robust solutions of

linear programming problems contaminated with un-

certain data. Mathematical programming, 88(3):411–

424.

Bertsimas, D. and Caramanis, C. (2010). Finite adaptability

in multistage linear optimization. IEEE Transactions

on Automatic Control, 55(12):2751–2766.

Bertsimas, D. and Dunning, I. (2016). Multistage robust

mixed-integer optimization with adaptive partitions.

Operations Research, 64(4):980–998.

Gabrel, V., Murat, C., and Thiele, A. (2014). Recent ad-

vances in robust optimization: An overview. Eu-

ropean journal of operational research, 235(3):471–

483.

Gicquel, C., Mi

egeville, N., Minoux, M., and Dallery, Y.

(2010). Optimizing glass coating lines: Mip model

and valid inequalities. European Journal of Opera-

tional Research, 202(3):747–755.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

234

Gorissen, B. L., Yanıko

glu,

I., and den Hertog, D. (2015).

A practical guide to robust optimization. Omega,

53:124–137.

Korte, B. H., Vygen, J., Korte, B., and Vygen, J. (2011).

Combinatorial optimization, volume 1. Springer.

Postek, K. and Hertog, D. d. (2016). Multistage adjustable

robust mixed-integer optimization via iterative split-

ting of the uncertainty set. INFORMS Journal on

Computing, 28(3):553–574.

Ruszczy

nski, A. and Shapiro, A. (2003). Stochastic pro-

gramming models. Handbooks in operations research

and management science, 10:1–64.

Subramanyam, A., Gounaris, C. E., and Wiesemann, W.

(2020). K-adaptability in two-stage mixed-integer ro-

bust optimization. Mathematical Programming Com-

putation, 12(2):193–224.

Two-Stage Adaptable Robust Optimization for Glass Production

235