Integration of Pricing and Production Scheduling Decisions: A

Mathematical Model

J. Mhanna

and H. Nouinou

CESI LINEACT, 54000 Nancy, France

Keywords:

Pricing, Production Scheduling, Parallel Machines, Mixed Integer Linear Programming, Periodic Ordering.

Abstract:

In today’s competitive manufacturing landscape, achieving operational efﬁciency and optimizing revenue gen-

eration are key objectives for make-to-order manufacturers. This paper presents a novel approach for integrat-

ing production scheduling and pricing decisions in a make-to-order manufacturing environment. We propose a

comprehensive mathematical model that addresses the complex interplay between production scheduling and

pricing strategies. By jointly optimizing these two critical aspects, manufacturers can enhance their competi-

tiveness and proﬁtability. The objective of the scheduling decisions is to minimize the total tardiness penalties

of jobs on a non-preemptive parallel machine environment, a widely used measure of customer service. Pricing

decisions on the other hand aim at maximizing the total revenue. A mixed integer linear programming model

is formulated and an algorithm is developed based on the ε-constraint approach to conduct the experimental

analysis. The algorithm aims to ﬁnd the best solutions, from the decision-maker’s perspective, by iteratively

adjusting production schedules and pricing decisions.

1 INTRODUCTION

In the dynamic landscape of make-to-order manu-

facturing, effective coordination between production

scheduling and pricing decisions is crucial for com-

panies to optimize their operational efﬁciency and

revenue generation. Traditionally, these two aspects

have been treated as separate entities, leading to sub-

optimal outcomes and missed opportunities. How-

ever, recognizing the inherent interdependencies be-

tween production scheduling and pricing strategies,

researchers and practitioners are increasingly focus-

ing on integrating these decisions to gain a competi-

tive advantage.

The integration of production scheduling and pric-

ing decisions presents a complex challenge due to

the dynamic nature of customer demands, evolving

market conditions, and limited production resources.

Manufacturers need to determine not only how to al-

locate production resources optimally but also how

to set prices that maximize revenue and satisfy cus-

tomer demand within speciﬁed delivery deadlines.

By jointly optimizing these decisions, companies can

enhance their ability to meet customer requirements

https://orcid.org/0009-0007-4460-5852

https://orcid.org/0000-0002-8712-4043

while maximizing proﬁtability.

To address this challenge, this paper proposes a

comprehensive mathematical model based on mixed-

integer linear programming that integrates production

scheduling and pricing decisions in a make-to-order

manufacturing environment. Our planning environ-

ment models the periodic ordering and scheduling de-

cisions that are commonly employed in the industry

(Russell and Taylor, 2006). In this context, orders are

typically accepted on a timely basis, with no new jobs

becoming available between consecutive orders. By

formulating the problem as a mathematical optimiza-

tion model, we aim to provide a systematic and rig-

orous approach for decision-making in this complex

environment.

Furthermore, the principle of ε-constraint is con-

sidered in order to ﬁnd the right balance between the

two objective functions, that is minimizing the total

tardiness penalty of orders and maximizing the total

proﬁt of the company. Leveraging mathematical pro-

gramming techniques and optimization methods, the

algorithm aims to ﬁnd optimal solutions by iteratively

adjusting the priority for one objective over the other

depending on the company’s strategy, i.e. increasing

proﬁt or improving customer satisfaction. By consid-

ering the dynamic nature of the environment, the al-

gorithm enables companies to adapt and respond to

Mhanna, J. and Nouinou, H.

Integration of Pricing and Production Scheduling Decisions: A Mathematical Model.

DOI: 10.5220/0012307700003639

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 221-228

ISBN: 978-989-758-681-1; ISSN: 2184-4372

221

changing market conditions and customer demands

effectively.

To validate the effectiveness of the proposed

mathematical model and algorithm, computational

experiments were conducted using arbitrary chosen

data and based on probability distributions. The im-

plementation results conﬁrm the effectiveness of the

proposed model, while the proposed algorithm pro-

vides a decision-maker-based-system able to help a

decision-maker determine the best compromise ac-

cording to their perspective between the two objective

functions and the executions time.

The remainder of this paper is organized as fol-

lows: Section 2 presents a brief literature review on

the integration of pricing and production scheduling

decisions in make-to-order manufacturing environ-

ment. The problem description along with the pro-

posed mathematical model are presented in Section

3. Section 4 presents an illustrative example to rep-

resent the solution structure provided by the model.

Then, computational experiments on the model using

a proposed algorithm are conducted in Section 5. Fi-

nally, conclusions and future directions are presented

in Section 6.

2 LITERATURE REVIEW

The close interplay between operational aspects such

as production planning and inventory policies, and

marketing decisions including demand management

and pricing strategies has long been acknowledged

in practical contexts (Chen. and Hall, 2022). Con-

sequently, it is essential to make coordinated mar-

keting and production decisions to maximize over-

all efﬁciency and proﬁtability throughout the supply

chain. Extensive literature surveys were conducted by

Eliashberg and Steinberg (1993), Chen and Simchi-

Levi (2012), and Chen. and Hall (2022), show-

ing considerable research attention devoted to Coor-

dinated Pricing and Production Scheduling (CPPS)

over the past decades. Among the vast array of re-

search and advancements in this ﬁeld, only a lim-

ited number of studies speciﬁcally addresses the de-

tailed scheduling of individual orders. Nevertheless,

as shown in (Chen. and Hall, 2022), many practical

examples can state the pertinence of coordinating pro-

duction scheduling and pricing decisions in make-to-

order systems. Driven by this practical relevance, two

categories of CPPS problems can be distinguished,

including problems with a single period pricing, and

problems with multiple periods pricing.

For the single-period pricing problem, orders

prices are decided at the beginning of the scheduling

horizon. Chen and Hall (2010) study the coordina-

tion of pricing and scheduling decisions in a make-to-

order environment. Assuming knowledge of a deter-

ministic non-increasing demand function, they study

three objective functions for the scheduling problem,

including the total work in progress, the total penalty

for orders delivered late, and the total capacity usage

while maximizing the total net proﬁt of the company.

Moreover, they assume that a single price is used for

each product along with its respective demand over

the entire scheduling horizon. They examine three

degrees of coordinating pricing and scheduling deci-

sions in order to conclude on the advantage of coordi-

nation in this context.

Liu et al. (2020) study the problem with a sin-

gle machine environment, where the manufacturer re-

ceives order inquiries from customers and has to al-

locate a price for each enquiry. They consider a

probability associated with the acceptance of the al-

located price by a customer and aim at maximizing

revenue while minimizing the total tardiness. To solve

this problem, they propose an efﬁcient heuristic after

proving that the problem is NP-hard.

Lu et al. (2013)’s work includes modeling cus-

tomer demand’s uncertainty. They focus on min-

imizing the expected production cost based on the

total weighted completion time. They design dy-

namic programming algorithms to solve the problem.

Their study highlights the advantage of coordination

in proﬁt maximization.

Wang and Wang (2019) investigate the pricing and

scheduling decisions coordination on a parallel ma-

chines environment, where the objective is to maxi-

mize revenue and minimize the total weighted tardi-

ness of accepted orders. They propose a mixed integer

linear programming model where products prices are

decided at the beginning of the planning horizon.

For the multi-period pricing problem, Yue et al.

(2019) study a particular problem motivated by the

practical setting where a manufacturer makes multi-

ple customized products from a common base prod-

uct. They use dynamic pricing to match capacity with

demand over a multi period planning horizon. Hence,

at the beginning of each period, the price and the pro-

duction schedule are decided for incoming orders on a

single machine environment. They consider that due

dates are equal to the end of each period, meaning

that a common due date is ﬁxed for orders arriving

at the beginning of each period. They propose dy-

namic programming algorithms to solve three variants

of the problem, including the total weighted comple-

tion time minimization, tardiness minimization with

rejection and without rejection.

In comparison to the existing literature, our

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

222

work makes a distinct contribution by introducing a

novel perspective on the multi-period pricing prob-

lem within the context of coordinated marketing and

production decisions. While the literature, exempli-

ﬁed by Yue et al. (2019), primarily considers a multi-

period setting where orders are scheduled based on

ﬁxed end-of-period deadlines, our study extends this

paradigm by allowing each order to possess a ﬂexi-

ble and arbitrary deadline, thereby reﬂecting the com-

plexities often encountered in real-world scenarios.

This departure from traditional scheduling deﬁnitions

permits a more accurate representation of practical

situations, where orders might be processed across

different periods depending on their individual dead-

lines. Furthermore, our proposed mathematical model

is designed not only to provide optimal solutions for

small instances but also serves as an initial step to-

wards tackling larger-scale instances using heuristics

and meta-heuristics.

3 PROBLEM DESCRIPTION

The problem under study involves scheduling orders

in an identical parallel machine environment taking

into account pricing decisions. The company pro-

poses a set of products and a range of prices for

each product and orders are received at speciﬁc arrival

times set by the company. The model then decides the

prices, the scheduling order and the machine assign-

ment for customers orders, so as to maximize revenue

and minimize production cost.

Following the Graham’s notation (Graham,

1966), the scheduling problem can be denoted as

∑

, where each order has a release date

at which it becomes available for scheduling,

a deadline d

at which it must be completed, and

a weight w

that refers to the penalty assigned to

an order if delayed. Furthermore, the objective

function is the total weighted tardiness of orders,

expressed as

∑

, where the tardiness of an

order T

= max{c

− d j, 0}, such as c

refers to the

completion time of the order. Finally, the scheduling

environment is composed of m identical parallel

machines. These notations are employed to describe

the classical scheduling problem and will evolve

in the following sections to accurately describe the

speciﬁc problem under consideration, taking into

account the pricing integration.

The scheduling problem P

∑

is NP-

hard since even the problem without release dates

∑

is NP-hard, as proved by Koulamas

(1994). The comparison between the latter and the

studied problem reveals their similarity, with the only

difference being the inclusion of the dynamic pricing

part in the studied problem. As a result, it is evident

that the studied problem is also NP-hard.

3.1 Assumptions

The mathematical model for the pricing and schedul-

ing decisions coordination takes into account the fol-

lowing assumptions inherited from the standard par-

allel machine scheduling problem with release dates

and due dates.

• Order preemption is not allowed, meaning that an

order can not be interrupted once it starts its pro-

cessing.

• Each order has a processing time.

• Each order has an arrival time and hence cannot

start processing before.

• Each order has a due date, and if that due date is

violated or not met, a penalty is incurred.

• Machines are identical.

• Each machine can process at most one order at a

time.

3.2 Notations

The proposed mathematical model is based on the fol-

lowing notations for sets and indices:

• M: set of ¯m identical parallel machines, with M =

{1,..., ¯m}.

• P: set of ¯p products proposed by the company,

with P = {1, ..., ¯p}.

• T : set of

t orders arrival times, with T = {t

,...,

t}.

• L

: set of

prices allowed for a product i ∈ P, with

= {1,...,

• D

: set of

orders of a product i ∈ P, with D

{1,...,

}, D

max

= max

i∈P

• pt

: processing time of a product i, with i ∈ P.

• w

: tardiness penalty of a product i ∈ P.

• d

: deadline of an order of product i ∈ P made at

time t ∈ T .

• f

: decreasing demand function with respect to the

product’s price for a product i ∈ P.

• q

: price of product i ∈ P of index l ∈ L

, such as

) is the associated demand.

• N: sufﬁciently large number.

Integration of Pricing and Production Scheduling Decisions: A Mathematical Model

223

3.3 Decision Variables

• T

i j

: tardiness of an order j of a product i made at

time t, with j ∈ D

, i ∈ P, and t ∈ T .

• C

i j

: completion time of an order j of product i

made at time t, with j ∈ D

, i ∈ P, and t ∈ T .

• x

: binary decision variable, which indicates the

price selected for a product order. This variable is

equal to 1 if price q

is ﬁxed for product i ∈ P at

period t, with l ∈ L

, and 0 otherwise.

• z

i j

: binary decision variable, which indicates if an

order of a product is made. This variable is equal

to 1 if order j ∈ D

of product i ∈ P is made at

time t, and 0 otherwise.

• A

i jt

: binary decision variable, which suggests the

orders assignments to machines. This variable is

equal to 1 if order j ∈ D

of product i ∈ P made

at time t ∈ T is assigned to machine k ∈ M, and 0

otherwise.

• y

i jtuvt

: binary decision variable, which indicates

the order of processed jobs. This variable is equal

to 1 if, on machine k ∈ M, order j ∈ D

of product

i ∈ P made at time t ∈ T is a direct predecessor of

order v ∈ D

of product u ∈ P made at time t

∈ T ,

and 0 otherwise.

3.4 Mathematical Model

The mathematical model (P0) presented here for the

problem of pricing and production scheduling was in-

spired from the Wang and Wang (2019)’s formulation.

Their model considers that prices are decided at the

beginning of the scheduling horizon and demand is

then ﬁxed consequently. The pricing integration part

was adapted for this mathematical model while con-

sidering that pricing decisions are made dynamically

at multiple order arrival times. Hence, the scheduling

decision must be made taking into account the con-

straint regarding orders arrival times.

The mathematical model (P0) is formulated as in-

dicated through equations (1) to (15):

Minimize

∑

t∈T

∑

i∈P

(

∑

j∈D

i j

−

∑

l∈L

) × x

)

(1)

Subject to:

∑

l∈L

= 1,∀t ∈ T,i ∈ P (2)

∑

j∈D

i j

∑

l∈L

) × x

,∀i ∈ P,t ∈ T (3)

∑

l∈L

) × x

− j ≥ D

max

× (z

i j

− 1),∀i ∈ P,

j ∈ D

,t ∈ T (4)

∑

k∈M

i jt

= z

i j

,∀i ∈ P, j ∈ D

,t ∈ T (5)

∑

u∈P

∑

v∈D

∑

∈T

i jtuvt

≤ A

i jt

,∀i ∈ P, j ∈ D

t ∈ T ,k ∈ M (6)

∑

i∈P

∑

j∈D

∑

t∈T

i jtuvt

≤ A

uvt

,∀u ∈ P,v ∈ D

∈ T ,k ∈ M (7)

∑

i∈P

∑

u∈P

∑

j∈D

∑

v∈D

∑

∈T

∑

t∈T

i jtuvt

∑

u∈P

∑

v∈D

∑

∈T

uvt

− 1,

∀k ∈ M

(8)

≥ C

i j

+ pt

− N × (3 − y

i jtuvt

− A

i jt

− A

uvt

∀i,u ∈ P,v ∈ D

, j ∈ D

,t ∈ T,t

∈ T, k ∈ M

(9)

i j

≥ t + pt

−N ×(1−z

i j

),∀i ∈ P, j ∈ D

,t ∈ T (10)

i j

≥ C

i j

− d

,∀i ∈ P, j ∈ D

,t ∈ T (11)

i j

≥ 0,∀i ∈ P, j ∈ D

,t ∈ T (12)

i j

≤ N × z

i j

,∀i ∈ P, j ∈ D

,t ∈ T (13)

i j

≥ 0,∀i ∈ P, j ∈ D

,t ∈ T (14)

i j

i jt

i jtuvt

∈ {0,1},∀i,u ∈ P, j ∈ D

v ∈ D

,l ∈ L

,t,t

∈ T, k ∈ M (15)

The objective function (1) minimizes the total tar-

diness penalty of orders while maximizing the total

revenue.

Constraint (2) veriﬁes that a single price is chosen for

each product ordered at a time t ∈ T .

Constraint (3) ﬁxes the total number of orders to be

scheduled for each product at each arrival time t ∈ T

to be equal to the total demand made.

Constraint (4) sets z

i j

= 0 in case

∑

l∈L

) × x

−

j ≥ 0, i.e. the actual demand is less than the maxi-

mum demand. On the other hand, in case z

i j

= 1 the

inequality remains valid.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

224

Constraint (5) states that each order of a product made

at an arrival time t ∈ T is assigned to a single machine.

Constraints (6) and (7) verify that if an order is as-

signed to a machine, then it is succeeded and preceded

by at most one order.

Constraint (8) ﬁxes the number of precedence rela-

tionships on each machine.

Constraints (9) and (10) set the completion time of

each order.

Constraints (11) and (12) set the tardiness of each

product.

Constraint (13) sets the completion times of unre-

quested orders to zero. Constraints (14) and (15) de-

ﬁne the domains of the decision variables.

4 ILLUSTRATIVE EXAMPLE

In order to illustrate the solution structure, we con-

sider the following instance: A manufacturer has

two types of products and two parallel machines.

Orders are received at three different arrival times,

T = {2, 5, 17}, and a deadline is associated with each

product’s order associated with an arrival time. In-

spired by Yalaoui (2012), the deadlines are generated

following the uniform distribution U[t + pt

,t + pt

((

∑

)/2)] with i ∈ P and t ∈ T. Table 1 presents

processing times, tardiness penalties, deadlines, and

the set of prices and demands for each product.

Table 1: Parameters of the illustrative example.

Product pt

/Time Price/Demand

1 4 2

6 / 2 8 / 1

10 / 5 7 / 2

27 /17 6 / 3

5 / 4

2 8 1

14 / 2 5 / 1

18 / 5 4 / 2

30 / 17 3 / 3

2 / 4

The mathematical model was implemented in

IBM CPLEX solver version 22.1.1.0, on a Intel(R)

Core(TM) i5-8350U CPU @ 1.70 GHz of 8 GB RAM

machine.

An optimal solution for the input described in Ta-

ble 1 was found in 648 seconds. The optimal objec-

tive value obtained is −57. Moreover, the selected

price for the ﬁrst product at times 2 and 5 is 7 with

two orders each, while at t = 17 the selected price of

this product is 6 with three orders. Moreover, for the

second product, the selected price is 5 for each of the

arrival times, resulting in a total of three orders.

As presented in Table 2, the selected price for the

Table 2: The selected price and demand for each product

and arrival time.

Product Time Price/Demand

2 7 / 2

5 7 / 2

17 6 / 3

2 5 / 1

5 5 / 1

17 5 / 1

Figure 1: Scheduling Process for Orders in Two Parallel

Machines.

ﬁrst product at times 2 and 5 is 7 with two orders each,

and at t = 17 the price of this product is 6 with three

orders. But for the second product, the selected price

is 5 with the associated demand at all the arrival times.

Figure 1 displays the solution scheduling struc-

ture. The order colored in grey is considered late as

its completion time exceeds the due date. In this case,

the total tardiness penalty is equal to 4 and the actual

beneﬁt is 61.

5 EXPERIMENTAL STUDY

The proposed model aims at minimizing the tardiness

penalty of the orders to improve service quality and

maximizing the total beneﬁt of the company at the

same time. In order to ﬁnd the best compromise be-

tween these two objectives, the ε-constraint method

Chankong and Haimes (2008) is considered. It con-

sists in optimizing one of the objective functions by

considering the other objective as an additional con-

straint. For the studied problem, we consider the min-

imization of the tardiness penalty, while considering

the following additional constraint on account of ben-

eﬁt maximization:

∑

i∈P

∑

t∈T

∑

l∈L

) × x

≥ α × MaxBene f it (16)

Such as, α ∈ [0, 1] represents a coefﬁcient ﬁxed by

the decision-maker indicating the minimum amount

Integration of Pricing and Production Scheduling Decisions: A Mathematical Model

225

of beneﬁt they are expecting to receive, while

MaxBene f it denotes the maximum beneﬁt that can be

obtained using the following equation:

MaxBene f it = t ×

∑

i∈P

max

l∈L

× f

)) (17)

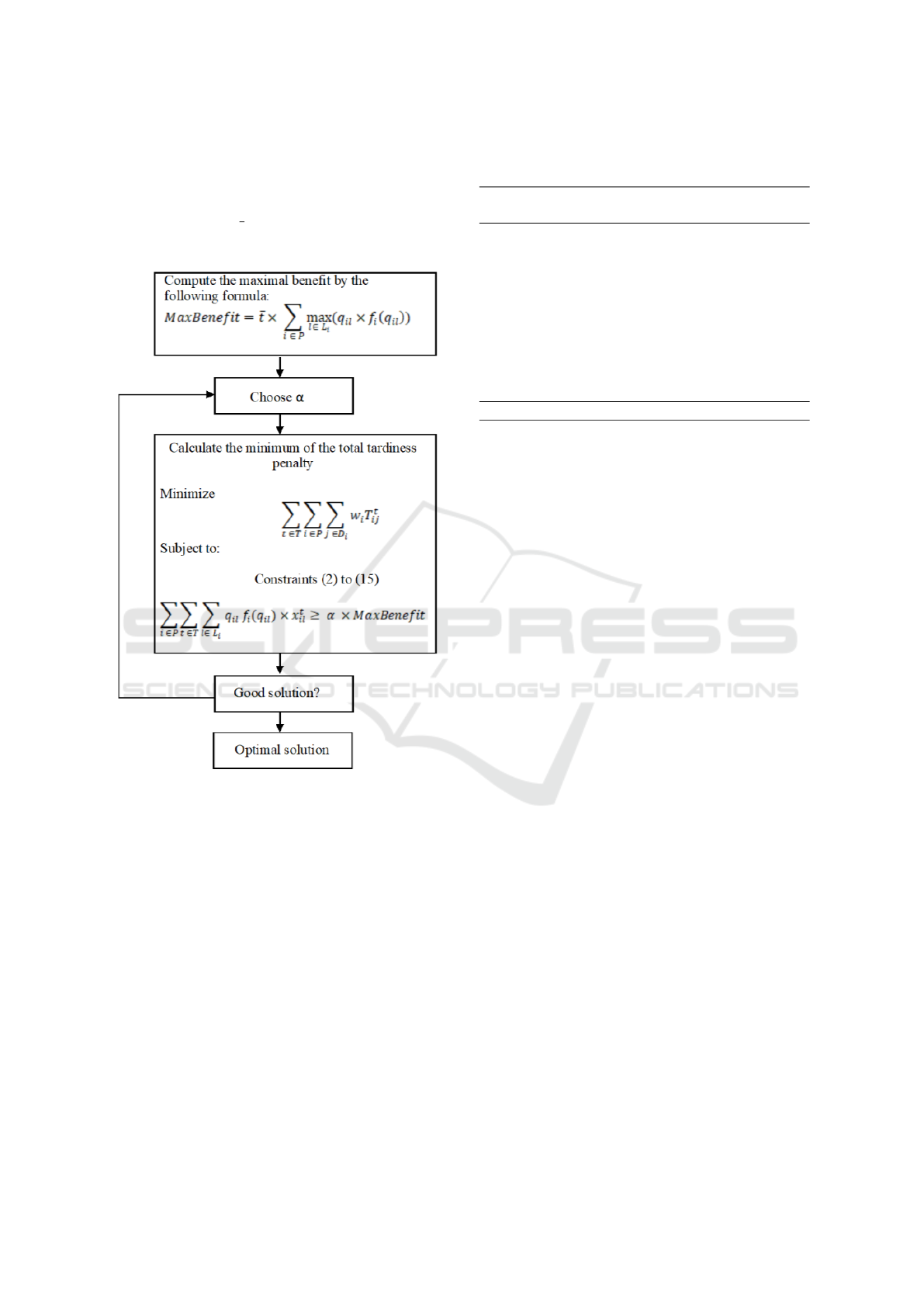
Figure 2: Resolution algorithm.

The ε-constraint based algorithm is depicted in

Figure 2. The algorithm starts by calculating the max-

imum beneﬁt following Equation (17). The α coefﬁ-

cient is then ﬁxed by the decision-maker. Next, the

model for the total tardiness penalty (TTP) is solved,

subject to the same constraints of problem (P0), in ad-

dition to Inequality (16). Finally, the optimal solution

associated with the chosen value of α is obtained and

the decision-maker decides whether to accept the so-

lution or choose another value for α.

By applying this algorithm to the illustrative ex-

ample presented in the previous section, the maxi-

mum beneﬁt obtained following Equation (17) is 87.

Table 3 presents the results for different values of α

and a limited execution time.

It must be noted that α = O.7 refers to the optimal

solution obtained by implementing the initial model

(P0) where the objective functions are expressed as a

Table 3: Implementation results of the algorithm on the il-

lustrative example.

α Orders

Delayed

orders

TTP GAP(%) Time(s)

0.1 6 0 0 0 0.7

0.2 6 0 0 0 0.8

0.3 6 0 0 0 0.8

0.4 6 0 0 0 0.8

0.5 8 0 0 0 1.3

0.6 9 0 0 0 3.6

0.7 10 1 4 0 15

0.8 13 5 34 70.16 > 1800

0.9 16 7 128 100 > 1800

1 21 14 312 98 > 1800

0.7 10 1 4 0 15

single objective function, this result was obtained in

648 seconds, as stated earlier. However, using the ε-

constraint algorithm, for α = 0.7 the result is obtained

within 15 seconds. Furthermore, Figure 3 displays the

Pareto front of non-dominated solutions for α rang-

ing from 0.1 to 0.7, with solutions for α = 0.8 to 1.0

representing the best outcomes obtained after an ex-

tended execution time of 1800 seconds. As depicted

in the ﬁgure, the two objectives, namely minimizing

TTP and maximizing beneﬁt, exhibit a conﬂict, signi-

fying that optimizing one objective comes at the ex-

pense of the other.

Figure 4 presents the mean computational time of

the algorithm for each alpha value over 10 arbitrary

generated instances, taking into account two products,

with four possible prices and demands each. The pro-

cessing times and the tardiness penalties for these in-

stances are generated following a uniform distribution

U[1,8]. Moreover, three arrival times for the incom-

ing orders are considered, and the deadlines are gen-

erated following the same uniform distribution as pre-

viously used in the illustrative example.

The results show that the algorithm quickly pro-

vides an optimal solution for the associated coefﬁ-

cient α between 0.1 and 0.7. However, for α greater

than 0.7, no optimal solution is obtained even after

half an hour of execution. In fact, for higher values of

α, the algorithm prioritizes fulﬁlling orders to achieve

minimal beneﬁt, which in turn prolongs the schedul-

ing process on the parallel machines.

6 CONCLUSION

This research contributes to the ﬁeld by providing a

comprehensive framework for integrating production

scheduling and pricing decisions in a make-to-order

manufacturing environment. By considering the inter-

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

226

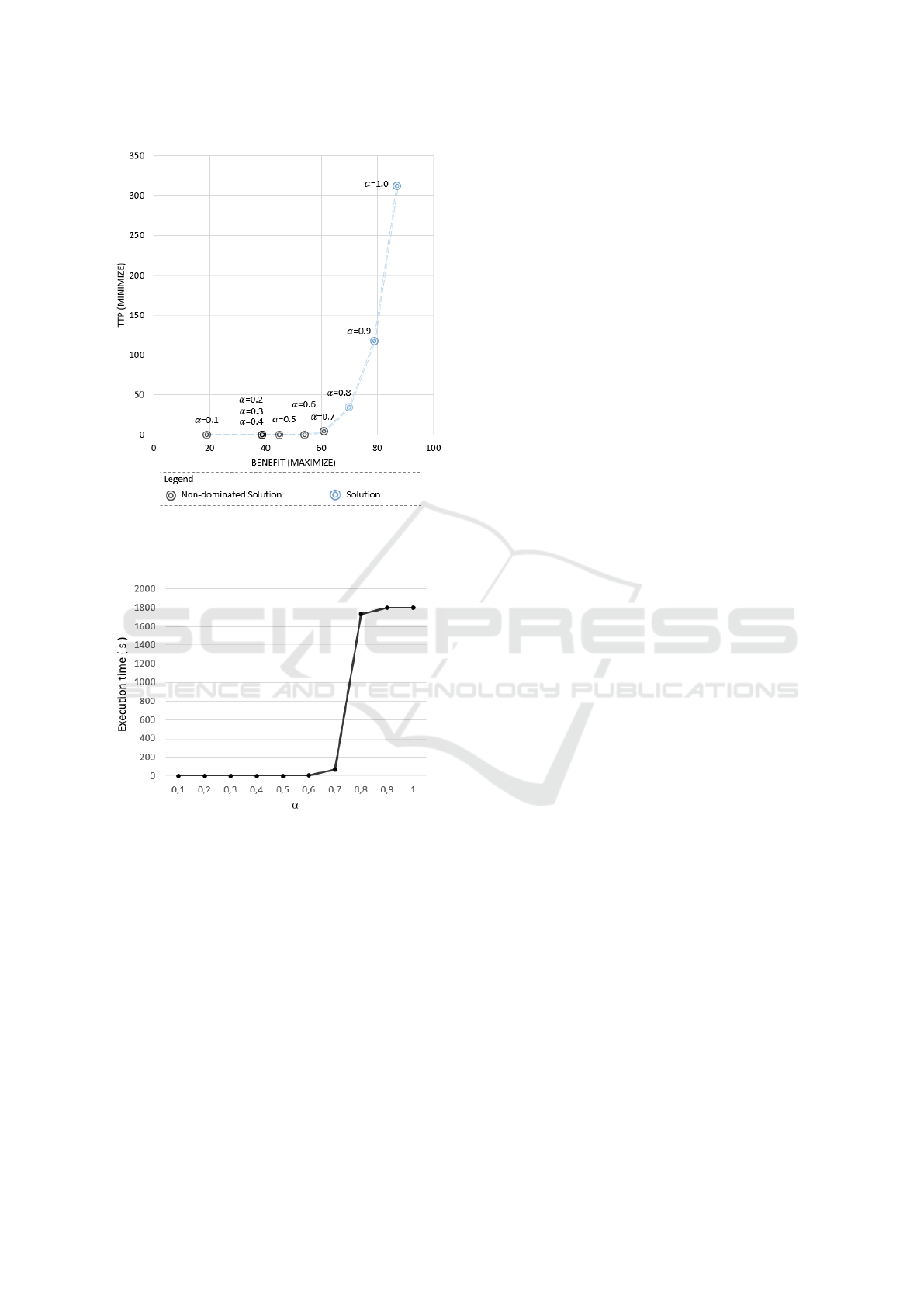
Figure 3: Pareto front of non-dominated solutions for α val-

ues (0.1 to 0.7) and best solutions (0.8 to 1.0) after a ﬁxed

execution time.

Figure 4: Mean Computational time of 10 arbitrary in-

stances with respect to different values of the coefﬁcient α.

dependencies between these decisions, manufactur-

ers can achieve better coordination, improve customer

satisfaction, and enhance their overall competitive-

ness in a dynamic market environment. In this pa-

per, a new mathematical model is proposed for pric-

ing and scheduling coordination on a parallel ma-

chine environment where arrival times are associated

with customers orders. A computational study is pre-

sented to conﬁrm the effectiveness of the proposed

mixed integer linear programming model. Using

the ε-constraint principle to conduct the experimen-

tal analysis, we provide insight for decision-makers

to ﬁnd the best compromise between revenue maxi-

mization and improving customer service. In future

work, it is important to focus on developing efﬁcient

algorithms that can effectively address large-scale in-

dustrial instances. In this regard, a promising resolu-

tion method lies in the application of Benders decom-

position, speciﬁcally tailored for tackling the multi-

objective nature of the integrated problem. Addition-

ally, drawing inspiration from the well-established lit-

erature on the mono-objective scheduling problem, a

method based on Tabu Search shows promise. As evi-

denced by Lara et al. (2016), Tabu Search has demon-

strated effectiveness in addressing the basic schedul-

ing problem. Extending its application to the in-

tegrated pricing and scheduling context could yield

valuable insights and solutions. Finally, more com-

plex machine environments can be studied in the fu-

ture.

REFERENCES

Chankong, V. and Haimes, Y. Y. (2008). Multiobjective

decision making: theory and methodology. Courier

Dover Publications.

Chen, X. and Simchi-Levi, D. (2012). Pricing and inventory

management.

Chen, Z.-L. and Hall, N. G. (2010). The coordination of

pricing and scheduling decisions. Manufacturing &

Service Operations Management, 12(1):77–92.

Chen., Z. L. and Hall, N. G. (2022). Supply chain schedul-

ing. pages 185–240. Springer.

Eliashberg, J. and Steinberg, R. (1993). Marketing-

production joint decision-making. Handbooks in op-

erations research and management science, 5:827–

880.

Graham, R. L. (1966). Bounds for certain multiprocessing

anomalies. Bell system technical journal, 45(9):1563–

1581.

Koulamas, C. (1994). The total tardiness problem: review

and extensions. Operations research, 42(6):1025–

1041.

Lara, A. F. B., Yalaoui, F., Dugardin, F., and Entzmann,

F. (2016). An efﬁcient heuristic to minimize the to-

tal tardiness in the parallel machines scheduling prob-

lem. Metaheuristics for production systems, pages

241–262.

Liu, Z., Lu, L., and Qi, X. (2020). Price quotation for or-

ders with different due dates. International Journal of

Production Economics, 220:107448.

Lu, L., Liu, Z., and Qi, X. (2013). Coordinated price quo-

tation and production scheduling for uncertain order

inquiries. IIE transactions, 45(12):1293–1308.

Russell, R. S. and Taylor, B. W. (2006). “Operations man-

agement: Quality and competitiveness in a global en-

vironment”. John Wiley & Sons Incorporated.

Wang, S. and Wang, X. (2019). Parallel machine scheduling

with pricing and rejection. In 2019 16th International

Conference on Service Systems and Service Manage-

ment (ICSSSM), pages 1–5. IEEE.

Integration of Pricing and Production Scheduling Decisions: A Mathematical Model

227

Yalaoui, F. (2012). Minimizing total tardiness in parallel-

machine scheduling with release dates. Interna-

tional Journal of Applied Evolutionary Computation

(IJAEC), 3(1):21–46.

Yue, Q., Chen, Z.-L., and Wan, G. (2019). Integrated pric-

ing and production scheduling of multiple customized

products with a common base product. IISE Transac-

tions, 51(12):1383–1401.

ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems

228