Hybrid Quanvolutional Echo State Network for Time Series Prediction

Rebh Soltani

1 a

, Emna Benmohamed

2 b

and Hela Ltiﬁ

3 c

Research Groups in Intelligent Machines, University of Sfax, National Engineering School of Sfax (ENIS),

BP 1173, Sfax, 3038, Tunisia

Department of Cyber Security, College of Engineering and Information Technology, Onaizah Colleges,

P.O. Box 5371, Onaizah, K.S.A.

Computer Science and Mathematics Department, Faculty of Sciences and Technology of Sidi Bouzid,

University of Kairouan, Tunisia

ﬁ

Keywords:

Echo State Network, Quantum Computing, Reservoir Computing, Quanvolution Filter.

Abstract:

Quantum Machine Learning (QML) combines quantum physics with machine learning techniques to enhance

algorithm performance. By leveraging the unique properties of quantum computing, such as superposition and

entanglement, QML aims to solve complex problems beyond the capabilities of classical computing. In this

study, we developed a hybrid model, the quantum convolutional Echo State Network, which incorporates QML

principles into the Reservoir Computing framework. Evaluating its performance on benchmark time-series

datasets, we observed improved results in terms of mean square error (MSE) and reduced time complexity

compared to the classical Echo State Network (ESN). These ﬁndings highlight the potential of QML to advance

time-series prediction and underscore the beneﬁts of merging quantum and machine learning approaches.

1 INTRODUCTION

QML is the fusion of machine learning and quantum

computing (Biamonte et al., 2017). The objective of

QML is to harness the computational advantages of-

fered by quantum computers, which can process data

at exponentially faster rates than classical comput-

ers. By leveraging quantum systems, algorithms are

developed to facilitate the continual improvement of

computer programs over time. QML capitalizes on

the inherent efﬁciency of quantum computers to ad-

dress machine learning problems. Notably, the uti-

lization of superposition quantum states enables the

simultaneous analysis of multiple states, leading to

substantial speedups. A key research focus lies in

the design of networks known as quantum neural net-

works (Altaisky et al., 2014), where every element,

including individual neurons and training algorithms,

operates on a quantum computer.

In the 1990s, the ﬁeld of quantum neural network

research began to emerge, as evidenced by early pub-

lications (Fern

andez P

erez et al., 2022). However, in

comparison to other areas of quantum machine learn-

https://orcid.org/0000-0002-5644-2049

https://orcid.org/0000-0002-3934-3962

https://orcid.org/0000-0003-3953-1135

ing discussed previously, neural networks in the quan-

tum realm have not yet attained the same level of

scientiﬁc maturity. This lack of progress can be at-

tributed to the inherent non-linearity of neural net-

work components conﬂicting with the linear nature

of quantum physics (Schuld et al., 2015). To over-

come this challenge, researchers have explored the

application of a quantum mechanical framework to

simulate the activation function of perceptrons. This

approach involves incorporating specialized measure-

ments and proposing non-linear quantum operators.

Notably, Schuld (Schuld et al., 2015) has described a

direct implementation of the activation function using

the quantum phase estimation approach and a circuit-

based model of quantum computation. These ad-

vancements offer promising avenues for bridging the

gap between neural networks and quantum mechan-

ics, thus unlocking new possibilities for quantum-

inspired machine learning paradigms (Chen et al.,

2022). Deﬁning quantum neural networks remains a

topic of ongoing debate and lacks a consensus, de-

spite recent efforts to construct neural network ver-

sions that rely solely on principles from quantum me-

chanics. The primary obstacle in developing a quan-

tum artiﬁcial neural network stems from the linear na-

ture of quantum physics, whereas artiﬁcial neural net-

works necessitate non-linearity (Schuld et al., 2015)

Soltani, R., Benmohamed, E. and Ltiﬁ, H.

Hybrid Quanvolutional Echo State Network for Time Series Prediction.

DOI: 10.5220/0012271600003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 2, pages 40-46

ISBN: 978-989-758-680-4; ISSN: 2184-433X

(Cao et al., 2017) (Zhao et al., 2019). Consequently,

many research papers have encountered challenges

in reproducing essential features of traditional neu-

ral networks, contributing to the absence of successful

replications in this regard.

We draw attention to the fact that despite sev-

eral studies on quantum neural networks (Gupta and

Zia, 2001), (Purushothaman and Karayiannis, 1997)

, (Bharti et al., 2022), and (Panella and Martinelli,

2011), no attempt has been made to explicitly model

non-linearity on amplitudes, suggesting that no really

effective quantum neural network has yet been pre-

sented. The Echo State Network (ESN) is a funda-

mental Recurrent Neural Network (RNN) model with

a sparse reservoir and a straightforward linear output

(Jaeger, 2002). It has found applications in various

domains, including human activity recognition, clin-

ical applications, distributed, embeddable and fed-

erated learning, and distributed intelligence applica-

tions (Sun et al., 2022) (Soltani et al., 2023). How-

ever, the ESN suffers from several fundamental chal-

lenges (Soltani et al., 2022). For instance, since the

reservoir is randomly created prior to training, deter-

mining the hyperparameters of the dynamic reservoir

typically involves experimentation (Liu et al., 2020).

The analysis of reservoir hyperparameters is a com-

plex task, and the initial connection and weight struc-

ture are unlikely to be in an optimal state. Conse-

quently, creating a highly efﬁcient reservoir that is

speciﬁcally tailored to certain tasks becomes chal-

lenging. To tackle these challenges, various tech-

niques have been proposed to address these issues.

One technique introduced a deterministic reservoir

topology that outperformed the standard ESN (Rodan

and Tino, 2010). In an alternative approach, a highly-

clustered ESN with a scale-free network structure was

utilized (Deng and Zhang, 2006). In pattern recogni-

tion, leak integral neurons were employed to improve

performance compared to conventional ESNs, utiliz-

ing ﬁlter neurons, delay variables, and readout (Jaeger

et al., 2007). These methods offered various opti-

mizations to the ESN model. The primary objective of

this study is to assess the viability and potential bene-

ﬁts of utilizing a quantum echo state network. Our fo-

cus lies in integrating the dynamic reservoirs of ESNs

with quantum computing to enhance the overall per-

formance of the network and unlock unprecedented

levels of efﬁciency. By leveraging the unique proper-

ties of quantum computing, we aim to explore novel

avenues for improving the capabilities of echo state

networks and achieving remarkable enhancements in

their performance.

In this study, we delve into the realm of Quanvo-

lutional Neural Networks (QNNs), a novel class of

models. QNNs leverage certain strengths of quan-

tum computation to enhance the capabilities of ESNs.

A pivotal contribution of QNNs is the introduc-

tion of quantum convolutional (quanvolutional) lay-

ers, which augment the conventional ESN architec-

ture. These quanvolutional layers operate in a man-

ner akin to classical convolutional layers, generating

feature maps through localized modiﬁcations of in-

put data. In contrast, quantum circuit-based quan-

volutional ﬁlters reshape speciﬁc subsets of data spa-

tially to extract features from the input. We propose

that leveraging features produced by random quanvo-

lutional circuits can enhance the accuracy of machine

learning models employed for time series forecasting.

This paper is structured as follows: Section 2 pro-

vides a comprehensive description of the ESN model.

In Section 3, we delve into the suggested Approach,

which combines quantum theory with the ESN, of-

fering a detailed exploration of the proposed model.

Section 4 is dedicated to the performance analysis and

presentation of experimental results. Finally, Section

5 concludes the article by summarizing the key ﬁnd-

ings and conclusions.

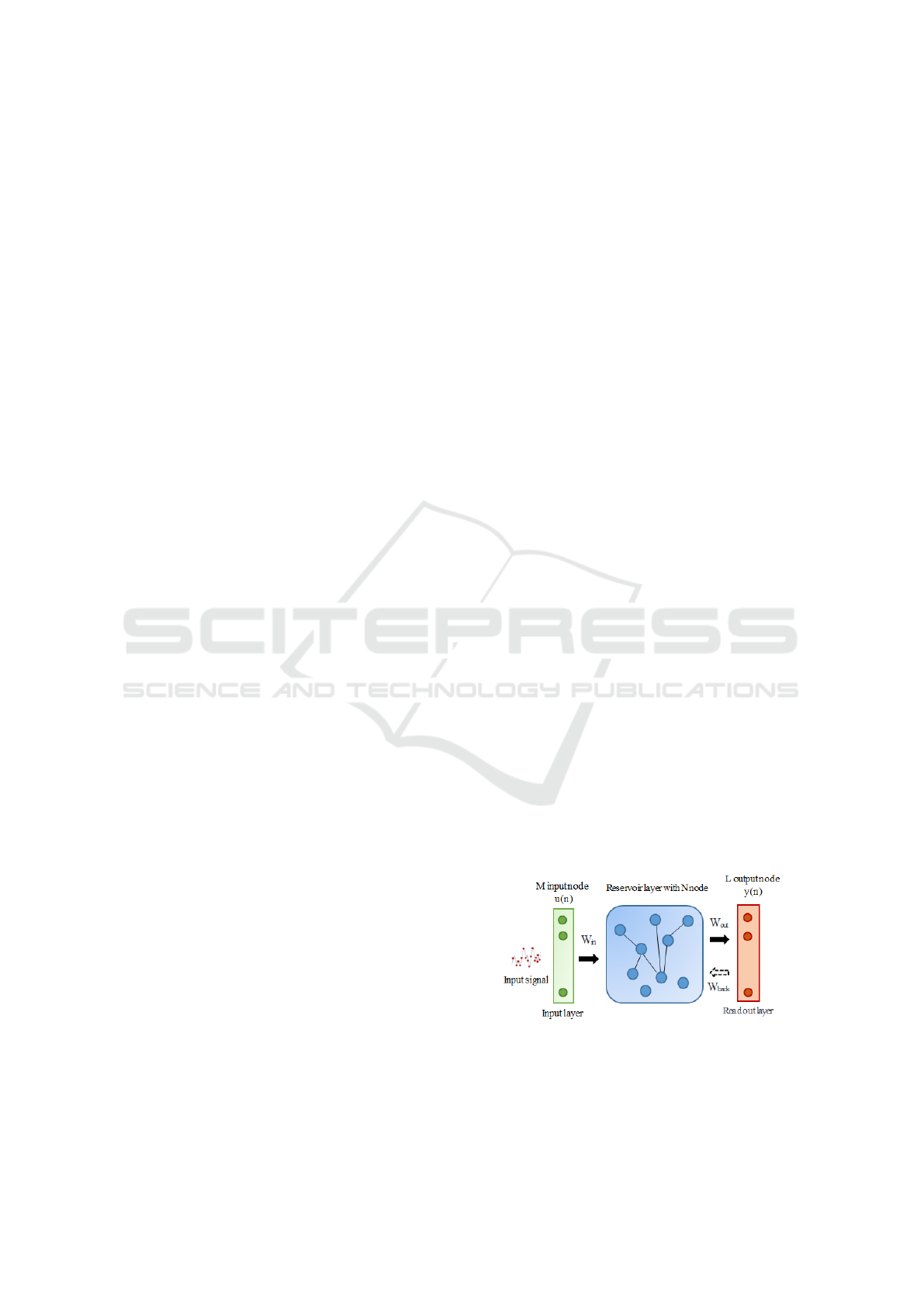
2 ECHO STATE NETWORK

Echo state networks (Soltani et al., 2023) are a type

of RNNs which has the ability to extract the time

correlation of time series data(Bouazizi et al., 2022)

(Bouazizi et al., 2023). For this reason, they are fre-

quently employed to tackle time series forecasting

tasks. As demonstrated in Fig. 1, ESN model uses

a reservoir whose state and dynamics play the role of

memory of past experiences, and from which we wish

to extract the relevant information through the readout

layer. Since just the weights in the readout layer may

be trained, the training time is kept to a minimum.

Considering that the network includes M input units,

Figure 1: The structure of ESN.

N internal compute nodes (i.e. reservoir layer neu-

rons), and L output units (as shown in Fig. 1). The

Hybrid Quanvolutional Echo State Network for Time Series Prediction

ESN can be modelled by :

x(n + 1) = f (W x(n) +W

u(n + 1) +W

back

y(n)) (1)

y(n + 1) = W

out

(x(n + 1), u(n + 1), y(n)) (2)

The internal state of ESN neurons is updating, as il-

lustrated in equations (1) and (2). The hidden layer

activation function is f. f is often a nonlinear function

such as tanh or sigmoid. The reservoir’s internal up-

dating state is denoted by x(n), while the output of the

linear function f

out

is denoted by y(n). W

represents

the input weights from the input to the reservoir layer.

The internal weights inside the reservoir are called W.

out

is the output weights from the reserve pool to

the readout layer and is the only one that needs to be

trained.W

back

is the backward weights from the read-

out to the reservoir layer.

3 HYBRID QUANTUM ESN

This section ﬁrst covers the basic concepts of quan-

tum mechanics. The model is then proposed, fol-

lowed by a full explanation.

3.1 Quantum

(Qubit): Conventional information is represented by

one or more bits. A bit can take the values 0, 1 or true,

false. A qubit can take on values of both |0⟩ and |1⟩

said in quantum superposition (Gupta and Zia, 2001).

This is in contrast to analog circuits which take values

between 0 and 1. The algebraic part of qubits is better

understood using Dirac notation. The |0⟩ states and

|1⟩ states are algebraically equivalent to the 0 and 1

of a classical bit. The phenomena of quantum super-

position is represented by the linear combinations of

both |0⟩ and |1⟩. As a result, various potential states

emerge:

|Ψ⟩ = α|0⟩ + β|1⟩ (3)

where α and β are complex values that make up a unit

norm vector:

∥α∥

+ ∥β∥

= 1 (4)

The coefﬁcients α and β reﬂect the probability ampli-

tude or for making shorter amplitude in a quantitative

sense. The probability of measuring |0⟩ is given by

the squared norm, while the probability of measuring

|1⟩ is given by the squared norm.The squared norm of

an amplitude reﬂects a probability (Biamonte et al.,

2017), hence ∥α∥

+ ∥β∥

= 1.

4 HYBRID QUANVOLUTIONAL

ESN MODEL

The idea behind this approach is that the quanvolution

ﬁlter can extract more relevant features from the input

data, which can improve the performance of the ESN.

Additionally, the quanvolution ﬁlter allows including

quantum mechanical properties, such as superposition

and entanglement, which could enhance the represen-

tational power of the ESN. Fig 2 presents in details

our proposed method.

1) The input data is transformed into a quantum

state, which is a mathematical representation of the

data in the quantum mechanical system (equation 3).

This can be done using techniques such as quantum

state encoding, which maps classical data to a quan-

tum state.

= e(u(t)) = e

iu(t)

= cos(u(t))+isin(u(t)) (5)

where u(t) is the input data at time t. 2) The quantum

state is then passed through a quantum random circuit

that applies a random sequence of quantum gates to

the qubit.

= g(i

) (6)

3) Next, the output of the random quantum circuit is

passed through a measurement gate.

= d(O

) =< O

> (7)

4) The output of the quanvolutional ﬁlter is a new in-

put that contains the relevant features extracted from

the input data. The new input is then used in the re-

current part of the ESN. the following equation can

describe the state dynamic of our model:

x(n + 1) = f (W x(n) +W

back

y(n)) (8)

5) The output of the ESN is then generated.

y(n + 1) = W

out

(x(n + 1), u(n + 1), y(n)) (9)

By incorporating the quanvolution ﬁlter and its asso-

ciated quantum computations, this approach aims to

extract relevant features from the input data and inte-

grate them into the ESN framework, potentially lead-

ing to improved performance in time series forecast-

ing tasks.

5 EXPERIMENTATIONS AND

RESULTS

5.1 Experimental Environment

The experiments conducted in this research employed

the PennyLane quantum machine learning library.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

Figure 2: Hybrid Quanvolutional Echo State Network.

The code utilized a local qubit simulator designated

as ”default.qubit” in PennyLane, enabling quantum

computations on a single qubit. This setup allowed

for executing gate-model instructions with ﬂexibility

in gate width, circuit depth, and ﬁdelity. The experi-

ments intentionally omitted the incorporation of noise

models to assess the effectiveness of the ideal univer-

sal quantum computational model compared to clas-

sical computational models. Future experimentation

could involve investigating the impact of noise or uti-

lizing alternative quantum hardware or simulators.

To construct the quantum ﬁlter in this implemen-

tation, a single qubit is considered. The size of the in-

put for the quanvolutional ﬁlters determines the num-

ber of qubits required for the circuit. In this particular

case, a 1-by-1 quanvolutional ﬁlter is employed, re-

sulting in a circuit with 1 qubit (n = 1).

Random 1-qubit gates are generated for the quan-

volutional ﬁlter, selected from the gate set [X(θ),

Y(θ), Z(θ), U(θ), P, T, H]. The value of θ represents

a randomly determined rotational parameter, and the

target qubit for each gate is also selected randomly.

We applied the ﬁrst training-test split to all

datasets. We further deduced a divide into train-

ing (75 %) and validation (25 %) for model selec-

tion. Bayesian Optimization was used to tweak the

hyper-parameter values on the validation set. We in-

vestigated the following conﬁgurations in our stud-

ies using Hybrid quanvolutional ESN: the number of

units [5, 500] in the reservoir layer, input scaling

[0.01, 1.5], and spectral radius [0.01, 1.5] for the most

part. We employed a single dense layer trained using

adam optimizer as the output readout, with a learn-

ing rate of 1e-5 , for the Mackey-Glass (MG) dataset

(Mackey and Glass, 1977), the model was trained for

100 epochs. Similarly, for the NARMA-10 dataset,

the model underwent 50 epochs of training. Follow-

ing model selection, we trained our models using the

chosen hyper-parametrameter on the whole training

set, evaluated their performance on the test set. We

carried out the same trials with ESN for compari-

son. In both instances, we used the same model se-

lection and performance evaluation procedure, look-

ing at the identical values for the training algorithm’s

hyper-parameters and the number of recurrent units.

The model’s performance was assessed by mea-

suring the mean square error and computation time

on the test set. The experiments were conducted in a

Python environment, utilizing a computer equipped

with an i5 CPU and 8.0 GB RAM. The results of

the quanvolutional ﬁlter applied to ESN method were

evaluated on the Mackey-Glass (Zhao et al., 2019)

and NARMA-10 (Connor et al., 1991) datasets which

are a classic example of a chaotic system and is often

used as a benchmark for testing the performance of

numerical methods for solving differential equations.

5.2 Mackey-Glass Time Series

Prediction

For the prediction of chaotic series, the Mackey-

Glass’ chaotic series is a widely used test (Fig. 2).

The following is MG’s mathematical model:

dx(t)

ax(t − τ)y

1 + x

(t − τ)

+ bx(t) (10)

The key parameters are set as a=0.2, b=-0.1, τ=17,

n=10. The results obtained on the Mackey-Glass

datasets are presented in Table 1, Table 2, Figure 3

and Figure 4.

Quanvolutional ESN model is computationally

more efﬁcient and faster in processing the data com-

pared to the ESN model.

Based on the provided results on Table 1 Fig 3

and 4, the Hybrid Quanvolutional ESN model out-

performed the ESN model in terms of both predic-

tive accuracy and computational efﬁciency. The Hy-

brid Quanvolutional ESN model achieved a lower

MSE, indicating better predictive performance on

Hybrid Quanvolutional Echo State Network for Time Series Prediction

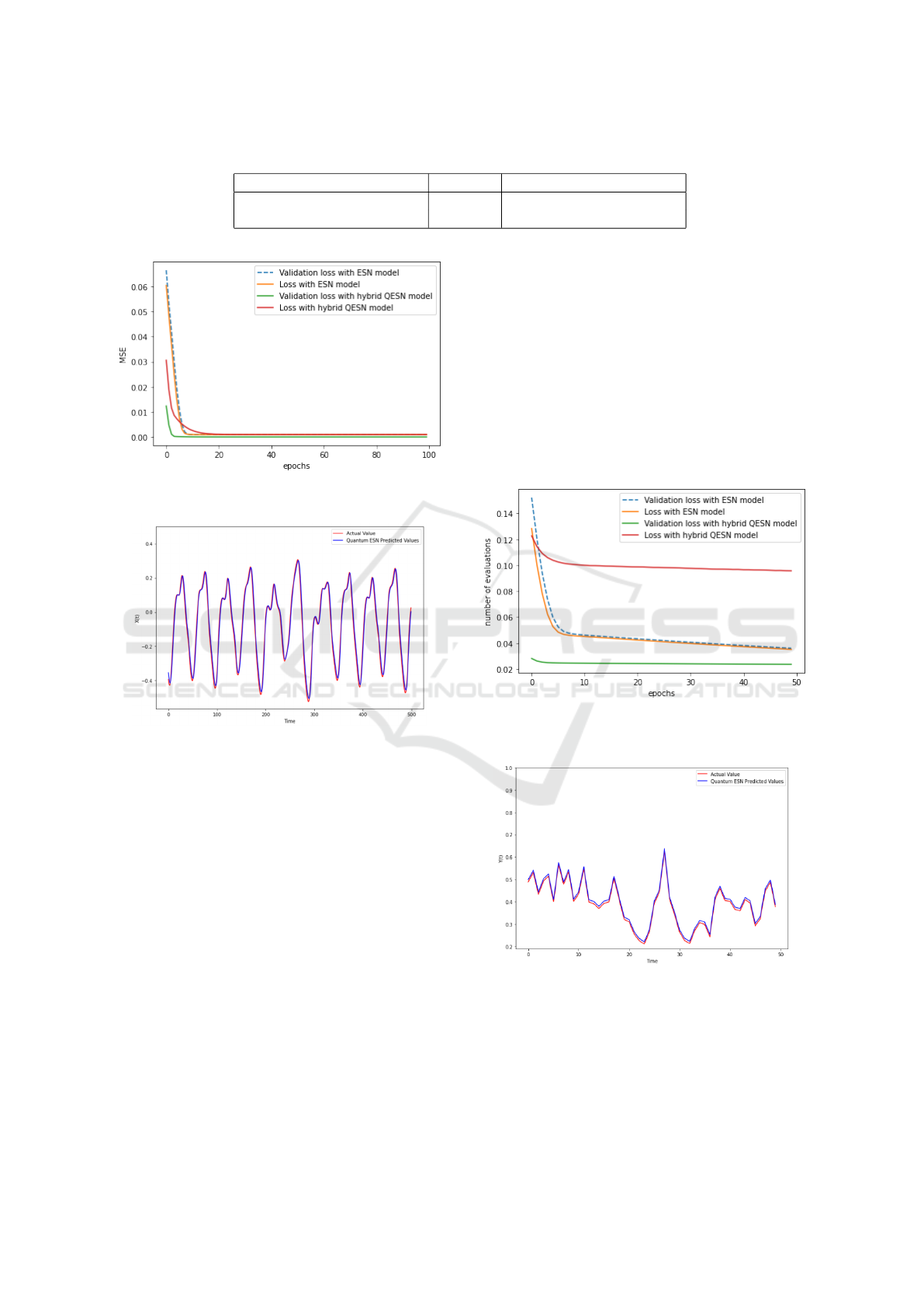
Table 1: Results on Mackey-Glass dataset.

Model MSE Time Complexity (second)

ESN 9.96e-05 116.74

Hybrid Quanvolutional ESN 5.05e-05 106.58

Figure 3: Evolution of training and validation loss during

train with MG dataset.

Figure 4: Real output and predicted output generated by

hybrid Qanvolutional ESN on MG dataset.

the Mackey-Glass dataset. Additionally, the Hybrid

Quanvolutional ESN model demonstrated a faster

processing time, making it more efﬁcient in handling

the dataset.

The results show that the quantum convolutional

ﬁlter applied to ESN method achieved a better perfor-

mance in terms of MSE and time complexity on both

datasets, compared to the classical ESN. This indi-

cates that the quantum convolutional ﬁlter can extract

more relevant features from the input data, which can

improve the performance of the ESN. In summary, the

proposed method shows a promising performance on

time series prediction problems, and it is worth to fur-

ther investigate this approach on other datasets and

problems.

5.3 NARMA-10 Time Series Prediction

one of the most popular tasks, known as NARMA-10

for NARMA deﬁned in (Connor et al., 1991), which

entails modeling the following order 10 systems:

y(t + 1) = c

y(t) + c

y(t)

∑

k−1

i=0

y(t − i) + c

x(t − (k − 1))x(t) + c

(11)

The important variables are set to k=10, c1=0.3,

c2=0.05, c3, and c4=0.1. The results obtained on the

NARMA-10 datasets are presented in Table 1, Table

2, Figure 3 and Figure 4.

Figure 5: Evolution of training and validation loss during

train with NARMA-10 dataset.

Figure 6: Real output and predicted output generated by

hybrid Qanvolutional ESN on NARMA-dataset.

Based on the provided results on Table 3, Fig 5

and 6, the Hybrid Quanvolutional ESN model outper-

forms the ESN model in terms of both predictive ac-

curacy and computational efﬁciency on the NARMA-

10 dataset. The Hybrid Quanvolutional ESN model

achieved a lower MSE, indicating superior predic-

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

Table 2: Results on Narma-10 dataset.

Model MSE Time Complexity (second)

ESN 0.04 677.48

Hybrid Quanvolutional ESN 0.02 479.52

tive performance. Additionally, the Hybrid Quanvo-

lutional ESN model demonstrated a faster processing

time, making it more efﬁcient in handling the dataset.

In conclusion, the Hybrid Quanvolutional ESN model

shows superiority over the ESN model for both MG

and NARMA-10 datasets. It achieves better predic-

tive accuracy and is more computationally efﬁcient.

These results suggest that the Hybrid Quanvolutional

ESN model could be a favorable choice for modeling

and predicting time series. However, it is important to

note that further analysis and experimentation may be

necessary to conﬁrm these ﬁndings and explore the

models’ generalizability to other datasets or scenar-

ios.

6 CONCLUSIONS

In this research, we suggested a new method for

time-series prediction using quanvolution ﬁlter ap-

plied to ESN. On the Mackey-Glass and NARMA

datasets, we assessed the method’s performance and

contrasted the outcomes with those obtained using

traditional ESN. The results shown that, when com-

pared to the traditional ESN, the suggested technique

outperformed it in terms of MSE and time complex-

ity on both datasets. This suggests that by extracting

more relevant features from the input data, the quan-

tum convolutional ﬁlter may enhance the effective-

ness of the ESN. It is crucial to note that the ﬁndings

are still in the research stage and that more studies are

required to prove the method’s efﬁcacy across a range

of issues and datasets.

REFERENCES

Altaisky, M. V., Kaputkina, N. E., and Krylov, V.

(2014). Quantum neural networks: Current status and

prospects for development. Physics of Particles and

Nuclei, 45:1013–1032.

Bharti, K., Cervera-Lierta, A., Kyaw, T. H., Haug, T.,

Alperin-Lea, S., Anand, A., Degroote, M., Heimonen,

H., Kottmann, J. S., Menke, T., et al. (2022). Noisy

intermediate-scale quantum algorithms. Reviews of

Modern Physics, 94(1):015004.

Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe,

N., and Lloyd, S. (2017). Quantum machine learning.

Nature, 549(7671):195–202.

Bouazizi, S., Benmohamed, E., and Ltiﬁ, H. (2022). Sa-

k2pc: Optimizing k2pc with simulated annealing for

bayesian structure learning. In International Confer-

ence on Hybrid Intelligent Systems, pages 762–775.

Springer.

Bouazizi, S., Benmohamed, E., and Ltiﬁ, H. (2023). A

novel approach of esn reservoir structure learning for

improved predictive performance. In 2023 IEEE Sym-

posium on Computers and Communications (ISCC),

pages 232–237. IEEE.

Cao, Y., Guerreschi, G. G., and Aspuru-Guzik, A. (2017).

Quantum neuron: an elementary building block for

machine learning on quantum computers. arXiv

preprint arXiv:1711.11240.

Chen, S. Y.-C., Wei, T.-C., Zhang, C., Yu, H., and Yoo, S.

(2022). Quantum convolutional neural networks for

high energy physics data analysis. Physical Review

Research, 4(1):013231.

Connor, J., Atlas, L., and Martin, D. (1991). Recurrent net-

works and narma modeling. Advances in neural infor-

mation processing systems, 4.

Deng, Z. and Zhang, Y. (2006). Complex systems modeling

using scale-free highly-clustered echo state network.

In The 2006 IEEE international joint conference on

neural network proceedings, pages 3128–3135. IEEE.

Fern

andez P

erez, I., Prieta, F. d. l., Rodr

ıguez-Gonz

alez, S.,

Corchado, J. M., and Prieto, J. (2022). Quantum ai:

Achievements and challenges in the interplay of quan-

tum computing and artiﬁcial intelligence. In Inter-

national Symposium on Ambient Intelligence, pages

155–166. Springer.

Gupta, S. and Zia, R. (2001). Quantum neural networks.

Journal of Computer and System Sciences, 63(3):355–

383.

Jaeger, H. (2002). Adaptive nonlinear system identiﬁcation

with echo state networks. Advances in neural infor-

mation processing systems, 15.

Jaeger, H., Luko

sevi

cius, M., Popovici, D., and Siewert, U.

(2007). Optimization and applications of echo state

networks with leaky-integrator neurons. Neural net-

works, 20(3):335–352.

Liu, J., Sun, T., Luo, Y., Yang, S., Cao, Y., and Zhai, J.

(2020). An echo state network architecture based on

quantum logic gate and its optimization. Neurocom-

puting, 371:100–107.

Mackey, M. C. and Glass, L. (1977). Oscillation and

chaos in physiological control systems. Science,

197(4300):287–289.

Panella, M. and Martinelli, G. (2011). Neural networks with

quantum architecture and quantum learning. Inter-

national Journal of Circuit Theory and Applications,

39(1):61–77.

Purushothaman, G. and Karayiannis, N. B. (1997). Quan-

tum neural networks (qnns): inherently fuzzy feedfor-

Hybrid Quanvolutional Echo State Network for Time Series Prediction

ward neural networks. IEEE Transactions on neural

networks, 8(3):679–693.

Rodan, A. and Tino, P. (2010). Minimum complexity echo

state network. IEEE transactions on neural networks,

22(1):131–144.

Schuld, M., Sinayskiy, I., and Petruccione, F. (2015). An

introduction to quantum machine learning. Contem-

porary Physics, 56(2):172–185.

Soltani, R., Benmohamed, E., and Ltiﬁ, H. (2022). Opti-

mized echo state network based on pso and gradient

descent for choatic time series prediction. In 2022

IEEE 34th International Conference on Tools with Ar-

tiﬁcial Intelligence (ICTAI), pages 747–754. IEEE.

Soltani, R., Benmohamed, E., and Ltiﬁ, H. (2023). Echo

state network optimization: A systematic literature re-

view. Neural Processing Letters, pages 1–35.

Sun, C., Song, M., Cai, D., Zhang, B., Hong, S., and Li, H.

(2022). A systematic review of echo state networks

from design to application. IEEE Transactions on Ar-

tiﬁcial Intelligence.

Zhao, J., Zhang, Y.-H., Shao, C.-P., Wu, Y.-C., Guo, G.-

C., and Guo, G.-P. (2019). Building quantum neural

networks based on a swap test. Physical Review A,

100(1):012334.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence