Regression Models for Bike Rental Prediction Based on External

Factors

Wenda Li

School of Philosophy, Renmin University of China, Beijing, China

Keywords: Data Mining, Regression Model, Intelligent Transportation.

Abstract: Recently public bike systems have been more and more popular for its environmental effects and accessibility

for daily use. Various researches have been conducted to improve all elements of the bike rental business,

such as determining the requirements for bikes in each bike station and designing the bike recycling route. In

order to develop more efficient bike systems, this paper applied two different kinds of regression models to

predict the demand for rental bikes considering weather and temporal factors based on actual data in a big

city. Three model frameworks are used in this paper, which are the backward stepwise selection model, ridge

regression and lasso. These models show that holidays, weather situations and humidity are negative factors

affecting the count while the weekday, working day, and feeling temperature are positive factors. The decision

tree models are used and show better performances than linear models. The result shows that the random

forest model has the best effect in predicting the demand for bikes. The study will contribute to the bike

system managers to determine the redistribution of bikes depending on external factors and utilize the total

amount of bikes placed in the system over a long period of time.

1 INTRODUCTION

Many countries have been running public bike

systems, such as New York’s city bike system and

Beijing’s shared bike system. The emergence of a

public bike system not only plays an important role in

environmental and health issues but effectively

compensates for the deficiency of public

transportation as well. Users can rent a bike from one

location and return it to a different bike station with

ease and this can save lots of time in travelling. Apart

from the convenience of the bike system, the

distribution of the bike system is also worth paying

attention to. The accessibility of public bikes for

residential areas and working places means that the

number of bikes at each location should be distributed

fairly and adequately. To avoid situations where there

are no bikes or slots at a bike station, it is important to

predict how many bikes will be needed in the future

since accurately predicting the demand of shared

bicycle users helps to achieve the matching of supply

and demand of shared bicycles.

The affecting reasons for public bikes demand

vary a lot with internal factors and external factors.

People’s preference to rent bikes for travelling and

commuting, how clean and the bikes look and how

comfortable bike users feel while in riding, are several

kinds of internal factors that influence people’s

choices of bike riding. These factors mostly represent

people’s perspectives about bike riding and they

inherent many aspects of views about ideas and

incentives, which implies that people’s need are

irrational, formed over a long time, affected by many

complex factors and it is difficult to capture by

measuring and setting variables and hared to predict

further. Thus, to accurately predict the future using of

bikes, using external data better fits the purpose and

statistical methods. One advantage of external data is

that many companies have shared their data, giving

access to data about time, weather and how the bikes

are used. What’s more, since people tend to react

quickly to the external factors, predictions based on

them can reflect the rental demand in a short term,

usually within a day, which can improve the accuracy

of the prediction. The bike managers can make very

timely and effective changes to the bike distribution.

This paper will propose multiple factors

regressions to predict the amount of bike renting in a

bike system using open-source data. First, this paper

will extract and explore the data of external factors,

such as weather condition, time and temperature and

sort them by day. Then, this paper will describe two

kinds of models--the linear regression models and tree

regression models. In each kind of model, this paper

Li, W.

Regression Models for Bike Rental Prediction Based on External Factors.

DOI: 10.5220/0012801900003885

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Analysis and Machine Learning (DAML 2023), pages 35-41

ISBN: 978-989-758-705-4

will provide an improved version of the basic model

so that the model’s accuracy is increased and the error

is reduced, improving the model’s prediction accuracy.

Finally, this paper will evaluate two kinds of models

and compare their predicting outcomes through MSE,

and CV errors. The best model among all the

considered models will be given and used to predict

the bike rental number in a short period of time.

2 LITERATURE REVIEW

Bike-sharing systems have become a popular research

topic in recent years. To develop more efficient bike-

sharing systems, researchers have examined the

distribution strategy of bikes, accessibility for users,

and predicting rental bike demand. The station areas

of Madrid's bike-sharing system were improved by

using a technique based on a geographic Information

System (GIS) that updated the information on

population and employment to estimate the

distribution of spatial needs (García-Palomares et al.,

2012). The problem was divided into two parts:

finding the needs for each level of station management

and contriving the best routes to design the bicycle

inventory (Schuijbroek et al., 2016).

Foreseeing the demand of bike users is essential

for managing the total supply and allocation of shared

bikes. Thus many researchers have concentrated on

the relative factors of bike demand. Zheng et al.

studied the influencing factors and utilized a cluster

strategy with similar patterns to simulate the effect of

weather conditions on usage numbers (Zheng et al.,

2018). An unobserved component model has been

applied to calculate the forecast of monthly rentals of

bikes of a BSS in Germany (Wirtgen et al., 2022).

With the deep neural network, the accuracy of

prediction can be improved and the flexible fitting of

the model can be achieved (Thirumalai and

Koppuravuri, 2017). Although numerous researchers

have investigated the overall demand and accessibility

of public bike-sharing systems, not many researches

focused on explaining certain influencing factors,

such as weather conditions and dates. In this study,

this paper will focus on predicting problems in public

bike rental demand considering weather and temporal

conditions.

In this paper, six algorithms will be used: (a).

Backward selection regression model (b) Ridge

regression (c)Lasso (d) Bagging (e) Random forest (f)

Boosting. As for the method, the boosting algorithm

presented very excellent performances in demands of

free-floating car service prediction (Alencar et al.,

2021). R. Simon et al. developed and compared the

state-of-the-art Random Forest algorithm and

Convolutional Neural Networks to better predict short

and long-term bike rental count (Ruffieux et al., 2017).

MLR and ARIMAX have been applied to predict the

travel time in BSS of Washington (Salih-Elamin and

Al-Deek, 2020). Li developed a BRNN through linear

regression to predict bikes and used GA to minimize

the schedule cost (Li, 2020).

The cross-validation method will be applied to the

training data and test data to find the best

hyperparameter. Then this study will consider which

is the best model with its corresponding performance.

In the last part, a variable importance analysis will be

carried out to determine which factor occupies the

most essential part of the regression model.

3 DATA PREPARATION AND

EXPLORATORY ANALYSIS

This research uses two-year data from the Rental Bike

Sharing Data Set that was obtained from the Kaggle

website (Fanaee-T and Gama, 2014). The data set time

starts from 2011, January and ends at 2012, December

and records the number of rental bikes for each hour

and each day. Table 1 shows the rental bike-sharing

data set variables and their corresponding description.

Table 1: Description of Variables in the Rental Bike Sharing Data Set.

Parameters Abb

. Classification

Date and time Hourly Date and timestamp Y-M-D

Number of total rentals Count Continuous Variable

Hour Hour Continuous Variable

Temperature Temp Continuous Variable

“feel like”temperature Atemp Continuous Variable

Relative Humidity Hum Continuous Variable

Wind speed Wind speed Continuous Variable

Season Season Categorical Variable

Holiday Holiday Categorical Variable

Workingday Workingday Categorical Variable

Weather Weathersit Categorical Variable

Week status Wstatus Categorical Variable

Day of the week Weekday Categorical Variable

DAML 2023 - International Conference on Data Analysis and Machine Learning

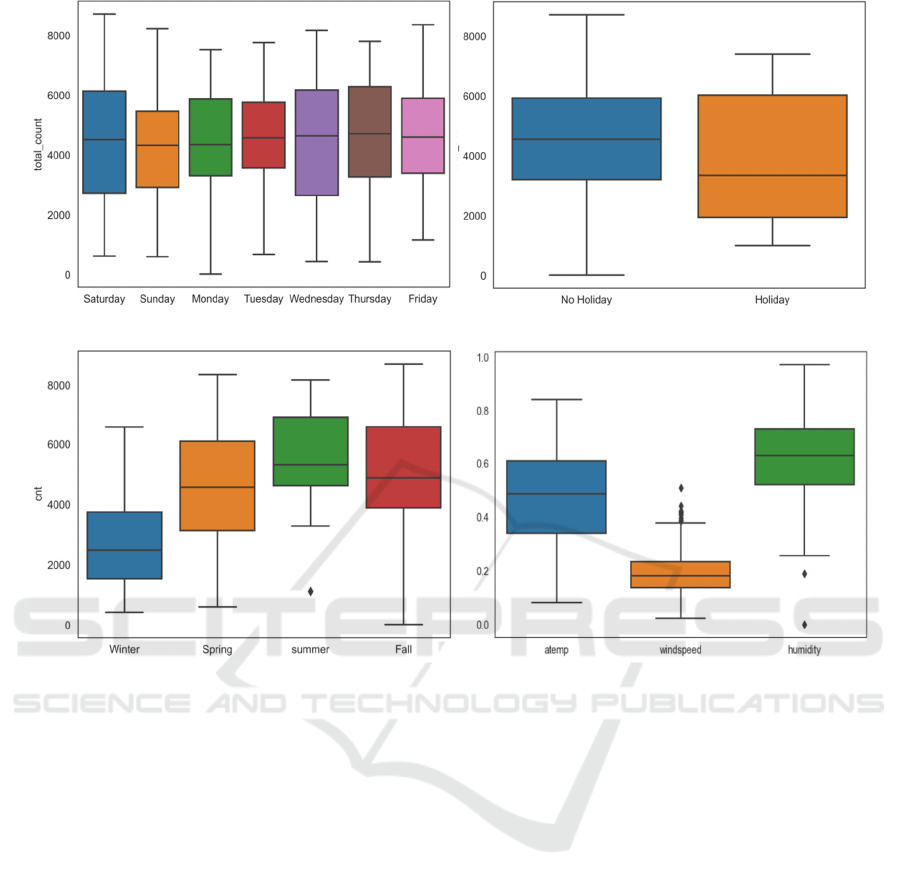
Figure 1: Boxplots for rental bike sharing data (Picture credit: Original).

Figure 1 represents the boxplots of the count of

rental bikes depending on the day of the week,

working day, season, and the distribution of weather

conditions. The rental count in holiday is less than that

in no holiday time and this can be witnessed in the top

right panel. The figure on bottom left of figure 1

presents rental bike use in winter is less than that in

other seasons, which reveals the seasonal effect of

weather use. This is probably because people use

fewer bikes to commute on holidays. Since the traffic

highly depends on weather conditions, the count

corresponding weather, such as little clouds (including

clear weather), mist, drizzle, snowstorm, recorded in

the data will significantly change the bike use demand.

In this study, the measurable weather factors such as

temperature, wind and humidity factors will also be

considered because they are important weather

indicators as well. The bottom right panel shows the

distribution of normalized measurable weather data. It

is worth noting that the temp and atemp are highly

positively correlated, which shows that they contain

the same information. Hence this paper is going to

ignore temp and use atemp in the following analysis.

In short, the predictors that will be considered

mainly include the temporal reasons and climate

reasons and the variables are Atemp, Hum, Wind

speed, Holiday, Working day, Weather, and Weekday.

The grid search method suggests choosing the best

settings by arranging all possible grids in the space of

parameters. Each grid axis represents a parameter of

the algorithm, and each point in the grid corresponds

to a specific combination of parameters (Ve and Cho,

2020). The bike rental data will be split into training

data set and a test data set using a 10-fold validation

test to find the best hyperparameters. Thus the data set

will be divided into two parts, each part containing half

of the full data set. 10 rounds of training and validating

will be applied and all the result validation errors will

be averaged to reduce the mean square error. Such

predictive accuracy and MSE control are optimized.

Regression Models for Bike Rental Prediction Based on External Factors

4 ANALYSIS OF INFLUENTIAL

FACTORS OF BIKE RENTAL

DATA BASED ON LINEAR

REGRESSION MODEL

4.1 Methodology

Backward stepwise selection and forward stepwise

selection are two easily applicable methods to

calculate the coefficients and quickly establish a

model using different counts of predictors. To the

characteristics of the backward method, backward

stepwise selection begins with the full least square

model that includes all predictors, and then eliminates

the predictor that is the least helpful one by one.

Since the variables satisfy that there are less

variables than the samples, this paper can apply

backward stepwise selection to the data.

The values that minimize the ridge regression

coefficient

estimates (Ridge) are



===

+−−

ijji

)(

βλββ

(1)

λ≥0 represents a parameter in (2) (James et al.,

2011). The second term



βλ

is called a shrinkage

penalty. Ridge regression improves the over least

squares because the ridge coefficient. estimates lead to

a substantial reduction in the variance of predictions

The lasso coefficients

(Lasso) minimize



===

+−−

ijji

)(

βλββ

(2)

The Lasso model has advantages in finding key

predictors because it can perform variable selection.

4.2 Model Development

The backward stepwise selection regression requires

us to determine how many variables k are to be applied

in the model. The test MSE in the training set is a

measure of fitting outcome. The lower the test MSE,

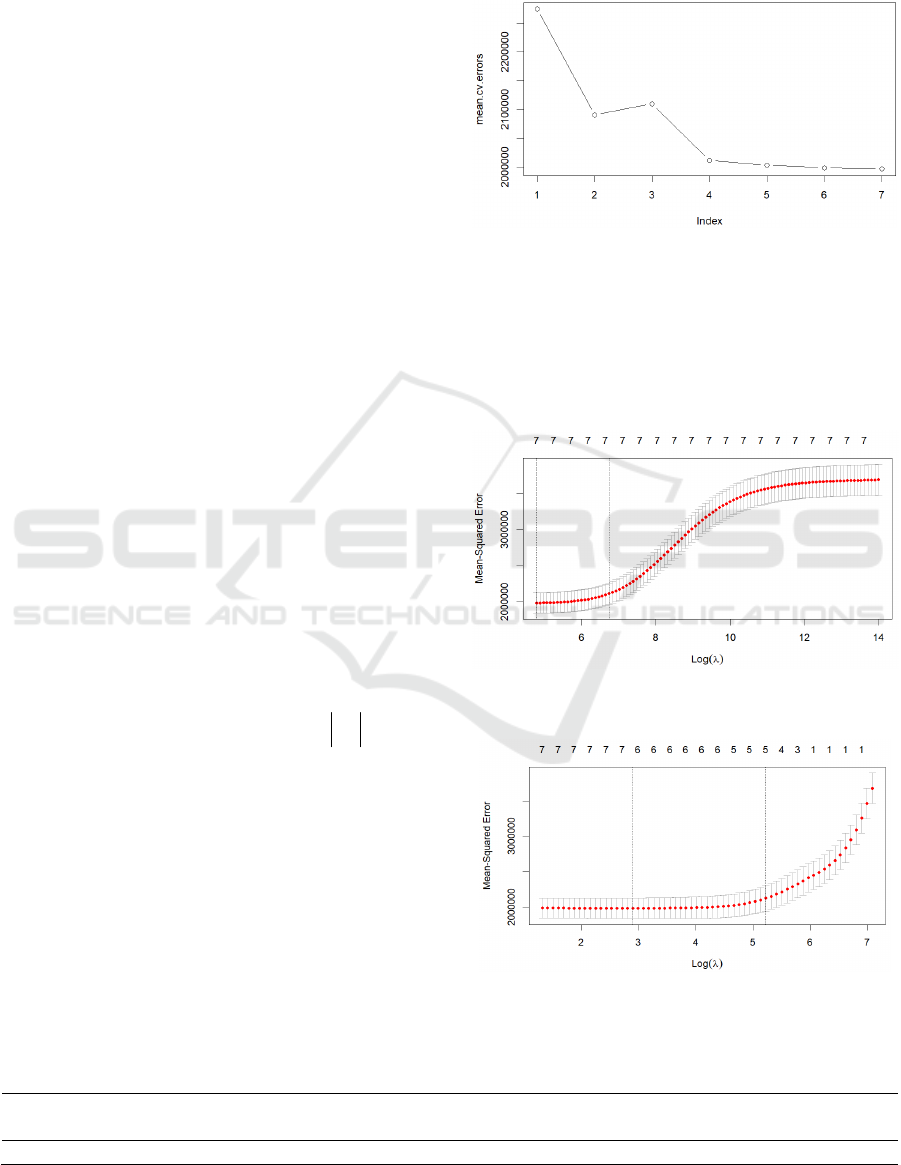
the better the model. Figure 2 shows the test MSE for

models corresponding with their numbers of variables.

The model with seven variables has the lowest test

MSE, which means it is the best model among the ones

considered. Table 2 shows the coefficients in the 7-

variable model.

Figure 2: Test MSE (Picture credit: Original).

The ridge regression and lasso select the hyper

parameter λ which results in the smallest test MSE and

this paper can minimize the cross-validation error

through the grid searching process. The process is

displayed in figure 3,4 and the coefficient outcome is

shown in table 3 and 4.

Figure 3: Grid search result for ridge regression (Picture

credit: Original).

Figure 4: Grid search result for Lasso (Picture credit:

Original).

Table 2: Coefficients of BSS.

Predictors (intercept) Holiday Weekday Working day Weathersit Atemp Hum

Wind

spee

Value 3451.77 -481.79 64.06 108.25 --506.73 7164.10 -1856.16 -3808.24

DAML 2023 - International Conference on Data Analysis and Machine Learning

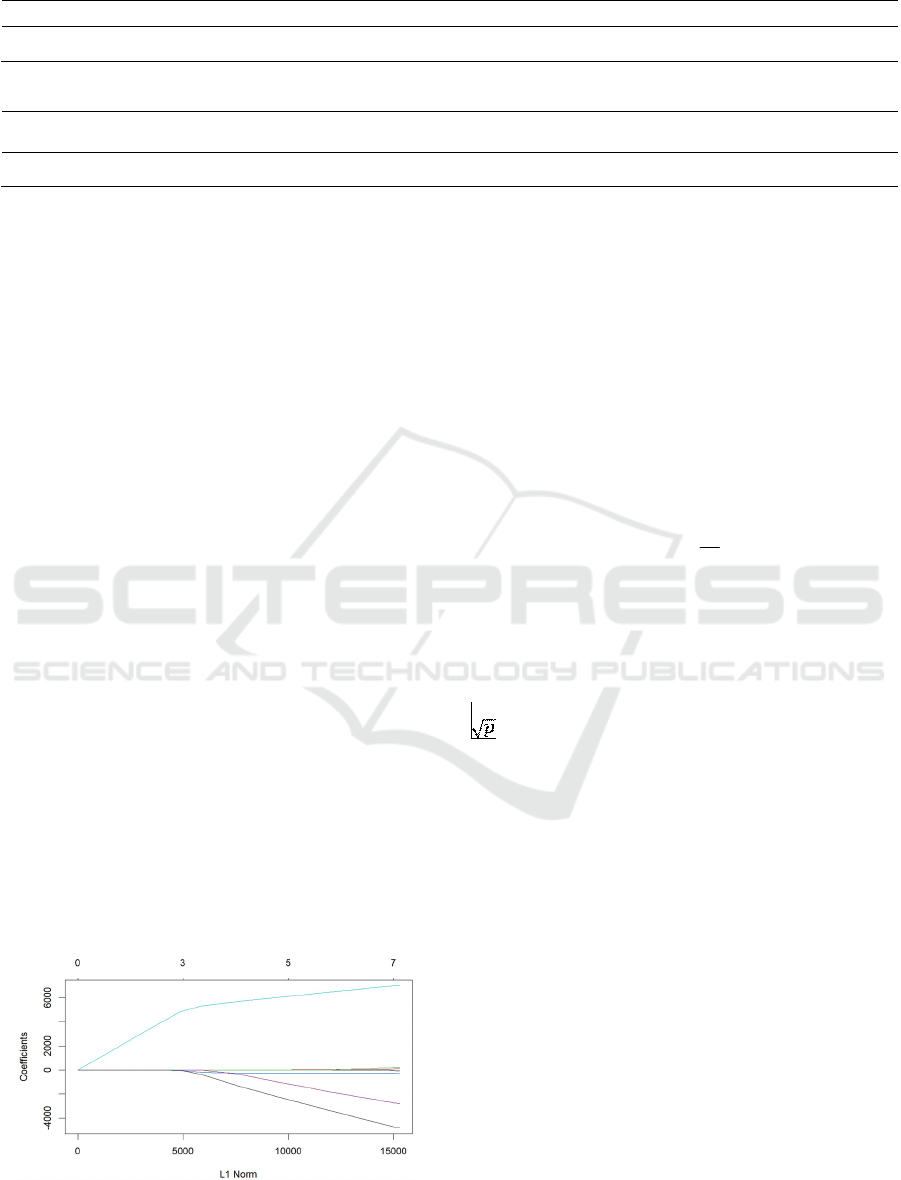
Table 3: Coefficients for Ridge Regression.

Predictors (intercept) Holiday Weekday Workingday Weathersit Atemp Hum Wind speed

value 3514.29 -467.52 61.02 111.46 -528.10 6716.66 -1612.89 -3285.63

Table 4: Coefficients for Lasso.

Predictors (intercept) Holiday Weekday Workingday Weathersit Atemp Hum Wind speed

value 3377.84 -404.70 56.36 78.45 -500.88 7064.51 -1691.33 -3540.10

From the ridge regression model, it can be seen

that when the holiday increases by one unit, the total

count of bikes (TCB) decreases by 467.52 units; this

is probably because on holiday people use less public

transportation to commute between workplace to

home. When the weekday increases by 1 unit, the TCB

increases by 61.02 unit; when working day increases

by 1 unit, the TCB increases by 111.46 unit; when

weathers increase by 1 unit, the TCB decreases by -

528.10 units; the coefficient outcome between weather

and TCB shows that extreme weather conditions hold

more people indoor. When atemp increases by 1 unit,

the TCB increases by 6716.66 units; when humidity

increases by 1 unit, the TCB decreases by 1612.89

units. Such an outcome reveals that people tend to

choose bike riding when the weather gets warmer and

drier. The overall outcome shows that holidays,

weathers and humidity are negative factors affecting

the TCB, while the weekday, and working day atemp

are positive factors.

From the lasso model, it is the same for the ridge

regression model that holiday, weather and humidity

are negative factors affecting the TCB, while the

weekday and workingday atemp are positive factors.

However, different from the ridge regression, the

atemp, humidity, and wind speed take up larger

importance in the lasso model.

The lasso regression coefficient estimates for the

bike rental data are displayed in figure 5. As λ

increases, the L1 Norm decreases. All coefficients

increases as the L1 Norm increases.

Figure 5: Lasso coefficients with L1 norm (Picture credit:

Original).

5 BIKE RENTAL DEMAND

PREDICTING MODEL BASED

ON TREES REGRESSION

MODEL

5.1 Model Introduction

Bagging is a general and efficient method for lowering

the variance in a statistical learning procedure. The

bagging algorithm can be expresses as the following

form (James et al., 2011):

).(

)(

bag



(3)

Random tree can enhance the bagged trees through

making a small tweak that makes the trees more

diverse. At each split of the tree, a subset of m (m<p)

predictors is randomly selected from the total set of p

predictors as split candidates. This paper choosed m=

here in our model consideration.

Boosting fits small trees to the residuals and adds

new decision trees to the fitted function, which

improves the model where it is weak.

Since there are 4 qualitative predictors in the

chosen 7 predictors of the model, this paper may apply

tree models to the data to improve the predicted result.

Trees are very explainable for the predictors and they

can more easily simulate the real decision-making

scenario for bike renting.

5.2 Model Development

The ordinary decision tree suffers from high variance.

Bootstrap aggregation can be a very useful method to

reduce the variance. This paper constructs B

regression trees using B bootstrapped training sets and

averages the resulting predictions. The individual tree

goes deep and is not pruned leading its high variance.

However, they also have rather low bias and to

compensate for the rising variance, averaging these

trees is necessary. In this way, trees are obtained in

proper range of variance and bias.

Regression Models for Bike Rental Prediction Based on External Factors

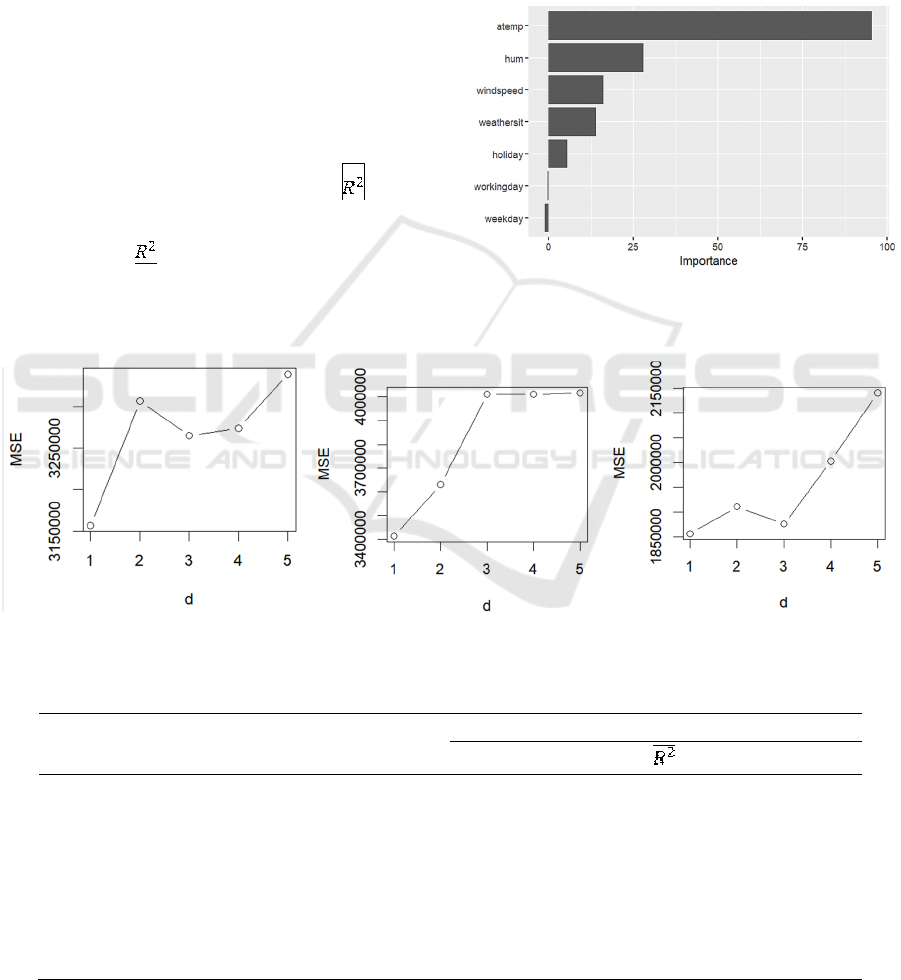
In the bagging procedure, mtry value of 7 is

chosen. In contrast, when a random forest model is

applied, the commonly acceptable mtry is 3 here.

The hyperparameters in boosting are B,λ, and d.

B is the number of trees, λ is the shrinkage parameter,

and d is the number of splits in each tree. They

determine the complexity of the boosted ensemble. A

single split in each tree makes it a stump, which works

well when d=1. The optimal hyperparameters for B

and λ is 50 and 0.2. The hyper parameter tuning output

is shown in figure 6.

6 RESULTS & DISCUSSION

After training all the regression models, the

performance of each of them in the Rental Bike

Sharing Data is evaluated through MSE,

and CV

errors. The model performs with the lowest MSE and

CV and highest

value is the best one. As table 5

shows, the tree model performs better than linear

models in the test result. Among the tree models the

random forest tree model performs best between other

tree models. The backward selection model has the

worst performance of the six models.

Variance importance analysis helps to identify the

most important features for each model. As it is shown

in figure 7, atemp, humidity and windspeed factors are

the most influential variables in the random tree model

and atemp is the most significant factor in all seven

predictors, which shows that temperature takes up

most of people’s consideration when choosing public

bikes.

Figure 7: Variance importance error for random forest

model (Picture credit: Original)

Figure 6: Lasso coefficients with L1 norm grid search result for boosting regression( Left Side:λ=0.05;Middle :λ=0.2;Right

Side:λ=0.5) (Picture credit: Original).

Table 5: Model Performance.

Testing

Models Hyperparameter MSE

Backward Selection Regression k=7 2117970 0.51 1996719

Ridge regression λ=121 2024368 0.53 1913997

Lasso λ=35 2022813 0.57 1906772

bagging mtry=7 1894905 0.65 1781000

Random Forest mtry=3 1828957 0.79 1671845

boosting d=1,B=50,λ=0.2 1879793 0.71 1742764

DAML 2023 - International Conference on Data Analysis and Machine Learning

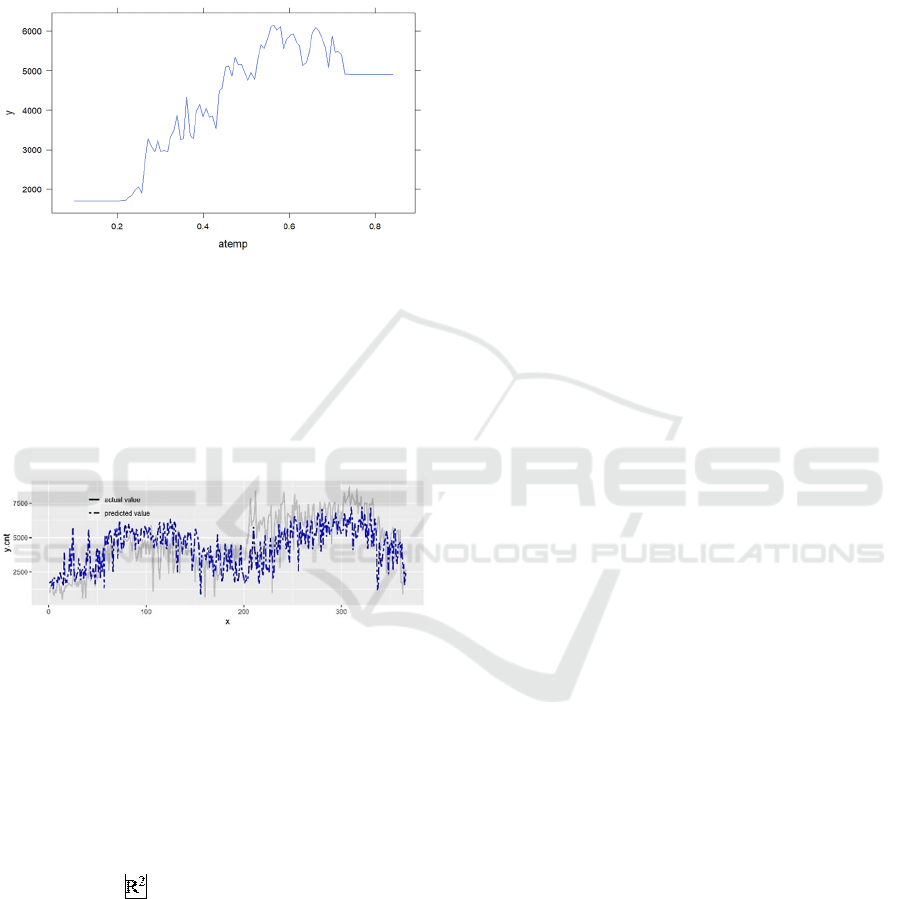
This paper also produces the partial dependence plot

for atemp variable. After accounting for all the

variables, the marginal effect of the selected variables

is illustrated in Figure 8. As the paper presumed, the

count of bikes first increases with atemp and at about

0.6 it reaches the climax, then decreases with atemp.

Figure 8: Partial independence plot for atemp variable

(Picture credit: Original).

Figure 9 shows the fitted values and the actual values

of the data by the random forest model. The model

fitting effect is good, as the two lines in the

comparison chart are very close. This can be

illustrated through that the model’s fitted value is

much around to the actual value.

Figure 9: Fitting plot for random forest (Picture credit:

Original)

7 CONCLUSION

The study mainly focuses on the bike renting count

prediction using the Bike Rental Sharing Data Set.

The analyzing outcome shows find that random forest

model improves the predicting result and its mean

square value,

and cross validation error best

compared to backward stepwise selection regression,

ridge regression, lasso,bagging, and boosting. This

leads to the conclusion that the random forest model

can be seen as a useful tool to predict bike demand.

From the result variance importance analysis, it can

infer that the most influential factors of bike rental

demand are temperature, humidity, and wind speed.

This conclusion can contribute to bike system

operation to predict the bike using demand more

accurately and determine the redistribution of bikes

more precisely.

REFERENCES

J. C. García-Palomares, J. Gutiérrez, and M. Latorre,

“Optimizing the location of stations in bike-sharing

programs: A GIS approach,” Applied Geography, vol.

35, Jul.2012, pp. 235-246, doi:10.1016/j.apgeog.2012.

07.002.

J.Schuijbroek, R. C. Hampshire and W. J. Van Hoeve,

“Inventory rebalancing and vehicle routing in bike

sharing systems,” European Journal of Operational

Research, vol. 257, Jun. 2016, pp. 992 – 1004,

doi:10.1016/j.ejor.2016.08.029.

Z. Zheng, Y. Zhou, L. Sun, “A Multiple Factor Bike Usage

Prediction Model in Bike-Sharing System,” In: Li, S.

(eds) Green, Pervasive, and Cloud Computing GPC

2018. Lecture Notes in Computer Science, vol 11204,

2019.

C. Wirtgen, M. Kowald, J. Luderschmidt, H. Hünemohr,

“Multivariate demand forecasting for rental bike

systems based on an unobserved component model,”

Electronics, vol. 11, Dec. 2022, pp. 4146,

2022,doi:10.3390/electronics11244146.

C.Thirumalai, and R. Koppuravuri, “Bike sharing

prediction using deep neural networks,” JOIV:

International Journal on Informatics Visualization, vol.

1, 2017, pp. 83-87,doi:10.30630/joiv.1.3.30.

V. A. Alencar, L. R.Pessamilio, F. Rooke, H. S. Bernardino,

and A. Borges Vieira, “Forecasting the carsharing

service demand using uni and multivariable models,”

Journal of Internet Services and Applications, vol. 12,

Dec. 2021, pp. 1-20,doi:10.1186/s13174-021-00137-8.

S. Ruffieux, N. Spycher, E. Mugellini and O. A. Khaled,

"Real-time usage forecasting for bike-sharing systems:

A study on random forest and convolutional neural

network applicability," 2017 Intelligent Systems

Conference (IntelliSys), London, UK, 2017, pp. 622-

631, doi: 10.1109/IntelliSys.2017.8324359.

R. Salih-Elamin, and H. Al-Deek, “Short-term prediction

for bike share systems' travel time under the effects of

weather conditions,” Advances in transportation

studies, vol. 50. Apr. 2020, pp. 81-94, doi:10.4399/

97888255317326.

S. Li, “A Decision Model for Bike Sharing Based on Big

Data Analysis,” Journal Européen des Systèmes

Automatisés, vol. 53, Apr. 2020,pp 283-288,

doi:10.18280/jesa.530216.

H. Fanaee-T, and J. Gama, “Event labeling combining

ensemble detectors and background knowledge,”

Progress in Artificial Intelligence, vol. 2, Jun. 2014, pp.

113-127,doi:10.1007/s13748-013-0040-3.

S. VE, and Y Cho, Y. “A rule-based model for Seoul Bike

sharing demand prediction using weather data,”

European Journal of Remote Sensing, vol. 53, Jun2020,

pp. 166-183, doi:10.1080/22797254.2020.1725789.

G. James, D. Witten, T. Hastie and R. Tibshirani. An

introduction to statistical learning. New York: Springer,

vol. 112, 2011, pp. 18.

Regression Models for Bike Rental Prediction Based on External Factors