Online Portfolio Selection of LQ45 Stocks Index with the Adaptive
Online Moving Average Method
Irkham Muhammad Fakhri
1
, Deni Saepudin
1
and Aniq Atiqi Rohmawati
1
1
Department of Informatics, Telkom University, Bandung, Indonesia
Keywords:
Portfolio, Aolma, Equal Weight, Sharpe Ratio
Abstract:
An online portfolio is a collection or composition of a fund in financial assets with specific returns held online.
Online portfolio selection can increase the chances of getting the right stocks. One way to choose an online
portfolio is using the Adaptive Online Moving Average (AOLMA) method. This method predicts stock returns
using adaptive decay variables from moving averages so that the predictive rate increases even more. In this
paper, portfolio selection using the Adaptive Online Moving Average (AOLMA) method is carried out on the
LQ45 stock index dataset from April 2012 to April 2022. The portfolio performance is then compared to the
Equal Weight Portfolio (EWP). This portfolio is superior to the equal-weight portfolio in terms of mean return.
1 INTRODUCTION
An online portfolio is a collection of funds distributed
as financial assets with a specific return. In this study,
the portfolio comprises companies from the LQ45 in-
dex. Portfolio selection was studied for the first time
in 1952 by Markowitz. He developed a fundamental
idea of mean-variance to calculate the percentage of
asset allocation (Markowitz, 1952). An online port-
folio is different from a traditional portfolio. The on-
line portfolio does not consider the return distribution
of historical data to manage the portfolio return and
risk. One method currently used in an online portfo-
lio is the Adaptive Online Moving Average algorithm
or AOLMA. AOLMA was developed based on tech-
nical analysis to predict future stock price movements
as seen from historical data, including opening, high-
est, lowest prices, and most importantly, the closing
price and the trading volume (Brown and Jennings,
1989). AOLMA focuses primarily on accurate fore-
casting of future prices to help investors create opti-
mal investment strategies. In this paper, a portfolio
from LQ45 index stocks is constructed by maximiz-
ing the portfolio’s return value. Online selection of
portfolios has been carried out using various meth-
ods. However, these various methods use quite a lot
of historical data and a reasonably long time to predict
a stock closing price or stock return in a period in an
online portfolio. AOLMA is here to overcome this by
only needing data on a stock’s latest period’s closing
price to get predictions of closing prices and returns
for future periods. AOLMA can periodically improve
the effectiveness of predictions by updating the de-
cay factor every period. Stocks are selected based
on stock return predictions from the Adaptive Online
Moving Average Algorithm. In addition, the portfo-
lio will be compared to the Equal Weight portfolio by
calculating the mean return, standard deviation, and
Sharpe ratio.
2 LITERATURE REVIEW
Many studies on online portfolio selection have been
conducted in line with the development of computa-
tional intelligence techniques that prioritize efficient
and practical processes for managing stock as online
assets. The selection of this online portfolio does
not pay attention to the distribution function to pre-
dict future returns. The selection of online portfolios
is made by considering the selection of artificial in-
telligence techniques as a predictor of asset returns
and optimal investment strategies. There are many
types of portfolio selection, such as benchmarks, fol-
lowing the winner strategy, following the loser strat-
egy, a combination of winner and loser strategies,
as well as meta-learning strategies. One version of
the benchmark-type portfolio is the market method,
which buys and holds or sells the same stocks as an
index (Li and Hoi, 2014). The market method is
implemented by distributing available capital evenly
Fakhri, I., Saepudin, D. and Rohmawati, A.
Online Portfolio Selection of LQ45 Stocks Index with the Adaptive Online Moving Average Method.
DOI: 10.5220/0012639200003848
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 3rd International Conference on Advanced Information Scientific Development (ICAISD 2023), pages 321-327
ISBN: 978-989-758-678-1
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
321

across all assets in the index in each period. An-
other version of the benchmark-type portfolios is the
Constant Rebalanced Portfolio (CRP) which allocates
capital to the assets with the same risk level in all pe-
riods (Tan et al., 1991). Exponential Gradient (EG)
is a portfolio selection version of the winning strat-
egy type with an exponential gradient value adjust-
ment that is used to allocate investments using his-
torical return data and strategies from stocks in the
portfolio (Helmbold et al., 1998). The next version
for portfolio selection for the winning strategy type
is the Online Newton Step (ONS) through the appli-
cation of the cumulative log return calculation equa-
tion with the Hessian matrix variable and the gradient
matrix (Agarwal et al., 2006). The adaptive method
is another version of the portfolio selection of win-
ning strategy types. This version can determine mul-
tiple selections of stocks for portfolios such as op-
timal constant log portfolio and rebalancing, adap-
tive Markowitz portfolio selection method, and index-
based portfolio selection method (Gaivoronski and
Stella, 2003). Portfolio selection following the loser
strategy has several versions. The first version is the
Anticorrelation method, this method uses the mean
return and cross-correlation matrix of various risky
stocks in dividing the proportion of portfolio stocks
based on stocks that perform well and stocks that per-
form poorly (Thrun et al., 2004). The next version
is passive aggressive mean reversion (PAMR) from
the application of the loss equation depending on the
mean return portfolio (Li et al., 2012). The Confi-
dence Weighted Mean Reversion (CWMR) method is
another version for selecting portfolio types follow-
ing a loser strategy, this version is based on a vector
design on a portfolio with a Gaussian distribution pro-
cess and the process of adjusting the distribution con-
stantly depends on the nature of the average reversion
(Li et al., 2013). The latest version in the portfolio
of types following a losing strategy is Robust Median
Reversion (RMR), this version predicts the strength
of the median L1 value and can be used for symp-
tom revision in a simple linear time frame so that it
is easy to use (Huang et al., 2016). The selection of
stocks in a pattern-matching portfolio combines the
following winner and following loser strategies and
consists of two processes. The first process is to de-
termine a sample with the aim of selecting an existing
historical price model through a benchmark that is al-
most aligned with the current price pattern. The sec-
ond process is to build a better portfolio enhancement
model with reference to the selected pricing model.
The method used in selecting this type of portfolio is
selecting a sample based on a non-parametric kernel
to find a consistent price model by considering the dif-
ferent Euclidean model distances, then constructing
a log-optimal portfolio based on capital growth the-
ory (Gy
¨
orfi et al., 2006). This method has the latest
version by selecting samples based on nonparametric
nearest neighbors and proposes a method of embed-
ding the model from the log of the best nonparamet-
ric nearest neighbors (Gy
¨
orfi et al., 2008). These two
methods were further developed with the existence
of a nonparametric sample selection method based
on correlation using various model correlation coef-
ficients and proposed a Correlation-driven Nonpara-
metric (CORN) learning algorithm (Li et al., 2011).
The metalearning strategy is a type of portfolio selec-
tion using various strategies combined to get a suit-
able portfolio. One strategy is the strategy of using
the Aggregating algorithm which can solve the prob-
lem of selecting online portfolios, and generalizing
the worst case of the Universal Portfolio (UP) algo-
rithm [4]. There are also those who directly imple-
ment meta-learning algorithm methods such as On-
line Newton Update (ONU) and Online Gradient Up-
date (OGU) with satisfactory success rates in select-
ing stocks for online portfolios (Das and Banerjee,
2011). There is also another strategy implemented
in this portfolio using the Follow the Leading His-
tory (FLH) algorithm which is implemented in such
a way that the basic data set is adjusted periodically
and continuously with each base expert making calcu-
lations for future prices. with the start being the time
period varies in historical data (Hazan and Seshadhri,
2009).
2.1 Portfolio Selection with Online
Moving Average Revision
The Online Moving Average Revision or abbreviated
OLMAR is the first online portfolio selection algo-
rithm to use a moving average variable that assumes
that stocks performing poorly in the present will per-
form better in the future and vice versa. The OL-
MAR is exploited from the Moving Average Rever-
sion approach which considers the expected return
and stock risk. There are two moving averages used in
the OLMAR, namely Simple Moving Average or ab-
breviated SMA algorithm and the Exponential Mov-
ing Average or abbreviated EMA algorithm (Li et al.,
2015). The SMA algorithm uses the arithmetic av-
erage of truncated historical prices (Johnston et al.,
1999). Whereas, the EMA algorithm takes more his-
torical stock prices and then assigns an exponential
weight to each stock price.
ICAISD 2023 - International Conference on Advanced Information Scientific Development
322

2.2 Portfolio Selection with Adaptive
Online Net Profit Maximization
Portfolio selection using the Adaptive Online Net
Profit Maximization or abbreviated AOLNPM algo-
rithm is a development of the Online Moving Aver-
age Revision (OLMAR) method. This is because OL-
MAR has several drawbacks such as the house limit
for the rate of return that must be set, the selection
of strategies that are found only take the appropri-
ate strategy without looking at other strategies that
may have higher returns, and OLMAR returns also
do not impose special conditions and there are no
transaction costs calculated in making portfolio strat-
egy changes. The purpose of adding NPM is to add
value to the transaction cost variable and then trans-
form the non-linear model into a linear programming
problem that is commensurate with changes in the
variable in the portfolio. Even though AOL NPM is
an updated model, there are still limitations such as
the risky assets taken are determined only by histori-
cal asset data even though asset volume must also be
considered and assets with small risks are not consid-
ered in selecting online portfolios. This is evidenced
by the application of AOLNPM to the MSCI, NYSE-
O, NYSE-N, and TSE index stocks. The cumulative
return results are satisfactory (Guo et al., 2021).
2.3 Portfolio Selection with Adaptive
Online Moving Average
Adaptive Online Moving Average (AOLMA) is an al-
gorithm that focuses on predicting stock movements
to determine optimal investment strategies. AOLMA
uses historical data analysis that comes from financial
markets such as historical stock prices and stock trad-
ing volume. The AOLMA uses technical analysis to
determine whether or not the trend will continue in a
stock. Instruments that can be used to carry out trend
analysis are trend lines, candlestick formations, and
other systematic visualizations. The AOLMA relies
on design to factor decay over a given period. The
AOLMA method is based on regression techniques,
namely techniques obtained from analyzing two dif-
ferent and separate variables to obtain an equation to
estimate returns effectively and accurately. Adaptive
Online Moving Average (AOLMA) works by adjust-
ing the stock decay factor gradually from the mov-
ing average according to stock performance (Li and
Hoi, 2012). The advantages provided by the AOLMA
method include predictions that are made faster and
in real time, the data needed is only the latest stock
close price data, and the effectiveness of the predic-
tion is further improved by updating the decay factor
value by adding and subtracting Y values.
2.4 Equal Weight Portfolio
qual weight portfolio is the simplest and easiest to
implement portfolio selection approach. An equal-
weight portfolio is based on giving each company the
same weight. This portfolio can be relied upon to
maximize stock returns in the portfolio and is very
easy to allocate to many stocks. Equal weight portfo-
lio can be formulated as follows (Brandel, ).
w
i
=
1
N
′
i = 1, 2, ....N, (1)
where w
i
is the weight i
th
stock in the portfolio,
and N is the number of stocks contained in the port-
folio.
3 METHODOLOGY
The design of all processes of a system that is in this
article is built-in visualization with the format in the
form of a flow chart (flowchart) containing a work-
flow explanation of the system design built for the ba-
sic work of the system from the beginning to the end
of the process as shown in Figure 1.
Figure 1: Methodology.
The initial step in creating this system was to input
all weekly stock price index data with the LQ45 index
in the period April 2012 - April 2022 by taking the
dataset from the Yahoo Finance website. The sample
dataset used is shown in Table 1.
Table 1: Dataset Sample.
Date Close Close Close Close Close
BBCA TLKM ASII PTBA INTP
30/04/2012 1610 1670 7270 3650 18850
07/05/2012 1600 1640 6885 3250 18150
14/05/2012 1510 1580 6840 3290 17300
21/05/2012 1450 1450 6585 3240 17200
28/05/2012 1420 1520 6335 3000 17250
The next stage is the data preprocessing stage.
Data preprocessing is carried out to prepare raw data
on LQ45 stocks that have been previously obtained
to be processed into data that is ready to be used in
the system created. This data preprocessing step fo-
cuses on data cleaning, namely eliminating or mod-
ifying incorrect or empty data values (missing val-
ues), and correcting inconsistent data. Furthermore,
Online Portfolio Selection of LQ45 Stocks Index with the Adaptive Online Moving Average Method
323

the data normalization process is carried out, data nor-
malization is the process of comparing data so that it
can be described as data with normal distribution.
3.1 Adaptive Online Moving Average
(AOLMA) Algorithm
The process of forming a portfolio by applying the
AOLMA algorithm is as follows:
1. Determine the first decay factor α
1
with 0 ≤ α
1
≤
1and the updating value of the next decay factor γ
with γ ≤ 0.001. The decay factor will be a vector
in the portfolio (α = (α
1
, α
2
, ..., α
m
)) in a period
(t) of an asset (i) ( i = 1, 2, . . . , m ).
2. Calculating stock predictions for period t with the
Simple Moving Average for the first 10 weeks.
3. Calculating stock predictions in period t + 1:
P
1
(t+1)
= a
(t+1)
.P
(t)
+ (1 − a
(t+1)
).P
′
(t)
(2)
Where P
t+1
is prediction close period t +1, a
t+1
is
period decay factor t+1, P
(t)
is close period t, and
P
′
(t)
is prediction close period t(from SMA predic-
tion calculations).
4. Calculating the expected stock return in the t+1
period:
r
′
(r+1)
= a
(t+1)
.1 + (1 − a
(t+1)
)P
(t)
.
r
′
t
r
t
(3)
Where r
′
(r+1)
is expected stock return period t+1,
a
(t+1)
is period decay factor t+1, r
′
t
is expected
stock return period t, and r
t
is period stock return
t.
5. Calculating the expected return of stock i in period
t:
r
′
(ti)
= a
(ti)
+ (1 − a
(ti)
).
r
′
(t−1)i
r
(t−1)i
(4)
the following formula is generated:
r
′
(ti)
−r
′
(ti)
= r
(ti)
−
r
′
(t−1)i
r
(t−1)i
−(1−
r
′
(t−1)i
r
(t−1)i
.a
(ti)
) (5)
Where r
′
(ti)
is expected stock return i period t, r
(ti)
is stock return i period t, a
(ti)
is stock decay factor
i period t, r
′
(t−1)i
is expected stock return i period
t-1, and r
(t−1)i
is stock return i period t-1.
6. Determine the conditions that occur in the portfo-
lio:
1st condition : r
(ti)
> r
′
(ti)
and r
(t−1)i
> r
′
(t−1)i
2nd condition : r
(ti)
> r
′
(ti)
and r
(t−1)i
≤ r
′
(t−1)i
3rd condition : r
(ti)
≤ r
′
(ti)
and r
(t−1)i
> r
′
(t−1)i
4rd condition : r
(ti)
≤ r
′
(ti)
and r
(t−1)i
≤ r
′
(t−1)i
If the first condition or 4th condition is found, the
decay factor coefficient is updated:
a
(ti)
= −(1−
r
′
(t−1)i
r
(t−1)i
< 0anda
(t+1)i
= a
(ti)
+γ (6)
If the 2nd condition or 3rd condition is found, the
decay factor coefficient is updated:
a
(ti)
= −(1−
r
′
(t−1)i
r
(t−1)i
≥ 0anda
(t+1)i
= a
(ti)
+γ (7)
Increasing and decreasing the value of the de-
cay factor can increase the accuracy as well as
adaptive updates in getting close stock price pre-
dictions and stock return predictions from the
AOLMA method.
7. Calculating the effectiveness of the Adaptive On-
line Moving Average (AOLMA) return predic-
tion. This is done by calculating the relative pre-
diction error of the stock at time j using the for-
mula.
Er
( j)
=



r
′
ji
− r
ji



r
ji
.100% (8)
and the average relative error of predictions:
Er =
1
n
n
∑
j=1



r
′
ji
− r
ji



r
ji
.100% (9)
Where Er(j) is a relative error of time stock pre-
diction j, Er is the average relative error, n is many
stocks in the portfolio, r
′
ji
is the expected Return
of stock i time j, and r
ji
is stock return i time j.
4 EVALUATION
4.1 Metric
In investigating the accuracy of the prediction results,
evaluation metrics are used, namely, the root means
square error is abbreviated as RMSE and the mean
absolute error is abbreviated as MAE (Chen et al.,
2021).
RMSE =
s
1
n
n
∑
i=1
(y
i
− y
′
i
)
2
(10)
ICAISD 2023 - International Conference on Advanced Information Scientific Development
324

MAE =
s
1
n
n
∑
i=1
|
y
i
− y
′
i
)
|
(11)
Where y
′
i
is the predicted stock return and y
i
is the ac-
tual stock return, and n is the total number of samples.
4.2 Sharpe Ratio
The Sharpe Ratio is a way of measuring the perfor-
mance of a portfolio. The way to evaluate portfolio
performance with the Sharpe ratio is to look at the
value of the portfolio’s expected return and portfolio
risk. If the Sharpe values the smaller the ratio, the
less good portfolio performance will result and vice
versa. The portfolio Sharpe ratio can be formulated
as follows (Iorio et al., 2018).
MAE =
R
exp
σ
p
(12)
Where S
p
is the Sharpe ratio, R
exp
is the Expected
return portfolio, and σ
p
is portfolio risk.
4.3 Testing Scenario
The application of the AOLMA algorithm to the
LQ45 stock index is carried out in the following
stages:
1. Predict the return of stocks that are on the LQ45
index using AOLMA with an initialization of a de-
cay factor (α) value of 0.5 with γ (modifier of de-
cay factor value) of 0.001. In this paper, a first de-
cay factor (α) value of 0.5 was chosen because it
is the middle range in the choice of value and a de-
cay factor value modifier γ of 0.001. The modifier
for the decay factor value γ must be smaller than
the decay factor value because the decay factor
update is carried out every period and the change
must not be too significant but can be effective
in predicting stock close prices and stock returns
from the AOLMA method.
2. Form a portfolio with 2 stocks, 3 stocks, and 5
stocks. Stocks are selected based on the com-
pany’s industrial activity sector.
3. The selection or determination of stocks taken ev-
ery week for the portfolio is based on AOLMA’s
return predictions where the stocks taken must
have one of the largest return predictions in the
list of stocks in the portfolio every week.
4. Form a portfolio with the same list of stocks as
the portfolio obtained from point 3 but the weight
used must be the same for each stock in the port-
folio (portfolio with the same weight).
5. Comparing the results of portfolio performance in
points 3 and 4 with the performance of stocks in
the portfolio list using the calculation of the mean
return value, standard deviation value, and Sharpe
ratio value for each portfolio.
6. Determines the best portfolio to be taken based
on its performance from the highest mean return
value and the highest Sharpe ratio value of the
portfolio in this test.
4.4 Experiment Result
The return prediction results and model evaluation for
all stocks that will be formed into several portfolios
are shown in Table 2.
Table 2: Evaluation of Return Prediction Results.
Stock RMSE MAE
BBCA 0,033205 0,023546
TLKM 0,036214 0,026868
ASII 0,045645 0,032404
PTBA 0,064316 0,047836
INTP 0,051624 0,039506
PTPP 0,075572 0,05426
PGAS 0,065342 0,044468
INDF 0,039979 0,028801
The value of the portfolio using the AOLMA
method compared to the portfolio with the same
weight was carried out with 2 stocks, 3 stocks, and
5 stocks from different sectors. A comparison of
the portfolio with 2 stocks is shown in Figure 3.
The first 2 stock portfolios consist of BBCA.JK and
TLKM.JK. The second portfolio of 2 stocks with
ASII.JK and PTBA.JK. The third portfolio of 2 stocks
with INTP.JK and PTPP.JK. The fourth portfolio of 2
stocks with PGAS.JK and INDF.JK.
Based on Table 3, the average return of the portfo-
lio with the method used in this article is better than
the equal weight method. The equal weight portfolio
has a relatively smaller risk value in terms of the risk
obtained from the standard deviation (smaller) and
also has better performance than AOLMA in terms
of Sharpe ratio (larger). Thus, on testing a portofolio
of 2 stocks, the AOLMA portofolio only provides a
better mean return than the equal-weight portofolio.
The value of the portfolio using the AOLMA
method compared to the portfolio with the same
weight carried out with 3 stocks is shown in Fig-
ure 5. The first 3 stock portfolios consist of
BBCA.JK, TLKM.JK, and ASII.JK. The second port-
folio of 3 stocks consists of BBCA.JK, TLKM.JK and
PTBA.JK. The third portfolio of 3 stocks consists of
BBCA.JK, TLKM.JK and INTP.JK. The fourth port-
Online Portfolio Selection of LQ45 Stocks Index with the Adaptive Online Moving Average Method
325

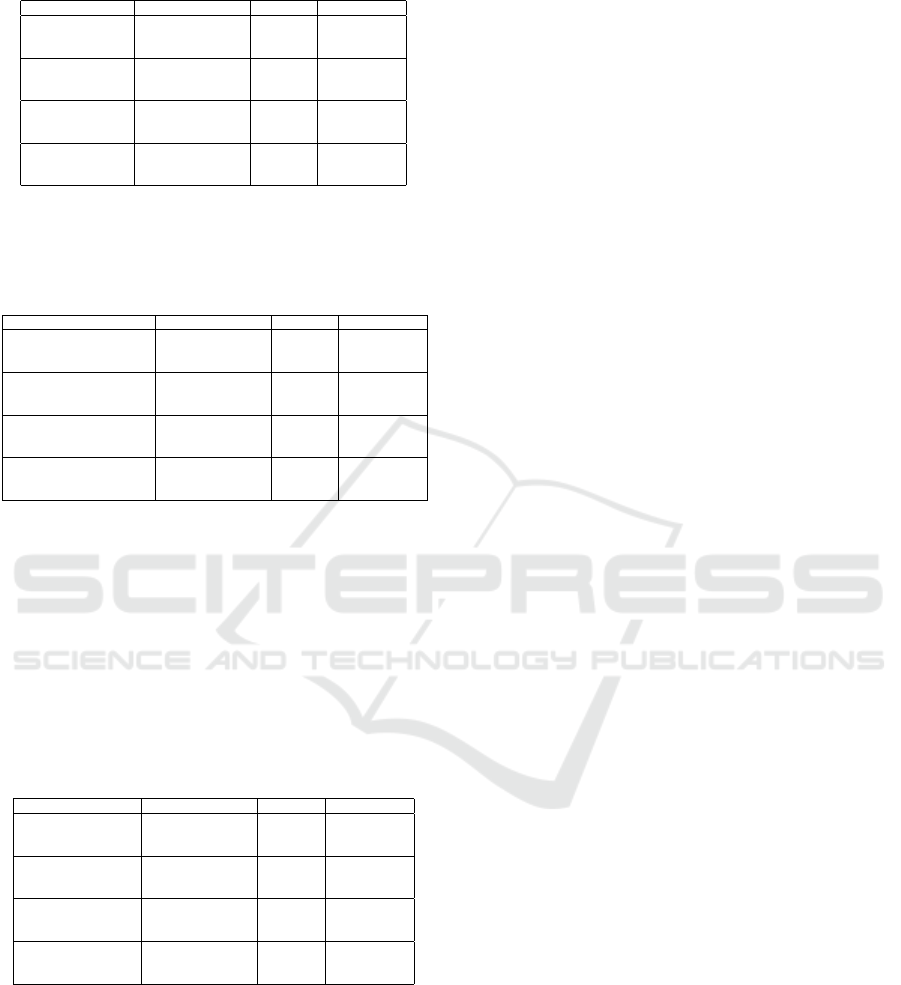
Table 3: Comparative Evaluation of Portfolio Value for 2
Stocks.
Portofolio Evaluation AOLMA Equal Weight
BBCA and TLKM Mean Return 1,00549 1,00323
Standard Deviation 0,03321 0,02836
Sharpe Ratio 30,2729 35,3713
ASII and PTBA Mean Return 1,00198 1,00156
Standard Deviation 0.05337 0,04074
Sharpe Ratio 18,7727 24,5833
INTP and PTPP Mean Return 1,00368 1,00161
Standard Deviation 0,05916 0,04826
Sharpe Ratio 16,9639 20,7519
PGAS and INDF Mean Return 1,00180 1,00055
Standard Deviation 0,05176 0,04052
Sharpe Ratio 19,3514 24,6889
folio of 3 stocks consists of BBCA.JK, TLKM.JK and
PTPP.JK stock.
Table 4: Comparative Evaluation of Portfolio Value for 3
Stocks.
Portofolio Evaluation AOLMA Equal Weight
BBCA, TLKM, and ASII Mean Return 1,00549 1,00253
Standard Deviation 0,03952 0.02957
Sharpe Ratio 25,4389 33,8964
BBCA, TLKM, and PTBA Mean Return 1,00348 1,00282
Standard Deviation 0,04689 0,03058
Sharpe Ratio 21,3965 32,7929
BBCA, TLKM, and INTP Mean Return 1,00452 1,00220
Standard Deviation 0,04286 0,03079
Sharpe Ratio 23,4342 32,5485
BBCA, TLKM, and PTPP Mean Return 1,00429 1,00318
Standard Deviation 0,05285 0,03451
Sharpe Ratio 18,9997 29,0654
Based on Table 4, the average return of the portfo-
lio with the method used in this article is better than
the equal weight method. The equal weight portfolio
has a relatively smaller risk value in terms of the risk
from standard deviation (smaller) and also has bet-
ter performance than AOLMA in terms of Sharpe ra-
tio (larger). In testing the portfolio of 3 stocks, the
AOLMA portfolio only provides a better mean return
than the equal-weight portfolio.
Table 5: Comparative Evaluation of Portfolio Value for 5
Stocks.
Portofolio Evaluation AOLMA Equal Weight
BBCA, TLKM, ASII, Mean Return 1,00468 1,00176
INTP, and INDF Standard Deviation 0,04361 0,02942
Sharpe Ratio 23,0342 34,0494
BBCA, TLKM, ASII, Mean Return 1,00347 1,00154
INTP, and PGAS Standard Deviation 0,05001 0,03227
Sharpe Ratio 20,0629 31,0356
BBCA, TLKM, ASII, Mean Return 1,00432 1,00216
INTP, and PTPP Standard Deviation 0,05483 0,03327
Sharpe Ratio 18,3153 30,1165
BBCA, TLKM, ASII, Mean Return 1,00484 1,00195
INTP, and PTBA Standard Deviation 0,04971 0,03043
Sharpe Ratio 20,2105 32,9218
The value of the portfolio using the AOLMA
method compared to the portfolio with the same
weight carried out with 5 stocks. The first 5
stock portfolios are BBCA.JK, TLKM.JK, ASII .JK,
INTP.JK , and INDF.JK. The second portfolio of 5
consists of BBCA.JK, TLKM.JK, ASII.JK, INTP.JK
and PGAS.JK. The third portfolio of 5 stock con-
sists of BBCA.JK, TLKM.JK, ASII.JK, INTP.JK,
and PTPP.JK. The fourth portfolio of 5 stock con-
sists of BBCA.JK, TLKM.JK, ASII.JK, INTP.JK and
PTBA.JK.
Based on Table 5, the average return of the portfo-
lio with the method used in this article is better than
the equal weight method. Portfolios of equal weight
have relatively smaller risk values in terms of standard
deviation risk (smaller) and also have better perfor-
mance than AOLMA in terms of Sharpe ratio (larger).
Thus, in testing a portfolio of 3 stocks, the AOLMA
portfolio only provides a better average return than a
portfolio with equal weight.
A portfolio comparison for 2 stocks, 3 stocks, and
5 stocks as a whole got the results that, the AOLMA
portfolio provides better performance in terms of
mean return alone. Whereas performance in terms
of standard deviation and Sharpe ratio of the equal
weight portfolio is better. That matter shows that the
AOLMA portfolio can get a bigger profit than the
equal portfolio weight, but the big profits are worth
the bigger risks too. Besides that, a portfolio con-
sisting of several stocks does not necessarily provide
better portfolio performance.
5 CONCLUSIONS
Experimental results for stock selection for a portfo-
lio of 2 stocks, 3 stocks, and 5 stocks with AOLMA
and EW show that the portfolio with AOLMA return
predictions has better performance than the mean re-
turn side compared to equal-weight portfolios, espe-
cially with stocks that have history of performance
good and uniform. If the stocks selected for selec-
tion with AOLMA have performance and movement
each week, the value and performance of the AOLMA
portfolio are lower than the equal-weight portfolio.
The portfolio with the best performance is the one
with the most stocks in the experiment is a portfo-
lio of 5 stocks whose performance is seen from the
Sharpe ratio. Although the portfolio with AOLMA’s
return prediction has a high return the risk that is ob-
tained is also higher, that is which makes the shape
ratio smaller. This indicates that the increased risk
is compensated by a higher increase in returns. In
further research, it is suggested to be able to expand
the method comparison for the selection of portfolios
used in addition to equal weight portfolio and perfect
the AOLMA method by changing the parameters used
or even combining them with another method.
ICAISD 2023 - International Conference on Advanced Information Scientific Development
326

REFERENCES
Agarwal, A., Hazan, E., Kale, S., and Schapire, R. (2006).
Algorithms for portfolio management based on the
newton method. In Proceedings of the 23rd interna-
tional conference on Machine learning, page 9–16.
Brandel, S. Markov regime switching model implementa-
tion to the stockholm stock market comparison with
equal weight portfolio,”(2017.
Brown, D. and Jennings, R. (1989). On technical analysis.
The Review of Financial Studies, 2:527–551.
Chen, W., Zhang, H., Mehlawat, M., and Jia, L. (2021).
Mean–variance portfolio optimization using machine
learning-based stock price prediction,”applied. Soft
Computing, 100:106943.
Das, P. and Banerjee, A. (2011). Meta optimization and
its application to portfolio selection. In Proceed-
ings of the 17th ACM SIGKDD international confer-
ence on Knowledge discovery and data mining, page
1163–1171.
Gaivoronski, A. and Stella, F. (2003). On-line portfolio se-
lection using stochastic programming. Journal of Eco-
nomic Dynamics and Control, 27:1013–1043.
Guo, S., Gu, J.-W., and Ching, W.-K. (2021). Adap-
tive online portfolio selection with transaction
costs. European Journal of Operational Research,
295:1074–1086.
Gy
¨
orfi, L., Lugosi, G., and Udina, F. (2006). Non-
parametric kernel-based sequential investment strate-
gies. Mathematical Finance: An International Jour-
nal of Mathematics, Statistics and Financial Eco-
nomics, 16:337–357.
Gy
¨
orfi, L., Udina, F., and Walk, H. (2008). Experiments
on universal portfolio selection using data from real
markets.
Hazan, E. and Seshadhri, C. (2009). Efficient learning algo-
rithms for changing environments. In Proceedings of
the 26th annual international conference on machine
learning, page 393–400.
Helmbold, D., Schapire, R., Singer, Y., and Warmuth, M.
(1998). On-line portfolio selection using multiplica-
tive upyears. Mathematical Finance, 8:325–347.
Huang, D., Zhou, J., Li, B., Hoi, S., and Zhou, S. (2016).
Robust median reversion strategy for online portfolio
selection. IEEE Transactions on Knowledge and Data
Engineering, 28:2480–2493.
Iorio, C., Frasso, G., D’Ambrosio, A., and Siciliano, R.
(2018). A p-spline based clustering approach for port-
folio selection. Expert Systems with Applications,
95:88–103.
Johnston, F., Boyland, J., Meadows, M., and Shale, E.
(1999). Some properties of a simple moving average
when applied to forecasting a time series,”journal. the
Operational Research Society, 50:1267–1271.
Li, B. and Hoi, S. (2012). On-line portfolio selec-
tion with moving average reversion. arXiv preprint
arXiv:1206.4626.
Li, B. and Hoi, S. (2014). Online portfolio selection: A
survey. ACM Computing Surveys (CSUR, 46:1–36.
Li, B., Hoi, S., and Gopalkrishnan, V. (2011). Corn:
Correlation-driven nonparametric learning approach
for portfolio selection. ACM Transactions on Intel-
ligent Systems and Technology (TIST, 2:1–29.
Li, B., Hoi, S., Sahoo, D., and Liu, Z.-Y. (2015). Moving
average reversion strategy for on-line portfolio selec-
tion. Artificial Intelligence, 222:104–123.
Li, B., Hoi, S., Zhao, P., and Gopalkrishnan, V. (2013).
Confidence weighted mean reversion strategy for on-
line portfolio selection. ACM Transactions on Knowl-
edge Discovery from Data (TKDD, 7:1–38.
Li, B., Zhao, P., Hoi, S., and Gopalkrishnan, V. (2012).
Pamr: Passive aggressive mean reversion strategy for
portfolio selection. Machine learning, 87:221–258.
Markowitz, H. (1952). Portfolio selection. journal of fi-
nance.
Tan, G., Kelly, P., Kim, J., and Wartell, R. (1991). Com-
parison of camp receptor protein (crp) and a camp-
independent form of crp by raman spectroscopy and
dna binding. Biochemistry, 30:5076–5080.
Thrun, S., Saul, L., and Sch
¨
olkopf, B. (2004). Advances
in neural information processing systems 16. In Pro-
ceedings of the 2003 Conference, page 47–110, Lon-
don, England. The MIT Press.
Online Portfolio Selection of LQ45 Stocks Index with the Adaptive Online Moving Average Method
327