Improving Performance of the K-Means Algorithm with the Pillar

Technique for Determining Centroids

Mustaqim Sidebang

, Erna Budhiarti Nababan

and Sawaluddin

Master of Informatics Program, Universitas Sumatera Utara, Medan, Indonesia

Faculty of Computer Science and Information Technology, Universitas Sumatera Utara, Medan, Indonesia

Faculty of Mathematics and Natural Sciences, Universitas Sumatera Utara, Medan, Indonesia

Keywords:

K-Means Algorithm, Pillar Technique, Determining Centroids.

Abstract:

The K-Means algorithm is a popular clustering technique used in many applications, including machine learn-

ing, data mining, and image processing. Despite its popularity, the algorithm has several limitations, including

sensitivity to the initialization of centroid values and the quality of clustering. In this paper, we propose a

novel technique called the ”pillar technique” to improve the performance of the K-Means algorithm. The

pillar technique involves dividing the dataset into smaller sub-datasets, computing the centroids for each sub-

dataset, and then merging the centroids to obtain the ﬁnal cluster centroids. We compare the performance

of the K-Means algorithm with and without the pillar technique on several benchmark datasets. Our results

show that the pillar technique improves the quality of clustering and convergence rate of the algorithm while

reducing computational complexity. We also compare our proposed approach with other centroid initializa-

tion methods, including K-Means++, and demonstrate the superior performance of the pillar technique. Our

ﬁndings suggest that the pillar technique is an effective method to improve the performance of the K-Means

algorithm, especially in large-scale data clustering applications.

1 INTRODUCTION

Grouping large data in today’s era has been made eas-

ier with the presence of advanced technology that can

be learned in machine learning. Data grouping in ma-

chine learning is called clustering and categorized as

unsupervised learning, which can be understood that

the processed data does not have a pattern, making it

not easy to cluster in a simple way. In data cluster-

ing, there are several algorithms, such as: K-Means

Algorithm, KMedoids, Fuzzy C-Means, and Density-

Based Spatial Clustering of Application with Noise

(DBSCAN) (Xu and Tian, 2015). The most widely

used clustering algorithm and one of the oldest al-

gorithms is the K-Means algorithm. In general, the

K-Means algorithm is referred to as a partition-based

algorithm where all clusters depend on the centroid

and are clustered based on data closest to the centroid

(Primartha, 2021).

The K-Means algorithm is considered to have a

disadvantage because determining the initial centroid

value randomly can lead to better or worse results

and excessive iteration, as well as poor cluster quality

(Barakbah and Kiyoki, 2009a). Wang & Bai (2016)

suggested that K-Means is highly sensitive to ran-

dom centroid determination, which can lead to group-

ing errors, and proposed other techniques to eliminate

dependence on randomly chosen initial centroid val-

ues (Wang and Bai, 2016). Wang and Ren (2021)

also expressed their opinion in their paper that the

K-Means++ algorithm, which is a derivative and de-

velopment of K-Means, has problems with randomly

determining initial centroid values and outliers in data

(Wang and Ren, 2021).

A variety of techniques and supporting algorithms

have attracted the attention of many researchers in

an effort to improve performance and optimize the

best results in the K-Means algorithm. Barakbah &

Kiyoki’s (2009) research proposes an idea based on

the supporting pillars of a building that support the

roof to remain sturdy as a good idea for determining

the initial centroid in the K-Means algorithm, which is

considered a weakness of K-Means in uncertain con-

ditions. This inspiration is called the Pillar technique

(Barakbah and Kiyoki, 2009b). Subsequent research

by Barakbah & Kiyoki (2009) succeeded in optimiz-

ing performance by calculating the accumulated dis-

tance metric between each data point and all previous

Sidebang, M., Nababan, E. and Sawaluddin, .

Improving Performance of the K-Means Algorithm with the Pillar Technique for Determining Centroids.

DOI: 10.5220/0012441600003848

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Advanced Information Scientiﬁc Development (ICAISD 2023), pages 52-59

ISBN: 978-989-758-678-1

centroids and selecting the data point with the max-

imum distance as the new initial centroid. The ex-

periment involved eight benchmark datasets with ﬁve

validity measures and execution time. The results of

this experiment showed that the Pillar algorithm can

optimize the initial centroid selection and improve the

precision of K-Means on all datasets and most of its

validity measures (Barakbah and Kiyoki, 2009a).

The ability of the Pillar technique in determining

initial centroids which is one of the most common

problems due to its random nature attracts the atten-

tion of researchers in implementing it for the needs

of handling and learning unsupervised learning. Ex-

periments carried out may not necessarily have the

same results as the success of previous researchers,

so the author is interested in solving the problem in

this initialization by using the Pillar technique as the

proposed method. In this paper, we hope to improve

the performance of the K-Means algorithm on the

dataset to be processed (Retno et al., 2020) (Putra

et al., 2017).

2 LITERATURE REVIEW

2.1 Unsupervised Learning

The machine learning learning process that is un-

labeled and unsupervised, therefore, does not have

easily categorized data formation patterns, is also

called unsupervised learning. Unsupervised learning

aims to discover hidden patterns in data and is com-

monly used in solving clustering problems (Wahyono,

2020). Unsupervised learning is a category of ma-

chine learning in which the processed dataset is unla-

beled or does not have a predetermined output. There-

fore, it can also be referred to as a process of process-

ing data that is unlabeled and unsupervised. Unsuper-

vised learning can be analogized to a teacher grading

a student’s answers, but the correctness of the answer

depends on how the teacher understands the question

without an answer key. Thus, unsupervised learning

is considered more subjective than supervised learn-

ing. In cases where the dataset is unlabeled and the

implicit relationships need to be discovered, unsuper-

vised learning is very useful. The non-relationship

condition is usually called clustering. Some unsuper-

vised learning algorithms include K-Means, Hierar-

chical Clustering, DBSCAN, Fuzzy C-Means, Self-

Organizing Map, and others (Primartha, 2021).

2.2 Clustering

Clustering is a very important tool in research pro-

cesses for solving various problems in several ﬁelds

such as archaeology, psychiatry, engineering, and

medicine. Clusters consist of points that are similar

to each other but different from points in other clus-

ters (Abo-Elnaga and Nasr, 2022). Clustering is also

commonly used in various ﬁelds as a tool for analyz-

ing social networks, detecting crimes, and software

engineering, as it helps to identify the pattern of a

process in searching and classifying data that have

characteristics between one data and another, which is

also known as clustering (Putra et al., 2017). Cluster-

ing has the advantage of wide applicability in pattern

recognition, machine learning, image programming,

and statistics. The purpose is to partition a set of data

with similar patterns into different groups (Wang and

Bai, 2016). Clustering analysis is one of the most im-

portant problems in data processing. Identifying simi-

larity groups among data sets has been widely applied

in several applications. The general approach for de-

termining a cluster from a data set is to minimize the

objective function after the number of clusters is de-

termined a priori (Kume and Walker, 2021).

2.3 K-Means Algorithm

Clustering using K-Means is an approach to dividing

data into similar groups and creating clusters. The

advantage of using the K-Means algorithm is that

it can cluster massive data quickly and efﬁciently.

The initial step of the K-Means algorithm is to de-

termine the initial centroids randomly (Abo-Elnaga

and Nasr, 2022). The K-Means algorithm identiﬁes

clusters by minimizing the clustering error (Wang and

Bai, 2016). With high simplicity, practicality, and ef-

ﬁciency, the K-Means algorithm has been success-

fully applied in various ﬁelds and applications, in-

cluding document clustering, market segmentation,

image segmentation, and feature learning. Generally,

clustering algorithms fall into two categories: hierar-

chical clustering and partition clustering (Liu et al.,

2020).

The K-Means algorithm is capable of clustering

large data, even multi-view data from different ta-

bles or datasets. In clustering data simultaneously on

each table to become multi-view. Clustering a large

amount of data is known as a technique for centroid-

based clustering by representing the number of clus-

ters and then obtaining good groups depending on

the ﬁnal constant value of the centroid (Retno et al.,

2020).

The clustering process in the K-Means algorithm

Improving Performance of the K-Means Algorithm with the Pillar Technique for Determining Centroids

uses the Euclidean distance as a measure of similarity

between data objects. The process of the K-Means

algorithm is as follows:

1. Preprocessing

Performing preprocessing steps beforehand is

necessary before applying the K-Means algorithm

to ensure that the processed data yields maximum

results. Preprocessing steps include data selec-

tion, data transformation, normalization, and oth-

ers, and the steps used depend on the requirements

and rules of the algorithm being used. Normaliza-

tion used in preprocessing is done using the Min-

Max method. The MinMax method is a normal-

ization method that equalizes the range of values

between large and small values. In data classi-

ﬁcation, data with large values will produce de-

viating results compared to data with small val-

ues. To adjust the measured values to the same

scale, all data will be normalized using the Min-

Max method. The MinMax method process can

be seen in equation 1 as follows:

′

x − xmin

xmax − xmin

(1)

2. Determining the number of clusters

Determining the number of clusters (K value) and

cluster centers or initial centroids. The number

of clusters is usually determined based on the de-

sired classes or groups according to the needs of

the processed data segment. In the K-Means al-

gorithm, the initial centroid value is determined

randomly in each cluster to start calculating its

Euclidean distance. Determining the K value in

the dataset being processed can be done using the

Elbow method. The Elbow method is a method

for ﬁnding the K value in clustering by determin-

ing the Within Sum Square Error (WSSE) value

(Zeng et al., 2019). The process of ﬁnding the

WSSE value can be seen in the following equa-

tion 2:

∑

distance(P

, C

)

(2)

3. Calculating the Euclidean distance

Performing the process of calculating the Eu-

clidean distance and taking the smallest value

as the closest distance to the cluster center. The

formula for calculating the Euclidean distance

can be seen in equation 3

d(x, C

) =

∑

= 1(x

− C

) (3)

4. Calculating the average value of data objects

Calculating the average value of data objects in

each cluster as the new centroid value. The new

centroid value will replace the initial centroid

value in the next calculation of Euclidean dis-

tance.

5. Iterating

Iterating from step two and three until reaching a

constant value in the iteration

As a measure of algorithm quality, Sum of Square Er-

ror (SSE) testing is performed to determine the qual-

ity of the clustering results. The formula for calculat-

ing SSE can be seen in equation 4.

SSE =

∑

= 1(x

− C

)

(4)

The result of the calculation of SSE approaching zero

indicates the good quality of the clustering. Con-

versely, if it produces a large value, it indicates the

poor quality of the clustering performed (Liu et al.,

2020). The sensitivity of clustering results due to the

random initial centroids has led many researchers to

study this issue, which may lead to suboptimal re-

sults. Research in this area has produced new meth-

ods, algorithms, or techniques for determining initial

centroids, such as Pillar, Range Order Centroid, Dy-

namic Artiﬁcial Chromosome Genetic Algorithm, K-

Means++, Centronit, Na

ıve Sharding, Principal Com-

ponent Analysis (PCA). This study improves the per-

formance of the K-Means algorithm by using the Pil-

lar technique.

2.4 Pillar Technique

K-Means is considered to have limitations due to its

inability to determine the appropriate number of clus-

ters, random centroid values, and high dependence on

the initial selection of cluster centers (Barakbah and

Kiyoki, 2009b) (Seputra and Wijaya, 2020). The Pil-

lar technique considers the placement pillars that must

be placed as far apart from each other as possible to

withstand the pressure distribution of the roof. Barak-

bah & Kiyoki (2009) stated that the Pillar technique

can optimize the K-Means algorithm for image seg-

mentation clustering in terms of precision and com-

putational time. The Pillar technique determines the

initial centroid position by accumulating the farthest

distance among them in the data distribution (Barak-

bah and Kiyoki, 2009a) (Wahyudin et al., 2016).

Each pillar is positioned according to the speci-

ﬁed number of k and adjusted to the angle or series

of data to be processed. This illustration aims to pro-

duce good centroids because the balance of the cen-

troid position is like pillars that support a building,

which remains sturdy.

The process of the Pillar technique in determining

the initial centroid is as follows:

1. First, determine the number of data (n) and the

number of clusters (k).

ICAISD 2023 - International Conference on Advanced Information Scientiﬁc Development

2. Calculate the median middle value (m) in the

dataset.

3. Determine the value (x) by calculating the dis-

tance value of the data object with the median (m).

4. Determine the data object value (y) by calculat-

ing the maximum value (x) as a candidate centroid

(DM).

5. Recalculate the value with the median (m) on the

candidate centroid (DM).

6. Iterate from the third to the ﬁfth process until

reaching the speciﬁed number of clusters (i=k).

7. Obtain the centroid value and perform the cluster-

ing process in the K-Means algorithm.

The result of the above steps is the determination

of the initial centroid in K-Means. The next step is

to continue with the process of calculating Euclidean

distance and generating the next centroid until it pro-

duces a constant value (Barakbah and Kiyoki, 2009b).

3 METHOD

3.1 Data Sources

The Data sources in this study was obtained from the

ﬁnancial institution Baitul Mal wa Tamwil (BMT) in

the Batang Kuis district of Deli Serdang Regency,

North Sumatra. The data consists of customer pro-

ﬁles and transactions taken in January 2023. The pre-

pared data to be processed is in the form of a .csv ﬁle

format that will be run on a program designed using

the Python programming language. The details of the

BMT Batang Kuis customer dataset.

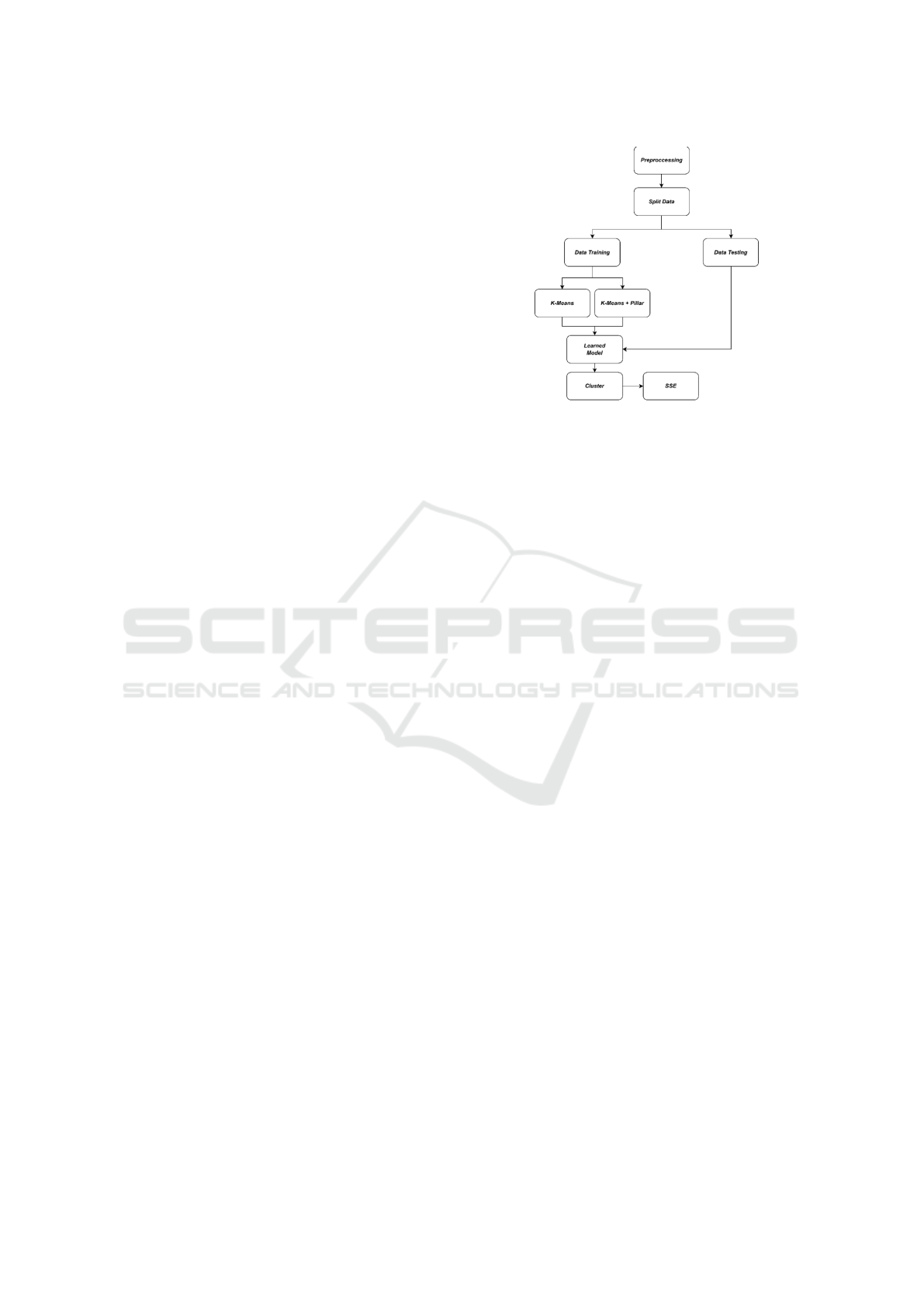
3.2 General Architecture

The process of implementing the K-Means algorithm

improved with the Pillar technique in determining the

initial centroid values involves several stages, start-

ing from preprocessing, K-Means clustering with the

Pillar technique, then testing the results with Sum

of Square Error (SSE), and a comparison experiment

will be conducted with K-Means that determines ini-

tial centroid values randomly to determine the per-

formance improvement with the proposed Pillar tech-

nique. The workﬂow of this method can be seen in

the following diagram:

3.3 Preprocessing

1. Data Selection

In the preprocessing stage, the attributes used

Figure 1: General architecture.

are occupation, age, major, and account balance.

These four attributes are selected based on their

good contribution variance to be processed due

to data correlation that only has 2 variants (1 and

0) such as gender, active/inactive, ownership, and

major.

2. Data Transformation

Numeric data is required to be processed by the

K-Means algorithm, in the available dataset non-

numeric attributes will be transformed into num-

bers. In this study, attributes such as teacher, em-

ployee, student, others will be transformed into

the order of 0,1,2,3 for the occupation attribute.

3. Normalization

Data normalization can also be referred to as nor-

malization, where normalization can be calculated

using the MinMax Normalization method. To

avoid outlier data in the K-Means Algorithm pro-

cess, the normalization process will be carried out

using the MinMax formula as in equation 1.

3.4 Spliting Data

Based on the main architecture in Figure 3.1, the data

will be split into two parts for training and testing

data. This process will use Random Sampling where

most of the data will be used as a sample for training

data in the algorithm to obtain a model, and a small

part of it will be used as testing data after the machine

learns from the previous training data, which is called

a model. The training data to be used is 80%, and 20%

is testing data. The training data and testing data.

Improving Performance of the K-Means Algorithm with the Pillar Technique for Determining Centroids

3.5 Determination of the Value of K

Using the Elbow Method

Determining the number of clusters from 3531 rows

of customer data in BMT Batang Kuis. The number

of clusters can be determined with a minimum of 2

clusters or less than the total rows of data. In this

study, the process of determining the number of clus-

ters used the Elbow method by knowing the Within

Sum Square Error (WSSE) on the comparison of clus-

ter 1 to cluster 20. The process of calculating the El-

bow method WSSE uses equation 2 and produces an

SSE graph in the form of an elbow as shown in Figure

Figure 2: Elbow chart.

The elbow-shaped line is a good point in the El-

bow method for determining the number of clusters,

and from Figure 3.2, it shows that the 3rd cluster is

the best point.

3.6 K-Means Clustering

Perform clustering using the K-Means Algorithm on

the training data using a value of K = 3 based on Fig-

ure 2. This step can be carried out through a process

similar to the general architecture of the K-Means al-

gorithm as follows:

Figure 3: K-Means algorithm.

Finding the closest value in each data by calculat-

ing the Euclidean distance using equation 2.1. The re-

sult of the Euclidean distance calculation will choose

the largest value as a candidate for the value of K, and

the average value of the candidate will be taken as the

next centroid value. Then, repeat the Euclidean dis-

tance calculation until the K value is constant. This

process can be done using the Python programming

language and will produce cluster data in the follow-

ing table 1:

Table 1: The result of K-Means clustering.

0 1 2 3 cluster

2232 0.242424 0.261128 0.666667 0.000005 0

1475 0.272727 0.338279 0.000000 0.000000 1

1235 0.242424 0.839763 0.666667 0.000000 2

440 0.196970 0.910979 0.666667 0.000370 2

2095 0.196970 0.035608 0.666667 0.000000 0

The K-Means clustering process shows the cen-

troid value of the black point between the blue and

yellow clusters as the resulting cluster. The visualiza-

tion data of transaction and age attributes can be seen

in the following Figure 4.

Figure 4: K-Means clustering.

3.7 K-Means Clustering with Pillar

Technique

The K-Means algorithm with the Pillar technique ini-

tially takes preprocessed data to avoid poor iteration

caused by existing data noise. Then, it goes through

the initial centroid value determination stage with the

Pillar technique, by ﬁnding the furthest value between

the data centers and determining the desired number

of clusters. Then, it calculates the Euclidean distance

and iterates until reaching a constant value or the cen-

troid value no longer changes

The general architecture using the Pillar technique

as the initial centroid determiner in the K-Means al-

gorithm can be seen in Figure 5.

The Pillar technique process located on the left

side of Figure 3.11 is a replacement for searching for

randomly determined initial centroid values. There-

fore, the next K-Means process is the same as in the

discussion process except for the initial centroid val-

ues.

ICAISD 2023 - International Conference on Advanced Information Scientiﬁc Development

Figure 5: K-Means algorithm with Pillar technique.

1. Spliting Data

2. Determining Initial Centroids Using the Pillar

Technique

The process of determining initial centroids based

on the ﬂowchart in Figure 6 on the left-hand side

indicates the process of sorting values from the

smallest to the largest to obtain the middle value

by ﬁnding the median value in the data row. The

resulting middle value is based on the length of

the row and the predetermined number of clusters,

which is three clusters

Table 2: Determining initial centroids using pillar tech-

nique.

0 1 2 3

706 0.666667 0.227273 0.0 0.026706

1412 0.000000 0.272727 0.0 0.896142

2118 0.666667 0.196970 0.0 0.531157

3. K-Means clustering Performing K-Means cluster-

ing process using initial centroid values in table

3.11. The clustering process in ﬁnding the Eu-

clidean values stops when the centroid values be-

come constant or no longer change, resulting in

the values shown in table 3:

Table 3: K-Means clustering with pillar technique.

0 1 2 3 index centroid

2395 0.666667 0.196970 0.000000 0.391691 1

932 0.666667 0.257576 0.000000 0.189911 1

3308 0.666667 0.212121 0.002270 0.578635 3

960 0.666667 0.257576 0.000000 0.181009 1

2393 0.666667 0.242424 0.000097 0.169139 1

The visualization results of K-Means clustering

with the Pillar technique can be seen in the fol-

lowing Figure 6:

Figure 6: K-Means Clustering with pillar technique.

4 SIMULATION AND RESULTS

4.1 K-Means Clustering Results with

Random Centroid Determining

The next clustering process uses the model estab-

lished in the discussion of 3.2.5 where the data used

is testing data with 4 variables of age, occupation,

balance, and traction attributes. Normalization using

MinMax and sorted.

Determining the number of clusters to be 3 based

on the Elbow method. The clustering results on test-

ing data can be seen in the following table 4:

Table 4: K-Means clustering.

0 1 2 3 cluster

1332 0.378788 0.317507 0.000000 0.002601 2

2815 0.196970 0.528190 0.666667 0.000003 0

2434 0.212121 0.317507 0.666667 0.000096 1

2843 0.212121 0.801187 0.666667 0.000620 0

2366 0.181818 0.967359 0.666667 0.000000 0

Producing cluster visualization with different col-

ors indicating each group that has a centroid value,

represented by a green point as seen in the following

Figure 7:

Figure 7: K-Means clustering result.

Improving Performance of the K-Means Algorithm with the Pillar Technique for Determining Centroids

4.2 K-Means Clustering Results with

Pillar Technique

The next clustering process is using the Pillar tech-

nique with the established model discussed, where the

data used is testing data with 4 variables of age, oc-

cupation, balance, and traction attributes. Normaliza-

tion using MinMax. Determining the initial centroids

using the Pillar technique, the selected data as initial

centroids can be seen in the following table 5:

Table 5: Determining the initial centroid with pillar tech-

nique.

0 1 2 3

1017 0.666667 0.212121 0.000000 0.985163

379 0.666667 0.212121 0.000000 0.486647

1001 0.666667 0.212121 0.007181 0.872404

After obtaining the unchanged centroid values, the

clustering process will result in clustering data on the

testing data which can be seen in the following table

Table 6: K-Means clustering with pillar technique result.

0 1 2 3 index centroid

2373 0.666667 0.242424 0.000602 0.759644 1

1247 0.666667 0.257576 0.000000 0.468843 2

1084 0.666667 0.257576 0.000000 0.810089 1

3076 0.666667 0.227273 0.000068 0.513353 2

2610 0.666667 0.257576 0.000060 0.100890 2

Generating a cluster visualization with different

colors indicating each cluster group, where each

group has its own centroid point represented by a

green dot, can be seen in Figure 8 as follows:

Figure 8: K-Means clustering with pillar technique result.

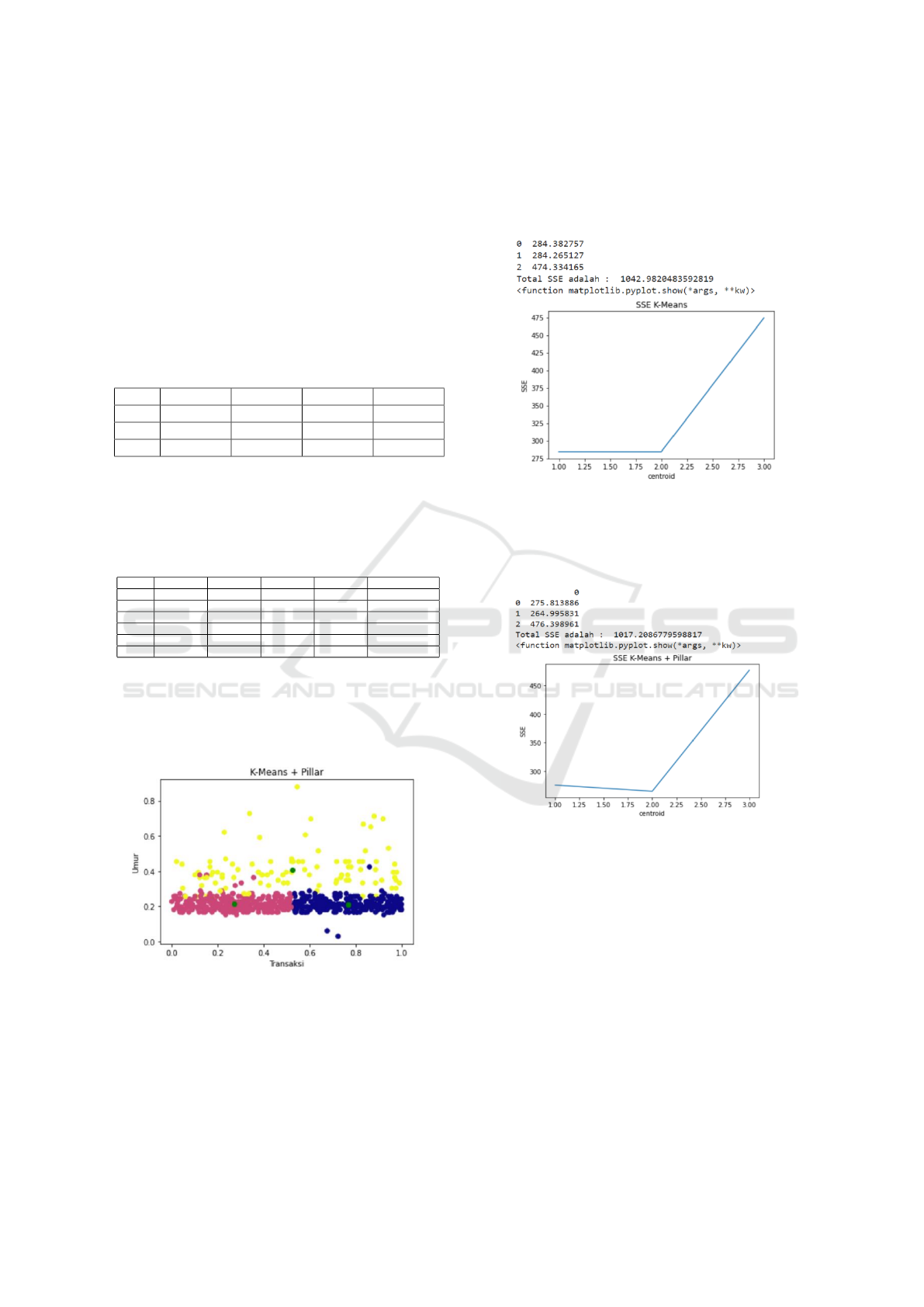
4.3 Sum of Square Error Testing

Citing all the process and result data from K-Means

Algorithm with randomly determined initial centroids

and K-Means with Pillar technique, testing is per-

formed with SSE. The data taken will be inserted into

the SSE calculation formula as in equation 2. The to-

tal SSE between K-Means with random centroids on

testing data resulted in a total of 1042.98 and can be

seen in the following ﬁgure 9:

Figure 9: SSE K-Means clustering.

The total SSE between K-Means with pillar tech-

nique on testing data resulted in a total of 1017.208

and can be seen in the following ﬁgure 10:

Figure 10: SSE K-Means clustering with pillar technique.

The comparison between the two, K-Means:

1042.98 ¿ K-Means + Pillar: 1017.208, where the

smallest total SSE is the best result in clustering.

5 CONCLUSION

The proposed research method obtained several con-

clusions based on the test results, including the fol-

lowing:

1. Based on the testing data used, better cluster re-

sults were obtained in K-Means clustering with

the Pillar technique compared to K-Means with

randomly selected initial centroids.

ICAISD 2023 - International Conference on Advanced Information Scientiﬁc Development

2. Based on the Sum Square Error (SSE) test, K-

Means with the Pillar technique increased by 1%

compared to K-Means with randomly selected ini-

tial centroids.

3. Changes in each experiment resulted in almost the

same value in clustering using K-Means with the

Pillar technique compared to K-Means with ran-

domly selected initial centroids, which produced

inconsistent clusters in each experiment.

REFERENCES

Abo-Elnaga, Y. and Nasr, S. (2022). K-means cluster in-

teractive algorithm based evolutionary approach for

solving bilevel multi-objective programming prob-

lems. AEJ - Alexandria Engineering Journal.

Barakbah, A. and Kiyoki, Y. (2009a). A New Approach for

Image Segmentation Using Pillar-Kmeans Algorithm.

World Academy of Science, Engineering and Tech-

nology.

Barakbah, A. and Kiyoki, Y. (2009b). A pillar algorithm

for k-means optimization by distance maximization

for initial centroid desgnation. united States.

Kume, A. and Walker, S. (2021). The utility of clusters and

a hungarian clustering algorithm. Plos One.

Liu, Y., Ma, S., and Du, X. (2020). A novel effective dis-

tance measure and a relevant algorithm for optimizing

the initial cluster centroids of k-means. IEEE Access.

Primartha, R. (2021). Algoritma Machine Learning. Infor-

matika Bandung, Bandung.

Putra, A., Zarlis, M., and Nababan, E. (2017). Performance

analysis of combined methods of genetic algorithm

and k- means clustering in determining the value of

centroid. In International Conference on Information

and Communication Technology.

Retno, S., Nababan, E., and Efendi, S. (2020). Initial cen-

troid of k-means algorithm using purity to enhance the

clustering results. International Journal of Trend in

Research and Development.

Seputra, K. and Wijaya, I. (2020). Penerapan algoritma

pillar untuk inisialisasi titik pusat k-means klaster di-

namis. Jurnal Teknologi Informasi dan Ilmu Komputer

(JTIIK.

Wahyono, Y. (2020). Machine Learning Konsep dan Imple-

mentasi. Gava Media, yogyakarta, 1 edition.

Wahyudin, I., Djatna, T., and Kusuma, W. (2016). Clus-

ter analysis for sme risk analysis documents based on

pillar k- means. Telkomnika.

Wang, X. and Bai, Y. (2016). A modiﬁed min max k-means

algorithm based on pso. Computational Intellegence

and Neuroscience.

Wang, Y. and Ren, J. (2021). Taxi passenger hot spot min-

ing based on a reﬁned k-means++ algorithm. IEEE

Access.

Xu, D. and Tian, X. (2015). A comprehensive survey of

clustering algorithms. Annals of Data Science.

Zeng, J., Wang, J., Guo, L., Fan, G., Zhang, K., and Gui, G.

(2019). Cell scene division and visualization based on

autoencoder and k-means algorithm. IEEE Access.

Improving Performance of the K-Means Algorithm with the Pillar Technique for Determining Centroids