Study on Wire-Controlled Differential Steering of Hub-Driven

Four-Wheel Electric Vehicle

Jin Chen, Fenggang Han and Yao Lu

Xiamen University of Technology, Xiamen, China

Keywords: Hub-Driven, Electronic Differential, Wire-Controlled Steering, Motor Rotational Speed, Ackermann

Steering Model.

Abstract: In order to research the differential steering control method of the hub-driven electric vehicle, an

Ackermann differential steering model applicable to low-speed driving of four-wheel electric vehicles is

established. A permanent magnet synchronous motor model is established using a double closed-loop

control of rotational speed loop and current loop combined with SVPWM algorithm. At the same time, four

motor controllers are used to control the rotational speed of four driving motors respectively, achieving

differential steering. The differential steering control system is built and simulated in the

MATLAB/Simulink environment. The simulation results show that the adopted Ackermann differential

steering control system can meet the requirements of low-speed differential steering of four-wheel electric

vehicles. Meanwhile, the PI rotational speed control system can achieve adaptive tracking of the given

speed, effectively improving the safety and stability of the vehicle during rotational speed change.

INTRODUCTION

In recent years, hub-driven electric vehicles have

received widespread attention. The technological

advantage of hub-driven lies in the elimination of

components such as mechanical differential

clutches, transmissions, and drive shafts, which

improves the space utilization rate and transmission

efficiency, as well as the layout structure, chassis

integrated control, and execution flexibility (Li- Du,

Peng).

In the research of hub-driven electric vehicles,

the steering system is one of the research hotspots.

One of the problems that need to be solved for

electric vehicles driven by hub motors is the

synchronization and coordination of each wheel,

namely the differential steering problem (L. Jian-

Termous). The main approach to the solution is to

coordinate the rotational speed of each driving motor

through the vehicle controller, or to realize it

through a special motor (Yuan, 2022). This paper,

based on the low-speed characteristics of four-wheel

electric vehicles during steering, analyzes the

vehicle steering dynamics, establishes the

Ackermann differential steering model, and analyzes

the mathematical model of the vehicle drive motor

to construct a double closed-loop control system of

the drive motor. The differential model is combined

with the motor system, and the motor rotational

speed is coordinated and controlled, and it is verified

and analyzed on the Simulink simulation platform.

DIFFERENTIAL STEERING

MODEL

2.1 Design of Differential Steering

Model

For low-speed vehicles, the differential strategy

adopted is the electronic differential analysis model

proposed by Ackermann-Jeantand. The assumptions

of this model are: (1) the vehicle body is rigid; (2)

the wheels are pure rolling motion, and the tire slip

and slide running state are not considered; (3) the

lateral deformation and lateral force of the tire are

proportional, and the tire material and structural

nonlinearity and the impact of the centrifugal force

causing changes in the tire’s vertical load are not

considered. The designed differential steering model

is as shown in Fig. 1.

248

Chen, J., Han, F. and Lu, Y.

Study on Wire-Controlled Differential Steering of Hub-Driven Four- Wheel Electric Vehicle.

DOI: 10.5220/0012280200003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 248-252

ISBN: 978-989-758-677-4

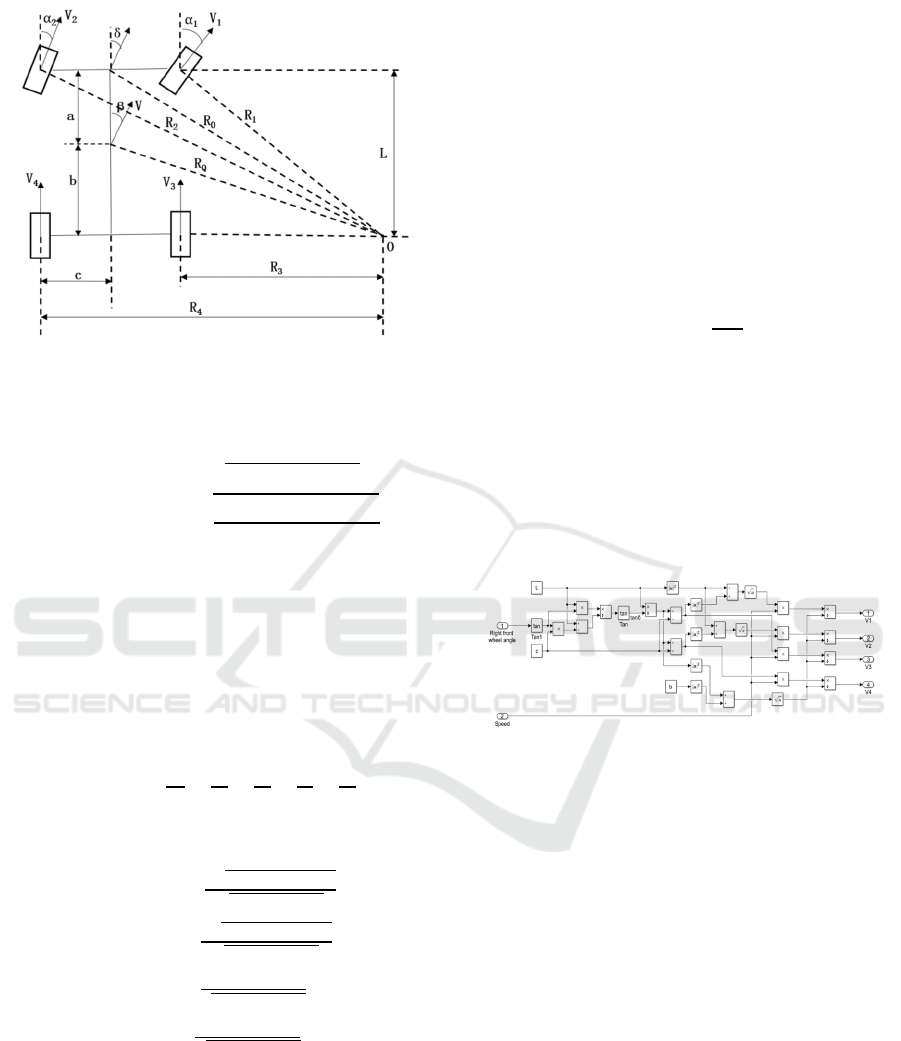
Figure 1: Differential Steering Model.

According to the Ackermann-Jeantand steering

model in Fig. 1, taking a right turn as an example,

we know from geometric relationships:

𝑅







𝑏







𝐿 tan 𝛿

⁄ 



(1)

𝑅







𝐿







𝐿 tan 𝛿

⁄

𝑐





(2)

𝑅







𝐿







𝐿 tan 𝛿

⁄

𝑐





(3)

𝑅



𝐿tan 𝛿

⁄

𝑐 (4)

𝑅



𝐿tan 𝛿

⁄

𝑐 (5)

From which we can get:

tan 𝛼



𝐿/𝐿 tan 𝛿

⁄

𝑐 (6)

Then we have:

tan 𝛿𝐿tan 𝛼





𝐿𝑐tan 𝛼



⁄

(7)

According to the Instantaneous Center of Rotation

(ICR) theorem, we know:















































(8)

The longitudinal speeds of each wheel can be

obtained as:

𝑉



















⁄



















⁄ 



(9)

𝑉



















⁄



















⁄ 



(10)

𝑉











⁄

















⁄ 



(11)

𝑉











⁄

















⁄ 



(12)

Where V is the speed of the omnidirectional

electric chassis centroid, V

are the longitudinal

motion speeds of each wheel respectively, L is the

wheelbase from the front axle and rear axle, c is half

of the track, a and b are the distances from the front

axle and rear axle to the vehicle centroid

respectively, R

are the steering radii of each

wheel around the rotation center O respectively, R

is the steering radius of the centroid around the

rotation center O, α

and α

are the steering angles of

the right front wheel and left front wheel

respectively, and δ is the vehicle’s Ackermann

steering angle.

2.2 Differential Steering Simulation

Model

The wheel speed is generally calculated from the

wheel rotational speed collected by the speed sensor.

The conversion formula from wheel speed to wheel

rotational speed is:

𝑣





(13)

Where v is the wheel speed, n is the wheel

rotational speed, and r is the radius of the tire.

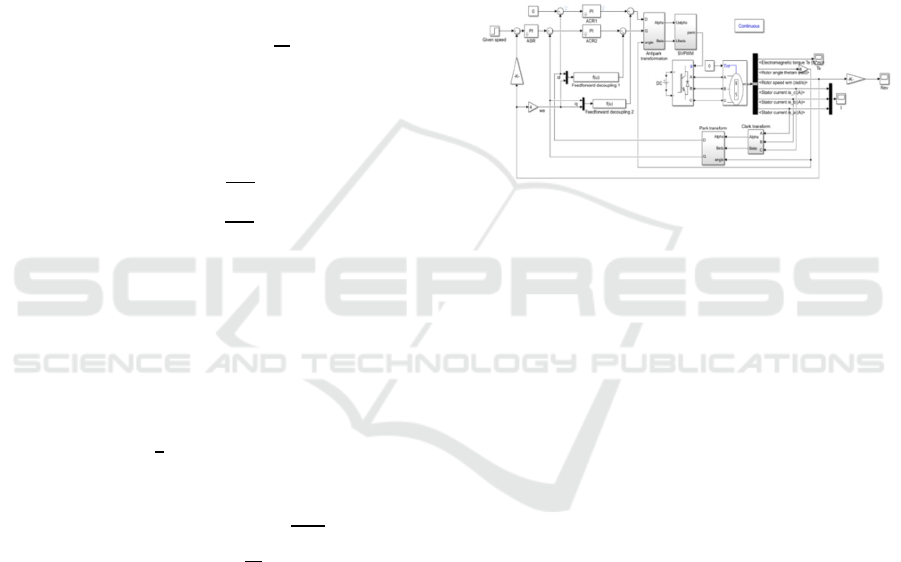
According to the established mathematical

model of the electric vehicle’s differential steering, a

differential steering system simulation model is built

in the MATLAB/Simulink environment. As shown

in Fig. 2, the vehicle speed and the right front wheel

steering angle serve as inputs, with the speeds of all

four wheels as the output.

Figure 2: Ackermann Steering System Simulation Model.

PMSM MODEL BASED ON PI

ROTATIONAL SPEED

CONTROL

Due to the excellent startup performance of the

Permanent Magnet Synchronous Motor (PMSM),

along with its good reliability, high security, and

high efficiency during rated operation, it can well

meet the requirements of vehicle drive motors. In

addition, such motors also have features such as

light weight, small size, and low rotor heating rate.

Therefore, PMSM is selected as the subject for

control analysis.

3.1 PMSM Mathematical Model

Since the stator induced electromotive force of the

PMSM is a sine wave, the use of coordinate

Study on Wire-Controlled Differential Steering of Hub-Driven Four- Wheel Electric Vehicle

249

transformation theory is a relatively effective

analysis method. The motor in the actual operation

process will inevitably be affected by the actual

environment, causing changes in the motor’s

resistance and inductance. To simplify the analysis

process, the following assumptions are made: (1)

The motor air gap magnetic field is uniform and

sinusoidal, the winding resistance and inductance

values are constant; (2) Saturation effects of the

magnetic circuit are ignored; (3) Magnetic hysteresis

and eddy current losses are not considered; (4) The

influence of the stator slots is neglected.

The three-phase voltage equation of the PMSM

model under the three-phase stator ABC coordinate

system is:



𝑢



𝑢



𝑢





𝑟 00

0 𝑟 0

00𝑟



𝑖



𝑖



𝑖











𝜓



𝜓



𝜓



 (14)

The mathematical model of the Permanent

Magnet Synchronous Motor established under the

synchronous rotating coordinate system is:



𝑢



𝑟𝑖











𝜔𝜓



𝑢



𝑟𝑖











𝜔𝜓



(15)

When the motor’s salient pole effect is not

considered, the magnetic linkage equation is:



𝜓



𝐿



𝑖



𝜓



𝜓



𝐿



𝑖



(16)

Using the principle of equal amplitude

transformation, the electromagnetic torque of the

Permanent Magnet Synchronous Motor is obtained:

𝑇









𝑛



𝜓



𝑖



𝐿



𝐿



𝑖



𝑖



 (17)

The mechanical motion equation of the motor is:



𝑇



𝑇



𝐵𝜔



𝐽







𝜔











(18)

Where u

and u

are the voltages of the d and q

axes; id and i

are the currents of the d and q axes; n

is the number of pole pairs; ψ

and ψ

are the direct-

axis and quadrature-axis components of the stator

magnetic linkage; ψ

is the magnetic linkage; L

and

are the direct-axis and quadrature-axis

inductances; r is the phase resistance of the stator; T

is the load torque of the motor; ω

and ω are the

mechanical and electrical angular speeds of the

motor; B and J are the damping coefficient and

moment of inertia.

3.2 Motor Simulation Model

According to the PMSM mathematical model, a

motor control system is established using the

rotational speed loop PI controller and current loop

PI controller dual-loop control combined with the

Space Vector Pulse Width Modulation (SVPWM)

algorithm. Fig. 3 is the overall structure diagram of

the motor control system, mainly including the

rotational speed control module, current control

module, voltage inverter module, SVPWM

algorithm module, and so on. A motor system

simulation model is built in the MATLAB/Simulink

environment.

Figure 3: Motor Simulation Model.

DIFFERENTIAL CONTROL

METHOD BASED ON MOTOR

ROTATIONAL SPEED

According to the differential model, motor model,

and speed- rotational speed conversion model, a

differential steering control system is established.

The collected vehicle speed and steering angle are

used as variable inputs to the differential steering

model. Through the model calculation, the wheel

speeds of the four wheels are obtained and converted

into desired rotational speed via the speed-rotational

speed conversion model. Then we have to calculate

difference between the desired speed and the actual

rotational speed of the motor and then input the

value to the PI controller to control the operation of

each hub motor and drive the vehicle to steer. The

schematic diagram of the differential steering system

is shown in Fig. 4.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

250

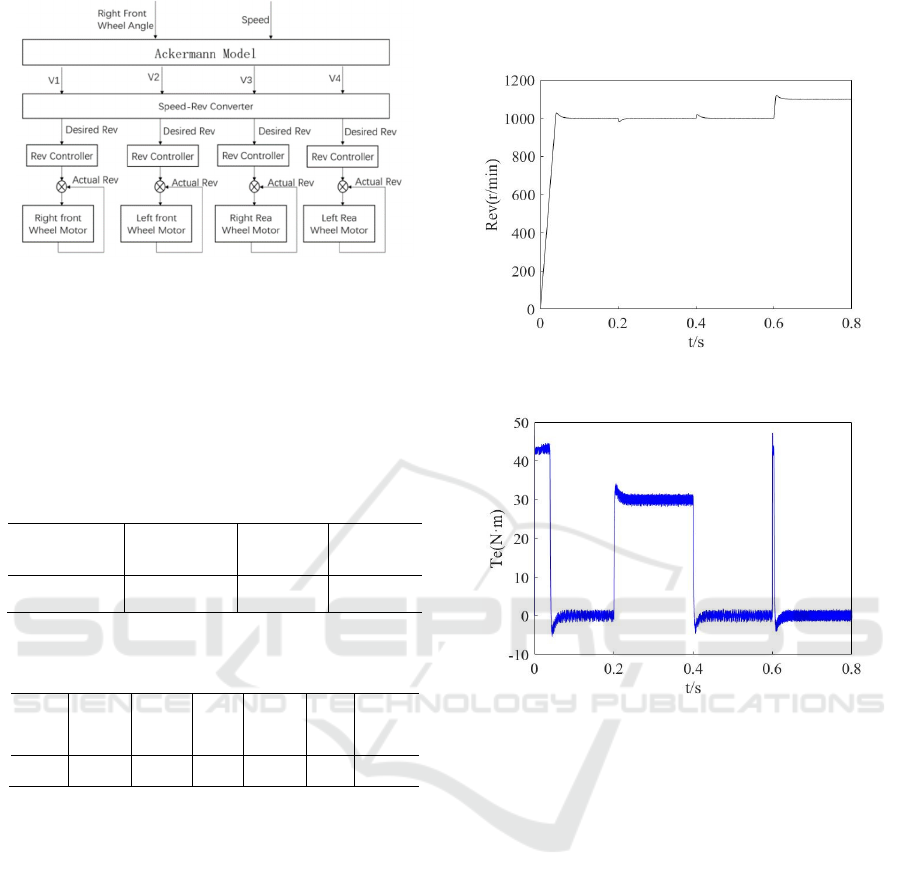
Figure 4: Differential Steering Control System.

SIMULATION RESULTS

ANALYSIS

The design parameters of the sample vehicle are as

shown in Table 1.

Table 1: Three Scheme comparing.

Parameter Name Wheelbase(m)

Tread

width(m)

Tire

radius(m)

Parameter Value 2.35 1.52 0.6

Motor parameters are as shown in Table 2.

Table 2: Three Scheme comparing.

Parameter

Name

Inductance

（H）

Resistance

（Ω）

Rotor

Flux

Linkage

（Wb）

Moment

of Inertia

（kg·m

）

Number

of Pole

Pairs

Damping

Coefficient

（N·m·s）

Parameter

Value

0.000835 0.11 0.1119 0.0016 4 0.0002024

5.1 Motor Performance Test

To verify whether the hub motor parameters can

meet various performance requirements, the

established motor system simulation model is tested

as follows: the initial load torque is set to zero, the

motor is started without load, the load is suddenly

added at 0.2s, and the load is removed at 0.4s; the

initial rotational speed is set to n=1000r/min, and at

0.6s, it is accelerated to n=1100r/min.

Simulation results show that when the motor

gradually accelerates from zero to the reference

rotational speed of 1000r/min, although there is an

overshoot, the response speed of the motor system is

fast, and the stability is relatively strong. It is evident

that the use of PI control rotational speed has strong

anti-interference capability and rapid adjustment

speed. Fig. 5 shows the rotational speed change

curve, Fig. 6 shows the electromagnetic torque

change curve.

Figure 5: Rotational Speed Change Curve.

Figure 6: Electromagnetic Torque Change Curve.

5.2 Differential Performance Test

Taking the right front wheel as an example, the

steering angle is set to 10°, the vehicle speed

v=10m/s, and a comparative test is carried out with

and without PI control. The simulation result is

shown in Fig. 7. The result shows that the right front

wheel with PI control has reduced the overshoot,

effectively weakening the overshoot phenomenon.

When a disturbance is added at t=0.3s, the right front

wheel’s rotational speed response time is short with

PI control, significantly enhancing the robustness of

the differential steering control system.

Study on Wire-Controlled Differential Steering of Hub-Driven Four- Wheel Electric Vehicle

251

Figure 7: Comparison of control curves for the right front

wheel.

Given a lower driving speed of v=15m/s, the right

front wheel’s steering angle changes uniformly from

[0, 50]. The wheel rotational speeds are shown in

Fig. 8. Through simulation analysis, when the

vehicle is turning, the rotational speed of the outer

wheels is higher than the inner wheels, which is

consistent with the actual situation, verifying the

correctness of the differential steering control

system. As the steering angle changes continuously,

the vehicle controls the hub motors of each wheel to

achieve differential steering through the differential

steering system and always maintains the condition

that the rotational speed of the outer wheel is higher

than the inner wheel, verifying the feasibility of the

differential steering system controlling the vehicle’s

steering movement.

Figure 8: Curve of speed change of each wheel.

CONCLUSION

Hub-driven electric vehicles have shown many

advantages in economy and vehicle control and are

one of the future development directions of cars.

Differential steering technology is one of its

essential performance indicators, and the quality of

the differential steering system affects the stability

and smoothness of vehicle travel. Therefore,

continuous exploration of differential steering is

essential.

This paper takes the hub-driven four-wheel

electric vehicle as the research object, establishes a

differential steering control system suitable for low-

speed steering, and verifies and analyzes this system

in the Simulink simulation platform. The results

show that the constructed permanent magnet

synchronous motor system has strong robustness.

The established steering control system can fully

meet the differential requirements, enhancing the

stability and security of the vehicle when steering.

This system is simple and practical and has some

reference value for future research on differential

steering systems.

REFERENCES

X. Li and R. Wang, “The future trends of in-wheel motors

for electric vehicles,” 2011 International Conference

on Consumer Electronics, Communications and

Networks (CECNet), Xianning, China, 2011, pp. 5390-

5393 https://doi.org/10.1109/CECNET.2011.5768782

Khan, Muhammad Arshad, Aftab, Muhammad Faisal,

Ahmed, Ejaz, et al. Robust Differential Steering

Control System for an Independent Four Wheel Drive

Electric Vehicle. International Journal of Automotive

Technology, 2019,20(1):87-97 https://doi.org/10.1007

/s12239-019-0008-9

Du, Peng, Ma, Zhongmin, Chen, Hao, et al. Speed-

adaptive motion control algorithm for differential

steering vehicle. Proceedings of the Institution of

Mechanical Engineers, Part D. Journal of Automobile

Engineering,2021,235(2/3):672-685 https://doi.org/10.

1177/0954407020950588

L. Jian, “Research Status and Development Prospect of

Electric Vehicles Based on Hub Motor,” 2018 China

International Conference on Electricity Distribution

(CICED), Tianjin, China, 2018, pp. 126-129

https://doi.org/10.1109/CICED.2018.8592598

Termous, Hussein, Shraim, Hassan, Talj, Reine, et al.

Coordinated control strategies for active steering,

differential braking and active suspension for vehicle

stability, handling and safety improvement. Vehicle

System Dynamics: International Journal of Vehicle

Mechanics and Mobility,2019,57(10/12):1494-1529

https://doi.org/10.1080/00423114.2018.1521001

W. Yuan and L. Xun, “Research on differential steering

control of an articulated steering vehicle via fuzzy-PID

control,” 2022 IEEE 4th International Conference on

Power, Intelligent Computing and Systems (ICPICS),

Shenyang, China, 2022, pp. 867-872 https://doi.org/

10.1109/ICPICS55264.2022.9873569

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

252