Multi-Coil Electromagnetic Field Calculation with Two Methods and

Software Implementation

Xiangyu Cheng

1,2

and Yan Zhang

3,*

The 38th Research Institute of China Electronics Technology Group Corporation, Hefei, China

Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei, China

Anhui Technical College of Water Resources and Hydroelectric Power, Hefei, China

Keywords: Electromagnetic Field, High Precision Computation, Software Development.

Abstract: There are many methods to calculate multi-coil composite electromagnetic fields, but which one is optimal

requires further research. The best method should take into account the calculation efficiency and calcula-

tion accuracy. We want the fastest operation time to obtain the ideal accuracy. This paper discusses the two

methods of series expansion and elliptic integration to calculate the multi-coil composite electromagnetic

field, finds that the elliptic integral method has better operation effect. Series expansion can be a supple-

mental option for certifying result. Lastly, A software program is written to realize data input, start calcula-

tion and final result display with a good human-machine interface.

INTRODUCTION

Lacking specialized high precision calculation tool

for electromagnetic field strength, we set about de-

veloping a kind of magnetic field calculation pro-

gram software. After contrast between series expan-

sion method and elliptic integral method, we find the

two methods are both effective on solving circle

current electromagnetic field, but the former is much

easier to control the resultant precision in computer

operation. Therefore, besides the traditional elliptic

integral method, series expansion method affords

another newer effective method optional for us when

we do high precision magnetic field calculation.

They are both convenient for us to figure out a visu-

alized magnetic cloud map meeting our majority

usage case.

Calculation for kinds of shapes of coil group is

badly needed with high frequency in High Magnetic

Field Laboratory of Chinese Academy of Science

(Ren Yong - He P.) and other institutional units. The

demand of the calculation is normally high-precision

(generally exceeding 0.01ppm). There is a consistent

rigid demand to work out many types of coil groups’

field strengths or homogeneity.

When we calculate the magnetic field strength,

we normally use these formulas or methods: like as

Biot-Savart Law (Binder P-M, 2016), Laplace Equa-

tions (Du Di, 2016), Maxwell Equations (Arbab A.I.,

Chovan Jaroslav), and so on. Those will further turn

out some complicated integral equations or other

forms, often impossibly solved artificially.

On another hand, magnets are composed of mul-

tiple coils with different locations and various shape

dimensions. A large amount of superconducting

wires are enriched in variable currents and section

shapes. All of these factors are hardly difficult to

calculate manually.

So, developing a kind of high fitness calculation

program based on high speed computer numerical

calculation is the only way to face all of these hard

cases (Zhilichev Y, Takahashi Keita).

We hope the program can be widely used in al-

most all kinds of magnet figuring. In this case, we

choose Matlab as development platform, because its

high performance of matrix arithmetic capability,

visualized figure output character, and fine operate

accuracy are attracted deeply for majority program-

mers (Ramana Reddy J.V.- Fang Xiaorong], also for

us.

The software adopts plenty of functions and

modularity program structures. That makes it have

strong readability and good transplantable. We pre-

serve some modular interfaces for latter improve-

ments for specific conditions and functional exten-

sions. It has a good graphic user interface for con-

venient and efficient inputting kinds of parameters.

The number for coils countable is limitless expanda-

ble. So it has a widely usage in practical magnetic

calculation fields.

138

Cheng, X. and Zhang, Y.

Multi-Coil Electromagnetic Field Calculation with Two Methods and Software Implementation.

DOI: 10.5220/0012276000003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 138-142

ISBN: 978-989-758-677-4

Computational accuracy is sufficient high for

MRI, NMR (Fang Xiaorong, 2014), and normal

electromagnetic calculations. The theory accuracy

reaches 10-14 estimated by software’s platform.

Actual measured accuracy arrived above 10-11 on

desktop computers. If running on large scale high

performance workstation, the computational accura-

cy should get further improvement.

MATHEMATICAL METHODS

There are two methods for counting single circular

current loop so far. They are separately series expan-

sion method and elliptic integral method. They are

both suitable for computer numerical calculation.

Correspondingly to two version programs are devel-

oped according to the methods. The distinction be-

tween the two methods is present in their modulari-

zation core processing function, and different in in-

put user interface. A brief overview summarized for

these calculating methods are shown as follows.

2.1 Series Expansion Method

Figure 1: The calculating model based on circular current

loop.

Suppose a circular current loop put in vacuum cir-

cumstance. Its radius is R. Current density is I. Es-

tablish a Cartesian coordinate system shown in Fig-

ure 1. By the symmetry, we can locate a point P(x,z)

by random. Select a current element

lId

of the tiny

part A on the circular loop (see Fig. 1).

So, by Biot-Savart Law, we can get the differen-

tial value of magnetic flux density at point P ex-

pressed as

4 r

rlI

⋅=

. (1)

In which,

kji

ZRRX

OAOP

+−−=

−=

θθ

sin)cos(

2/1222

)cos2(

RXXZRr −++=

jil

θθθθ

cossin

)sincos(

RdRd

RRdd

+−=

Put

、

into (1). By integral operation

on angle

in the interval

]2,0[

, we get the mag-

netic flux density generated by current element A at

point P:



−++

2/3222

)cos2(

cos

RXXZR

(2)

]

)cos2(

sin

)cos2(

sin

[

]

)cos2(

sin

)cos2(

sin

[

)cos2(

sin

2/3222

−++



−

θθ

RXXZR

(3)

Result zero is derived from the zero summation

of odd function integral in the symmetric interval.



−++

−

2/3222

)cos2(

)cos(

RXXZR

dXR

(4)

Assuming dimensionless variables

RZz /=

RXx /=

, substituting the magnetic flux density

RIB 2/

at the center of the circle as the ref-

erence value, and writing

/ BBb

, (2) and (4) can be reformed as:



−++

2/322

)cos21(

cos

xxz

(5)



−++

−

2/322

)cos21(

)cos1(

xxz

(6)

Substituting

1 xz ++=

，

/2xq =

, we

get



−−

−=

θθθη

2/32/3

cos)cos1(

dqzb

(7)



−−=

−−

θθθη

2/32/3

)cos1()cos1(

dxqzb

(8)

Operating

2/3

)cos1(

−

with Taylor ex-

pansion, the finally results are got:

Multi-Coil Electromagnetic Field Calculation with Two Methods and Software Implementation

139

]

)2(642

)12(531

)24(42

)14(53

[

2/3

−

∞

−

⋅

⋅⋅⋅⋅

−⋅⋅⋅⋅

⋅

−⋅⋅⋅





(9)

]})

)2(642

)12(531

)24(42

)14(53

[

222

2/3

qxz

⋅−−+⋅

⋅⋅⋅⋅

−⋅⋅⋅⋅

⋅

−⋅⋅⋅



∞

−



. (10)

Equations (3), (9) and (10) comprise the magnet-

ic series solution of single circular current loop

(

Pawel Bienkowski, 2012

). These kinds of gradual

convergence expressions of series in last term are

especially suitable for multiply accumulative calcu-

lation within computer solving.

By controlling the last term’s accuracy of series

solution, we can limit the finally resultant numerical

precision in a needed range.

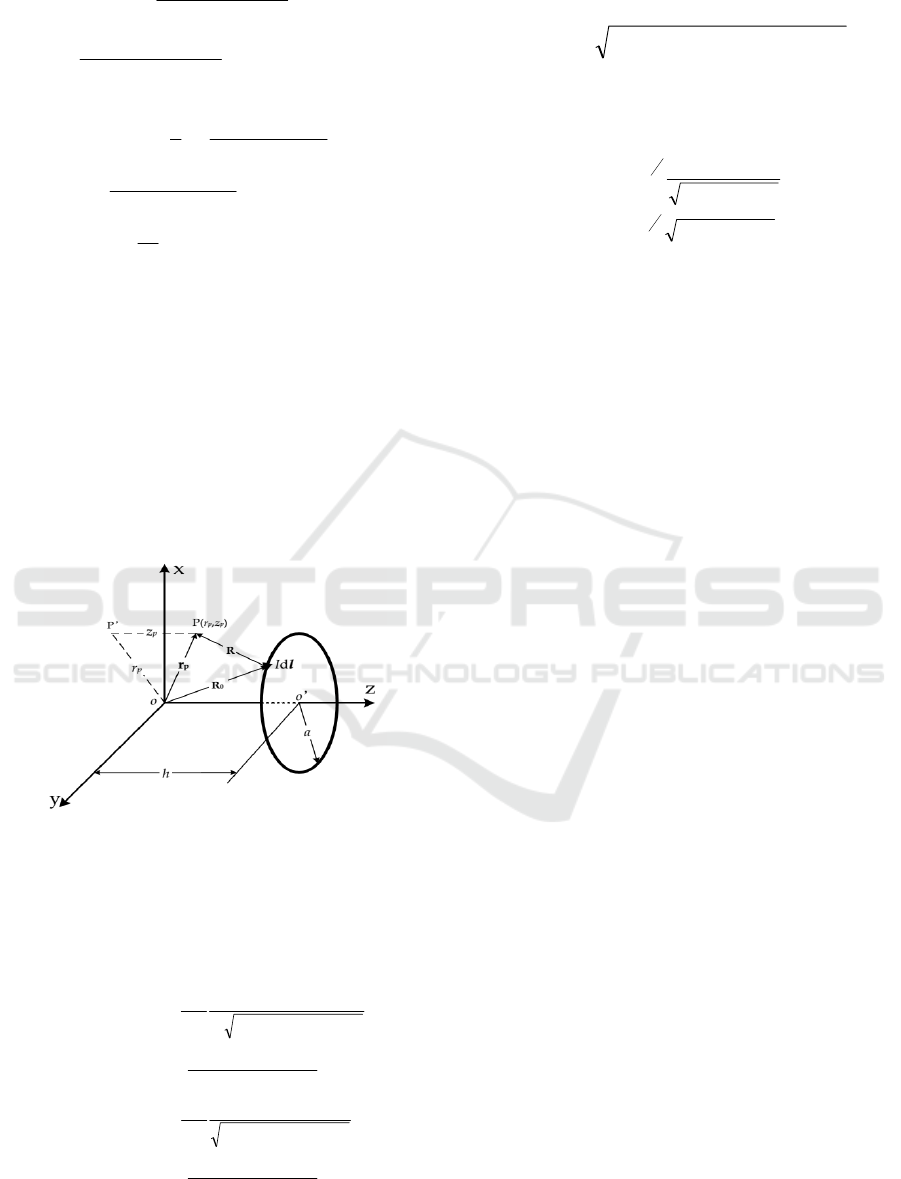
2.2 Elliptic Integral Method

Figure 2: Calculate circular current loop by elliptic inte-

gral.

For a ideal current carrying ring of center coor-

dinate O(0,0,h), radius a, current I (shown in Fig. 2),

The magnetic flux density at arbitrary space point

P(rp,zp) is expressed as (

Reich Felix A.

Martin N.























−+−

−⋅

−++













−+−

−++

−⋅

−++

−

)(

)()(

)(

)()(

),(

)(

)()(

)(

)()(

),(

222

hzar

zrB

hzar

hzarr

zrB

ppz

ppp

ppr

(11)

Where,

is vacuum permeability,

])()/[(4

hzarark

ppp

−++=

)(kK

and

)(kE

are separately elliptic integral

of the first kind and the second kind, and expressed

as:











−=

−



sin1)(

sin1

)(

αα

dkkE

(12)

The advantage of this kind of method is that we

can directly utilize the integrated elliptic integral

computing module integrated in Matlab to figure it

out. So the computing efficiency is very high. Com-

putational accuracy can be controlled by pass pa-

rameter Tol in the module. That is unnecessary to

expand the elliptic integral for recalculating in pro-

gram manually.

2.3 Other Methods

Besides the elliptic integral and series expansion

method, some other methods (Vlasko-Vlasov V. K.,

Pathak Aritro.) also to be considered as choices for

calculating the magnetic field intensity of solenoid

with electric current are as follows: calculating with

integral module integrated in Matlab software (nu-

merical/character expression integral module), reck-

on in helical angle on solenoid (see Fig. 3), arithme-

tic combining helical angle with section shape (see

Fig. 4). For separately defects, these methods are

nullified finally. The flaws are described as follows:

Calculating with integral module integrated in

Matlab software includes numerical and character

expression integral module. The arithmetic speed is

too slow despite higher accuracy. It may be spend 20

minutes in computing 10 current circles with a nor-

mal desktop computer. For certain coil, it has usual-

ly size of several hundreds of current circles. In this

case, the operating time is too long to acceptable.

The efficiency of reckoning in helical angle is al-

so very slow. Despite the module is more accurate,

the calculating speed is unimaginable. Because the

relative value of coil diameter to conductor diameter

is very high (generally larger than 100), causing the

lead angle less than atan2(1,pi*100)*180/pi =0.1824

゜

=10'57", facing such a little angle value, and for

pursuing high efficient calculation, the lead angle

should be negligible.

The computing speed is mostly unimaginable

low if helical angle and section shape are concur-

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

140

rently put into account. For a desktop computer, the

computing may lead to system halted, also even for

small workstation. It is completely unnecessary

when conductor diameter is far less than coil diame-

ter because computational efficiency is more appre-

ciative than tiny precision improvement.

Figure 3: Coil model accounted helical angle.

Figure 4: Coil model accounted conductor section shape.

PROGRAM

IMPLEMENTATION

We chose Matlab software to apply the calculation

method because of its high computational efficiency,

nice precision, favorable visualization, running in-

dependently and good platform portability (maybe

suitable for Windows, Linux, Unix, Ios, etc.).

Start

GUI

parameters

input

Manual

input

Importing

Excel

data

Getting

Parameters

Single point

field

Sylinder

field

measurement

area

selection

Sphere

field

measurement

area

selection

Meshing

the

region

Calculating the

whole coil

field

Calculating a

single circle unit

field

elliptic integral

method

（accuracy control

and singularity

avoidance ）

series expansion

method

（accracy and

convergency

control ）

Result

output

Figure field

strength

cloud map

Computing

the homogeneity

Result

output

Figure field

homogeneity

cloud map

Figure 5: The basic principle flow chart of arithmetic pro-

cedure.

Circle

current

data

Computing

expansion

term

Does

it meet the

precision

demand ?

Reach the limited

maximum iteration

Single current

field strength

Figure 6: Internal series expansion count process flow chart.

The basic principle flow chart of arithmetic proce-

dure (see Fig. 5) and internal series expansion count

process are drawn in Figure 6.

RESULTS AND CONCLUSIONS

A superconducting magnet consisted of 4 coils in

detail listed in Table 1 is tested. We found the results

(see Fig. 7) are highly accordant between elliptic

integral method and series expansion method. So the

series expansion method is verified as an effective

method well as traditional elliptic integral method.

The former’s accuracy can be easily controlled by

total expanding term numbers.

ACKNOWLEDGMENTS

This work was financially supported by the Key

Research and Development Projects of the Ministry

of Science and Technology of China through grant

2020YFA0711600 and 2020YFA0711603.

Table 1: Configurations of superconducting magnet coils.

Inner

radius

(mm)

Outer

radius

(mm)

Section

coordinate

Zmin(mm)

Section

coordinate

Zmax(mm)

Radial

turns

Axial

layers

Current

(A)

49 100 35 145 52 100 114.62

49 100 -35 -145 52 100 114.62

113 165 30 150 62 92 114.62

113 165 -30 -150 62 92 114.62

165.5 200 30 150 50 100 114.62

165.5 200 -30 -150 50 100 114.62

Helical line

parameter equations:

x=r*cos(Theta);

y=r*sin(Theta);

z=Dire*P*Theta/

(

)

;

Current element

parameter equations

：

x=(r+rb)*cos(Theta);

y=(r+rb)*sin(Theta);

z=Dire*P*Theta/(2*pi)+za;

Multi-Coil Electromagnetic Field Calculation with Two Methods and Software Implementation

141

Figure 7: Calculation results of magnetic field strength and

homogeneity.

REFERENCES

Ren Yong, Kuang Guangli, Chen Wenge. Analysis of the

Experimental Results for the Nb3Sn Model Coil Being

Built in China[J]. Journal of Superconductivity and

Novel Magnetism. Oct. 2015, Vol. 28, No. 10, pp. 2941-

2944. https://doi.org/10.1007/s10948-015-3110-x

Yong Ren, Guangli Kuang, Wenge Chen. Quench Simula-

tion of the Hybrid Magnet Superconducting Outsert

Being Built in China[J]. Journal of Fusion Energy.

Oct. 2015, Vol. 34, No. 5, pp. 1146-1150. https://

doi.org/ 10.1007/s10894-015-9933-4

Yong Ren, Guangli Kuang, Wenge Chen. Analy-

sis of the Magnetic Forces Generated in the Hybrid

Magnet Being Built in China[J]. Journal of Fusion

Energy. Aug. 2015, Vol. 34, No. 4, pp. 733-738.

https://doi.org/10.1007/s10894-015-9876-9

He P., Chen W. G., Chen Z. M. Pressure Drop Calcula-

tion of Gas Path for Heat Treatment System of Nb3Sn

Superconducting Coils[J]. Physica C-

Superconductivity and Its Applications. Jun. 2012, Vol.

476, pp. 73-76. https://doi.org/10.1016/j.

physc.2012.02.011

Binder P-M, Grace Alyssa L., Hui Kaleonui J. Magnetic

Field in the Plane of a Physical Dipole[J]. European

Journal of Physics. Jul. 2016, Vol. 37, No. 4.

https://doi.org/10.1088/0143-0807/37/4/045203

Du Di, He Peng, Zeng Yongchao. Dynamics of paramag-

netic squares in uniform magnetic fields[J]. Journal of

Magnetism and Magnetic Materials. Nov. 2016, Vol.

417, pp. 100-105. https://doi.org/10.1016/j.

jmmm.2016.05.032

Arbab A.I., Is the Electromagnetic Field in a Medium a

Fluid or a Wave?[J]. Optik, Feb. 2017, Vol. 130, pp.

154-161. https://doi.org/10.1016/j.ijleo.2016.10.130

Chovan Jaroslav, Slodicka Marian. Induction Hardening

of Steel with Restrained Joule Heating and Nonlinear

Law Formagnetic Induction Field: Solvability[J].

Journal of Computational and Applied Mathematics.

Feb. 2017, Vol. 311, pp. 630-644. https://doi.org/

10.1016/j.cam.2016.08.016

Zhilichev Y. Simulation of Critical Currents in Bulk Su-

perconductors by Modified FEA and Hybrid Meth-

ods[J]. IEEE Transactions on Applied Superconductiv-

ity. Jun. 2017, Vol. 27, No. 4, pp. 5. https://doi.

org/10.1109/tasc.2016.2631475

Takahashi Keita, Ainslie Mark D., Fujishiro Hiroyuki.

Pulsed-Field Magnetizing Characteristics of Rectangu-

lar-Shaped Gd-Ba-Cu-O Bulk Using Split-and Sole-

noid-Type Coils[J]. IEEE Transactions on Applied

Superconductivity. Jun. 2017, Vol. 27, No. 4.

https://doi.org/10.1109/TASC.2016.2625764

Ramana Reddy J.V., Sugunamma V., Sandeep N. Effect of

Frictional Heating on Radiative Ferrofluid Flow over a

Slendering Stretching Sheet with

Aligned Magnetic Field[J]. European Physical Jour-

nal Plus. Jan. 2017, Vol. 132, No. 1, pp. 7-20.

https://doi.org/10.1140/epjp/i2017-11287-1

Evstaf'ev A.M., Yakushev A.Ya., Sereda A.G. A Simula-

tion Mathematical Model of a Traction Transformer

with Tapped Secondary Windings[J]. Russian Electri-

cal Engineering. May. 2016, Vol. 87, No. 5, pp. 275-

281. https://doi.org/10.3103/S1068371216050072

Fang Xiaorong, Wang Nanfei, Zhang Jianfeng. Three-

Dimensional Visualization of Maize Roots Based

on Magnetic Resonance Imaging. Agriculture and Life

Sciences[J], Journal of Zhejiang University. 2014, Vol.

40, No. 2, pp. 181-187. https://www.webofscience.

com/wos/alldb/full-record/CSCD:5099879

Pawel Bienkowski, Hubert Trzaska. Electromagnetic

Measurements in the Near Field. IET Digital Library;

SciTech Publishing Inc. 2012, pp. 89-111.

https://doi.org/10.1049/SBEW042E

Reich Felix A., Stahn Oliver, Mueller Wolfgang H. The

Magnetic Field of a Permanent Hollow Cylindrical

Magnet[J]. Continuum Mechanics and Thermodynam-

ics. Sep, 2016, Vol. 28, No. 5, pp. 1435-1444.

https://doi.org/10.1007/s00161-015-0485-7

Martin N. Wilson. Superconducting Magnets. Clarendon

Press Oxford. 1983, pp. 34-40.

Vlasko-Vlasov V. K., Glatz A., Koshelev A. E. Aniso-

tropic Superconductors in Tilted Magnetic Fields[J].

Physical Review B. Jun. 2015, Vol. 91, No. 22.

https://doi.org/10.1103/PhysRevB.91.224505

Pathak Aritro. An Elementary Argument for

the Magnetic Field Outside a Solenoid[J]. European

Journal of Physics. Jan. 2017, Vol. 38, No. 1.

https://doi.org/10.1088/0143-0807/38/1/015201

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

142