Can HP-protein Folding Be Solved with Genetic Algorithms? Maybe not

Reitze Jansen

1 a

, Ruben Horn

2,3 b

, Okke van Eck

3 c

, Kristian Verduin

1 d

Sarah L. Thomson

4 e

and Daan van den Berg

1 f

Department of Computer Science, University of Amsterdam, Netherlands

Helmut-Schmidt-University, Hamburg, Germany

Department of Computer Science, VU Amsterdam, Netherlands

Napier University, Edinburgh, U.K.

Keywords:

Protein Folding, Genetic Algorithms, Evolutionary Computing, Constraints, Constraint Hierarchy.

Abstract:

Genetic algorithms might not be able to solve the HP-protein folding problem because creating random indi-

viduals for an initial population is very hard, if not impossible. The reason for this, is that the expected number

of constraint violations increases with instance size when randomly sampling individuals, as we will show in

an experiment. Thereby, the probability of randomly sampling a valid individual decreases exponentially with

instance size. This immediately prohibits resampling, and repair mechanisms might also be non-applicable.

Backtracking could generate a valid random individual, but it runs in exponential time, and is therefore also

unsuitable. No wonder that previous approaches do not report how (often) random samples are created, and

only address small instances. We contrast our ﬁndings with TSP, which is also NP-hard, but does not have

these problems.

1 PROTEIN FOLDING

The exact way in which a protein folds is immensely

important. Within the human body, the long chains

of amino acids (“aminos”) that make up our proteins

perform their biological function only when spatially

folded in a certain way. For many, their folded shape

is a state of minimum energy – of which a protein can

have multiple (Levitt, 1983; Unger and Moult, 1993).

Conversely, a folding deﬁciency can lead to a higher

than minimum energy, which causes the conforma-

tion to be unstable. Proteins in unstable conforma-

tions have the tendency to unfold, which is a known

cause for Alzheimer’s, Parkinson’s, diabetes, and fa-

tal insomnia (Lee et al., 2000; Thomas et al., 1995;

Dobson, 1999).

Not just for this reason the subject is intensively

studied. In medical sciences, diseases are combated

https://orcid.org/0009-0007-0029-2882

https://orcid.org/0000-0001-6643-5582

https://orcid.org/0000-0002-3600-5183

https://orcid.org/0009-0005-8754-7635

https://orcid.org/0000-0001-6971-7817

https://orcid.org/0000-0001-5060-3342

with artiﬁcially synthesized proteins, which also at-

tain their stability from their exact conformational de-

tails (Leader et al., 2008; Zhao and Lu, 2011; Don-

dapati et al., 2020). The exact mechanics of the

folding process are notoriously complex (Creighton,

1988; Dill and MacCallum, 2012), but stability result-

ing from a conformation is known to closely depend

on the interplay of the aminos (Levitt, 1982; Levitt,

1983; Dill, 1985). In exploring the nature of confor-

mations, researchers moved to utilize simpliﬁed mod-

els, such as the HP-model. Algorithmic protein fold-

ing, particularly in the HP-model, aims at ﬁnding the

maximum stability conformation of a protein, and at

understanding how to get there.

Within the HP-model, proteins are chains of con-

nected aminos which are all labeled as either being

hydrophobic (H) or polar (P) (Lau and Dill, 1989),

and precede one another on adjacent vertices in a

(usually 2- or 3-dimensional) rectangular lattice (Fig-

ure 1). Non-connected H-amino’s can form attracting

bonds when placed on neighbouring lattice vertices,

each of which reduces the free energy of the attained

conformation by one. So the more H-bonds the folded

Jansen, R., Horn, R., van Eck, O., Verduin, K., Thomson, S. and van den Berg, D.

Can HP-protein Folding Be Solved with Genetic Algorithms? Maybe not.

DOI: 10.5220/0012248500003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 131-140

ISBN: 978-989-758-674-3; ISSN: 2184-3236

131

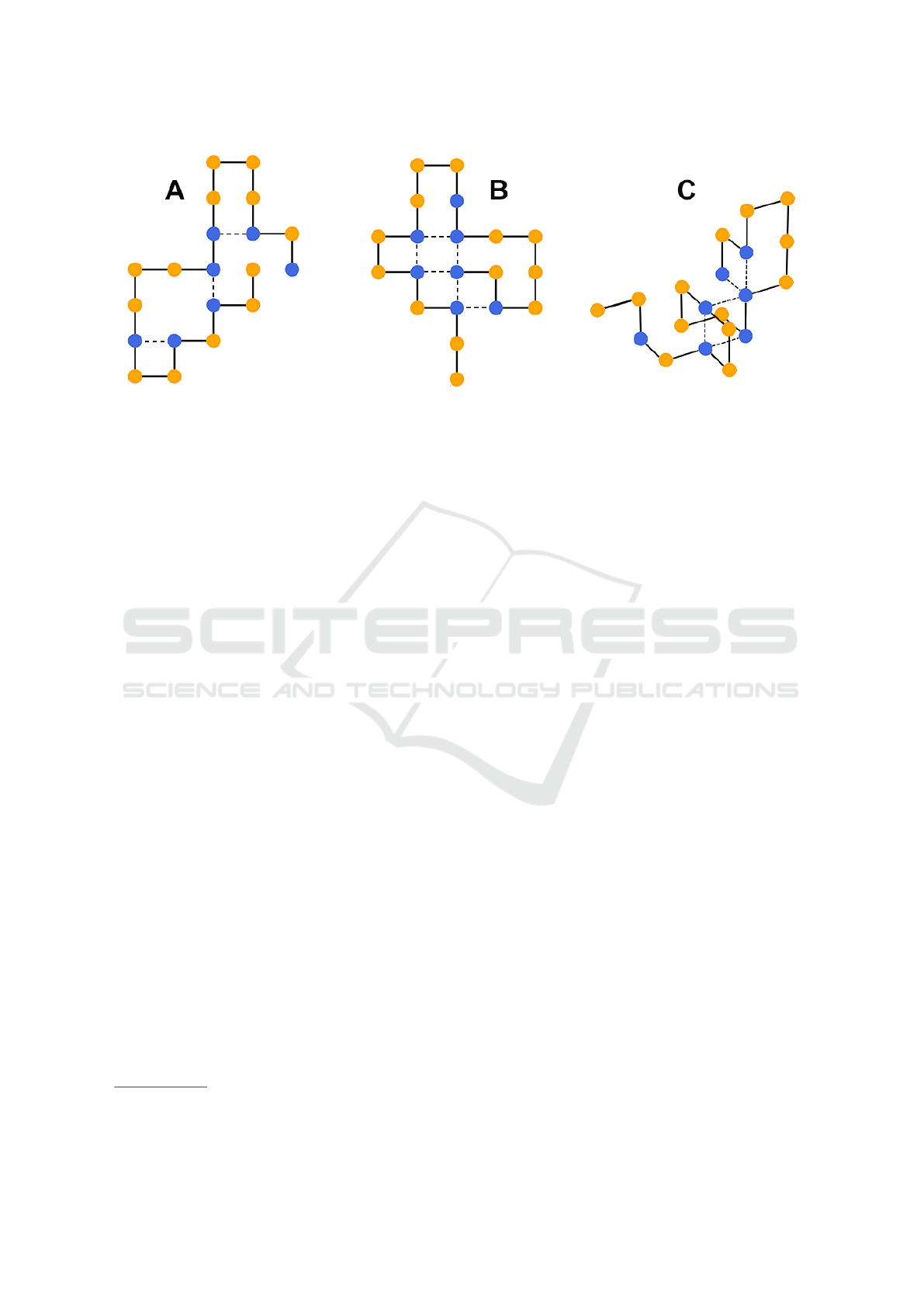
Figure 1: The HP-protein folding problem pertains ﬁnding the lowest stability conformation for a certain protein. Depending

on the fold, a protein conformation can have different stability values, which are given by the number of H-bonds (dashed

lines) of the corresponding conformation. In subﬁgures A and B, the protein is folded in 2D with stability -3 and -6 respec-

tively. In subﬁgure C, it is folded in 3D with a stability of -5.

protein has, the lower its stability value

and the less

likely the protein is to spontaneously unfold. The free

energy (or stability) of a conformation c for an amino

acid sequence seq = [a

,..,a

], is thereby the mini-

mization of:

S(c) =

∑

i=1

i−1

∑

j=1

)

where f

indicates whether a

and a

are ﬁrst neigh-

boring H-aminos, deﬁned as:

) =







−1

if a

= a

= H ∧ |i − j|̸= 1

∧ d(a

) = 1

0 otherwise

in which d(a

) is the Manhattan distance between

two aminos on the lattice (van Eck and van den Berg,

2023). Two unconnected H-aminos that are ﬁrst

neighbors are said to form a bond between them, as

illustrated with the dashed lines in Figure 1. Thereby,

the HP-protein folding problem is a minimization

problem: a quest to ﬁnd the conformation with the

lowest stability value, or equivalently, the highest

number of H-bonds formed between neighbouring H-

aminos.

The HP-model preserves the NP-completeness

and NP-hardness of the protein folding problem

(Berger and Leighton, 1998; Hart and Istrail, 1997),

which entails that neither ﬁnding a maximally sta-

ble conformation nor verifying a given conforma-

tion is actually maximally stable can be done in

polynomial time – under the assumption that P ̸=

Confusingly enough, a lower stability value means a

more stable protein

NP. Even though the HP-model is a strongly sim-

pliﬁed representation of natural protein folding, the

number of possible conformations is still immense

(Unger and Moult, 1993), and ﬁnding a minimum-

energy conformation is intractable with the capabil-

ities of modern-day computers for any realistic in-

stance size. As one consequence, researchers are fo-

cusing on (meta)heuristic approaches instead of exact

algorithms.

But this approach is not without problems ei-

ther, due to the overwhelming number of invalid in-

dividuals in the search space. The vast majority of

metaheuristic algorithms starts off with a population

of randomly chosen individuals (Eiben and Smith,

2015), and although Eiben and Smith also discuss

the possibility of nonrandom initialization, mostly for

speciﬁc problem settings, many authors will opt for a

uniformly random initial population. Maaranen et al.

take a slightly stronger position even, abiding by the

practice that initial individuals should be “as evenly

distributed as possible” (Maaranen et al., 2004). We

also closely follow this position: at the very least, ran-

dom initialization of an initial population should be

uniformly random, and unbiased. Or even more care-

fully put: at the very least we want uniformly random

sampling to be available, in order to obtain an unbi-

ased initial population for our evolutionary algorithm,

if we choose to have so.

However, even this most modest wish appears to

be a formidable problem for protein folding in the HP-

model, as we will show shortly. Uniformly randomly

sampling a conformation from the space of all pos-

sible conformations might not be possible in deter-

ministic polynomial time for this problem. To make

matters worse, stochastic uniform random sampling is

also problematic, as it appears the conformation space

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

132

gets saturated with invalid instances as n increases.

As a direct consequence, it might be impossible to

sample a uniformly random initial population, e.g. for

use by a genetic algorithm. For this reason, it is ques-

tionable how suitable genetic algorithms are for solv-

ing the HP-protein folding problem.

We will demonstrate these problems by examin-

ing 40,000 random folds for ‘neutralized’ proteins in

2D and 3D without any preassumptions, and then sim-

ply count the number of constraint violations (or col-

lisions) that occur for each protein (Figure 2). The

results show that the number of expected collisions

increases in n, making the sampling of valid random

initial individeals ever less feasible. But before that,

we will have a look at existing approaches for fold-

ing proteins with genetic algorithms. Unsurprisingly,

none of these are unproblematic.

2 EXISTING GA-APPROACHES

There have been various attempts at solving HP-

protein folding with genetic algorithms since 1993, of

which some are summarized below. Many of them are

part of the same ‘line’ of papers, initiated by Unger

and Moult in 1993 (Unger and Moult, 1993).

Generally speaking, one can represent a confor-

mation relative to the lattice (a sequence of lattice di-

rections denotes the conformation) or relative to the

chain (a sequence of left - right - up - down

turns). If the step back to the previous amino is

prevented however, we can reduce the conformation

space enormously (at least from O(4

) to O(3

)), al-

though the other representations could have imple-

mentational advantages when it comes to crossover

and mutation. In none of the cases below however,

we found any motivation for why authors opt for ei-

ther of the two representations.

The early study by Unger and Moult compared a

Monte Carlo approach to a genetic algorithm for HP-

protein folding (Kirkpatrick et al., 1983; Unger and

Moult, 1993). They use a two-dimensional Cartesian

lattice and imply that folds are encoded relative to

the chain (Patton et al., 1995). Their Monte Carlo

approach starts from a ‘random coil conformation’,

but the details of the GA’s initialization are not listed.

In the parent selection however, some details are ex-

posed: if during crossover all the three possible angles

at which to join the partial folds results in collisions,

new parents are sampled. The GA is run for 300 gen-

erations with a population size of 200, and perfectly

solves all instances with a size below 64 within less

than 600,000 evaluations. But notably, they do not re-

port the number of invalid conformations generated,

nor the number of times resampling is required in mu-

tation, crossover or initialization.

In a 1995 followup work by Patton et al., a stan-

dard GA was employed to HP-protein folding on a

3D Cartesian lattice (Patton et al., 1995). Individuals

with collisions are tolerated in the populations, but

penalized in the evaluation. Their modiﬁcations con-

sistently result in lower-energy conformations after

much fewer evaluations. So it appears that temporar-

ily allowing invalid conformations in a metaheuristic

allows for better end solutions – found quicker. But

this observation should be considered as a very early

hypothesis.

Nine years later, a followup study by Custodio et

al. implement four modiﬁcations to Patton et al.’s ap-

proach (Cust

odio et al., 2004). These authors conse-

quently also penalize conformations containing col-

lisions. Their selection method preserves diversity

by progressively replacing individuals with equal or

better offspring. For recombination, they use multi-

point crossover, which is contingent on the length of

the chain. They also experiment with using islands

to create a better initial population “(with fewer col-

lisions)”. Additionally, they propose an alternative

ﬁtness function which rewards more compact con-

formations. Their representation of the folded struc-

ture is relative to the lattice. These modiﬁcations re-

sult in a better average performance and within the

3,500,000 evaluations the best solutions are almost as

good as when using the method by Unger and Moult

or Patton et al. The fact that their work is published

could be a testimony to the success of allowing col-

lisions rather than resampling, but the reader should

understand that 3.5 million evaluations is a lot.

In 2005, a study by Bui and Sundarraj on genetic

algorithms for two-dimensional HP-protein folding

appeared(Bui and Sundarraj, 2005). In this work,

secondary structures of the longest hydrophobic sub-

section were separately evolved. During random ini-

tialization, the longest hydrophobic subsection is se-

lected at random from the library of secondary struc-

tures instead of being sequentially folded. When a

collision occurs and cannot be resolved by rotation,

the individual is recreated. The top-half of the initial-

ized individuals from the ﬁrst generation. Using tour-

nament selection, one-point crossover is performed to

create offspring before applying mutations across the

whole chain with a probability depending on the gen-

eration. If the mutation falls within a hydrophobic

subsection that was sampled from the library of sec-

ondary structures, it is replaced by a new secondary

structure. If possible, any collisions introduced by

crossover and mutation are resolved, or the individual

is discarded. To do this, the chain is re-folded start-

Can HP-protein Folding Be Solved with Genetic Algorithms? Maybe not

133

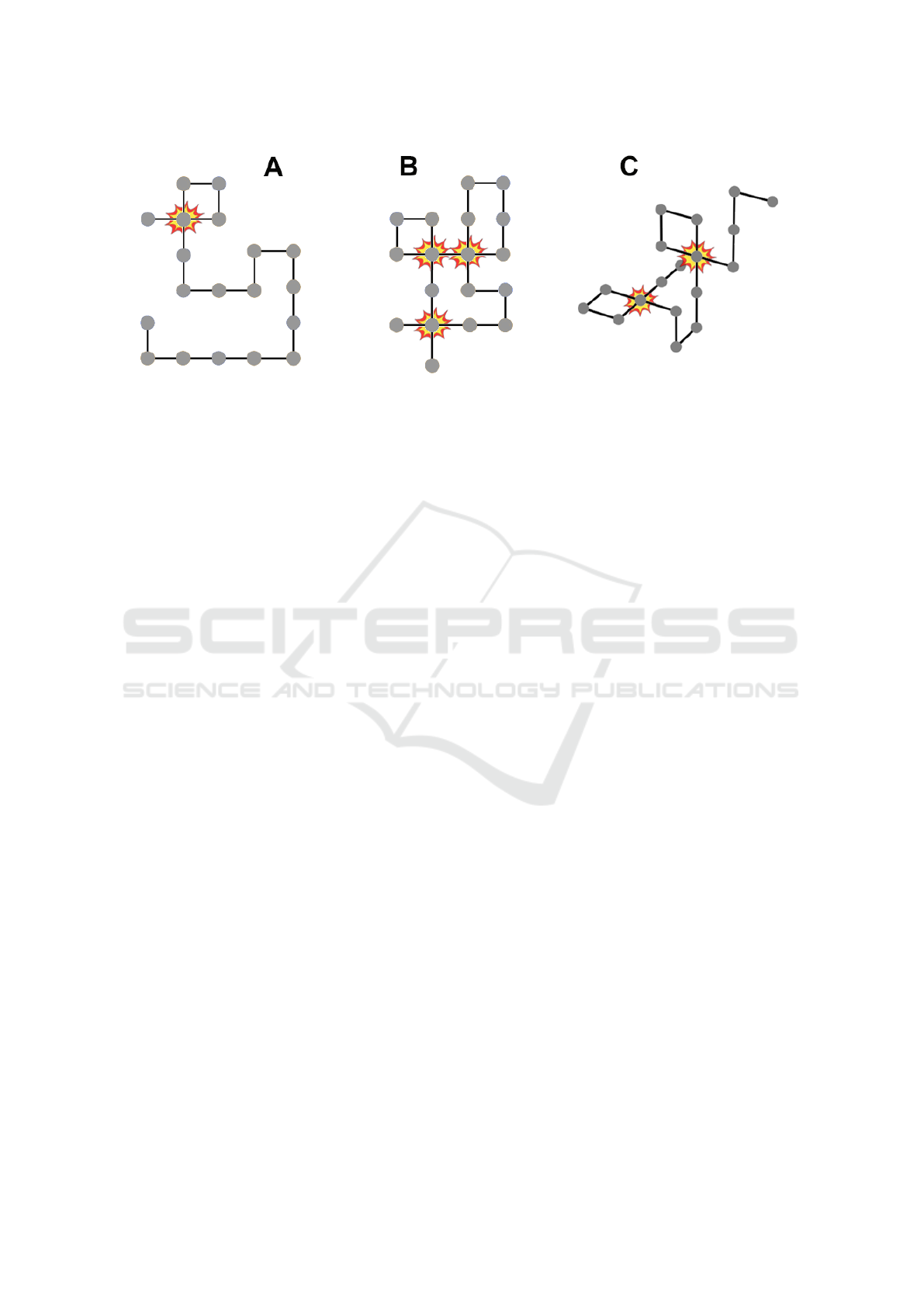
Figure 2: In HP-protein folding, ﬁnding valid conformations to evaluate is a problem. When randomly folding ‘neutral’

HP-proteins, constraint violations (or: ‘collisions’) occur quite frequently. For a protein consisting of n aminos, the minimum

number of constraint violations for any fold in 2D or 3D is 0, the maximum is n − 3.

ing from the secondary structure if present and from

the beginning if not and in the case of a collision,

a random possible direction is selected. Using two

simple refolding schemes (patterns and replacements

for 4 and 6 neighboring aminos), local optimization

is applied to the new individuals before progressively

creating the next generation by replacing the worst

parent or individual in the whole population with the

best offspring if it is better. Preceding the execution

of the main algorithm, the library of secondary struc-

tures is initialized using the same GA with some addi-

tional constraints for the longest hydrophobic subsec-

tion in the chain. Over 100,000 generations, the best

results of this approach are at least as good as those

by Unger and Moult’s and also (very close to) per-

fect for selected instances with a length of up to 100.

Summarizing, this work is another example of how

many tailor-made repair mechanisms are required to

solve HP-protein folding. These authors have one for

initialization, crossover and mutation, and by reading

their study, there’s no guarantee the algorithm won’t

get stuck on trying to ﬁnd zero-collision conforma-

tions. True, these might practically not occur often

at all, but as we will show, the proportion of invalid

inviduals in the conformation space grows as n in-

creases, so this is a problem worth of recognition.

Bui and Sundarraj themselves give no numbers on of-

ten their resampling methods are invoked, and if they

ever get stuck, for either initialization, mutation, or

crossover.

Four years later, a hybrid approach by Lin and

Hsieh involved a genetic algorithm combined with

the Taguchi method and particle swarm optimization

(Lin and Hsieh, 2009) (for the Taguchi method see

(Kaytako

glu and Akyalc¸ın, 2007)). Following repro-

duction using roulette-wheel selection and two-point

crossover using tournament selection, the Taguchi

method using random pairs replaces the bottom-half

of the population. A random subsection of the chain

is selected for mutation, on which a Particle Swarm

Optimization (PSO) algorithm is applied, but crucial

details such as the maximum number of its iterations

are not mentioned. Finally, hill climbing is performed

on a random subsection of the chain. Their represen-

tation of the folded structure is also relative to the lat-

tice, but the treatment of collisions is not described.

Over 2,000 generations and using a population of be-

tween 100 and 300, their algorithm consistently ﬁnds

lower-energy conformations than the experiment by

Unger and Moult, however the number of function

evaluations is not compared directly. A fair conclu-

sion for now is to say we do not know enough about

their experiment to draw direct conclusions, but we

suspect at the very least that authors also did not solve

the collision problem. Fairer would be to say that this

experiment needs to be replicated to obtain useful data

about their collision number and treatment.

A different approach, using multi-objective opti-

mization is proposed by Garza-Fabre et al. (Garza-

Fabre et al., 2015). Their experiment also allows for

individuals with collisions whose number, along with

the number stability of the conformations, make up

the two optimization criteria. Through neighboring

non-dominated solutions, it may be possible to ex-

plore the search space more effectively and escape

them. Their experiments on both two- and three-

dimensional Cartesian lattices are encoded relative

to the chain, and these authors ﬁnd that (proportion-

ally) biasing the optimization criteria to favor a re-

duction in collisions is necessary and yields better re-

sults compared to single-objective optimization. The

advantage of this approach becomes clear with in-

creased evaluations. However, this approach still re-

sults in searching a very large state space containing

mostly invalid conformations, and hence an efﬁcient

restriction of the search space to only those without

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

134

collisions would be preferable. Nonetheless, we feel

that the bias values in their experiment hold the po-

tential to elucidate the fundamentals of this problem,

and are therefore of signiﬁcant interest.

A 2016 study by Wang et al. proposed a ge-

netic algorithm with cloning of top individuals and

crossover followed by ‘chaotic mutation’ for the re-

maining individuals in the population (Wang et al.,

2016). Their conformation representation is relative

to the chain. They do not describe how the random

initialization of the population or the genetic opera-

tors treat collisions, but these authors claim their ap-

proach is signiﬁcantly more likely to ﬁnd the “per-

fect” conformation compared to standard GAs, even

for some long chains.

In a recent study on a 2D triangular lattice, au-

thors combine hill climbing and tabu search in a hy-

brid genetic algorithm, somewhat similar to the stud-

ies by Unger & Moult and Lin & Hsieh (Boumedine

and Bouroubi, 2021). The initial population is created

randomly, and collisions are resolved by resampling

the individual but again, authors do not mention how

often this happens. Offspring are generated by ei-

ther mutation or tabu search with random single point

crossover followed by hill climbing. This makes their

GA non-standard, and the frequency and treatment of

invalid conformations is not reported. Abiding by an

elitist approach, only the best offspring is considered

for the new population, which does not contain dupli-

cates. The use of local and tabu search makes it im-

possible to gauge the number of evaluations. Again,

we feel that there is no conclusive evidence about the

sampling distribution, which might be worth a closer

look.

The last study discussed in this paper is by Atari

and Majd, who introduce a ‘quantum genetic algo-

rithm’ (Atari and Majd, 2022). Their conformation

encoding is relative to the lattice, using two qubits

for every subsequent amino acid. The ﬁrst population

is initialized with equal probability for every confor-

mation. The population is sampled from the quan-

tum state by comparing a random variable to the am-

plitude of each qubit. Using the best individual, the

quantum population is updated by aligning it with the

best sampled individual. If the algorithm converges

on a local optimum, some individuals are randomly

recreated to induce diversity. This approach implies

the penalization of conformations with collisions, but

this is not described explicitly. We had some trouble

getting the details of this this study explicit, but as

the most recent publication, it is nonetheless included

in the overview. A deﬁnite answer of how (random)

sampling occurs, and how and how often collisions

were treated was not found however.

A rather disturbing observation from these studies

is that many of these limit the length n to 64. In some,

the length is set to n ≤ 100, but this is nowhere near

the length of real proteins, which can contain up to

2,000 aminos (Alberts et al., 2003). Could it be that

not only random sampling is impossible, but iterative

algorithms as a whole should be disqualiﬁed for the

HP-protein folding problem?

3 SOLUTION SAMPLING

Reviewing the literature on the subject, it appears safe

to say that sampling the conformation space presents

a stubborn problem for genetic algorithm approaches

on HP-protein folding. In our view, the issue boils

down to the following three questions:

1. Is it possible to sample, with uniform probabil-

ity, a single conformation from the space of all

possible valid conformations, for the HP-protein

folding problem?

2. If this is possible in deterministic time, what time

complexity does such a uniform probability sam-

pling algorithm have?

3. If this is not possible, what is the (stochastically

expected) number of resamples needed to obtain

a randomly sampled conformation, and how does

this number scale in n?

We think the answers to these questions might have

far reaching consequences. For now, it appears there

are two common strategies in publications up to this

point.

1. One option is to include only valid solutions in

the search space, by rejecting, preserving and re-

pairing strategies (Unger and Moult, 1993; Bui

and Sundarraj, 2005; Boumedine and Bouroubi,

2021; Garza-Fabre et al., 2015). There are at least

three problems with this approach:

(a) Repair mechanisms such as found in the

above literature, could distort the uniformity of

the sample distribution from the conformation

space. Put differently: repairing invalid sam-

ples might bias the sample, and stochastically

miss good or even optimal solutions as a result.

(b) The expected number of required samples

might increase in n for HP-protein folding. For

some problems, such as the traveling tourna-

ment problem, this number in fact increases so

fast that the random sampling method in itself

becomes unfeasible, let alone the accompany-

ing genetic algorithm (Verduin et al., 2023b).

Possibly for this reason, most above studies

Can HP-protein Folding Be Solved with Genetic Algorithms? Maybe not

135

have n ≤ 64, and only 3 studies have instances

of n ≤ 100 aminos (Bui and Sundarraj, 2005;

Wang et al., 2016; Boumedine and Bouroubi,

2021). Most proteins in nature are at least

twice as long, but can range up to 2,000 aminos

in length (Alberts et al., 2003). Considering

the exponential growth of the number of con-

formations in n, serious doubt could be raised

on whether one can uniformly sample random

real-life sized instances even in the vastly sim-

pliﬁed HP-model, let alone solve them with

a genetic algorithm. One key insight should

come from an assessment pertaining how the

ratio of valid to invalid conformations develops

in the exponential conformation space growth.

Probably not very good, as we will shortly see.

rithm exists, such as a form of backtracking, the

time complexity of the sampling procedure be-

comes an immediate concern. Maybe for that

reason, we did not ﬁnd a single study applying

that approach. It is an open question whether

a deterministic polynomial time uniform sam-

pling algorithm exists.

2. Alternatively, one might allow but penalize

conformation collisions (Patton et al., 1995;

Cust

odio et al., 2004; Garza-Fabre et al., 2015),

which potentially allows a genetic algorithm to

converge on a better conformation via invalid

ones. However, the search space size increases

dramatically, as invalid conformations become

ever more common in n, possibly making the en-

tire experiment unfeasible. Additionally, the pe-

nalization strategy for collisions presents yet an-

other optimization problem (Runarsson and Yao,

2000). Conversely, this approach might conserve

the connectedness of the ﬁtness landscape, possi-

bly unbiasing search algorithms, which might be

beneﬁcial.

So far, the emerging image is not a comfortable one.

Is it

uberhaupt possible to randomly sample from the

conformation space with uniform probability for the

HP-protein folding problem? Maybe not. But if so,

what are the (expected) time budgets involved for dif-

ferent protein lengths n? And how does this inﬂu-

ence the operation of GAs on the problem, or restrict

crossover and mutation operators? So many ques-

tions.

In this paper, we will start the quest for answers

by simply counting the number of collisions for dif-

ferent values of n, and rigorously characterizing them.

Although the experimental setup is quite modest, the

results could be quite fundamental.

4 EXPERIMENT & RESULTS

In the experiment, we randomly fold 1000 ‘neutral-

ized’ proteins for lengths n ∈ {5,10,15...195,200} on

both a 2D lattice and a 3D lattice without any pre-

assumptions, and counted the number of collisions

(Fig. 2). ‘Neutralize’ means we simply stripped the

amino’s ‘hydrophobic’ and ‘polar’ labels, to empha-

size we are only interested in valid conformations,

not optimal ones (Fig. 2). We place the aminos one

by one, every subsequent placement randomly choos-

ing a location ∈ {left, right, straight} for

2D, and ∈ {left, right, straight up, down}

for 3D. As such, we abide by a chain-relative repre-

sentation, but excluding backward collisions. While

placing, we increment the number of constraint vio-

lations (n

violations

) every time an amino is placed on a

lattice vertex that already has one or more previously

placed aminos.

The minimum value for n

violations

of any confor-

mation is 0, in case the random result happens to be

a completely self-avoiding walk, while the maximum

value for n

violations

is n − 4, because it’s impossible to

place the ﬁrst 4 aminos on a previously occupied lat-

tice vertex, after which every k

amino can be placed

on top of the (k − 4)

amino. As a consequence, the

maximum-collision conformation has the shape of a

layered coil, and there are exactly 2 such conforma-

tions: one consisting of left turns only, and the other

consisting of right turns only. The number of zero-

violation conformations on the other hand, is much

higher than 2. As one indication, a zero-violations

conformation with exactly one left turn followed by

zero or more straights and then exactly one right

turn is (n − 2) · (n −3), for all n > 3 (since having two

turns in a conformation of just 3 aminos is impossi-

ble). This observation is important, because it imme-

diately gives rise to the suspicion of an asymmetric

distribution for the number of violations. This suspi-

cion is empirically corroborated in our results, which

will be discussed shortly. All generation was done on

a contemporary desktop computer, and took at most

three days of continuous running time. Our Python

source code is publicly available (Anonymous, 2023).

For every length n, the number violations for each

of the 1,000 conformations was recorded, and taken

to histogram (Figure 3). It turns out that these vio-

lation distributions can be closely characterized by a

beta-binomial function, which can be used to model

probability densities for discrete but ﬁnite numbers of

interdependent events. To which extent the distribu-

tion is a theoretically credible model for random con-

formations in the HP-model is debatable. For safety,

let’s just say we use this speciﬁc curve because it gen-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

136

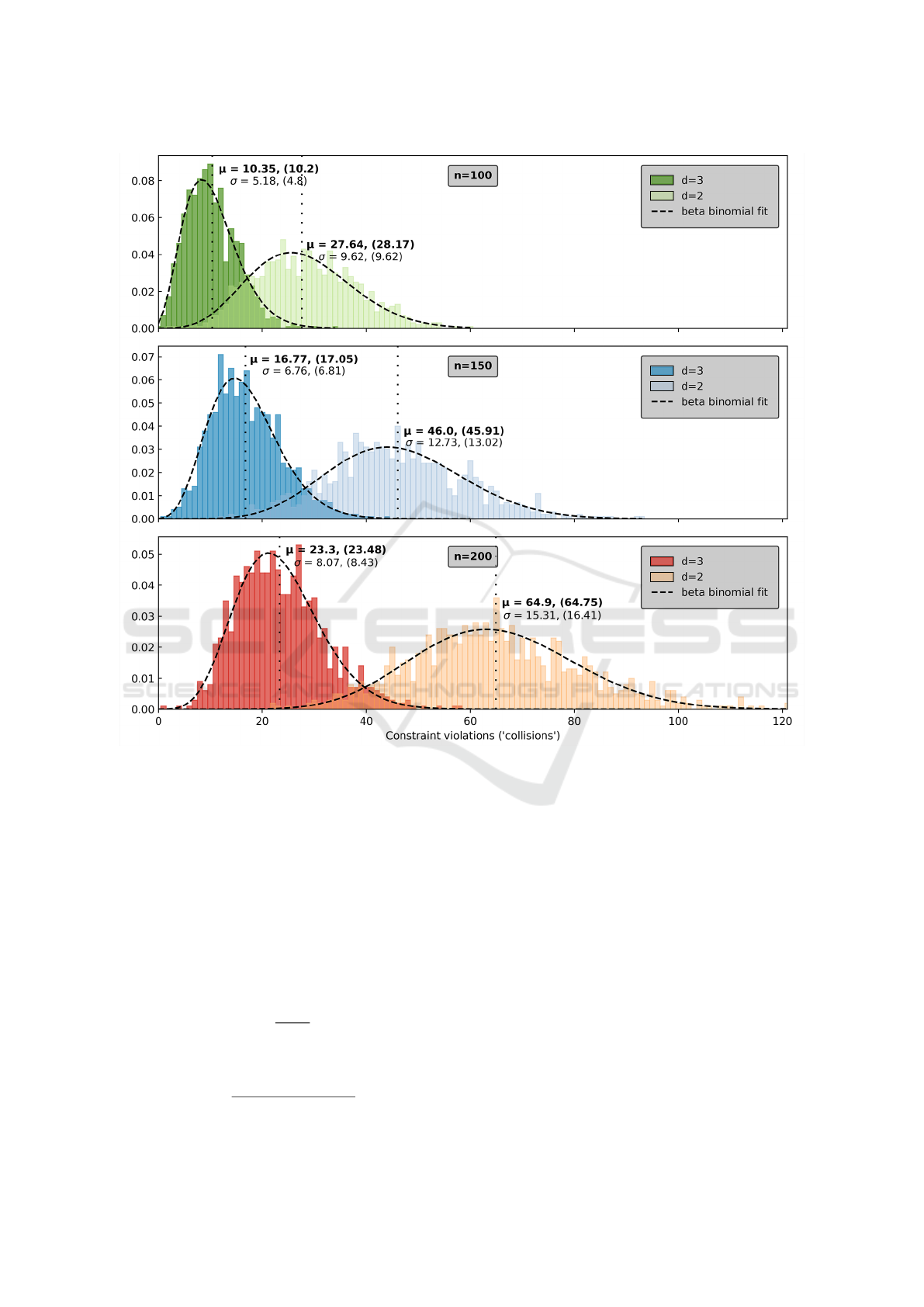
Figure 3: The frequency of constraint violations (‘collisions’) for random protein conformations of length n = 100, 150,200

in both 2 and 3 dimensions increase with n. Vertically dotted lines denote the mean (µ) of the ﬁtted distribution, the value in

brackets is the actual value of µ taken from the data, and similar for σ.

eralizes so well, and thereby allows us to extrapolate.

The beta binomial function takes two ﬁt-

parameters α and β, which have no predictive signiﬁ-

cance by themselves, but rather control the skewness.

Fits were made using Python’s SciPi package and

were relatively tight (an exhaustive list of all param-

eters can be found in the repo: (Anonymous, 2023)),

but typically, larger values of n have tighter ﬁts. Once

the ﬁts have been made, a generalized µ and σ can be

extracted as

µ =

nα

α + β

(1)

and

σ =

nαβ(α + β + n)

(α + β)

(α + β + 1)

(2)

Subsequently, µ and σ themselves can also be char-

acterized in n, which can be seen in Figure 4. The

ﬁrst two subﬁgures reveal that the number of expected

constraint violations increases linearly in the length of

the proteins (Figure 4, left) (ﬁt details for all param-

eters can be found in the repo: (Anonymous, 2023)).

For 2D random folds, the expected number of con-

straint violations behaves like

violations

= 0.3678n (3)

whereas in 3D random folds, the number of constrain

violations behaves like:

violations

= 0.1295n (4)

Although a linear increase is quite innocuous in many

problem solving contexts, in this case it is quite se-

vere. These numbers show an increase in expected

Can HP-protein Folding Be Solved with Genetic Algorithms? Maybe not

137

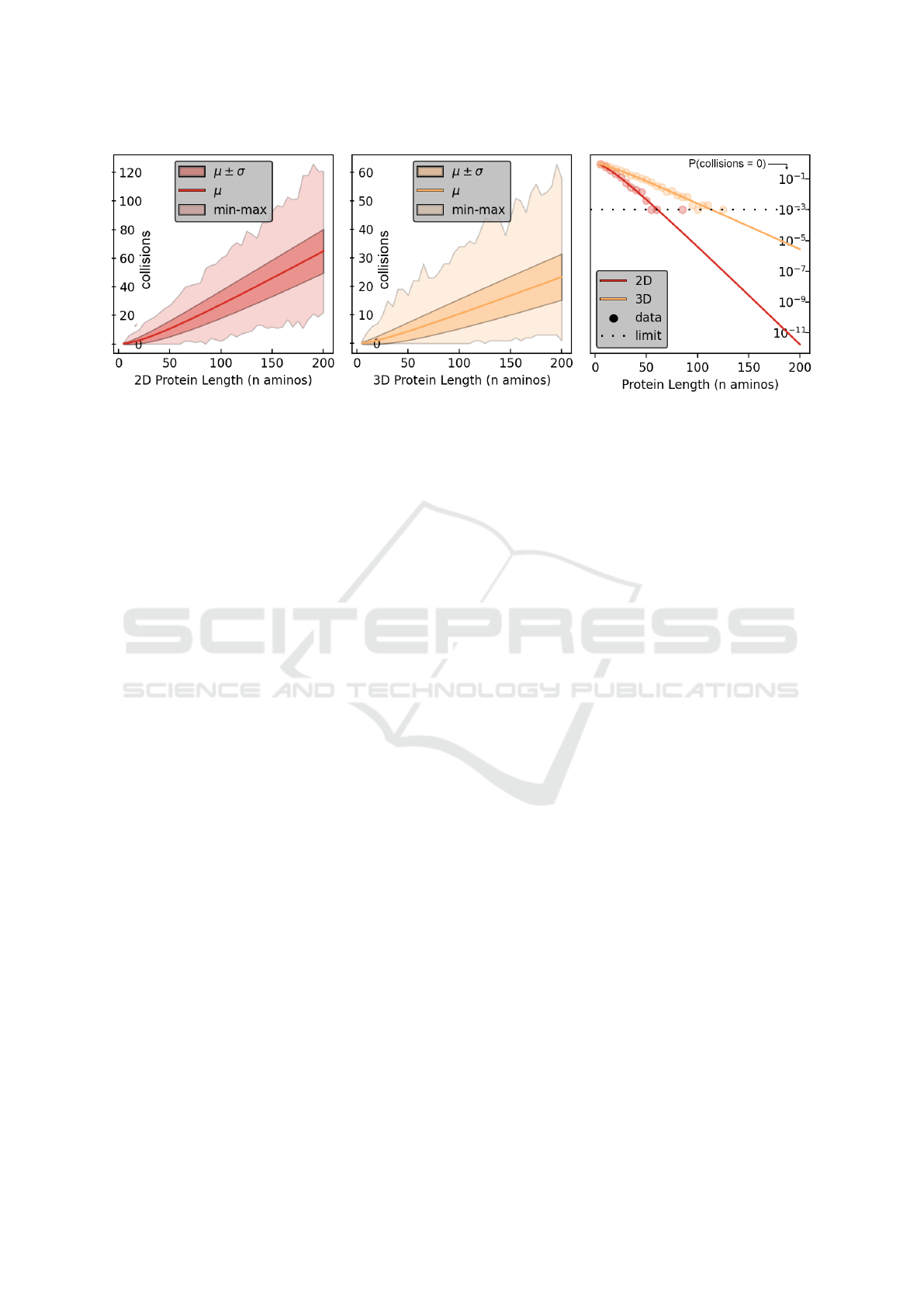
Figure 4: Left, Middle: The number of expected constraint violations (collisions) in folded protein conformations increases

linearly in the protein length, but slower in 3D than in 2D. Right: The chance of randomly sampling a zero-collision confor-

mation drops exponentially in n, but slightly slower in 3D than in 2D.

collisions as proteins get longer, and that might ex-

plain why none of the previous studies actually ran-

domly sample from the conformation space (without

problems): it simply cannot be done. A very, very pe-

culiar observation is that the 0.3678 coefﬁcient of the

2D violations is very close to 1/e.

In the classic HP-protein folding problem, for any

random conformation to be evaluated, it needs to have

zero violations, and this probability rapidly drops to

zero for larger values of n (Figure 4, right subﬁgure).

The probability of sampling a zero-violation confor-

mation in 2D is

(violations=0)

= 2.6024 · e

−0.1294n

(5)

which is a disheartening decrease in n. For 3D, the

probability of sampling a zero-violation conformation

(violations=0)

= 1.7629 · e

−0.0654n

(6)

which is less bad, but still not good. Presumably, the

dimensional increase, and thereby the degrees of free-

dom press both constants a bit, increasing the chance

of zero violations for random folds in 3D, as com-

pared to 2D.

5 CONCLUSION & DISCUSSION

Although the setup of this experiment is quite mod-

est, the implications could be huge. With an expected

number of collisions increasing in n, and a zero-

collision sample rapidly decreasing in n, it is very

hard, if not impossible, to sample valid initial solu-

tions for lengths up to n = 200, let alone more biolog-

ically realistic lengths of up to n = 2000. This result

reveals a rather disturbing reality: iterative heuristic

algorithms, a rather weak class in the spectrum, might

not be usable for HP-protein folding with any realistic

value of n, simply because we cannot uniformly ran-

domly sample from the conformation space. More-

over, we also suspect that the trouble with crossover

and mutation operators stem from the same source:

too many constraint violations. For smaller numbers

of n, some (possibly non-uniform) sample-and-repair

methods exist, which might or might not compro-

mise the metaheuristic’s performance, but for larger

numbers of n, there might not exist any reasonable

method of randomly generating initial solutions. This

just adds up to the fact that HP-protein folding is al-

ready NP-hard, thereby also disqualifying the elite

class of exact algorithms, even for lengths of ‘only’

200 aminos.

These conclusions paint a bleak picture for the

problem’s future, but there might be some ways for-

ward. Ultimately, we want to know whether it is

possible to uniformly randomly sample a conforma-

tion for the HP-protein folding problem in determin-

istic time, and what the lowest possible time com-

plexity for that random sampling algorithm would be.

Maybe, despite previously mentioned efforts, such a

sampling algorithm exists, but has simply never been

found yet. The same might be true for universally

applicable crossover and mutation operators; maybe

these still exist, but remain to be designed. Further-

more, problems like n-queens and traveling salesman

have proven to heavily rely on the existence of an efﬁ-

cient representation; considering the diversity in ear-

lier studies on HP-protein folding, this might be an-

other line worth exploring.

So things look quite disheartening, but things

could be worse. As it turns out, the traveling tourna-

ment problem also does not have a uniform sampling

method (yet), other than recreating invalid individu-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

138

als. And for this problem, the constraint violations

increase quadratically instead of linearly, becoming

infeasible from n = 12 already (Verduin et al., 2023b;

Verduin et al., 2023a). But things could be better, too.

For a problem such as TSP, uniformly randomly sam-

pling can be done in deterministic linear time (θ(n)):

1. Start with a full list of unpicked cities, and an

empty tour.

2. Add a randomly picked city from the list of un-

picked cities, and add it to the tour.

3. Delete that city from the list of unpicked cities.

4. If the list of unpicked cities is not empty, go back

to 2.

While this algorithm might be considered too triv-

ial to explicitly write down, it important to realize

that this method produces a uniformly random valid

TSP-solution in deterministic linear time. Point 3 is

important in this sense. Many programmers opt for

a boolean ‘picked marker’ for each city, and sim-

ply pick a new random city when an already chosen

city is accidentally picked. This will work for up to

very large instances without any noticeable delays,

and might even stochastically improve runtimes, as

deletion from a data structure such as an array is ex-

tremely expensive compared to ﬂipping a bit in a list

of boolean picked markers.

So it exists for TSP, but does such a uniform prob-

ability linear time selection algorithm also exist for

NP-protein folding? We do not think so. The best

we can do (for now) appears to be randomly sampling

a conformation by assigning all aminos a random di-

rection ∈ {left, right, straight}, relative to the

chain. Although this does guarantee that all confor-

mations have equal probability, it also includes a lot

of invalid conformations with colliding aminos. The

obvious solution is just to resample a few times until

we pick a valid solution, but how feasible is this ap-

proach as instances get bigger? Not very feasible, it

seems. For now, the race is on to ﬁnd a determinis-

tic polynomial time uniform sampling method, which

might or might not exist. For the future of this prob-

lem, it is of utmost importance.

REFERENCES

Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K.,

Walter, P., and Chaffey, N. (2003). Molecular biology

of the cell. 4th ed. Oxford University Press.

Anonymous (2023). Repository containing source

material: https://anonymous.4open.science/r/PF-

sampling/README.md.

Atari, M. and Majd, N. (2022). 2d hp protein folding us-

ing quantum genetic algorithm. In 2022 27th Inter-

national Computer Conference, Computer Society of

Iran (CSICC), pages 1–8.

Berger, B. and Leighton, T. (1998). Protein folding in the

hydrophobic-hydrophilic (hp) is np-complete. In Pro-

ceedings of the second annual international confer-

ence on Computational molecular biology, pages 30–

39.

Boumedine, N. and Bouroubi, S. (2021). A new hybrid

genetic algorithm for protein structure prediction on

the 2d triangular lattice. Turkish Journal of Electrical

Engineering and Computer Sciences, 29(2):499–513.

Bui, T. N. and Sundarraj, G. (2005). An efﬁcient genetic al-

gorithm for predicting protein tertiary structures in the

2d hp model. In Proceedings of the 7th Annual Con-

ference on Genetic and Evolutionary Computation,

GECCO ’05, page 385–392, New York, NY, USA. As-

sociation for Computing Machinery.

Creighton, T. E. (1988). The protein folding problem. Sci-

ence, 240(4850):267–267.

Cust

odio, F. L., Barbosa, H. J. C., and Dardenne, L. E.

(2004). Investigation of the three-dimensional lattice

hp protein folding model using a genetic algorithm.

Genetics and Molecular Biology, 27(4):611–615.

Dill, K. A. (1985). Theory for the folding and stability of

globular proteins. Biochemistry, 24(6):1501–1509.

Dill, K. A. and MacCallum, J. L. (2012). The

protein-folding problem, 50 years on. science,

338(6110):1042–1046.

Dobson, C. M. (1999). Protein misfolding, evolution and

disease. Trends in biochemical sciences, 24(9):329–

332.

Dondapati, S. K., Stech, M., Zemella, A., and Kubick,

S. (2020). Cell-free protein synthesis: a promis-

ing option for future drug development. BioDrugs,

34(3):327–348.

Eiben, A. E. and Smith, J. E. (2015). Introduction to evolu-

tionary computing. Springer.

Garza-Fabre, M., Rodriguez-Tello, E., and Toscano-Pulido,

G. (2015). Constraint-handling through multi-

objective optimization: The hydrophobic-polar model

for protein structure prediction. Computers & Opera-

tions Research, 53:128–153.

Hart, W. E. and Istrail, S. (1997). Robust proofs of np-

hardness for protein folding: general lattices and en-

ergy potentials. Journal of Computational Biology,

4(1):1–22.

Kaytako

glu, S. and Akyalc¸ın, L. (2007). Optimization of

parametric performance of a pemfc. International

Journal of Hydrogen Energy, 32(17):4418–4423.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).

Optimization by simulated annealing. Science,

220(4598):671–680.

Lau, K. F. and Dill, K. A. (1989). A lattice statistical me-

chanics model of the conformational and sequence

spaces of proteins. Macromolecules, 22(10):3986–

3997.

Can HP-protein Folding Be Solved with Genetic Algorithms? Maybe not

139

Leader, B., Baca, Q. J., and Golan, D. E. (2008). Protein

therapeutics: a summary and pharmacological classi-

ﬁcation. Nature reviews Drug discovery, 7(1):21–39.

Lee, C., Park, S.-H., Lee, M.-Y., and Yu, M.-H. (2000).

Regulation of protein function by native metastabil-

ity. Proceedings of the National Academy of Sciences,

97(14):7727–7731.

Levitt, M. (1982). Protein conformation, dynamics, and

folding by computer simulation. Annual review of bio-

physics and bioengineering, 11(1):251–271.

Levitt, M. (1983). Protein folding by restrained energy min-

imization and molecular dynamics. Journal of molec-

ular biology, 170(3):723–764.

Lin, C.-J. and Hsieh, M.-H. (2009). An efﬁcient

hybrid taguchi-genetic algorithm for protein fold-

ing simulation. Expert Systems with Applications,

36(10):12446–12453.

Maaranen, H., Miettinen, K., and M

akel

a, M. M. (2004).

Quasi-random initial population for genetic algo-

rithms. Computers & Mathematics with Applications,

47(12):1885–1895.

Patton, A. L., Punch, W. F., and Goodman, E. D. (1995). A

standard ga approach to native protein conformation

prediction. In Proceedings of the 6th International

Conference on Genetic Algorithms, page 574–581,

San Francisco, CA, USA. Morgan Kaufmann Publish-

ers Inc.

Runarsson, T. and Yao, X. (2000). Stochastic ranking for

constrained evolutionary optimization. IEEE Trans-

actions on Evolutionary Computation, 4(3):284–294.

Thomas, P. J., Qu, B.-H., and Pedersen, P. L. (1995). De-

fective protein folding as a basis of human disease.

Trends in biochemical sciences, 20(11):456–459.

Unger, R. and Moult, J. (1993). Genetic algorithms for pro-

tein folding simulations. Journal of Molecular Biol-

ogy, 231(1):75–81.

van Eck, O. and van den Berg, D. (2023). Quantifying

instance hardness of protein folding within the hp-

model. (accepted for publication at CIBCB’23).

Verduin, K., Thomson, S. L., and van den Berg, D.

(2023a). Too constrained for genetic algorithms. too

hard for evolutionary computing. the traveling tourna-

ment problem (to appear at ecta 2023).

Verduin, K., Weise, T., and van den Berg, D. (2023b). Why

is the traveling tournament problem not solved with

genetic algorithms?

Wang, S., Wu, L., Huo, Y., Wu, X., Wang, H., and Zhang,

Y. (2016). Predict two-dimensional protein folding

based on hydrophobic-polar lattice model and chaotic

clonal genetic algorithm. In Yin, H., Gao, Y., Li, B.,

Zhang, D., Yang, M., Li, Y., Klawonn, F., and Tall

on-

Ballesteros, A. J., editors, Intelligent Data Engineer-

ing and Automated Learning – IDEAL 2016, pages

10–17, Cham. Springer International Publishing.

Zhao, L. and Lu, W. (2011). D-peptide-based drug discov-

ery aided by chemical protein synthesis. Israel Jour-

nal of Chemistry, 51(8-9):868–875.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

140