Modelling Drag Forces on a Wheelchair Racing Simulator

Ateayeh Bayat

1,3

and Félix Chénier

1,2,3

Department of Systems Engineering, École de Technologie Supérieure (ÉTS), Montreal, Canada

Department of Physical Activity Sciences, Université du Québec à Montréal (UQAM), Canada

Centre for Interdisciplinary Research in Rehabilitation of Greater Montreal (CRIR), Canada

Keywords: Racing Wheelchair, Simulator, Dynamic Model, Drag Force.

Abstract: A racing wheelchair simulator is a stationary device that allows para-athletes to train inside, in different

simulated conditions (e.g., rolling resistance, wind). Apart from improving performance during training

sessions, it also allows researchers to study the biomechanics of the propulsion in a laboratory, which is

important because wheelchair racing can cause musculoskeletal disorders and pain in athletes. For these

reasons, the realism of these simulators is paramount, and having a model that reproduces a non-linear

relationship between drag force, wheeling speed and wind speed is one of the criteria for achieving this

realism. In this work, we develop and characterize such a model through empirical data recorded on a racing

track, and then implement it on a racing wheelchair simulator with a haptic controller. Propelling on this

simulator proved to be somewhat less challenging than real-life conditions, with a measured resistance force

approximately 5 N lower than during real propulsion conditions. However, the resistance expectedly

increased as simulated face wind increased. These results show a promising avenue for racing wheelchair

athletes, both for training and assessing/correcting their biomechanics.

1 INTRODUCTION

Wheelchair sports have gained recognition for their

positive impact on enhancing power, improving

quality of life, increasing social participation, and

reducing medical complications (Slater & Meade,

2004). However, a notable percentage of individuals

who rely on manual wheelchairs for daily mobility,

ranging from 30% to 73%, experience

musculoskeletal disorders (MSDs) and shoulder or

wrist pain due to repetitive loading during

propulsion (Boninger et al., 2002; Finley & Rodgers,

2004). The risk of developing MSDs is even higher

in wheelchair sports compared to regular wheelchair

use, as the shoulder endures increased strain (Finley

& Rodgers, 2004; Slater & Meade, 2004).

Preserving musculoskeletal integrity is crucial for

manual wheelchair users to maintain an active

lifestyle, underscoring the importance of targeted

sports training to mitigate the elevated risk of MSDs.

In comparison to other wheelchair sports such as

basketball, tennis, or cycling, wheelchair racing is

associated with a higher incidence of injuries

(Roussot, 2014; Taylor & Williams, 1995). Thus,

monitoring propulsion and studying its

biomechanics holds significant importance in

improving users’ health. However, due to the limited

availability of measuring instruments, the

biomechanics of wheelchair racing remain

understudied. To overcome the challenges of

measuring and controlling various propulsion

parameters in real-world settings, the use of in-

laboratory devices, called simulators, becomes

essential. These devices simulate wheelchair

propulsion in a controlled and safe environment,

enabling the measurement of different propulsion-

related parameters and facilitating proper and safe

propulsion training for users (Arlati et al., 2020;

MacGillivray et al., 2020).

To ensure that research findings apply to real-life

conditions, laboratory experiments must employ

instruments that accurately replicate realistic

dynamics (Vanlandewijck et al., 2001). In the case of

stationary devices, it is crucial to model the non-

linear relationship between wheelchair speed and

resistance force. In wheelchair racing, this force

comprises two primary components: 1) a constant

and viscous component influenced by factors such as

track hardness, tire pressure, wheel size, and the

normal force exerted on the ground; and 2) a

Bayat, A. and Chénier, F.

Modelling Drag Forces on a Wheelchair Racing Simulator.

DOI: 10.5220/0012223300003587

In Proceedings of the 11th International Conference on Spor t Sciences Research and Technology Support (icSPORTS 2023), pages 187-193

ISBN: 978-989-758-673-6; ISSN: 2184-3201

187

component that is proportional to the square of the

wheelchair velocity relative to the air, considering

factors such as athlete’s body position, aerodynamic

profile, and air density (Barbosa et al., 2016; van der

Woude et al., 2001). However, stationary devices on

the market (e.g. Invacare Corp., Revolution Sports

Inc.), employ mechanical rollers to support the rear

wheels of racing wheelchairs and fail to replicate the

intricate non-linear relationship between wheelchair

speed, rolling resistance, and air resistance.

To address these challenges, we first modelled

the relationship between total drag force and

airspeed using empirical data, in order to accurately

model propulsion on a stationary simulator with

greater realism. Then, building upon the previous

work of Chénier et al. (2014), we developed a

wheelchair racing simulator that aims to accurately

reproduce this non-linear resistance force, so that

our system provides users with realistic feedback

during propulsion, enhancing the overall simulation

experience. The aim of this communication is to

present our methodological development and

compare the propulsion forces between real and

simulated conditions.

2 METHODS

This study is composed of two phases. In the first

phase, the equation relating the total resistance force

and speed is developed and characterized using

propulsion data from two wheelchair racing athletes

on a racing track. In the second phase, this equation

is implemented on the simulator and the ability of

the simulator to reproduce this equation is tested

with a wheelchair racing athlete.

2.1 Phase 1. Racing Wheelchair

Dynamic Equations

The simulator needs a dynamic model of the racing

wheelchair to be implemented on it. This model is

expressed by:

𝐹

ulsion

𝐹

dra

𝑚𝑎

(1)

where 𝐹

propulsion

is the resulting linear force from

the propulsive moments applied by the user on the

pushrims that moves the wheelchair forward; 𝐹

drag

the force applied by the environment on the

wheelchair/athlete to prevent its movement; 𝑚 is the

mass of the wheelchair/athlete, and 𝑎 is the

wheelchair acceleration. The drag force is modelled

as:

𝐹

drag

𝜇



𝑚𝑔  𝜇



𝑚𝑔𝑣

wheelchair

𝜇





𝑣

wheelchai

𝑣

win





(2)

where 𝜇



and 𝜇



are the constant and viscous

terms of the rolling resistance, and 𝜇



is the air drag

coefficient, proportional to the square of the

difference between the wheelchair speed and the tail

wind speed.

To characterize this equation, a first experiment

took place on the Ben-Leduc 400m exterior racing

track of Marcel-Laurin Park, Montreal, CA. Two

wheelchair racing athletes were recruited for a study

on the characterization of drag forces during racing

wheelchair propulsion: 1) male, right-handed,

cerebral palsy, T34 classification; 2) female, right-

handed, double tibial amputee, T54 classification.

They gave their informed consent, and the project

was approved by the ethics committee of Université

du Québec à Montréal, #CIEREH 2022–4098. They

used their own racing wheelchair, where we replaced

one rear wheel with an instrumented racing wheel

similar to the one described in Chénier et al. (2021).

This instrumented wheel records the propulsive

forces and moments at a sampling rate of 2500 Hz.

We weighed the instrumented wheelchair and athlete

using 3 portable scales placed under each wheel.

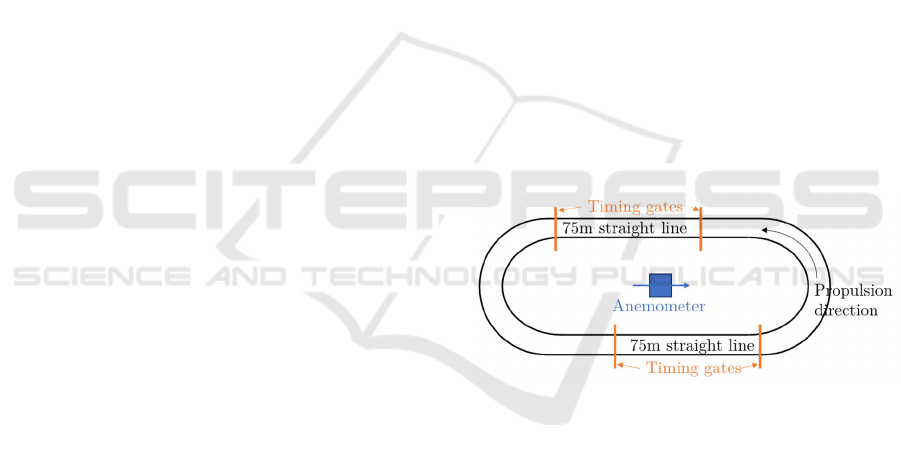
Figure 1: Racing track setup for determining the

coefficients of the dynamic equation.

The athletes were asked to propel at different

constant speeds of 14 to 20 km/h, controlled using a

bicycle computer. The pushrim moments were

measured using the instrumented wheel, which was

synchronized to timing gates delimiting two 75m

straight line zones as pictured in Fig. 1. Four

measurements per speed were done, with the

instrumented wheel installed on both sides. The tail

wind speed 𝑣

wind

was measured continually using an

anemometer (PCE VA-20). Since 𝑚𝑎  0 at a

constant speed, the total drag resistance 𝐹

drag

was

measured using the instrumented wheel using

𝐹

drag

𝐹

propulsion

. Due to assumed symmetry,

𝐹

propulsion

2𝑀

propulsion

/𝑟

wheel

where 𝑟

wheel

is the

radius of the rear wheel. This means that the

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

188

coefficients 𝜇



, 𝜇



and 𝜇



can be characterized by a

least square optimization using the following

equation:

2𝑀

propulsion

𝑟

wheel

𝜇



𝑚𝑔  𝜇



𝑚𝑔𝑣

wheelchair

𝜇





𝑣

wheelchai

𝑣

win





(3)

with 𝑀

propulsion

being measured by the instrumented

wheel, 𝑣

wheelchair

by the timing gates, and 𝑣

wind

the anemometer.

All 75-meter bouts were segmented using the

timing gates. Then, to compensate for inertial forces

due to anteroposterior body movement, only

complete propulsion cycles were processed: for each

bout, 𝑀

propulsion

was cut from the start of the first

push up to the start of the last push and was

averaged over this span.

The difference of 𝑀

propulsion

between both sides

(trials with the instrumented wheel on the left vs.

right) was 0.9 ± 3.7 Nm. There seems to be no side

bias, which suggests that 𝐹

drag

can effectively be

estimated using only one wheel. Characterizing

Eq. (3) yielded 𝜇



 0.00599, 𝜇



 0.000785 and

𝜇



 1.0187, for a coefficient of determination of

𝑅



 0.606.

2.2 Phase 2. Racing Wheelchair

Simulator

Fig. 2 shows the racing wheelchair simulator,

including both the roller and the racing wheelchair.

The wheelchair’s rear wheels sit on one roller that is

controlled by a 120-volt brushless servomotor and

drive.

Figure 2: UQAM Racing Wheelchair Simulator.

A force sensor is installed into the wheelchair

supports that hold the wheelchair in place, as seen in

Fig.3. By its location, it captures all the

anteroposterior forces between the simulator and the

wheelchair, including the inertial forces due to body

movements.

Real-time information from the force sensor is

fed to an admittance control loop using a real-time

computer (SpeedGoat). The admittance control is a

category of haptic controllers that controls the

relationship between force and speed. In this

controller, the input is the force and the controller

regulates the speed as dictated by the dynamic

equation to simulate (Cavenago et al., 2018). This

control system was chosen for the wheelchair racing

simulator as it is suited for controlling systems with

high inertia (Chenier et al., 2014; Keemink et al.,

2018). Fig. 4 shows the block diagram for an

admittance control block. Both the dynamic model

and speed controller (a proportional-integral—PI

controller) were implemented using Simulink Real-

Time on the SpeedGoat computer.

Figure 3: Force Sensor Location.

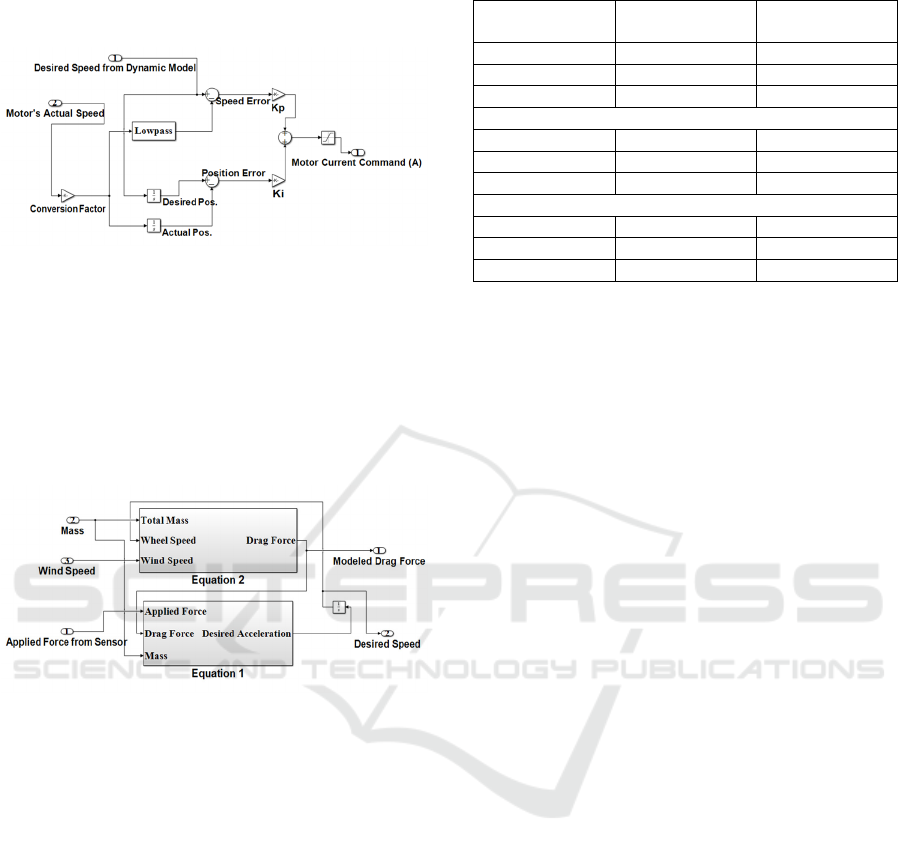
Figure 4: Block Diagram of Admittance Control.

The Simulink implementation of this simulator is

a novel modular structure where each part of the

system (e.g., force sensor input, dynamic model,

speed controller) is a separate block designed for

code reuse, and that includes its own unit test

procedure. This structure helps to easily add blocks

or iteratively enhance the system, avoiding

redesigns. It also uses predefined configuration

settings that will help researchers from other labs to

integrate this work into other wheelchair simulators,

Modelling Drag Forces on a Wheelchair Racing Simulator

189

using different versions of MATLAB/Simulink. Fig.

5 and Fig. 6 show the block diagram of the speed

controller and dynamic model respectively.

Figure 5: Block Diagram of Speed Controller.

In the speed controller (Fig. 5), the conversion

factor for the motor drive is defined based on the

radius ratio of the wheel, roller, and motor shaft.

This speed signal is then filtered by a low-pass

Bessel filter of order 2 with a cutoff frequency of

20 Hz. The gains for the PI controller were defined

based on the Ziegler method, and then modified by

trial and error, for final values of Kp = 7 and Ki = 5.

Figure 6: Block Diagram of Racing Wheelchair Dynamic

Model.

Equations 1 and 2 were implemented inside the

dynamic model (Fig. 6), which gives two outputs:

the modelled drag force is based on Eq. (2), and it

allows calculating a desired speed based on Eq. (1).

After calibrating the system (essentially

removing the force sensor offset), the simulated

parameters such as the wind speed can be sent in

real time to the simulator, allowing for the change of

the propulsion conditions inside the same propulsion

acquisition.

2.3 Experimental Test of the Racing

Simulator

Participant 2 of Phase 1 was re-invited for a test

experiment of the UQAM Racing Wheelchair

Simulator. His own racing wheelchair was affixed to

the simulator and the right wheel was replaced by

the instrumented wheel.

Table 1: Steady-state propulsion on the simulator.

Task Wheelchair

speed (km/h)

Wind speed

(m/s)

1101

2100

310-1

Rest

4121

5120

612-1

Rest

7141

8140

914-1

The athlete propelled on the simulator in three

blocks of constant speed, each segmented into three

wind speeds (no wind, 1 m/s tail wind, 1 m/s face

wind), as shown in Table 1 where a positive wind

speed value is a tail wind. He propelled for each

segment for the time equivalent to 75 m and had a

rest between blocks. Speed was controlled using a

bicycle computer.

After the propulsion, he answered a few quick

questions about his perception of the realism and

usefulness of the simulator.

2.3.1 Measured Parameters and Analysis

To verify the ability of the speed controller to match

the desired speed, we compared the desired speed to

the real speed.

Then, to verify the ability of the simulator to

match the desired drag force, we used the propulsive

moment measured by the instrumented wheel

(𝑀

propulsion

) to calculate the average measured drag

force 𝐹

drag

using the same method as in phase one.

The 𝐹

drag

(modelled) is the output of Equation 2

which was implemented in Dynamic Model Block.

For each task of Table 1, the average measured drag

force was compared to the average drag force

modelled by the simulator.

3 RESULTS

Fig. 7 presents a comparison of the desired and real

speed in m/s for a few pushes during task 5

(12 km/h, no wind) as an example. Overall, the RMS

of the error was of 0.0413 m/s for the controller.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

190

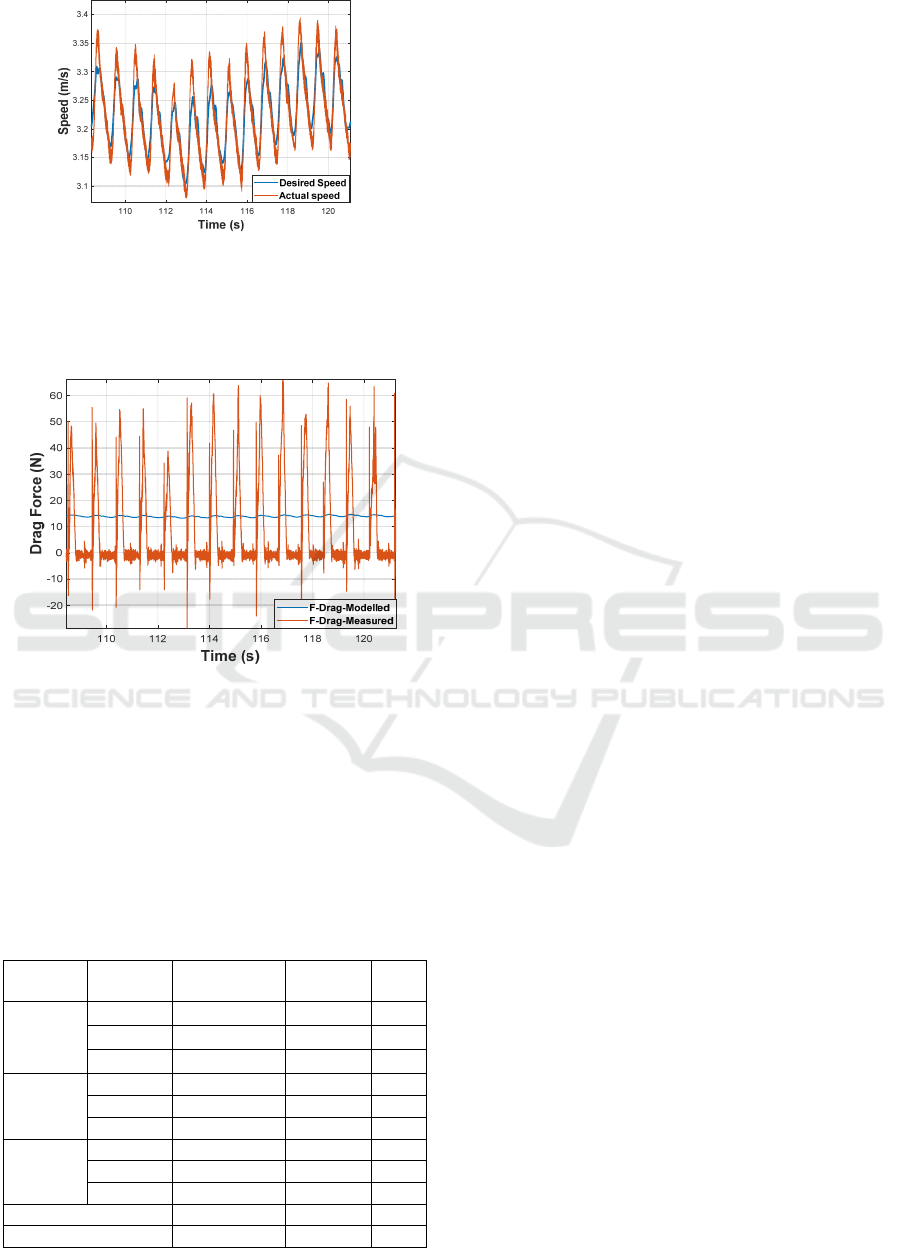
Figure 7: Desired and Real speed during a few pushes at

12 km/h block and 0 m/s wind speed segment.

Fig. 8 shows the modelled and measured drag force

during the same pushes as Fig. 7.

Figure 8: Values of modelled and measured 𝐹

drag

during a

few pushes at 12 km/h block and 0 m/s wind speed

segment.

Table 2 compares average values of modelled

and measured forces for all propulsion tasks during

the complete cycles with constant speed. As we

observe, the average value of drag force that the user

really

overcame (measured 𝐹

drag

) was lower than the

Table 2: Average values of modelled and measured drag

force in different propulsion conditions on the simulator.

ind spee

(m/s)

Avg. Model’

𝐹

dra

(N)

Avg. Meas.

𝐹

dra

(N)

Diff.

(N)

Block1

10 km/h

1 6.8 2.2 -4.6

0 11.5 6.9 -4.6

-1 17.7 12.6 -5.1

Block2

12 km/h

1 8.2 3.4 -4.8

0 13.8 8.1 -5.7

-1 21.2 16.2 -5.0

Block3

14 km/h

1 10.2 4.7 -5.5

0 16.7 11 -5.7

-1 23.1 20.3 -2.8

Mean 14.4 9.5 -4.9

Std. 5.7 6.1 0.9

one modelled by Eq. (2) (modelled 𝐹

drag

) by about

4.9 N, which suggests that it was easier to propel on

the simulator than in real conditions. The mean

value and standard deviation of these two forces

show that their difference is only a constant value.

4 DISCUSSION

Propelling on the simulator proved to be easier for

the athlete than intended. This discrepancy between

the modelled and measured drag forces may be

attributed to the lag in the controller’s response to

rapid changes. The controller fails to follow the

desired speed during rapid transitions, as depicted in

Fig. 7. Consequently, the wheel may accelerate

faster than it should during the first portion of the

push, resulting in a lower resistance.

This finding is particularly intriguing when we

compare this simulator with the LIO simulator

(Chenier et al., 2014) that uses a similar admittance-

based controller. However, in the LIO simulator, the

input force is measured by two instrumented wheels

instead of a force sensor at the rear of the

wheelchair. As a result of reading the external force

directly applied to the wheel, the LIO simulator’s

controller uses this information in a feed-forward

configuration to directly compensate for the

perturbation applied by the user. In contrast, the

current simulator substitutes the instrumented wheel

with a force sensor, following the configuration in

Pizzaro-Chong (2020). This modification enhances

the affordability, both in terms of cost and time, as

the athletes do not need to change their wheels for

instrumented wheels on the simulator. Furthermore,

this change facilitates the capture of all forces,

including the inertial forces due to body movement,

which may enhance the realism of the simulator

(Chenier et al., 2016). However, the drawback of

using the force sensor is that we could not

implement such a feedforward, as we do not

measure the force applied on the pushrims by the

user. Consequently, the controller could not react as

fast to these external perturbations. This is especially

important for a racing wheelchair simulator, where

the athletes apply high forces, at high speed, during

short amounts of time.

To address this limitation, we propose including

a physical inertia such as a flywheel in a future

iteration of the simulator, in addition to the

electronic inertia provided by our admittance

controller. This additional physical inertia will

compensate instantly for most of the perturbation

exerted by the user while letting the controller reach

Modelling Drag Forces on a Wheelchair Racing Simulator

191

a steady state using a similar proportional-integral

architecture.

Overall, the athlete’s perception of the

experiment was highly positive. He expressed great

satisfaction with the simulation, noting its similarity

to real conditions, where changes in wind speed

affect the sensation of resistance. From a training

aspect, the advantage of the simulator lies in

providing a controlled training environment without

the challenges faced when practising outdoors,

particularly in colder climates where exterior racing

tracks are unavailable during winter. However, the

athlete did mention a slight disparity in the

perceived amount of resistance compared to

overground conditions, which aligns with the

observations from the results.

The primary limitation of this study is the

restricted speed range in which the racing

wheelchair was evaluated. To comprehensively

assess its performance, higher speeds should be

investigated. However, due to the availability of only

one motor that lacked sufficient strength to

accommodate higher desired speeds, this objective

could not be achieved within the scope of this study.

Additionally, the participant pool was limited to a

single individual, which restricted the ability to fully

comprehend the simulator’s strengths and

weaknesses. Including a larger number of

participants would provide valuable insights in this

regard.

Future studies on the validation of this simulator

should investigate not only the drag mean force, but

other biomechanical variables such as instantaneous

force, power, and speed on both real and simulated

tracks. This comparison will establish the

simulator’s potential as a valuable tool to evaluate

the biomechanics of wheelchair racing, and

eventually as a better training tool for athletes.

5 CONCLUSION

The availability of a dependable stationary device

for racing wheelchair athletes, facilitating ecological

biomechanical measurement and training, is of

paramount importance. The simulator presented in

this work, along with the suggested dynamic model,

holds promise in serving this purpose. By adjusting

the resistance experienced by athletes according to

wind speed and their applied force, a more realistic

biomechanical assessment and training experience

can be achieved.

REFERENCES

Arlati, S., Colombo, V., Ferrigno, G., Sacchetti, R., &

Sacco, M. (2020). Virtual reality-based wheelchair

simulators: A scoping review. Assistive Technology,

32(6), 294—305. https://doi.org/10.1080/10400435.

2018.1553079

Barbosa, T. M., Forte, P., Estrela, J. E., & Coelho, E.

(2016). Analysis of the Aerodynamics by

Experimental Testing of an Elite Wheelchair Sprinter.

Procedia Engineering, 147, 2—6. https://doi.org/

10.1016/j.proeng.2016.06.180

Boninger, M. L., Souza, A. L., Cooper, R. A., Fitzgerald,

S. G., Koontz, A. M., & Fay, B. T. (2002). Propulsion

patterns and pushrim biomechanics in manual

wheelchair propulsion. Archives of Physical Medicine

and Rehabilitation, 83(5), 718–723. https://doi.org/

10.1053/apmr.2002.32455

Cavenago, F., Voli, L., & Massari, M. (2018). Adaptive

Hybrid System Framework for Unified Impedance and

Admittance Control. Journal of Intelligent & Robotic

Systems, 91(3–4), 569–581. https://doi.org/10.1007/s

10846-017-0732-1

Chenier, F., Bigras, P., & Aissaoui, R. (2014). A New

Wheelchair Ergometer Designed as an Admittance-

Controlled Haptic Robot. IEEE/ASME Transactions

on Mechatronics, 19(1), 321—328. https://doi.org/

10.1109/TMECH.2012.2235079

Chenier, F., Gagnon, D. H., Blouin, M., & Aissaoui, R.

(2016). A Simplified Upper-Body Model to Improve

the External Validity of Wheelchair Simulators.

IEEE/ASME Transactions on Mechatronics, 21(3),

1641–1649. https://doi.org/10.1109/TMECH.2016.252

7240

Chénier, F., Pelland-Leblanc, J.-P., Parrinello, A., Marquis,

E., & Rancourt, D. (2021). A high sample rate,

wireless instrumented wheel for measuring 3D

pushrim kinetics of a racing wheelchair. Medical

Engineering & Physics, 87, 30–37. https://doi.org/

10.1016/j.medengphy.2020.11.008

Finley, M. A., & Rodgers, M. M. (2004). Prevalence and

identification of shoulder pathology in athletic and

nonathletic wheelchair users with shoulder pain: A

pilot study. Journal of Rehabilitation Research and

Development, 41(3B), 395—402. https://doi.org/

10.1682/jrrd.2003.02.0022

Keemink, A. Q., van der Kooij, H., & Stienen, A. H.

(2018). Admittance control for physical human—robot

interaction. The International Journal of Robotics

Research, 37(11), 1421—1444. https://doi.org/10.117

7/0278364918768950

MacGillivray, M. K., Eng, J. J., Dean, E., & Sawatzky, B.

J. (2020). Effects of Motor Skill-Based Training on

Wheelchair Propulsion Biomechanics in Older Adults:

A Randomized Controlled Trial. Archives of Physical

Medicine and Rehabilitation, 101(1), 1–10. https://doi

.org/10.1016/j.apmr.2019.07.017

Pizarro-Chong, A. D. (2020). Development and Validation

of the Control Loops for the Haptic Interfaces of a

Standard Manual Wheelchair Simulator. 177.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

192

Richter, W. M., Kwarciak, A. M., Guo, L., & Turner, J. T.

(2011). Effects of Single-Variable Biofeedback on

Wheelchair Handrim Biomechanics. Archives of

Physical Medicine and Rehabilitation, 92(4), 572–

577. https://doi.org/10.1016/j.apmr.2010.11.001

Roussot, M. (2014). Upper limb injuries in athletes

participating at the London 2012 Paralympic Games

[Master Thesis, University of Cape Town].

https://open.uct.ac.za/handle/11427/13312

Slater, D., & Meade, M. A. (2004). Participation in

recreation and sports for persons with spinal cord

injury: Review and recommendations.

NeuroRehabilitation, 19(2), 121–129.

Taylor, D., & Williams, T. (1995). Sports injuries in

athletes with disabilities: Wheelchair racing.

Paraplegia, 33(5), 296—299. https://doi.org/10.1038

/sc.1995.67

van der Woude, L. H. V., Veeger, H. E. J., Dallmeijer, A.

J., Janssen, T. W. J., & Rozendaal, L. A. (2001).

Biomechanics and physiology in active manual

wheelchair propulsion. Medical Engineering & Physics,

23(10), 713–733. https://doi.org/10.1016/S 1350-

4533(01)00083-2

Vanlandewijck, Y., Theisen, D., & Daly, D. (2001).

Wheelchair Propulsion Biomechanics: Implications for

Wheelchair Sports. Sports Medicine, 31(5), 339–367.

https://doi.org/10.2165/00007256-200131050-00005

Modelling Drag Forces on a Wheelchair Racing Simulator

193