A Survey and Analysis of Evolutionary Operators for Permutations

Vincent A. Cicirello

Computer Science, School of Business, Stockton University, 101 Vera King Farris Dr, Galloway, NJ, U.S.A.

Keywords:

Crossover, Evolutionary Algorithms, Fitness Landscape Analysis, Java, Mutation, Open Source, Permutation.

Abstract:

There are many combinatorial optimization problems whose solutions are best represented by permutations.

The classic traveling salesperson seeks an optimal ordering over a set of cities. Scheduling problems often

seek optimal orderings of tasks or activities. Although some evolutionary approaches to such problems utilize

the bit strings of a genetic algorithm, it is more common to directly represent solutions with permutations.

Evolving permutations directly requires specialized evolutionary operators. Over the years, many crossover

and mutation operators have been developed for solving permutation problems with evolutionary algorithms.

In this paper, we survey the breadth of evolutionary operators for permutations. We implemented all of these

in Chips-n-Salsa, an open source Java library for evolutionary computation. Finally, we empirically analyze

the crossover operators on artiﬁcial ﬁtness landscapes isolating different permutation features.

1 INTRODUCTION

Combinatorial optimization often involves searching

for an ordering of a set of elements to either mini-

mize a cost function or maximize a value function. A

classic example is the traveling salesperson (TSP), in

which we seek the tour of a set of cities (i.e., simple

cycle that includes all cities) that minimizes cost (Pa-

padimitriou and Steiglitz, 1998). Many scheduling

problems in a variety of domains also involve search-

ing for an ordering of a set of elements (e.g., jobs,

tasks, activities, etc) that either minimizes or maxi-

mizes some objective function (Huang et al., 2023;

Ding et al., 2023; Xiong et al., 2022; Geurtsen et al.,

2023; Li and Wang, 2022; Pasha et al., 2022).

When faced with such an ordering problem, you

can turn to evolutionary computation. Although it is

certainly possible to represent solutions to ordering

problems with bit strings to enable using a genetic al-

gorithm and its standard operators, it is more com-

mon to more directly represent solutions with permu-

tations. But to evolve a population of permutations

requires the use of specialized evolutionary operators.

Many crossover and mutation operators were de-

veloped over the years for evolving solutions to per-

mutation problems. Some like Edge Recombina-

tion (Whitley et al., 1989) assume that a permutation

represents edges such as for the TSP and are designed

so children inherit edges from parents. Others like

https://orcid.org/0000-0003-1072-8559

Precedence Preservative Crossover (Bierwirth et al.,

1996) transfer precedences from parents to children,

such as for scheduling problems where completing

a given task earlier than others may improve solu-

tion ﬁtness. Operators like Cycle Crossover (Oliver

et al., 1987) enable children to inherit element posi-

tions from parents. Several studies examine the vari-

ety of problem features that can be important to solu-

tion ﬁtness for permutation problems (Campos et al.,

2005; Cicirello, 2019; Cicirello, 2022b). This is why

the literature is so rich with crossover and mutation

operators for permutations.

In this paper, we survey the breadth of evolution-

ary operators for permutations. We discuss how each

operator works, runtime complexity, and the problem

features that each operator focuses upon. Addition-

ally, we implemented all of the operators in Chips-n-

Salsa (Cicirello, 2020), an open source Java library

for evolutionary computation, with source code avail-

able on GitHub (https://github.com/cicirello/Chips-n-

Salsa). We specify our assumptions and other prelim-

inaries in Section 2. Sections 3 and 4 survey permu-

tation mutation and crossover operators, respectively.

In Section 5, we perform ﬁtness landscape analysis

of the crossover operators on artiﬁcial landscapes that

isolate different permutation features. This comple-

ments our prior analysis of mutation operators (Ci-

cirello, 2022b). We discuss conclusions in Section 6.

288

Cicirello, V.

A Survey and Analysis of Evolutionary Operators for Permutations.

DOI: 10.5220/0012204900003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 288-299

ISBN: 978-989-758-674-3; ISSN: 2184-3236

2 PRELIMINARIES

Assumptions: When discussing the runtime for im-

plementations of an operator, we assume that a per-

mutation is represented as an array of elements. The

runtime of some operators may be different if permu-

tations are instead represented by linked lists. We as-

sume both parents of a crossover are the same length,

although some may generalize to different length par-

ents. We use n to denote permutation length.

We assume that operators alter the parent permuta-

tions, i.e., mutation mutates the input permutation and

crossover transforms parents into children. In most

cases, this does not impact algorithm complexity, but

in other cases it does. The runtime of a few mutation

operators is O(1) with this assumption, but O(n) if a

new permutation was instead created.

Permutation Features: For each evolutionary

operator, we discuss the features of permutations that

the operator enables offspring to inherit from parents.

We analyze the operational behavior of the crossover

operators in this paper, including a ﬁtness landscape

analysis in Section 5. For the mutation operators,

some of the insights come from our prior work on ﬁt-

ness landscape analysis (Cicirello, 2022b). The per-

mutation features that we consider are as follows:

• Positions: Does mutation change a small number

of element positions? Does crossover enable chil-

dren to inherit absolute element positions from

parents? For example, element x is at index i in

a child if it was at index i in one of its parents.

• Undirected edges: If the permutation represents a

sequence of undirected edges (e.g., x adjacent to y

implies an undirected edge between x and y), does

mutation change a small number of edges? Does

crossover enable inheriting undirected edges? For

example, x and y are adjacent in a child if they are

adjacent in one of the parents.

• Directed edges: This is like above, but where

a permutation represents a sequence of directed

edges, such as for the Asymmetric TSP (ATSP).

• Precedences: Consider that a permutation repre-

sents a set of precedences. For example, x appear-

ing anywhere prior to y implies a preference for

x over y. Maybe a job for a scheduling problem

instance is critical to schedule earlier than others.

Does mutation change a small number of prece-

dences? Does crossover enable children to inherit

precedences from parents?

• Cyclic precedences: This feature is similar to the

above, but such that the precedences implied by

the permutation follow some unspeciﬁed rotation.

3 MUTATION OPERATORS

There are many mutation operators for permutations.

Some are so ubiquitous that it is difﬁcult to attribute

their origin to any speciﬁc work. Where possible, we

cite the mutation operator’s origin. Many of these,

however, are commonly utilized without speciﬁc at-

tribution, and their origins likely lost to history. If

additional reference is needed, there are many studies

to consult (Bossek et al., 2023; Cicirello, 2022b; Sut-

ton et al., 2014; Serpell and Smith, 2010; Eiben and

Smith, 2003; Valenzuela, 2001).

Swap: Swap mutation (also known as exchange)

chooses two different elements uniformly at random

and swaps them. Its runtime is O(1). It is a good

general purpose mutation because it is a small ran-

dom change regardless of the characteristics (e.g., po-

sitions, edges, precedences) most important to ﬁtness.

Adjacent Swap: This is swap mutation restricted

to adjacent elements. It tends to be associated with

very slow search progress (Cicirello, 2022b) due to

a very small neighborhood size compared to other

available mutation operators, and is thus of more lim-

ited application. Its runtime is O(1).

Insertion: Insertion mutation (also known as

jump mutation) removes a random element and rein-

serts it at a different randomly chosen position. Its

worst case and average case runtime is O(n) since

all elements between the removal and insertion points

shift (n/3 elements on average). It is worth consid-

ering in cases where the permutation represents a se-

quence of edges since an insertion is equivalent to re-

placing only 3 edges. It is shown especially effective

when permutation element precedences are important

to the problem (Cicirello, 2022b). However, it is a

poor choice when positions of elements impact ﬁt-

ness, because it disrupts the positions of a large num-

ber of elements (n/3 on average).

Reversal and 2-change: Reversal mutation

(also known as inversion) reverses a random sub-

permutation. Its runtime is O(n). Within a TSP

context, reversal is approximately equivalent to 2-

change (Lin, 1965), deﬁned as replacing two edges

of a tour to create a new tour. However, some

reversals don’t change any edges (e.g., reversing

the entire permutation). We include both a rever-

sal mutation and a true 2-change mutation in the

Chips-n-Salsa library (Cicirello, 2020). Reversal is

a good choice when a permutation represents undi-

rected edges. However, it is too disruptive in other

cases, including when a permutation represents di-

rected edges, such as for the ATSP, because it changes

the direction of n/3 directed edges on average.

3opt: The 3opt mutation (Lin, 1965) was orig-

A Survey and Analysis of Evolutionary Operators for Permutations

289

inally speciﬁed for the TSP within the context of a

steepest descent hill climber (i.e., systematically it-

erate over the neighborhood). The 3opt neighbor-

hood consists of all 2-changes and 3-changes, where

a k-change removes k edges from a TSP tour and re-

places them with k edges that form a different valid

tour. Our implementation in Chips-n-Salsa (Cicirello,

2020) generalizes 3opt from TSP tours to permu-

tations by assuming a permutation represents undi-

rected edges, independent of what it actually repre-

sents, and then randomizes the “edge” selection. Its

runtime is O(n). Like reversal, 3opt is worth consid-

ering when permutations represent undirected edges,

but it is too disruptive in all other cases.

Block-Move: A block-move mutation removes a

random contiguous block of elements, and reinserts

the block at a different random location. It generalizes

insertion mutation from single elements to a block of

elements. Like insertion mutation, it is appropriate

when permutations represent edge sequences (undi-

rected or directed) and it is equivalent to replacing

three edges. It is too disruptive in other contexts. Its

worst case and average case runtime is O(n).

Block-Swap: A block-swap (or block inter-

change) swaps two random non-overlapping blocks.

It generalizes swap mutation from elements to blocks.

It also generalizes block-move, since a block-move

swaps two adjacent blocks. Like block-move, it is ap-

propriate when permutations represent edges (undi-

rected or directed). In that context, it replaces up to

four edges. It is too disruptive in other contexts. Its

worst case and average case runtime is O(n).

Cycle: Cycle mutation’s two forms, Cycle(kmax)

and Cycle(α), induce a random k-cycle (Cicirello,

2022a). They differ in how k is chosen. Cycle(kmax)

selects k uniformly at random from {2,...,kmax}.

Cycle(α) selects k from {2,. ..,n}, with probabil-

ity of choosing k = k

′

proportional to α

′

−2

where

α ∈ (0.0, 1.0). Cycle(α)’s much larger neighborhood

better enables local optima avoidance. The worst case

and average runtime of Cycle(kmax) is a constant

that depends upon kmax. The worst case runtime of

Cycle(α) is O(n), while average runtime is a constant

that depends upon α. Both forms are effective when

element positions impact ﬁtness. Fitness landscape

analysis also suggests that it may be relevant in other

cases provided kmax or α carefully tuned.

Scramble: Scramble mutation, sometimes called

shufﬂe, picks a random sub-permutation and random-

izes the order of its elements. Its worst case and av-

erage runtime is O(n). It is usually too disruptive.

Surprisingly, it is effective for problems where per-

mutation element precedences are most important to

ﬁtness (Cicirello, 2022b), likely because the vast ma-

jority of pair-wise precedences are retained (e.g., all

involving at least one element not in the scrambled

block, and on average half of the precedences where

both elements are in the scrambled block).

Uniform Scramble: We introduced uniform

scramble mutation (Cicirello, 2022b) within research

on ﬁtness landscape analysis. In the common form of

scramble, the randomized elements are together in a

block, while in uniform scramble they are distributed

uniformly across the permutation. Each element is

chosen with probability u, and the chosen elements

are scrambled. Its worst case runtime is O(n) and av-

erage case is O(un). The work that introduced it con-

sidered the case of u = 1/3 to affect the same num-

ber of elements on average as scramble. In that case,

uniform scramble was too disruptive for general use.

We posited that it may be useful to periodically kick

a stagnated search (scramble might be useful for that

purpose as well). Lower values of u may be more ef-

fective for general use, but has not been explored.

Rotation: Chips-n-Salsa (Cicirello, 2020) in-

cludes a rotation mutation that performs a random cir-

cular rotation. It chooses the number of positions to

rotate uniformly at random from {1, ...,n − 1}. We

have neither used it ourselves in research, nor have we

seen others use it, so its strengths and weaknesses are

unknown. It is not possible to transform one permuta-

tion into any other simply via a sequence of rotations.

Thus, it is not likely effective as the only mutation op-

erator in an EA, but might be useful in combination

with others. Runtime is O(n).

Windowed Mutation: Several mutation opera-

tors involve choosing two or three random indexes

into the permutation. Window-limited mutation con-

strains the distance between indexes (Cicirello, 2014).

For example, window-limited swap chooses two ran-

dom elements that are at most w positions apart. Win-

dowed versions of swap, insertion, reversal, block-

move, and scramble are all potentially applicable to

some problems. Like adjacent swap, which is a win-

dowed swap with w = 1, we posit that they likely lead

to slow search progress in most cases if w is too low.

We include them here to be comprehensive, but their

strengths are unclear. The runtime of windowed swap

is O(1), and the runtime of the others is O(min(n,w)),

or just O(w) if we assume that w < n.

Algorithmic Complexity: Table 1 summarizes

the worst case and average case runtime of the mu-

tation operators. The bottom portion concerns the

windowed mutation operators. The notation Swap(w)

means windowedswap with window limit w, and like-

wise for the other windowed operators.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

290

Table 1: Runtime of the mutation operators.

Mutation Worst case Average case

Swap O(1) O(1)

Adjacent Swap O(1) O(1)

Insertion O(n) O(n)

Reversal O(n) O(n)

2-change O(n) O(n)

3opt O(n) O(n)

Block-Move O(n) O(n)

Block-Swap O(n) O(n)

Cycle(kmax) O((

kmax

)

) O((

kmax

)

Cycle(α) O(n) O((

2−α

1−α

)

Scramble O(n) O(n)

Uniform Scramble O(n) O(un)

Rotation O(n) O(n)

Swap(w) O(1) O(1)

Insertion(w) O(w) O(w)

Reversal(w) O(w) O(w)

BlockMove(w) O(w) O(w)

Scramble(w) O(w) O(w)

4 CROSSOVER OPERATORS

There are many crossover operators for permutations.

We describe the behavior of each here, and discuss the

permutation features that they best enable inheriting

from parents, conﬁrmed empirically in Section 5.

Cycle Crossover (CX): The CX (Oliver et al.,

1987) operator picks a random permutation cycle of

the pair of parents. Child c

inherits the positions of

the elements that are in the cycle from parent p

, and

the positions of the other elements from parent p

Likewise, child c

inherits the positions of the ele-

ments in the cycle from p

, and the positions of the

other elements from p

A permutation cycle is a cycle in a directed graph

deﬁned by a pair of permutations. The vertexes of

this hypothetical graph are the permutation elements.

This graph has an edge from x to y if and only

if the index of x in permutation p

is the same as

the index of y in permutation p

. As an example,

consider permutations p

= [0,1,2,3,4,5] and p

[2,1, 4,5, 0,3]. The graph consists of the directed

edges: {(0,2), (1,1),(2, 4),(3,5),(4,0), (5,3)}. We

don’t actually need to build the graph. There are

three permutation cycles in this example: a 2-cycle in-

volving elements {3,5}, a 3-cycle involving elements

{0,2, 4}, and a singleton cycle with {1}.

CX picks a random index, computes the cycle

containing the elements at that index, and exchanges

those elements to form the children. In this exam-

ple, if any of {0,2, 4} is the random element, then

the children will be: c

= [2, 1,4, 3,0, 5] and c

[0,1, 2,5, 4,3]. Runtime is O(n).

CX strongly transfers positions from parents to

children. Every element in a child inherits its position

from one of the parents. Children also inherit all pair-

wise precedences from one or the other of the parents.

For example, all elements in a child that inherited po-

sitions from p

retain the pairwise precedences from

, and similarly for the elements inherited from p

The cycle exchange likely breaks many edges.

Edge Recombination (ER): ER (Whitley et al.,

1989) assumes that a permutation represents a cyclic

sequence of undirected edges, such as for the TSP.

Using a data structure called an edge map (Whitley

et al., 1989) for efﬁcient implementation, the set of

undirected edges that appear in one or both parents is

formed. Each child is then created only using edges

from that set. It is thus an excellent choice for prob-

lems where permutations represent undirected edges,

but it is unlikely to perform well otherwise.

Consider an example with p

= [3,0,2,1, 4]

and p

= [4,3,2,1,0]. Parent p

includes the

undirected edges { (3,0),(0, 2),(2,1),(1,4), (4,3)},

and p

includes {(4,3),(3,2), (2,1),(1, 0),(0,4)}.

The union of these is the set of undirected edges

{(3,0), (0,2),(2, 1),(1,4),(4,3), (3,2),(1, 0),(0,4)}.

Initialize child c

with the ﬁrst element of p

= [3]. The 3 is adjacent to 0, 2, and 4 in the edge

set. Choose the one that is adjacent to the fewest

elements that are not yet in the child. In this case, 0 is

adjacent to three elements, and 2 and 4 are adjacent

to two elements each. Break the tie randomly.

Consider that the random tie breaker resulted in 4

to give us c

= [3,4]. The 4 is adjacent to 0 and 1

in the edge set, both of which are adjacent to two

elements that haven’t been used yet, so pick one of

these randomly. Assume that we chose 1 to arrive at

= [3, 4,1]. The 1 is adjacent to 0 and 2, which are

also the only remaining elements and thus another

tie. Pick one at random, such as 0 in this example, to

obtain c

= [3,4,1,0]. Finally add the last element:

= [3,4,1,0,2]. The other child c

is formed in a

similar way, but initialized with the ﬁrst element of

. The runtime of ER is O(n).

Enhanced Edge Recombination (EER):

EER (Starkweather et al., 1991) works much like

ER, forming children from edges inherited from the

parents. However, EER attempts to create children

that inherit subsequences of edges that the parents

have in common. Efﬁcient implementation utilizes a

variation of ER’s edge map that is augmented to label

the edges that the parents have in common. Each

child is generated similarly to ER, except that the

decision on which element to add next prefers edges

that start common subsequences. See the original

A Survey and Analysis of Evolutionary Operators for Permutations

291

presentation of EER (Starkweather et al., 1991) or

our open source implementation for full details.

Like ER, the runtime of EER is O(n) and it strongly

enables inheriting undirected edges from parents, but

not so much other permutation features.

Order Crossover (OX): OX (Davis, 1985) begins

by selecting two random indexes to deﬁne a cross re-

gion similar to a two-point crossover for bit strings.

Child c

gets the positions of the elements in the re-

gion from parent p

, and the relative ordering of the

remaining elements from p

but populated into c

be-

ginning after the cross region in a cyclic manner. The

original motivating problem was the TSP, which is

likely why they chose to insert the relatively ordered

elements after the cross region wrapping to the front

since it gets all the relatively ordered elements to-

gether if you view the permutation as a cycle. Child c

is formed likewise, inheriting positions of elements in

the region from p

and the relative order of the other

elements from p

. Runtime is O(n).

Consider an example with p

= [0, 1,2, 3,4, 5,6, 7]

and p

= [1,2,0,5,6,7,4,3]. Let the random cross

region consist of indexes 2 through 4. Child c

gets the elements at those indexes from p

, such

as c

= [x, x,2, 3,4,x, x,x], where each x is a place-

holder. The rest of the elements are relatively or-

dered as in p

, i.e., in the order 1,0, 5,6, 7, but pop-

ulated into c

beginning after the cross region to ob-

tain c

= [6,7,2,3,4,1,0,5]. Likewise, initialize c

with the elements from the cross region of p

to get

= [x,x,0, 5,6, x,x,x]. Then, populate it after the

cross region with the remaining elements relatively

ordered as in p

to obtain c

= [4,7, 0,5, 6,1,2,3].

OX is effective for edges, since it enables inher-

iting large numbers of edges. All adjacent elements

within the cross region represent edges inherited from

one parent. Getting the relative order of the remaining

elements from the other parent tends to inherit many

edges from that parent, although some edges will be

broken where the cross region elements had been pre-

viously. Unlike ER and EER, OX’s behaviorfor edges

is independent of whether they are undirected or di-

rected edges, such as for the TSP or the ATSP. OX

is not effective for other features. Many precedences

are ﬂipped due to how OX populates the relatively or-

dered elements after the cross region wrapping to the

front. And although the positions of the elements in

the cross region are inherited by the children, the ma-

jority of the elements are positioned in the children

rather differently than the parents.

Non-Wrapping Order Crossover (NWOX):

The NWOX operator (Cicirello, 2006) is similar to

OX. However, the relatively ordered elements popu-

late the child from the left end of the permutation,

jumping over the cross region, and continuing to the

right end. Consider the earlier example with parents

= [0,1,2,3,4,5,6,7] and p

= [1, 2,0,5,6,7,4,3],

and the same random cross region. Child c

is still

initialized with the cross region from p

as c

[x,x,2, 3,4, x,x,x]. But the relatively ordered ele-

ments, 1,0,5,6,7, from p

, ﬁll in from the left to

obtain c

= [1,0,2,3,4,5,6,7]. Likewise initialize

= [x, x,0, 5,6,x, x,x], but ﬁll in relatively ordered

elements from the left to get c

= [1,2, 0,5, 6,3,4,7].

Unlike OX, NWOX is very effective for cases

where element precedences are important to ﬁtness,

the original motivation for NWOX. Every pairwise

precedence relation in a child is present in at least one

of the parents. However, NWOX breaks more edges

than OX. And like OX, NWOX tends to displace el-

ements from their original positions, although less so

than OX. Runtime is O(n).

Uniform Order Based Crossover (UOBX):

UOBX (Syswerda, 1991) is a uniform analog of OX

and NWOX. It is controlled by a parameter u, which

is the probability that a position is a ﬁxed-point. That

is, child c

gets the position of the element at in-

dex j in parent p

with probability u. The rela-

tive order of the remaining elements comes from the

other parent. Consider p

= [3,0,6,2,5,1,4,7] and

= [7,6,5,4,3,2,1,0], u = 0.5, and that indexes

0, 3, 4, and 6 were chosen as ﬁxed points. Child

is initialized with c

= [3,x, x,2, 5,x,4,x]. The

remaining elements are relatively ordered as in p

(i.e., 7, 6, 1, 0), and inserted into the open spots

left to right to obtain c

= [3,7,6,2,5,1,4,0]. Like-

wise, c

gets the elements at the ﬁxed points from p

= [7,x,x,4, 3,x,1,x]. The other elements are then

relatively ordered as in p

(i.e., 0, 6, 2, 5) to obtain

= [7,0, 6,4, 3,2,1,5].

With UOBX, all pairwise precedences within the

children are inherited from one or the other of the

parents (just like with NWOX). This is because the

ﬁxed points have same relative order as the parent

where they originated, and the others the same rel-

ative order as in the other parent. For other prob-

lem features, UOBX may be relevant if u is carefully

tuned. For example, UOBX is capable of transferring

many element positions to children if u is sufﬁciently

high. UOBX likely breaks many edges since the ﬁxed

points are uniformly distributed along the permuta-

tion. However, if u is low, it may retain many edges

from parents. Runtime is O(n).

Order Crossover 2 (OX2): Syswerda introduced

OX2 in the same paper as UOBX (Syswerda, 1991).

He originally called it order crossover, but others be-

gan using the name OX2 (Starkweather et al., 1991)

to distinguish it from the original OX, and that name

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

292

has stuck. OX2 is rather different than OX. OX2 be-

gins by selecting a random set of indexes. Syswerda’s

original description implied each index equally likely

chosen as not chosen. In our implementation in

Chips-n-Salsa (Cicirello, 2020), we provide a pa-

rameter u that is the probability of choosing an in-

dex. For Syswerda’s original OX2, set u = 0.5. The

elements at those indexes in p

are found in p

Child c

is formed as a copy of p

with those ele-

ments rearranged into the relative order from p

. In

a similar way, the elements at the chosen indexes

in p

are found in p

. Child c

becomes a copy

of p

but with those elements rearranged into the

relative order from p

. Consider an example with

= [1,0,3,2,5,4,7,6] and p

= [6,7,4,5,2,3,0,1],

and random indexes: 1, 2, 6, and 7. The elements

at those indexes in p

, ordered as in p

, are: 7, 4,

0, 1. Rearrange these within p

to produce c

[7,4, 3,2, 5,0,1,6]. The elements at the random in-

dexesin p

, ordered as in p

, are: 0, 3, 7, 6. Rearrange

these within p

to produce c

= [0,3, 4,5, 2,7,6,1].

OX2 is closely related to UOBX. Each child pro-

duced by OX2 can be produced by UOBX from the

same pair of parents, but different random indexes,

and vice versa. However, the pair of children pro-

duced by OX2 will differ from the pair produced by

UOBX. Thus, OX2 and UOBX are not exactly equiv-

alent. It is unclear whether there are cases when one

outperforms the other. They should be effective for

the same problem features. OX2’s runtime is O(n).

Precedence Preservative Crossover (PPX):

Bierwirth et al introduced two variations of a

crossover operator focused on precedences, both of

which they referred to as PPX (Bierwirth et al., 1996).

We refer to the two-point version as PPX, and we con-

sider the uniform version later. Both variations were

originally described as producing one child from two

parents. In our implementation in Chips-n-Salsa (Ci-

cirello, 2020), we generalize this to produce two chil-

dren. In the two-point PPX, two random cross points,

i and j, are chosen. Without loss of generality, assume

that i is the lower of these. Child c

inherits every-

thing left of i from p

, and likewise c

everything left

of i from p

. Let k = j − i + 1. Child c

inherits the

ﬁrst k elements left-to-right from p

that are not yet

in c

, and similarly for the other child. The remaining

elements of c

come from p

in the order they appear

in p

, and likewise for the other child.

Consider p

= [7,6, 5,4, 3,2, 1,0] and p

[0,1, 2,3, 4,5,6,7] with random i = 3, j = 5, and

k = j− i+ 1 = 3. The ﬁrst i = 3 elements of c

come

from p

, i.e., c

= [7,6, 5], and likewise c

= [0,1, 2].

The next k = 3 elements of c

are the ﬁrst 3 ele-

ments of p

that are not yet in c

, which results in

= [7, 6,5, 0,1, 2]. Similarly, c

= [0,1,2,7,6,5].

Complete c

with the remaining elements of p

that

are not yet in c

from left to right. The ﬁnal c

[7,6, 5,0, 1,2,4,3] and c

= [0,1, 2,7, 6,5,3,4].

The children created by PPX inherit all prece-

dences from one or the other of the parents. How-

ever, many edges are broken relative to the parents,

and very fewpositions are inherited. Runtime is O(n).

Uniform Precedence Preservative Crossover

(UPPX): We refer to the uniform version of

PPX (Bierwirth et al., 1996) as UPPX. It originally

produced one child from two parents, but we general-

ize to create two children. Generate a random array of

n booleans (Bierwirth et al originally speciﬁed array

of ones and twos). Let u be the probability of true. We

added this u parameter,which was not present in Bier-

wirth et al’s version. For original UPPX, set u = 0.5.

To form child c

iterate over the array of booleans. If

the next value is true, then add to c

the ﬁrst element

of p

not yet present in c

, and otherwise add to c

the ﬁrst element of p

not yet present. Form child c

at the same time, but true means add to c

the ﬁrst el-

ement of p

not yet present in c

, and otherwise the

ﬁrst element of p

not yet present.

UPPX focuses on transferring precedences from

parents to children. The original case, u = 0.5, is

unlikely suitable when edges or positions are impor-

tant to ﬁtness. However, higher or lower values of u

increases likelihood of consecutive elements coming

from the same parent. Thus, tuning u may lead to

an operator relevant for problems like the TSP where

edges are critical to ﬁtness. Runtime is O(n).

Partially Matched Crossover (PMX): Goldberg

and Lingle introduced PMX (Goldberg and Lingle,

1985; Goldberg, 1989). PMX initializes children c

and c

as copies of parents p

and p

. It deﬁnes a

cross region with a random pair of indexes, which de-

ﬁnes a sequence of swaps. For each index i in the

cross region, let x be the element at index i in p

, and

y be the element at that position in p

. Swap elements

x and y within c

, and swap x and y within c

Consider p

= [0,1, 2,3, 4,5,6,7] and p

[1,2, 0,5, 6,7,4,3], and random cross region from in-

dex 2 to index 4, inclusive. Child c

is initially

a copy of p

: c

= [0,1,2,3,4,5,6,7]. Swap the

2 with the 0 (i.e., elements at index 2 in the par-

ents): c

= [2,1,0,3,4,5,6,7]. Next, swap the 3

with the 5 (i.e., elements at index 3 in the parents):

= [2,1,0,5,4,3,6,7]. Finally, swap the 4 with

the 6 (i.e., elements at index 4 in the parents): c

[2,1, 0,5, 6,3,4,7]. Follow the same process for the

other child to get: c

= [1,0, 2,3, 4,7,6,5].

In the original PMX description, the indexes of the

elements to swap were found with a linear search, and

A Survey and Analysis of Evolutionary Operators for Permutations

293

since the average size of the cross region is also linear

(i.e., n/3 on average), PMX as originally described

required O(n

) time. The runtime of our implemen-

tation in Chips-n-Salsa (Cicirello, 2020) is O(n). In-

stead of linear searches, we generate the inverse of

each permutation in O(n) time to use as a lookup ta-

ble to ﬁnd each required index in constant time.

The cross region has an average of n/3 elements,

due to which each child inherits n/3 element positions

on average from each parent. Thus, children inherit a

signiﬁcant number of positions from the parents (at

least 2n/3 on average). Although the cross region of

each child includes consecutive elements (i.e., edges)

from the opposite parent, many edges are broken else-

where, so PMX is disruptive for edges. However,

PMX preserves precedences well.

Uniform Partially Matched Crossover

(UPMX): UPMX uses indexes uniformly dis-

tributed along the permutations rather than PMX’s

contiguous cross region (Cicirello and Smith, 2000).

Parameter u is the probability of including an index.

The elements at the chosen indexes deﬁne the swaps

in the same way as in PMX. Runtime is O(n).

Consider p

= [7,6, 5,4, 3,2, 1,0] and p

[1,2, 0,5, 6,4,7,3], and random indexes 3, 1, and 6.

Initialize c

= [7,6,5,4,3,2,1,0]. Element 4 is at in-

dex 3 in p

, and 5 is at that index in p

. UPMX swaps

the 4 and 5 to obtain c

= [7,6,4,5,3,2,1,0]. Ele-

ments 6 and 2 are at index 1 in p

and p

. UMPX

swaps the 6 and 2 to get c

= [7, 2,4, 5,3, 6,1, 0]. Ele-

ments 1 and 7 are at index 6 in p

and p

. Swap the 1

and 7 to get the ﬁnal c

= [1, 2,4,5,3,6,7,0]. Follow

the same process to derive c

= [7,6, 0,4, 2,5,1,3].

Children inherit positions and precedences from

parents to about the same degree as in PMX. The uni-

formly distributed indexes likely break most edges.

But if u is low, many edges may also be preserved.

Position Based Crossover (PBX): Barecke and

Detyniecki designed PBX to strongly focus on posi-

tions (Barecke and Detyniecki, 2007). One of PBX’s

objectives is for a child to inherit approximately equal

numbers of element positions from each of its parents.

PBX proceeds in ﬁve steps. It ﬁrst generates a list

mapping each element to its indexes in the parents.

Consider p

= [2,5, 1,4, 3,0] and p

= [5,4, 3,2, 1,0].

The list of index mappings would be [0 → (5,5),1 →

(2,4),2 → (0, 3),3 → (4,2), 4 → (3,1),5 → (1,0)].

Mapping 1 → (2, 4) means that element 1 is at index

2 in p

and index 4 in p

. Step 2 randomizes the or-

der of the elements in this list, e.g., [3 → (4,2),5 →

(1,0),0 → (5, 5),2 → (0,3), 1 → (2,4),4 → (3,1)].

Also at this stage, PBX chooses a random subset of

elements (each element chosen with probability 0.5),

and swaps the order of the indexes of those elements.

For this example, elements 5 and 1 are chosen. Map-

ping 5 → (1,0) becomes 5 → (0,1), and 1 → (2,4)

becomes 1 → (4,2). This results in [3 → (4,2),5 →

(0,1),0 → (5, 5),2 → (0,3), 1 → (4,2),4 → (3, 1)].

Step 3 begins populating the children by iterating

this list, and for each mapping e → (i

) it at-

tempts to put element e at index i

in c

and in-

dex i

in c

, skipping any if the index is occupied.

For this example, we’d have: c

= [5, x, x,4, 3,0] and

= [x,5,3,2, x,0]. Step 4 makes a second pass try-

ing the index from the other parent to obtain: c

[5,x,1,4,3,0] and c

= [x,5, 3,2, 1,0]. One ﬁnal pass

places any remaining elements in open indexes: c

[5,2, 1,4, 3,0] and c

= [4,5, 3,2, 1,0].

PBX is strongly position oriented, although less

so than CX since PBX’s last pass puts some elements

at different indexes than either parent. But unlike CX,

PBX children inherit equal numbers of element posi-

tions from parents on average. As a result, children

also inherit approximately equal numbers of prece-

dences from parents, but many edges are disrupted

since inherited positions are not grouped together.

The runtime of PBX is O(n).

Heuristic-Guided Crossover Operators: We

are primarily focusing on crossover operators that

are problem-independent, and which do not require

any knowledge of the optimization problem at hand.

However, there are also some powerful problem-

dependent crossover operators that utilize a heuristic

for the problem. We discuss a few of these here, al-

though these are not currently included in our open

source library (Cicirello, 2020). One of the more

well known crossover operators of this type is Edge

Assembly Crossover (EAX) (Watson et al., 1998)

for the TSP, which utilizes a TSP speciﬁc heuris-

tic. Many have proposed variations and improve-

ments to EAX (Sanches et al., 2017; Nagata and

Kobayashi, 2013; Nagata, 2006), including adapt-

ing to other problems (Nagata et al., 2010; Na-

gata, 2007). Another example of a crossover oper-

ator guided by a heuristic is Heuristic Sequencing

Crossover (HeurX) (Cicirello, 2010), which was orig-

inally designed for scheduling problems, and which

requires a constructive heuristic for the problem.

EAX and its many variations are focused on prob-

lems where edges are most important to solution ﬁt-

ness, whereas HeurX is primarily focused on prece-

dences. There are other crossover operators that rely

on problem-dependent information (Freisleben and

Merz, 1996), and utilize local search while creating

children (Barecke and Detyniecki, 2022).

Algorithmic Complexity: The runtime (worst

and average cases) of the crossover operators in this

section, except the heuristic operators, is O(n).

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

294

5 CROSSOVER LANDSCAPES

In this section, we analyze the ﬁtness landscape char-

acteristics of the crossover operators. We use the Per-

mutation in a Haystack problem (Cicirello, 2016) to

deﬁne ﬁve artiﬁcial ﬁtness landscapes, each isolating

one of the permutation features listed earlier in Sec-

tion 2. In the Permutation in a Haystack, we must

search for the permutation that minimizes distance to

a target permutation. The optimal solution is obvi-

ously the target, much like in the OneMax problem

the optimal solution is the bit string of all one bits.

However, the Permutation in a Haystack provides a

mechanism for isolating a permutation feature of in-

terest in how we deﬁne distance. To focus on ele-

ment positions, we use exact match distance (Ronald,

1998), the number of elements in different positions

in the permutations. We deﬁne ﬁtness landscapes for

undirected and directed edges using cyclic edge dis-

tance (Ronald, 1997) and cyclic r-type distance (Cam-

pos et al., 2005), respectively. Cyclic edge distance

is the number of edges in the ﬁrst permutation, but

not in the other, if the permutations represent undi-

rected edges, including an edge from last element to

ﬁrst. Cyclic r-type distance is its directed edge coun-

terpart. We use Kendall tau distance (Kendall, 1938),

the minimum number of adjacent swaps to transform

one permutationinto the other,to deﬁne a ﬁtness land-

scape for precedences. We use Lee distance (Lee,

1958) to deﬁne a landscape characterized by cyclic

precedences. This last permutation feature, and corre-

sponding distance function, were derived from a prin-

cipal component analysis in our prior work (Cicirello,

2019; Cicirello, 2022b), and we are unaware of any

real problem where this feature is important.

For all landscapes, we use permutation length

n = 100, and generate 100 random target permuta-

tions. We use an adaptive EA that evolves crossover

and mutation rates to eliminate tuning these a priori.

Each population member (p

,σ

) consists of a

permutation p

, crossover rate c

, mutation rate m

and a σ

. In a generation, parent permutations p

cross with probability c

(which parent is i is arbi-

trary), and each permutation mutates with probability

. We use swap mutation because it is simple and

works reasonably well across a range of features. The

and m

are initialized randomly in [0.1, 1.0], and

mutated with Gaussian mutation with standard devia-

tion σ

, constrained to [0.1,1.0]. The σ

are initialized

randomly in [0.05,0.15] and mutated with Gaussian

mutation with standard deviation 0.01, constrained to

[0.01, 0.2]. The population size is 100, and we use

elitism with the single highest ﬁtness solution surviv-

ing unaltered to the next generation. We use binary

number of generations (log scale)

100

average solution cost

Swap

EER

NWOX

UOBX

OX2

PPX

UPPX

PMX

UPMX

PBX

Figure 1: Crossover comparison for element positions.

tournament selection. As a baseline, we use an adap-

tive mutation-only EA with swap mutation to exam-

ine whether the addition of a crossover operator im-

proves performance. For UOBX, OX2, and UPPX,

we use u = 0.5 as suggested by their authors; and we

use u = 0.33 for UPMX for the same reason.

We use OpenJDK 17, Windows 10, an AMD

A10-5700 3.4 GHz CPU, and 8GB RAM. We use

Chips-n-Salsa version 6.4.0, as released via the

Maven Central repository, and not a development

version to ensure reproducibility. The distance

metrics for the Permutation in a Haystack are from

version 5.1.0 of JavaPermutationTools (JPT) (Ci-

cirello, 2018). The source code of Chips-n-Salsa

(https://github.com/cicirello/Chips-n-Salsa) and JPT

(https://github.com/cicirello/JavaPermutationTools)

is on GitHub; as is the source of the ex-

periments, and the raw and processed data

(https://github.com/cicirello/permutation-crossover-

landscape-analysis).

Figures 1 to 5 show the results on the ﬁve land-

scapes. The x-axis is number of generations at log

scale, and the y-axis is solution cost averaged over

100 runs. A black line shows the mutation-only base-

line to make it easy to see which crossover opera-

tors enable improvement over the mutation-only case.

Subtle differences among them are not particularly

important, as we are only identifying which crossover

operators are worth considering for a problem based

upon permutation features. Inspect the raw and sum-

mary data in GitHub for a ﬁne-grained comparison.

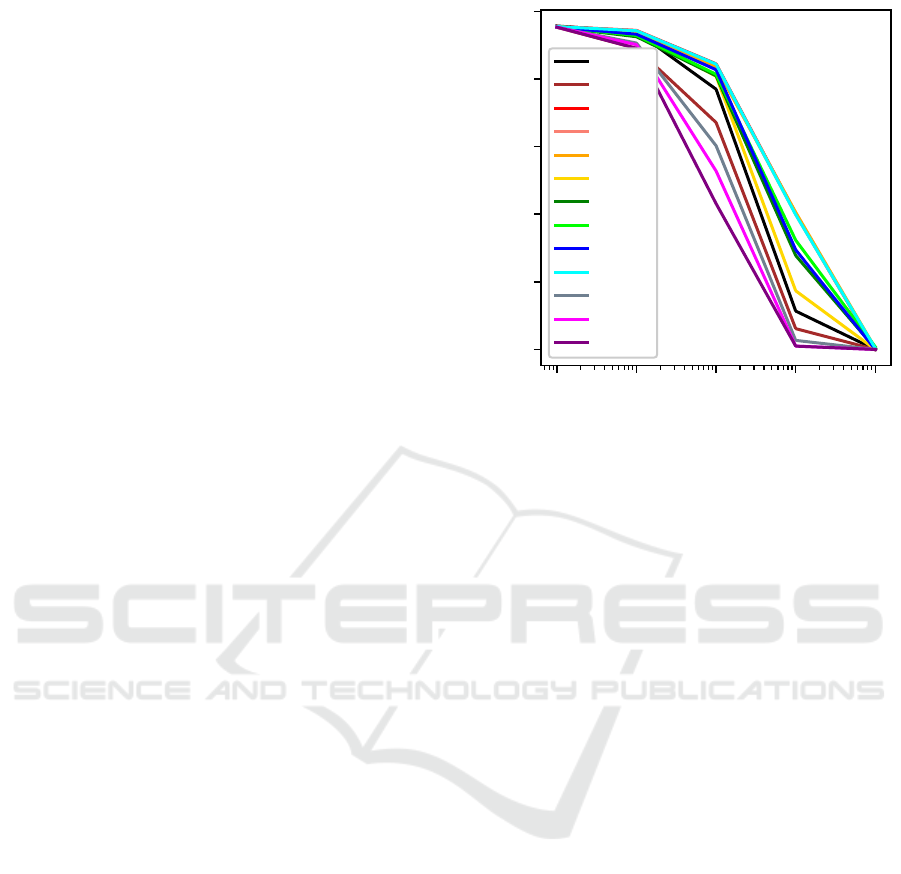
Optimizing Element Positions: In Figure 1, we

see four crossover operators optimize element posi-

A Survey and Analysis of Evolutionary Operators for Permutations

295

number of generations (log scale)

average solution cost

Swap

EER

NWOX

UOBX

OX2

PPX

UPPX

PMX

UPMX

PBX

Figure 2: Crossover comparison for undirected edges.

number of generations (log scale)

average solution cost

Swap

EER

NWOX

UOBX

OX2

PPX

UPPX

PMX

UPMX

PBX

Figure 3: Crossover comparison for directed edges.

tions better than mutation alone: CX, PMX, UPMX,

and PBX. Although UOBX and OX2 perform worse

than baseline, they may also be relevant for positions

if u is carefully tuned as discussed in Section 4.

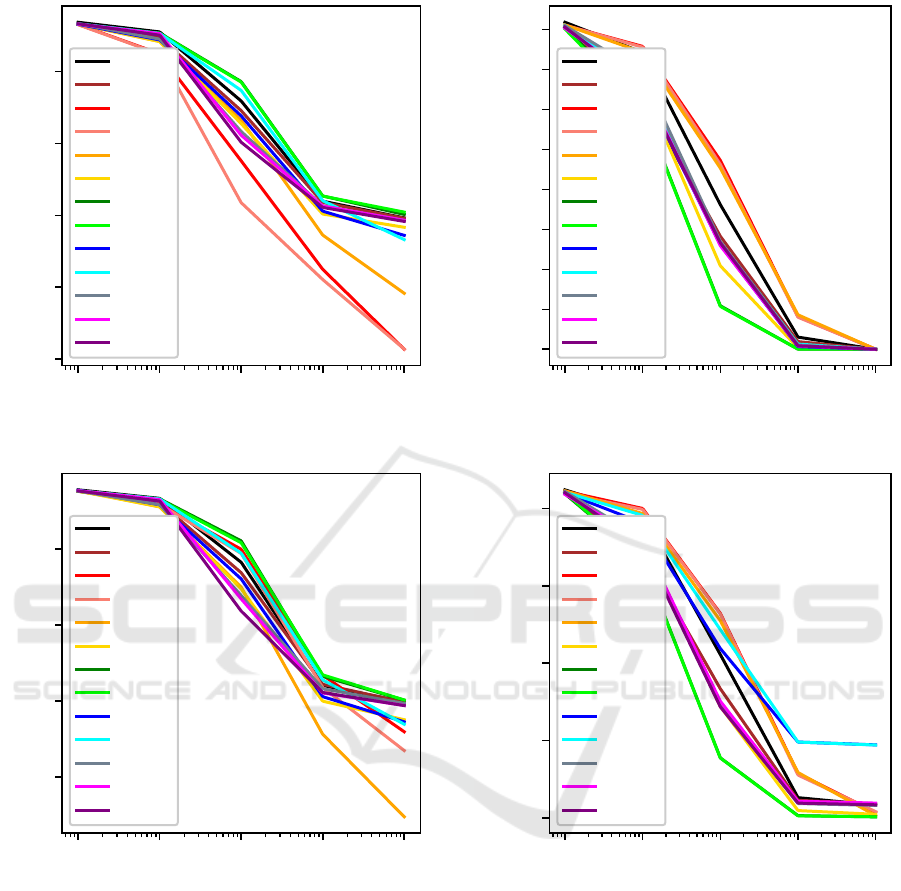
Optimizing Undirected Edges: Figure 2 shows

that only EER, ER, and OX optimize undirected edges

better than the mutation-only baseline.

Optimizing Directed Edges: For directed edges

(Figure 3), only OX performs substantially better than

the mutation-only baseline. For long runs, others

(EER, ER, NWOX, PPX, UPPX) begin to outperform

the baseline, but by much smaller margins than OX.

Although not seen here, with carefully tuned u,

number of generations (log scale)

250

500

750

1000

1250

1500

1750

2000

average solution cost

Swap

EER

NWOX

UOBX

OX2

PPX

UPPX

PMX

UPMX

PBX

Figure 4: Crossover comparison for precedences.

number of generations (log scale)

500

1000

1500

2000

average solution cost

Swap

EER

NWOX

UOBX

OX2

PPX

UPPX

PMX

UPMX

PBX

Figure 5: Crossover comparison for cyclic precedences.

UOBX, OX2, and UPMX may be relevant for edges

(undirected or directed) as discussed in Section 4.

Optimizing precedences: Several crossover op-

erators optimize precedences (Figure 4) better than

the mutation-only baseline, including: CX, NWOX,

UOBX, OX2, PPX, UPPX, PMX, UPMX, and PBX.

Optimizing Cyclic Precedences: Figure 5 shows

the cyclic precedences results, which reveal many

crossover operators superior to mutation alone: CX,

NWOX, UOBX, OX2, PMX, UPMX, and PBX. Note

that some of these strongly overlap on the graph.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

296

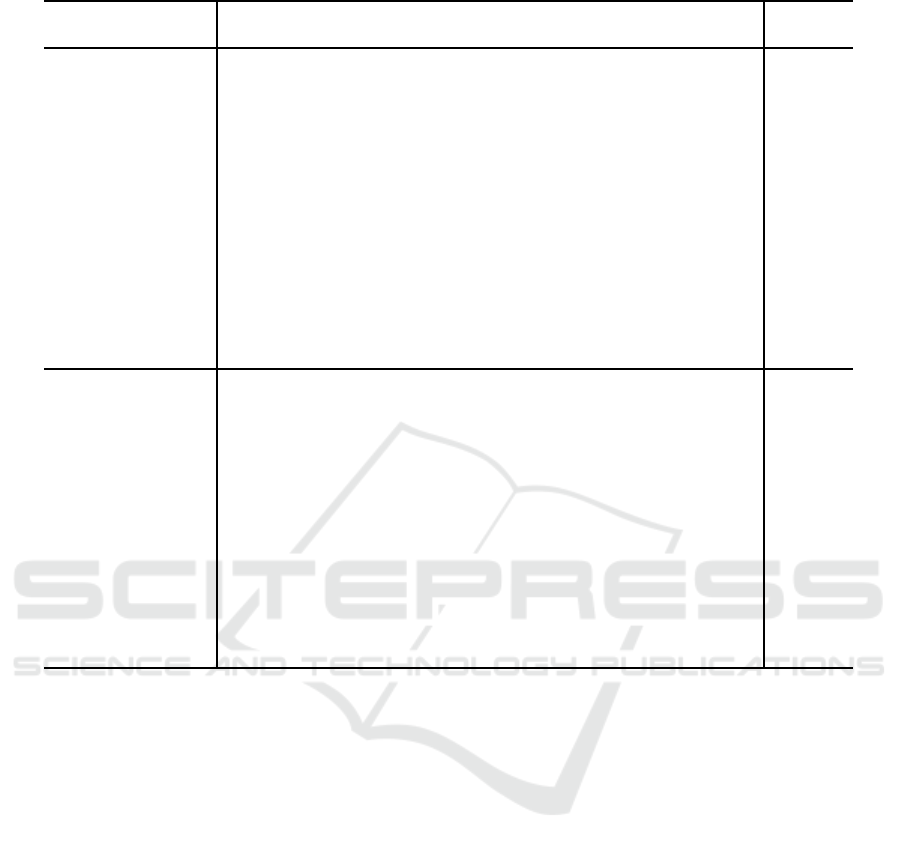
Table 2: Evolutionary operator characteristics: Xmeans effective for feature, and ? means may be effective if carefully tuned.

Undirected Directed Cyclic Limited

Operator

Positions Edges Edges Precedences Precedences /Special

CX X X X

ER X

EER X

OX X X

NWOX X X

UOBX ? ? ? X X

OX2 ? ? ? X X

PPX X

UPPX ? ? X

PMX X X X

UPMX X ? ? X X

PBX X X X

EAX X X

HeurX X

Swap X X X X X

Adjacent Swap X

Insertion X X X X

Reversal X

2-change X

3opt X

Block-Move X X

Block-Swap X X

Cycle(kmax) X ? ? ? ?

Cycle(α) X ? ? ? ?

Scramble X

Uniform Scramble ? ? ? ? ?

Rotation X

6 CONCLUSIONS

Table 2 maps the evolutionary operators to the permu-

tation features they effectively optimize. The top and

bottom parts of Table 2 focus on crossover and muta-

tion operators, respectively. The crossover operator to

feature mapping in the top of Table 2 is as derived in

Section 5. The mutation operator to feature mapping

in the bottom of Table 2 is partially derived from our

prior research (Cicirello, 2022b). In some cases (indi-

cated with a question mark), applicability of an evo-

lutionary operator for a feature may require tuning a

control parameter, such as u for uniform scramble or

the various uniform crossover operators.

One objective of this paper is to serve as a sort of

catalog of evolutionary operators relevant to evolving

permutations. Another objective is to offer insights

into which operators are worth considering for a prob-

lem based upon the characteristics of the problem. If a

ﬁtness function for a problem is heavily inﬂuenced by

a speciﬁc permutation feature, the insights from this

paper can assist in narrowing the available operators

to those most likely effective. If a ﬁtness function is

inﬂuenced by a combination of features, then an op-

erator that balances its behavior with respect to that

combination of features may be a good choice.

In future work, we plan to dive deeper into the

behavior of the operators whose strengths are less

clear. The crossover operators UOBX, OX2, UPPX,

and UPMX include a tunable parameter, as do the mu-

tation operators uniform scramble, Cycle(kmax), and

Cycle(α). Although our empirical analyses identiﬁed

problem features for which these operators are well

suited, we also hypothesized that it may be possible

to tune their control parameters for favorable perfor-

mance on other permutation features. Future work

will explore more deﬁnitively answering whether or

not such tuning can extend the applicability of these

operators to more features.

A Survey and Analysis of Evolutionary Operators for Permutations

297

REFERENCES

Barecke, T. and Detyniecki, M. (2007). Memetic algorithms

for inexact graph matching. In 2007 IEEE Congress

on Evolutionary Computation, pages 4238–4245.

Barecke, T. and Detyniecki, M. (2022). The effects of inter-

action functions between two cellular automata. Com-

plex Systems, 31(2):219–246.

Bierwirth, C., Mattfeld, D. C., and Kopfer, H. (1996). On

permutation representations for scheduling problems.

In The 4th International Conference on Parallel Prob-

lem Solving from Nature, pages 310–318, Berlin, Hei-

delberg. Springer.

Bossek, J., Neumann, A., and Neumann, F. (2023). On

the impact of operators and populations within evolu-

tionary algorithms for the dynamic weighted traveling

salesperson problem. arXiv:2305.18955.

Campos, V., Laguna, M., and Mart´ı, R. (2005). Context-

independent scatter and tabu search for permuta-

tion problems. INFORMS Journal on Computing,

17(1):111–122.

Cicirello, V. A. (2006). Non-wrapping order crossover: An

order preserving crossover operator that respects ab-

solute position. In Proceedings of the Genetic and

Evolutionary Computation Conference (GECCO’06),

volume 2, pages 1125–1131. ACM Press.

Cicirello, V. A. (2010). Heuristic sequencing crossover: In-

tegrating problem dependent heuristic knowledge into

a genetic algorithm. In Proceedings of the 23rd Inter-

national Florida Artiﬁcial Intelligence Research Soci-

ety Conference, pages 14–19. AAAI Press.

Cicirello, V. A. (2014). On the effects of window-limits on

the distance proﬁles of permutation neighborhood op-

erators. In Proceedings of the 8th International Con-

ference on Bio-inspired Information and Communica-

tions Technologies, pages 28–35.

Cicirello, V. A. (2016). The permutation in a haystack

problem and the calculus of search landscapes.

IEEE Transactions on Evolutionary Computation,

20(3):434–446.

Cicirello, V. A. (2018). JavaPermutationTools: A java li-

brary of permutation distance metrics. Journal of

Open Source Software, 3(31):950.1–950.4.

Cicirello, V. A. (2019). Classiﬁcation of permutation dis-

tance metrics for ﬁtness landscape analysis. In Pro-

ceedings of the 11th International Conference on Bio-

inspired Information and Communication Technolo-

gies, pages 81–97. Springer Nature.

Cicirello, V. A. (2020). Chips-n-salsa: A java library of cus-

tomizable, hybridizable, iterative, parallel, stochastic,

and self-adaptive local search algorithms. Journal of

Open Source Software, 5(52):2448.1–2448.4.

Cicirello, V. A. (2022a). Cycle mutation: Evolving per-

mutations via cycle induction. Applied Sciences,

12(11):5506.1–5506.26.

Cicirello, V. A. (2022b). On ﬁtness landscape analysis of

permutation problems: From distance metrics to mu-

tation operator selection. Mobile Networks and Appli-

cations.

Cicirello, V. A. and Smith, S. F. (2000). Modeling ga per-

formance for control parameter optimization. In Pro-

ceedings of the Genetic and Evolutionary Computa-

tion Conference, pages 235–242. Morgan Kaufmann.

Davis, L. (1985). Applying adaptive algorithms to epistatic

domains. In Proceedings of the 9th International Joint

Conference on Artiﬁcial Intelligence, pages 162–164,

San Francisco, CA, USA. Morgan Kaufmann.

Ding, J., Chen, M., Wang, T., Zhou, J., Fu, X., and Li,

K. (2023). A survey of ai-enabled dynamic manu-

facturing scheduling: From directed heuristics to au-

tonomous learning. ACM Computing Surveys.

Eiben, A. E. and Smith, J. E. (2003). Introduction to Evolu-

tionary Computing. Springer, Berlin, Germany.

Freisleben, B. and Merz, P. (1996). New genetic local

search operators for the traveling salesman problem.

In Parallel Problem Solving from Nature–PPSN IV,

pages 890–899, Berlin, Heidelberg. Springer.

Geurtsen, M., Didden, J. B., Adan, J., Atan, Z., and Adan,

I. (2023). Production, maintenance and resource

scheduling: A review. European Journal of Opera-

tional Research, 305(2):501–529.

Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-

timization and Machine Learning. Addison Wesley.

Goldberg, D. E. and Lingle, R. (1985). Alleles, loci, and

the traveling salesman problem. In Proceedings of the

1st International Conference on Genetic Algorithms,

pages 154–159.

Huang, B., Zhou, M., Lu, X. S., and Abusorrah, A. (2023).

Scheduling of resource allocation systems with timed

petri nets: A survey. ACM Computing Surveys,

55(11).

Kendall, M. G. (1938). A new measure of rank correlation.

Biometrika, 30(1/2):81–93.

Lee, C. (1958). Some properties of nonbinary error-

correcting codes. IRE Trans Inf Theory, 4(2):77–82.

Li, M. and Wang, G.-G. (2022). A review of green shop

scheduling problem. Information Sciences, 589:478–

496.

Lin, S. (1965). Computer solutions of the traveling sales-

man problem. The Bell System Technical Journal,

44(10):2245–2269.

Nagata, Y. (2006). New eax crossover for large tsp

instances. In Parallel Problem Solving from Na-

ture - PPSN IX, pages 372–381, Berlin, Heidelberg.

Springer.

Nagata, Y. (2007). Edge assembly crossover for the capac-

itated vehicle routing problem. In Evolutionary Com-

putation in Combinatorial Optimization, pages 142–

153, Berlin, Heidelberg. Springer.

Nagata, Y., Br¨aysy, O., and Dullaert, W. (2010). A penalty-

based edge assembly memetic algorithm for the vehi-

cle routing problem with time windows. Computers

& Operations Research, 37(4):724–737.

Nagata, Y. and Kobayashi, S. (2013). A powerful genetic

algorithm using edge assembly crossover for the trav-

eling salesman problem. INFORMS Journal on Com-

puting, 25(2):346–363.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

298

Oliver, I. M., Smith, D. J., and Holland, J. R. C. (1987). A

study of permutation crossover operators on the trav-

eling salesman problem. In Proceedings of the Second

International Conference on Genetic Algorithms and

Their Application, pages 224–230, USA. L. Erlbaum

Associates Inc.

Papadimitriou, C. H. and Steiglitz, K. (1998). Combinato-

rial Optimization: Algorithms and Complexity. Dover

Publications, Mineola, NY, USA.

Pasha, J., Elmi, Z., Purkayastha, S., Fathollahi-Fard, A. M.,

Ge, Y.-E., Lau, Y.-Y., and Dulebenets, M. A. (2022).

The drone scheduling problem: A systematic state-

of-the-art review. IEEE Transactions on Intelligent

Transportation Systems, 23(9):14224–14247.

Ronald, S. (1997). Distance functions for order-based en-

codings. In IEEE Congress on Evolutionary Compu-

tation, pages 49–54.

Ronald, S. (1998). More distance functions for order-based

encodings. In IEEE Congress on Evolutionary Com-

putation, pages 558–563.

Sanches, D., Whitley, D., and Tin´os, R. (2017). Build-

ing a better heuristic for the traveling salesman prob-

lem: Combining edge assembly crossover and parti-

tion crossover. In Proceedings of the Genetic and Evo-

lutionary Computation Conference, pages 329–336,

New York, NY, USA. Association for Computing Ma-

chinery.

Serpell, M. and Smith, J. E. (2010). Self-adaptation of mu-

tation operator and probability for permutation repre-

sentations in genetic algorithms. Evolutionary Com-

putation, 18(3):491–514.

Starkweather, T., McDaniel, S., Mathias, K., Whitley, D.,

and Whitley, C. (1991). A comparison of genetic se-

quencing operators. In Proceedings of the Fourth In-

ternational Conference on Genetic Algorithms, pages

69–76.

Sutton, A. M., Neumann, F., and Nallaperuma, S. (2014).

Parameterized runtime analyses of evolutionary algo-

rithms for the planar euclidean traveling salesperson

problem. Evolutionary Computation, 22(4):595–628.

Syswerda, G. (1991). Schedule optimization using genetic

algorithms. In Davis, L., editor, Handbook of Genetic

Algorithms. Van Nostrand Reinhold.

Valenzuela, C. L. (2001). A study of permutation oper-

ators for minimum span frequency assignment using

an order based representation. Journal of Heuristics,

7(1):5–21.

Watson, J., Ross, C., Eisele, V., Denton, J., Bins, J., Guerra,

C., Whitley, D., and Howe, A. (1998). The traveling

salesrep problem, edge assembly crossover, and 2-opt.

In Parallel Problem Solving from Nature - PPSN V,

pages 823–832, Berlin, Heidelberg. Springer.

Whitley, L. D., Starkweather, T., and Fuquay, D. (1989).

Scheduling problems and traveling salesmen: The ge-

netic edge recombination operator. In Proceedings

of the 3rd International Conference on Genetic Al-

gorithms, pages 133–140, San Francisco, CA, USA.

Morgan Kaufmann Publishers Inc.

Xiong, H., Shi, S., Ren, D., and Hu, J. (2022). A survey of

job shop scheduling problem: The types and models.

Computers & Operations Research, 142:105731.

A Survey and Analysis of Evolutionary Operators for Permutations

299