Semi-Supervised Fuzzy C-Means for Regression

Gabriella Casalino

, Giovanna Castellano

and Corrado Mencar

Dept. of Computer Science, University of Bari Aldo Moro, Italy

Keywords:

Fuzzy Clustering, Semi-Supervised Clustering, Regression, Discretization.

Abstract:

We propose a method to perform regression on partially labeled data, which is based on SSFCM (Semi-

Supervised Fuzzy C-Means), an algorithm for semi-supervised classiﬁcation based on fuzzy clustering. The

proposed method, called SSFCM-R, precedes the application of SSFCM with a relabeling module based on

target discretization. After the application of SSFCM, regression is carried out according to one out of two

possible schemes: (i) the output corresponds to the label of the closest cluster; (ii) the output is a linear

combination of the cluster labels weighted by the membership degree of the input. Some experiments on

synthetic data are reported to compare both approaches.

1 INTRODUCTION

One of the methodologies at the heart of machine

learning is Semi-Supervised Learning (SSL), a fusion

of supervised and unsupervised learning, which was

developed as a result of the widespread availability of

unlabeled data in many ﬁelds and, at the same time,

the dearth of labeled data. Indeed, in many real-world

applications, a huge amount of data is continuously

generated, but only a few of them are labeled. La-

beling data is indeed time-consuming, and sometimes

it is not possible due to the large volume of data, the

speed of acquisition, or both. Cyber attacks, fraudu-

lent transactions, or anomalies in monitoring systems

are just a few examples where labeling all data is in-

feasible.

To overcome these limitations, SSL methods try to

use as much unlabeled data as possible while requir-

ing only a small amount of labeled data to drive pre-

diction. Depending on the characteristics of the pre-

dicted output, two different approaches can be located

under the SSL umbrella: Semi-Supervised Classiﬁ-

cation and Semi-Supervised Regression (Kostopoulos

et al., 2018).

Numerous studies over the past years have dealt

with the use of Semi-Supervised Classiﬁcation ap-

proaches in many real-world applications such as

text analysis (Duarte and Berton, 2023), e-health

(Qayyum et al., 2023; Casalino et al., 2023; Kmita

https://orcid.org/0000-0003-0713-2260

https://orcid.org/0000-0002-6489-8628

https://orcid.org/0000-0001-8712-023X

et al., 2022), image analysis (Qiu et al., 2023; Liu

et al., 2023b), learning analytics (Liu et al., 2023a),

manufacturing (Kim et al., 2023; Leite et al., 2020),

energy management (Hao and Xu, 2023), just to men-

tion a few. Moreover, semi-supervised extensions of

clustering algorithms are often used for classiﬁcation

by exploiting the information deriving from the few

available labels (Gonz

alez-Almagro et al., 2023).

In contrast, few works deal with Semi-Supervised

Regression, which is still a lightly touched instance of

SSL. Notable SSR techniques are the COREG (Zhou

et al., 2005) and the SSKR (Semi-Supervised Kernel

Regression) (Wang et al., 2006) algorithms. Kang et

al. (Kang et al., 2016) introduce representative SSR

algorithms such as Co-training, kernel, and graph-

based regression methods.

In this work we propose SSFCM-R, a semi-

supervised regression method that leverages the

Semi-Supervised Fuzzy C-Means algorithm (SS-

FCM), previously employed for semi-supervised clas-

siﬁcation (Pedrycz and Waletzky, 1997). SSFCM-R

extends SSFCM by adding some components useful

to perform a prediction task linked to regression, start-

ing from partially labeled data. At the core of the

SSFCM-R method is a relabeling process based on

a discretization of the available target values that en-

ables the application of the SSFCM-based classiﬁer.

After the application of SSFCM, regression is carried

out according to one out of two possible schemes: (i)

the output corresponds to the label of the closest clus-

ter; (ii) the output is a linear combination of the clus-

ter labels weighted by the membership degree of the

Casalino, G., Castellano, G. and Mencar, C.

Semi-Supervised Fuzzy C-Means for Regression.

DOI: 10.5220/0012195100003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 369-375

ISBN: 978-989-758-674-3; ISSN: 2184-3236

369

input. Three different discretization strategies have

been compared to identify the most effective. They

group data in subsets, called bins, which are assigned

to continuous outputs, on the basis of different criteria

(equal width distribution, quantiles, k-means). Syn-

thetic data, of different complexity, have been gener-

ated to study the robustness of the proposed method.

Also, different labeling percentages have been consid-

ered to study the algorithm behavior when the number

of available labels decreases. Finally, the inﬂuence of

the size of bins on the regression results has been an-

alyzed.

The paper is organized as follows. In section 2

the proposed algorithm is formalized. The results of

the numerical experiments are discussed in Section 3.

Section 4 concludes the work and future directions of

this research are outlined.

2 THE PROPOSED METHOD

The proposed SSFCM-R extends SSFCM (Semi-

Supervised Fuzzy C-Means) (Pedrycz and Waletzky,

1997), which was originally designed for classiﬁca-

tion, by adding some mechanisms useful to accom-

plish a regression task.

2.1 SSFCM

SSFCM is a semi-supervised version of the FCM

(Fuzzy C-Means) algorithm, which exploits partially

labeled data to drive the clustering process. The al-

gorithm generates clusters from a set of data that can

be completely or partially labeled, by minimizing the

following objective function:

J =

∑

k=1

∑

j=1

+ α

∑

k=1

∑

j=1



− b



(1)

where K is the number of clusters, N is the number of

samples, u

∈ [0, 1] is the membership degree of sam-

ple x

in the k-th cluster; d

is the Euclidean distance

between x

and the center c

of the k-th cluster; m is

the fuzziﬁcation parameter (we will assume m = 2).

Peculiar to SSFCM is the introduction of vari-

ables b

= b(x

), where b : X 7→ {0, 1} is such that

b(x) = 1 iff x is pre-labeled, i.e., its class value is

known, and f

= 1 iff the j-th sample has the k-th

class label, 0 otherwise (notice that f

is undeﬁned

when b

= 0). The regularization parameter α ≥ 0

weights the second term of the objective function, that

uses the class information; according to (Pedrycz and

Waletzky, 1997), its value is the ratio of unlabeled

data over all available data.

The outcome of SSFCM is a partition matrix U =





and a set of K cluster centroids

∑

j=1

∑

j=1

(2)

that minimize (1). The details of the optimization

schema are reported in (Pedrycz and Waletzky, 1997).

2.2 SSFCM-R

The core strategy of SSFCM-R is to consider the class

label as the output of the function to be approximated.

In order to enable regression through SSFCM, we ﬁrst

extend the original algorithm by admitting the possi-

bility that the number of clusters (K) is greater than

or equal to the number of class labels (C). In other

words, different clusters can be assigned to the same

class label. This extension is necessary because a

function can have approximately the same value in

different regions of the domain.

In this respect, the variables f

occurring in (1)

are re-interpreted as follows: f

= 1 if the j-th sam-

ple has the same class label as the k-th cluster pro-

totype, 0 otherwise. This change of interpretation re-

quires evaluating the class label of a cluster prototype.

To this pursuit, before starting the SSFCM clustering

process, K labeled data are randomly chosen to ini-

tialize the prototypes, so that each cluster prototype is

associated with a class label.

Once the clustering process is complete, the clas-

siﬁcation of an unlabeled data sample is based on

a matching method using the derived labeled proto-

types. Speciﬁcally, an unlabeled data sample is as-

signed the label of the closest prototype, according to

the Euclidean distance.

Differently from SSFCM, where class labels do

not have any speciﬁc structure, in SSFCM-R the class

labels are numbers. Thus, SSFCM-R consists of the

following three main stages:

1. Pre-processing: a discretization process and a

subsequent relabeling process is applied to the tar-

get values to reduce the regression problem to one

of classiﬁcation;

2. Clustering is performed as in SSFCM;

3. Post-processing: given the discrete output values

provided by SSFCM-based classiﬁcation, the ﬁ-

nal predicted output value is computed as either

by looking at the closest cluster, or by a linear

combination of the discrete output values of all

clusters.

FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications

370

2.2.1 Pre-Processing

Suppose that a set D of partially labeled data is avail-

able, representing an unknown function f : X → Y .

The set D consists of tuples (x, y), where x ∈ X and

y ∈ Y ∪ {}. (The tuple (x, ) represents an unla-

beled data sample.) The goal of regression is to ﬁnd a

model that approximates f starting from D.

Let

L = {(x, y) ∈ D|y 6= }

the subset of labeled data samples of D. We assume

that L has cardinality N

> 0. Let Y = {y ∈ Y |(x, y) ∈

L} the set of numerical labels. The set Y is discretized

into C intervals; for each interval [a

, b

], i = 1,2, . . . ,C

the subset Y

= Y ∩ [a

, b

] is computed (i.e., the subset

of labels falling in the i-th interval) and the average

value ˆy

is considered. The set of labels is therefore

Y = { ˆy

|i = 1, 2, . . . ,C}.

The dataset D is then transformed into a new

dataset

D so that each labeled sample (x, y) is replaced

with (x, ˆy

), where ˆy

is the average of the subset Y

the

label y belongs to. The number C of bins is a hyper-

parameter that should be ﬁxed in advance.

We consider three different discretization strate-

gies:

D1: Equal-width discretization, separating all possi-

ble values into C bins, each having the same

width;

D2: Equal-frequency discretization, separating all

possible values into C bins, each having the same

amount of observations;

D3: The intervals are deﬁned on the basis of the cen-

troids produced by K-Means clustering.

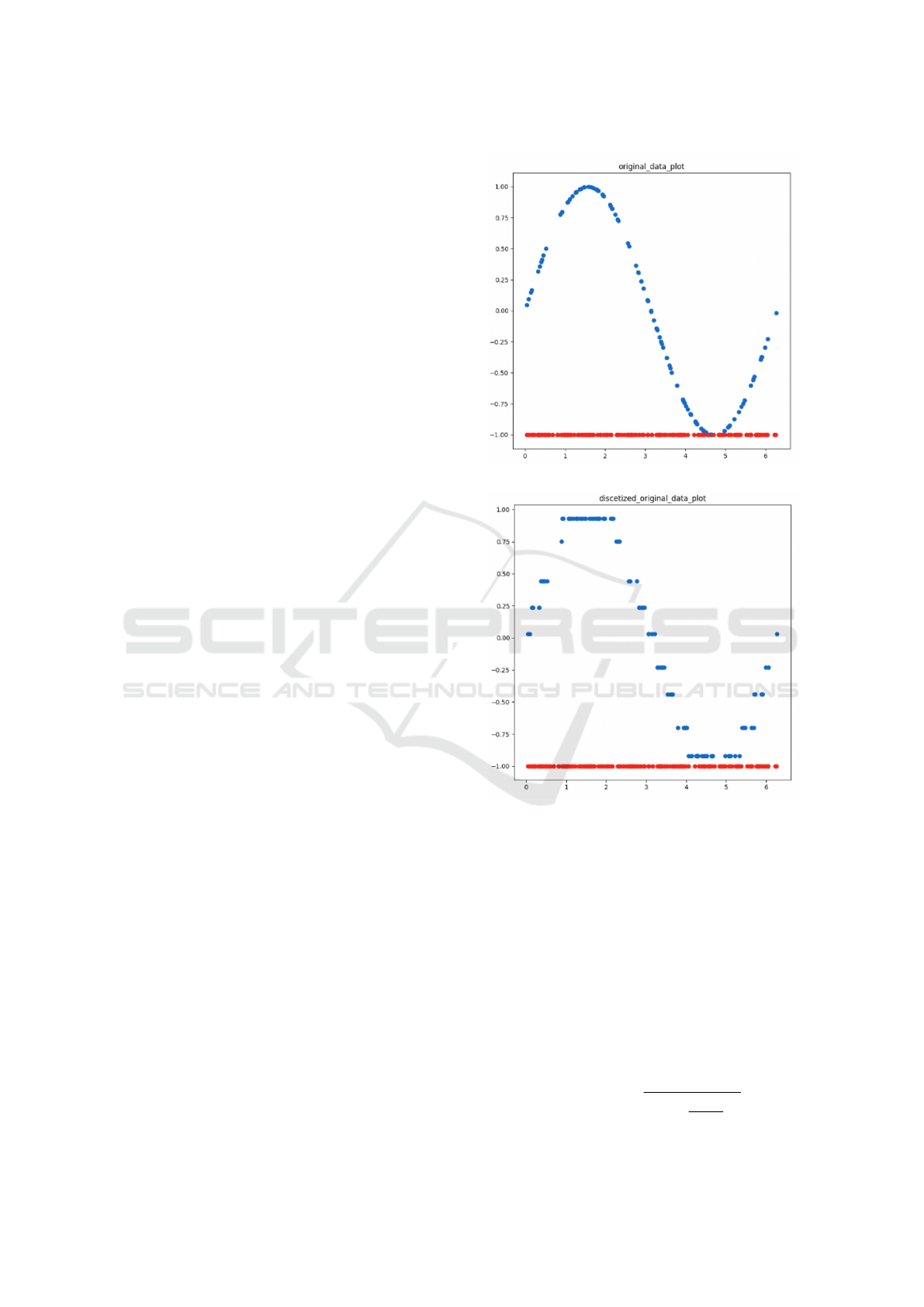
As an example, ﬁg. 1 shows the values of the sine

function in [0, 2π], before and after the discretization

step. The ﬁrst plot (ﬁg. 1a) represents the sine func-

tion with partially labeled data (red dots correspond

to unlabeled data). The second plot (ﬁg. 1b) displays

the target values after equal width discretization, with

the number of bins equal to the 10% of labeled data

(in this case C = 9).

2.2.2 Clustering

The pre-processed dataset

D is used as input to SS-

FCM, as described in Sec. 2.1. The output is a col-

lection of labeled cluster prototypes (c

, ˆy

) where

ˆy

∈

Y and a partition matrix U = [u

] of each data

sample (either labeled or unlabeled) to each cluster.

2.2.3 Post-Processing

Given a new input x ∈ X , the estimated value y can be

computed according to one out of two possible strate-

(a)

(b)

Figure 1: Original partially labeled data obtained by sine

function (a) and equal width discretized data with 9 bins

(b).

gies:

(max) The closest prototype c

to x is determined;

then, the estimated value y

max

corresponds to

the class label ˆy

;

(sum) The membership degrees of x to each clus-

ter are determined by using the formula used

in SSFCM to compute the membership de-

grees for unlabeled data (Pedrycz and Walet-

zky, 1997):

(x) =

∑

h=1



d(x,c

)

d(x,c

)



Semi-Supervised Fuzzy C-Means for Regression

371

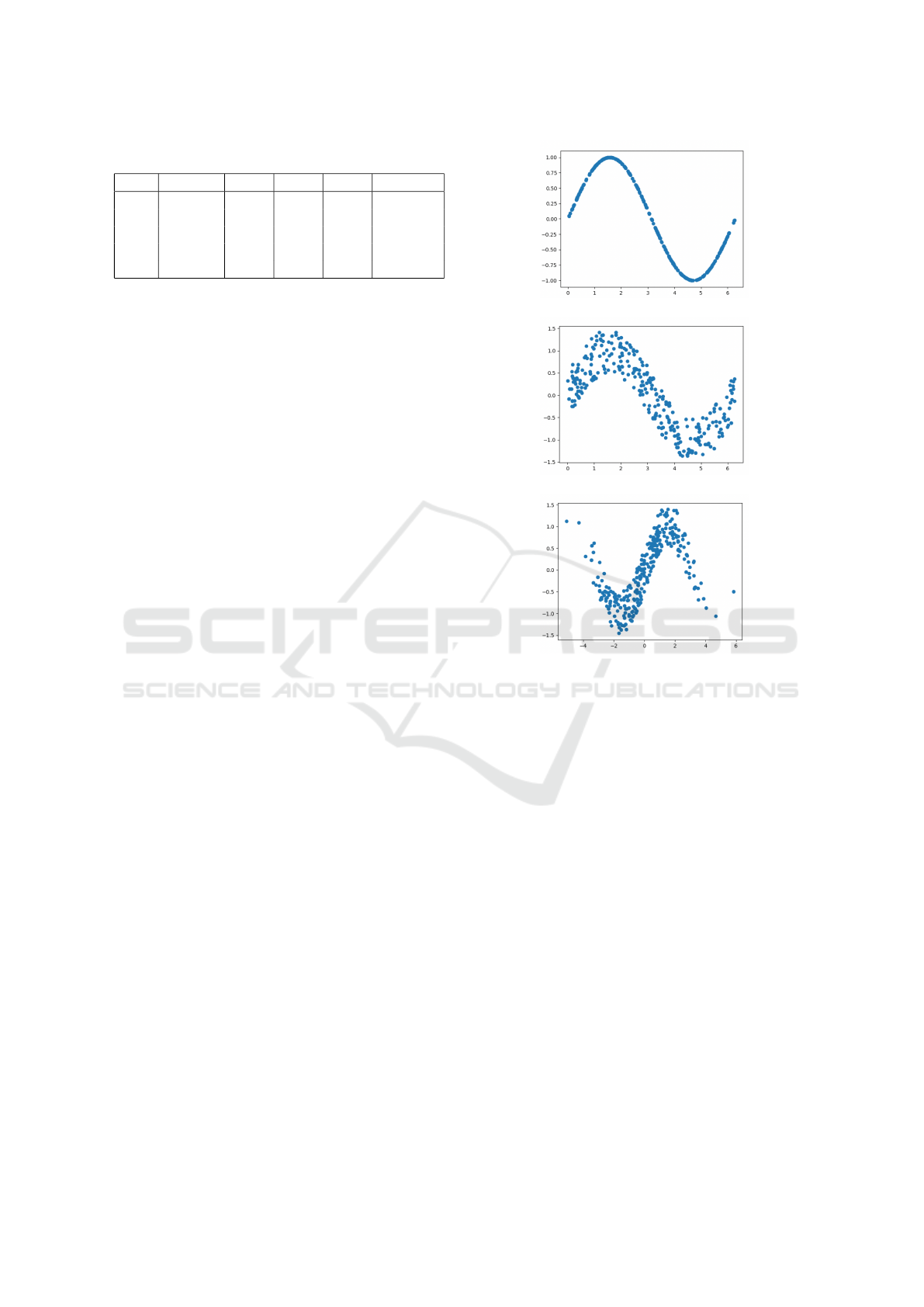
Table 1: Example of results given by SSFCM-R.

x Labeled ˆy y

sum

max

y (target)

3.67 No  -0.31 -0.70 -0.50

3.95 Yes -0.70 -0.66 -0.70 -0.72

1.06 Yes 0.93 0.91 0.93 0.87

2.25 Yes 0.75 0.73 0.75 0.77

3.98 No  -0.40 -0.70 -0.74

Since

∑

k=1

(x) = 1, then the estimated value

y corresponds to the weighted average

sum

∑

k=1

(x) ˆy

Table 1 shows an example of results obtained by

SSFCM-R for ﬁve data points (labeled and not la-

beled). The third column shows the class, in terms

of discretized bin value, that has been assigned. The

last column indicates the real output for the given in-

put. Two more values are reported: y

sum

and y

max

which are estimated according to the two aforemen-

tioned strategies.

3 EXPERIMENTS

Some experiments have been conducted to verify the

effectiveness of the proposed approach, by varying

the discretization strategy, the percentage of labeled

data, and the number of bins used for discretization.

Moreover, three synthetic datasets, of different com-

plexity, have been created. For the sake of simplic-

ity, bi-dimensional data have been produced, where

the second dimension is the value to predict. Noise

has been added to the simplest dataset with different

distributions (uniform and normal), thus making the

predictive problem more complex to solve.

Partial labeling has been simulated in order to

evaluate the robustness of the proposed algorithm in

the presence of unlabeled data at varying frequen-

cies. Particularly, eight labeling percentages have

been considered, namely: 10%, 30%, 50%, 60%,

70%, 80%, 90%, and 100%. Also, three different bin

sizes have been compared by considering the 10%,

20%, and 30% of labeled data. Different bin sizes

have been used, from 3 to 90.

The standard Mean Square Error (MSE) and the

computational time (TIME) have been used as evalu-

ation metrics for the comparison. We compare the er-

rors obtained with the two post-processing methods:

MSE sum and MSE max.

(a) S1.

(b) S2.

Figure 2: Synthetic datasets.

3.1 Data

Figure 2 shows the three synthetic dataset S1, S2, and

S3 created as follows:

• S1 consists of the evaluation of the sine function

on 300 data points generated with a uniform dis-

tribution in the interval [0, 2π]: Y = sin X where

X ∼ U([0, 2π])

• S2 consists of the evaluation of the sine function

on 300 data points generated with a uniform dis-

tribution in the interval [0, 2π] as in S1 plus a noise

term with uniform distribution: Y = sin X + ε

where X ∼ U([0, 2π]) and ε ∼ U([−0.5, 0.5])

• S3 consists of the evaluation of the sine func-

tion on 300 points generated from a normal dis-

tribution plus a noise term with uniform distri-

bution: Y = sinX + ε where X ∼ N(0, π) and

ε ∼ U([−0.5, 0.5])

FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications

372

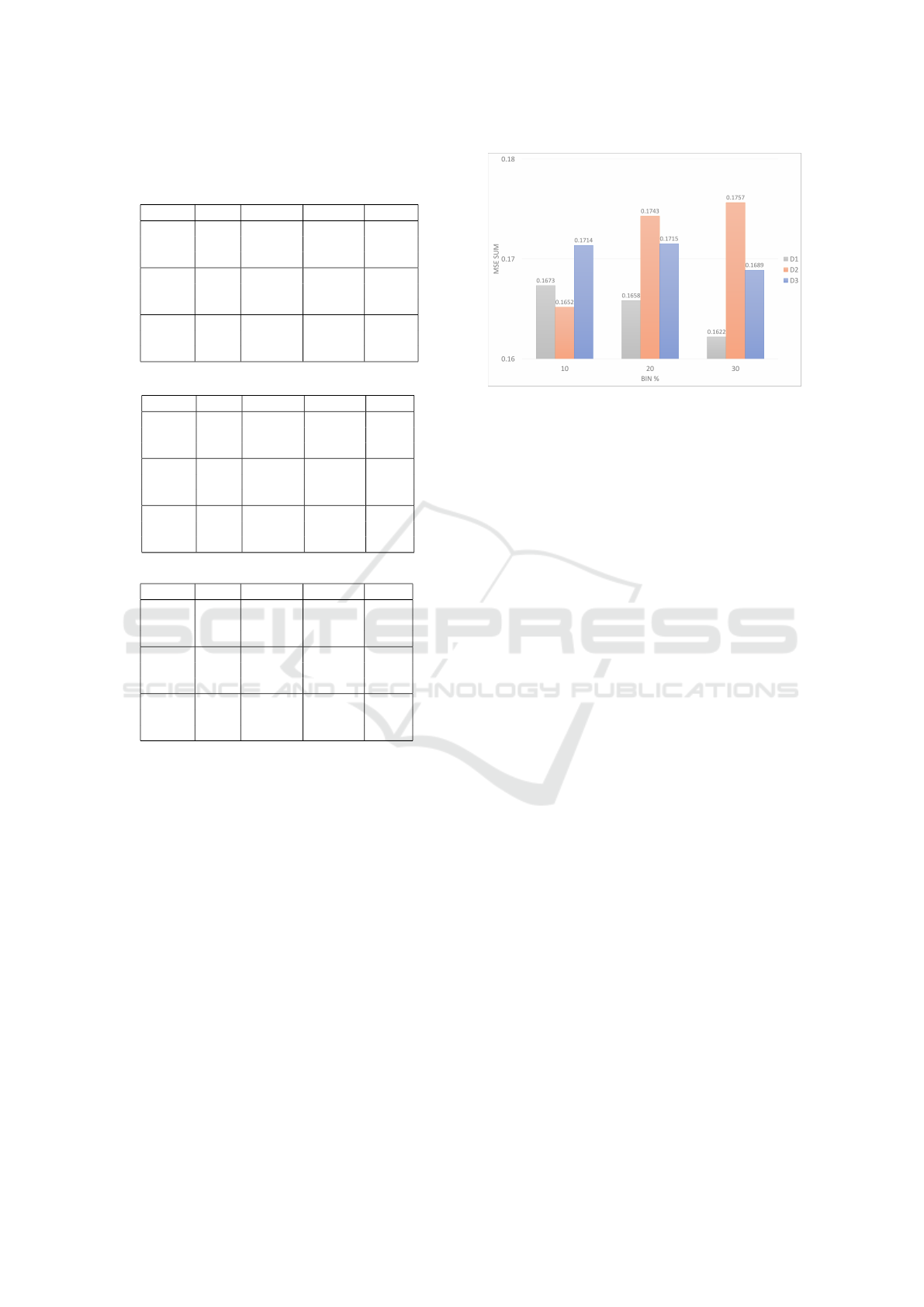
Table 2: Comparison of different discretization strategies,

varying the percentages of adopted bins, with S1, S2, and

S3 datasets.

Strategy Bin % MSE max MSE sum Time

D3 10 0.18 0.12 130.20

20 0.20 0.12 390.63

30 0.18 0.10 687.84

D2 10 0.15 0.12 110.80

20 0.18 0.13 326.19

30 0.27 0.14 1228.27

D1 10 0.17 0.11 82.33

20 0.19 0.13 397.84

30 0.19 0.10 626.00

(a) S1 dataset.

Strategy Bin % MSE max MSE sum Time

D3 10 0.22 0.19 104.78

20 0.18 0.18 448.68

30 0.22 0.18 939.75

D2 10 0.20 0.17 91.56

20 0.20 0.17 402.34

30 0.21 0.18 969.61

D1 10 0.21 0.19 106.71

20 0.18 0.18 385.93

30 0.20 0.18 724.61

(b) S2 dataset.

Strategy Bin % MSE max MSE sum Time

D3 10 0.26 0.20 110.07

20 0.26 0.21 383.59

30 0.26 0.22 666.51

D2 10 0.29 0.21 97.49

20 0.30 0.22 323.47

30 0.30 0.20 833.30

D1 10 0.25 0.19 90.64

20 0.23 0.19 309.12

30 0.23 0.20 635.72

3.2 Results

Table 2 shows the numerical results obtained by vary-

ing the bin percentages, the discretization methods,

and the datasets. Average measures over all the la-

beling percentages have been reported for the three

datasets S1, S2, and S3.nExpectedly, as the complex-

ity of data increases, errors also increase, but this is

not the only parameter to consider. In fact, the MSE

max obtained with the discretization D1, and bin %

30 on the simplest data S1, is higher than the error

obtained with D1 on S3, the most complex dataset.

Thus, different combinations of parameters, affecting

the regression results, are analyzed. The computa-

tional time is strictly proportional to the number of

bins; this is observed for each data and discretization

method.

To better analyze the results, charts focusing

on each parameter (discretization method, bin per-

Figure 3: Average MSE values varying the discretization

method and the bin percentages, over the labeling percent-

ages and the datasets.

centages, labeling percentages, and post-processing

method) and varying the others, have been reported.

Figure 3 compares the three discretization methods,

by varying the bin percentages. Average values over

the labeling percentages and the three datasets have

been reported. It is observed that the equal width

strategy (D1) has the lowest MSE on average, regard-

less of the dataset complexity. Also, by increasing the

bin percentage, the equal width strategy provides the

lowest MSE, with respect to the other two approaches.

Moreover, the equal width strategy has also the lowest

computational time, in seconds, among all the consid-

ered strategies (D1=373.21, D2=487.00, D3=429.12).

For this reason, we now focus on the equal width dis-

cretization strategy, and analyze the inﬂuence of the

labeling percentage and the bin size, in terms of MSE

sum and MSE max, averaged on all the remaining pa-

rameters.

Figure 4a shows the inﬂuence of the labeling

percentages by averaging the results from different

datasets, and bin percentages. It could be observed

that the labeling percentage strongly affects the pre-

dictions. Indeed, as expected, as the number of labels

increases, the error decreases. However, with a label-

ing percentage lower than 60% the algorithm is not

stable, and peaks could be observed in the graph. As

the labeling percentage increases over 60% the error

signiﬁcantly decreases. It is also observed that MSE

sum is signiﬁcantly lower than MSE max when the

percentage of labeled data is low, while both converge

to similar values for higher labeling percentages.

We analyzed the inﬂuence of the bin size on the re-

sults to identify the best percentage. Figure 4b shows

the average measures over the three datasets, varying

the labeling percentages. It could be observed that the

bin percentage does not inﬂuence the predictive capa-

bility of the algorithm, returning comparable errors.

Semi-Supervised Fuzzy C-Means for Regression

373

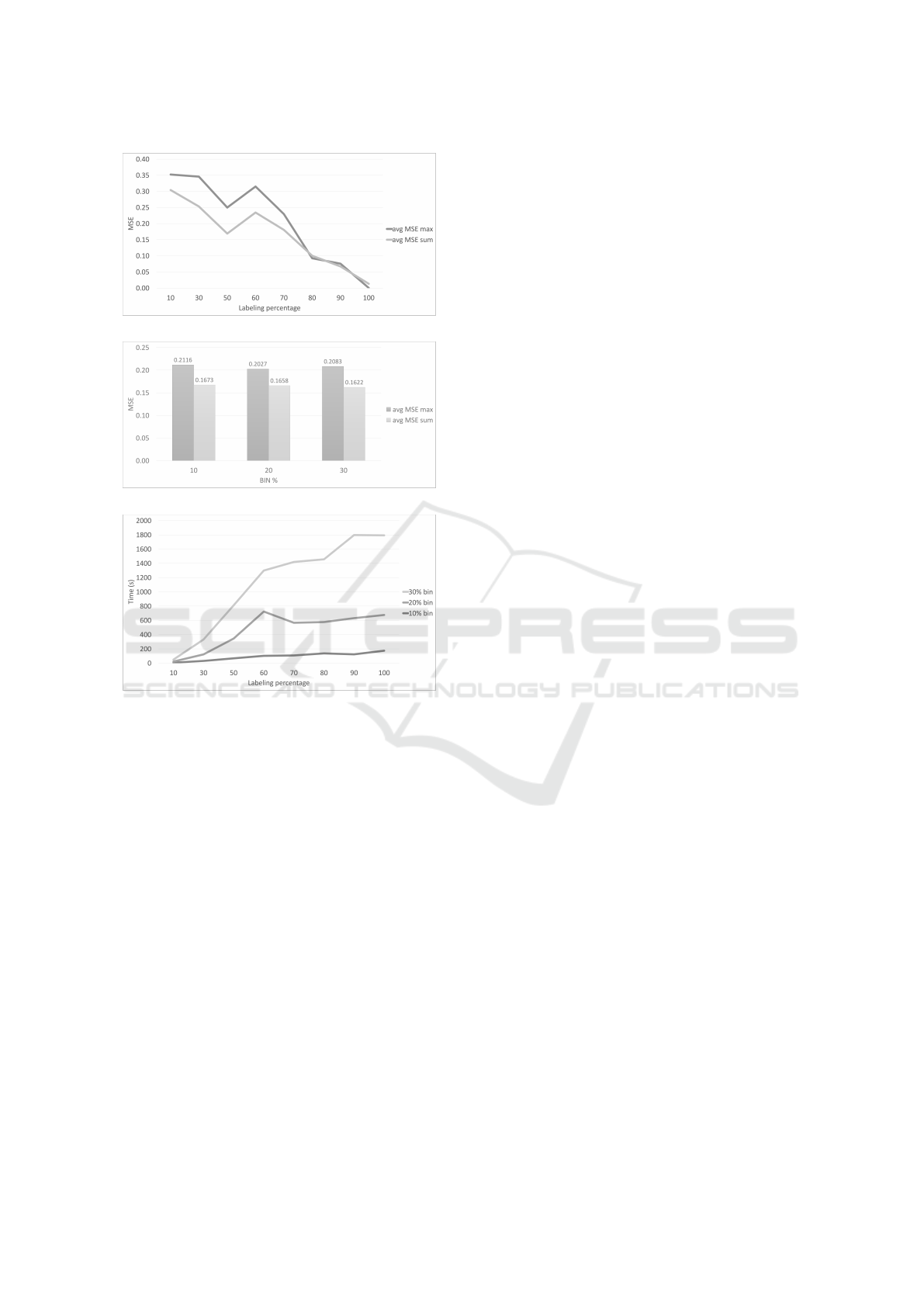
(a)

(b)

(c)

Figure 4: Effectiveness and efﬁciency of SSCFCM-R with

equal width discretization.

Finally, the value (in seconds) of computational

time for the equal width discretization, varying the la-

beling percentage and the bin percentage, are summa-

rized in Fig. 4c, by averaging results over all datasets.

It can be seen that computational time increases as

the percentage of bins and the labeling percentage in-

crease. Overall, since the bin size does not inﬂuence

the effectiveness of the methods, whilst it does inﬂu-

ence the computational time, a small number of bins

(10% of labeled data), is the best choice for both high

efﬁciency and effectiveness.

4 CONCLUSIONS

We have proposed SSFCM-R, an extension of the

Semi-Supervised Fuzzy C-Means (SSFCM) algo-

rithm that is suitable for regression. SSFCM-R lever-

ages a discretization mechanism to move from a con-

tinuous domain (useful to solve a regression problem)

to a discrete one (that SSFCM is able to process). To

this aim three different discretization strategies have

been compared, based on equally sized bins (subsets

of data), percentiles, and k-means. Experiments have

been performed to analyze the effectiveness of the

proposed approach in different conditions. Particu-

larly, the inﬂuence of data complexity, discretization

strategy, labeling percentage, and number of bins, on

the results, has been studied. In this preliminary work,

synthetic data has been produced for controlled exper-

iments. The equal width strategy has been proven to

be the more effective, with a lower error if compared

with the other discretization strategies. Also, whilst

the number of labeled data inﬂuences the results, re-

sulting in low performances for labeling percentages

lower than 60%, the number of adopted bins does not.

Thus, since the computational time is strictly related

to the number of bins, a small number is preferable.

Finally, the post-processing method sum has shown to

always achieve lower errors than the max method.

Overall, this is the ﬁrst attempt to modify SSFCM

for regression. This study has been useful to iden-

tify the parameters that mostly affect the results and

which of them allow the algorithm to perform better.

Future work will be devoted to studying different dis-

cretization strategies, not depending on the labeling

percentage and the data complexity. Also, the effec-

tiveness of the proposed approach will be evaluated

on real-world applications, and it will be compared

with other semi-supervised regression algorithms.

ACKNOWLEDGEMENTS

G. Casalino acknowledges funding from the Euro-

pean Union PON project Ricerca e Innovazione 2014-

2020, DM 1062/2021. G. Castellano’s work is par-

tially supported by the FAIR - Future AI Research

(PE00000013) project, Spoke 6 - Symbiotic AI (CUP

H97G22000210007), under the NRRP MUR program

funded by NextGenerationEU. All the authors are

members of the INdAM GNCS research group. The

authors thank the students Michele Gabriele Addati

and Nunziangelo Bruno for their contribution to de-

veloping the code and running the experiments.

REFERENCES

Casalino, G., Castellano, G., Hryniewicz, O., Leite, D.,

Opara, K., Radzieskewska, W., and Kaczmarek-

Majer, K. (2023). Semi-supervised vs. supervised

learning for mental health monitoring: a case study on

FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications

374

the classiﬁcation of bipolar disorder episodes. Journal

of Applied Mathematics and Computer Science, 33(3).

Duarte, J. M. and Berton, L. (2023). A review of semi-

supervised learning for text classiﬁcation. Artiﬁcial

Intelligence Review, pages 1–69.

Gonz

alez-Almagro, G., Peralta, D., De Poorter, E., Cano,

J.-R., and Garc

ıa, S. (2023). Semi-supervised con-

strained clustering: An in-depth overview, ranked tax-

onomy and future research directions. arXiv preprint

arXiv:2303.00522.

Hao, L. and Xu, Y. (2023). Semi-supervised learning based

occupancy estimation for real-time energy manage-

ment using ambient data. IEEE Internet of Things

Journal.

Kang, P., Kim, D., and Cho, S. (2016). Semi-supervised

support vector regression based on self-training with

label uncertainty: An application to virtual metrology

in semiconductor manufacturing. Expert Systems with

Applications, 51:85–106.

Kim, G., Choi, J. G., Ku, M., and Lim, S. (2023). De-

veloping a semi-supervised learning and ordinal clas-

siﬁcation framework for quality level prediction in

manufacturing. Computers & Industrial Engineering,

181:109286.

Kmita, K., Casalino, G., Castellano, G., Hryniewicz, O.,

and Kaczmarek-Majer, K. (2022). Conﬁdence path

regularization for handling label uncertainty in semi-

supervised learning: use case in bipolar disorder mon-

itoring. In 2022 IEEE International Conference on

Fuzzy Systems (FUZZ-IEEE), pages 1–8. IEEE.

Kostopoulos, G., Karlos, S., Kotsiantis, S., and Ragos, O.

(2018). Semi-supervised regression: A recent review.

Journal of Intelligent & Fuzzy Systems, 35(2):1483–

1500.

Leite, D., Decker, L., Santana, M., and Souza, P. (2020).

Egfc: Evolving gaussian fuzzy classiﬁer from never-

ending semi-supervised data streams – with applica-

tion to power quality disturbance detection and clas-

siﬁcation. In 2020 IEEE International Conference on

Fuzzy Systems (FUZZ-IEEE), pages 1–9.

Liu, Z., Kong, W., Peng, X., Yang, Z., Liu, S., Liu,

S., and Wen, C. (2023a). Dual-feature-embeddings-

based semi-supervised learning for cognitive en-

gagement classiﬁcation in online course discussions.

Knowledge-Based Systems, 259:110053.

Liu, Z., Lai, Z., Ou, W., Zhang, K., and Huo, H.

(2023b). Discriminative sparse least square regression

for semi-supervised learning. Information Sciences,

636:118903.

Pedrycz, W. and Waletzky, J. (1997). Fuzzy clustering with

partial supervision. IEEE transactions on systems,

man, and cybernetics. Part B, Cybernetics, 27(5):787–

95.

Qayyum, A., Tahir, A., Butt, M. A., Luke, A., Abbas, H. T.,

Qadir, J., Arshad, K., Assaleh, K., Imran, M. A., and

Abbasi, Q. H. (2023). Dental caries detection using

a semi-supervised learning approach. Scientiﬁc Re-

ports, 13(1):749.

Qiu, L., Cheng, J., Gao, H., Xiong, W., and Ren, H. (2023).

Federated semi-supervised learning for medical image

segmentation via pseudo-label denoising. IEEE Jour-

nal of Biomedical and Health Informatics.

Wang, M., Hua, X.-S., Song, Y., Dai, L.-R., and Zhang,

H.-J. (2006). Semi-supervised kernel regression.

In Sixth International Conference on Data Mining

(ICDM’06), pages 1130–1135. IEEE.

Zhou, Z.-H., Li, M., et al. (2005). Semi-supervised regres-

sion with co-training. In IJCAI, volume 5, pages 908–

913.

Semi-Supervised Fuzzy C-Means for Regression

375