Fault Diagnosis with Stacked Sparse AutoEncoder for Multimode

Process Monitoring

Yahia Kourd

, Messaoud Ramdani

, Riadh Toumi

and Ahmed Samet

Laboratory of Electrical Engineering and Renewable Energy, Faculty of Science and Technology,

Mohamed-Cherif Messaadia University, Souk Ahras, 41000, Algeria

Department of Electronics, Faculty of Engineering, Badji-Mokhtar University, Annaba, 23000, Algeria

Keywords: Fault Diagnosis, Process Monitoring, Principal Component Analysis, Sparse PCA and AutoEncoder.

Abstract: Traditional process monitoring generally assumes that process data follow a Gaussian distribution with

linear correlation. Nevertheless, this sort of restriction cannot be satisfied in reality since many industrial

processes are nonlinear in nature. This work provides an enhanced multivariate statistical process

monitoring technique based on the Stacked Sparse AutoEncoder and K-Nearest Neighbor (SSAE-KNN).

This approach consists of developing a model by using Stacked Sparse AutoEncoder (SSAE) to get the

residual space, which is the main tool in detecting and reconstructing the potential missing data by residual

space. The monitoring statistics in this space are constructed using KNN rules; the threshold values for

SSAE-KNN process monitoring are estimated utilizing the Kernel Density PDF Estimation (KDE) method,

and an enhanced Sensor Validity Index (SVI) is proposed to detect faulty data based on the reconstruction

approach. The experimental results using actual data from a photovoltaic power station connected at the site

of OuedKebrit, located in north-eastern Algeria, reveal the effectiveness of the proposed scheme and show

its capacity to detect and identify sensor failures.

https://orcid.org/ 0000-0002-4370-5700

https://orcid.org/ 0000-0002-6726-1155

1 INTRODUCTION

Data mining can extract hidden and usable

information from massive datasets, where possible

correlations may be utilized for automated anomaly

detection and associated issue root cause

identification. In general, Statistical Process Control

(SPC) charts enable the visualization of process

development and the identification of abnormal

changes (

Qin S. J., 2012

and

Yin S. et al, 2014)

However, most standard SPC methods like PCA

(Principal Components Analysis) work well only if

the correlations are linear, which is a poor

approximation of the real world. Deep learning is an

unsupervised approach that can provide a better

representation using a deep learning algorithm and

has recently proved extremely effective in several

fields (

Hinton G. E. et al, 2006

). As part of deep

learning approaches, we present the Stacked Sparse

AutoEncoder (SSAE) to reconstitute the input data

(

Xu J. et al 2016

). The K-nearest neighbor rule is one

of the population-based learning strategies, which

uses the closest samples to classify objects in an n-

dimensional feature space. It is the simplest way of

learning; the number of k defines how numerous

nearest neighbors will be grouped for classification

with the Euclidean distance metric commonly used

to compute the distance between data points (

Wang

G. et al, 2015

). The Squared Prediction Error (SPE)

index is used to identify detection. It is developed by

introducing the KNN rule and its associated control

limits established by Kernel Density Estimation

(KDE) (

Odiowei P. E. et al, 2010

). Additionally, the

Sensor Validity Index (SVI) is proposed as a way of

detecting faulty sensors. The findings reveal that,

when compared to the contribution plot, the

proposed technique is more effective at diagnosis the

faulty sensor. In this paper discusses the application

of a Stacked Sparse AutoEncoder (SSAE) that has

been trained to recreate the input data acquired

during normal operation. Then, using KNN, create

monitoring statistics in the residual space of the

Kourd, Y., Ramdani, M., Toumi, R. and Samet, A.

Fault Diagnosis with Stacked Sparse AutoEncoder for Multimode Process Monitoring.

DOI: 10.5220/0012194400003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 237-242

ISBN: 978-989-758-670-5; ISSN: 2184-2809

237

SSAE model. The paper is structured as follows: A

brief overview of basic concepts is presented in

Section 2. The recommended approaches for

multimode process monitoring are shown in Section

3. The validation of the methods is realized by

experiments conducted in section 4, utilizing real

data from solar power plants. The last section

concentrates on a discussion of the results obtained

and conclusions.

2 METHODS USED

2.1 Stacked Sparse AutoEncoder

Deep Learning has recently demonstrated

outstanding performance on a variety of tasks. It has

been utilized in the past for visual analysis and

picture identification, but not for process

monitoring. Models of deep neural networks with a

hidden layer called the bottleneck layer are used to

extract features. To begin, the input data X

= 1, 2,

3,....N is translated as follows into a hidden layer

represented by the function h

shown as follows:

= f(x

) = sigm(W

x+b

) (1)

Where b1 and W

are respectively the bias and the

weight between the input part and the hidden layer

and sigm(x) is a sigmoid function chosen to get more

bounded and uniformly distributed embedding. In

the decoding layer, h

is translated to the output

represented by x. In this stage, we employ the

activation function shown below:

= g(h

) = sigm(W

h+b

) (2)

Where W

and b

are respectively the bias and the

weight between the hidden layer and the output layer

(x). The bottleneck network whose learning criteria

contain a sparsity penalty in the bottleneck part is

named Stacked Sparse AutoEncoder (SSAE) (

Yin J.

et al, 2019). The aim of this network is to estimate its

output (prediction of the input) as similarly as

possible to its input, thus through optimizing the cost

function described by:

(3)

Where λ and β are respectively the coefficient that

establishes the weight decay and the sparsity penalty

terms, m: is the number of the hidden nodes.

Equation (3) consist of the reconstruction error, the

regularization term and the last term is sparsity

penalty, where KL(ρp

) is the Kullback-Leibler

divergence, it is used to compute the difference

between ρ and p

, those are the constraint utilized

during learning. The back propagation algorithm is

utilized to find the appropriate parameters W

, W

, b

and to minimize the cost function.

2.2 K-Nearest Neighbor

Firstly, the KNN rule is a supervised classification

algorithm that is nonparametric. The goal of

supervised classification is to predict the unknown

sample of data using a set of labeled samples. The

detection approach works on the assumption that a

sample under control will take values in the

neighborhood of the training data. Then, if a new

sample deviates too much from the data under

control, it considers out-of-control. A cumulative

distance between new sample and its k closest

neighbors included in the learning sample is

computed to analyze the distance between each new

sample and the data under control. Because the KNN

rule is a nonlinear classifier, it could address many

limitations such as process nonlinearity.

Furthermore, since the FD-KNN technique finds

flaws based on local neighbors of comparable

batches, it is ideally suited for multimodal data sets

in which batches may be divided into subgroups

with distinct characteristics (

Ren Z. et al, 2021).

2.3 Kernel Density Estimation

KDE is a method for generating a smooth PDF

(Probability Density Function) from a collection of

random samples and fitting it to a data set. It’s often

used to estimate PDFs, particularly for univariate

random data. The KDE may be used with the Q and

statistics since they are both univariate, despite

the fact that the process they describe is multivariate.

The PDF g(y) of a random variable y may be

estimated from its m samples, y

, j = 1,...,m, as

follows:

(4)

Where h is the bandwidth while K is a kernel

function. The significance of bandwidth selection

and strategies for achieving an optimal value are

detailed in (Xiong

L. et al, 2007). The probability is

obtained by integrating the density function across

a continuous range. Assuming the PDF g(y), the

likelihood of y being smaller than c at a given

significance level, a is given by:

(5)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

238

As a result, the threshold of the monitoring statistics

Q can be determined using their corresponding PDF

estimates:

(6)

2.4 Contribution Plot

There are numerous approaches for fault isolation.

Contribution plots may be used for this purpose

(

Bougheloum W. et al, 2019

). This technique is often

based on the contribution rate from each variable to

determine which variable contributes the most to the

Q statistic; the contribution of variable j is computed

as follows:

(7)

Where :

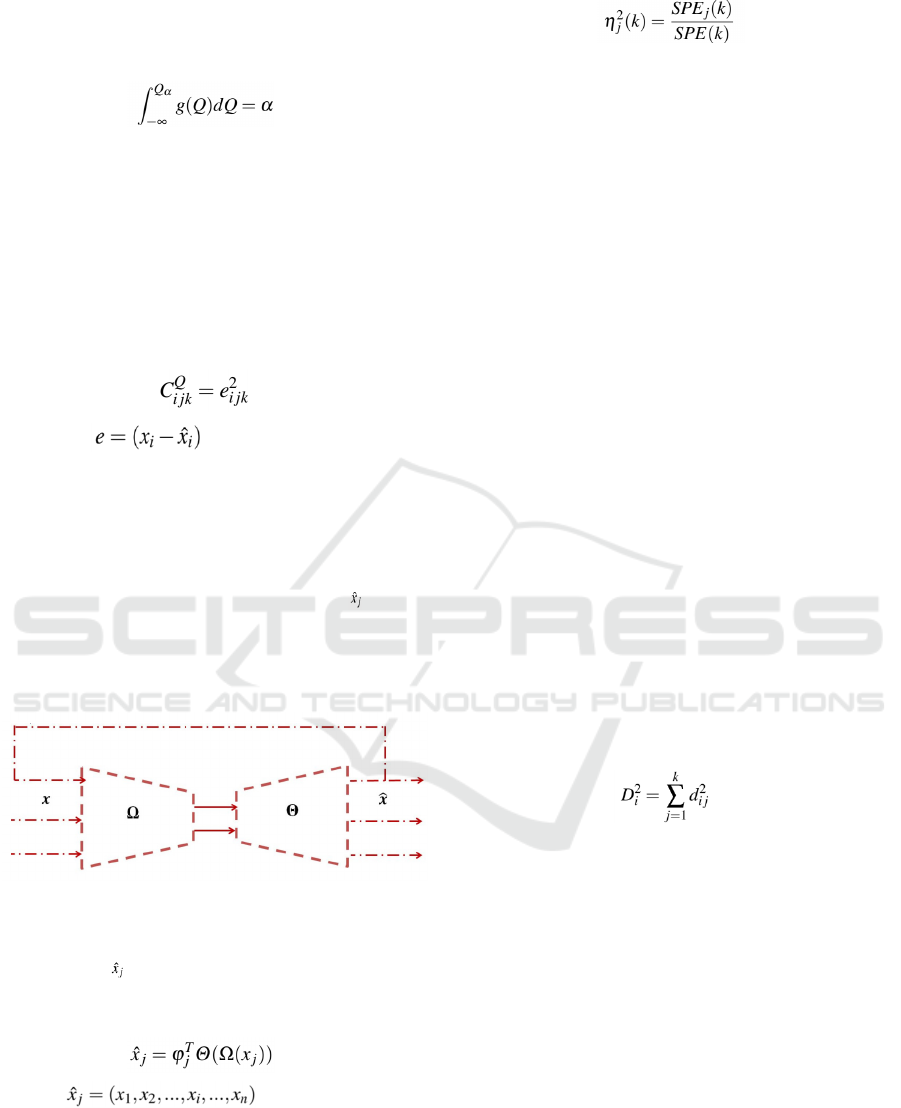
2.5 Sensor Validity Index

This method is based on the principle of

reconstructing all the variables from the moment of

detection by calculating the validity indexes of the

sensors. The reconstructed measurement can be

obtained iteratively, estimated, and re-estimated

until convergence, as indicated in Figure 1. This is

why, and similarly, in order to restructure the faulty

data, it is essential to detect the fault in a unique.

Figure 1: The schema of the reconstruction principal used.

The method requires predicting the process

measurement by substituting the j

process variable

with the predicted one and continuing the procedure

until the algorithm converges as follows:

(8)

Where: ,

is the

column of the identity matrix.

The Sensor Validity Index (SVI) is a sensor

effectiveness assessment in which, regardless of the

number of principal components of the faults, a

specified range should be present (

Bouzena

et al.,

201

7), it is defined as follows:

(9)

SPE

is the j

quadratic prediction error calculated

after reconstruction, while SPE is the quadratic

global prediction error computed before

reconstruction. A faulty sensor’s validity index must

converge towards zero.

3 FAULT DETECTION BASED ON

SSAE-KNN

The suggested technique is consisted of offline

modelling and online monitoring. The specified

stages are explained as follows:

3.1 Offline Modeling

Offline modeling steps’ include the following:

1. Training data is collected and normalized under

normal conditions.

2. The model is trained using the SSAE cost

function, deep nonlinear and dynamic features are

extracted from the input data.

3. The monitoring statistic is built using the

extracted feature with the model’s reconstruction

error.

4. In the extracted feature, finding k nearest

neighbors for input data x.

5. Calculate the KNN squared for each sample. The

KNN squared distance of sample i ( 𝐷





) is

described as:

(10)

Where 𝑑





indicates the squared Euclidean distance

between sample i to its j

closest neighbor.

6. KDE establishes a 𝐷





threshold for fault

detection. The threshold 𝐷





with a significance level

may be established because the distribution of 𝐷





can be approximated by a noncentral chi-square

distribution (

Verdier G. et al.,

201

1).

3.2 Online Monitoring

The fault detection section for an incoming

unclassified sample x has five steps:

1. The samples used for the test is standardized.

2. The dynamic enhanced data are transmitted into

a well-trained SSAE, which calculates the

residual feature and reconstruction error.

3. D



and SPE statistical quantities are calculated.

4. The problem is detected using the threshold

Fault Diagnosis with Stacked Sparse AutoEncoder for Multimode Process Monitoring

239

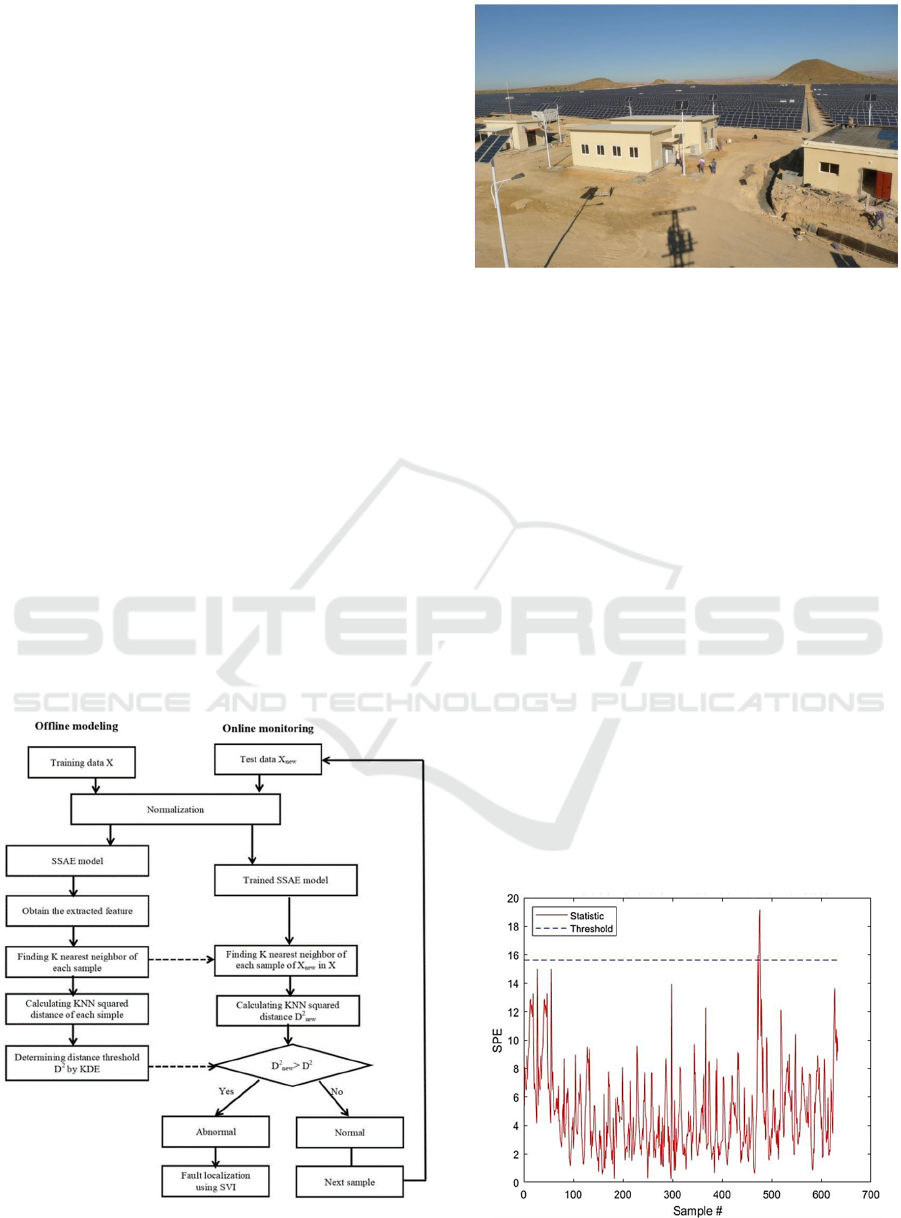
determined in step 6. If the statistical quantity

exceeds the threshold, the fault has occurred.

5. Using the contribution plot and sensor validity

index SVI to identify the faulty sensor. To

provide a more intuitive picture, the flow chart of

the proposed multimode process monitoring

technique based on the Stacked Sparse

AutoEncoder and K nearest neighbour scheme is

summarized in Figure 2.

4 CASE STUDY OF

IMPLEMENTATION

4.1 Process Description Used

The case study is about the solar power plant of

Oued Keberit, which is located near the city of

Souk-Ahras in north-eastern Algeria; close the

Tunisian border, shown in Figure 3. It is located in

latitude 35

’

”

north and longitude 7

’

”

East

(Toumi R. et al, 2019). The temperature varies

between 22.9 and 26.3 degrees Celsius in the

summer and as low as 10.2 degrees Celsius in the

winter. This gives an ideal setting for solar energy

project development. In our study, the model inputs

consist of solar power plant parameters, the hidden

layer that represents learned features, and the output

layer with the same dimension of the input layer that

represents reconstruction (Soualmia A. et al., 2016).

Figure 2: Flow chart of proposed fault detection method.

Figure 3: Photovoltaic Power Station of Oued Kebrit.

To demonstrate the usefulness of the suggested

technique, we examine data from the grid-connected

photovoltaic solar plant at Oued Kebrit. This data

includes the following parameters: Total Radiation,

Temperature, Wind Speed, Humidity, and Pressure,

we have a total of 05 parameters, indicating that we

have five sensors monitoring the observations

throughout a thirty-day period (2018). To develop

the SSAE model, a data matrix X was constructed

using N = 633 observations indicating the process

normal functioning. The data in such a matrix are

centered and scaled using the data means and

standard deviations. For the monitoring model, a

vector of measures comprised of the 05 variables

described previously was selected.

4.2 Simulations Results

In this context, we will present the results of the

suggested multimode process monitoring technique,

which is primarily used to identify sensor problems.

To show the monitoring method’s validity and the

advantages of fault detection, we created a

multimode monitoring model using a dataset from a

Figure 4: Evolution of the SPE index in normal state.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

240

solar power plant that had five variables and 633

samples. Under normal conditions, both the standard

technique based on SPE statistics and the SSAE-

KNN monitoring statistics suggest that all samples

are contained within the relevant zones depicted in

Figure 4-5.

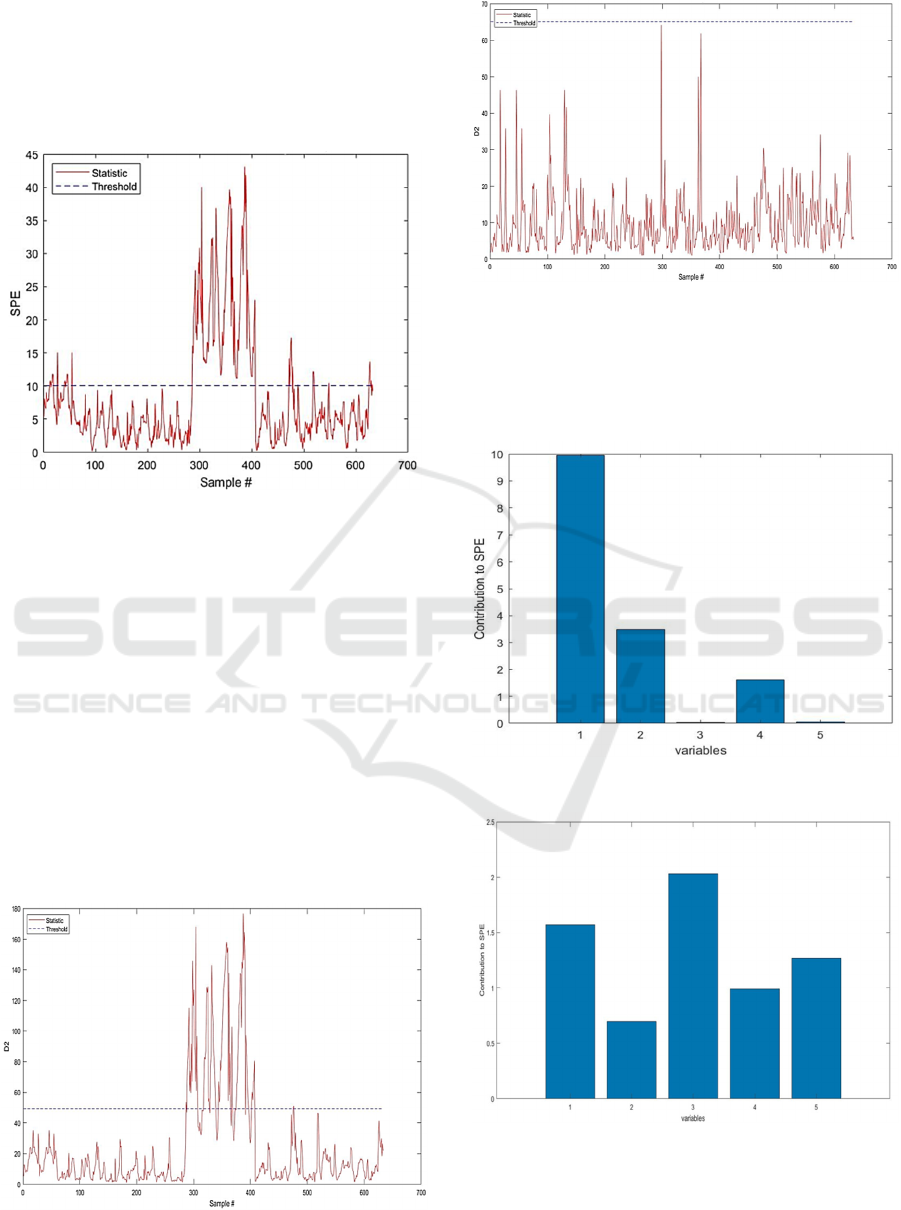
Figure 5: Evolution of the SPE index in faulty state.

After discovering a fault, it is required to determine

which sensor is faulty; this is accomplished using

the contribution plot. The evolution of the

contribution plots in the presence of a problem

affecting the first sensor measuring total radiation

and the fourth sensor measuring humidity is shown

in Figure 8(a)-(b). The usual technique fails to

identify the infected fourth sensor. Then, using the

reconstruction approach, we used the enhanced

sensor validity index (SVI). The fault localization of

all faulty variables is depicted in Figure 9(a)-(b).

Consequently, SVI based on reconstruction

approaches of the offending variable measures is

effectively used and gives better performance

compared to the conventional approach.

Figure 6: Evolution of the monitoring index based on

KNN in normal state.

Figure 7: Fault detection using SSAE-KNN.

The proposed SSAE-KNN method gives better

performance in fault detection, which appears

clearly in false alarm detection in the validation and

the test steps.

(a) Evolution of Contribution plot of the 1

sensor.

(b) Evolution of Contribution plot of the 4

sensor.

Figure 8: Localization of fault based on Contribution plot.

Fault Diagnosis with Stacked Sparse AutoEncoder for Multimode Process Monitoring

241

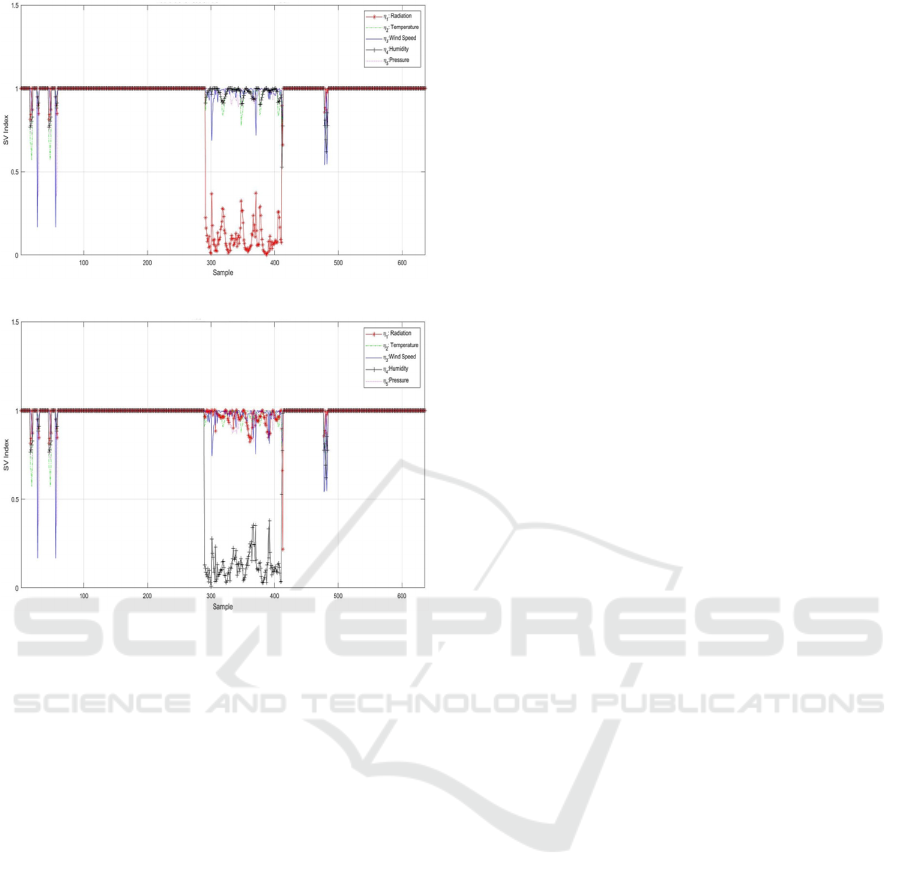
(a) Evolution of Sensor validity index of the 1

sensor.

(b) Evolution of Sensor validity index of the 4

sensor.

Figure 9: Localization of fault based on Sensor Validity

Index.

5 CONCLUSIONS

This work proposes a multimode process monitoring

approach based on the Stacked Sparse AutoEncoder

(SSAE) and K-Nearest Neighbour (KNN). The input

data is rebuilt using SSAE, and monitoring statistics

are generated using the KNN rule, with their related

thresholds determined using Kernel Density

Estimation (KDE). To detect malfunctioning

sensors, an improved Sensor Validity Index (SVI)

based on the reconstruction technique is proposed.

The experimental findings from a solar power plant

indicate the usefulness of the proposed system and

its ability to detect and diagnose sensor failures.

ACKNOWLEDGEMENT

This work is supported by the Directorate General of

Scientific Research and Technological Development

(DGRSDT) and Laboratory of Electrical Engineering

and Renewable Energy LEER of Algeria.

REFERENCES

Qin S. J., (2012) “Survey on data-driven industrial process

monitoring and diagnosis,” Annual Reviews in

Control, vol. 36, pp. 220–234.

Yin S., S. Ding X., Xie X., and Luo H., (2014) “A review

on basic data-driven approaches for industrial process

monitoring,” IEEE Transactions on Industrial

Electronics, vol. 61, pp. 6418–6428.

Hinton G. E. and Salakhutdinov R. R., (2006) “Reducing

the dimensionality of data with neural networks,”

Science, vol. 313, pp. 504–507.

Xu J., Xiang L., Liu Q., Gilmore H., Wu J., Tang J., and

Madabhushi A., (2016) “Stacked sparse autoencoder

(SSAE) for nuclei detection on breast cancer

histopathology images,” IEEE Transactions on

Medical Imaging, vol. 35, pp. 119–130.

Wang G., Liu J., Li Y., and Shang L., (2015) “Fault

detection based on diffusion maps and k-nearest

neighbor diffusion distance of feature space,” Journal

of Chemical Engineering of Japan, vol. 48, no. 9, pp.

756–765.

P. E. Odiowei and Y. Cao, (2010) “Nonlinear dynamic

process monitoring using canonical variate analysis

and kernel density estimations,” IEEE Transactions on

Industrial Informatics, vol. 6, pp. 36–45.

Yin J. and Yan X., (2019) “Mutual information–dynamic

stacked sparse autoencoders for fault detection,”

Industrial & Engineering Chemistry Research, vol. 58,

pp. 21614–21624, Nov. 2019.

Ren Z., Tang Y., and Zhang W., (2021) “Quality-related

fault diagnosis based on k-nearest neighbor rule for

non-linear industrial processes,” International Journal

of Distributed Sensor Networks, vol. 17, p.

155014772110559.

Xiong L., Liang J., and Qian J., (2007) “Multivariate

statistical process monitoring of an industrial

polypropylene catalyzer reactor with component

analysis and kernel density estimation,” Chinese Journal

of Chemical Engineering, vol. 15, pp. 524–532.

Bougheloum W. and Ramdani M., (2019) “Accurate

quality control charts via sparsityreconstruction for

multimode process monitoring,” International Journal

of Control, Energy and Electrical Engineering

(CEEE), vol. 11, pp. 8–11.

Bouzenad K. and Ramdani M., (2017) “Multivariate

statistical process control using enhanced bottleneck

neural network,” Algorithms, vol. 10, p. 49.

Verdier G. and Ferreira A., (2011) “Adaptive mahalanobis

distance and knearest neighbor rule for fault detection

in semiconductor manufacturing,” IEEE Transactions

on Semiconductor Manufacturing, vol. 24, pp. 59–68.

Toumi R., Kourd Y., and Ramdani M., (2019)“Data driven

photovoltaic power station monitoring using robust

sparse representation,” in 2019 1

International

Conference on Sustainable Renewable Energy

Systems and Applications (ICSRESA), IEEE.

Soualmia A. and Chenni R., (2016) “Modeling and

simulation of 15mw grid-connected photovoltaic system

using PV syst software,” in 2016 International

Renewable and Sustainable Energy Conference

(IRSEC), IEEE.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

242