Dual-Arm Compliance Control with Robust Force Decomposition

William Freidank

1,2

, Konrad Ahlin

and Stephen Balakirsky

Department of Mechanical Engineering, Georgia Institute of Technology, 801 Ferst Dr, Atlanta, Georgia, U.S.A.

Georgia Tech Research Institute, 640 Strong Street, Atlanta, Georgia, U.S.A.

Keywords:

Dual-Arm Control, Compliance Control, Artiﬁcial Potential Field, Secant Method, Force Decomposition,

Beam Method, Robot, Robotic, Manipulator.

Abstract:

Realtime, compliant control of dual-arm robots has been an open area of investigation for versatile object

manipulation. Recent research has focused on leader-follower, hybrid, and impedance control techniques.

This paper proposes a guaranteed-convergence artiﬁcial potential ﬁeld in order to leverage its advantages in

computational speed and functional quality. Additionally, compliance control is integrated using a novel force

decomposition method. Experiments are performed on a 14 Degree-of-Freedom (DoF) dual-carriage rail,

with two UR5e robots to validate the new method’s accuracy and demonstrate the feasibility of the uniﬁed

controller.

1 INTRODUCTION

Robotics have steadily gained greater responsibility

in industrial settings, especially in structured and pre-

dictable assembly operations. One major challenge

to broader implementation is the inability to adapt

highly task-speciﬁc solutions to new objects and situ-

ations (Kousi et al., 2018). Dual-arm, compliant ma-

nipulators promise greater versatility in the push for

reliably performing maintenance operations with un-

predictable disturbances and features.

There are two kinds of compliance: internal and

external. A human uses “external” compliance when

using their arms and hands to install an object guided

by a peg and socket. The force felt from the socket

correcting the orientation of the peg during insertion

allows the human to adjust the insertion to comply

with the actual geometry. A human uses “internal”

compliance when an object cannot be grabbed at an-

ticipated positions. For example, if the object is larger

due to a design change, the human will feel the ob-

ject’s larger size forcing the human to “comply” with

a greater spacing of their arms and hands. The prob-

lem of internal compliance is unique to systems with

more than one simultaneous grasp point.

In robotics, compliance control may be realized

passively through innovative mechanical designs such

as variable stiffness actuators (Wolf et al., 2016) or

actively through more classical methods such as par-

allel force/position, impedance, or admittance control

(Calanca et al., 2016)(Seraji, 1994). In the active

case, compliant control may be seen as a form of con-

tinuous feedback force control. Compliance can be

achieved at the level of the object, at the level of robot

joints, or both, as explored in (Ren et al., 2021).

(Hu et al., 2021) proposed two techniques of solv-

ing the internal and external compliant forces for

dual-arm compliant control: a master-slave force con-

trol and a shared force control. The master-slave tech-

nique assumes an expected force and torque at one

manipulator’s end-effector, reducing the number of

unknown variables to only those at the other manip-

ulator, and then solves the system uniquely. Vari-

ations of this approach have been used elsewhere

(Xian et al., 2017)(Gao et al., 2022). In the second

method, the shared force technique allows for object-

level force commands, but suffers from an undeter-

mined system of equations. (Song et al., 2021) ex-

plored the control of internal and external forces when

employing the shared force technique. The primary

challenge in question becomes properly decompos-

ing applied forces into internal and external contribu-

tions at the robot end-effectors. Pseudoinverse-based

methods have the advantage of being readily extended

to k number of manipulators, as leveraged in (Song

et al., 2022). (Walker et al., 1991) proposed a No-

Squeeze pseudoinverse designed to yield end-effector

wrenches that are free from internal effects on the ob-

ject. However, their method imposes the requirement

of equal load distribution, which may not correspond

to real operating conditions. A further exploration

was made in (Erhart and Hirche, 2015) of the prob-

lems arising frrom unintended internal wrenches pro-

duced by different pseudoinverses, presenting an an-

616

Freidank, W., Ahlin, K. and Balakirsky, S.

Dual-Arm Compliance Control with Robust Force Decomposition.

DOI: 10.5220/0012177300003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 616-623

ISBN: 978-989-758-670-5; ISSN: 2184-2809

alytically inspired parameterized inverse. In this pa-

per, we propose a shared-force technique that avoids

mathematical optimizations in favor of a closed form

solution drawing upon a physically inspired analysis

incorporating established models in classical statics.

A robust control methodology may use simultane-

ous path planning and compliance control to achieve a

larger trajectory objective. However, compliant con-

trol for large or heavy objects may require the co-

ordinated control of multiple robotic manipulators.

In such high-dimensional problems, choice of a path

planning method comes down to computation time as

a function of algorithm complexity, which for search-

based methods, such as A* and Rapidly-exploring

Random Trees (RRT), increases exponentially with

the dimensions of space (LaValle, 2006). Neither can

reliably solve the path planning problem with real-

time capability in a fourteen-dimensional space, as

necessary for the robot cell used for our research.

Artiﬁcial Potential Fields (APF), which are

function-based approaches to path planning, offer

compelling advantages for path planning in high di-

mensional spaces. APF uses a goal location and

obstacles to calculate a simulated “potential” func-

tion, the gradient of which acts as a pseudo-force

that directs the manipulators toward the target. The

complexity of the APF algorithm scales linearly with

space dimensions rather than exponentially making

it ideal for high DoF path planning (Khatib, 1985)

(Khatib, 1986). APF has well-known disadvantages

for mobile robotics (Omar et al., 2016), but these

performance issues can be alleviated by adjusting

the potential function using an approach called the

“Secant Method” (Ahlin et al., 2018). Furthermore,

APF theory can be extended to manipulators. (Kim

et al., 2021) demonstrated that the Secant Method can

plan for two, six-DoF manipulators to have coordi-

nated motion. In their research, coordinated control

alongside a mechanical compliance device known as a

“wifﬂetree” allowed two manipulators to carry a pay-

load that was heavier than either could have carried

individually. In this work, we adopt insights from

(Kim et al., 2021). First, the path planning will be

solved in real-time at approximately 500 Hz to match

the controller. (Kim et al., 2021) used this frequency

to ensure that the two manipulators’ end-effectors

maintained the same relative position, despite varia-

tions and errors that manifested during path execu-

tion. Second, we compute the path plan in Cartesian

task space and translate the commanded pseudo-force

to joint space via a Jacobian transpose. Error values

can thus remain in the task space domain, which im-

proves the relevance of the error to real-world appli-

cations and eliminates the need to translate the target

location to joint space.

The general formulation of a dual-arm coopera-

tive manipulation task is sketched in Figure 1. Each

manipulator may have n

joints for a total of n = Σn

degrees of freedom. A common base frame with co-

ordinates {B} stands as a ﬁxed global frame for the

combined system. Further coordinate frames are es-

tablished for the end-effectors, {E1} and {E2}, as

well as the manipulated object, {O}. The grasp points

at which each manipulator contacts the object are

known a priori, and are prescribed as constant homo-

geneous transforms in the object’s ﬁxed frame,

and

. As a matter of convention, a manipulator’s

end-effector is deﬁned as the feature which should co-

incide with one of an object’s grasp-points.

{B}

{E1}

{E2}

{O}

{G1} {G2}

Figure 1: Dual-arm cooperative manipulation scenario.

2 COORDINATED CONTROL

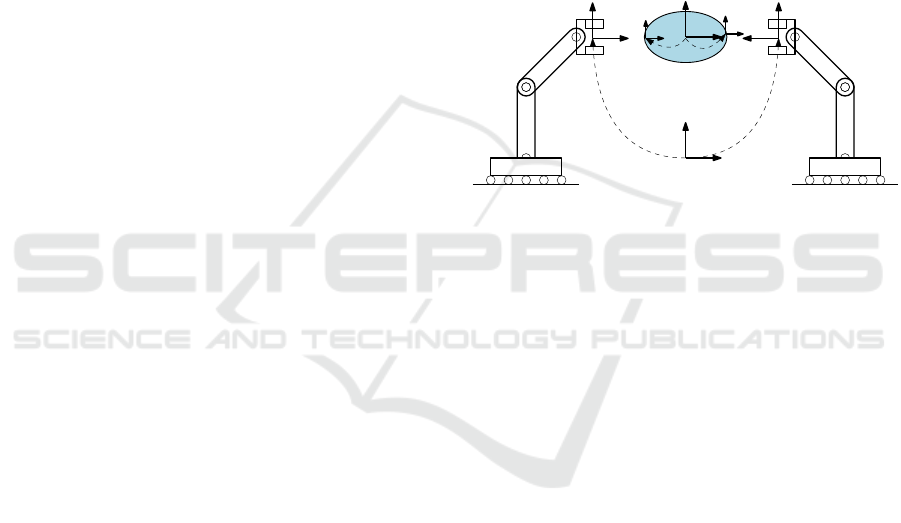
2.1 Coordinated Potential Field

The combined controller should retain its capacity to

direct each arm independently and allow for seamless

transition from individual to cooperative manipula-

tion. To retain independent functionality, a separate

instance of the Secant controller (Ahlin et al., 2018)

is initially assigned to each robot chain, forming the

potential ﬁelds {Ψ

, Ψ

}, where each ﬁeld is conﬁg-

ured for its respective manipulator’s task-space goal.

In a cooperative task, the two ﬁelds are conﬁgured

with the same goal so that both chains act collabo-

ratively. However, further modiﬁcation is required

to enforce a relative constraint between the manipu-

lators to avoid crushing, twisting, or otherwise vio-

lating the volumetric properties of a held object. To

enforce the desired cooperative kinematic constraint

between the manipulators, we deﬁne and generate a

secondary potential ﬁeld Φ(z) whose task-space tar-

get is the shared object frame {O}. The gradient of

this ﬁeld, evaluated at the ith end-effector, provides a

new spring force which acts in contrast to any relative

offset between the manipulators. The new, modiﬁed

gradient at the ith manipulator for APF control is cal-

culated as:

Dual-Arm Compliance Control with Robust Force Decomposition

617

∇

∂Ψ

)

∂z

∂Φ(z

)

∂z

(1)

This arrangement can be understood in Figure 2. An

important consideration: this research is using the Se-

cant Method to create a trajectory in Cartesian space.

As such, dynamic effects such as gravity and Coriolis

effects do not need to be considered within the plan-

ner. These terms are accounted for in the arm con-

trollers and in the force proﬁle read by the sensors.

2.2 Incorporating Grasp Offset

To maintain coherent robot motion in cooperative

mode, the gradients {

∂Ψ

∂z

∂Ψ

∂z

} should be nominally

evaluated at an identical location. This conﬁguration

would allow each manipulator to share a ﬁnal link

when invoking the inverse Jacobian, resulting in a

common center of rotation for the combined manip-

ulator. This is accomplished by establishing a virtual

Tool Center Point (vTCP) for each manipulator, de-

rived from the grasp transformation.

(

)

= (

)

−1

(2)

In this manner, the robot end-effector will nomi-

nally coincide with the grasp feature while the vTCP

will coincide with the object’s body origin. While the

vTCP is reserved as the last link in each kinematic

chain, it is excluded from all obstacle avoidance cal-

culations.

Finally, disturbances or errors may result in tran-

sitory or ﬁxed offsets between the vTCPs, leaving

the shared object frame ambiguously deﬁned. We re-

solve the ambiguity by approximately inferring {O}

in real-time as the average of the vTCP poses. For

the position component, this is easily computed as the

element-wise mean of both. For the orientation com-

ponent, we use the 50% quaternion spherical linear

interpretation (SLERP) between the two orientations.

(

)

(

)

{B}

{T }

Figure 2: Dual-arm coordinated control.

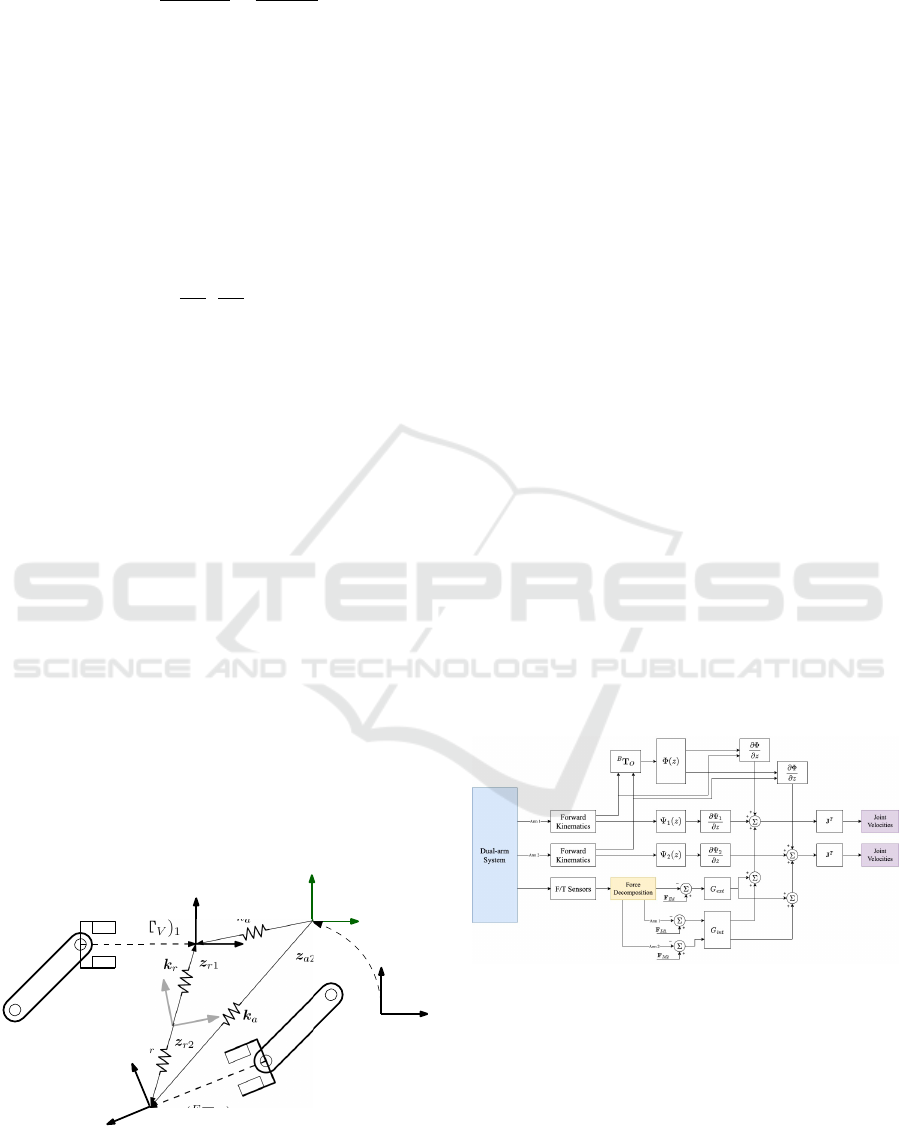
3 COMPLIANCE CONTROL

3.1 Overview

Let a convention for generalized forces, or wrenches,

be deﬁned:





(3)

where the wrench is composed of a linear force f and

a torque τ applied at some point x.

Compliance can be implemented in an artiﬁcial

potential ﬁeld by superimposing a new class of forces

onto the gradient of the map. The forces are con-

structed according to the laws

= k

⊙ (F

− F

) (4)

where k

is a vector of gain factors whose entries cor-

respond to each respective element of a generalized

force vector, and which are applied to a wrench via

the Hadamard product with the ⊙ operator. F

is the

current external wrench applied to the object and F

is the desired or commanded external wrench.

In the dual-arm condition, as in any similar coop-

erative manipulation task, an additional internal force

is introduced as an artifact of its over-constrained na-

ture. The internal force can be decomposed in a sim-

ilar manner as to the external and with the same sub-

scripted meanings:

= k

⊙ (F

− F

) (5)

The integration of these two compliance forces

into the APF controller is detailed in Figure 3. The

subsequent sections investigate how to accurately de-

termine F

and F

Figure 3: Dual-arm coordinated and compliant control.

3.2 F/T Equivalence

In these operations, it is often necessary to convert

forces from one point of application to another while

maintaining an equivalent effect on the rigid body.

This requirement is most often introduced when a ma-

nipulator’s force-torque sensor does not coincide with

the tool center point, as will be the case in coopera-

tive manipulation tasks involving a volumetric object.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

618

The matrix transferring a spatial wrench at point α to

point β is

Ω



⌊r

γ→α

×⌋ I



(6)

where ⌊·×⌋ forms the skew-symmetric matrix for

cross-product operations and r

γ→α

is the vector drawn

from the point γ to the point α.

Where it is necessary to perform a change of basis

from {A} to {B}, it shall be noted as x

Unless otherwise stated, we express all vectors and

wrenches in a ﬁxed common work frame {W }.

3.3 Determining External Force

The analysis completed by (Walker et al., 1991) of a

rigid body assumes a ﬁrm grasp transmits both forces

and moments at the point of contact. Let F

be the

contact forces at the ith of k total grasp points ex-

pressed in work frame coordinates. From a free-body

diagram analysis, the net force exerted externally on

the object can be expressed generally as

= W F

(7)

with

= [F

, ..., F

]

(8)

W =



. . . I

⌊r

×⌋ I

. . . ⌊r

×⌋ I



(9)

where W is known as the grasp matrix in the R

spa-

tial context, r

is the vector drawn from the object

frame to the ith grasp point, and all vectors are ex-

pressed in the common work frame.

We further stipulate that the force-torque sensor

might not be coincident with the end-effector of the

robot chain. Therefore, so as to calculate forces as

applied at the sensor, we replace the vectors r

with

, the vector drawn from the object frame to the ith

chain’s F/T sensor. In this way, the end-effector chain

is considered a rigid component of the grasped object,

and the net object force can be expressed as a function

of the F/T sensor readings F

. In the dual-arm sce-

nario shown in Figure 4, these relationships reduce to

W F

(10)

with





(11)

W =



Ω



(12)

In general, the external force F

includes not only

external loads but also the effects of gravity and any

dynamic forces arising from the acceleration of the

body. This is observed from the sum of forces and

moments for a dynamic rigid body with constant mass

{X, Y, Z}

(a)

{X, Y, Z}

(

)

(b)

Figure 4: (a) Dual-arm cooperative object detail. (b) End-

effector chain detail.

and inertial properties. However, a rigorous consider-

ation of inertial effects is not the focus of the present

investigation. We assume small acceleration and ve-

locity throughout, resulting in small dynamical terms

in comparison to external disturbances. As the in-

corporation of the dynamical terms is linear, they can

thus be neglected. We also consider the effect of grav-

ity as an external disturbance rather than accounting

for it directly, since the mass of the object is unknown.

In practice, zeroing of F

sufﬁces to account for grav-

ity, and we establish:

= F

(13)

3.4 Determining Internal Force

Established methods in literature isolate the internal

force contribution of a given manipulator by subtract-

ing the expected wrench

in an unloaded internal

condition from the reported wrench.

int

= F

−

(14)

To obtain

, the authors have pre-multiplied (10)

by the inverse of the grasp matrix to isolate F

. How-

ever, in over-constrained systems, the grasp matrix

has a nonzero null space and cannot be inverted ex-

cept approximately by a pseudoinverse, as investi-

gated in (Walker et al., 1991). These linear ap-

proximations are merely mathematical optimizations

rather than informed studies, resulting in poor accu-

racy along certain axes.

Rather than make use of a pseudoinverse, we pro-

pose modeling the handled object as a statically inde-

terminate beam. This model assumes the object has

a fairly uniform cross-section and structural stiffness.

In the case of transverse forces and moments (Fig-

ure 5), the one-dimensional reactionary wrench at the

constraint a units away from the external wrench ap-

plication upon a beam of length l can be calculated

according to (Roark et al., 2012).

T,a

( f , τ) =

− f

(l − a)

(l + 2a) +

6τa

(l − a) (15)

Dual-Arm Compliance Control with Robust Force Decomposition

619

T,a

(t, τ) =

f a

(l − a)

− 4al + 3a

) (16)

where R is the linear reactionary force, M is the reac-

tionary torque, f is the load force, and τ is the load

torque.

Figure 5: Statically indeterminate beam (transverse forces).

The longitudinal case (Figure 6) may be similarly

calculated (Hibbeler, 2011).

L,a

( f ) = f



a − l



(17)

L,a

(τ) = τ



a − l



(18)

Figure 6: Statically indeterminate beam (longitudinal

forces).

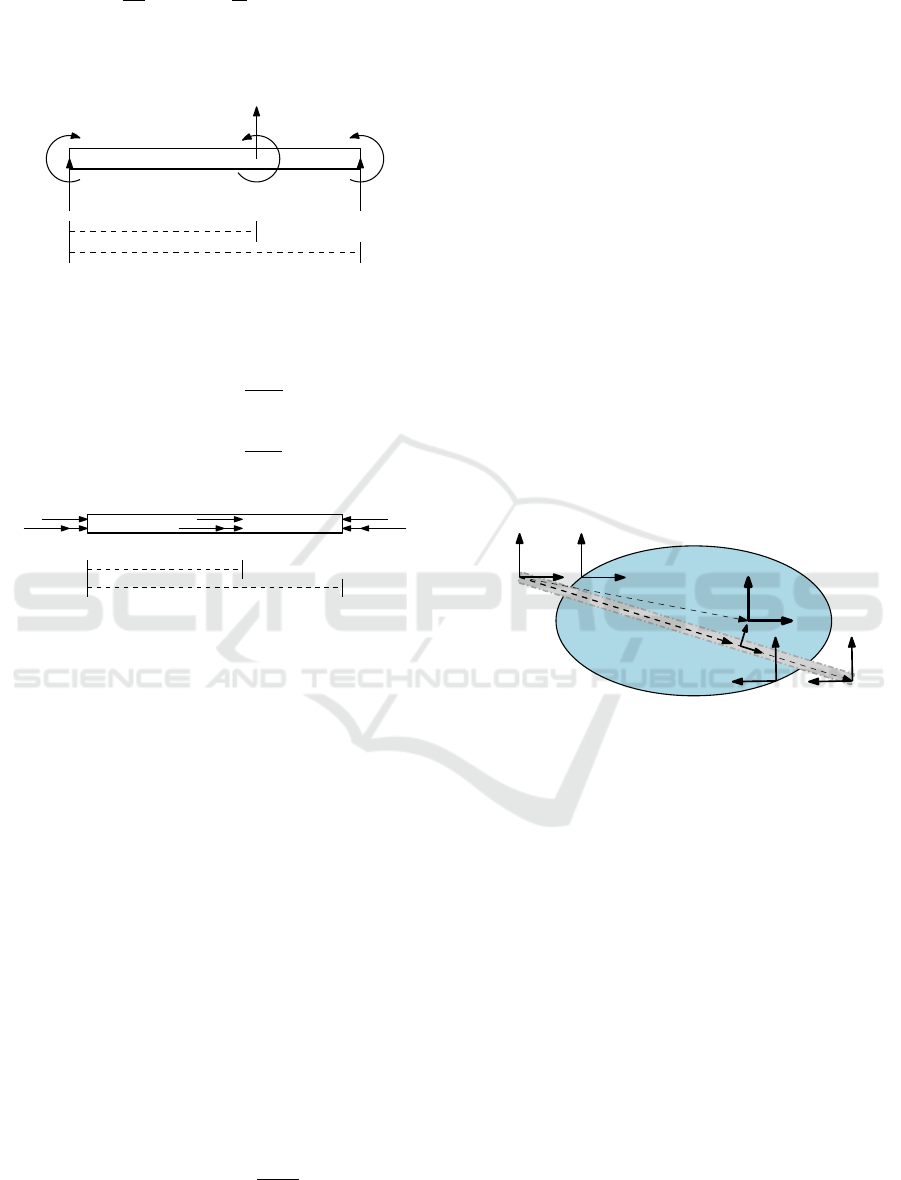
The question now arises as to which physical

points should be associated with the ends of the mod-

eled beam, or beam phantom. An intuitive option is

to deﬁne the beam phantom as the line joining the two

grasp points. However, the end-effector chains them-

selves can be seen as forming part of a larger rigid

body containing the shared object. Here, the nuances

of the manipulation problem can become more rele-

vant, such as the comparative stiffness of the object

and end-effector chain. We proceed with a method

based on the second observation and assume a more

accurate model admits to the entire structure con-

tributing to the combined deformation effects. The

force-torque sensors of either arm shall be the termi-

nation points of the beam phantom, with the span of

the vector g joining them termed the grasp line (Fig-

ure 7).

The phantom point of force application {

O} is de-

ﬁned by orthogonal projection of the object origin

onto the grasp line. In this way, the equivalent offset

a is maintained, which is critical for model validity.

˜o

= Proj

) =

(19)

{a, l} = {||r

˜o

||, ||g||} (20)

where r

is the vector drawn from the F/T sensor of

manipulator 1 to the shared object center O. Addition-

ally, {

O} is oriented so as to always align its x-axis

with the longitudinal axis of the beam. Since internal

forces do not affect object motion and thus do not ap-

pear in the net object force F

, the result of (10) may

be used for the purpose of calculating the expected

wrenches in the internally unloaded condition. The

object force is transferred to {

O} by F/T equivalence,

and then expressed in the coordinates of {

O}, allow-

ing systematic application of the beam equations with

resultant wrenches

expressed in the same frame.

˜o

Ω

(21)







L,a

˜o

T,a

˜o

j, τ

˜o

−R

T,a

(−f

˜o

k, τ

˜o

L,a

(τ

˜o

−M

T,a

(−f

˜o

k, τ

˜o

−M

T,a

˜o

j, τ

˜o







(22)

where

k are the unit identity vectors. Note that, in

practice, care must be taken to properly account for

sign differences caused by the coordinate convention.

{O}

{S1}

{

˜o

{S2}

{G1}

{G2}

Figure 7: Statically indeterminate beam phantom.

It is desirable to compute compliance in the

object-ﬁxed frame. This permits, for instance, a con-

stant squeeze force along a particular axis of the ob-

ject, regardless of its orientation or that of the end-

effectors with respect to it. Therefore, before the gain

factors are applied,

is transferred to and expressed

in the original object frame, {O}.

Ω

(23)

Note that it has not been necessary to perform

identical calculations on the second manipulator. This

is because, by deﬁnition, internal forces do not con-

tribute to object motion. If the internal forces con-

tributed by the ith manipulator are transferred to and

expressed in the same frame, then

= 0 (24)

Since there are only two manipulators, this expands

= −

(25)

The internal gain factors k

are applied and the results

expressed in work frame coordinates.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

620

(a) (b)

Figure 8: (a) Experiment upright posture. (b) Experiment

horizontal posture.

4 FORCE DECOMPOSITION

EXPERIMENTS

To illustrate the advantage of our beam method, static

experiments are performed on a mock object manip-

ulation problem. The object is a 1” aluminium ex-

trusion and is grasped by 2-ﬁnger grippers with ap-

proximately 470 mm of separation. F/T readings are

recorded by an ATI Axia80 placed in the end-effector

chain of one of the manipulators. It should be men-

tioned that the ﬁnger grippers will always provide

forces, but due to their relatively small contact sur-

face, may not provide reactionary torques along all

axes. To help determine the true boundary condi-

tions, two different grasp postures are evaluated (Fig-

ure 8). The upright posture minimizes the gripper

surface area that would contribute a torque in the z-

axis, while the horizontal posture maximizes it. Lin-

ear force along the y-axis and torque along the z-axis

are independently applied at seven different points

along the beam. The measured F/T response is com-

pared to the expected values yielded by the Moore-

Penrose pseudoinverse (PINV), the No-Squeeze pseu-

doinverse (Walker et al., 1991), our beam method,

and a simply-supported (SS) model. The simply-

supported model assumes the grippers transmit no

torque; by removing the torque entries of F

, the

grasp matrix W becomes square with a unique non-

approximate inverse. As anticipated, the simply-

supported model best predicts experimental F/T read-

ings in the upright conﬁguration; however, our beam

method provides substantial improvements in the hor-

izontal posture, as shown in Table 1.

First, it is noted that the beam and pseudoinverse

predictions for f

in response to a linear force con-

verge when the point of force application is near

the geometric center of beam. In this regard, the

beam method provides the greatest advantage when

the shared object has a center of gravity which does

not coincide with its volumetric center, or when it has

an off-center interface point with the environment.

The experiments yield one modiﬁcation that must

be made: both manipulators share equally the load in-

Table 1: Minimum and maximum F/T sensor prediction er-

ror ϵ, as a percentage of |F

ext

|, in response to a static load

applied at a range of locations ±20% of the distance be-

tween the sensors in the horizontal posture. Lower is better.

Isolated Force

ϵ PINV No-Squeeze SS Beam

1.5—31 2.6—36 1.9—17 0.9—8.7

2.4—30 3.3—33 5.7—22 0.0—5.1

Isolated Torque

ϵ PINV No-Squeeze SS Beam

88—140 110—160 19—74 6.5—47

64—81 76—92 26—42 5.2—31

duced by a linear force applied longitudinally along

the beam (that is, along the denoted x-axis), regard-

less of where it is applied. While the beam method

theory is in disagreement, it is simple to revise it to

accommodate:

′

L,a

( f ) = f



−1



(26)

5 LIVE APPLICATION ANALYSIS

A typical benchmark for manipulation tasks is the

peg-in-hole problem, serving as a primary primitive

for applied multi-axis compliance in insertion con-

texts. To benchmark our dual-arm system with im-

proved force decomposition, we design a peg-in-hole

problem (Figure 9) in which both internal and exter-

nal compliance are required along a transverse axis.

Internal compliance may be necessary when the ex-

pected and actual object geometries do not match,

which we simulate by using object handles mis-

aligned by about 40 mm. To highlight the advantage

of the beam method, the mating point is located non-

centrally between the two manipulators, at a point

20% along the total length. To demonstrate external

compliance, the mating peg location is erroneously

perturbed, and a large 45

◦

chamfer is added to the peg

sockets to lengthen the distance over which compli-

ance is employed. Additionally, the use of two sepa-

rate mating features provide a rotational constraint to

demonstrate both linear and angular responses. The

mating point is taken as the center-point between the

two features.

Our dual-arm system is comprised of two UR5e

collaborative robot arms, each attached to a respective

rail carriage to form a total of 14 DoF. The rail car-

riages are individually powered by Parker-Hanniﬁn

Dual-Arm Compliance Control with Robust Force Decomposition

621

Figure 9: Aluminium extrusion with misaligned handles

and two peg sockets. Beam length is not to scale in this

sketch.

IPA04-HC motor controllers. F/T readings for each

manipulator are obtained using the internal UR5e sen-

sors. Manipulator 1 uses a Robotiq 2F-85 gripper, and

manipulator 2 uses a longer 2F-140 model. To ensure

the transmission of torque at the grasp points, the ob-

ject is grasped in a horizontal posture.

5.1 Isolated Force Application

We simulate the interactions between the peg and hole

by applying a transverse force f

at the mating point.

The metrics of interest are the reported internal force

int,y

and torque τ

. Since only an external force is

in fact being applied during the experiment, f

int,y

and

int,z

should remain constant. For completeness, this

experiment is performed twice, once with external

control enabled and again with it disabled. When

enabled, the same control gains are used across the

tested force decomposition methods. It is noted that

the baseline internal force caused by gripping the mis-

aligned handles varies depending on the force decom-

position method employed. This is accounted for by

subtracting the prior baseline reading before analysis.

Table 2: Maximum internal force and torque in response to

a simulated peg-in-hole interaction with the Beam method

and control disabled. Lower is better.

Component Method

(as % of |F

ext

|) PINV No-Squeeze Beam

Linear, f

int

15 16 0.8

Torque, τ

int

13 15 4.1

From Tables 2 and 3, it is clear that the beam

method provides an improvement in registered inter-

nal loading in all conditions, with maximum beneﬁt

when the control gains are lowest (emulated at the

limit by disabled control). Improvements over the

Moore-Penrose pseudoinverse are maximum at 18x

in linear force and 3x in torque. Against the No-

Squeeze method, the Beam technique offers maxi-

mum improvements of 15x in force and 3x in torque.

Table 3: Maximum internal force and torque in response to

a simulated peg-in-hole interaction with the Beam method

and control enabled. Lower is better.

Component Method

(as % of |F

ext

|) PINV No-Squeeze Beam

Linear, f

int

3.5 4.5 1.1

Torque, τ

int

10 20 5.9

5.2 Peg-in-Hole Demonstration

The complete system is run on actual hardware with

control enabled. The purpose of the demonstration is

to show the collective functioning of the planner and

compliance technique in the real-world context of a

mating problem. Figure 9 is a still frame from the

demonstration recording. The demonstration success-

fully mates the rotationally constrained object with an

initial error neighboring 6

◦

in rotation and 2.5cm in

vertical distance. The direct-contact insertion phase

completes in approximately ﬁve seconds. Greater er-

ror could be tested using larger socket chamfers. Os-

cillations are present once both pegs fully thread into

the sockets, particularly along the axis of the rail car-

riages. This is a stability problem associated with the

force impulses upon contact with a rigid surface. Re-

ducing the force response gain and increasing posi-

tional stiffness alleviates these oscillations.

Figure 10: Dual peg-in-hole demonstration.

6 CONCLUSION

Coordinated dual-arm control of a shared object has

been achieved using a modiﬁed artiﬁcial potential

ﬁeld controller as the basis for path planning. For

demonstration, the system was able to solve an an-

gularly constrained, non-central peg-in-hole prob-

lem. Future work may involve demonstrating static

and dynamic object collision avoidance, leveraging

the novel capabilities of the Secant Method. More-

over, compliance has been incorporated into the con-

troller using a physically driven nonlinear model. Our

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

622

method of force decomposition achieves better re-

sults in experiment, up to an order of magnitude, than

common methods in literature. Future improvements

to the technique could include modeling interaction

torques as a force-couple with known moment arm

rather than a concentrated torque; this would match

the physical scenario more closely in certain conﬁg-

urations. Internal compliance might also be adjusted

so as to use each manipulator’s gripper point as the

respective center of rotation, while still sharing the

object center for external compliance and object-level

trajectory planning. Object mass and inertia proper-

ties, neglected here, could be incorporated into the

equations of motion. A Kalman ﬁlter could be ex-

plored for smoothing reactions to impulsive contact

forces and reducing oscillations. Taken together, this

work forms the basis for future dual-arm collabora-

tive object manipulation, including the exploration of

intelligent insertion strategies to improve speed and

repeatability.

REFERENCES

Ahlin, K. J., Sadegh, N., and Hu, A.-P. (2018). The se-

cant method: Global trajectory planning with variable

radius, solid obstacles. In Dynamic Systems and Con-

trol Conference, volume 51913, page V003T32A015.

American Society of Mechanical Engineers.

Calanca, A., Muradore, R., and Fiorini, P. (2016). A re-

view of algorithms for compliant control of stiff and

ﬁxed-compliance robots. IEEE/ASME Transactions

on Mechatronics, 21(2):613–624.

Erhart, S. and Hirche, S. (2015). Internal force analysis and

load distribution for cooperative multi-robot manipu-

lation. IEEE Transactions on Robotics, 31(5):1238–

1243.

Gao, M., Zhou, H., Yang, Y., Dong, Z., and He, Z. (2022).

An intelligent master–slave collaborative robot system

for cafeteria service. Robotics and Autonomous Sys-

tems, 154:104121.

Hibbeler, R. C. (2011). Mechanics of materials. Prentice

Hall, Boston, 8th ed edition.

Hu, B., Yan, L., Han, L., and Yu, H. (2021). Coordinated

compliance control of dual-arm robot astronaut for

payload operation. International Journal of Advanced

Robotic Systems, 18(3):17298814211012850.

Khatib, O. (1985). Real-time obstacle avoidance for manip-

ulators and mobile robots. In Proceedings. 1985 IEEE

international conference on robotics and automation,

volume 2, pages 500–505. IEEE.

Khatib, O. (1986). The potential ﬁeld approach and opera-

tional space formulation in robot control. pages 367–

377. Springer.

Kim, R., Balakirsky, S., Ahlin, K., Marcum, M., and

Mazumdar, A. (2021). Enhancing payload capacity

with dual-arm manipulation and adaptable mechani-

cal intelligence. Journal of Mechanisms and Robotics,

13(2).

Kousi, N., Michalos, G., Aivaliotis, S., and Makris, S.

(2018). An outlook on future assembly systems in-

troducing robotic mobile dual arm workers. Procedia

CIRP, 72:33–38. 51st CIRP Conference on Manufac-

turing Systems.

LaValle, S. M. (2006). Planning algorithms. Cambridge

university press.

Omar, R., Sabudin, E., CK, C. K. M., et al. (2016). Po-

tential ﬁeld methods and their inherent approaches for

path planning. volume 11, pages 10801–10805. Asian

Research Publishing Network (ARPN).

Ren, X., Huang, L., and Zhao, M. (2021). Prioritized hier-

archical compliance control for dual-arm robot stable

clamping.

Roark, R. J., Young, W. C., Budynas, R. G., and Sadegh,

A. M. (2012). Roark’s formulas for stress and strain.

McGraw-Hill, New York, 8th ed edition. OCLC:

ocn769455976.

Seraji, H. (1994). Adaptive admittance control: an approach

to explicit force control in compliant motion. In Pro-

ceedings of the 1994 IEEE International Conference

on Robotics and Automation, pages 2705–2712 vol.4.

Song, X., Huang, H., Xu, W., and Li, B. (2022). A ro-

bust force controller of multi-robot cooperative ma-

nipulators for carrying task. In 2022 IEEE Interna-

tional Conference on Robotics and Biomimetics (RO-

BIO), pages 987–992, Jinghong, China. IEEE.

Song, X., Mao, H., Huang, H., Xu, W., and Li, B. (2021).

A Dynamic Adaptive Impedance Controller for Force

Tracking of Dual-arm Manipulators in Uncertain Con-

tact Environment. In 2021 IEEE International Con-

ference on Robotics and Biomimetics (ROBIO), pages

1674–1681, Sanya, China. IEEE.

Walker, I. D., Freeman, R. A., and Marcus, S. I. (1991).

Analysis of Motion and Internal Loading of Ob-

jects Grasped by Multiple Cooperating Manipula-

tors. The International Journal of Robotics Research,

10(4):396–409.

Wolf, S., Grioli, G., Eiberger, O., Friedl, W., Grebenstein,

M., Hoppner, H., Burdet, E., Caldwell, D. G., Car-

loni, R., Catalano, M. G., Lefeber, D., Stramigioli,

S., Tsagarakis, N., Van Damme, M., Van Ham, R.,

Vanderborght, B., Visser, L. C., Bicchi, A., and Albu-

Schaffer, A. (2016). Variable stiffness actuators: Re-

view on design and components. IEEE/ASME Trans-

actions on Mechatronics, 21(5):2418–2430. Cited By

:266.

Xian, Z., Lertkultanon, P., and Pham, Q.-C. (2017). Closed-

chain manipulation of large objects by multi-arm

robotic systems. IEEE Robotics and Automation Let-

ters, 2(4):1832–1839.

Dual-Arm Compliance Control with Robust Force Decomposition

623