A One-Vs-One Approach to Improve Tangled Program Graph
Performance on Classification Tasks
Thibaut Bellanger
1,2 a
, Matthieu Le Berre
1 b
, Manuel Clergue
1 c
and Jin-Kao Hao
2 d
1
LDR, ESIEA, 38 rue des Docteurs Calmette et Guérin, 53000 Laval, France
2
LERIA, Université d’Angers, 2 Boulevard Lavoisier, 49045 Angers, France
Keywords:
Genetic Programming, Classification, Tangled Program Graph, Ensemble Learning, Evolutionary Machine
Learning.
Abstract:
We propose an approach to improve the classification performance of the Tangled Programs Graph (TPG).
TPG is a genetic programming method that aims to discover Directed Acyclic Graphs (DAGs) through an
evolutionary process, where the edges carry programs that allow nodes to create a route from the root to a
leaf, and the leaves represent actions or labels in classification. Despite notable successes in reinforcement
learning tasks, TPG’s performance in classification appears to be limited in its basic version, as evidenced by
the scores obtained on the MNIST dataset. However, the advantage of TPG compared to neural networks is
to obtain, like decision trees, a global decision that is decomposable into simple atomic decisions and thus
more easily explainable. Compared to decision trees, TPG has the advantage that atomic decisions benefit from
the expressiveness of a pseudo register-based programming language, and the graph evolutionary construction
prevents the emergence of overfitting. Our approach consists of decomposing the multi-class problem into a set
of one-vs-one binary problems, training a set of TPG for each of them, and then combining the results of the
TPGs to obtain a global decision, after selecting the best ones by a genetic algorithm. We test our approach on
several benchmark datasets, and the results obtained are promising and tend to validate the proposed method.
1 INTRODUCTION
Since their original proposal, back in the 1960s (Mor-
gan and Sonquist, 1963), decision trees (DTs) have
gained popularity as a machine learning model due
to their low computational cost, their interpretability,
their simple and fast construction process, their ro-
bustness, and their ability to deal with heterogeneous
data or missing data (Hastie et al., 2009). However,
traditional methods for constructing DTs, which em-
ploy a greedy approach in selecting nodes for subtree
construction, suffer from two primary issues. Firstly,
they often lead to suboptimal tree structures. Secondly,
DTs are susceptible to overfitting, which can be mit-
igated through techniques such as pruning. Another
drawback of DTs is the limited expressiveness of the
splitting functions used at each node, which are typi-
cally limited to hyperplanes. This limitation hampers
a
https://orcid.org/0009-0000-9764-5996
b
https://orcid.org/0009-0007-6592-2590
c
https://orcid.org/0000-0001-8661-0026
d
https://orcid.org/0000-0001-8813-4377
the ability of DTs to capture complex decision bound-
aries. To address these challenges, various approaches
have been proposed in the literature, and the improve-
ment of DTs remains an active research area. Costa et
al. recently published a comprehensive survey (Costa
and Pedreira, 2022) highlighting the ongoing efforts to
enhance DTs. One promising approach to constructing
DTs involves leveraging evolutionary algorithms. In
a recent survey on evolutionary machine learning by
Telikani et al. (2021), the authors discuss the applica-
tions of evolutionary algorithms in machine learning,
including the evolutionary induction of DTs and the
evolutionary design of DT components. Another ap-
proach improving the performance of decision trees
involves the use of directed acyclic graphs (DAGs)
instead of traditional tree structures, resulting in deci-
sion graphs (DGs). By allowing nodes to be shared
between decision branches, DGs offer more compact
representations compared to DTs (Zhu and Shoaran,
2021; Sudo et al., 2019). The approach designed by
Zhu and Shoaran (2021), Tree in Tree, outperforms
traditional DTs on several benchmark datasets. How-
ever, the construction of DGs introduces additional
Bellanger, T., Berre, M., Clergue, M. and Hao, J.
A One-Vs-One Approach to Improve Tangled Program Graph Performance on Classification Tasks.
DOI: 10.5220/0012167700003595
In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 53-63
ISBN: 978-989-758-674-3; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
53

complexity, as the model structure is no longer bound
to a tree.
Kelly and Heywood (2017) proposed an innovative
method called Tangled Program Graph (TPG), which
combines DGs and an evolutionary design process, as
a genetic programming framework for solving rein-
forcement learning tasks.
TPG manipulates graphs where nodes correspond
to decisions made based on scores calculated by the
programs carried by the edges. When a node is ter-
minal, we call it a leaf and it is assigned an action
or a class label. The construction of the TPG graph
involves an evolutionary process, incorporating new
nodes through mutation and selecting the most promis-
ing graphs based on a fitness function. Notably, TPG
has demonstrated impressive performance in reinforce-
ment learning tasks, often outperforming classical re-
inforcement learning algorithms on Atari benchmark
games (Bellemare et al., 2013). Furthermore, TPG
exhibits lower complexity, making it a compelling al-
ternative to traditional methods (Kelly and Heywood,
2017). The emergent modularity of TPG enables train-
ing agents on multiple games simultaneously, facili-
tating knowledge transfer between tasks (Kelly and
Heywood, 2018). Moreover, as noted in (Mei et al.,
2022), TPG can learn modules (or teams) to solve the
decomposed problem instead of solving the problem
as a whole. This feature can be leveraged to improve
the explainability of the model, as the learned modules
can be interpreted as subtasks of the original problem.
However, the performance of the basic TPG in
classification tasks is limited, as evidenced by modest
accuracy scores on the MNIST dataset. To extend the
applicability of TPG, Kelly et al. proposed incorporat-
ing a memory component, enabling its application to
time series forecasting (Kelly et al., 2020). The perfor-
mance of the TPG on some challenging problems is
comparable to that of state-of-the-art methods, without
having to predefine the size of a sliding window of
observations.
Interestingly, this approach has also good per-
formances on symbolic regression problems. Smith
et al. (2021) show that TPG can be used to address
the CIFAR-10 benchmark, an image classification
problem which has several issues for genetic pro-
gramming applied to classification: cardinality of the
dataset, multi-class classification and diversity mainte-
nance. Beside TPG, they use several modified selec-
tion mechanisms, such as fitness sharing or lexicase
selection. Their approach exhibits interesting results
on the CIFAR-10 benchmark, with generated models
much less complex in terms of inference computation.
However, this is obtained at the cost of a decreased
accuracy and important induction time. Sourbier et al.
explored the use of TPG to address imbalanced classi-
fication problems (Sourbier et al., 2022). They adapted
the selection mechanism by employing metrics tailored
to imbalanced problems, aiming to achieve improved
performance when the Imbalance Order of Magnitude
(IOM) remains low. However, their findings revealed a
significant drop in performance when the IOM reached
4, indicating a substantial class imbalance. Finally, one
main interest of generating models with TPG is the
opportunity to produce final standalone code that can
be very fast and efficient in inference, allowing them
to run on embedded devices as noted by Desnos et al.
(2022).
One other way to improve the performance of clas-
sification methods is to act on the problem itself. One-
vs-one decomposition belongs to this kind of approach,
and has been used for addressing multi-class classifica-
tion problems (Kang et al., 2015) by binary classifiers.
This technique involves breaking down a multi-class
problem into multiple binary classification problems,
where each binary problem focuses on distinguishing
one class from another. The key advantage of this
approach lies in its ability to leverage binary classi-
fiers, which are often simpler to construct compared to
multi-class classifiers. However, one of the main draw-
backs of this method is the need to build individual
classifiers for each pair of classes, which increases the
computational burden and requires a decision strategy
to choose the final class. Despite these limitations,
one-vs-one decomposition has been widely adopted in
the field of machine learning due to its ability to over-
come certain challenges associated with multi-class
classification tasks. By converting the original multi-
class problem into multiple binary problems, it enables
the use of well-established binary classification algo-
rithms and techniques. Furthermore, the simplicity
of binary classifiers facilitates their construction and
reduces the complexity of the learning process. How-
ever, it is important to note that the performance of the
one-vs-one approach heavily depends on the choice of
decision strategy and the overall design of the classifi-
cation system. In recent years, various extensions and
modifications to the one-vs-one decomposition method
have been proposed to further enhance its effectiveness.
These include the introduction of decision templates,
ensemble methods, and boosting techniques, among
others (Kang et al., 2015). These advancements aim to
address the limitations and challenges associated with
one-vs-one decomposition, improving its efficiency
and overall performance. As a result, the one-vs-one
approach continues to be an active area of research in
the field of machine learning, with ongoing efforts to
refine and optimize its application in various domains.
TPG is a recent learning method that shows very
ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications
54

promising results for reinforcement learning problems
but performs poorly on classification problems. In this
paper, we propose improvements to achieve satisfac-
tory results in both performance and complexity on
a benchmark problem set. In particular we show that
integrating TPG with the one-vs-one decomposition
approach and an ensemble technique optimized with
genetic algorithms greatly improves the performance
of TPG on classification problems while keeping the
complexity of the generated models relatively low.
The remainder of this article is organized as fol-
lows. In Section 2 we present our approach. Section
3 shows the experimental setup and the datasets we
used. The results we obtained are presented and dis-
cussed in Section 4. Finally, in Section 5 we present
our conclusions and discuss future work.
2 PROPOSED APPROACH
2.1 Tangled Program Graph
The Tangled Program Graph (TPG) is a novel learning
methodology that combines the principles of genetic
programming with the formalism of program repre-
sentation as a graph. Introduced by Stephen Kelly in
2017 (Kelly and Heywood, 2017), this approach has
gained attention for its application in the field of rein-
forcement learning, particularly in the evaluation of
its performance against neural networks on the Atari
benchmark.
As the name implies and as shown in Figure 1, the
TPG operates on a graph structure, where the graph
nodes fulfill distinct roles. The nodes can be catego-
rized as follows: root nodes, which serve as starting
points for decision-making processes; internal nodes,
previous root nodes that currently contribute to deci-
sion paths; and leaves, representing potential actions
or decisions. When a specific path leads to a leaf node,
the corresponding action or decision is inferred.
These nodes are connected by edges, with each
edge carrying a program. Programs process inputs
and produce an output. Input data is represented by
arrays of real numbers called registers, which can be
of three types: internal, external, or constant registers.
The external register is only accessible for reading and
contains the input data of the dataset. The size of the
external register depends on the number of features
in the dataset. The internal register is of fixed size
and contains the values calculated by a program on
an edge. This register is reset before each program
execution. It stores intermediate results and the final
result, which helps choose the node to move towards.
The constant register is also a fixed-size register that
R
1
R
0
R
2
N
2
N
1
N
0
N
3
N
4
N
6
N
5
N
7
L
4
L
3
L
2
L
1
L
0
L
5
L
6
L
7
L
8
Figure 1: An example of TPG, with decision made from root
node R
0
to leaf L
3
.
can be parameterized. It consists of a set of constants
used, for example, in comparison instructions. The
distribution of the register is also parameterizable. The
values in the constant register are set relative to those
in the external register, which means the minimum
and maximum values of the external register are also
the minimum and maximum values in the constant
register. The intermediate values are then calculated
based on the chosen distribution, which can be linear,
exponential, logarithmic, or hyperbolic tangent.
To illustrate, consider the example of translating a
TicTacToe grid into an array of nine integers, where
each square is encoded using the set 0, 1, 2. Addition-
ally, constants such as 0, 1, and 2 can be included for
comparison purposes.
Programs in the TPG consist of a series of instruc-
tions that operate on the registers, including math-
ematical operations such as addition or subtraction,
conditional tests like comparing internal, external and
constant registers, function applications, and more.
While Kelly and Heywood (2017) define a standard
instruction set for the TPG, it is adaptable to the spe-
cific problem being addressed, allowing for variations
in the instruction set to suit different contexts and re-
quirements.
The decision-making process within a graph struc-
ture follows a sequence of steps. It begins by selecting
a root node as the initial starting point for decision-
making. This root node then becomes the current node,
marking the beginning of the process. At each current
node, an examination takes place, wherein all outgo-
ing edges connected to the current node are assessed.
Each edge carries a program that takes the registers as
input parameters. These programs are subsequently
executed, and the output values they generate are com-
puted. The calculated values are stored in the internal
register. The first instructions can compute interme-
diate values, and the last instruction defines the final
A One-Vs-One Approach to Improve Tangled Program Graph Performance on Classification Tasks
55

value of the program, stored in the first slot of the
internal register, R[0]. Among these values, the pro-
gram that yields the maximum value is chosen as the
selected program. Once the program with the highest
output value has been determined, the corresponding
edge connected to the current node is traversed. This
traversal leads to a new node, which then becomes the
updated current node. The process is repeated itera-
tively, with the updated current node serving as the
starting point for the next iteration. This iterative pro-
cedure continues until a leaf node is reached within the
graph. Upon reaching a leaf node, the decision asso-
ciated with that specific leaf is extracted, representing
the final outcome of the decision-making process. By
following this systematic approach, the graph-based
decision-making process effectively navigates through
the interconnected nodes and edges, utilizing program
evaluations and comparisons to guide the selection of
the most promising paths and ultimately extracting the
corresponding decision from the reached leaf node.
The design of the graph in the TPG methodology
follows an evolutionary process across iterations, en-
suring the refinement and enhancement of the graph’s
structure. While the initial graph is generated ran-
domly, subsequent iterations adhere to a defined logic
outlined as follows.
Firstly, each root node within the graph is evaluated
based on specific criteria relevant to the problem at
hand. In classification scenarios, a precision score can
be assigned, whereas simulations involve averaging
scores obtained over multiple trials.
Next, the underperforming root nodes are elimi-
nated from the graph and replaced with clones of ex-
isting nodes. The selection of parent nodes for cloning
is performed randomly, with the probability of selec-
tion based on the fitness of nodes present in the graph.
Cloning entails creating new nodes by duplicating the
edges and programs of the chosen node.
Furthermore, a mutation operator is applied to each
new root node. Building upon Kelly and Heywood
(2017) implementation, a set of eight potential muta-
tions can occur for a given root node. These mutations
encompass various modifications, including the addi-
tion or removal of edges, redirection of existing edges,
program renewal, addition, removal, or modification of
instructions within a program, as well as the exchange
of two instructions.
It is worth noting that throughout this process, the
resulting graph remains acyclic. When a node is cre-
ated, its edges are solely directed towards nodes gen-
erated in previous iterations, ensuring the absence of
cycles. Moreover, once a node is inserted into the
graph, its list of edges remains unaltered, preserving
the acyclic nature of the graph.
By iteratively evaluating and replacing root nodes,
applying mutations, and maintaining the acyclic graph
structure, the TPG methodology dynamically refines
the graph, improving its adaptability and optimizing
its performance in solving complex problems.
The output of the TPG is a DAG. This DAG accu-
mulates introns as it evolves. To clean up the output
DAG, we have added a reduction phase. Starting from
the root of the DAG and using the training dataset, we
analyze the decision-making process by traversing the
graph to detect unnecessary edges and nodes. This
phase significantly reduces the size of the output DAG,
without modifying its training score.
2.2 Ensemble and Decomposition
Approach
2.3 Tested Methods
The proposed algorithm 1 addresses the problem of
improving classification performance through an iter-
ative process using what we call widgets. A widget
is a binary classifier on the subproblem obtained by
filtering instances of the original multiclass problem
on two classes. The algorithm iteratively generates and
updates ensembles of widgets for each class pair, grad-
ually improving the classification performance. The
process involves constructing subproblems based on
misclassified instances or those correctly classified by
a short majority vote and generating new widgets for
these subproblems. Through this iterative approach,
the algorithm aims to achieve improved classification
accuracy.
For each class pair, a set of M widgets is generated
by TPG on the problem P(i, j) . The initial ensemble
e
i, j
is constructed using these widgets, and its score
score
i, j
is computed by a majority vote.
Next, a counter k is initialized to 0, and a while
loop is entered, which continues until the ensemble
score score
i, j
reaches or exceeds a threshold of 0.99
or the maximum number of iterations N is reached.
Within each iteration of the loop, a subproblem
P
′
(i, j) is constructed as an empty set. Each instance x
in the original problem P(i, j) is examined, and if it is
misclassified by the current ensemble e
i, j
or correctly
classified by a majority of just one vote, it is added to
P
′
(i, j).
A new widget n is generated on the subproblem
P
′
(i, j) , and it is added to the ensemble e
i, j
. The up-
dated ensemble score score
i, j
is computed, and the
counter k is incremented.
The loop continues until the ensemble score
reaches the threshold or the maximum number of it-
erations is reached. At this point, the ensemble e
i, j
ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications
56

is subjected to an ensemble optimization step to fur-
ther enhance its performance. Since the problem of
choosing the optimal subset of voters is NP-hard, as
shown in appendix, we choose a genetic algorithm to
optimize the ensemble.
Overall, the algorithm iteratively generates and
updates ensembles of widgets for each class pair,
gradually improving the classification performance.
Through this iterative approach, the algorithm aims to
achieve improved classification accuracy.
Its complexity is linear with the number of samples
and quadratic with the number of classes. However, al-
though binary decomposition results in quadratic com-
plexity with the number of classes, the sub-datasets
generated by the decomposition limit this impact as
they have fewer samples and only consist of two
classes. Overall, with well-balanced datasets, the com-
plexity remains linear with samples and classes.
for each class pair (i, j) where i < j do
e
i, j
← generate M widgets on P(i, j);
score
i, j
← compute the score of e
i, j
;
k ← 0; while score
i, j
≤ 0.99 and k < N
do
P
′
(i, j) ← {};
for each instance x of P(i,j) do
if x is misclassed by e
i, j
or x is
correctly classed by one vote
then
P
′
(i, j) ← P
′
(i, j) + x;
end
end
n ← generate one widget on P
′
(i, j);
e
i, j
← e
i, j
+ n;
score
i, j
← compute the score of e
i, j
;
k ← k + 1;
end
e
i, j
← ensemble optimize(e
i, j
);
end
Algorithm 1: Ensemble construction.
3 EXPERIMENTS
3.1 Tested Methods
We test our approach against the classical implemen-
tation of TPG as proposed in (Kelly and Heywood,
2017). In addition, we also present the results of
several intermediary methods with particular features
gradually added. The choices of continuous integra-
tion for the different methods are explained in Section
4.
The proposed improvements are as follows.
• TPGE, which stands for TPG Ensemble, is a
method that generates N TPGs and makes them
vote to classify instances.
• BD is a binary decomposition, as described in Sec-
tion 2.2. This implementation involves generating
one TPG per sub-problem and having them vote
as a group.
• BDE, which stands for Binary Decomposition En-
semble, builds upon BD by generating N TPGs per
sub-problem and having them vote as a group.
• BDEO, which stands for Binary Decomposition
Ensemble Optimized, is based on BDE. The ob-
jective is to generate N TPGs per sub-problem,
starting with independently generating N/2 TPGs,
and then generating the remaining N/2 by consid-
ering only the instances from the sub-problems
that were poorly handled or under tension by the
first N/2 TPGs. We then have this ensemble vote.
• BDGA, which stands for Binary Decomposition
with Genetic Algorithm, uses a genetic algorithm
to select K out of N TPGs for each sub-problem,
aiming to maintain performance while reducing
the size of the output program.
3.2 Datasets
In order to compare methods, we choose 9 classi-
fication datasets: Connect-4, Proteins, USPS, Sen-
seit, Pendigits, Optical Recognition, MNIST, Fashion-
MNIST and Letters, as shown in Table 1. We run each
method ten times on each dataset. We have chosen
these datasets for several reasons. Firstly, they are the
same datasets used by (Zhu and Shoaran, 2021), who
used a method similar to ours. Secondly, the datasets
vary in terms of the number of instances and classes,
allowing us to identify the strengths and weaknesses
of our methods.
Table 1: Datasets’ shape.
Datasets Train Test Features Labels
CONNECT4 45.3k 22.3k 126 3
LETTER 13.4k 6.6k 16 26
MNIST 60k 10k 784 10
OPTRECO 3.8k 1.8k 64 10
PENDIGITS 7.5k 3.5k 16 10
PROTEIN 11.9k 5.9k 357 3
SENSEIT 78.8k 19.7k 100 3
USPS 7.3k 2k 256 10
FASHION 60k 10k 784 10
A One-Vs-One Approach to Improve Tangled Program Graph Performance on Classification Tasks
57

3.3 Parameters Setting
TPG parameters have been set experimentally, and
their are shown in Table 2.The voting process, which
requires us to generate a larger number of graphs, led
us to reduce the number of iterations to 100 instead
of 1000. Considering the logarithmic nature of the
accuracy curve in training and testing with respect to
the number of iterations, it became evident that this
parameter had the greatest impact on execution time
while having a limited effect on performance as shown
in section 4. In addition, we only activate addition,
substraction, multiplication, minimum, maximum and
test instructions. Indeed, mathematical functions have
not shown any convergence improvements in our con-
text, and consume a lot of execution time compared to
basic instructions.
Table 2: TPG parameters.
Parameter Value
Maximum number of iterations 100
Number of roots 100
Maximum number of edge per node 5
Percentage of roots kept per iteration 0.3
Number of instruction per program 3
Probability of edge addition 0.2
Probability of edge suppression 0.2
Probability of generating new program 0.2
Probability of rerouting edge 0.2
Probability of instruction modification 0.2
Probability of instructions swap 0.2
Constant register distribution Linear
The experiments were performed on a Gigabyte
AMD EPYC 7003 DP server system, with 2 AMD
ROME 7662 processors and Linux operating system.
All tested algorithms were implemented in the C lan-
guage, using p-thread library for parallelizing widgets
assemblies construction.
4 RESULTS
We present in this section the results of the different ap-
proaches from the original TPG implementation to our
final proposition which include all our contributions.
• Table 3 presents the performance on the training
datasets for each of our models. It serves as our
fitness during the models’ learning process.
• Table 4 presents the performance on the test
datasets for each of our models. The performance
on the test data allows us to compare our methods
and evaluate their effectiveness.
• Table 5 presents the complexity and portability of
the models, demonstrating their lightweight nature,
which we quantify by the number of output nodes.
• Table 6 presents the training time required for each
model. Genetic algorithms are often criticized for
their long convergence time. However, we have
achieved an acceptable training time for our mod-
els.
For each model, we present the mean across 10
independent runs with different seeds and the stan-
dard deviation. The performances are reported in per-
centage, the complexity in number of nodes, and the
execution time in hours, minutes, and seconds.
The original implementation of the TPG shows dis-
appointing performance in classification compared to
its performance on reinforcement learning problems.
With 1000 iterations, the TPG reaches a convergence
plateau, as shown in Figure 2. This figure clearly
demonstrates that the number of nodes in the graph in-
creases almost linearly, while the performance exhibits
a logarithmic behavior. One possible explanation for
this phenomenon, known as bloat, is the presence of
introns in the TPG’s output DAG. The reduction phase
is essential to keep only the useful nodes in the graph.
Figure 3 illustrates the evolution of the total number of
nodes compared to the number of useful nodes with-
out introns. It can be observed that the number of
nodes is reduced by a factor of 1000, which offers a
significant advantage in terms of portability and ex-
plainability. The reduction phase is performed only at
the end of the evolutionary process to avoid impacting
the diversity of the node population. Consequently,
the execution time also increases almost linearly, cor-
related with the total number of nodes, as shown in
Figure 4.
For the subsequent implementations, we selected
100 iterations to limit the decrease in performance com-
pared to a drastic reduction in execution time. Among
the tested methods, TPG exhibits the highest standard
deviation across all datasets. The number of labels
in the datasets has a significant impact on the perfor-
mance of TPG alone, but also on the improvements
we have made. The final decision made by our imple-
mentation is obtained through a vote, so a dataset with
three labels will have three voters, while a dataset with
ten labels will have 45 voters. Datasets such as PRO-
TEIN, CONNECT4, and SENSEIT are the ones that
benefit the least from our methods’ improvements. In
contrast, the performance of the binary decomposition
optimized by the genetic algorithm is not compara-
ble to TPG’s performance on LETTER, which has 26
labels.
Binary decomposition brings improvements to all
datasets with more than four labels, and voting helps
ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications
58

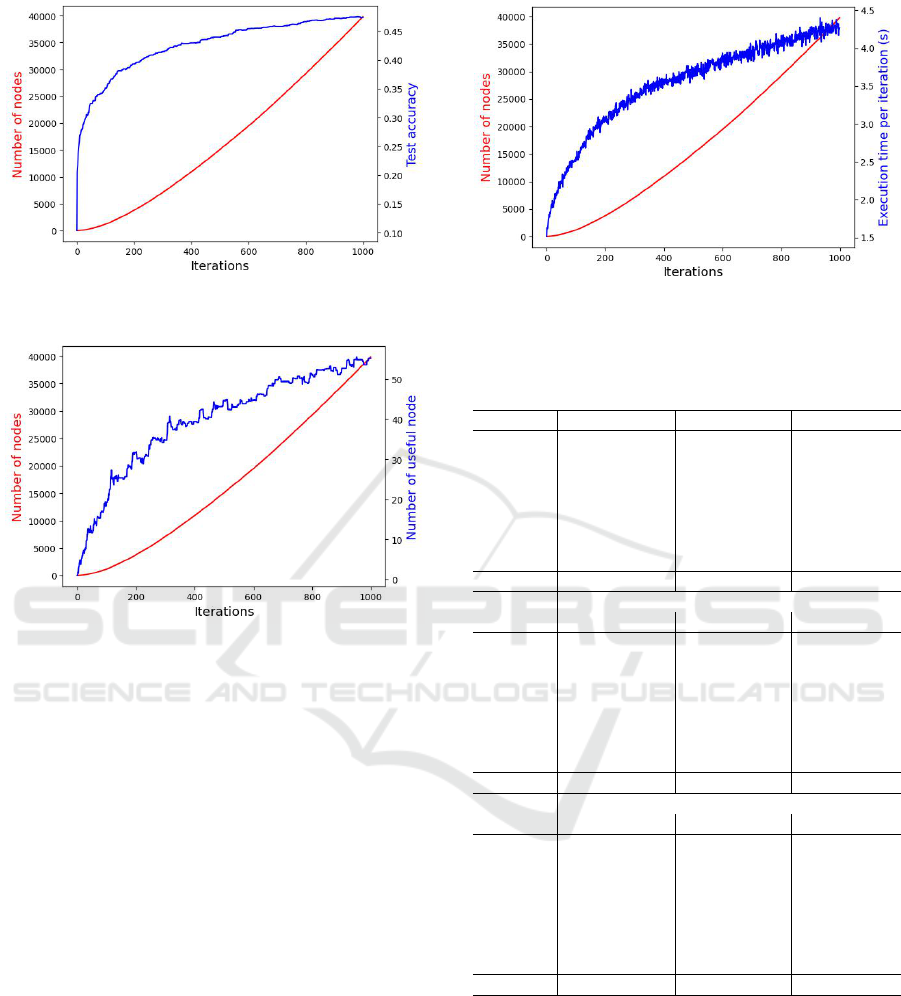
Figure 2: Test accuracy in blue and number of nodes in red
against iterations | MNIST.
Figure 3: Reduced DAG in blue and full DAG in red against
iterations | MNIST.
to enhance the results while reducing the standard
deviation.
The optimized ensembles, considering instances
that are difficult to handle or under tension, primarily
result in performance gains (BDEO > BDE) while re-
ducing execution time and the number of nodes. This
can be attributed to faster node evaluation in the opti-
mized ensemble, as only a subset of instances is con-
sidered. Convergence is also faster for these subsets,
resulting in smaller widgets and, consequently, fewer
nodes.
Finally, the genetic algorithm allows us to decrease
the number of nodes for all datasets. However, the
reduction in the number of nodes is less significant for
datasets with fewer than four labels, while the execu-
tion time increases for these datasets. This is partly
due to the low performance of the widgets, which leads
to an increase in the number of iterations of the genetic
algorithm.
For datasets with more labels, and with similar ex-
ecution times and performances, the genetic algorithm
enables a reduction of nearly 50% in the number of
nodes.
Figure 4: Execution time in blue and number of nodes in red
against iterations | MNIST.
Table 3: Performances on train (%).
*Based on best test score from (Zhu and Shoaran, 2021).
CONNECT4 LETTER MNIST
TPG100 67.34±0.45 15.77±1.2 34.59±1.11
TPG1K 69.18±0.62 24.41±2.1 46.76±1.3
TPGE 66.92±0.33 26.41±0.81 63.22±1.38
BD 67.51±0.27 78.77±0.65 82.48±0.37
BDE 67.46±0.17 82.83±0.19 89.25±0.11
BDEO 74.92±0.41 99.57±0.05 98.42±0.05
BDGA 75.62±0.28 99.95±0.02 98.73±0.05
TnT* 88.44±0.07 99.78±0.02 99.09±0.03
OPTRECO PENDIGITS PROTEIN
TPG100 43.32±1.98 48.58±2.94 48.47±0.67
TPG1K 58.65±2.63 66.34±1.66 51.19±0.74
TPGE 64.74±1.1 69.71±1.3 46.37±0.06
BD 92.45±0.64 92.03±0.57 50.09±0.49
BDE 96.99±0.17 96.08±0.09 49.38±0.49
BDEO 99.99±0.02 99.96±0.01 68.85±0.36
BDGA 100.0±0.0 100.0±0.01 69.93±0.55
TnT* 99.99±0.01 99.69±0.04 86.71±0.21
SENSEIT USPS FASHION
TPG100 66.79±2.0 47.41±2.24 39.94±1.63
TPG1K 70.83±0.67 60.25±2.18 55.46±1.03
TPGE 71.47±0.2 62.23±0.87 53.46±1.73
BD 71.77±0.85 90.26±0.32 75.96±0.55
BDE 76.11±0.13 95.41±0.11 80.77±0.07
BDEO 79.52±0.25 99.96±0.01 89.14±0.07
BDGA 81.6±0.22 99.98±0.01 89.84±0.12
TnT* 90.92±0.02 100
5 CONCLUSION
In this article, we presented an approach which com-
bines the TPG with One-vs-One binary decomposition
of classification with an ensemble technique enhanced
by a genetic algorithm.
We compared our approach to classical TPG, and
results have shown that our approach outperforms TPG
for classification problems with a large number of
A One-Vs-One Approach to Improve Tangled Program Graph Performance on Classification Tasks
59

Table 4: Performances on test (%) .
CONNECT4 LETTER MNIST
TPG100 67.25±0.5 15.55±1.28 35.09±1.29
TPG1K 69.03±0.70 24.24±2.18 47.35±1.42
TPGE 66.85±0.32 26.2±0.8 64.34±1.45
BD 67.44±0.35 76.89±0.79 82.88±0.54
BDE 67.31±0.16 81.36±0.29 89.86±0.08
BDEO 74.04±0.47 89.85±0.21 95.31±0.11
BDGA 74.51±0.31 91.52±0.32 95.44±0.12
TnT* 82.84±0.02 94.37±0.03 96.11±0.09
OPTRECO PENDIGITS PROTEIN
TPG100 41.85±2.01 47.14±4.07 47.83±0.59
TPG1K 55.61±3.39 63.32±2.33 49.95±0.98
TPGE 64.26±1.14 65.81±1.25 46.24±0.06
BD 87.18±1.03 87.86±1.53 49.23±0.74
BDE 93.01±0.18 93.45±0.12 48.3±0.41
BDEO 94.74±0.33 95.69±0.27 61.37±0.53
BDGA 94.64±0.55 95.98±0.19 60.95±0.55
TnT* 94.52±0.55 95.69±0.16 66.63±0.30
SENSEIT USPS FASHION
TPG100 66.56±1.91 45.28±2.18 39.79±1.63
TPG1K 70.55±0.74 56.71±2.36 55.16±1.06
TPGE 71.16±0.19 59.21±0.95 53.2±1.61
BD 71.35±0.94 85.41±0.78 75.46±0.47
BDE 75.92±0.17 91.23±0.18 80.29±0.13
BDEO 78.55±0.2 92.52±0.2 85.31±0.2
BDGA 80.67±0.3 93.38±1.9 85.59±0.23
TnT* 84.09±0.09 94.37
classes. However, the results have also shown that
our approach does not provide noticeable improve-
ments when the number of classes is less or equal to
four. Moreover, this improvement in accuracy does
not come at the expense of model complexity. The size
of the models remains the same order of magnitude as
those obtained with the traditional Tangled Program
Graph. The learning time also remains in the same
order of magnitude.
In future work, we will focus on the amelioration
of the TPG itself, in order to improve the core method
of our process. The program generation could be im-
proved by drawing inspiration from the decision trees,
especially feature selection. Instruction set may also
need some tuning, with a specialization considering
the problem.
ACKNOWLEDGMENTS
We are grateful to the reviewers for their valuable com-
ments and suggestions which helped us to improve the
paper. Support from the Region "Pays de la Loire"
for the first author (PhD scholarship) is also acknowl-
edged.
Table 5: Model size (with reduction) .
CONNECT4 LETTER MNIST
TPG100 8±2 14±5 19±7
TPG1K 37±13 43±12 55±14
TPGE 814±28 1.6k±56 2k±41
BD 26±9 2k±59 373±26
BDE 2.7k±43 194.3k±295 37.1k±255
BDEO 1.9k±47 116.6k±359 37.6k±224
BDGA 1.3k±52 66.4k±467 29.6k±774
TnT* 143k 108k 111k
OPTRECO PENDIGITS PROTEIN
TPG100 20±9 20±6 7±4
TPG1K 52±7 49±9 30±8
TPGE 1.9k±60 1.8k±59 850±52
BD 192±15 135±13 29±6
BDE 19.5k±154 14k±187 2.7k±125
BDEO 10.8k±98 8.5k±103 2.6k±77
BDGA 5.8k±101 4.6k±145 2.2k±114
TnT* 820 11k 300
SENSEIT USPS FASHION
TPG100 11±5 17±5 23±8
TPG1K 31±9 46±10 53±16
TPGE 1.1k±50 1.8k±74 2.4k±87
BD 19±5 210±21 238±19
BDE 2.3k±48 21.4k±178 24.1k±192
BDEO 2.3k±64 12.9k±144 26.8k±181
BDGA 1.4k±105 6.9k±1998 20.6k±448
TnT* 116k 740
REFERENCES
Bellemare, M. G., Naddaf, Y., Veness, J., and Bowling, M.
(2013). The Arcade Learning Environment: An Evalua-
tion Platform for General Agents. Journal of Artificial
Intelligence Research, 47:253–279.
Cook, S. A. (1971). The Complexity of Theorem-Proving
Procedures. In Proceedings of the Third Annual ACM
Symposium on Theory of Computing, STOC ’71, page
151–158, New York, NY, USA. Association for Comput-
ing Machinery.
Costa, V. G. and Pedreira, C. E. (2022). Recent Advances in
Decision Trees: an Updated Survey. Artificial Intelligence
Review, 56:4765–4800.
Desnos, K., Bourgoin, T., Dardaillon, M., Sourbier, N.,
Gesny, O., and Pelcat, M. (2022). Ultra-Fast Machine
Learning Inference through C Code Generation for Tan-
gled Program Graphs. In 2022 IEEE Workshop on Signal
Processing Systems (SiPS), pages 1–6, Rennes, France.
IEEE.
Hastie, T., Tibshirani, R., and Friedman, J. (2009). Additive
Models, Trees, and Related Methods. In Hastie, T., Tibshi-
rani, R., and Friedman, J., editors, The Elements of Statis-
tical Learning: Data Mining, Inference, and Prediction,
Springer Series in Statistics, pages 295–336. Springer,
New York, NY.
ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications
60

Table 6: Learning Time .
CONNECT4 LETTER MNIST
TPG100 1m38s±8s 45s±3s 3m38s±11s
TPG1K 33m28s±3m 12m46s±1m 59m2s±6m
TPGE 2m1s±1s 1m5s±1s 6m7s±9s
BD 1m20s±8s 1m25s±3s 2m43s±4s
BDE 2h40m±2m 2h46m±54s 4h30m±2m
BDEO 1h25m±2m 1h14m±16s 2h58m±1m
BDGA 1h53m±6m 1h16m±15s 3h4m±3m
OPTRECO PENDIGITS PROTEIN
TPG100 13s±1s 26s±2s 24s±4s
TPG1K 3m25s±25s 6m34s±30s 6m59s±52s
TPGE 16s 38s±1s 25s
BD 7s±1s 12s±1s 19s±2s
BDE 10m40s±10s 25m2s±39s 32m56s±25s
BDEO 5m29s±6s 10m14s±10s 22m38s±20s
BDGA 5m35s±6s 10m52s±11s 25m4s±1m
SENSEIT USPS FASHION
TPG100 3m12s±20s 25s±1s 3m31s±16s
TPG1K 56m4s±7m 6m8s±16s 51m8s±5m
TPGE 3m22s±4s 0m30s 4m5s±2s
BD 2m6s±9s 16s±1s 2m22s±3s
BDE 3h52m±2m 24m24s±8s 4h28m±3m
BDEO 2h19m±1m 14m11s±12s 2h42m±2m
BDGA 4h56m±19m 12m11s±3m 2h53m±3m
Kang, S., Cho, S., and Kang, P. (2015). Constructing a Multi-
Class Classifier using One-Against-One Approach with
Different Binary Classifiers. Neurocomputing, 149:677–
682.
Kelly, S. and Heywood, M. (2018). Emergent Tangled Pro-
gram Graphs in Multi-Task Learning. In Proceedings
of the Twenty-Seventh International Joint Conference on
Artificial Intelligence, pages 5294–5298, Stockholm, Swe-
den.
Kelly, S. and Heywood, M. I. (2017). Emergent Tangled
Graph Representations for Atari Game Playing Agents.
In McDermott, J., Castelli, M., Sekanina, L., Haasdijk, E.,
and García-Sánchez, P., editors, Genetic Programming,
volume 10196, pages 64–79. Springer, Cham. Lecture
Notes in Computer Science.
Kelly, S., Newsted, J., Banzhaf, W., and Gondro, C. (2020).
A Modular Memory Framework for Time Series Predic-
tion. In Proceedings of the 2020 Genetic and Evolution-
ary Computation Conference, pages 949–957, Cancún
Mexico. ACM.
Mei, Y., Chen, Q., Lensen, A., Xue, B., and Zhang, M.
(2022). Explainable Artificial Intelligence by Genetic
Programming: A Survey. IEEE Transactions on Evolu-
tionary Computation, 27(3):621–641.
Morgan, J. N. and Sonquist, J. A. (1963). Problems in the
Analysis of Survey Data, and a Proposal. Journal of the
American Statistical Association, 58(302):415–434.
Smith, R. J., Amaral, R., and Heywood, M. I. (2021). Evolv-
ing Simple Solutions to the CIFAR-10 Benchmark using
Tangled Program Graphs. In 2021 IEEE Congress on
Evolutionary Computation (CEC), pages 2061–2068.
Sourbier, N., Bonnot, J., Majorczyk, F., Gesny, O., Guyet,
T., and Pelcat, M. (2022). Imbalanced Classification with
TPG Genetic Programming: Impact of Problem Imbal-
ance and Selection Mechanisms. In GECCO 2022 - Ge-
netic and Evolutionary Computation Conference, pages
1–4, Boston, United States.
Sudo, H., Nuida, K., and Shimizu, K. (2019). An Efficient
Private Evaluation of a Decision Graph. Lee, K. (eds)
Information Security and Cryptology – ICISC 2018. Lec-
ture Notes in Computer Science, volume 11396, pages pp
143–160 Springer, Cham.
Telikani, A., Tahmassebi, A., Banzhaf, W., and Gandomi,
A. H. (2021). Evolutionary Machine Learning: A Survey.
ACM Computing Surveys, 54(8):161:1–161:35.
Zhu, B. and Shoaran, M. (2021). Tree in Tree: from De-
cision Trees to Decision Graphs. Advances in Neural
Information Processing Systems.
APPENDIX
In this paper, we used a basic genetic algorithm to
optimize subset of voters in the ensemble of widgets
for each class pair. Intuitively, finding the best subset
of voters in an assembly seems to be a difficult prob-
lem. To confirm this, in this section we show that this
problem is NP-hard in the case of binary choice. To
show that a problem is NP-hard, all we need to do is
find a polynomial reduction from a problem known to
belong to this class to our problem. To do this, we’ll
proceed step by step:
1. we’ll transform 3-SAT, an NP-hard problem, into
a problem we’ll call 3to5-SAT ;
2. we’ll transform 3to5-SAT into our problem of se-
lecting the best binary voting subset in an assembly
considering two classes.
In this way, it will be possible to transform 3-SAT into
our problem in polynomial time, thus proving that the
problem of selecting the best subset of voters is NP-
hard, and justifying the use of metaheuristics to solve
it.
3-SAT to 3to5-SAT
Let’s start with the first step, and introduce 3-SAT
and 3to5-SAT. These are logical problems, consist-
ing of Boolean variables and clauses composed of a
number of literals. A literal is either a variable or its
negation. The first problem is 3-SAT: an instance is
characterized by a set of N Boolean variables and M
clauses, each clause consisting of 3 literals. A clause
is said to be satisfied if at least one of its literals is
true. A 3-SAT instance is considered satisfied if all
A One-Vs-One Approach to Improve Tangled Program Graph Performance on Classification Tasks
61

its clauses are satisfied by an instantiation of the N
variables. This problem has been proved to be NP-
complete (Cook, 1971). The second problem is de-
fined here as 3to5-SAT: an instance is characterized
by a set of N
′
Boolean variables and M
′
clauses, each
clause consisting of 5 literals. A clause is said to be
satisfied if at least three of its literals are true. A 3to5-
SAT instance is considered satisfied if all its clauses
are satisfied by an instantiation of the N
′
variables.
The existence of this problem is justified in the second
part of the demonstration.
Let’s show that it’s possible to transform any 3-
SAT instance into a 3to5-SAT instance in polynomial
time. Let (x
1
,x
2
,x
3
) be a 3-SAT clause, and transform
it into two 3to5-SAT clauses, by introducing four new
variables x
4
, x
5
, x
6
and x
7
. The two clauses formed are
(x
1
,x
2
,x
4
,x
5
,x
6
) and (x
3
, ¯x
4
, ¯x
5
,x
6
,x
7
) . Next we show
that : (1) if x
1
, x
2
and x
3
are false, then it is not possible
to find an instantiation of x
4
, x
5
, x
6
and x
7
satisfying
both 3to5-SAT clauses and (2) if at least one of the
three variables x
1
, x
2
and x
3
is true, then it is possible
to find at least one instantiation of x
4
, x
5
, x
6
and x
7
satisfying both 3to5-SAT clauses. In the first case, x
1
,
x
2
and x
3
are false, so we have to set x
4
, x
5
and x
6
to
true to satisfy the first clause, i.e. at least three of the
literals are true. In that case, it is not possible to satisfy
the second clause : x
3
, ¯x
4
and ¯x
5
are false, the number
of literals set to true will be less or equal to two. In
the second case, at least one of the three variables x
1
,
x
2
and x
3
is true. Using a truth table 7, we show that
is it is possible to find at least one assignment to x
4
,
x
5
, x
6
and x
7
allowing to satisfy both of the 3to5-SAT
clauses.
Table 7: 3to5-SAT truth table for the first case .
Initial variables Added variables
x
1
x
2
x
3
x
4
x
5
x
6
x
7
⊥ ⊥ ⊥ Unsatisfiable
⊤ ⊥ ⊥ ⊥ ⊤ ⊤ ⊤
⊥ ⊤ ⊥ ⊥ ⊤ ⊤ ⊤
⊥ ⊥ ⊤ ⊤ ⊤ ⊤ ⊤
⊥ ⊤ ⊤ ⊤ ⊤ ⊤ ⊤
⊤ ⊥ ⊤ ⊤ ⊤ ⊤ ⊤
⊤ ⊤ ⊥ ⊤ ⊤ ⊤ ⊤
⊤ ⊤ ⊤ ⊤ ⊤ ⊤ ⊤
Let w be a 3-SAT instance with N variables and
M clauses, the transformation produces a 3to5-SAT
instance f (w) with N + 4 × M variables and 2 × M
clauses. If f (w) is unsatisfiable, then w is also unsat-
isfiable. Otherwise, the instanciation of the N + 4M
variables of f (w) allows to instantiate the N variables
of w . As it’s possible to transform any 3-SAT instance
into a 3to5-SAT instance in polynomial time, the 3to5-
SAT problem is NP-complete.
3to5-SAT to Best Binary Voting Subset
In decision version, in opposition at optimization ver-
sion, we can define the best binary voting subset
problem by N voters and M targets. Each voter can
recognize or misclassified each target. So, for all
(i, j) ∈ {1,..,N} × {1,..,M} , we define a
i, j
= 1 if the
voter i recognize the target j , a
i, j
= −1 otherwise. A
target j ∈ {1,..,M} is said recognized only if there are
more voters recognizing it than voters misclassifying
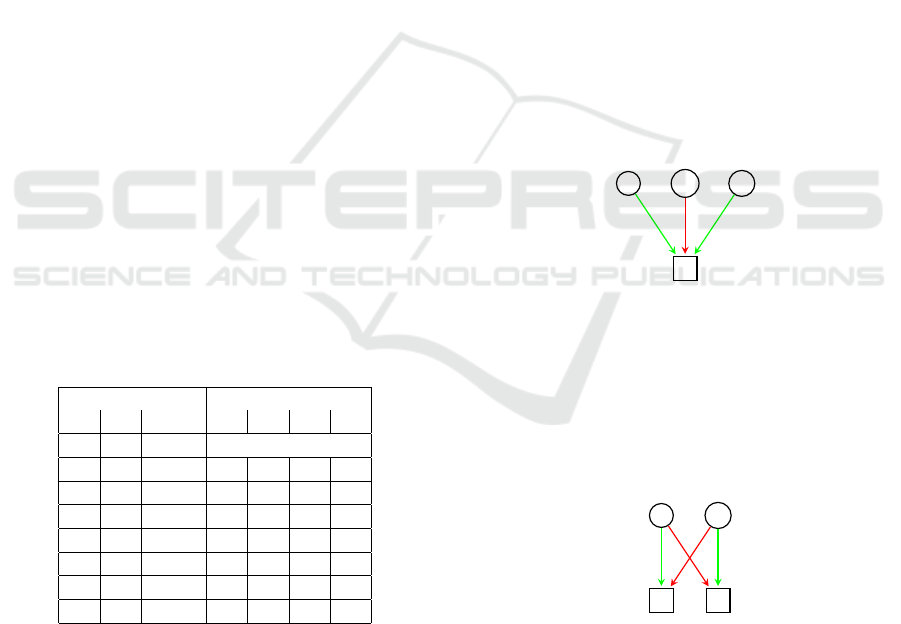
it. In the figure 5, we represent the relation between
3 voters and a target. A relation can be positive, i.e.
the voter recognize the target or negative, i.e. the voter
misclassify the target. Positive and negative relations
will be represented edges, respectively weighted at 1
and -1. For reasons of clarity, we will represents posi-
tive and negative relations with respectively green and
red edges. The target will be recognize only if the sum
of incoming edges weigths considering selected voters
is greater than zero. In the figure, the target t can be
recognized if (1) v
j
is not selected and at least one of
v
i
and v
k
is selected or (2) all the voters are selected.
v
i
v
j
v
k
t
Figure 5: Relations between targets and voters .
Let K ≤ M be an integer representing the goal, is
it possible to find a subset of voters allowing to well
classify at least K targets? We show that this problem
is NP-Hard. Let w be an instance of 3to5-SAT, defined
by N
′
variables and M
′
clauses. For each variable x
i
,
we create two voters x
i
and ¯x
i
, and two targets t
i
and
¯
t
i
,
linked as shown in figure 6.
x
i
¯x
i
t
i
¯
t
i
Figure 6: Logical coherence widget.
Here, x
i
recognizes t
i
and misclassifies
¯
t
i
, and ¯x
i
recognizes
¯
t
i
and misclassifies t
i
:
• if we select none or both of x
1
and ¯x
1
, then none
of the targets is recognized;
• if we select only x
i
, then t
i
is recognized and
¯
t
i
is
misclassified;
ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications
62

• if we select only ¯x
i
, then t
i
is misclassified and
¯
t
i
is
recognized.
x
1
¯x
1
x
2
¯x
2
x
3
¯x
3
x
4
¯x
4
x
5
¯x
5
c
1
Figure 7: Clause satisfaction.
Next, for each clause j ∈ {1,..,M
′
} , we create a
target c
j
. Then, we add positive relations between c
j
and all literals contained in the clause, and negative
relations between c
j
and negations of all literals con-
tained in the clause. To recognize c
j
, we will have
to select at least 3 of the 5 literals of the clause. The
figure 7 shows links between voters and targets for a
clause (x
1
,x
2
,x
3
,x
4
,x
5
).
Finally, the instance of the best binary voting sub-
set is defined by 2 × N
′
voters, i.e. two for each vari-
able and 2×N
′
+M
′
targets, i.e. two for each variables
and one for each clause. We also define K = N
′
+ M
′
.
For all i ∈ {1,..,N
′
} , it is not possible to recognize t
i
and
¯
t
i
at once. So, the number of recognized targets
will be less or equal to K . With this in mind, if we find
a subset of voters recognizing K targets, then, for all
j ∈ {1,..,M
′
} , c
j
will be recognized, while ensuring
logical coherence, as all variables will be instanciated
to true or false, not both. In this case, the solution of
the best binary voting subset will produce a solution
for the 3to5-SAT instance. The figure 8 presents the
instance of best binary voting subset produced by the
instance of 3to5-SAT defined by five variables and one
clause (x
1
,x
2
,x
3
,x
4
,x
5
) . With K = 6 , at least 3 of the
5 voters representing the literals of the clause will be
selected, involving the satisfaction of the 3to5-SAT in-
stance. As 3to5-SAT is NP-Hard, then the best binary
voting subset problem so is.
x
1
¯x
1
x
2
¯x
2
x
3
¯x
3
x
4
¯x
4
x
5
¯x
5
t
1
¯
t
1
t
2
¯
t
2
t
3
¯
t
3
t
4
¯
t
4
t
5
¯
t
5
c
1
Figure 8: Clause satisfaction with logical coherence.
Optimization of Classifier Subset
Let (i, j) be a class pair, the widget generation process
produce K graphs, each graph trained to separate the
classes i and j . In this section, we will detail the opti-
mization process allowing to maximize the precision
of the (i, j) assembly, by selecting K
′
≤ K graphs. For
each graph k ∈ {1, ..,K} , we declare a binary deci-
sion variable X
K
, expressing the selection of the k -th
classifier in the assembly. A solution of this problem
is represented by a binary vector X = (X
1
,X
2
,...,X
K
) .
We experimented the optimization of this problem with
the linear solver Gurobi, but it took too much time to
be efficient. Instead of exact resolution, the optimiza-
tion is done by a classical genetic algorithm, set as
follows:
• the initial population is generated randomly, except
for the first solution for which we set all decision
variables to 1 since all classifiers are selected;
• we implemented a 2-point crossover, and a binary
mutation inverting decision variables values;
• the selection processes are elitist whether for re-
production or survival.
The number of iterations, population size, selection
size, crossover and mutation probabilities are respec-
tively set to 3000, 1000, 1000, 1 and 0.02.
P ← initialization of the population;
for each iteration iter ∈ {1,nbIter} do
S ← randomly generated pairs of P’s
solutions;
C ← crossover+mutation on S;
P ← sorted(P +C);
P is shrinked to its original size;
end
return P[0];
Algorithm 2: Genetic algorithm for classifiers selection.
A One-Vs-One Approach to Improve Tangled Program Graph Performance on Classification Tasks
63