Hybrid LSTM-Fuzzy System to Model a Sulfur Recovery Unit

Jorge S. S. J

unior

1 a

, J

ome Mendes

2 b

, Francisco Souza

3 c

and Cristiano Premebida

1 d

University of Coimbra, Institute of Systems and Robotics, DEEC, Coimbra, Portugal

University of Coimbra, CEMMPRE, ARISE, Department of Mechanical Engineering, Coimbra, Portugal

Radboud University, Dept. Analytical Chemistry & Chemometrics, 6525 AJ Nijmegen, The Netherlands

Keywords:

Neo-Fuzzy Neuron System, Long Short-Term Memory, Industrial Processes, Interpretability.

Abstract:

Dealing with the dynamics of an industrial process using machine learning techniques has been a paradigm

throughout decades of technological advancement. Motivated by addressing this problem, the present work

proposes the hybridization of a neo-fuzzy neuron system (NFN) with a long short-term memory network

(LSTM), the NFN-LSTM model. The fuzzy part guarantees interpretability through linguistic terms asso-

ciated with membership functions that allow an effective mapping of the input variables in its universe of

discourse with respect to the output. On the other hand, the LSTM part explores high-level representations

useful for sequential data in dynamic processes. In this work, a sulfur recovery unit is used as a case study,

whose dynamics are mainly associated with peak values in the estimation of residual hydrogen sulﬁde. The

proposed NFN-LSTM model is compared with state-of-the-art methods, such as standalone LSTM, GAM-

ZOTS (generalized additive models using zero-order Takagi-Sugeno fuzzy system), iMU-ZOTS (extension of

GAM-ZOTS), ALMMo-1 (autonomous learning of a multimodel system from streaming data), iNoMO-TS

(iterative learning of multivariate fuzzy models using novelty detection), and SVR (support vector regression).

Analyzing the results, the proposed model performed similarly to standalone LSTM, and both outperformed

the other methods. Finally, NFN-LSTM manages to balance interpretability and accuracy.

1 INTRODUCTION

The reliability and explainability of artiﬁcial intelli-

gence (AI) models applied to modeling industrial pro-

cesses are pivotal to increasing the adoption of AI

in Industry 4.0 (Souza et al., 2022). The advent of

complexity and nonlinearity in modern industrial sys-

tems requires computational technologies to grow at

the same pace. However, the rapid progress of AI has

led to very complex models, the majority of which are

difﬁcult to understand and explain. As a result, these

models lack a connection with human operators, mak-

ing it challenging to support reasoning or enhance un-

derstanding of the process.

It is common to see Deep Learning (DL) solu-

tions widespread in modeling complex nonlinear pro-

cesses, mainly due to the capacity to achieve high

levels of data representation. For example, in (Yuan

et al., 2020) the authors employed a long short-term

https://orcid.org/0000-0001-6263-3602

https://orcid.org/0000-0003-4616-3473

https://orcid.org/0000-0001-6362-9349

https://orcid.org/0000-0002-2168-2077

memory network (LSTM) to learn quality-relevant

hidden dynamics of a penicillin fermentation process

and a debutanizer column. The study in (Guo et al.,

2021) proposes a soft sensor based on the denoising

autoencoder (DAE) and mechanism-introduced gated

recurrent units (MGRUs) whose performance is vali-

dated by predicting the rotor thermal deformation of

a rotary air preheater. Although the two DL models

follow the dynamic trend of the outputs with good ac-

curacy (especially LSTMs), they can present a large

number of parameters and complexity that harm a

clear understanding of the extracted features and the

internal mechanism of the model (interpretability is-

sues) (Jiang et al., 2021).

Traditional machine learning techniques can also

be appreciated to model complex nonlinear processes

in a more interpretable way than DL. As a moti-

vation to reach interpretable models, an approach

called GAM-ZOTS was proposed in (Mendes et al.,

2019a) to learn univariate zero-order Takagi-Sugeno

(T-S) fuzzy models through a backﬁtting algorithm.

Then, an extension of the GAM-ZOTS was proposed

in (Mendes et al., 2019b), the iMU-ZOTS, where

S. S. Júnior, J., Mendes, J., Souza, F. and Premebida, C.

Hybrid LSTM-Fuzzy System to Model a Sulfur Recovery Unit.

DOI: 10.5220/0012165100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 281-288

ISBN: 978-989-758-670-5; ISSN: 2184-2809

281

the model learns iteratively, i.e., new fuzzy rules are

added using a novelty detection criterion which de-

tects if new data is not represented by the current

model.

The union of deep and traditional techniques can

be advantageous in exploring a balance between ac-

curacy and interpretability, resulting in a more reli-

able hybrid approach for application in sensitive ar-

eas such as industrial processes. The use of fuzzy

systems as a foundation to treat the interpretability

side exploits the universe of discourse of the input

data, easy notation readability, and a symbolic struc-

ture with comprehensible mapping of linguistic vari-

ables to fuzzy sets, despite suffering from accuracy

in many complex problems (Moral et al., 2021). The

survey in (J

unior et al., 2023) shows, through exam-

ples in the literature, that the combination of fuzzy

systems and deep learning (the deep fuzzy systems)

allows an effective trade-off between interpretability-

accuracy when dealing with the individual limitations

of DL and FS. This survey also shows the lack of ap-

propriate discussions in the literature about these hy-

brid models, as there is no consensus on how to quan-

tify or qualify the interpretability with potential ﬁne

adjustments from the initial design of the models.

The present work proposes a neo-fuzzy neuron ar-

chitecture hybridized with LSTM, the NFN-LSTM

model, for regression problems in industrial pro-

cesses. The proposed model contributes to reach-

ing an effective interpretability-accuracy trade-off by

combining the good interpretability of the NFN model

and the accuracy of the LSTM. The fuzzy part of the

proposed model allows a mapping of the input-output

relations with the easy readability of what happens

globally in the system. On the other hand, the LSTM

part transforms the fuzziﬁed variables to reach a high

level of representation that can follow the system’s

dynamics and express good accuracy. The case study

chosen for this work is the estimation of residual hy-

drogen sulﬁde in the tail stream of a sulfur recovery

unit, whose dynamics are perceived partly through

manual control of the gas and air ﬂows by human op-

erators and partly through a closed-loop algorithm for

airﬂow.

The rest of the paper is structured as follows: Sec-

tion 2 presents the topics that underlie this study.

Then, the proposed hybrid approach of neo-fuzzy

neuron with LSTM is presented in Section 3. The

implementation and validation of the proposed NFN-

LSTM model are presented in Section 4. Finally, Sec-

tion 5 concludes the paper.

2 BACKGROUND

In this section, an overview of topics related to the

hybrid approach proposed in Section 3 will be pre-

sented, namely neo-fuzzy neuron (Section 2.1) and

Long Short-Term Memory networks (Section 2.2).

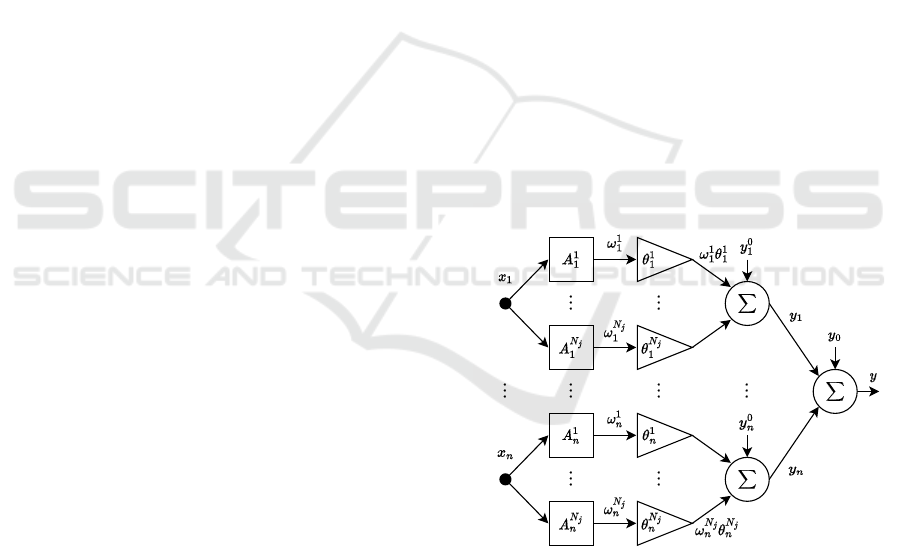
2.1 The Neo-Fuzzy Neuron Model

A neo-fuzzy neuron (NFN) system incorporates mul-

tiple univariate additive zero-order Takagi-Sugeno (T-

S) fuzzy systems represented by the following uni-

variate fuzzy rules (Yamakawa, 1992):

: IF x

(k) ∼ A

THEN y

(k) = θ

, (1)

where x(k) = [x

(k), ··· , x

(k)] are input variables for

the k −th sample (k = 1, ··· , K), R

= 1, · ·· , N

;

j = 1, ··· , n) depicts the i

-th rule of j-th variable (for

a total of N

individual rules). The antecedent part

is deﬁned by the linguistic terms A

through fuzzy

membership functions (MFs) µ

. The consequent

part is deﬁned by θ

parameters that express the out-

put of the univariate model y

. Figure 1 exhibits the

diagram of the described NFN system.

ConsequentMF

Figure 1: Neo-fuzzy neuron system.

The output of a NFN comprises the sum of the ad-

ditive univariate models, where each model represents

an input variable x

j| j=1,···,n

y[x(k)] = y

∑

j=1

(k)], (2)

with

(k)] = y

∑

(k)]θ

, (3)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

282

where y

is the bias of the global model, y

is the

bias of the individual model y

(k)] ( j = 1, ··· , n),

(k)] is the normalized form of the membership

function µ

. Learning an NFN is often achieved us-

ing the backﬁtting algorithm, and the Least Squares

Method.

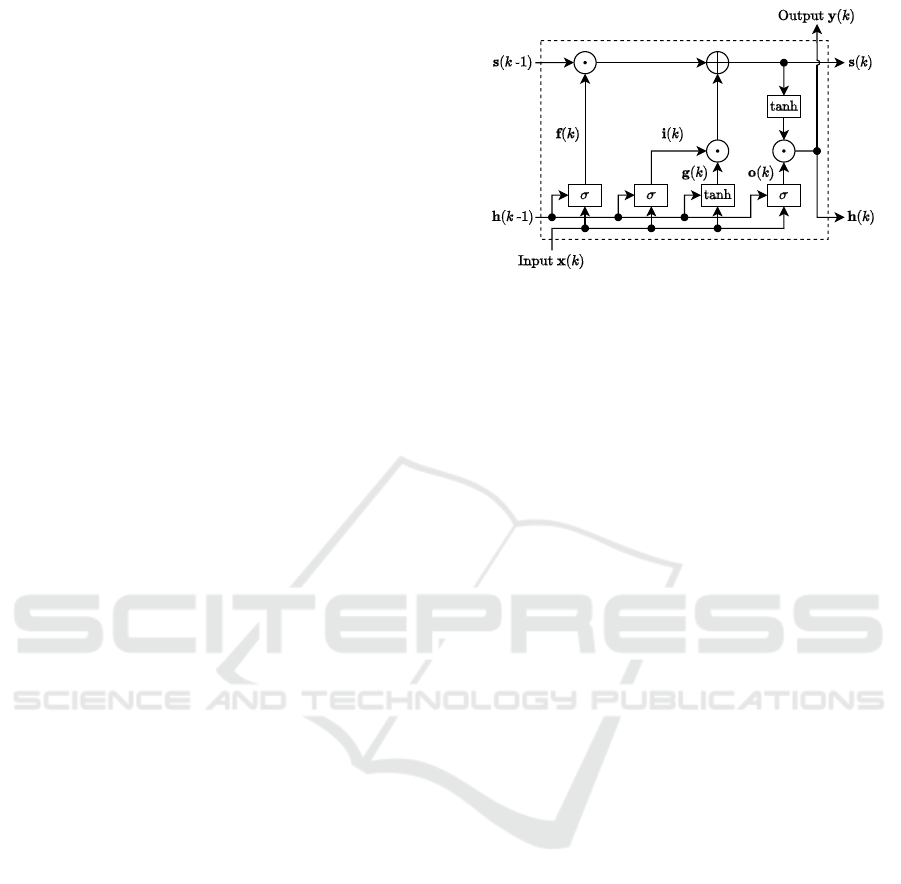
2.2 The Long Short-Term Memory

Networks

Long Short-Term Memory networks (LSTMs) were

developed in 1997 and are mainly used in model-

ing tasks that use long temporal sequences (Hochre-

iter and Schmidhuber, 1997; Goodfellow et al.,

2016). Sequential data in the time domain are

processed through nonlinear elements called gates.

These gates are commonly activated using sigmoidal

functions (deal with irrelevant inputs and irrelevant

memory contents) and hyperbolic tangent functions

(avoid vanishing/exploding gradients) (Zarzycki and

Ławry

nczuk, 2021).

The main formulations computed at instant k

within an LSTM with the structure illustrated in Fig-

ure 2 are (Zarzycki and Ławry

nczuk, 2021):

i(k) = σ



x(k) + W

h(k − 1) + b



, (4)

f(k) = σ



x(k) + W

h(k − 1) + b



, (5)

g(k) = tanh



x(k) + W

h(k − 1) + b



,(6)

o(k) = σ



x(k) + W

h(k − 1) + b



, (7)

s(k) = f(k) ⊙ s(k − 1) + i(k ) ⊙ g(k), (8)

h(k) = o(k) ⊙ tanh(s(k)), (9)

where i(k), f(k), g(k) and o(k) are input, forget, state

candidate and output gates, respectively, with respec-

tive recurrent weight matrices W

, W

, in-

put weight matrices W

, W

, and biases

, b

. The variables x(k), s(k ) and h(k) rep-

resent, respectively, the input, cell state and hidden

(output) vectors at k-th instant. The symbol ⊙ is the

Hadamard (element-wise) product of the vectors.

A standalone LSTM has an internal mechanism

that is difﬁcult to interpret because it has a high num-

ber of parameters required for the ports, in addition to

making direct input-output mapping difﬁcult to sim-

plify its structure without compromising performance

(Lees et al., 2022). One of the techniques used in the

literature to overcome the interpretability issue is the

attention mechanism that prioritizes the importance of

input features (Gandin et al., 2021; Liu et al., 2021).

Figure 2: Representation of the Long Short-Term Memory

unior et al., 2023).

3 PROPOSED NFN-LSTM MODEL

3.1 Motivation

The need to develop a model that expresses reliabil-

ity in its internal functioning comes partly from ex-

ploring interpretability, which can be addressed by

fuzzy systems whose membership functions convey

the individual impact of inputs on output. Reliability

is also achieved when the model to be developed can

efﬁciently estimate characteristics of a given system,

such as dynamics and nonlinearity, with a high level

of accuracy. In this context, LSTMs can be used for

achieving such characteristics in systems represented

by temporal sequences, as stated in Section 2.2.

The literature on eXplainable Artiﬁcial Intelli-

gence (XAI) shows the difﬁculty in guaranteeing mu-

tual excellence between interpretability and accuracy,

therefore using the concept of a trade-off between

both that allows a balancing with potential to be

increasingly explored in the future (Angelov et al.,

2021; J

unior et al., 2023). Given this concept, the

present work proposes a new model that considers the

interpretability capacity of fuzzy systems and the ac-

curacy capacity of LSTMs in a hybrid structure.

3.2 NFN-LSTM Model

In this study, a LSTM network is implemented in a

hybrid way to the neo-fuzzy neuron system to reach

the representation portrayed in Figure 3, the NFN-

LSTM model. The resulting fuzzy rules of the pro-

posed NFN-LSTM model are expressed as:

: IF x

(k) ∼ A

THEN y

(k) = LSTM

· θ

, (10)

where R

(i = 1, ··· , N) represents the i-th fuzzy rule

for a total of N global rules. These rules consider

in ascending order each i

-th MF (i

= 1, ··· , N

) of

Hybrid LSTM-Fuzzy System to Model a Sulfur Recovery Unit

283

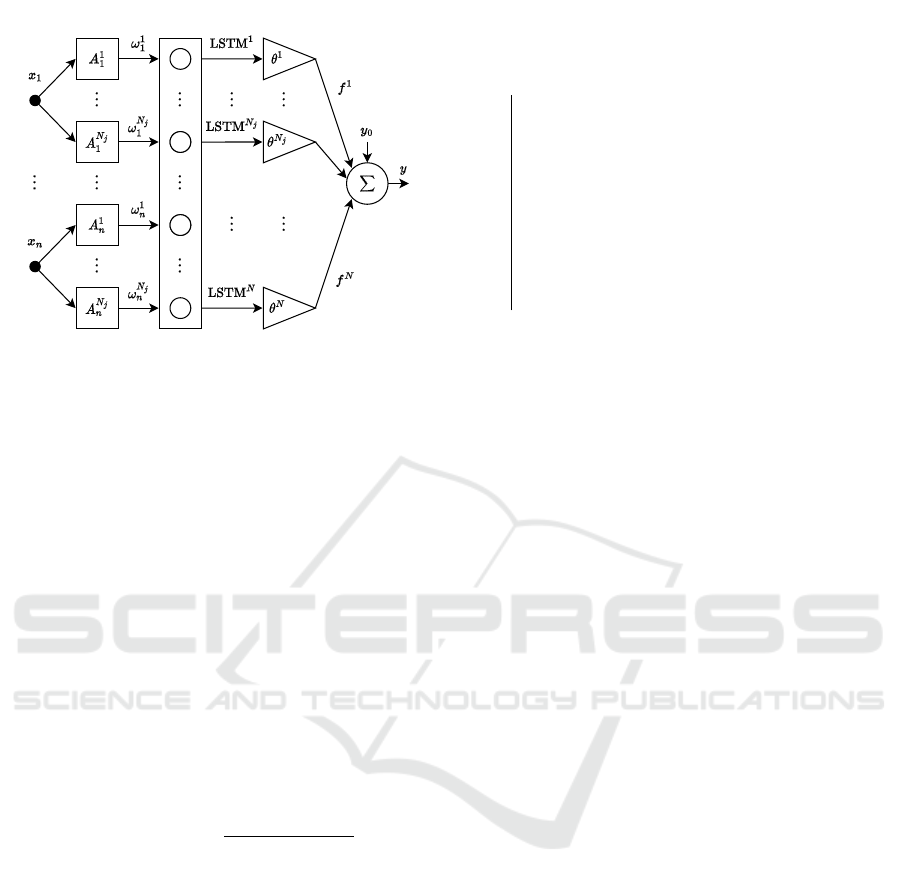
MF LSTM Consequent

Figure 3: Representation of the NFN-LSTM model.

each j−th variable ( j = 1, · ·· , n) according to Fig-

ure 3 (therefore N = n · N

). LSTM outputs are repre-

sented by parameters LSTM

that accompany the con-

sequent parameters θ

. The MFs used in the hybrid

model are of the complementary triangular form that

can be activated at the instant k in pairs (at most, for a

given input x

), i.e. (Silva et al., 2014):

∑

(k)] = µ

(k)] + µ

(k)] = 1.

(11)

The output of the hybrid model is expressed as:

y[x(k)] = y

∑

i=1

j| j=1,···,n

(k)], (12)

where y

is a bias and



, ··· , ω



≡

, ··· , ω

(13)

≡ ω

(k)] =

(k)]

∑

(k)]

(14)

j| j=1,···,n

(k)] = LSTM

(ω

, ··· , ω

) · θ

(15)

As noted in Section 2.2 and Figure 3, it becomes

an arduous task to try to establish a direct relation-

ship between the inputs ω

and outputs LSTM

the LSTM due to the high complexity of its internal

mechanism. For this reason, the outputs LSTM

de-

scribed in Eq. (15) are deﬁned as dependent variables

of all inputs ω

, ··· , ω

4 RESULTS

This section deals with the implementation of the

NFN-LSTM proposed in this work. Section 4.1 de-

ﬁnes the case study and the choice of state-of-the-art

Input: Input variables

x : {(x

(k), ··· , x

(k))}

k=1

, each one

with N

MFs, time steps, LSTM layers

begin

Compute triangular MFs based on

Eq. (11);

Normalize MFs and obtain



, ··· , ω



according to Eq. (13) and Eq. (14);

Compute LSTM

(ω

, ··· , ω

) (LSTM

outputs) based on Eq. (4)-(9);

Obtain the consequent parameters

j| j=1,···,n

(k)] using Eq. (15);

Estimate the ﬁnal output using Eq. (12);

end

Output: Estimated output

y : {y(k)}

k=1

Algorithm 1: NFN-LSTM learning.

methods to compare with NFN-LSTM. Next, the ex-

perimental results of the methods analyzed in Section

4.2 are presented and discussed.

4.1 Case Study

The model proposed in this paper was implemented

using an industrial case study that deals with the es-

timation of residual hydrogen sulﬁde (H

S) in the

tail stream of a Sulfur Recovery Unit (SRU) (Fortuna

et al., 2007). SRU has four sulfur lines that operate in

parallel through two separate combustion chambers,

where one is fed with MEA gas (from the gas wash-

ing plants) rich in H

S and the other is fed with SWS

gas (from sour water stripping plants) rich in H

S and

ammonia (NH

) (Fortuna et al., 2003). Correct es-

timation of residual H

S is understood as having the

ability to detect peaks in their values as they indicate

undesirable behavior of the SRU (Souza et al., 2022).

To estimate the residual H

S, ﬁve variables are

used (Curreri et al., 2021):

1. x

: MEA gas fed to the ﬁrst combustion chamber;

2. x

: air fed to the ﬁrst combustion chamber, that

regulates the combustion of MEA gas to supply

oxygen for the reaction;

3. x

: automatically controlled air ﬂow to improve

the stoichiometric ratio [H

S] − 2[SO

];

4. x

: total gas fed to the second combustion cham-

ber, composed of SWS gas and additional MEA

gas (required when SWS gas is too low);

5. x

: total air fed to the second combustion cham-

ber, composed of air ﬂow for the combustion of

SWS gas and an additional air ﬂow to keep gas

input constant.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

284

−1

0 2000 4000 6000 8000 10000

Sample

−1

Output

Figure 4: Input and output data from SRU.

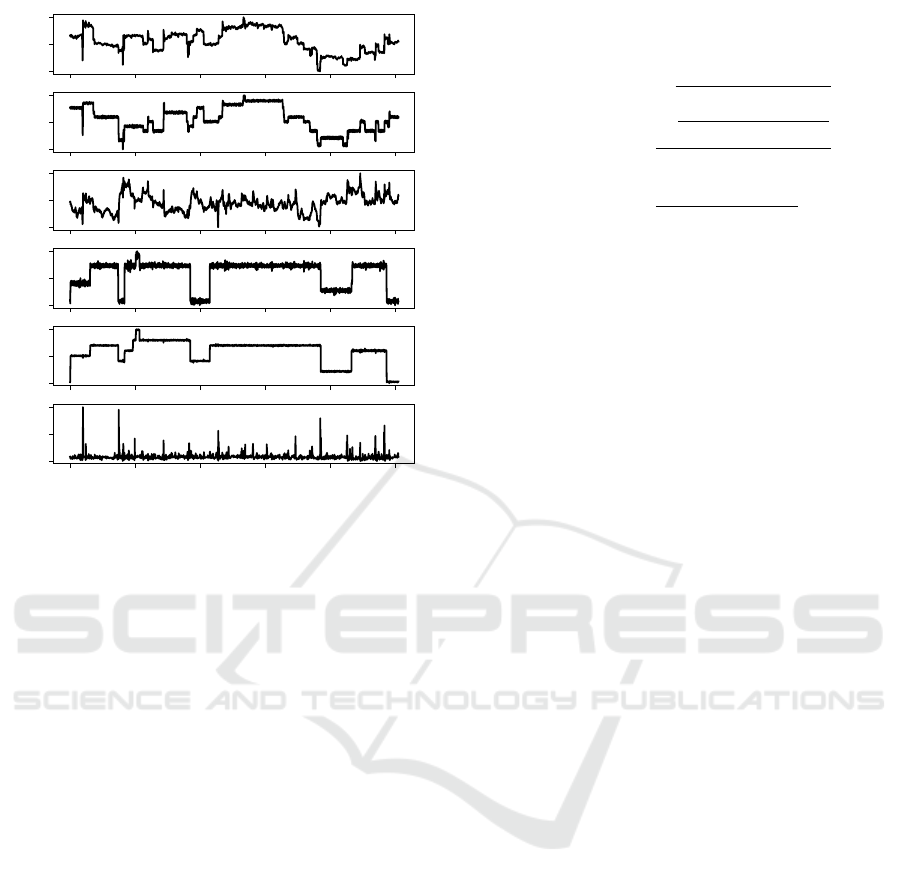
Figure 4 shows the dataset used to implement

the proposed model, which has x

, ··· , x

as inputs

and the residual H

S as output, each containing K =

10081 samples. This dataset was split into 60%

training, 10% validation, and 30% testing (i.e., 6094,

1008, and 3024 samples, respectively).

The proposed NFN-LSTM is validated through

comparison with the following methods:

• LSTM: standalone long short-term memory net-

work (Hochreiter and Schmidhuber, 1997);

• GAM-ZOTS: generalized additive models using

zero-order T-S fuzzy systems learned by backﬁt-

ting algorithm (Mendes et al., 2019a);

• iMU-ZOTS: iterative learning for a model com-

posed of the sum of multiple univariate zero-order

T-S fuzzy systems (Mendes et al., 2019b);

• ALMMo-1: autonomous learning of a multimodel

system from streaming data (ﬁrst-order predictor)

(Angelov et al., 2018);

• iNoMO-TS: iterative learning of multi-input

multi-output T-S fuzzy models using novelty de-

tection (J

unior et al., 2021);

• SVR: support vector regression (Vapnik, 1999).

The training and testing datasets are used for

learning the presented models. The validation dataset

is exclusively used in the hybrid model to individually

verify the model’s tendency to behave with unknown

data throughout training in several epochs.

The performance of the proposed model is val-

idated using Normalized Root Mean Square Error

(NRMSE) and Mean Absolute Error (MAE):

NRMSE =

∑

k=1

[y(k) − ˆy(k)]

max(y) − min (y)

, (16)

MAE =

∑

k=1

y(k) − ˆy(k)

, (17)

where K is the total number of samples, y(k) and

ˆy(k) are the real and estimated outputs of the sys-

tem at k-th sample, respectively, and max (y) and

min(y) are the maximum and minimum values of out-

put y = [y(1), ·· · , y(K)]. The smaller the NRMSE

and MAE values (closer to zero), the better the per-

formance of the method to be validated.

Experiments with NFN-LSTM, LSTM, ALMMo-

1, iNoMO-TS, and SVR were performed using Spy-

der 5 (Python, PyTorch). On the other hand, exper-

iments with GAM-ZOTS and iMU-ZOTS were per-

formed using MATLAB 2022a and C language. Each

one of the experiments was performed 10 times on an

AMD Ryzen 4800H CPU @ 2.90 GHz, with 16GB

DDR4 and 512GB PCIe SSD.

4.2 Implementation

The proposed model has been implemented with 5

membership functions (N

= 5) for each j−th vari-

able ( j = 1, ··· , 5), being the total number of fuzzy

rules N = n · N

= 5 · 5 = 25 as the dimension of

the input and output of the LSTM. The part with

LSTM has only one hidden layer and one-step fore-

casting. The learning process uses the Adam algo-

rithm (Kingma and Ba, 2014) as optimizer, mean

squared error (MSE) as loss function, 100 epochs, and

learning rate 10

−1

decaying stepwise by 0.95 every

ﬁve epochs.

Figure 5 shows the losses for the 100 epochs of the

best trial (out of 10). The comparison results between

the real and estimated outputs in training and testing

stages of the best trial are shown in Figure 6. The

training error values obtained were NRMSE = 0.0348

and MAE = 0.0422, while the testing error values

were NRMSE = 0.0401 and MAE = 0.0417.

In Figure 5, the training and validation cost func-

tions converged satisfactorily, indicating that the pro-

posed model responds well to unknown data. Figure 6

shows that the model reached some peaks as expected

from the SRU dataset, although there are still op-

portunities to improve performance and address more

peaks concerning the system’s dynamic. The fuzzy

rule base obtained from the training of the NFN-

Hybrid LSTM-Fuzzy System to Model a Sulfur Recovery Unit

285

Figure 5: Loss functions for training and validation.

Figure 6: Results of the proposed NFN-LSTM model for

estimating H

S residual in the tail stream of SRU.

LSTM model (best trial), in the form of Eq. (10), is

represented below.

Fuzzy rules for x

(k):

IF x

(k) ∼ A

THEN y

(k) = 5.18 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 5.03 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 5.47 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 4.85 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 6.66 · LSTM

Fuzzy rules for x

(k):

IF x

(k) ∼ A

THEN y

(k) = 5.27 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 4.50 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 5.03 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 3.43 · LSTM

IF x

(k) ∼ A

THEN y

(k) = −0.03 · LSTM

Fuzzy rules for x

(k):

IF x

(k) ∼ A

THEN y

(k) = 2.11 · LSTM

IF x

(k) ∼ A

THEN y

(k) = −0.14 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 0.21 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 3.62 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 2.24 · LSTM

Fuzzy rules for x

(k):

IF x

(k) ∼ A

THEN y

(k) = 3.92 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 3.94 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 5.58 · LSTM

IF x

(k) ∼ A

THEN y

(k) = −0.55 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 5.00 · LSTM

Fuzzy rules for x

(k):

IF x

(k) ∼ A

THEN y

(k) = 4.00 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 2.56 · LSTM

IF x

(k) ∼ A

THEN y

(k) = 0.05 · LSTM

IF x

(k) ∼ A

THEN y

(k) = −2.52 · LSTM

IF x

(k) ∼ A

THEN y

(k) = −0.17 · LSTM

4.3 Discussion

Different methods may present distinct behaviors to

attempt a fair comparison of performance. Thus, the

main parameters of the methods compared in this sec-

tion were adjusted as follows:

• LSTM: one hidden layer, one-step forecasting,

25 for input and output dimension, 100 epochs,

learning rate 10

−1

decaying stepwise by 0.95 ev-

ery ﬁve epochs, Adam optimizer.

• GAM-ZOTS: it

max

= 100 (max. number of itera-

tions), ξ = 10

−3

(termination condition), N

= 5

(ﬁxed number of rules), backﬁtting algorithm.

• iMU-ZOTS: it

max

= 100 (max. number of itera-

tions), ξ = 10

−3

(termination condition), N

= 5

(ﬁxed max. number of rules), M

= 0.8 (thresh-

old for novelty detection), backﬁtting algorithm.

• ALMMo-1: Ω = 10 (for initializing covariance

matrices), λ = 0.8 (threshold for adding new

rules), η = 0.1 (forgetting factor).

• iNoMO-TS: it

max

= 100 (max. number of iter-

ations), N

= 0.3 (threshold for novelty detec-

tion), S

= 0.6 (threshold for similarity detec-

tion), σ

ini

= 10 (elements of the initial covariance

matrix).

• SVR: C = 1 (regularization parameter), epsilon =

0.1 (threshold for non-penalty associated with er-

rors), radial basis function kernel.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

286

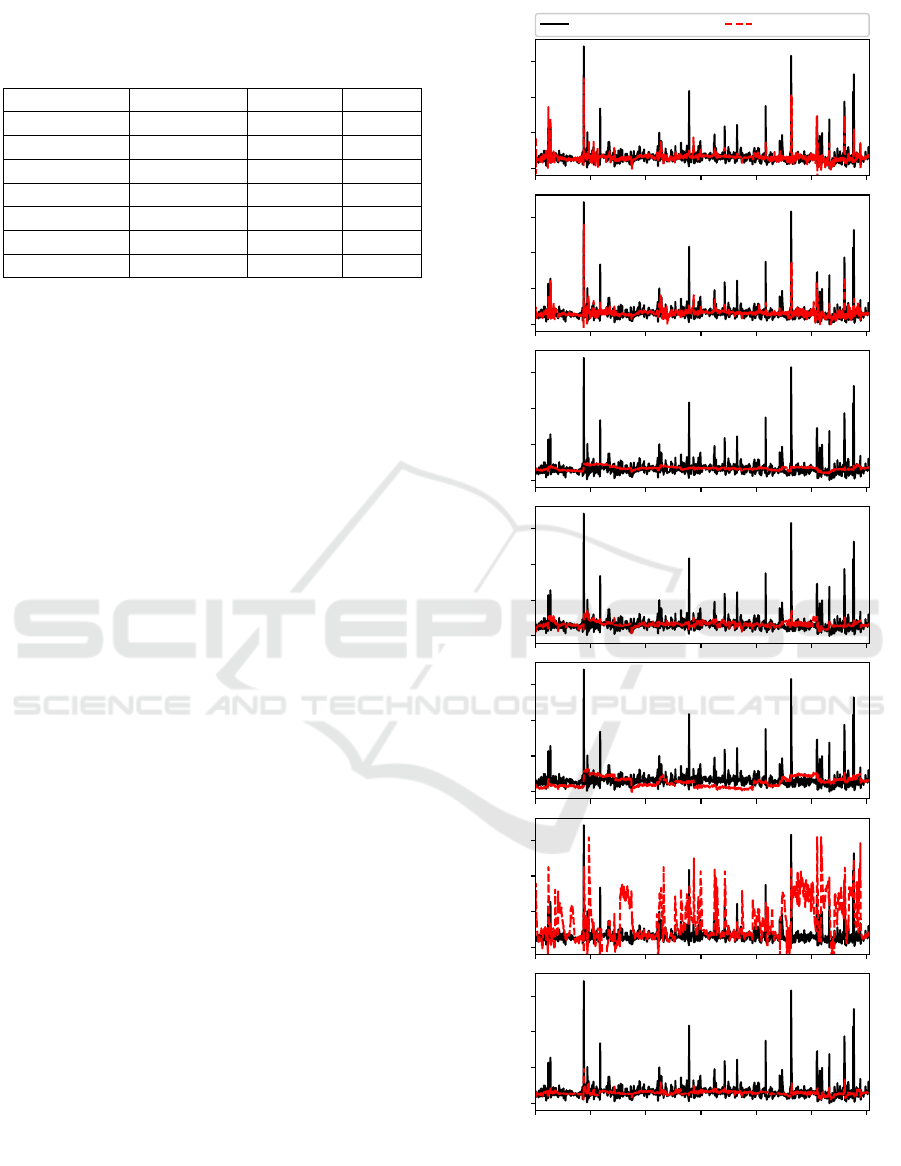
Table 1: Testing results of the proposed NFN-LSTM,

LSTM, GAM-ZOTS, iMU-ZOTS, ALMMo-1, iNoMO-TS,

and SVR.

Method Elapsed (s) NRMSE MAE

NFN-LSTM 2.7672 0.0414 0.0425

LSTM 2.4712 0.0436 0.0452

GAM-ZOTS 4.7521 0.0542 0.0509

iMU-ZOTS 1.8751 0.0529 0.0518

ALMMo-1 13.6527 0.0649 0.0794

iNoMO-TS 353.5502 0.2003 0.2332

SVR 1.3709 0.0510 0.0428

Table 1 presents the average elapsed training time

and the average testing error values of 10 trials of the

proposed model, LSTM, GAM-ZOTS, iMU-ZOTS,

ALMMo-1, iNoMO-TS, and SVR, whose best aver-

age performance is highlighted in bold. Figure 7 com-

pares the outputs of the best-learned models across 10

trials in the testing phase.

It can be noticed that the proposed model and the

LSTM had similar performance in estimation qual-

ity. This fact does not occur in the other methods,

especially GAM-ZOTS and iMU-ZOTS, which have

a neo-fuzzy neuron model with a similar structure

that provided the basis for the proposed method. Fur-

thermore, ALMMo-1 and iNoMO-TS did not obtain

efﬁcient estimation despite their adaptive learning,

whose ﬁnal number of membership functions for each

input variable (as well as fuzzy rules) was equal to

12 and 15, respectively. Still, Figure 7 shows the

instability expressed by iNoMO-TS and the low es-

timation quality by SVR, although it presents error

values close to the NFN-LSTM and LSTM. In addi-

tion to achieving good accuracy and estimation qual-

ity, the proposed model (NFN-LSTM) manages to ex-

press good interpretability in a global way that can be

analyzed on the learned fuzzy rules.

5 CONCLUSIONS

The present study proposed a hybrid method involv-

ing a neo-fuzzy neuron system with long short-term

memory, the NFN-LSTM model, with a positive bal-

ance between interpretability and accuracy. Inter-

pretability can be analyzed by the inﬂuence of in-

puts on the output with the learned fuzzy rules, and

accuracy is veriﬁed by the quality of the output es-

timation and associated errors. The case study in

an industrial system showed the viability and power

of NFN-LSTM over the LSTM, GAM-ZOTS, iMU-

ZOTS, ALMMo-1, iNoMO-TS, and SVR methods,

due to the results and the additional task of detect-

ing important peak values for the application. Fu-

− 1.0

− 0.5

0.0

0.5

O utput (N FN -LSTM )

− 1.0

− 0.5

0.0

0.5

O utput (LSTM )

− 1.0

− 0.5

0.0

0.5

O utput (G AM -ZO TS)

− 1.0

− 0.5

0.0

0.5

O utput (iM U-ZO TS)

− 1.0

− 0.5

0.0

0.5

O utput (ALM M o-1)

− 1.0

− 0.5

0.0

0.5

O utput (iN oM O -TS)

0 500 1000 1500 2000 2500 3000

Sam ple

− 1.0

− 0.5

0.0

0.5

O utput (SVR)

Real Output Estimated Output

Figure 7: Comparison of testing outputs of the NFN-LSTM,

LSTM, GAM-ZOTS, iMU-ZOTS, ALMMo-1, iNoMO-TS,

and SVR.

Hybrid LSTM-Fuzzy System to Model a Sulfur Recovery Unit

287

ture works will explore the use of other methods in

a hybrid way to the neo-fuzzy neuron to improve the

interpretability-accuracy trade-off.

ACKNOWLEDGEMENTS

Jorge S. S. J

unior is supported by Fundac¸

ao para

a Ci

encia e a Tecnologia (FCT) under the grant

ref. 2021.04917.BD. This research was supported

by the ERDF and national funds through the

project InGestAlgae (CENTRO-01-0247-FEDER-

046983), and by the FCT project UIDB/00048/2020.

REFERENCES

Angelov, P. P., Gu, X., and Pr

ıncipe, J. C. (2018). Au-

tonomous Learning Multimodel Systems From Data

Streams. IEEE Transactions on Fuzzy Systems,

26(4):2213–2224.

Angelov, P. P., Soares, E. A., Jiang, R., Arnold, N. I., and

Atkinson, P. M. (2021). Explainable artiﬁcial intelli-

gence: an analytical review. WIREs Data Mining and

Knowledge Discovery.

Curreri, F., Patan

e, L., and Xibilia, M. (2021). Soft Sen-

sor Transferability between Lines of a Sulfur Recov-

ery Unit. IFAC-PapersOnLine, 54(7):535–540.

Fortuna, L., Graziani, S., Rizzo, A., and Xibilia, M. G.

(2007). Soft Sensors for Monitoring and Control of

Industrial Processes. Springer Science & Business

Media.

Fortuna, L., Rizzo, A., Sinatra, M., and Xibilia, M. (2003).

Soft analyzers for a sulfur recovery unit. Control En-

gineering Practice, 11(12):1491–1500.

Gandin, I., Scagnetto, A., Romani, S., and Barbati, G.

(2021). Interpretability of time-series deep learning

models: A study in cardiovascular patients admitted

to Intensive care unit. Journal of Biomedical Infor-

matics, 121:103876.

Goodfellow, I., Bengio, Y., Courville, A., and Bengio, Y.

(2016). Deep learning. MIT press Cambridge.

Guo, R., Liu, H., Wang, W., Xie, G., and Zhang, Y.

(2021). A Hybrid-driven Soft Sensor with Com-

plex Process Data Based on DAE and Mechanism-

introduced GRU. In 2021 IEEE 10th Data Driven

Control and Learning Systems Conference (DDCLS),

pages 553–558.

Hochreiter, S. and Schmidhuber, J. (1997). Long Short-

Term Memory. Neural Computation, 9(8):1735–1780.

Jiang, Y., Yin, S., Dong, J., and Kaynak, O. (2021). A

Review on Soft Sensors for Monitoring, Control, and

Optimization of Industrial Processes. IEEE Sensors

Journal, 21(11):12868–12881.

unior, J. S. S., Mendes, J., Ara

ujo, R., Paulo, J. R., and

Premebida, C. (2021). Novelty Detection for Iterative

Learning of MIMO Fuzzy Systems. In 2021 IEEE

19th International Conference on Industrial Informat-

ics (INDIN), pages 1–7.

unior, J. S. S., Mendes, J., Souza, F., and Premebida, C.

(2023). Survey on Deep Fuzzy Systems in regression

applications: a view on interpretability. International

Journal of Fuzzy Systems, pages 1–22.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Lees, T., Reece, S., Kratzert, F., Klotz, D., Gauch, M.,

Bruijn, J. D., Sahu, R. K., Greve, P., Slater, L., and

Dadson, S. J. (2022). Hydrological concept formation

inside long short-term memory (LSTM) networks.

Hydrology and Earth System Sciences, 26(12):3079–

3101.

Liu, X., Shi, Q., Liu, Z., and Yuan, J. (2021). Using LSTM

Neural Network Based on Improved PSO and Atten-

tion Mechanism for Predicting the Efﬂuent COD in a

Wastewater Treatment Plant. IEEE Access, 9:146082–

146096.

Mendes, J., Souza, F., Ara

ujo, R., and Rastegar, S.

(2019a). Neo-Fuzzy Neuron Learning Using Backﬁt-

ting Algorithm. Neural Computing and Applications,

31(8):3609–3618.

Mendes, J., Souza, F. A. A., Maia, R., and Ara

ujo, R.

(2019b). Iterative Learning of Multiple Univariate

Zero-Order T-S Fuzzy Systems. In Proc. of the

The IEEE 45th Annual Conference of the Industrial

Electronics Society (IECON 2019), pages 3657–3662.

IEEE.

Moral, J. M. A., Castiello, C., Magdalena, L., and Mencar,

C. (2021). Explainable Fuzzy Systems. Springer In-

ternational Publishing.

Silva, A. M., Caminhas, W., Lemos, A., and Gomide, F.

(2014). A fast learning algorithm for evolving neo-

fuzzy neuron. Applied Soft Computing, 14:194–209.

Souza, F., Offermans, T., Barendse, R., Postma, G., and

Jansen, J. (2022). Contextual Mixture of Experts: In-

tegrating Knowledge into Predictive Modeling. IEEE

Transactions on Industrial Informatics, pages 1–12.

Vapnik, V. (1999). The nature of statistical learning theory.

Springer science & business media.

Yamakawa, T. (1992). A Neo Fuzzy Neuron and Its Appli-

cations to System Identiﬁcation and Prediction of the

System Behavior. Proc. of the 2nd Int. Conf. on Fuzzy

Logic & Neural Networks, pages 477–483.

Yuan, X., Li, L., and Wang, Y. (2020). Nonlinear Dynamic

Soft Sensor Modeling With Supervised Long Short-

Term Memory Network. IEEE Transactions on In-

dustrial Informatics, 16(5):3168–3176.

Zarzycki, K. and Ławry

nczuk, M. (2021). LSTM and GRU

Neural Networks as Models of Dynamical Processes

Used in Predictive Control: A Comparison of Mod-

els Developed for Two Chemical Reactors. Sensors,

21(16).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

288