Can Ensemble Learning Approaches for Offside Detection Work?

Kurt Dylan Buttigieg

, David Suda

and Mark Anthony Caruana

Department of Statistics and Operations Research, University of Malta, Msida, MSD2080, Malta

Keywords: Football, Offside Detection, Random Forests, Boosting, Ensemble Learning.

Abstract: The analysis of data collected from various recreational activities and professional sports is essential to obtain

more information on the activity in question or to make better data-driven decisions. Most literature related

to offside detection related to the efficacy of manual offside detection or the use of an offside detection

algorithm. In this study, the focus shall be on the detection of offside judgements in football/soccer using

ensemble learning approaches such as random forest type algorithms, boosting type algorithms and majority

voting. For random forests, we also consider three corresponding extensions: regularized random forests,

guided regularized random forests, and guided random forests. Moreover, five boosting approaches are

considered, namely: Discrete AdaBoost, Real AdaBoost, Gentle AdaBoost, Gradient Boosting and Extreme

Gradient Boosting. Gentle AdaBoost is the best performing model on most metrics, except for sensitivity,

where Extreme Gradient Boosting performs best. Furthermore, soft majority voting among the models

considered is capable of improving the Cohen’s Kappa and the F

score but does not provide improvements

on other metrics.

1 INTRODUCTION

The offside rule in football is considered to be one of

the most complex and critical rules that a referee has to

abide by during a match. It is primarily enforced by two

referees, one for each side of the pitch, known as

linesmen or assistant referees. Each linesman runs on

one side of the pitch from the half-way line up to the

goal line and is the referee in charge of enforcing the

offside rule for his side of the pitch. Rules in football

are defined in the Laws of The Game (LOTG),

maintained by the International Football Association

Board (IFAB), which consists of 17 different laws.

Law 11 concerns the offside rule which explicitly

defines an offside offence in the game of football and

how it should be enforced by the referees. The law

states that a player is in an offside position if any part

of the head, body or feet of such player is in the

opponents’ half of the pitch and closer to the attacking

goal line than the ball and the penultimate member of

the defending team. The player in an offside position is

only penalised for the offence if such player touches or

plays the ball, interferes with an opponent by

https://orcid.org/0000-0002-7861-7479

https://orcid.org/0000-0003-0106-7947

https://orcid.org/0000-0002-9033-1481

preventing them from playing the ball, obstructs an

opponent from the ball, challenges an opponent for the

ball, or impacts an opponent’s ability to play the ball in

any other way. Since offside detection by a referee is

subject to human error, the assistance of computational

means to detect offside are of utmost importance. As

shall be seen in the literature review, most literature in

this aspect focus on the use of an offside detection

algorithm. In this study, an alternative focus on

machine learning techniques is taken. Images taken

from a broadcasted television camera are used for

offside detection. The images do not consider whether

a player is interfering with play or not, as the referee

can easily take this decision. Therefore, the aim of this

study is to identify whether an attacking player’s head,

shoulders, hips, knees or feet are in an offside position

at the time the image is taken or the video is stopped.

2 LITERATURE REVIEW

Several authors studied the manual accuracy of

assistant referees for offside judgement in football

Buttigieg, K., Suda, D. and Caruana, M.

Can Ensemble Learning Approaches for Offside Detection Work?.

DOI: 10.5220/0012159800003587

In Proceedings of the 11th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2023), pages 34-44

ISBN: 978-989-758-673-6; ISSN: 2184-3201

(Oudejans et al., 2005; Helsen et al., 2006; Gilis et al.,

2008; Catteeuw et al., 2010). These authors conclude

that, in a significant number of cases (between 17-

33%), the judgment given by these referees was

erroneous. Moreover, it has also been established that

during the first 15-minute match period, the error in

judging offside is significantly higher than in other

match periods, with a percentage error of 38.5%.

(Helsen et al., 2006). In one of the earliest studies

investigating the applicability of mathematical

concepts for offside detection, a multiple camera

system and an offside detection algorithm was used

in real-time was by (D'Orazio et al., 2009). This led

to a classification accuracy of 77.8%. Another article

concludes that the most suitable form for offside

detection is camera-based player tracking, with a

decrease in accuracy error of around 40% (Henderson

et al., 2014). The use of contour mapping to identify

players that are in an offside position has also been

applied (Patil et al., 2018). An infrared camera system

and a MATLAB script were also used to detect

offside (Lopez and Jenkins, 2019). The system had no

misclassification errors, however, the players had to

wear several reflective markers and the system may

confuse one player with another. The dataset we shall

use in this paper has also been used (Panse and

Mahabaleshwarkar, 2020). In this paper, TV-

broadcasted images and a vanishing point algorithm

were used to identify the playing area. DBSCAN and

the k-means clustering algorithms were used to

classify players into teams. An offside detection

algorithm was also constructed to detect offside from

the collected dataset, giving an F

score of 0.85.

Another study used two cameras and several

algorithms to construct the dataset, followed by an

offside detection algorithm. They obtained precision,

recall and F

scores between 0.6 and 0.67 (Uchida et

al., 2021). Finally, the use of multiple cameras and

several algorithms to establish the players' positions,

followed by an offside detection algorithm

conditioned on the players' positions, has also been

studied (Siratanita et al., 2021). The accuracy was of

98.5%. Despite much of the literature focusing on the

use of an offside detection algorithm, none of the

literature found looked into the use of machine

learning techniques to detect offside, in particular

ensemble learning approaches. Ensemble learning

methods combine the prediction of multiple models

to provide a combined output. In this paper, we look

at the use of these methods to determine whether

these can offer an improvement over both linesmen

and the oft resorted to offside detection algorithm.

3 METHODOLOGY

In this section we shall go through a number of

ensemble learning approaches which we will make use

of in this paper. The first is random forests (RF),

which uses the bagging approach (also known as

bootstrap aggregating), to train multiple decision trees

which are then eventually considered collectively to

obtain a predictive model (Breiman, 2001). Aside from

the bagging step, random forests also require two

settings - the number of variables randomly sampled as

candidates at each split and the minimum number of

vectors of observations in the terminal nodes. In

random forests, the splits are determined using the Gini

impurity. In regularised random forests (RRF), the

impurity decrease of variables which have not yet

been used in any of the trees of the random forest is

penalised by a coefficient of regularisation 𝜐 (Deng

and Runger, 2012). Therefore, a feature which has not

yet been selected in any of the nodes in the forest

needs to have a high impurity decrease to be selected

for the split. Further extensions include guided

regularized random forests (GRRF) and guided

random forests (GRF). In guided regularized

random forests, the penalisation parameter is not kept

constant for all features, but is a function of the

importance in a previously trained random forest. We

thus have two important parameters, 𝜐 and 𝜏, where 𝜏

is a coefficient of importance (Deng and Runger,

2013). Guided random forests, on the other hand, set

the penalisation parameter 𝜐=1 and rely solely on

the coefficient of importance (Deng, 2013).

The class of random forest algorithms represents

one type of ensemble learning, where multiple trees

are generated, trained in parallel, and combined at a

later stage. Another class of algorithms are boosting

algorithms. In this case, classifiers are trained

sequentially, and the most recent classifier is trained

depending on the previous classifier. One of the

earliest known boosting classifiers is discrete

AdaBoost (Freund and Schapire, 1997). In discrete

AdaBoost, each observation is initially given equal

weighting, but then at every iteration, each classifier

is given a new weighting depending on the

classification error, based on the exponential loss

function. This is repeated for a set number of

iterations until a final classifier is given. An extension

to discrete AdaBoost is real AdaBoost (Friedman et

al., 2000) which uses class probabilities instead of

discrete classes in the computation of the weights.

Finally, we also have gentle AdaBoost, where direct

optimisation of the exponential loss is replaced by

Newton’s method (Friedman et al., 2000). In these

three cases, the number of trees (iterations of the

Can Ensemble Learning Approaches for Offside Detection Work?

algorithm) 𝐵, the maximum depth of each tree, the

shrinkage parameter 𝛼 and the subsampling rate 𝜗

are all important parameters of these algorithms.

Gradient Boosting, on the other hand, is an

alternative boosting approach that uses pseudo

residuals as target variables to build trees rather than

the classifiers themselves (Friedman, 2001).

Extreme Gradient Boosting, also referred to as

XGBoost, uses the number of leaves in the tree at the

current iteration and L

regularisation with the loss

function, and is known to achieve better accuracy at

higher speeds (Chen and Guestrin, 2016). Important

parameters of both algorithms are: the number of

boosting iterations 𝐵, the maximum tree depth, the

minimum number of vectors of observations in the

terminal nodes of each tree, the shrinkage parameter

𝛼the subsampling rate 𝜗 and the column subsampling

rate 𝜖. Additionally, XGBoost also has regularisation

coefficients 𝛽 and 𝜂 which are associated with the

number of leaves and L

regularisation term. An

extension to XGBoost is XGBoost with dropout,

where a fraction of the trees, 𝜃∈

[

0,1

]

, are dropped

at each iteration. Also, one can also specify a

probability 𝜆∈

[

0,1

]

which defines whether the tree

dropout technique is used.

Following this overview of the types of methods

and relevant parameters which will be assessed in this

paper with the aim of offside detection, a description

of the dataset under study shall be given, after which

detail about the grid search for the model parameters

shall be provided. This is followed by the chosen

parameters based on the different models’ Cohen’s

Kappa, and in the end, the different performance

criteria of the different models shall be analysed.

4 APPLICATION

4.1 Dataset

The dataset used for this analysis contains several

images taken from publicly broadcasted videos on

television (Panse and Mahabaleshwarkar, 2020).

Moreover, a pose estimation algorithm was used to

detect the body parts of each player in the image and

convert them to x-y coordinates (Bridgeman et al.,

2019). The x-y coordinates of the head, shoulders,

hips, knees and feet for each player in the frame are

obtained using the mentioned pose algorithm. All the

images are 2560 by 1440 pixels and the x-y

coordinates are the pixel coordinates of the respective

players and body parts. The DBSCAN and the k-

means clustering algorithms to detect the goalkeeper

and referee and classify players into teams.

Specifically, since the DBSCAN algorithm also

classifies noisy data, it was used to detect the

goalkeeper and the referee in the frame, while the k-

means algorithm was used to classify the players into

teams (Panse and Mahabaleshwarkar, 2020).

Following this, each row of data is therefore an image

with several numerical variables indicating the

coordinates of each body part of the players. Since

there are 10 players in each team (excluding the

goalkeeper), 9 body parts and 2 coordinates (x and y),

there are 180 variables for each team. The defending

goalkeeper includes a further 18 variables in the

dataset, together with the target variable indicating 1

for offside and 0 otherwise. This gives a total of 379

variables.

Figure 1: An example on the use of the camera_angle

variable and the solution to the missing data problem.

Evidently, a broadcasting camera does not capture the

whole football pitch and a camera is directed manually.

Because of this, a camera placed on the side of the pitch

between the two halves does not include all the players

in the frame, leading to missing data in the dataset,

corresponding to players which are not in the frame. To

cater for this, an additional binary variable was created

indicating the camera’s direction, denoted as

camera_angle, which can either be showing the left or

the right-hand sides of the pitch. This variable takes the

value 0 if the camera is directed to the left or the value

1 if the camera is directed to the right. As an example,

consider the two-dimensional image in Figure 1

(taking camera_angle as 1), where Area B is the area

being captured by the broadcasting camera while Areas

A and C are the remaining areas not captured by the

camera. Using the camera_angle variable, the missing

x-y coordinates for the missing players were taken as

the coordinates on the far bottom left or the far bottom

right of the frame. Specifically, the x-coordinate when

the camera is directed to the left is taken as 2560 (i.e.,

far right) while the x-coordinate when the camera is

directed to the right is taken as 0 (i.e., far left). The y-

coordinate is taken constantly for both cases as 1440,

representing the bottom of the frame. This is also

depicted in the example of Figure 1, where the

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

coordinates of the players in Area A are taken as the

furthest position to the bottom left of Area B,

represented by the purple point. This applies to all

variables characterizing different body parts. In this

way, the missing data problem for the players is

eliminated and the new coordinates are not affecting

the offside decision.

Another missing data problem was present for the

defending goalkeeper, where the frame of several

images was slightly to the right or to the left and the

goalkeeper was out of the frame. The position of this

goalkeeper is significant to the offside decision and

thus, the variable indicating the camera direction was

used again to input the respective coordinates.

Particularly, if the camera is directed to the left and the

goalkeeper’s coordinates are missing, the x-coordinate

of the goalkeeper is taken as 0 (i.e., far left) and is taken

as 2560 (i.e., far right) if the camera is directed to the

right. The y-coordinate is taken as 720, indicating that

the goalkeeper is in the middle of the frame. This is

also pictured in Figure 1, where the out-of-frame

defending goalkeeper has been given the rightmost

coordinates. As done for the missing data problem for

the players, this solution was applied to all variables

characterizing different body parts. The camera_angle

variable indicating the camera’s direction shall also be

included in the models during training.

The names of the features in the dataset for the

players are in the form A-B-

-E, where 𝛢∈{1, 2} for

the two different teams, 𝐵∈{0, 1, …, 9} denotes the

𝐵

left-most player in team Α , 𝛤∈{0, 1, …, 8}

denotes the Γ

body part of player Β in team Α, while

𝐸∈{x, y} is either the x or y coordinate of body part Γ

of player Β in team Α . Note that Team 1 is taken

constantly as the team attacking from the left to the

right side of the pitch. Thus, if camera_angle = 0 (i.e.,

the camera is directed to the left side of the pitch),

Team 1 denotes the defending team, and if

camera_angle = 1 (i.e., the camera is directed to the

right side of the pitch), Team 1 denotes the attacking

team. Moreover, for the set 𝛤, 0 denotes the player’s

head, 1, 2, 3 and 4 denote the player’s left shoulder,

hip, knee, and foot respectively, while 5, 6, 7 and 8 -

denote the player’s right foot, knee, hip and shoulder

respectively. As an example, the variable Team1-0-2-

x is the x-coordinate in the frame of the left hip of the

left-most player of team 1. The goalkeeper variable

names follow a similar but simpler structure.

Specifically, the variable takes the form GK-

-E,

where the sets 𝛤 and 𝐸 are as defined previously for

the players. As an example, GK-6-y denotes the y-

coordinate in the frame of the right knee of the

defending goalkeeper.

The data is imbalanced since only 26.5% of the

images include at least one player in an offside

position. Python’s imblearn library was used to apply

SMOTE-NC on this dataset. In the balanced dataset,

69.31% of the vectors of observations are used for

training while the remaining 30.69% are used for

testing, where 192 vectors of observations are used for

training for each class.

4.2 Model Parameters for Grid Search

The model parameter sets used for grid search shall

now be discussed. For all the models to be trained, 3-

fold cross-validation shall be used, and the vectors of

observations in each of the folds are the same across all

models. This was done to reduce any bias and to keep

equal conditions between different models for

comparison. Cohen’s Kappa shall be the performance

metric utilised to identify the optimal hyperparameters

across different models in the grid search, since equal

importance is given to all the classes and no class’s

performance needs to be optimised more than the other

classes. The well-known R package caret shall be used

for generic model training. The package easily trains

different models from different packages by tuning

hyperparameters using 𝐾 -fold cross-validation, and

then chooses the best performing model depending on

a defined metric.

Random Forest

For the random forest, the randomForest package is

used, where two hyperparameters are optimised; the

number of variables randomly sampled as candidates

at each split and the minimum number of vectors of

observations in the terminal nodes. A grid search is

conducted where the number of variables sampled is

taken from the set {5, 6, 7, …, 18, 19, 20, 35, …, 350,

365, 379} with a total of 40 different values. The values

for the minimum number of vectors of observations in

the terminal nodes are taken from the set {1, 3, 6, 9,

12 } . Therefore, there are a total of 200 different

combinations in the grid. The number of trees in the

random forest is fixed at 500, since the prediction error

of a random forest goes to a limiting value almost

surely as the number of trees increases (Breiman,

2001). Thus, setting the number of trees to 500 is

adequate for our problem.

RRF, GRRF

and GRF

The RRF package has been created to apply the

extensions to random forests (Deng and Runger,

2012; Deng and Runger, 2013; Deng, 2013). For all

RRF, GRRF and GRF, the number of trees shall also

Can Ensemble Learning Approaches for Offside Detection Work?

be fixed at 500 and the number of variables randomly

sampled for splits is optimised as in random forests.

Moreover, 𝐶 and the coefficient of importance 𝜏 are

optimised as follows. For RRF, 𝜐 is optimised from

{0.1, 0.2, …, 0.9, 1} and 𝜏 is kept constant at 0. For

GRRF, both 𝜐 and 𝜏 are optimised from {0, 0.1, 0.2,

…, 0.9, 1}, but excluding the combination

(

𝜐, 𝜏

)

( 0,0). For GRF, 𝜐 is kept constant at 1 and 𝜏 is

optimised from {0, 0.1, 0.2, …, 0.9, 1}. Thus, for

RRF, there are a total of 400 combinations of

different model parameters to consider while 4800

model combinations are available for GRRF and 440

different parameter combinations for GRF.

Discrete, Real and Gentle AdaBoost

For the three AdaBoost algorithms, the ada package

implementation in caret shall be used. The number of

trees 𝐵 , the maximum depth of each tree, the

shrinkage parameter 𝛼 and the subsampling rate 𝜗

are all parameters which need to be optimised.

AdaBoost was initially created to work on weak

learners and decisions stumps, indicating that the

maximum depth should be 1. However, when

considering trees with a maximum depth of 1 (thus

having a boosted model consisting of weak learners)

the models performed significantly worse than those

with a depth greater than 1. Therefore, stronger

learners with an increased tree depth will be

considered. For each of the three AdaBoost models,

the number of trees 𝐵 shall be optimised from the set

{ 100, 200, …, 900, 1000 } while the shrinkage

parameter 𝛼 and the subsampling rate 𝜗 shall both be

optimised from the set {0.25, 0.5, 0.75, 1}. The set of

tree depth values to be optimised shall be {3, 5, 7, 9}.

Thus, the grid consists of 640 combinations.

Gradient Boosting and Extreme Gradient Boosting

The caret implementation of the h2o package in R shall

be used for the implementation of Gradient Boosting,

where the logistic loss function is used for binary

classification. More information on other loss

functions available here (Click et al., 2022). The

number of boosting iterations 𝐵

shall be optimised

from the set {100, 200, …, 500}, the maximum tree

depth shall be taken from {3, 5, 7}, while the minimum

number of vectors of observations in the terminal

nodes of each tree shall be optimised from the set {3,

6, 9, 12 } . Additionally, the optimal value for the

shrinkage parameter 𝛼 will be obtained from the set

{0.05, 0.1, 0.25, 0.5}, while the best values for both the

https://github.com/buttigiegkurt/offside-paper

subsampling rate 𝜗 and the column subsampling rate

𝜖 will be taken from {0.5, 0.75, 1}. This gives 2160

different combinations in our grid search. Thus, due

to 3-fold cross-validation, 6480 models need to be

trained.

For Extreme Gradient Boosting, two different grid

searches shall be created. The first approach is the

simple Extreme Gradient Boosting without the tree

dropout while the second approach includes tree

dropout. The xgboost R package shall be used in this

study, which caters for both extreme gradient boosted

trees and the corresponding dropout version. For the

first approach, the seven different parameters are

optimised as follows; the number of boosting iterations

𝐵 is optimised from the set {50, 100, 150, 200, 300},

the maximum tree depth is optimised from the set {3,

5, 7, 9}, the shrinkage parameter 𝛼 is optimised from

the set {0.05, 0.1, 0.25, 0.5}, the subsampling rate 𝜗

and the column subsampling rate 𝜖 are both optimised

from the set {0.5, 0.75, 1}, the coefficient 𝛽 which

determines the influence of 𝑀



is optimised from the

set {0, 1}, and the coefficient 𝜂 which determines the

influence of the L

regularization term is optimised

from the set {0.5, 1, 2}. This gives a total of 4320

different combinations in the grid search. In the second

approach, the 4320 combinations used in the first

approach are once again considered, together with the

optimisation of the dropout fraction 𝜃 and the dropout

probability 𝜆 from the set { 0.25, 0.5 } . Thus, the

optimal model is obtained from 17280 combinations.

4.3 Statistical Models

In this section, the models for offside detection are

trained using the training offside dataset and

optimised using the hyperparameter sets. Cohen’s

Kappa shall be considered when training and testing

models as the cost of incorrectly classifying a non-

offside case is equal to the cost of incorrectly

classifying an offside case. Other testing metrics

including the accuracy, sensitivity and specificity are

given at the end of the section after the models have

been trained, wherein a comparison of the models and

feature importance are considered. Due to space

limitations, the reason for hyperparameter choice and

the figures plotting the performance results for

hyperparameter optimisation using grid search are

given in the supplementary material

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

Random Forest

For random forests, lower values for the minimum

number of vectors of observations in the terminal

nodes give a slightly better model and, more

evidently, increasing the number of variables sampled

declines the performance of the model. The optimal

set of parameters is 6 for the number of variables

sampled and 3 for the minimum number of vectors of

observations in terminal nodes, giving an average

validation performance of 0.443. Training a model on

the full training set using the two optimal parameters

gives a training accuracy of 100% and a Kappa of 1,

indicating that all training vectors of observations are

classified correctly. This shows that, despite the

implementation of parameter tuning, some overfitting

may still be present in the trained model. Testing the

model on the testing set leads to a Kappa of 0.488.

The prediction error of a random forest goes to a

limiting value almost surely as the number of trees

increases.

RRF, GRRF and GRF

For RRF, it can be noted that higher values for the

coefficient of regularization drastically improve the

performance of the models. The values 0.9 and 1 are

similar in terms of performance while values in the

range [ 0.1, 0.6 ] are shown to have poor model

performance. Recall that 𝜐= 1 gives the standard

random forest, meaning that low regularization

parameters are not beneficial for this dataset. The

optimal model obtained has 𝜐= 0.9 and the number

of variables sampled equal to 11, giving an average

validation performance of 0.398 when considering

the Kappa metric. Training using the mentioned

optimal parameters on the whole training set gives a

model which predicts all training vectors of

observations correctly, indicating some overfitting

once again. Furthermore, testing the model on the

testing set gives a Kappa of 0.410.

Three parameters shall be optimised when

considering the GRRF approach, the two coefficients

and the number of variables sampled. Lower values

for both the coefficients lead to a more dispersed set

of line graphs, indicating that taking one of the

coefficients close to 1 leads to similar models

irrespective of the other coefficient. Moreover,

different values for the number of variables sampled

does not seem to be affecting model performance as

the line graph is consistent across the x-axis. The

optimal set of parameters is given by (𝜐, 𝜏) = (0.8,

0.3), with the number of variables sampled equal to

350, giving an average Kappa validation metric of

0.430. Training a model on the optimal parameters

and applying it on the full dataset leads to an accuracy

of 100%, predicting all training vectors of

observations correctly. Despite this, testing the model

on the testing set gives a Kappa of 0.410. Once more,

due to the significant decrease in performance from

the training set to the testing set, model overfitting

which was not eliminated from parameter tuning may

still be present.

The final extension to random forests which still

needs to be considered is GRF. Increasing the number

of variables sampled reduces the model performance,

with higher values for the coefficient of importance

leading to a more accelerated decline in the Kappa

metric. Despite this, all variations of the coefficient

lead have similar performance for low values of the

number of variables sampled during splits. The

optimal average validation Kappa is given when 𝜏=

0.8 and the number of variables sample is equal to 5.

Training these parameters on the full training set

produces a model with an accuracy of 100% once

more. Testing the model on the testing set gives a

Kappa of 0.559.

Comparing the three models, the RRF and GRRF

models performed equally well on the testing set,

predicting 17 offsides out of the total 32 and 122

onsides out of 138. However, the GRF performed

slightly better in predicting both the offside and

onside images, with 18 offsides detected and 131

onsides. Moreover, the performance of the GRF is

marginally better than the standard random forest,

with 4 more images classified correctly. This

indicates that, contrary to RRF and GRRF, the GRF

approach may have a slight advantage over standard

random forests for this offside detection dataset.

Next, the focus shall move on to boosting, where

Discrete, Real and Gentle AdaBoost are considered.

Discrete, Real and Gentle AdaBoost

The optimal model for Discrete AdaBoost has a

shrinkage parameter of 1, a subsampling parameter of

1, includes just 100 trees and a maximum tree depth

of 3. The average validation Kappa performance for

this model is given by 0.417. Similar to the random

forest model, the Discrete AdaBoost model has a

100% accuracy on the training set, whereas testing the

same model on the testing set gives a Kappa of 0.428,

incorrectly predicting 34 vectors of observations.

The Real AdaBoost approach performed similarly

in terms of validation performance as the optimal

model having a shrinkage parameter of 0.5, a

subsampling parameter of 0.25, a maximum tree

depth of 5 and 100 trees gives an average Kappa of 0.409.

Can Ensemble Learning Approaches for Offside Detection Work?

The performance of models with a subsampling value

of 1 or the combination (𝛼, 𝜗) = (1, 0.25) seems to

differ over different maximum tree depths whereas

the other combinations do not suggest such difference

over distinct tree depths. As in discrete AdaBoost, the

model gives a perfect prediction over the training set.

Fitting the model on the testing set provides a Kappa

of 0.408. The Real AdaBoost model performed well

in predicting onside however only half of the offside

images where correctly predicted. This translates to a

15.63% lower performance in predicting the positive

class.

Finally, for Gentle AdaBoost, the optimal model

has a shrinkage parameter of 0.25, a subsampling

parameter of 0.25, a maximum tree depth of 7 and

includes 200 trees. This model gives an average

validation Kappa of 0.417 and, once again, a 100%

accuracy on the full training set. With a testing Kappa

of 0.668, only 5 offside and 11 onsides where

incorrectly classified in the testing set, indicating that

Gentle AdaBoost is the best performing technique up

till now.

Gradient Boosting and Extreme Gradient Boosting

The optimal validation Kappa of 0.352 is obtained

when the number of trees is the boosted model is 100,

the maximum tree depth is 5, the minimum number

of vectors of observations in the terminal nodes is 9,

together with a shrinkage of 0.1, a subsampling

parameter of 0.5, and a column subsampling

parameter 0.75. This optimal model gives an accuracy

of 99.74% with just one vector of observations

classified incorrectly. As noted in the previously

trained models, overfitting may once again be present

in the Gradient Boosting model. Upon testing the

constructed model, a testing Kappa of 0.519 is

derived. This shows that Gradient Boosting is a very

valid technique on this dataset, performing quite well

on the testing dataset.

A value of 1 is the worst performing value for both

the subsampling and column subsampling

parameters. There does not seem to be a significant

difference between the values of 0.5 and 0.75, and the

performance is somewhat constant across the

different number of trees for most of the

combinations. Moreover, different values for

maximum tree depth also do not seem to be affecting

model performance. It is clear that the higher

shrinkage values of 0.25 and 0.5 perform worse than

the lower values of 0.05 and 0.1. Additionally, the

performance is constant across different number of

trees and does not depend on the L

regularization

coefficient as the Kappa metric does not seem to

change with the mentioned coefficient. Despite this,

the coefficient for the number of terminal nodes

regularization parameter does seem to impact the

performance as the value 0, i.e., not including this

regularization term, leads to a better Kappa

performance when compared to the value of 1, i.e.,

including the mentioned regularization term.

The optimal combination has an average validated

Kappa metric of 0.391, where the number of boosting

iterations 𝐵 is 50, the maximum tree depth is 5, the

shrinkage parameter 𝛼 is 0.1, the subsampling rate 𝜗

and the column subsampling rate 𝜖 are both 0.75, the

coefficient 𝛽 which determines the influence of 𝑀



0, and the coefficient 𝜂 which determines the

influence of the L

regularization term is 1. Training

a model on this set of parameters on the full training

set, a model predicting all training vectors of

observations correctly is once again obtained,

indicating that, despite all the regularization measures

taken in Extreme Gradient Boosting, overfitting may

still be present. Testing the trained model on the

testing set, a Kappa of 0.541 is derived.

For extreme gradient boosting with dropout,

17280 parameter combinations have been considered.

For the column subsampling parameter, the value of

0.5 seem to be performing better than the other two

values and for the subsampling parameter, the value

0.75 seems to give the better averaged performance.

With regard to maximum tree depth, there does not

seem to be a significant difference between the

different values, however a maximum tree depth of 3

gave a lower performance in five of the nine

combinations of the two subsampling parameters.

Different values for the L

regularization

coefficient do not seem to influence the performance

of the model, however the value 0 for the number of

terminal nodes regularization coefficient slightly

improves the performance of the model. Moreover,

for lower number of trees, the shrinkage value of 0.05

performs the worst compared with other values,

however improves when the number of trees

increases. Different values for the two dropout

parameters do not seem to be significantly affecting

the performance, however increasing the number of

trees is beneficial and the performance seems to

converge between 150 and 200 trees. Following this,

the optimal validation performance obtained

corresponds to the model with 300 boosting

iterations, a maximum tree depth of 5, a shrinkage 𝛼

of 0.05, a subsampling rate 𝜗 of 0.75, a column

subsampling rate 𝜖 of 0.5, a coefficient 𝛽 of 0 (which

determines the influence of 𝑀



), a coefficient 𝜂 of 0.5

(which determines the influence of the L

regularization term), a dropout fraction 𝜃 of 0.25 and

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

a dropout probability 𝜆 also of 0.25. This

combination gives a validated Kappa of 0.396.

Training a model on the full training set using the

mentioned parameter gives a model predicting

99.48% of the training vectors of observations

correctly with just one vector of observations in each

class classified incorrectly. Moreover, testing this

model gives a testing Kappa of 0.473.

Comparing the approach without dropout with the

one with dropout, the first approach performed better

on the testing set than the corresponding dropout

version. Although several regularization parameters

are being considered, overfitting may still be present

in all the two models as the training performance are

relatively high compared to the testing ones. The

introduction of just two additional values in each of

the two dropout parameters presented another

computational challenge as this multiplied the

number of models to be trained in the grid search by

4. Apart from taking weeks to finish the dropout

model, the memory required to store the model

outputs needs also to be taken into consideration as

these grids need to be split and saved separately to

avoid out-of-memory problems. This is also a

limitation as more combinations can be considered to

better optimise model performance. Moreover, tree

dropout seems to decrease model performance for this

dataset and the slightly simpler Extreme Gradient

Boosting without dropout is preferred.

Model Comparisons and Variable Importance

Next, the testing performances for each model are

presented and discussed. Table 1 summarises several

binary performance metrics, including the accuracy,

the precision and sensitivity, together with the F

score and specificity.

The Gentle AdaBoost model clearly performed

best on the testing set, obtaining the highest

performance in all but one metric. According to the

accuracy metric, the second-best model is the GRF,

followed by the gradient boosted one. However, the

score depict a slightly different picture since,

according to this metric, the Extreme Gradient

Boosting model is the second-best model, followed

by GRF.

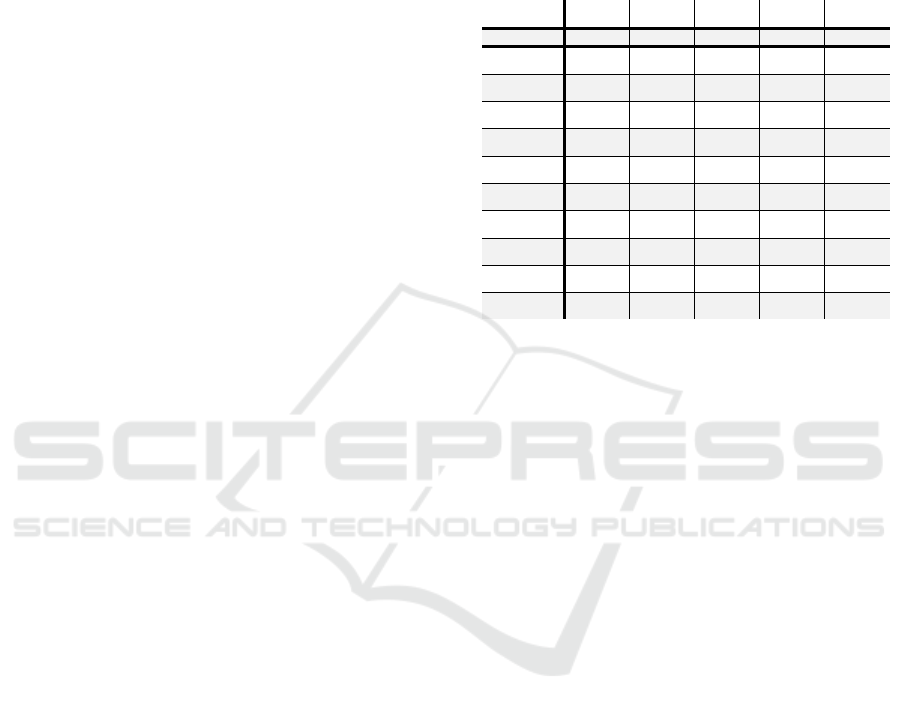
Table 1: Testing performance metrics for each model

considered for the offside dataset. RF is random forest, RRF

is regularized random forest, GRRF is guided regularized

random forest, GRF is guided random forest, DA is discrete

AdaBoost, RA is real AdaBoost, GA is Gentle AdaBoost,

GB is gradient boosting, EGB is extreme gradient boosting,

EGBD is extreme gradient boosting with dropout, A is

accuracy, P is precision, Se is sensitivity, Sp is specificity.

A P Se F

RF 0.853 0.630 0.531 0.576 0.928

RRF 0.818 0.515 0.531 0.523 0.884

GRRF 0.818 0.515 0.531 0.523 0.884

GRF 0.876 0.720 0.563 0.632 0.949

DA 0.800 0.477 0.656 0.553 0.833

RA 0.824 0.533 0.500 0.516 0.899

GA 0.906 0.808 0.656 0.724 0.964

GB 0.871 0.727 0.500 0.593 0.957

EGB 0.841 0.558 0.750 0.640 0.862

EGBD 0.818 0.512 0.688 0.587 0.848

The sensitivity metric, which can be considered as the

accuracy of a model on the positive class (i.e., the ratio

of the true offsides to all of the offsides), was the only

metric which Gentle AdaBoost did not perform the

best in. Extreme Gradient Boosting performed better in

terms of the sensitivity metric, with 75% of the testing

positive cases classified correctly.

With regards to the random forest and its

extensions, GRF improved the performance over the

standard random forest, however, the other two

extensions diminished the performance by 3.5%

accuracy. Moreover, for Extreme Gradient Boosting,

the dropout extension does not seem to improve on the

model without dropout as all the metrics indicate a

reduction in performance.

For variable importance, a type of ensemble is

proposed to consider all the models together. For both

random forests and boosting, the change in node purity

is utilised (Breiman, 2001), where the importance is

estimated as the average of the total decrease in node

impurities from the splits in the decision nodes over all

the trees in the ensemble. To estimate the importance

of each variable across all models, the importance

vectors of the 14 models are combined into a 379 × 14

matrix which is then scaled by dividing the importance

of each model by its standard deviation. Note that the

importance vectors are only scaled and not centred as

this will lead to negative importance for variables with

an importance of 0 (i.e., not used in the model).

Following this, the importance of each variable is

summed across all models, leading to a total variable

importance vector of size 379.

Can Ensemble Learning Approaches for Offside Detection Work?

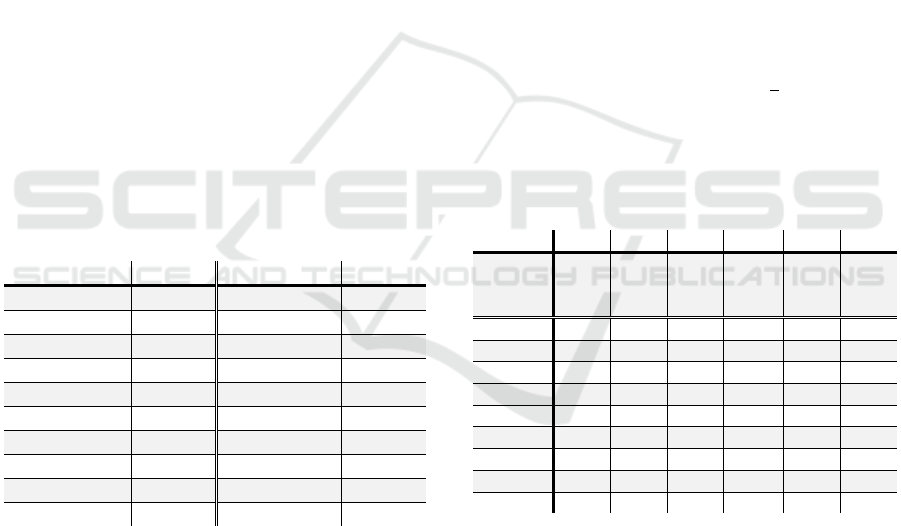
Table 2 shows the top 20 attributes of the total

variable importance vector. The most important

variable is GK.4.x, which corresponds to the x-

coordinate of the left foot of the goalkeeper, followed

by Team1.3.3.x, corresponding to the x-coordinate of

the left knee of the third leftmost player of the team

attacking from left to right in the image. The reason

for the importance of the GK.4.x attribute is

understandable and expected as the position of the

goalkeeper is crucial for offside judgement in the

majority of cases. The other variables are much less

important than GK.4.x, indicating that this is by far

the most dominant variable. The difference in

importance between the other attributes is

considerably less pronounced and all seem to provide

approximately equal contribution. One can also

notice that 8 out of the top 10 attributes correspond to

the x-coordinate, which is slightly expected as the

offside line is primarily dependant on the horizontal

position of the players. Moreover, another conclusion

from variable importance is the significance of the

coordinates of the players’ head and left shoulder and

left knee (body parts 0, 1 and 4), which are part of 9

out of the top 10 attributes.

Table 2: Twenty of the most important attributes calculated

by first considering the 14 models, then scaling and

summing the variable importance (Var. Imp.) for each

model. Refer to Section 4.1 for interpretation of attribute

abbreviation.

Attribute Var. Imp. Attribute Var. Imp.

46.15

16.655

Team1

26.32

Team2

16.41

Team1

21.35

Team2

16.285

Team2

20.455 Team2

16.26

20.282 Team2

15.12

Team2

20.281 Team2

14.95

Team1

20.058 GK

14.841

Team2

17.584 Team1

14.53

Team1

17.409 Team2

14.324

Team2

17.065 Team1

14.219

The scaled feature importance for each of the models

separately are given in the supplementary material.

The variable importance for the RF, RRF, GRRF and

GRF models do not seem to follow any particular

pattern, however the guided approaches to random

forests (GRRF and GRF) utilised the GK.4.x variable

more than the two other bagging approaches. For the

Discrete, Real and Gentle AdaBoost models, these

techniques seem to signify that the three leftmost

players (for both teams) in the dataset are the most

influential. This may be due to the images not

including all the players and thus focusing on the first

two to three players of each team. In the case of

Gentle AdaBoost, this model utilises the goalkeeper

coordinates the most. For Gradient Boosting,

Extreme Gradient Boosting, and Extreme Gradient

Boosting with dropout, these three techniques all

provide a different view on which attribute is the most

important. Despite this, the three models indicate that

the x-coordinate is more useful than the y-coordinate

of the players in the image. In the next section, a soft

majority approach shall be applied.

5 SOFT MAJORITY VOTING

In soft majority voting, the class predicted

probabilities from the 𝑑 different models are used to

obtain the final predicted probabilities. The latter are

directly obtained by taking the average of the former.

Formally, let 𝓅



be the class probability for model 𝑗

for a vector of observations predicted as class 𝑙. Then,

the predicted class 𝑦

(



)

produced by soft majority

voting is given by 𝑦

(



)

=argmax



(

,…,

)





∑

𝓅







Table 3: Testing set summary table for soft majority voting.

GA denotes Gentle AdaBoost, EGB denotes Extreme

Gradient Boosting, A is accuracy, K is Kappa, P is

precision, Se is sensitivity, Sp is specificity.

KP S

Sin

Model

Perform

0.906

(GA)

0.668

(GA)

0.808

(GA)

0.750

(EGB)

0.964

(GA)

0.724

(GA)

2 0.90

0.668 0.808 0.65

0.964 0.724

3 0.90

0.668 0.808 0.65

0.964 0.724

4 0.894 0.63

0.75

0.65

0.949 0.70

5 0.894 0.63

0.75

0.65

0.949 0.70

0.90

0.661 0.759 0.688 0.949 0.721

7 0.90

0.669 0.742 0.719 0.942 0.73

8 0.894 0.654 0.719 0.719 0.935 0.719

9 0.90

0.684 0.76

0.719 0.949 0.742

10 0.888 0.621 0.724 0.65

0.942 0.689

This approach is applied on the trained models from

Section 4 in this paper. The models are first ranked

depending on their Kappa performance on the testing

set and the top 𝑗 models are taken for 𝑗=2,…,10.

Table 3 shows the performance metrics for the soft

majority voting ensembles.

Comparing the underlying models to the soft

majority voting ones, there is a slight improvement in

the Kappa and F

metrics. The Kappa increased from

0.668 for the Gentle AdaBoost model to 0.689 for the

top 9 model while the F

increased from 0.724 for the

Gentle AdaBoost model to 0.742, also for the top 9

model. The accuracy does not change from the Gentle

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

AdaBoost model to the soft majority voting ensemble

models and the sensitivity decreased when compared

to the Extreme Gradient Boosting model. This shows

that the effect of soft majority voting on the predictive

abilities of the models is mixed, with some

improvement on certain performance criteria, and

slight deterioration in other cases.

6 CONCLUSIONS

In this study we have seen that ensemble learning,

proves to be an improvement over the manual

approach, with 9% of the decisions being erroneous,

as opposed to 17-33% (as stated in Section 2). Gentle

AdaBoost proves to be the most effective model

across most performance criteria, but Extreme

Gradient Boosting is the model with the best recall.

Furthermore, through variable importance analysis, it

was found that the x-coordinate of the goalkeeper’s

foot was by far the most important, followed by other

variables of similar contribution. When analysing the

10 most important variables, it was generally found

that the x-coordinate was more important than the y

coordinate of the body parts of the respective players.

Finally, soft majority voting managed to maintain the

same level of accuracy, improve Cohen’s Kappa and

the F

score, but deteriorated the sensitivity,

specificity and precision.

The ensemble approaches applied in this paper

have generally shown to fare comparably to other

papers discussed in the literature review in terms of

success. If one compares the performance of an

offside detection algorithm on the same dataset

(Panse and Mahabaleshwarkar, 2020), it has not been

successful in providing a better performance in terms

of precision (0.87), sensitivity (0.91) and F

score

(0.85). However, given the respectable performance

ensemble learning methods have shown in taking

good decisions on offside situations, it would be

worth exploring further whether ensemble learning

methods, or other machine learning methods in

general, can act as useful tools for this purpose, on

their own or in conjunction with offside detection

algorithms.

REFERENCES

Breiman, L. (2001). Random forests. In Machine learning,

45(1), 5–32. Springer.

Bridgeman, L., Volino, M., Guillemaut, J., Hilton, A.

(2019). Multiperson 3D pose estimation and tracking in

sports. In 2019 IEEE/CVF Conference on Computer

Vision and Pattern Recognition Workshops (CVPRW),

2487-2496. IEEE Xplore.

Catteeuw, P., Gilis, B., Wagemans, J., Helsen, W. (2010).

Offside decision making of assistant referees in the

English Premier League: Impact of physical and

perceptual-cognitive factors on match performance. In

Journal of Sports Sciences, 28(5), 471-481. Taylor &

Francis.

Chen, T., Guestrin C. (2016). XGBoost: A Scalable Tree

Boosting System. In Proceedings of the 22nd ACM

SIGKDD International Conference on Knowledge

Discovery and Data Mining, 785–794. ACM Digital

Library.

Click, C., Malohlava, M., Candel, A., Roark, H., Parmar,

V. (2022). Gradient Boosting Machine with H2O.

H2O.ai, 7

edition.

Deng, H. (2013). Guided Random Forest in the RRF

Package. In arXiv.

Deng, H., Runger, G. (2012). Feature selection via

regularized trees. In The 2012 International Joint

Conference on Neural Networks (IJCNN), 1-8. IEEE

Xplore.

Deng, H., Runger, G. (2013). Gene selection with guided

regularized random forest. In Pattern Recognition

46(12), 3483-3489. Science Direct.

D'Orazio, T., Leo, M., Spagnolo, P., Mazzeo, P. L., Mosca,

N., Nitti, M., Distante, A. (2009). An Investigation into

the Feasibility of Real-Time Soccer Offside Detection

from a Multiple Camera System. In IEEE Transactions

on Circuits and Systems for Video Technology, 19(12),

1804-1818. IEEE Xplore.

Freund, Y., Schapire, R. (1997). A decision-theoretic

generalization of online learning and an application to

boosting. In Journal of Computer and System Sciences,

55, 119–139. Science Direct.

Friedman, J. (2001). Greedy Function Approximation: A

Gradient Boosting Machine. In Annals of Statistics,

29(5), 1189-1232. IMS.

Friedman, J., Hastie, T., Tibshirani, R. (2000). Additive

logistic regression: a statistical view of boosting (with

discussion). In Annals of Statistics, 28(2) 337–407.

IMS.

Gilis, B., Helsen, W., Catteeuw, P., Wagemans, J. (2008).

Offside decisions by expert assistant referees in

association football: Perception and recall of spatial

positions in complex dynamic events. In Journal of

Experimental Psychology: Applied, 14(1), 21–35. APA.

Helsen, W., Gilis, B., Weston, M. (2006). Errors in judging

“offside” in association football: Test of the optical

error versus the perceptual flash-lag hypothesis.

Journal of Sports Sciences, 24(5), 521-528. https://doi.

org/10.1080/02640410500298065

Henderson, A., Lai, D., Allen, T. (2014). A Modern

Approach to Determine the Offside Law in

International Football. In Procedia Engineering, 72,

138-143. Science Direct.

Lopez, E., Jenkins, P. (2019). Offside Detection System

Using an Infrared Camera Tracking System. In World

Journal of Mechanics, 9(6), 163-176. Scientific

Research Publishing.

Can Ensemble Learning Approaches for Offside Detection Work?

Oudejans, R., Bakker, F., Verheijen, R., Gerrits, J.,

Steinbrückner, M., Beek, P. (2005). How position and

motion of expert assistant referees in soccer relate to the

quality of their offside judgements during actual match.

In International Journal of Sport Psychology (IJISP),

36, 3-21.

Panse, N., Mahabaleshwarkar, A. (2020). A Dataset

Methodology for Computer Vision based Offside

Detection in Soccer. In 3rd International Workshop on

Multimedia Content Analysis in Sports (MMSports’20),

19-26. ACM.

Patil, P.N., Salve, R.J., Pawar, K.R., Atre, P.M. (2018).

Offside Detection in the Game of Football Using

Contour Mapping. In International Journal of Research

in Engineering and Science (IJRES), 6(4), 66-69.

Siratanita, S., Chamnongthai, K., Muneyasu, M. (2021). A

Method of Football-Offside Detection Using Multiple

Cameras for an Automatic Linesman Assistance

System. In Wireless Personal Communications, 118,

1883–1905. Springer.

Uchida, I., Scott, A., Shishido, H., Kameda, Y. (2021).

Automated Offside Detection by Spatio-Temporal

Analysis of Football Videos. In Proceedings of the 4th

International Workshop on Multimedia Content

Analysis in Sports (MMSports'21), Association for

Computing Machinery, 17–24. ACM.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support