CASP: Computer Aided Specimen Placement for Robot-Based

Component Testing

Julian Hanke

, Matthias Stueben

, Christian Eym

uller

, Maximilian Enrico M

uller,

Alexander Poeppel

and Wolfgang Reif

Institute for Software and Systems Engineering, Augsburg University, Universit

atsstraße 6a, Augsburg, Germany

Keywords:

Industrial Robots, Destructive Component Testing, Robot Modeling, Robot-Based Testing.

Abstract:

The manufacturing industry is undergoing a signiﬁcant transformation in the context of Industry 4.0, and pro-

duction is shifting from mass products to individual products of batch size one. Moreover, the increasing

complexity of components, e.g., due to additive manufacturing, makes the testing setups of components even

more complex. Due to the low quantities of the components, it is not proﬁtable to build test benches for each

individual component to test a large number of different forces and torsions to ensure the needed product qual-

ity. In order to be able to test various components ﬂexibly through different motions, we developed a concept

to perform robot-based destructive component testing with industrial robots. The six degrees of freedom and

the broad working range of an industrial robot make it possible to apply forces and torques to different prod-

ucts. Since industrial robots cannot apply the same forces and torques in all axis positions, a position must

be calculated where the specimen can be tested. Therefore, we propose an approach for automatic specimen

placement, which includes a format to map applicable forces and torques of industrial robots. Furthermore,

we present an algorithmic approach to execute an automatic feasibility check for the required test motions and

an automatic specimen placement using an exemplary robot-based component testing bench.

1 INTRODUCTION

In the context of Industry 4.0, the manufacturing

industry is undergoing a signiﬁcant transformation.

Production is shifting from mass production to mass

customization (Lasi et al., 2014), where each compo-

nent is unique. In order to ensure the quality of these

unique products, it is also necessary to adapt the way

of testing such products. Additionally, the increasing

complexity of components, e.g., due to additive man-

ufacturing (Wong and Hernandez, 2012), also makes

the test setup of components more and more complex.

For example, components that have to withstand a

large variety of forces and torsions in later applica-

tions must also be able to withstand this wide variety

of forces and torsions on the test bench. Due to the

low quantities of the components, it is not proﬁtable to

build complex test benches for each component. Nev-

https://orcid.org/0000-0002-0692-1965

https://orcid.org/0009-0003-2292-0086

https://orcid.org/0009-0004-9468-3881

https://orcid.org/0000-0002-2737-3881

https://orcid.org/0000-0002-4086-0043

ertheless, it is essential to test these components to en-

sure the quality of each component. Therefore, a test

stand is required to test many components ﬂexibly.

Component testing is generally distinguished between

destructive (DT) and non-destructive component test-

ing (NDT). Destructive component testing is testing a

component until it irreversibly deforms. This deter-

mines a component or specimen’s material behavior

or performance under extreme conditions (e.g., strong

acid, high forces, high torques, or high temperatures).

Non-destructive testing aims to test components with-

out destroying them so they can continue to be used

for their intended purpose. NDT methods are, e.g., ra-

diographic, visual, or ultrasonic testing. The focus of

this work is on DT with mechanical and fracture test-

ing, a process in which high forces and torques are ap-

plied to components until they break (Howard Kuhn,

2000). Standard testing machines in custom rigs usu-

ally only cover simple movements and are specially

designed to meet the test requirements of a single

component. In order to be able to test various com-

ponents ﬂexibly through different movements, we de-

veloped a concept to perform robot-based destructive

component testing with industrial robots. The high

374

Hanke, J., Stueben, M., Eymüller, C., Müller, M., Poeppel, A. and Reif, W.

CASP: Computer Aided Specimen Placement for Robot-Based Component Testing.

DOI: 10.5220/0012155000003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 374-382

ISBN: 978-989-758-670-5; ISSN: 2184-2809

number of movement directions (six degrees of free-

dom) and the extensive working range of a six-axis

industrial robot make it possible to apply forces and

torques to different products. Industrial robots, how-

ever, cannot apply the same forces and torques in all

axis positions. Since destructive material testing of-

ten requires very high forces and torques, the axis po-

sition of the robots must be adjusted to achieve the

required torques or forces. Consequently, the position

of the component, where it can be tested with the help

of robots, must be calculated. We propose a com-

puter aided specimen placement approach (CASP)

for robot-based component testing to overcome the

abovementioned challenges. This paper makes the

following contribution in this area:

1. Introducing a mapping format for applicable

forces and torques of different poses for industrial

robots.

2. Automatic feasibility check to evaluate test mo-

tions depending on the required forces and

torques.

3. Constraint based automatic specimen placement

for an exemplary robot-based component testing

bench.

The presented paper is divided into six sections.

section 2 describes an example of a ﬂexible robot test

bench with two heavy-duty industrial robots. Sec-

tion 3 summarizes the current state of the art in robotic

component testing and provides an overview of used

technologies. The concept of a computer aided spec-

imen placement for robot-based component testing is

described in Section 4. In Section 5, we evaluated our

approach with the help of a selected use case. Sec-

tion 6 concludes with a brief outlook on further re-

search.

2 ROBOT-BASED TESTING

FACILITY SETUP

The central part of the testing facility consists of a

clamping ﬁeld

⃝ which is 7 m long and 2.5 m wide

(see Figure 1). This ﬁeld allows the ﬂexible place-

ment of components or specimens of different sizes

in any position. We use two KUKA KR1000 ti-

tan (KUKA AG, 2023a) robots

⃝ with one-ton load

capacity each to apply forces and torques to mounted

components. Both robots have a maximum reach of

(3202 mm and an overlapping workspace. In addition,

both robots are equipped with force-torque sensors to

measure the generated forces or torques and perform

force- or torque-controlled testing motions. This fa-

2 x KUKA

KR1000 Titan

Clamping Area

Figure 1: The facility for robot-based component testing

consists of a clamping area (7 m length x 2.5 m width) for

the ﬂexible positioning of testing components or specimen

and two KUKA KR1000 titan heavy-duty industrial robots.

cility was ﬁrst proposed and described in more detail

in our previous work (Hanke et al., ).

3 STATE OF THE ART

The area of using robots for component testing can

roughly be divided into two categories, namely robot-

assisted and robot-based. In the ﬁrst category, the

robot assumes merely a supporting role, and other

testing machines perform the mechanical component

tests. An example of this supporting role is the combi-

nation of a stationary test machine with a robot, e.g.,

in automated tensile testing, where the robot loads the

test specimen into the testing machine (ZwickRoell

GmbH & Co. KG, 2023b). The use of robots in the

area of medical technology represents a transition be-

tween robot-assisted and robot-based component test-

ing. Since robots offer the advantage of high move-

ment ﬂexibility and reproducible conditions, they are

often used to imitate human movements. Kebbach

et al. uses, e.g., an industrial robot to move and

load a knee endoprosthesis according to the motions

which are delivered by a musculoskeletal multi-body

model (Kebbach et al., 2019). The most common use

cases for robot-based destructive component testing

are test rig concepts in the form of hexapods, also

known as Stewart platforms. They consist of a sta-

tionary platform (base) and a mobile platform on top.

Both platforms are connected via six connecting struts

(legs), each varying lengths independently to allow

six degrees of freedom (6 DoFs). The test structures

are mounted between the ﬁxed base cell and the mov-

able platform on top to apply multi-axial loads. They

are also used in the medical technology domain men-

CASP: Computer Aided Specimen Placement for Robot-Based Component Testing

375

tioned earlier to mimic human motions, e.g., chew-

ing motions (Alemzadeh and Raabe, 2007). In ad-

dition, they are also suitable for performing fatigue

tests, static and dynamic stiffness tests, or damping

measurements of large structures or components. Var-

ious universities are conducting research on perform-

ing destructive component tests with these platforms,

e.g., the University of Cachan (France) (Nierenberger

et al., 2014) or the Hamburg University of Technology

(Germany) (Technische Universit

at Hamburg, 2022).

Stewart platforms are already expanding the range of

applications of classic testing machines. Classic test-

ing machines often consist of one or more linear test-

ing cylinders (ZwickRoell GmbH & Co. KG, 2023a)

and can apply either force or torque in one direc-

tion. In contrast, hexapods allow superimposed loads

since they can apply forces and torques simultane-

ously. However, due to its construction, the range of

motion is restricted, and in contrast to an industrial

robot, the forces and torques that can be achieved in

different positions are very similar, and the compo-

nent placement is not a signiﬁcant task in this domain.

A robotic domain for the placement of components

is, e.g., the object placement planning and optimiza-

tion for robot manipulation tasks. Lozano-Perez et

al. (Lozano-Perez et al., 1987) proposed a solution to

the grasp and motion planning problem in early times,

and following, this problem has been extensively re-

searched. Contributions in this area address three

challenges according to Haustein et al. (Haustein

et al., 2019) or Harada et al. (Harada et al., 2014):

1. To place a component, the object’s physical prop-

erties and the environment must be considered.

2. The robot must be able to reach the component.

3. Human preferences, stability, and clearance from

other obstacles must be determined.

These challenges are transferable to robot-based com-

ponent testing, especially challenges 1 and 2, which

play an essential role in automated component place-

ment. Physical properties are given by the component

itself or by the clamping ﬁxture for the component.

The environment is deﬁned, e.g., by the clamping area

where the component will be mounted. Moreover, the

robot must not only reach the component but also ap-

ply the required forces and torques at this position,

which is a further challenge to the above mentioned

challenges for robot manipulation tasks. Human pref-

erences, stability, and clearance from other obstacles

need to be considered, but in our use case, they play a

subordinate role. In addition to the challenges above,

different technologies for calculating and simulating

the whole component test are needed. e.g., to cal-

culate a collision-free path planning for the starting

point of a component test or to determine the length

of a testing motion that depends on physical material

properties. The open-source Robot Operating Sys-

tem (ROS) offers software libraries and tools to build

such a robot application (Quigley, 2009). Combined

with MoveIt, it enables motion planning and calculat-

ing inverse kinematics (Coleman et al., 2014). Actual

motions can be visualized with rviz, a 3D visualizer

for ROS, or with NVIDIA Isaac Sim. Isaac Sim is

a photorealistic robotics simulation application tool

that offers physically-accurate virtual environments to

build and test complex robot applications (NVIDIA

Corperation, 2022). The Isaac SDK & ROS/ROS2

interface provides seamless connectivity and interop-

erability to applications built in ROS or ROS2. In

the future, the framework ORBIT will extend rigid

and soft body simulation (Mittal et al., 2023). This

is needed to simulate, e.g., the robot movements un-

der load depending on the material characteristics. To

solve the problem of specimen placement for robot-

based component testing, we introduced a ﬁrst ap-

proach by using mixed reality to help a worker place

the component manually (Filipenko et al., 2020). Ex-

tending and automating this process using the tech-

nologies mentioned above, we are the ﬁrst to present a

novel approach for Computer Aided Specimen Place-

ment for robot-based component testing to the best of

our knowledge.

4 CONCEPT

To cover the full spectrum of Computer Aided Spec-

imen Placement (CASP) for robot-based component

testing, we began by modeling testing motions, which

deﬁne the required forces and torques with their cor-

responding directions and orientations. In the follow-

ing subsection, we describe how the Jacobian matrix

can calculate the static force torque model. Next, the

concept for representing the force torque model and

how we appropriately store the calculated forces and

torques are presented. The last subsection describes

how the presented concepts are used to calculate an

appropriate component placement.

4.1 Modeling Testing Motions for

Robot-Based Component Testing

In our previous work (Hanke et al., ), we used test-

ing motions to deﬁne which forces or torques will

be applied to a component or specimen. We distin-

guish between multiple testing motions, deﬁned by

load paths, which can be modeled as illustrated in Fig-

ure 2. Here, a test motion consists of one or more

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

376

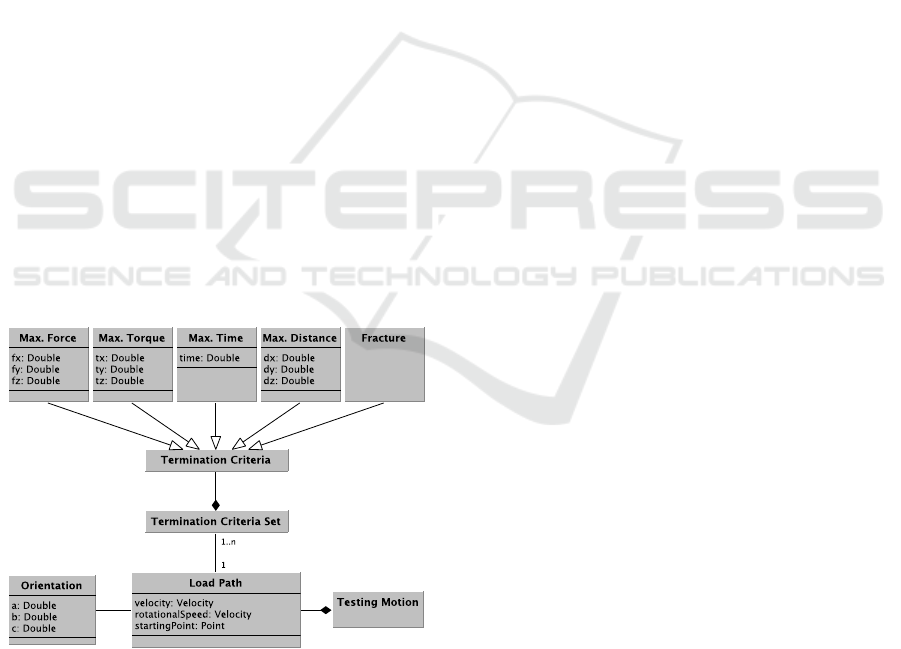
load paths. This enables the deﬁnition of superim-

posed load paths (e.g., force and torque simultaneous)

and classic loads (e.g., only a force). Each load path

includes one or more termination criteria set to en-

able ﬂexibility in the termination of the load paths.

These sets include one or more termination criteria.

In this way, different termination criteria can be com-

bined arbitrarily. All termination conditions within a

set must be fulﬁlled simultaneously ( conjuctive op-

erator) for the set to be fulﬁlled. Termination criteria

sets are linked disjunctive, meaning that the load path

terminates once one of its termination criteria sets is

fulﬁlled. A force criterion, e.g., can be combined

within a set with a time criterion to specify how long

the force should be applied. Furthermore, the lengths

of the load paths can be deﬁned in the respective di-

rection. These can be determined in advance with the

help of a Finite Element Analysis (FEM) simulation.

The termination criterion fracture can terminate the

motion when the specimen breaks. The parameters of

this termination criterion determine how breaks are

detected, e.g., by a rapid force drop. Motions can

be represented by a velocity, e.g., rotational speed for

circular movements, in one direction with a given ori-

entation. So every load path needs, in addition to its

speed, a speciﬁed orientation a, b, c in a known coor-

dinate system, e.g., in our case, in the base coordinate

system of the robot. Each testing motion starts at a

speciﬁc starting point for the robot. Components or

specimens are usually installed in clamping ﬁxtures

for testing. These clamping devices usually specify

the height z of the starting point for the load path and

Figure 2: Representation of testing motions. Each testing

motion is a composition of one or more load paths that in-

clude one or more termination criteria, which deﬁne, e.g.,

the range of motion or the maximum forces and torques to

be applied to the component. Each test motion starts at a

particular starting point for the robot (which has to be cal-

culated) with a predeﬁned orientation a, b, c and a velocity

or a rotational speed.

the robot’s orientation with z as the robot’s impact di-

rection. The robot starting point’s missing cartesian

position x, y must be calculated. Since the forces that

a robot can apply are highly dependent on its pose, an

appropriate choice of x, y, can be critical for the feasi-

bility of a testing motion. For this calculation, a rep-

resentation of the robots’ possible forces and torques

is needed, which is covered in the next section.

4.2 Calculation of Static Force Analysis

Model

Using industrial robots for component testing adds

complexity to the process of positioning the compo-

nent for testing. It is essential to consider the object’s

reachability when placing it for testing. Although a

robot is generally more ﬂexible than a linear actua-

tor, it may not be able to reach every position on the

clamping surface. Even when the robot can reach a

position, it may not be the best option as the maxi-

mum force cannot be achieved in every position, such

as when the robot arm is fully extended.

To determine the best starting pose for the robot,

we extended our model, which we ﬁrst introduced

in (Filipenko et al., 2020), that analyzes the static

force using the robot’s Jacobian matrix to estimate the

maximum forces that can be applied. The static cal-

culations aim to establish the connection between the

forces generated by the end effector and the torques

applied to the joints, assuming the robot is in an equi-

librium conﬁguration suitable for component testing.

Let γ

denote the vector of generalized end-effector

forces with γ



, µ



. Here, f

are the 3-

dimensional force contributions, and µ

are the 3-

dimensional torque contributions. The relationship

between the end-effector forces γ

and the vector τ of

joint torques is, according to (Siciliano et al., 2010),

determined by the transpose of the geometric Jaco-

bian J, which is subject to the manipulator’s joint con-

ﬁguration q.

τ = J

(q)γ

(1)

Hence, the maximum component testing force γ

max

the end-effector can be calculated using the inverted

transpose of the geometric Jacobian J and the avail-

able joint torques τ

avail

. To calculate the available

joint torques, the joint space dynamic model of the

end-effector (Siciliano et al., 2010) is consulted:

B(q) ¨q +C(q, ˙q) ˙q +g(q) = τ − J

(q)γ

(2)

B(q) is a 6 × 6 symmetric, positive-deﬁnite matrix

representing the joint space inertia matrix. C(q, ˙q) is a

6 × 6 matrix such that C(q, ˙q) ˙q is the vector of Corio-

lis and centrifugal terms. g(q) is the vector of gravity

CASP: Computer Aided Specimen Placement for Robot-Based Component Testing

377

terms. As component testing is performed at very low

velocities and accelerations, e.g., 5 mm/min for our

chosen use-case of a steel specimen(ISO, 2019), we

assume that both ˙q and ¨q are equal to 0. Thus, we can

simplify the joint space dynamic model and rewrite

Equation 2 as follows:

(q)γ

= τ − g(q) (3)

To calculate the highest possible end-effector forces

denoted by γ

,max

, with a speciﬁed joint conﬁguration

q and a maximum joint torque τ

max

, the following for-

mula is used:

max



J(q)



−1

(τ

max

− g(q)) (4)

In order to exclude singularity positions, a check

of det(J(q)) ̸= 0 was added to the model calcula-

tion. Otherwise, it cannot be solved unambiguously,

and wrong values will be calculated. Furthermore,

depending on the speciﬁc robot pose, the gravity

term either increases or decreases the maximum end-

effector forces (e. g., when pushing downwards, the

robot’s weight will increase the end-effector forces).

This equation (4) estimates the highest reachable end-

effector forces and torques. The dynamics are cal-

culated using an internal library function from the

KUKA.Load (KUKA AG, 2023b) software. As a re-

sult, we are able to increase the component testing

forces well above 10 kN, which is beyond the robot’s

payload class. In order to be able to use the calcula-

tion for automatic specimen placement, the following

section describes a representation format to store the

calculation.

4.3 Representation of the Force Torque

Model

When attempting to ﬁnd a suitable placement for the

specimen, the maximum forces and torques the robot

can exert in a given pose need to be known. Calculat-

ing these values online for each considered position

is computationally intensive and takes a signiﬁcant

amount of time, which is unacceptable in practice. In

order to reduce the required time, we calculate these

values ofﬂine for samples evenly spread throughout

the workspace and store the results in a database. This

database is then used to approximate the values on-

line.

The force-torque model stores the sampled end-

effector poses and the maximum forces and torques

the robot can exert in these. The same cartesian posi-

tion can be reached with different joint positions, and

the mapping from cartesian poses to possible forces

and torques is, therefore, not unique. Instead, it de-

pends on the speciﬁc solution of the inverse kinemat-

ics solver used. Therefore, the chosen joint positions

to reach the end-effector pose are also stored. This

means that, in most cases, multiple entries of possible

joint positions and the applicable forces/torques are

stored for each cartesian pose. For most poses, a typ-

ical six-axis industrial manipulator has eight different

solutions to the inverse kinematics (Siciliano et al.,

2010). The amount of sampled cartesian poses that

can be stored and searched efﬁciently are already a

limiting factor of the model, thus storing eight differ-

ent solutions per sample is not advisable. While the

problem of different inverse kinematics solutions can

not be ignored, and it is recommended to reduce the

amount of data by limiting the considered cartesian

poses and joint positions as much as possible for the

given application. In our case study, for example, we

have restricted the cartesian poses to the space above

the clamping area and limited the joint positions to

exclude overhead and elbow-down positions for the

majority of cases. The amount of joint positions to be

stored has thus been reduced considerably. The exact

bounds to choose, of course, depend heavily on the

application and the employed robot. In our applica-

tion, the cartesian workspace has a size of 7× 3×3 m.

Bounds on joint positions are most relevant for the

robot’s ﬁrst (base) and third (elbow) joints in our use

case. These are both limited to the range of 120°.

Wider bounds are used for the other joints.

Mathematically, we describe our force-torque

model by two functions. We refer to the set of all

stored joint positions as Q, and the set of all stored

cartesian end-effectors poses as E. The function p

maps a cartesian pose e to the set of joint positions

that are stored in Q and brings the end-effector clos-

est to e:

p(e) = {q ∈ Q|NN(e, E) = FK(q)} (5)

Here, NN(e, E) stands for the nearest neighbour of

the cartesian pose e that is contained in E. FK is the

forward kinematics function that calculates the end

effector pose for each of the given joint positions q.

Since the function p is based on the nearest neighbor

search, p(e) is never empty (assuming that the poses

in E and the joint positions in Q are not empty and

correspond to each other). However, p(e) can contain

multiple joint positions.

The second function, m(q), maps joint positions

to the maximum forces and torques:

m(q) =



(q), f

−

(q), t

−

(q)



= ( f

, f

), f

−

= ( f

−

, f

−

, f

−

)

= (t

, t

), t

−

= (t

−

, t

−

, t

−

)

(6)

Positive and negative forces ( f

and f

−

) and

torques (t

and t

−

) are considered separately since

they are not necessarily of equal magnitude. For

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

378

example, pushing and pulling is not always possi-

ble with the same amount of force. The indices

x, y, z, a, b, c indicate the respective direction of the

force or torque relative to the global base coordinate

system.

In practice, we store the data of the force torque

model in a relational database to enable efﬁcient stor-

age and querying. The function m(q) can then be

computed as a simple lookup operation, given that the

values of q are the result of the calculation of p(e) and

are thus directly contained in the database. The com-

putation of p(e) is slightly more complex due to the

nearest neighbor search required. Otherwise, it corre-

sponds to a simple database query as well. The for-

ward kinematics FK(q) are not computed directly but

given by the association of poses and joint positions

in the database.

The following Section describes the calculation of

specimen poses and feasibility checks.

4.4 Specimen Placement and Feasibility

Check

The goal of the specimen placement is to ﬁnd a suit-

able position for the specimen to be tested, given

a speciﬁcation of the testing motion and the force-

torque model of the robot used. The orientation

(a, b, c) of the specimen is ﬁxed by the speciﬁcation of

the testing motion. The height z is determined by the

physical constraints of the clamping mechanism to a

single value. Hence, the specimen placement proce-

dure needs to determine the robot’s starting position

(x, y, z) and the resulting component placement point.

Besides the placement of the specimen, and thus

the end-effector pose, the joint positions used to reach

this end-effector pose also need to be determined be-

cause not all solutions of the inverse kinematics might

be able to create the required forces and torques.

Hence, the vector of joint positions q is an additional

output of the algorithm.

The following pseudocode gives a basic overview

of our procedure to ﬁnd feasible poses to execute the

predeﬁned testing motion.

F ← f easibleStartingPoints(E, Q)

for (e, q) ∈ F do

if f easibilityCheck(e, q) then

return (e, q)

end if

end for

The procedure f easibleStartingPoints(E, Q) re-

turns all poses and the associated joint positions

from the stored poses E and joint positions Q,

where the robot can produce the forces and torques

( f

, f

, t

) speciﬁed at the start of the test-

ing motion:

∈ [ f

−

, f

], f

∈ [ f

−

, f

], f

∈ [ f

−

, f

]

∈ [t

−

, t

], t

∈ [t

−

, t

], t

∈ [t

−

, t

]

(7)

The values of f

, f

−

, t

, and t

−

are found using the

force-torque model as described in Section 4.3. Can-

didates for the starting poses are found by query-

ing the database of the force-torque model with the

required orientation and height (z, a, b, c). In case

z is speciﬁed as an interval, a range query can ef-

ﬁciently retrieve all database entries within the re-

quested range.

In this way, specimen poses, and joint positions

suitable for the beginning of the testing motion are

found. However, ensuring that the robot can pro-

duce enough force at the beginning of the motion is

not enough since both the robot’s position and the

requirements of the load path can change through-

out a testing motion. Therefore we use a feasibil-

ity check (referred to as f easibilityCheck(e, q) for a

cartesian starting pose e and corresponding joint po-

sitions q in the above algorithm) over the entire test-

ing motion to ﬁnd a feasible position. The proce-

dure f easibilityCheck incrementally iterates through

the given testing motion and checks the requirements

along the entire testing motions with a given step size.

For a predicted pose along the testing motion e

, all

joint positions from p(e

) are selected close enough

to the joint position of the previous pose in the mo-

tion. The remaining joint positions are then checked

using m(q) to determine whether they can fulﬁll the

force and torque requirements of the testing motion.

If a starting pair (e, q) passes the feasibility check

for each testing motion, it is returned, and the proce-

dure terminates. Subsequently, the component place-

ment point can be derived from the start point of the

robot, e.g., with the help of a cad model. Next, the

physical specimen placement occurs, and the robot

can execute the testing motions.

In case no feasible solution can be found, three

fallback strategies are suggested to the user that, in

our practical experience, can often lead to still ﬁnd-

ing a suitable solution. They all involve manually ad-

justing some parts of the physical setup (usually the

clamping mechanism for the specimen) and rerunning

the specimen placement procedure with the new pa-

rameters. The three fallback strategies that we suggest

are as follows:

1. Adjust Height Requirements: Different mount-

ing strategies for the specimen can lead to differ-

ent speciﬁcations of the parameter z, i.e., the spec-

imen’s required height. Changing this value often

CASP: Computer Aided Specimen Placement for Robot-Based Component Testing

379

creates new solutions for specimen placement.

2. Change Orientation by Right Angles: In prac-

tice, due to the structure of typical clamping

mechanisms, it is often easy to change to orien-

tation of the specimen by multiples of 90°. This

can be a relatively simple way to ﬁnd a usable pa-

rameter set.

3. Manual Parameter Adjustment: The last fall-

back strategy is manually picking a completely

different orientation, e.g., using a different clamp-

ing ﬁxture for the specimen.

Even with simple component tests, very high

forces or torques are often required, which industrial

robots cannot apply in all positions. To provide guid-

ance in ﬁnding a proper orientation for the third fall-

back strategy, we provide a visual representation for

a chosen orientation and height z of the force-torque

model stored in the database in the Form of a two-

dimensional heatmap (see Figure 3). On the right side

of the graphic, the legend shows the forces the robot

can apply in kN. The scale goes from 0 (dark pur-

ple) up to 35 kN (bright yellow). The distribution of

the forces is approximately circular around the robot

as a center point. The less the robot is stretched, the

more force it can exert. This indicates that axis 1 is

not the limiting factor in this type of testing motion.

The falloff on the polar longitudinal axis indicates the

inﬂuence of axes 2 and 3. At the outer circle, the

force breaks off very quickly because the robot can

no longer reach these points, and therefore, the force

is zero.

5 CASE STUDY

We evaluated our approach in our robot-based test-

ing facility described in section 2. To evaluate our

concept, we selected a tensile test, a classic mate-

rial testing case study (see Figure 4). In standardized

Kuka

KR 1000

Robot Reach in 10 dm

Force in kN

Figure 3: Visualization of a plane with the selected height

z = 130 cm of applicable pulling forces in z-direction for

the orientation of a = −90

◦

, b = 0

◦

, c = 180

◦

in robot world

coordinates. The forces are given in kN, and the reach of the

robot in the middle is given in dm.

tensile tests, the specimen is loaded in one direction

until it breaks to test material characteristics. Steel

was chosen as the material for the tensile specimen,

which needs a maximum force of up to 25 kN until it

breaks. The lower clamping jaw for the specimen de-

termines the options to mount the chosen test setup on

our clamping area. To determine the starting height

z = 130 cm for the component test, we can measure

the height of the end effector as a sum of the lower

clamping jaw plus the length of the specimen plus

the length of the end effector with the f/t torque sen-

sor mounted combined with the upper clamping jaw

(yellow part in Figure 4). Since the clamping places

the specimen perpendicular to the clamping ﬁeld and

the test motion points in the direction of the clamped

specimen, we obtain a = −90

◦

, b = 0

◦

, c = 180

◦

for

the load path orientation (see the green force direction

arrow in Figure 4) with a maximum force of −25 kN

for f z as it is a pull motion in the robot base coor-

dinate system. The last step is determining the dis-

tance the robot needs to travel to ensure it can build

up the force of 25 kN over the entire distance. This

Height

Lower Clamping

Jaw

Steel Specimen

Upper Clamping Jaw

with F/T Sensor

Force Direction

(A, B, C)

Component

Placement Point

Robot Starting

Point (x, y, z)

Figure 4: Tensile test setup: Attachment of the clamping

jaws with clamped tensile specimen between the clamping

ﬁeld (bottom) and the robot end effector (top), consisting of

the f/t sensor and the upper clamping jaw. The green given

force direction indicates in which direction the force is to

be applied to the specimen by the robot.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

380

can be done, for example, with the help of a FEM

simulation. In our example, the distance was circa

10 cm. The test motion can be entered into our pro-

gram with the help of a small UI. We have carried

out our feasibility check and the resulting component

placement with this data. Our algorithm has selected

the position x = 50 cm, y = 156 cm, and z = 130 cm

for the robot starting point, corresponding to the po-

sition shown in Figure 4. This also denotes that the

robot can apply the required forces for our chosen use

case. Finally, we performed the actual component test

to ensure that the robot could apply the forces for the

given testing motion and the calculated starting pose,

which includes the pose E and joint positions Q. For

further validation of our force model, we performed

an experimental test at different positions with differ-

ent heights. The calculated values corresponded to

the experimentally determined values with a margin

of ± 300 N. However, these are negligible unless us-

ing the test bench at its ultimate limits of the forces or

torques. In order to be able to state how exactly the

values are deviating, more research is planned, which

will be described in more detail in the next section.

6 CONCLUSION

One challenge of robot-based component testing is

specimen placement since industrial robots cannot

achieve all forces or torques in every position. Our

CASP (Computer Aided Specimen Placement) ap-

proach for robot-based component testing solves this

challenge by calculating a position for the specimen

placement where the robots can test it. We ﬁrst

extended our developed model for testing motions,

which includes load paths consisting of forces and

torques, the corresponding directions, and the start-

ing point to be determined by the testing motion. A

further advantage of this model is the representation

of superimposed loads that only a few standard test

rigs can muster. Moreover, we have developed a

description and storage format for robot forces and

torques depending on the robot’s orientation and po-

sition. With the help of the combination of these two

developments, we have presented an algorithm that

performs an automatic feasibility check for the re-

quired test motions and calculates the automatic spec-

imen placement. In our case study, we brieﬂy ex-

plained our testing facility and evaluated the compo-

nent placement by choosing a classical use case for

material testing (standardized tensile tests). Our ap-

proach automatically calculated a placement for the

test specimen of this use case, and we successfully

performed the actual test afterward. In addition, we

conducted an experimental comparison of our force

model and identiﬁed slight deviations between our

model and the actual applicable forces. An initial as-

sumption leading to this deviation is the impact of the

mounted periphery, e.g., the weight of the end effec-

tor or the cable tow, as this is currently not included

in our calculation model. In further research, we will

conduct more experimental comparisons to determine

the deviations and thus better deﬁne the boundaries

more precisely. Finally, we are investigating how

the computer aided specimen placement can be sim-

ulated, e.g., for collision detection and extended for

multi-robot component tests. For this purpose, we are

already simulating the motion to the calculated start-

ing point of the test motion with the help of ROS2,

MoveIt, and NVIDIA Isaac Sim (see Figure 1 for our

Isaac Sim Model). We also want to combine the robot

motion simulation with a physical simulation of the

specimen with the framework ORBIT to simulate the

entire test sequence later on.

ACKNOWLEDGEMENTS

This work partly presents the results of the project

WiR Augsburg which was funded by the German Fed-

eral Ministry of Education and Research (BMBF) and

the Bavarian Government.

REFERENCES

(2019). Metallic materials, Tensile testing, Part 1: Method

of test at room temperature. Standard DIN EN 6892-

1:2019, DIN Deutsches Institut f

ur Normung e. V.,

Berlin, DE.

Alemzadeh, K. and Raabe, D. (2007). Prototyping artiﬁ-

cial jaws for the bristol dento-munch robo-simulator;

’a parallel robot to test dental components and mate-

rials’. In 2007 29th Annual International Conference

of the IEEE Engineering in Medicine and Biology So-

ciety, pages 1453–1456.

Coleman, D., Sucan, I., Chitta, S., and Correll, N. (2014).

Reducing the Barrier to Entry of Complex Robotic

Software: a MoveIt! Case Study.

Filipenko, M., Poeppel, A., Hoffmann, A., Reif, W., Mon-

den, A., and Sause, M. (2020). Virtual commission-

ing with mixed reality for next-generation robot-based

mechanical component testing. In ISR 2020; 52th In-

ternational Symposium on Robotics, pages 1–6.

Hanke, J., Eym

uller, C., Reichmann, J., Trauth, A., Sause,

M., and Reif, W. Software-deﬁned testing facility

for component testing with industrial robots. ETFA,

September 06-09, 2022, Stuttgart, to be published.

Harada, K., Tsuji, T., Nagata, K., Yamanobe, N., and Onda,

H. (2014). Validating an object placement planner

CASP: Computer Aided Specimen Placement for Robot-Based Component Testing

381

for robotic pick-and-place tasks. Robotics and Au-

tonomous Systems, 62(10):1463–1477.

Haustein, J. A., Hang, K., Stork, J., and Kragic, D. (2019).

Object placement planning and optimization for robot

manipulators. In 2019 IEEE/RSJ International Con-

ference on Intelligent Robots and Systems (IROS),

pages 7417–7424. IEEE.

Howard Kuhn, D. M. (2000). ASM Handbook: Volume 8:

Mechanical Testing and Evaluation. Asm Handbook.

ASM International, 10 edition.

Kebbach, M., Grawe, R., Geier, A., Winter, E.,

Bergschmidt, P., Kluess, D., Lima, D., Woernle, C.,

and Bader, R. (2019). Effect of surgical parameters on

the biomechanical behaviour of bicondylar total knee

endoprostheses - a robot-assisted test method based on

a musculoskeletal model. Scientiﬁc Reports, 9:1–11.

KUKA AG (2023a). KR 1000 titan.

https://www.kuka.com/en-de/products/robot-

systems/industrial-robots/kr-1000-titan (accessed

on: 16.05.2023).

KUKA AG (2023b). KUKA Robot Selector.

https://www.kuka.com/en-de/products/robot-

systems/software/cloud-software/kuka-robot-selector

(accessed on 09.05.2023).

Lasi, H., Fettke, P., Kemper, H.-G., Feld, T., and Hoffmann,

M. (2014). Industry 4.0. Business & information sys-

tems engineering, 6(4):239–242.

Lozano-Perez, T., Jones, J., Mazer, E., O’Donnell, P., Grim-

son, W., Tournassoud, P., and Lanusse, A. (1987).

Handey: A robot system that recognizes, plans, and

manipulates. In Proceedings. 1987 IEEE Interna-

tional Conference on Robotics and Automation, vol-

ume 4, pages 843–849.

Mittal, M., Yu, C., Yu, Q., Liu, J., Rudin, N., Hoeller,

D., Yuan, J. L., Tehrani, P. P., Singh, R., Guo, Y.,

Mazhar, H., Mandlekar, A., Babich, B., State, G., Hut-

ter, M., and Garg, A. (2023). Orbit: A uniﬁed simula-

tion framework for interactive robot learning environ-

ments.

Nierenberger, M., Poncelet, M., Pattofatto, S., Hamouche,

A., Raka, B., and Virely, J. (2014). Multiaxial Testing

of Materials Using a Stewart Platform: Case Study of

the Nooru-Mohamed Test. Experimental Techniques,

38(2):74–83.

NVIDIA Corperation (2022). NVIDIA Isaac SDK.

https://developer.nvidia.com/isaac-sdk (accessed on

14.03.2023).

Quigley, M. (2009). ROS: an open-source Robot Operating

System. In ICRA 2009.

Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G.

(2010). Robotics: Modelling, Planning and Control.

Technische Universit

at Hamburg

(2022). Hexapod Pr

ufanlage.

https://www.tuhh.de/hexapod/startseite.html (ac-

cessed on 14.03.2023).

Wong, K. V. and Hernandez, A. (2012). A review of addi-

tive manufacturing. International scholarly research

notices, 2012.

ZwickRoell GmbH & Co. KG (2023a).

uﬂabor f

ur große Bauteilpr

ufungen.

https://www.zwickroell.com/de/services/prueﬂabor-

werkstoffpruefung-bauteilpruefung/ (accessed on

21.05.2023).

ZwickRoell GmbH & Co. KG (2023b).

RoboTest R Robotic Testing System.

https://www.zwickroell.com/products/automated-

testing-systems/robotest-r-robotic-testing-system/

(accessed on: 16.05.2023).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

382