∆ SFL: (Decoupled Server Federated Learning) to Utilize DLG Attacks

in Federated Learning by Decoupling the Server

Sudipta Paul

and Vicenc¸ Torra

Department of Computing Science, Ume

a University, Sweden

Keywords:

Federated Learning, Privacy, Attack, Data Poisoning.

Abstract:

Federated Learning or FL is the orchestration of centrally connected devices where a pre-trained machine

learning model is sent to the devices and the devices train the machine learning model with their own data,

individually. Though the data is not being stored in a central database the framework is still prone to data

leakage or privacy breach. There are several different privacy attacks on FL such as, membership inference

attack, gradient inversion attack, data poisoning attack, backdoor attack, deep learning from gradients attack

(DLG). So far different technologies such as differential privacy, secure multi party computation, homomor-

phic encryption, k-anonymity etc. have been used to tackle the privacy breach. Nevertheless, there is very

little exploration on the privacy by design approach and the analysis of the underlying network structure of

the seemingly unrelated FL network. Here we are proposing the ∆SFL framework, where the server is being

decoupled into server and an analyst. Also, in the learning process, ∆SFL will learn the spatio information

from the community detection, and then from DLG attack. Using the knowledge from both the algorithms,

∆SFL will improve itself. We experimented on three different datasets (geolife trajectory, cora, citeseer) with

satisfactory results.

1 INTRODUCTION

In federated learning, an orchestration of edge devices

train machine learning models independently with the

data they have and send the updated gradients after

training to the central cloud. There, at the central

cloud, all the gradients get collected from the user de-

vices. Then an average of the gradients is calculated

by the central server and then the machine learning

model is updated centrally and it does not store the

gradients afterwards. In this way, the data at the users’

devices does not need to be uploaded to a centralized

dataset. In addition, this approach allows to use a

huge amount of data. Nevertheless, it has been shown

that this FL system is also prone to some vicious pri-

vacy attacks such as inverted gradient reconstruction

attack (Geiping et al., 2020), model reconstruction at-

tack (Krishna et al., 2019; Luo et al., 2021), backdoor

attack (Xie et al., 2019), poisoning attack (Cao et al.,

2019) etc. Also, there is a limit for the number of

devices to be used due to the lack of computational

resources in real-life FL setup. One solution is to an-

alyze the internal network structure of the data when

https://orcid.org/0000-0001-6561-997X

https://orcid.org/0000-0002-0368-8037

the gradients are updated. Acknowledging all that,

an open question has been asked in (Kairouz et al.,

2021), which is - “Is studying network structure suf-

ﬁcient to provide defense against data poisioning and

privacy preservation in the FL setup?”.

All of these attacks intend to point out the vul-

nerabilities and faults in federated learning. This per-

mits the development of new solutions with stronger

privacy guarantees. Motivated by these types of at-

tacks, in this paper we propose a novel FL system

which depends on the analysis of the spatio structure

of the seemingly disconnected data from the users.

The system decouples the computation of the model

from users’ gradients to avoid data reconstruction by

the server. More precisely, our system includes a data

analyst who receives the gradients from clients, anal-

yses their structure and provides estimated data from

a randomised version of the gradient structure. Then,

a cloud central server updates the model using this es-

timated data, and send the model to the clients. Here

we use the DLG attack (deep learning from gradients)

(Zhu et al., 2019) to estimate the data. In this attack

with the help of distance between gradients, dummy

data and labels one can infer (highly accurate) data.

As stated above, these data are used by the server to

Paul, S. and Torra, V.

T SFL: (Decoupled Server Federated Learning) to Utilize DLG Attacks in Federated Learning by Decoupling the Server.

DOI: 10.5220/0012150700003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 577-584

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

577

update the model. The analyst and the server are ex-

pected to be independent and that do not collide. We

call the system, ∆SFL for decoupled server FL.

The main contributions of this work are:

• We propose a new privacy-preserving updating

method for the FL framework where, from the

DLG attack, we are learning and updating the cen-

tral model. To our best knowledge, this is the ﬁrst

of its kind.

• We propose to decouple the server into two parts,

i.e. the server and the analyst, where the honest

but curious analyst has the hold of the gradients

and the server has the hold of the model parame-

ters. Also, both of them do not have any knowl-

edge of each other’s hold of information.

• The time to converge of the machine learning

model in the proposed system is similar to that of

in the FedAvg setup

1.1 Privacy Setup in ∆SFL

To understand the privacy setup of this framework,

we need some concepts and deﬁnitions. They are re-

viewed in this section.

Community Detection Algorithms: They build a

partition of a graph. The algorithms we use are:

a) Louvain algorithm (Blondel et al., 2008), b) Fast

Greedy (Clauset et al., 2004), c) Leading Eigen (New-

man, 2006), d) Edge Betweenness (Girvan and New-

man, 2002). Among these algorithms, Louvain and

Fast Greedy are similar in terms of speed and num-

ber of communities detected. The Edge Betweenness

algorithm is the slowest among these four.

Modularity: It is a beneﬁt function to study the

graph structure where it reﬂects the concentration of

edges within the “communities” with respect to the

random distributions of edges between all nodes re-

gardless of the communities. Modularity is usually

denoted by Q and deﬁned as follows:

Q = (Number of edges within communities)

− (expected number of such edges)

From the community structure of a graph, one can

infer the dynamics of the groups inside the graph net-

work. Metrics that characterise the communities can

be led to the leakage of sensitive information of users.

We have seen that the modularity function informs

about how concentrated are the communities inside

a graph network. The analyst has as a target to min-

imise the value of the modularity function to blur the

communities. This is achieved by adding more edges

between the communities randomly. In this way, it

becomes tough by the server to point out the ground

truth communities.

Density: The selection of nodes in a community

occurs on the basis of its density (Coleman and Mor

1983). It is determined based on the number of edges

and nodes in that particular node’s adjacency graph.

It can be deﬁned as the following:

Density(v

) =

′

(|V

′

|(|V

′

| − 1)/2)

(1)

where, v

is the j

node in the graph G and it’s ad-

jacency graph is A

< V

′

> and |E

′

|,|V

′

| are the

number of edges and nodes in A

. Generally, the

nodes in the boundary have more density than the

nodes in the central. Therefore it is easier to attack

a node by knowing its density. We will give an exam-

ple later that after going through our protection frame-

work the density becomes almost similar for all the

nodes.

Privacy Cost: This can be measured as the number

of edges that have been added to change the commu-

nity structure for the lowest possible value of the mod-

ularity (Takbiri et al., 2019). Therefore privacy cost

reveals how much distortion has occurred while pro-

tecting the original graph structure. Suppose the set of

communities is C = {c

,..,c

}, Total number of

nodes are |V | = N and divided into the i communities,

N = n

+ n

,... + n

. As we will see in our algo-

rithm (Algorithm 1), the ways to have new edges are





−m)

−o)

. Where, n

are the num-

ber of nodes in the chosen communities and m,o is

the number of nodes in both the chosen communities

that already has an edge with the other community.

Therefore, this is the maximum cost for our privacy

protection.

Degree of Anonymity Achieved: It is deﬁned

as the normalised entropy achieved by the nodes

of the framework towards the attacker (Nilizadeh

et al., 2014; Cai et al., 2019). The maximum en-

tropy is H

max

= log N. The entropy of a node is

= −

∑

j=1

p(c

)log

p(c

), where p(c

) is the ra-

tio of node in A

to that of c

community. There-

fore, the normalised entropy would be (H

max

−

∑

j=1

)/H

max

. Also, 0 ≤normalised entropy ≤ 1

DLG Attack: We will use a method to infer data

from the newly arranged gradients after the edge ad-

dition. DLG attack (Zhu et al., 2019) is the ﬁrst of

its kind and gets to retrieve data with very less mean

square error from the vanilla FL framework. DLG at-

tack uses a dummy model, data and labels to create

dummy gradients and then it minimises the distance

between the original and the dummy gradients. The

main basis of this attack is that the distance is twice

differentiable. The analyst discards the gradients and

the data after this step.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

578

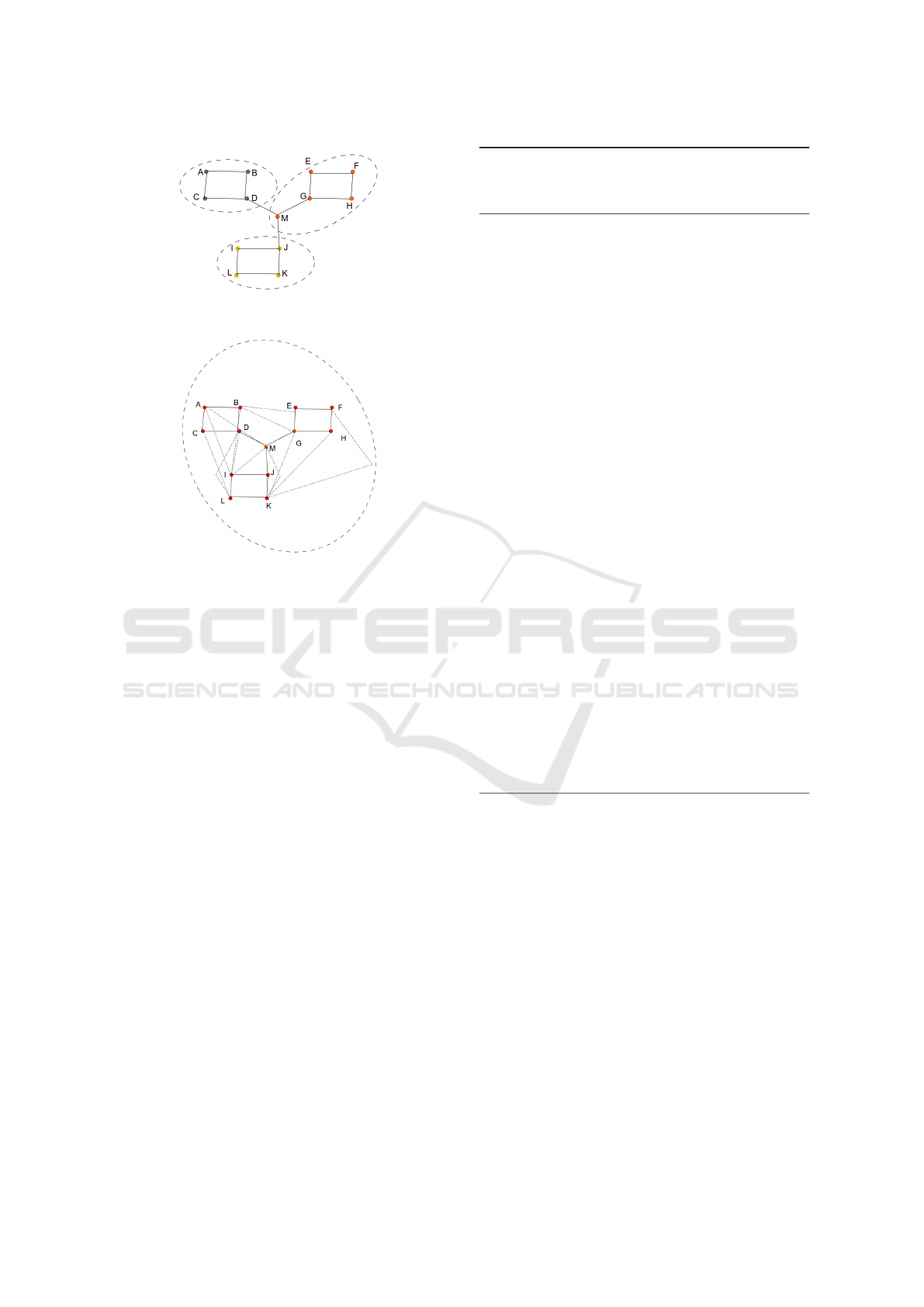
Figure 1: A graph with 13 nodes and 3 communities.

Figure 2: After privacy protection with 1 community.

1.1.1 Some Examples

Let us consider the graph in Fig.1. The densities

for all the nodes are: A=0.6, B=0.6, C=0.6, D=0.5,

E=0.6, F=0.6, G=0.5, H=0.6, I=0.6, J=0.5, K=0.6,

L=0.5, M=0.5. In contrast, for Fig.2 densities are

A=0.4, B=0.4, C=0.5, D=0.4, E=0.5, F=0.5, G=0.3,

H=0.5, I=0.4, J=0.5, K=0.4, L=0.4, M=0.4. These

results show that the density value does not inform

which one is a boundary node and which one is

in the center. The normalised entropy for the pro-

tected graph is 0.289, which suggests that after go-

ing through our privacy framework the example graph

will only reveal approximately 30% of the data at

most against the attacker.

2 OUR FRAMEWORK

In our framework we decouple the server to avoid data

reconstruction attacks from the gradients. Then, a

data analyst receives the gradients and use it to pro-

duce synthetic data which is sent to the server. The

community structure of the gradients is blurred by the

analyst to improve the privacy guarantees. Algorithm

1 details the computations. We give a ﬂow-chart of

this algorithm in Fig. 3. The FL system starts initial-

ising the model of the central server (global model)

and then proceeds in each round as follows.

Algorithm 1: ∆ SFL

The K clients are indexed by 1, 2, 3, 4, .. ., k, .. .

b is the batch size, α is the learning rate, t is the number of

training round, DB

is the data at device k.

Require: w (This is the pre-trained model at the cen-

tral server)

= φ (an array to save the gradients)

← set of ready clients

At the Server:

for each round t = 1,2,3, ... do

Train w with inferred data

Send the model back to the user devices for test-

ing

end for

Keep the model if it reaches to better testing accu-

racy or to a threshold

At the Analyst:

.store = ∇g(w)

Compute the Graph G from dg

Calculate L from G (Community Detection step)

for (Q ≃ 0) do

Choose communities to pick nodes from at ran-

dom

Choose nodes at random from the picked com-

munities

Connect the nodes if they already do not have an

edge between them

end for

Form a new graph G

′

Update Q and L from G

′

return the inferred data from G

′

to the central

server

At the Clients:

Train w with DB

return ∇g(w) = α∇g

(w) to the Analyst

1. The server sends the model parameters and model

to the ready user device pool,

2. The devices train the model with their data,

3. The model sends the trained gradients to the ana-

lyst

4. The analyst predicts the graph,

5. A round of community detection is done by the

analyst,

6. The analyst tries to decrease the modularity by

adding edges among the communities,

7. When the modularity converges a DGL attack is

being done by the analyst to infer the data from

the converged graph

8. The analyst sends the inferred data to the server

T SFL: (Decoupled Server Federated Learning) to Utilize DLG Attacks in Federated Learning by Decoupling the Server

579

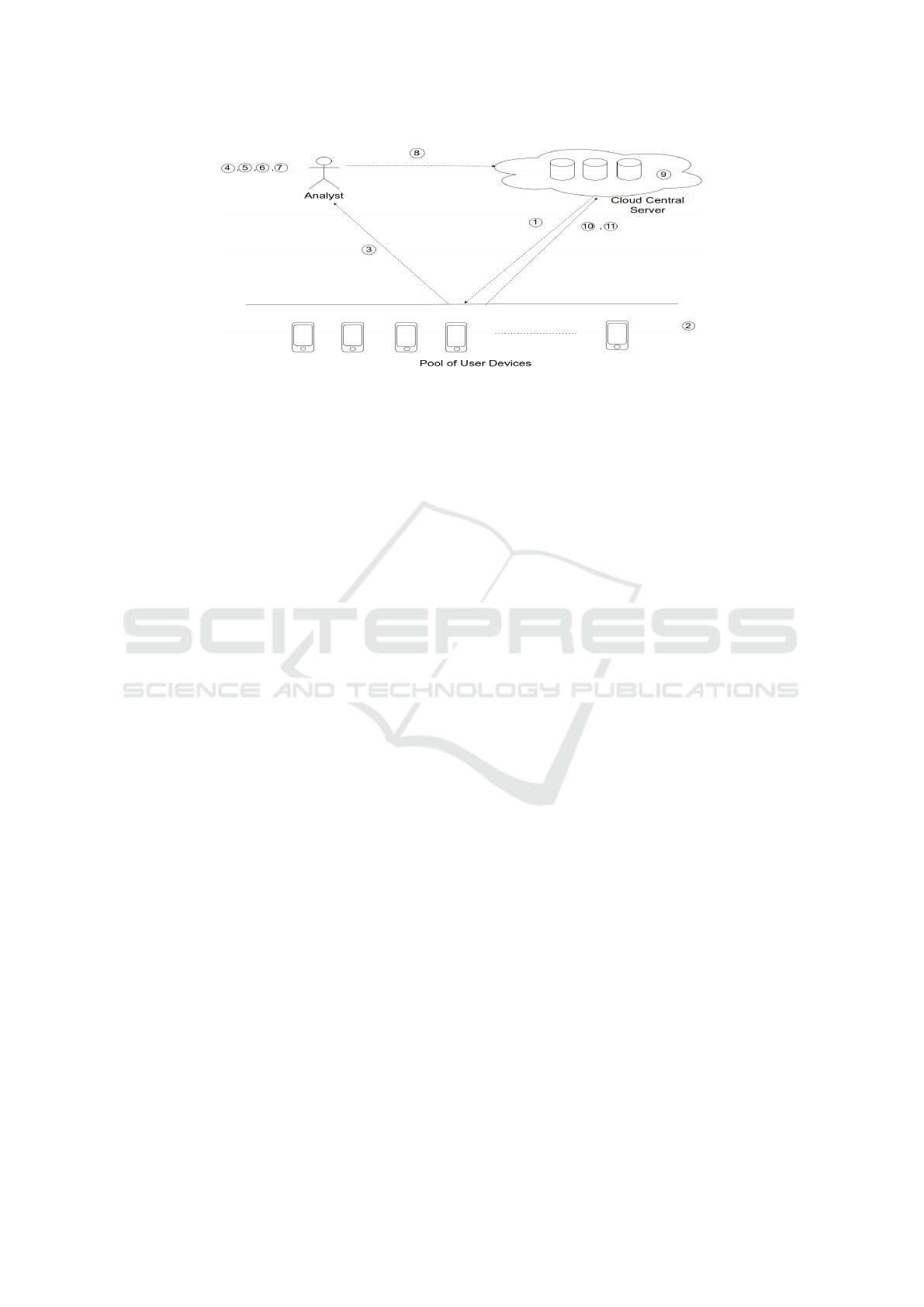
Figure 3: Flow chart of ∆SFL.The explanation is given in Section 2.

9. The model at the central server get trained by the

inferred data

10. This model again sent back to the user devices for

testing,

11. If the tested model gets better testing accuracy or

reaches a certain threshold of accuracy the server

will keep the model, else another cycle will start

We change the number of users in every training

round. The tunable hyperparameters of the machine

learning model involved in the whole setup are local

epoch e, learning rate α and batch size is b. They

are the same for all the local devices as well as at the

central server.

3 EXPERIMENT AND ANALYSIS

This section is dedicated to the study of the proposed

algorithm by using different datasets. Here we are

using three real-life dataset. The description of the

dataset and the results are separated in three different

subsections.

3.1 System Description

For the reproducibility purpose, we describe the sys-

tem on which we did our experiments. As one can

see, we do not use any GPU. The system speciﬁca-

tion is - UBUNTU 20.04.2 LTS, 64-bit Kernel Linux

5.8.0-44-generic x86 64 FOCAL FOSSA 1.20.4 OS

with 32.6 GiB of memory and Intel(R) Xeon(R) W-

1250P CPU 4.10GHz. The R-studio with R-version

3.6.1, Keras(version 2.2.5.0) and Tensor Flow(version

2.0.0) have been used, with a steady internet connec-

tion of 881.83 Mbit/s download speed and a 898.74

Mbit/s upload speed. For experiment purposes, we

used R version 4.2.0 (2022-04-22) - “Vigorous Cal-

isthenics” and the following packages: igraph, tidy-

verse, sqldf, dplyr, tensorﬂow, keras.

3.2 Results

In the next subsections we review the results on three

datasets we have considered.

3.2.1 Geolife Trajectory Dataset

This GPS trajectory information (Zheng et al., 2008;

Zheng et al., 2009) was gathered over four years by

178 users in the (Microsoft Research Asia) Geolife

project (from April 2007 to October 2011). This

dataset’s GPS trajectory is represented as a series of

time-stamped points, each of which comprises lati-

tude, longitude, and altitude information. There are

17,621 trajectories in this dataset, with a total dis-

tance of 1,251,654 kilometers and a length of 48,203

hours. Different GPS recorders and GPS phones cap-

tured these trajectories, which have a variety of sam-

pling rates. Every 15 seconds or 510 meters per point,

91 percent of the trajectories are logged in a dense

representation.

This dataset recoded a wide range of users’ out-

side activities, including not just daily activities like

going home and going to work, but also recreational

and sporting activities like shopping, sightseeing, eat-

ing, hiking, and cycling. Many study domains can

beneﬁt from this trajectory dataset, including mobil-

ity pattern mining, user activity detection, location-

based social networks, location privacy, and location

recommendation. There are 182 user’s data in total,

out of which 73 are being labeled with the mode of

transportation. We used these 73 users’ data to pre-

train the neural network model. The task for the FL

framework is to recommend a mode of transport for

a user. In Fig. 4a we can see the trend of testing ac-

curacy vs the number of users in the rounds of train-

ing after certain number of edges have been added.

The detected communities for different algorithms are

given in Fig.6 and the converged graph is given in the

Fig.9a. In the time of experiment, for every partition

SECRYPT 2023 - 20th International Conference on Security and Cryptography

580

Table 1: Some statistics of the experiment.

Dataset

name

No. of

Communities

at the beginning

No. of

communities

at the end

Accuracy at

the beginning

(rounded)

Accuracy at

the end

(rounded)

Overall time

in proposed

system

(in seconds,

averaged)

Overall time

in FedAvg

(in seconds,

averaged)

Geolife

Trajectory

11 1 90.88±1.35 97.62±1.12 7363.67 7022.89

Citeseer 450 1 92.62±0.62 99.12±0.3 43,496.82 39852.18

Cora 110 1 95.683±0.5 99.87±0.2 40,185.63 36998.26

of users we do the experiment for 100 times and take

an average of the testing accuracy.

From the result in Fig.4 it is evident that we need

atleast 20 users on the average in a round for this

dataset to learn something. We also can see that the

more users the better the learning and that adding

more edges does not reduce the testing accuracy at

all.

By comparing Fig.6 and Fig.9a we can see that

there are signiﬁcant visual changes in the structure of

the graphs occurred by the process of adding edges.

From Table 1 we can also see the same which has

been depicted in the Fig.9a.

3.2.2 Citeseer Dataset

The CiteSeer (Getoor, 2005; Sen et al., 2008) collec-

tion contains 3312 scientiﬁc papers that are divided

into six categories. There are 4732 linkages in the ci-

tation network. A 0/1-valued word vector describes

each publication in the dataset, indicating the exis-

tence or absence of the associated term from the dic-

tionary. There are 3703 distinct terms in the dic-

tionary. In the Citeseer dataset nodes correspond to

documents, and edges correspond to citations, where,

each node feature corresponds to the bag-of-words

representation of the document and belongs to one

of the academic topics. Both of them are benchmark

datasets in graph learning. Here, the task is the clas-

siﬁcation of the scientiﬁc papers. In Fig.4b we can

see the trend of the no. of users vs the testing accu-

racy for this dataset. Even when an abundant number

of edges have been integrated, the testing accuracy is

never less than 90% in the learning task.

From the result in Fig.4b it is evident that we need

atleast 20 users on the average in a round for this

dataset to learn appropriately. From the results in

Fig.7 and Fig. 9c we observe that adding edges is

changing the number of detected communities.

3.2.3 Cora Dataset

The Cora dataset (learning group At UMD, 2015)

contains 2708 scientiﬁc papers that are divided into

seven categories. There are 5429 linkages in the ci-

tation network. A 0/1-valued word vector describes

each publication in the dataset, indicating the exis-

tence or absence of the associated term from the dic-

tionary. There are 1433 distinct terms in the dictio-

nary. Here too, the learning task is the classiﬁcation

of the scientiﬁc papers. In Fig.4c we can see the trend

of no. of users vs the testing accuracy for this dataset.

From the result in Fig.4c it is evident that we need

at least 30 users on average in a round for this dataset

to learn. From the results in Fig.8 and Fig.9b it is evi-

dent that adding edges is indeed changing the number

of detected communities.

3.3 Analysis

There are three main new parts in the updating part

of the proposed ∆SFL algorithm, i.e. the community

detection, addition of new edges among the commu-

nities and the DLG attack.

Suppose, that after the step “Compute the graph

G = (V,E) from dg

” in Algorithm 1 we get the graph

G. Then after the addition of edges between commu-

nities we get the graph G

′

= G⊕g where G

′

= (V,E

′

g = (V

′

, p) and |V

′

| ≤ |V |, V

′

∈ V . Now, in G

′

the number of nodes remains constant and g is be-

ing made randomly, the probability of having or not

having an edge between two nodes is independent of

whether it was in the original graph or not. Therefore,

after the DLG attack on the gradient network G

′

in the

retrieved data the previous relationship of the original

distributed data is preserved with an addition of ex-

tra noisy edges. Therefore, privacy is being preserved

here locally by default of the system design.

For the ﬁrst part or for the analysis of the perfor-

mance of the community detection algorithm with re-

spect to the FL framework, we need to go through

Table 2. Here we can see that, for different datasets,

the Edge Betweenness algorithm performs the worst

T SFL: (Decoupled Server Federated Learning) to Utilize DLG Attacks in Federated Learning by Decoupling the Server

581

with respect to the time. Louvain and Fast Greedy

algorithms works almost similar and best for our ap-

proach. Time-wise the Leading-Eigen algorithm also

performs similar as the previous two algorithms. Here

we took “time” as the quantity to measure the perfor-

mance because we need to produce gradient updates

that are similar to that of the Fedavg algorithm. The

same can be observed for the overall proposed algo-

rithm and that off Fedavg in Table 1. From the de-

scription in Section 1.1 and Algorithm 1 it is clear

that they are capable of revealing the hierarchical and

spatio information of a dataset in the form of detect-

ing communities. Therefore, this community detec-

tion is itself a form of information retrieval and is cre-

ating the basis of adding more random edges among

the communities and the DLG attack.

We observe the effects of adding extra edges till 10

edges in Fig.4 for three different datasets as discussed

above. From the results it is evident that though we

are adding more abundant edges (which can be seen

as abundant data or “noise”) the testing accuracy is

not getting destroyed by it at all. Another result that

can be deducted roughly from this result is that if the

total number of users is N then our proposed algo-

rithm approximately needs N/3 number of devices in

a round to start reaching testing accuracy above 50%.

From Fig. 5, 6, 7, 8 and 9 we can observe the effect of

adding edges on top of different “communiﬁed graph

networks” for different datasets at the beginning and

at the end of modularity convergence. With the help

of these ﬁgures and Table 1 we can conclude that

more single vertices in a dataset the more the number

of communities, more time overhead but less number

of devices to be needed in a round to reach more than

50% testing accuracy in a round of edge addition.

The third part is to see the effect of the DLG

attack. With the help of the distance between the

gradients, a dummy model, dummy data and a ma-

chine learning task – this attack can retrieve a dataset

with (high accuracy) only from the gradients. In our

approach the referred data from the DLG attack is

formed with the help of the protected graph and the

gradients. As the protected graph is a changed ver-

sion of the original one and the DLG attack itself does

not reveal all the data but a portion of it — the new

referred data is different from the actual data, which

is full of redundant information. Nevertheless, it ac-

tually increases the testing accuracy of the machine

learning model as shown in the Table 1 by comparing

the columns “Accuracy at the beginning (rounded)”

and “Accuracy at the end (rounded)”. The analyst

do not store the referred data or any gradients or any

information about it, and the central server only has

the hold of the referred data and the machine learning

model. The central server similarly, never stores the

referred data but only stores the model parameters.

Therefore, through these three new parts the pri-

vacy of the users is preserved and the machine learn-

ing model is gaining better testing accuracy.

4 CONCLUSIONS

In this paper, we have introduced a framework for fed-

erated learning in which we decouple a data analyst

and the central server. This is to increase the privacy

guarantees of the model. We have described some of

the experiments performed with adequate examples

and experiments.

For future work, we intend to extend this work

in the domain of dynamic graphs and node churning.

Where we will see how the federated learning frame-

works can be described in terms of these techniques

with privacy protection beneﬁts and utility.

Table 2: Statistics about the Community Detection algo-

rithms.

Algorithm Dataset

Community

Detection

Time

(averaged in seconds)

Louvain

Geolife

Trajectory

0.16

Citeseer 4.05

Cora 3.67

Fast

Greedy

Geolife

Trajectory

0.16

Citeseer 4.18

Cora 3.61

Leading

Eigen

Geolife

Trajectory

0.19

Citeseer 5

Cora 4.32

Edge

Betwenness

Geolife

Trajectory

0.58

Citeseer 62.34

Cora 59.8

ACKNOWLEDGEMENTS

This research was partially funded by the Wallen-

berg AI, Autonomous Systems and Software Program

(WASP) funded by the Knut and Alice Wallenberg

Foundation.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

582

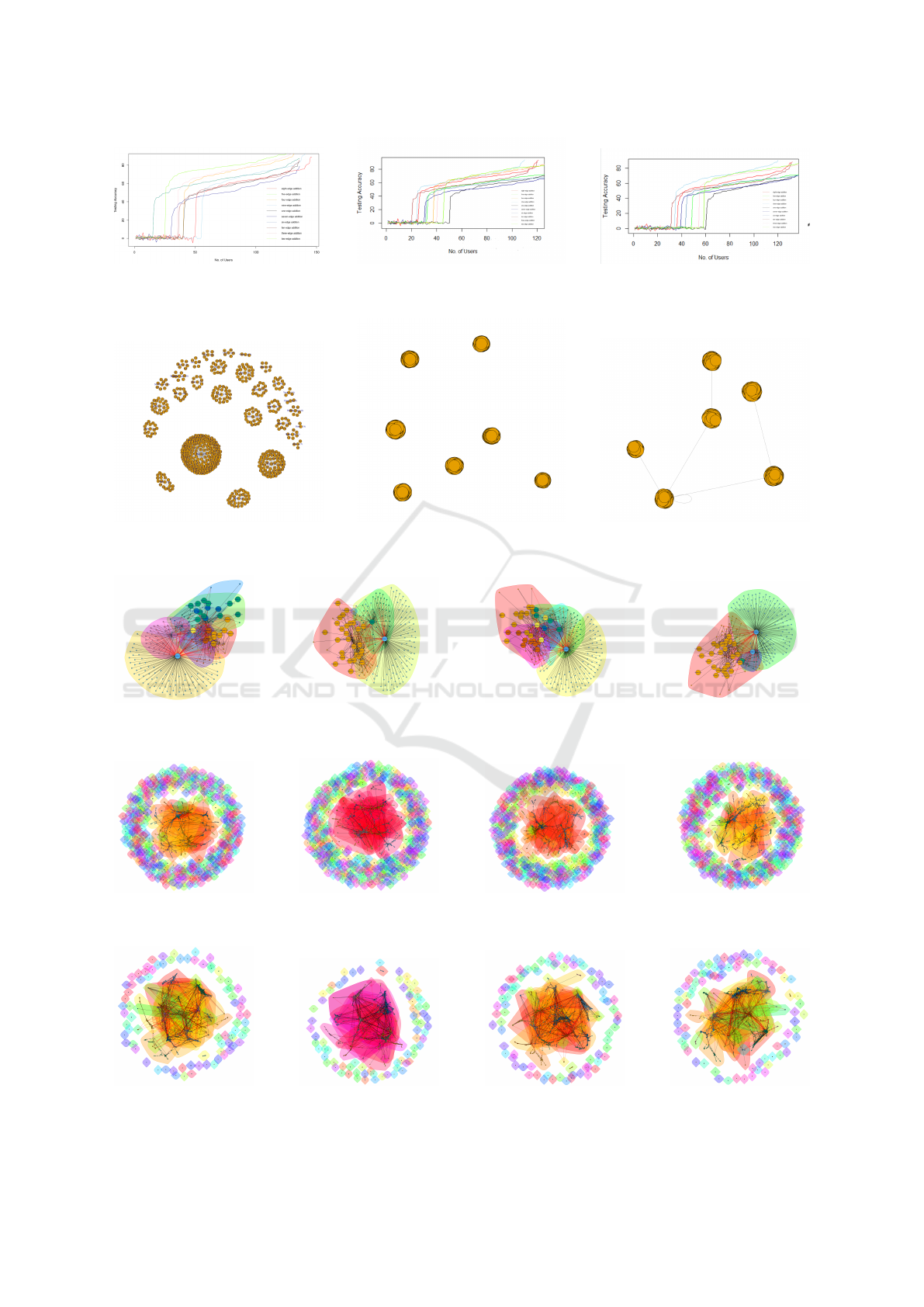
(a) Geolife Trajectory Dataset. (b) Citeseer Dataset. (c) Cora Dataset.

Figure 4: Testing accuracy vs Number of Users.

(a) Geolife trajectory dataset. (b) Cora Dataset. (c) Citeseer Dataset.

Figure 5: Before Community Detection.

(a) Louvain. (b) Leading Eigen. (c) Fast Greedy. (d) Edge Betweenness.

Figure 6: Community detection in the beginning for Geolife Trajectory Dataset.

(a) Louvain. (b) Leading Eigen. (c) Fast Greedy. (d) Edge Betweenness.

Figure 7: Community detection in the beginning for Citeseer Dataset.

(a) Louvain. (b) Leading Eigen. (c) Fast Greedy. (d) Edge Betweenness.

Figure 8: Community detection in the beginning for Cora Dataset.

T SFL: (Decoupled Server Federated Learning) to Utilize DLG Attacks in Federated Learning by Decoupling the Server

583

(a) Geolife trajectory dataset. (b) Cora Dataset. (c) Citeseer Dataset.

Figure 9: After Convergence Achieved in modularity by adding edges in case of Louvain Algorithm.

REFERENCES

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-

vre, E. (2008). Fast unfolding of communities in large

networks. Journal of statistical mechanics: theory

and experiment, 2008(10):P10008.

Cai, B., Zeng, L., Wang, Y., Li, H., and Hu, Y. (2019).

Community detection method based on node density,

degree centrality, and k-means clustering in complex

network. Entropy, 21(12):1145.

Cao, D., Chang, S., Lin, Z., Liu, G., and Sun, D. (2019).

Understanding distributed poisoning attack in fed-

erated learning. In 2019 IEEE 25th International

Conference on Parallel and Distributed Systems (IC-

PADS), pages 233–239.

Clauset, A., Newman, M. E., and Moore, C. (2004). Finding

community structure in very large networks. Physical

review E, 70(6):066111.

Coleman, T. F. and Mor

e, J. J. (1983). Estimation of sparse

jacobian matrices and graph coloring blems. SIAM

journal on Numerical Analysis, 20(1):187–209.

Geiping, J., Bauermeister, H., Dr

oge, H., and Moeller, M.

(2020). Inverting gradients-how easy is it to break pri-

vacy in federated learning? Advances in Neural Infor-

mation Processing Systems, 33:16937–16947.

Getoor, L. (2005). Link-based classiﬁcation. In Advanced

methods for knowledge discovery from complex data,

pages 189–207. Springer.

Girvan, M. and Newman, M. E. (2002). Community struc-

ture in social and biological networks. Proceedings of

the national academy of sciences, 99(12):7821–7826.

Kairouz, P., McMahan, H. B., Avent, B., Bellet, A., Bennis,

M., Bhagoji, A. N., Bonawitz, K., Charles, Z., Cor-

mode, G., Cummings, R., et al. (2021). Advances and

open problems in federated learning. Foundations and

Trends® in Machine Learning, 14(1–2):1–210.

Krishna, K., Tomar, G. S., Parikh, A. P., Papernot, N.,

and Iyyer, M. (2019). Thieves on sesame street!

model extraction of bert-based apis. arXiv preprint

arXiv:1910.12366.

learning group At UMD, S. (2015). Relational dataset

repository.

Luo, X., Wu, Y., Xiao, X., and Ooi, B. C. (2021). Fea-

ture inference attack on model predictions in vertical

federated learning. In 2021 IEEE 37th International

Conference on Data Engineering (ICDE), pages 181–

192.

Newman, M. E. (2006). Finding community structure in

networks using the eigenvectors of matrices. Physical

review E, 74(3):036104.

Nilizadeh, S., Kapadia, A., and Ahn, Y.-Y. (2014).

Community-enhanced de-anonymization of online so-

cial networks. In Proceedings of the 2014 acm sigsac

conference on computer and communications secu-

rity, pages 537–548.

Sen, P., Namata, G., Bilgic, M., Getoor, L., Galligher, B.,

and Eliassi-Rad, T. (2008). Collective classiﬁcation in

network data. AI magazine, 29(3):93–93.

Takbiri, N., Shao, X., Gao, L., and Pishro-Nik, H. (2019).

Improving privacy in graphs through node addition.

In 2019 57th Annual Allerton Conference on Com-

munication, Control, and Computing (Allerton), pages

487–494. IEEE.

Xie, C., Huang, K., Chen, P.-Y., and Li, B. (2019). Dba:

Distributed backdoor attacks against federated learn-

ing. In International Conference on Learning Repre-

sentations.

Zheng, Y., Li, Q., Chen, Y., Xie, X., and Ma, W.-Y.

(2008). Understanding mobility based on gps data. In

Proceedings of the 10th international conference on

Ubiquitous computing, pages 312–321.

Zheng, Y., Zhang, L., Xie, X., and Ma, W.-Y. (2009). Min-

ing interesting locations and travel sequences from

gps trajectories. In Proceedings of the 18th interna-

tional conference on World wide web, pages 791–800.

Zhu, L., Liu, Z., and Han, S. (2019). Deep leakage from

gradients. Advances in Neural Information Processing

Systems, 32.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

584