Implicit Multilinear Modeling of Air Conditioning Systems
Torben Warnecke
1 a
and Gerwald Lichtenberg
2 b
1
Deutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany
2
Faculty of Life Sciences, Hamburg University of Applied Sciences, Ulmenliet 20, 21033 Hamburg, Germany
Keywords:
Multilinear Algebra, Differential-Algebraic Models, State-Space Models, Tensor Decomposition, HVAC,
Air-Conditioning, Building Automation, Building Simulation.
Abstract:
The publication explores the applicability of implicit multilinear model approaches in air conditioning systems.
Implicit multilinear time-invariant models offer a structure that allows for the representation of most of the
fundamental physical equations of HVAC systems. Since the implicit multilinear time-invariant model class
is closed, it enables a component-based modeling approach to represent various types of HVAC systems with
different combinations of components. Multilinear time-invariant models are usually represented by tensors.
With HVAC-Systems having a large number of inputs and states, the models can be efficiently represented
in a decomposed manner, resulting in a matrix representation. As an example, the model of a precision
climatization hutch with a PI controller is derived and simulated.
1 INTRODUCTION
In this paper, an example model is provided to demon-
strate the applicability of implicit multilinear time-
invariant (iMTI) models for HVAC-Systems (Heat-
ing, Ventilation and Air Conditioning) working with
humid air. The energy equations of HVAC-Systems
mostly consist of linear combination of mass flows
and thermodynamic states, such as temperatures or
enthalpies (specific energy content of mass), e.g. in
the first law of thermodynamics applied to fluids.
Such equations typically exhibit a multilinear time-
invariant structure, as shown in (Lichtenberg et al.,
2022), (Pangalos et al., 2013) and (Pangalos et al.,
2014). A multilinear time-invariant structure can be
derived from the fundamental physical equations of
thermodynamic states and the energy conservation
principles of humid air systems. For the example of a
precision climatization hutch, typical thermodynamic
approaches, e.g. shown in (Yao and Yu, 2018), were
used. Usually, these systems are approximated using
linearized state-space models. However, this paper
proposes a modeling method with fewer approxima-
tions, allowing for direct utilization of most of the
fundamental physical equations.
a
https://orcid.org/0009-0004-3037-8634
b
https://orcid.org/0000-0001-6032-0733
2 MULTILINEAR MODELS
Recently, the implicit multilinear model framework
has been introduced. Firstly in an explicit form in
(Pangalos et al., 2013) and an implicit form in (Licht-
enberg et al., 2022). The multilinear model method
serves as a compromise between slow but accurate
nonlinear and fast but linear models. Furthermore,
linear and binary models can be fully represented us-
ing the multilinear structure. The multilinear func-
tions enable the utilization of tensor algorithms and
multilinear algebra, since the model structure and
parameter-space can be represented by tensors. This
facilitates the usage of tensor decomposition methods
and enhances the efficient use of multilinear models
in simulations or other applications, like control and
automation.
2.1 Implicit Multilinear State-Space
Modeling
Expanding the explicit multilinear time-invariant
(eMTI) model format into the implicit multilinear
time-invariant (iMTI) format allows the multiplica-
tion of state derivatives
˙
x ∈ R
n
with states x ∈ R
n
,
inputs u ∈ R
m
and/or outputs y ∈ R
r
. This enables
the representation of broken rational functions within
implicit multilinear models. More importantly, the
iMTI model class is a closed model class, mean-
440
Warnecke, T. and Lichtenberg, G.
Implicit Multilinear Modeling of Air Conditioning Systems.
DOI: 10.5220/0012138200003546
In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 440-447
ISBN: 978-989-758-668-2; ISSN: 2184-2841
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ing that any combination with different iMTI mod-
els results in the overall model still being an iMTI
model. This includes representation of series, par-
allel and feedback connections, as demonstrated in
(Lichtenberg et al., 2022). An iMTI model can be ex-
pressed as the inner tensor product of the model tensor
H ∈ R
2n+m+r
z }| {
2 × ... ×2×e
, with e being the application spe-
cific number of equations, and the monomial tensor
M(
˙
x,x,u,y) ∈ R
2
2n+m+r
by
0 = h H | M(
˙
x,x,u,y)i . (1)
The model tensor can be decomposed using the
canonical polyadic (CP)-representation, shown in
(Kruppa, 2017), and normalization methods proposed
in (J
¨
ores et al., 2022) into the norm-1 structure matrix
F ∈ R
(2n+m+r)×R
and the parameter matrix Φ ∈ R
e×R
,
with R as the model rank given by the number of over-
all terms
H =

F,Φ

. (2)
In the decomposed form, the implicit system of equa-
tions can be constructed from the structure matrix F
and parameter matrix Φ without reconstructing the
full tensor by inserting the matrices into the normal-
ized factored polynomial
0 =
R
∑
k=1
Φ
j,k
2n+m+r
∏
i=1
(1− | F
i,k
| +F
i,k
v
i
) (3)
with the variables v =



˙
x
x
u
y



for all j ∈ {1,2...e}.
3 PHYSICS OF AIR
CONDITIONING SYSTEMS
To simplify the following equations and provide
a rough overview of the given dynamics, an iso-
baric, respectively ambient pressure, system is con-
sidered, allowing the use of isobaric material proper-
ties. Because kinetic and potential energy differences
in air streams of AC (air conditioning)-systems are
small compared to enthalpy differences, those are ne-
glected.
3.1 Enthalpy of Wet Air
The state of humid air can be adequately described by
the independent states of temperature and humidity
along with the isobaric material properties of dry air
and water vapor. The specific enthalpy
h = c
d
ϑ + c
v
µϑ + h
0
µ (4)
of wet air can be calculated with the temperature ϑ
in
◦
C and absolute humidity µ in kg
water
/kg
air
, where
c
d
represents the heat capacity of dry air, c
v
the heat
capacity of water vapor in the air and h
0
the evapora-
tion enthalpy. Equation (4) is a multilinear function of
temperature ϑ and humidity µ due to the second term
of the equation, whereas the first and third terms are
linear.
3.2 Energy and Humidity Transfer of a
Wet Air Stream
To describe the energy absorbed by a mass flow q
m
of air, the first law of thermodynamics for stationary
flowing fluids can be applied. To calculate the change
in enthalpy h
V
and humidity µ
V
in a given reference
volume V , the following differential equations can be
obtained
ρV
˙
h
V
= q
m
(h
in
− h
out
), (5)
ρV ˙µ
V
= q
m
(µ
in
− µ
out
), (6)
with ρ as density of the air, h
in
as enthalpy of the en-
tering and h
out
as enthalpy of the exiting air.
The assumption is made that the air is well-mixed in-
side the reference volume and the air states are the
same throughout the volume (principle of concen-
trated masses and lumped parameters). This assump-
tion holds for small distances/volumes and high ve-
locities. This means that the exiting air states are
equal to the air states of the reference volume and the
equations (5) and (6) can be rewritten as
ρV
˙
h
V
= q
m
(h
in
− h
V
), (7)
ρV ˙µ
V
= q
m
(µ
in
− µ
V
). (8)
For higher resolution or larger systems, multiple in-
terconnected volumes (cells) can be used, as in CFD
or FEM calculations.
To calculate the temperature ϑ
V
of the reference vol-
ume, the additional algebraic equation
h
V
= c
d
ϑ
V
+ c
v
µ
V
+ h
0
ϑ
V
µ
V
(9)
is needed. Eq. (4) can be used for calculating the
enthalpy h
in
of the entering air stream from its tem-
perature ϑ
in
and humidity µ
in
. Substituting (4) and
(9) into (7) results in
ρV
˙
h
V
=c
d
q
m
ϑ
in
+ h
0
q
m
µ
in
+ c
v
q
m
ϑ
i
nµ
in
− q
m
h
V
.
(10)
The differential equations (8) and (10) can
be transformed into an implicit state-space model
with the states x =

h
V
µ
V

|
, inputs u =

q
m
ϑ
in
µ
in

|
and output y = ϑ
V
as follows
0 =ρV ˙x
1
+ u
1
x
1
− c
d
u
1
u
2
− h
0
u
1
u
3
− c
v
u
1
u
2
u
3
(11)
0 =ρV ˙x
2
+ u
1
x
2
− u
1
u
3
(12)
Implicit Multilinear Modeling of Air Conditioning Systems
441

with the additional algebraic output equation
0 = x
1
− c
d
y − c
v
x
2
− h
0
yx
2
. (13)
The structure matrix F of the iMTI model is
F =











0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1 1 0 0
0 0 0 0 1 1 1 0 0 0 0
0 1 1 1 0 0 1 0 1 0 0
0 0 1 1 0 0 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0 0
1 0 0 0 0 1 0 0 0 0 0











.
(14)
The parameter matrix Φ is
Φ
|
=

















0 0 −c
d
−1 −h
0
0
0 −c
d
0
0 −c
v
0
0 0 −c
v
0 0 −h
0
1 0 0
0 0 1
0 1 0
ρV 0 0
0 ρV 0

















. (15)
In the upcoming chapter, an iMTI model of an ac-
tual air conditioning system is developed to further
investigate the practical applicability of this modeling
approach.
4 EXAMPLE: CLIMATIZATION
HUTCH
A precision climatization hutch for magnetic field
measurements of magnets needed in particle ac-
celerators will act as example for this study. The
temperature in the climatization hutch needs to main-
tain at 21±0.1
◦
C, to prevent warping of the magnets
due to thermal expansion during the measurements.
Therefore, the hutch is cooled by a recirculating air
conditioning system, which is operated with a con-
stant air flow and a high air exchange rate of approx.
20
1
/h (which means that the air volume is completely
replaced 20 times per hour). The system is shown
in the Figure 1. The hutch itself is located inside an
industrial hall. The air conditioning system consist
of a duct system, a water-air heat exchanger with
a mixing-valve operated with cooling water and a
fan. The mixing valve is controlled by a PI-controller.
Figure 1: Climatization hutch with a recirculating air con-
ditioning system (in grey).
4.1 Component-Based Modeling
The model consists of interconnected sub-models, in-
cluding the room, air duct, dry water-air heat ex-
changer, mixing valve, walls, floor and PI controller.
In the following sections each component will be de-
scribed by thermodynamic equations.
4.1.1 Room
The thermodynamic behavior of the room can be de-
scribed by the change
˙
E
room
of energy content of the
room air. Often climatization zones are described by
multiple cells, e.g. a 3-cell model with an air-supply,
working and air-return cell, as shown in (Yao and Yu,
2018). To reduce the number of equations in this pa-
per, a simpler one-cell model is represented. As be-
fore such a cell is considered well-mixed.
The example includes the energy exchange Q
vent
due
to ventilation, energy losses Q
wall
towards the walls,
energy losses Q
f loor
towards the floor and internal
heat sources Q
int
(like the magnet and the magnet
power supplies). The heat losses from the fan mo-
tor are part of the internal heat sources, since it is a
closed system.
The change of energy content of the room can be fur-
ther described by the mass m
r
times the change
˙
h
r
in
enthalpy of the room air. The dynamic energy conser-
vation law results in
m
r
˙
h
r
= Q
vent
+ Q
wall
+ Q
f loor
+ Q
int
. (16)
The water content of the air is modeled by the dy-
namic mass conservation law, also called the conti-
nuity or transport equation. The change ˙µ
r
in abso-
lute humidity (mass of water per mass of air) can be
calculated with the entering and exiting water vapor
SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
442

mass flows. For simplification no internal gain rates
of water vapor are modeled, only the exchanged vapor
mass flow q
m,µ,vent
due to ventilation is considered.
The transport equation for the water vapor results in
m
r
˙µ
r
= q
m,µ,vent
. (17)
Eq. (4) can be used to calculate the temperature ϑ
r
implicitly from the enthalpy h
r
and humidity µ
r
of the
room air
h
r
= c
d
ϑ
r
+ c
v
µ
r
ϑ
r
+ h
0
µ
r
. (18)
4.1.2 Air Duct
The air duct system supplies and removes air from
the room. The energy rate Q
vent
between the supplied
air by the AC-unit and the room air is modeled using
the first law of thermodynamics for stationary flowing
fluids
Q
vent
=q
m,air
(c
d
(ϑ
sup
− ϑ
r
) + c
v
(µ
sup
ϑ
sup
− µ
r
ϑ
r
)
+ h
0
(µ
sup
− µ
r
)),
(19)
where q
m,air
is the mass flow of the exchanged air,
ϑ
sup
the temperature of the supplied air and µ
sup
the
absolute humidity of the supplied air.
The exchange rate q
m,µ,vent
of water vapor due to ven-
tilation is calculated by
q
m,µ,vent
= q
m,air
(µ
sup
− µ
r
). (20)
4.1.3 Dry Water-Air Heat Exchanger
A heat exchanger can be modeled by the energy con-
tent of the 2 liquids inside the exchanger and the en-
ergy storage of the exchange material itself. Over-
all the model has 3 energy storages. The concept of
concentrated masses and lumped parameters is used
and each storage is represented by one cell with one
according mass. It is also possible to use multi-cell
approaches for the different materials.
In the climatization hutch, the heat exchanger is
used for cooling the air, but it is only operated with
temperatures above 14°C, so the heat exchanger al-
ways operates in dry operation mode and no conden-
sation appears.
The energy content of the air is modeled based on
its average enthalpy h
a,av
and air mass m
a
inside the
heat exchanger. The airflow q
m,air
is similar in the
whole system. The incoming air has the states of the
room air (temperature ϑ
r
and humidity µ
r
) since it is
directly extracted from the room. Duct heat losses are
neglected. Since the heat exchanger is operated in a
dry mode, the exiting humidity µ
sup
equals the incom-
ing humidity µ
r
. The average enthalpy h
a,av
is calcu-
lated by the mean value of the entering and exiting
enthalpies h
r
and h
sup
h
a,av
=
h
r
+ h
sup
2
. (21)
The enthalpy h
r
can be calculated with (18). The
supply temperature ϑ
sup
can be calculated implicitly
from the enthalpy h
sup
and humidity µ
r
by
h
sup
= c
d
ϑ
sup
+ c
v
µ
r
ϑ
sup
+ h
0
µ
r
. (22)
The change m
a
˙
h
a,av
in energy content of the air in-
cludes heat dissipated from the airflow and heat trans-
fer to the heat exchange material. The power balance
for the air results in
m
a
˙
h
a,av
=q
m,air
(h
r
− h
sup
)
+ k
a
A
a
η
ex
(ϑ
ex,w
− ϑ
a,av
),
(23)
where k
a
is the heat transfer coefficient of the air-side,
A
a
the heat transfer surface of the air-side, η
ex
the heat
exchange efficiency and ϑ
ex,w
the surface temperature
of the heat exchanger on the water-side.
The change in energy content of the heat exchange
material is modeled by the change
˙
ϑ
ex,w
in tempera-
ture of the material on the water-side, the mass m
ex
of
the material and its heat capacity c
ex
. The change in
energy content includes the heat transfer between the
water and heat exchange material, as well as the heat
transfer between the air and heat exchange material
m
ex
c
ex
˙
ϑ
ex,w
=k
w
A
w
(ϑ
w,av
− ϑ
ex,w
)
+ k
a
A
a
η
ex
(ϑ
a,av
− ϑ
ex,w
),
(24)
with the heat transfer coefficient k
w
of the water-side,
the heat transfer surface A
w
of the water-side and the
average temperature ϑ
w,av
of the water inside the heat
exchanger.
The energy content of the water is modeled by its
mass m
w
, its heat capacity c
w
and its average tempera-
ture ϑ
w,av
, which is calculated by the mean of the inlet
and outlet temperatures ϑ
w,in
and ϑ
w,out
ϑ
w,av
=
ϑ
w,in
+ ϑ
w,out
2
. (25)
As for the air, the change in energy content of the
water is similar to the heat absorbed by the water flow
q
m,w
and the heat transfer from the heat exchange ma-
terial
m
w
c
w
˙
ϑ
w,av
=c
w
q
m,w
(ϑ
w,in
− ϑ
w,out
)
+ k
w
A
w
(ϑ
ex,w
− ϑ
w,av
).
(26)
4.1.4 Mixing Valve
A valve inside the water circuit is used to control the
output of the heat exchanger. For precision cooling
usually a mixing circuit with a mixing valve is used.
Implicit Multilinear Modeling of Air Conditioning Systems
443

The 3-way mixing valve is positioned at the inlet wa-
ter stream, as it can be seen in Figure 1. With the
mixing valve, the hotter outlet water can be mixed in
the cold feed water, raising the inlet water tempera-
ture of the heat exchanger. With an additional pump
the circuit is operated with a constant water flow q
m,w
,
so unnecessary oscillation can be avoided. To avoid
damaging pressure spikes the actuator response time
T
valve
is high. The change ˙x
valve
of the valve posi-
tion is modeled as an integrator over the difference
between the valve position x
valve
and control signal
u
controller
divided by the response time T
valve
˙x
valve
=
u
controller
− x
valve
T
valve
. (27)
The water inlet temperature ϑ
w,in
of the heat ex-
changer is calculated using the mixing equation
ϑ
w,in
= x
valve
ϑ
w, f eed
+ (1 − x
valve
)ϑ
w,out
, (28)
with ϑ
w, f eed
as the feed temperature of the primary
cooling water supply and ϑ
w,out
as the water outlet
temperature of the heat exchanger.
4.1.5 Wall and Floor
The walls and floor act as additional thermal energy
storages and transfer heat with the room and environ-
ment. The change in energy content of these struc-
tures is modeled by the change
˙
ϑ
wall,i
of their tem-
peratures times their masses m
wall,i
and heat capacity
c
wall,i
. The transferred heat is linearly depending on
the temperature differences between the wall and ad-
jacent zones. The power balance results in
m
wall,i
c
wall,i
˙
ϑ
wall,i
=k
in,i
A
wall,i
(ϑ
r
− ϑ
wall,i
)
+ k
out,i
A
wall,i
(ϑ
amb,i
− ϑ
wall,i
),
(29)
with the inner heat transfer coefficient k
in,i
, the heat
transfer surface A
wall,i
, the outer heat transfer coeffi-
cient k
out,i
and the ambient temperature ϑ
amb,i
, which
is the hall temperature in case of the walls and the
ground temperature in case of the floor.
The heat Q
wall,i
transferred between the room and the
wall/floor can be calculated by
Q
wall,i
= k
in,i
A
wall,i
(ϑ
wall,i
− ϑ
r
). (30)
In the example, the walls have been modeled as one
wall, with their surfaces added to each other. The
floor is modeled separately.
4.1.6 PI Controller
A PI controller is implemented in the model to main-
tain the desired room temperature. The controller sig-
nal u
controller
consists of a proportional and an inte-
grating part. The proportional part is calculated via a
gain of K
P
on the control error between the set tem-
perature ϑ
set
and the room temperature ϑ
r
. The inte-
grating part is calculated via a gain of K
I
on the inte-
grated control error. The equations of the PI controller
result in
˙x
I
=ϑ
set
− ϑ
r
, (31)
u
controller
=K
P
(ϑ
set
− ϑ
r
) + K
I
x
I
. (32)
These equations describe the behavior of the com-
ponents of the precision climatization hutch and can
be used for simulation and analysis.
4.2 Overall Model
The overall model is built from the implicit state-
space models of the single components. In the fol-
lowing those state-space models and the connection
equations will be shown.
Since no condensation or humidity sources are
modeled, the humidity is constant and could be
treated as a parameter for the model. For demon-
stration purposes, it remains as a variable, it is ex-
pected that in further research those effects can be
represented with iMTI models (see chapter 7).
The state-space model of the room has the states

x
1
x
2

|
=

h
r
µ
r

|
, inputs

u
1
... u
5

|
=

Q
vent
Q
wall
Q
f loor
Q
int
q
m,µ,vent

|
and out-
puts

y
1
y
2

|
=

ϑ
r
µ
r

|
. The equations of the
state-space model are
0 = m
r
˙x
1
− u
1
− u
2
− u
3
− u
4
,
0 = m
r
˙x
2
− u5,
0 = c
d
y
1
− x
1
+ h
0
x
2
+ c
v
x
2
y
1
,
0 = x
2
− y
2
.
(33)
The air duct state-space model has the inputs

u
6
... u
10

|
=

ϑ
r
µ
r
q
m,air
ϑ
sup
µ
sup

|
and outputs

y
3
y
4

|
=

Q
vent
q
m,µ,vent

|
. The
equations of the state-space model are
0 =c
d
u
8
u
9
− c
d
u
6
u
8
− y
3
− h
0
u
7
u
8
+ h
0
u
8
u
10
− c
v
u
6
u
7
u
8
+ c
v
u
8
u
9
u
10
,
0 =u
8
u
10
− u
7
u
8
− y
4
.
(34)
The duct model is connected to the room model
via the connection equations
0 = u
1
− y
3
,
0 = u
5
− y
4
,
0 = u
6
− y
1
,
0 = u
7
− y
2
,
0 = u
10
− y
2
.
(35)
SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
444

The state-space model of the heat ex-
changer has the states

x
3
x
4
x
5

|
=

h
a,av
ϑ
ex,w
ϑ
w,av

|
, inputs

u
11
... u
15

|
=

q
m,air
ϑ
r
µ
r
q
m,w
ϑ
w,in

|
, outputs

y
5
y
6

|
=

ϑ
sup
ϑ
w,out

|
and auxiliary z
1
= ϑ
a,av
.
The equations of the state-space model are
0 =2c
d
u
11
u
12
− 2u
11
x
3
− m
a
˙x
3
+ 2h
0
u
11
u
13
+ 2c
v
u
11
u
12
u
13
+ A
a
η
ex
k
a
x
4
− A
a
η
ex
k
a
z
1
,
0 =A
w
k
w
x
5
− x
4
(A
w
k
w
+ A
a
η
ex
k
a
)
− c
ex
m
ex
˙x
4
+ A
a
η
ex
k
a
z
1
,
0 =A
w
k
w
x
4
− A
w
k
w
x
5
− c
w
m
w
˙x
5
+ 2c
w
u
14
u
15
− 2c
w
u
14
x
5
,
0 =h
0
u
13
− x
3
+ c
d
z
1
+ c
v
u
13
z
1
,
0 =2x
3
− c
d
u
12
− c
d
y
5
− 2h
0
u
13
− c
v
u
12
u
13
− c
v
u
13
y
5
,
0 =2x
5
− u
15
− y
6
.
(36)
The heat exchanger model is connected to the rest of
the model with
0 = u
12
− y
1
,
0 = u
13
− y
2
,
0 = u
9
− y
5
.
(37)
The state-space model of the walls has the state x
6
=
ϑ
wall
, the inputs

u
16
u
17

|
=

ϑ
r
ϑ
amb

|
and out-
put y
7
= Q
wall
. The equations of the state-space
model are
0 =A
wall
k
wall,in
u
16
− A
wall
(k
wall,in
+ k
wall,out
)x
6
+ A
wall
k
wall,out
u
17
− c
wall
m
wall
˙x
8
,
0 =A
wall
k
wall,in
x
6
− A
wall
k
wall,in
u
16
− y
7
.
(38)
The state-space model of the floor has the state x
7
=
ϑ
f loor
, inputs

u
18
u
19

|
=

ϑ
r
ϑ
ground

|
and out-
put y
8
= Q
f loor
. The equations of the state-space
model are
0 =A
f loor
k
f loor,in
u
18
− A
f loor
(k
f loor,in
+ k
f loor,out
)x
7
+ A
f loor
k
f loor,out
u
19
− c
f loor
m
f loor
˙x
9
,
0 =A
f loor
k
f loor,in
x
7
− A
f loor
k
f loor,in
u
18
− y
8
.
(39)
The wall and floor model is connected to the rest with
0 = u
16
− y
1
,
0 = u
18
− y
1
,
0 = u
2
− y
7
,
0 = u
3
− y
8
.
(40)
The state-space model of the mixing valve has
the state x
8
= x
valve
, inputs

u
20
u
21
u
22

|
=

u
controller
ϑ
w, f eed
ϑ
w,out

|
and output y
9
= ϑ
w,in
.
The equations of the state-space model are
0 =u
20
− x
8
− T
valve
˙x
8
,
0 =u
22
− y
9
+ u
21
x
8
− u
22
x
8
.
(41)
The valve model is connected to the system model
with
0 = u
22
− y
6
,
0 = u
15
− y
9
.
(42)
The controller state-space model has the state x
9
= x
I
,
inputs

u
23
u
24

|
=

ϑ
set
ϑ
r

|
and output y
10
=
u
controller
. The equations of the state-space model are
0 =u
23
− u
24
− ˙x
9
,
0 =K
P
u
23
− y
10
− K
P
u
24
+ K
I
x
9
.
(43)
The controller model is connected to the system
model with
0 = u
24
− y
1
,
0 = u
20
− y
10
.
(44)
The resulting input and disturbance signals of the
overall model are
u
open
= [
u
4
u
8
u
11
u
14
u
17
u
19
u
21
u
23
]
|
= [
Q
int
q
m,air
q
m,air
q
m,w
ϑ
amb
ϑ
ground
ϑ
w, f eed
ϑ
set
]
|
.
(45)
The redundant inputs u
8
and u
11
have been replaced
by one input. The linear connection equations have
been reduced by exchanging the variables y
i
and u
j
with one similar auxiliary variable z
k
. In case of the
variables ϑ
r
and µ
r
, they have been replaced by simi-
lar output variables.
The overall model has 9 states, 7 inputs, 2 out-
puts and 9 auxiliaries. The structure matrix F can be
stored as sparse boolean matrix and has the dimen-
sions R
36×47
with 63 elements of one. The parameter
matrix Φ can be stored as a sparse matrix with dimen-
sions R
20×47
with 76 nonzero elements. The values
for the model parameters are shown in the appendix.
This model construction process demonstrates
that it is possible to directly represent a thermody-
namic modeling approach of an HVAC system in an
iMTI model. In the next chapter, simulation results
are provided to showcase a practical application of the
model.
5 SIMULATION
For simulation, the system of equations (3) is solved
using the ode15i-solver from Matlab version 2022b.
Implicit Multilinear Modeling of Air Conditioning Systems
445

Therefore initial values of the states and input trends
are needed. The simulation represents the operation
of 4 hours of an imaginary summer day in Germany.
5.1 Initial Conditions
For this example, the initial states are set as follows
x
0
=[
43488 0.008 43488 23 23
23 17 0 0
]
|
.
(46)
This refers to initial temperatures of 23
◦
C for the
room and walls, as well as the air and water inside
the heat exchanger and the heat exchange material it-
self. The initial floor temperature is set to 17
◦
C, since
it is directly exposed to the ground. The initial room
humidity is set to 8 × 10
−3
kg
water
/kg
air
. The mixing
valve is completely closed and the initial controller
signal is set to zero.
With the states and first input signals initial
guesses for the state derivatives and outputs can be
calculated with Eq. (3). The numerical solver
vpasolve for symbolic equations is used.
Figure 2: Input temperatures, mass flows and heatload.
5.2 Input Signals
The trends of the input signals are shown in Figure
2. The figure displays the temperature input signals
ϑ
amb
, ϑ
ground
, ϑ
w, f eed
and ϑ
set
, which are nearly held
constant for better traceability of the model behavior,
as well as the mass flows q
m,air
and q
m,w
of the air and
water. Also the inner heatload Q
int
of the climatiza-
tion hutch is shown and represented as an rectangular
function (in kW ). This could represent when a magnet
is powered and measurements of the magnetic field
are conducted.
5.3 Results
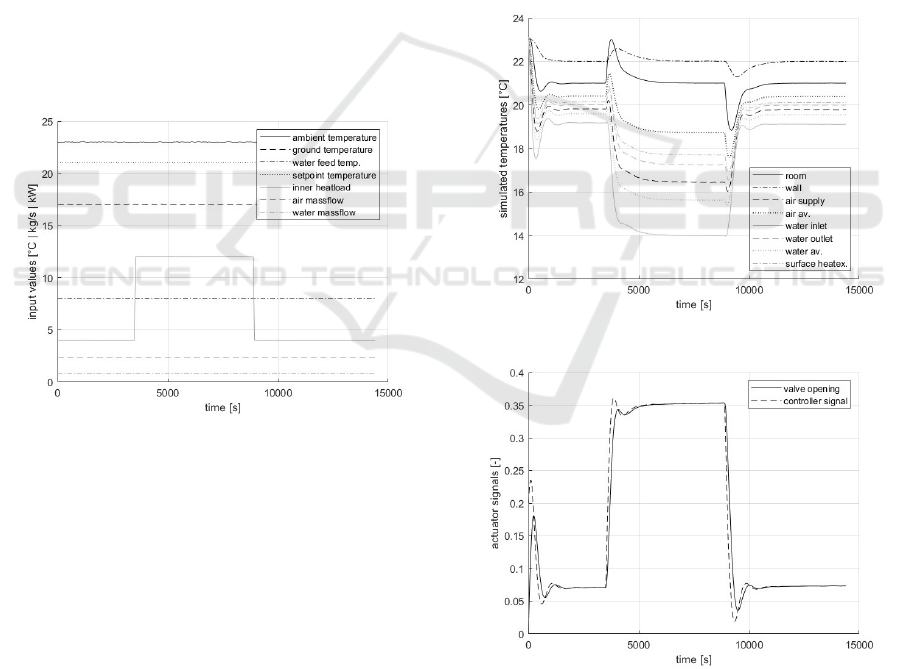
Figure 3 presents the computed temperature trends,
including the states: ϑ
wall
, ϑ
w,av
, ϑ
ex,w
, and the output
and auxiliary variables: ϑ
r
, ϑ
sup
, ϑ
w,in
, ϑ
w,out
. Figure
4 shows the controller signal u
controller
and the valve
position x
valve
. Based on experience with precision
climatization, the results appear reasonable.
Notably, the responses to the up and down step
of the inner heatload differ qualitatively from each
other, particularly in the trend of the valve opening
x
valve
. This difference could be attributed to the non-
linearities of the mixing valve’s sub-model, as other
variables in multilinear terms are held constant.
Further research into other air conditioning sys-
tems, especially those using variable airflow and sys-
tems with humidification and dehumidification re-
quirements, may reveal more of such behavior.
Figure 3: Simulated temperature signals.
Figure 4: Simulated control signal and valve opening.
SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
446

6 CONCLUSION
Implicit MTI models prove to be a suitable exten-
sion of the eMTI class for modeling complex HVAC-
systems. These models can directly represent most
physical laws and equations of HVAC systems, and
offer the advantage of being a closed model class,
simplifying component-based modeling and the use
of standardized methods. They can be utilized in
model-based applications, like nonlinear model pre-
dictive control to optimize competing goals, like en-
ergy consumption, comfort and technical compli-
ances.
However, there are some limitations of the appli-
cability of the iMTI class in HVAC systems. Non-
integer exponents can’t be represented by the iMTI
formula, which may arise from empirical analysis for
calculating convection heat transfer coefficients or dy-
namic flow resistances.
7 OUTLOOK
To account for the cooling of air below the saturation
temperature ϑ
sat
, which would involve the air cooler
operating in a wet mode where condensation occurs
and the air dehumidifies, additional binary signals are
required. The resulting system would be a hybrid sys-
tem with both binary and continuous signals, as well
as additional inequality constraints. Future research
will focus on investigating how binary variables can
be implemented and simulated within the iMTI class.
Furthermore, the overall system can be potentially
reduced further by redundant equations, variables and
unnecessary states. This reduces storage capacity and
computation time. Future research will explore auto-
mated methods for reduction of iMTI models.
ACKNOWLEDGMENTS
T.W. (DESY) acknowledges funding of the technical
design phase of Petra IV granted by the Beh
¨
orde f
¨
ur
Wissenschaft, Forschung, Gleichstellung und Bezirke
(BWFGB) of the Freie und Hansestadt Hamburg
under the contract BWFG/F|97236, as well as by
the Bundesministerium f
¨
ur Bildung und Forschung
(BMBF) under the contract DES21TDR.
REFERENCES
J
¨
ores, N., Kaufmann, C., Schnelle, L., Y
´
a
˜
nez, C., Pangalos,
G., and Lichtenberg, G. (2022). Reduced cp represen-
tation of multilinear models. Proceedings of the 12th
International Conference on Simulation and Modeling
Methodologies, Technologies and Applications.
Kruppa, K. (2017). Comparison of tensor decompo-
sition methods for simulation of multilinear time-
invariant systems with the mti toolbox * *this work
was partly supported by the project observe of the
federal ministry for economic affairs and energy ger-
many (grant-no.: 03et1225b). IFAC-PapersOnLine,
50(1):5610–5615.
Lichtenberg, G., Pangalos, G., Cateriano Y
´
a
˜
nez, C., Luxa,
A., J
¨
ores, N., Schnelle, L., and Kaufmann, C. (2022).
Implicit multilinear modeling. at - Automatisierung-
stechnik, 70(1):13–30.
Pangalos, G., Eichler, A., and Lichtenberg, G. (2013). Ten-
sor systems - multilinear modeling and applications.
Proceedings of the 3rd International Conference on
Simulation and Modeling Methodologies, Technolo-
gies and Applications.
Pangalos, G., Eichler, A., and Lichtenberg, G. (2014). Hy-
brid multilinear modeling and applications. Advances
in Intelligent Systems and Computing, page 71–85.
Yao, Y. and Yu, Y. (2018). Modeling and control in air-
conditioning systems. Springer Berlin.
APPENDIX
Parameters
A
a
A
f loor
A
w
20.8m
2
102.3m
2
5.22m
2
A
wall
c
d
c
ex
240.8m
2
1006
J
/kgK 477
J
/kgK
c
f loor
c
v
c
w
900
J
/kgK 1860
J
/kgK 4200
J
/kgK
c
wall
h
0
k
a
650
J
/kgK 2.501 × 10
6
J
/kg 600
W
/m
2
K
k
f loor,in
k
f loor,out
K
I
2
W
/m
2
K 2
W
/m
2
K −2 × 10
−4
1
/Ks
K
P
k
w
k
wall,in
−0.1
1
/K 1000
W
/m
2
K 3
W
/m
2
K
k
wall,out
m
a
m
ex
3
W
/m
2
K 0.4341kg 42.5kg
m
f loor
m
r
m
w
70000kg 418.8kg 27.75kg
m
wall
T
valve
η
ex
770.4kg 120s 0.85
Implicit Multilinear Modeling of Air Conditioning Systems
447