Joint Stiffness Adjustment of a Pneumatic Driven Exoskeleton

Pavel Venev

, Dimitar Chakarov

and Ivanka Veneva

Institute of Mechanics, Bulgarian Academy of Sciences, “Acad. G. Bonchev” str., Block 4, Sofia 1113, Bulgaria

Keywords: Exoskeleton, Upper Limb, Transparency, Pneumatic, Cylinders, Stiffness, Torque, Air Pressure,

Closed Chambers, Gravity Compensation.

Abstract: The work studies an exoskeleton on the upper limb intended for rehabilitation and training. To meet the

requirements of rehabilitation exoskeletons for transparency on the one hand and efficiency on the other, a

pneumatic actuation with a wide range of control pressure is offered. The subject of the work is the

development of a pneumatic drive that allows simultaneous adjustment of stiffness and torque in the joints of

the exoskeleton. For this purpose, pressure in the cylinder chambers both higher and lower than atmospheric

is used. The work presents the structure of the exoskeleton and a model of pneumatic actuation in the joints

of the exoskeleton. Equations are derived for the torque and joint stiffness resulting from the elasticity of the

air in the closed chambers of the pneumatic cylinders. The work proposes one approach to adjust the stiffness

at certain joint position. In this position, the joint torque is varied by creating pressure profiles in the two

chambers, so the joint stiffness is adjusted in addition to the joint torque. The change in joint torque due to

elastic deviations from the set position is also evaluated. An example of compensating gravity loads and

providing transparency through pneumatic actuation is shown.

1 INTRODUCTION

An alternative to conventional manual therapy for

improving motor function in post-stroke patients is

the use of robotic exoskeletons for rehabilitation

(Manna, 2018). The rehabilitation exoskeleton must

be able to create a large force to support, assist and

guide the patient's arm in the early stages of recovery,

as well as to follow the human arm without resistance

by responding to the movements performed by the

patient in the full recovery stage (Jarrasse, 2014).

Therefore, in the control of rehabilitation

exoskeletons, two ideal modes can be defined that

encompass all therapeutic interventions: 'robot in

charge' and 'patient in charge' (Veneman, 2006). In

the "robot in charge" mode, it is important that the

robot has sufficient force and power to realize the

desired motion with relatively high impedance. In the

“patient in charge” mode, it is important that the

interaction forces between the exoskeleton and the

human are low, in other words, the perceived

https://orcid.org/0000-0001-7809-3540

https://orcid.org/0000-0002-2312-5725

https://orcid.org/0000-0001-5501-7668

impedance of the patient must be low. The key feature

here is transparency.

In order to provide safety and transparency to the

interaction, there are two main approaches to change

the mechanical impedance of the structure: active and

passive. Electric motors and other active actuators are

used to control the impedance of rehabilitation

exoskeletons through an active approach. Active

impedance control is based on the use of sensors and

feedback. Impedance control successfully manages

patient-exoskeleton interaction in all modes of

therapeutic interventions (Courtois G., 2021).

The passive approach involves a natural and

inherently safe actuator. Pneumatic actuation has a

natural compliance and allows to achieve inherent

safety and transparency in the rehabilitation process

in a passive manner (Morales, 2011). Pneumatic

actuation also allows impedance control via the active

approach. There are different types of pneumatic

actuators. The best known are conventional

pneumatic cylinders and rotary pneumatic motors. On

the one hand, they are characterized by large size,

Venev, P., Chakarov, D. and Veneva, I.

Joint Stiffness Adjustment of a Pneumatic Driven Exoskeleton.

DOI: 10.5220/0012119200003546

In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 361-368

ISBN: 978-989-758-668-2; ISSN: 2184-2841

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

361

high weight and rigidity of construction, but on the

other hand, when mounted in the fixed base, they

provide the advantages of pneumatic actuation.

Pneumatic actuators are usually operated at

pressures higher than atmospheric pressure. Recently,

some soft pneumatic actuators that are activated by

vacuum have been developed (Yang D., 2017). Using

the effect of mechanical deformation to generate

controlled force, vacuum-actuated mechanisms have

been successfully developed and used for soft robotic

systems (Matthew A., 2017). Vacuum actuators have

many advantages over positive pressure actuators.

For example, this type of actuator offers implicitly

safe operation as the actuation force is limited by the

magnitude of atmospheric pressure (Tawk Ch., 2019),

also this leads to improved actuator life and

durability.

An upper limb pneumatic powered exoskeleton

has been developed for training and rehabilitation

assisted by interactions in virtual scenes (Chakarov

D., 2019). A study was conducted where the

exoskeleton driven by pneumatic cylinders with

positive pressure was compared with the case where

the exoskeleton was driven by pneumatic cylinders

with vacuum pressure (Chakarov D., 2022). This

study shows that vacuum pressure drive reduces

stiffness and results in high transparency and patient

safety. However, low stiffness is associated with poor

force response and low efficiency when performing

"robot-in-charge" operations. The combination of

transparency requirements on the one hand and

efficiency requirements on the other can be achieved

by pneumatic actuators with a wide range of control

pressures.

The subject of this work is the development and

investigation of a pneumatic actuation for the

exoskeleton that allows simultaneous adjustment of

stiffness and torque in the joints of the exoskeleton.

The goal of the work is to create an approach to adjust

the stiffness of the joint and the torque in the joint by

driving the pressures in the chambers both higher and

lower than atmospheric pressure.

2 STRUCTURE AND MODEL OF

PNEUMATIC ACTUATION IN

EXOSKELETON JOINTS

A prototype of a lightweight upper limb exoskeleton

has been developed by the authors (Chakarov D.,

2022). The mechanical structure of the exoskeleton

consists of two arms. Each arm includes pairs of

identical rotational joints for the movements of the

clavicle J1, J2, shoulder J3, J4 and elbow J5, J6, as

shown in Figure 1a), b). The joints have the following

range of movement: J1(15°), J2 (15°), J3(120°), J4

(120 °), J5 (150 °), J6 (135 °). Each arm has a total of

6 degrees of mobility, mimicking the natural

movement of the human arm from back to elbow.

Each arm of the exoskeleton has six movable

segments (1, 2, 3, 4, 5 and 6) made primarily of

aluminium alloy. Plastic shells with straps are placed

on the segments for attachment to the human limb

(Figure 1b). This structure was chosen for designing

the arm exoskeleton using uniform universal joints

and thus avoid more complex solutions involving

circular guide and triaxial joints.

J2 J3

Figure 1: Exoskeleton of the upper limbs: a) structural

scheme; b) prototype.

For each joint of the exoskeleton, a drive unit

including pneumatic cylinders and cable

transmissions was created. The drive unit of each

joint is built as a separate device located in the fixed

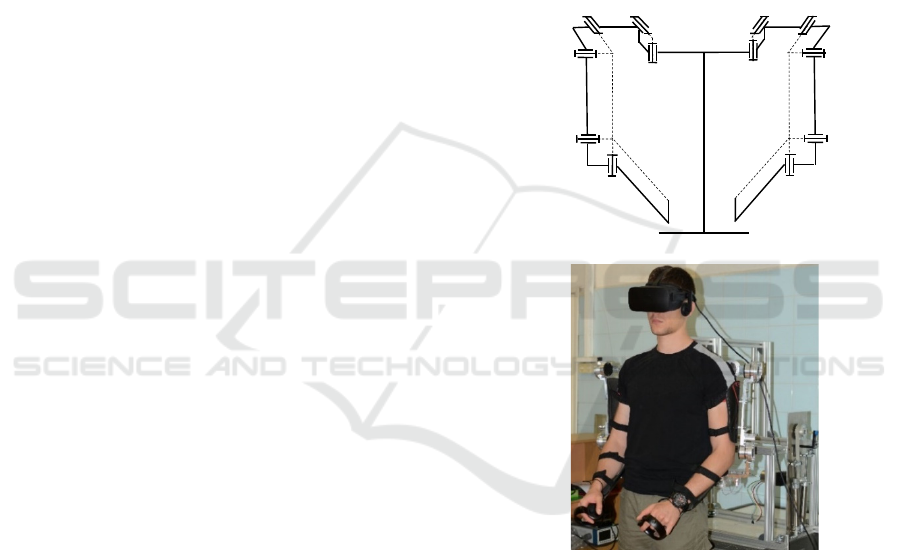
base. A scheme of the drive unit is shown in Figure 2.

The base has a bearing wheel 1 with a cable reel R1

mounted on it. Bowden cables T1, T2 are used to

connect the reel R1 and a similar reel located in the

exoskeleton joint. The radius of reel R

is r = 0.032

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

362

Figure 2: Scheme of the pneumatic drive of exoskeleton

joints.

The pneumatic drive unit includes a pair of

pneumatic cylinders C1, C2 mounted in the base and

a belt transmission as shown in Figure 2. Pneumatic

cylinders with a diameter of D = 0,032 m are used.

The areas on either side of the cylinder piston are s

804 10

-6

m and s

= 725 10

-6

m. The transmission

includes a timing belt B

and an additional wheel 2

for transmitting the motion from the pneumatic

cylinders to the wheel 1. The cylinders

simultaneously drive opposite sides of the belt B1.

The left chamber of one cylinder is connected to the

right chamber of the other cylinder by piping, and the

other right and left chambers are connected by

another piping (Figure 2). The piping of each pair is

connected to three parallel valves, one of which

supplies pressurized air to the chambers, the other

connects the chambers to vacuum pressure, and the

third connects the chambers to atmospheric pressure.

Pressure sensors are installed on each line.

The work evaluates the interaction between the

patient and the exoskeleton in so-called "patient in

charge" modes. In this mode, the exoskeleton does

not generate active forces. The resisting forces are

determined only by the mechanical impedance of the

exoskeleton. The resisting force applied to the

operator's hand is determined by the inertial,

frictional and gravitational forces as well as the

elastic forces of the pneumatic actuator.

The joint torque Q

of the resistive force applied

to the operator's arm to overcome the mechanical

impedance of the exoskeleton is determined

according to equation:

pgfr

QQQQQ +++=

(1)

Above: Q

presents the torque created by the

motor and the transmissions inertia as well as the

exoskeleton inertia; Q

represents the friction torque

which is mainly the result of the friction forces

generated in pneumatic actuators and Bowden cables;

is the torque created by the exoskeleton gravity;

is a difference of torques Q

and Q

produced

by the forces in the two pneumatic cylinders,

represented by the equality

pbpap

QQQ −=

(2)

If one of the chambers of the pneumatic cylinders

closes, it generates an elastic force caused by the

change in the volume of the enclosed air. The

variation of the chamber volume is calculated from

the initial piston position X

as presented in Figure 2.

Assuming that air is an ideal gas undergoing an

isothermal process (Czmerk, A., 2017), the rate of

change of pressure p and the change of volume V in

the closed chamber of the cylinder can be expressed

by the equation of the polytrophic process

CVp =

(3)

where C is a constant.

Once in the initial position of the cylinders X

(Figure 2), the chamber a of the pneumatic cylinders

is closed with a pressure p

and the volume V

(a)

of the

chamber is represented as a function of the piston area

and chamber length, equation (3) takes the form:

a210

C)ss(Xp =+

(4)

where s

and s

are the areas on either sides of the

piston and C

is a constant.

After the arm movements are performed, the

piston makes a deviation x from the initial position X

(Figure 2) and the pressure p

in the closed chamber

changes. After that, equation (3) should take a new

form:

a210a

C)ss)(xX(p =+−

(5)

The above equations give the equality for the pressure

change p

as a function of piston deflection x

−

(6)

The torque of the elastic force in chamber a at

deviation of the pistons x from the initial position X

is obtained by the equation

)rs(s

−

(7)

where r is the radius of reel R

of Figure 2.

In the same way, when in the initial position of the

cylinders X

, chamber b is closed with pressure p

and the piston makes a deviation x from the initial

Joint Stiffness Adjustment of a Pneumatic Driven Exoskeleton

363

position X

, (Figure 2), equation (3) allows to draw up

the following equalities

b210

210

C)ss)(xXL(p

)ss)(XL(p

=++−=

=+−

(8)

xX-L

)X-(Lp

(9)

where L is the cylinder length and C

is a constant.

The equation for the torque of the elastic actuator

due to the displacement of the pistons x from the

initial position X

in chamber b is obtained in a similar

way

)rs(s

xX-L

)X-(Lp

(10)

If either of the chambers a or b of the cylinders

is open to the atmosphere, the air in it does not change

its pressure and volume, so that the moments

generated by the pneumatic forces in the chambers

are constant as defined by the equations

r)s(spQ

21atmpa

(11)

r)s(spQ

21atmpb

(12)

In equations (5) - (10) piston deviation x is

determined by the deviation q at the joint angle and

the radius r of the wheel R

as follows

(13)

The behavior of closed pneumatic cylinders

according to (7) and (10) behaves like a variable

compliance spring. The stiffness of the joint driven by

pneumatic cylinders can be determined as a derivative

of the joint torque (2) about the joint deviation,

according to the equality:

pbpap

K −=

∂

−

∂

(14)

After differentiation of equations (7) and (10),

taking into account (13), the equations for the joint

stiffness as a result of the elasticity of the air in

chambers a and b are obtained as follows

)rs(s

)x(X

K +

−

−=

(15)

)rs(s

)xX-(L

)X-(Lp

K +

−=

(16)

If one of the chambers is open to the atmosphere,

according to (11) (12) and (14) it follows that

p(a,b)

=const. and the joint stiffness in chambers a and

b is

(17)

(18)

3 JOINT STIFFNESS

ADJUSTMENT

In this work, the possibility of adjusting the stiffness

in a certain joint position is investigated. In this

position, the joint torque changes linearly for 10

values, from zero at the first point to one positive

value at the last point. For each point, the pressures in

the two chambers are changed so that the joint

stiffness is adjusted in addition to the joint moment.

The joint moment and joint stiffness are evaluated at

the piston initial location corresponding to the certain

joint position when the deviations from this location

are zero (x=0). The length of the cylinder and the

initial location of the piston are selected respectively

L=0.125 m and X

=0.0625 m (Figure 2). According

to (2), (7), (10), the pressure in the chambers is

changed linearly to obtain a linear moment variation.

Three pressure variation profiles are proposed: A.

Generation of minimum stiffness by vacuum

pressure; B. Variable stiffness generation with

vacuum pressure and chamber opening; C.

Generation of high stiffness by pressures higher than

atmospheric pressure.

A. Generation of minimum stiffness by

vacuum pressure.

Vacuum pressure in chamber b of the cylinders

is used to generate low stiffness values. Chamber a in

this phase is open to the atmosphere p

atm

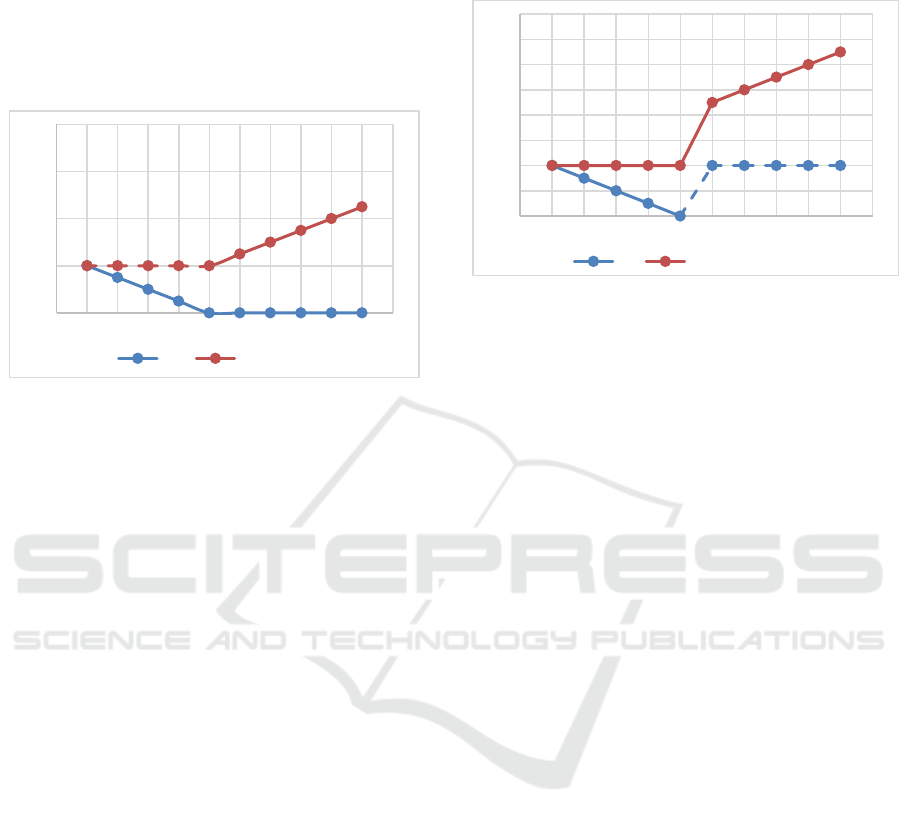
. Figure 3

shows the pressure variation in chamber a and in

chamber b at which the joint moment Q

increases

linearly. In the first phase, the pressure in chamber b

drops smoothly from p

=100 kPa and reaches full

vacuum p

=0, and chamber a is open p

atm

, and

generates no stiffness. The joint stiffness is

determined by relation (14, 16 and 17) for x=0 and

the joint moment is determined by relations (2), (10)

and (11) for x=0.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

364

In the second phase, chamber a closes and the

pressure in it increases smoothly, while the pressure

in chamber b is kept p

=0. In this case both chambers

are closed, the joint stiffness is determined by

equations (14), (15) and (16) for x=0 and the joint

moment is determined by equations (2), (7) and (10)

for x=0.

Figure 3: Profile A of pressure variation in chambers a and

b of the pneumatic cylinders.

Figure 6 shows the variation of joint moment from

0 to 11. 3 Nm as well as the variation of joint stiffness

at the ten pressure points. The joint stiffness is

minimum in the case when one chamber has full

vacuum p

=0 and the other chamber is open to the

atmosphere. The moment in this position is

determined by the atmospheric pressure p

=100 kPa.

Further the moment increases as chamber a is closed

with higher pressures p

>100 kPa, at which the

stiffness also increases.

B. Variable stiffness generation with vacuum

pressure and chamber opening.

Here, a vacuum pressure profile is proposed as a

modification of profile A, in which the stiffness is

increased by opening the vacuum chamber and using

atmospheric pressure.

Figure 4 shows the pressure variation in chamber

a and chamber b at which the joint moment Q

increases linearly. In the first phase, the pressure in

chamber b drops smoothly from atmospheric pressure

=100 kPa to full vacuum p

=0, and chamber a is

closed in this phase with atmospheric pressure p

=100

kPa. Since both chambers are closed the joint stiffness

is determined by the relation (14), (15) (16) for x=0

and the joint moment is determined by equations (2),

(7) and (10) for x=0.

In the second phase, chamber b is open to the

atmosphere, (p

= p

atm

)

and in chamber a, the pressure

increases by such values that the moment in the joint

increases linearly. In this case, chamber a is closed

and chamber b is open and the joint stiffness is

determined by relationships (14), (15) and (18). The

moment in the joint is determined by (2), (7) and (12).

The piston deviations are zero (x=0).

Figure 4: Profile B of pressure variation in chambers a and

b of the pneumatic cylinders.

Figure 6 shows the variation of joint moment (2)

as well as the variation of joint stiffness (14). The

joint stiffness changes in a similar way as in profile

A, but at higher values. In contrast to the previous

case, the increase in stiffness is achieved by chamber

a being closed at a pressure equal to atmospheric in

the first phase, and chamber b being opened to

atmosphere in the second phase. Switching between

the two stiffness values is easily achieved by closing

and opening to atmosphere the chambers of the

cylinders.

C. Generation of high stiffness by pressures

higher than atmospheric pressure.

To generate high stiffness, different profiles can

be created at pressures higher than atmospheric

pressure and the chambers closed. Thus, it is possible

to achieve the desired joint moment and high

stiffness. Figure 5 shows a variation of pressures in

chamber a and chamber b in which the joint moment

(2) increases linearly and the pressure profile is

similar to that of cases A and B, but at higher values.

In the first phase, chamber a is closed with pressure

=200 kPa, and the pressure in chamber b drops

smoothly from p

=200 kPa to p

atm

. Since both

chambers are closed, the moment is determined by

(2),(7), and(10) and the joint stiffness is determined

by the relation (14),(15), and (16). The piston

deviations are zero (x=0).

In the second phase, chamber b is closed with

pressure p

=200 kPa , and the pressure in chamber a

increases by such values that the moment in the joint

increases linearly. Here both chambers are closed, the

joint moment and joint stiffness are determined by the

same relationships.

100

200

300

400

01234567891011

pa[kPa]

point No

pb[kPa]

pb pa

100

150

200

250

300

350

400

01234567891011

pa[ kPa]

pb[kPa]

point No

pb pa

Joint Stiffness Adjustment of a Pneumatic Driven Exoskeleton

365

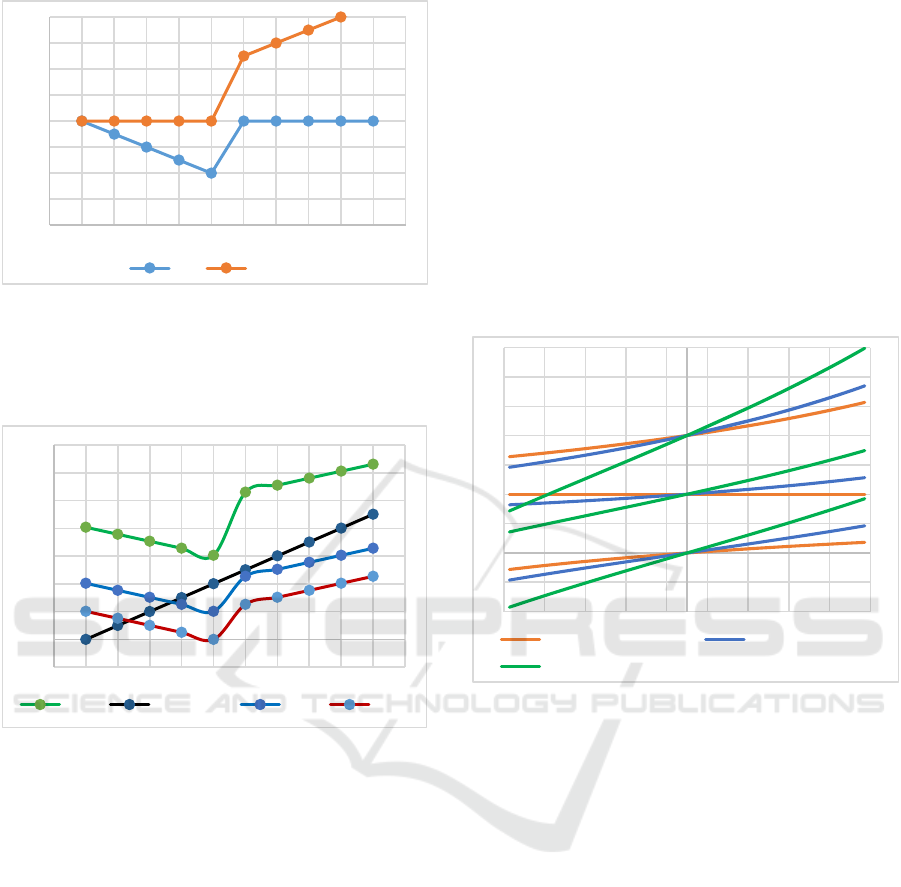
Figure 5: Profile C of pressure variation in chambers a and

b of the pneumatic cylinders.

Figure 6 shows the variation of joint moment (2)

as well as the variation of joint stiffness (14).

Figure 6: Variation in joint torque and joint stiffness for the

three pressure profiles A, B and C.

The joint stiffness profile is similar to the previous

cases, but the stiffness values are higher. Of course it

is possible to generate stiffness with other

modification profiles. A characteristic of the

proposed profiles A, B and C is that a minimum

stiffness is generated not at zero value but at an

average value of the joint moment (5Nm for the

considered case). It can be equal to an average value

of the joint moment created by static loads on the

exoskeleton for the position under consideration.

Transparency in this position will be maximized. At

any other time in the joint, the stiffness will be higher.

4 JOINT TORQUE ASSESSMENT

When the patient deviates the exoskeleton from the

initial position in which any of the cylinder chambers

is closed, resistive forces arise as a result of the

elasticity of the closed gas. When both chambers are

closed the moment from the elastic forces is

determined from equations (2), (7) and (10) as a

function of the deviation from the initial position x.

For a deviation x = [-0.014; 0.014] m which

corresponds according to (13) to a deviation in the

joint angle q = [-0. 436;0. 436] rad, the variation of

the joint moment is shown on Figure 7. The figure

shows the variation of the moment in the joint from

initial values of 0, 5 and 10 Nm (points 1, 5 and 9 in

the graph of Figure 6) at three stiffness values

corresponding to the three pressure profiles A, B and

C in the graph of Figure 6. Profile A shows the

smallest moment variations at all three points.

Figure 7: Variation of the joint torque Qp from initial values

of 0, 5 and 10 Nm, corresponding to the three pressure

profiles A, B and C.

In the "patient in charge" mode, when the patient

performs independent movements, the exoskeleton

should provide transparency. For this purpose, the

resistive forces due to the mechanical impedance of

the exoskeleton must be compensated. In low

dynamic mode, only resistance of gravity and

stiffness can be taken into account. Then torque (1) of

forces applied to the patient's hand is sum of moments

of gravity forces and compensatory forces of the

pneumatic drive

pgh

QQQ +=

(19)

In order to achieve transparency, compensatory

forces with minimum stiffness must be generated. To

compensate for gravity loads, it is appropriate to use

the moment from the pneumatic drive achieved at

pressures generating the lowest stiffness. Thus, with

profile A (Figure 6), the lowest stiffness value is

achieved at 5 Nm. Figure 8 shows the variation of the

moment from the pneumatic drive at an initial value

100

150

200

250

300

350

400

01234567891011

pa[kPa]

pb[kPa]

point No

pb pa

-2,5

0,0

2,5

5,0

7,5

10,0

12,5

15,0

17,5

01234567891011

[Nm/rad

point No

Qp [Nm]

K (C) Qp (A,B,C) K (B) K (A)

-5,0

-2,5

0,0

2,5

5,0

7,5

10,0

12,5

15,0

17,5

-0,45 -0,35 -0,25 -0,15 -0,05 0,05 0,15 0,25 0,35 0,45

Qp [Nm

]

q [rad]

Pressure profile A Pressure profile B

Pressure profile C

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

366

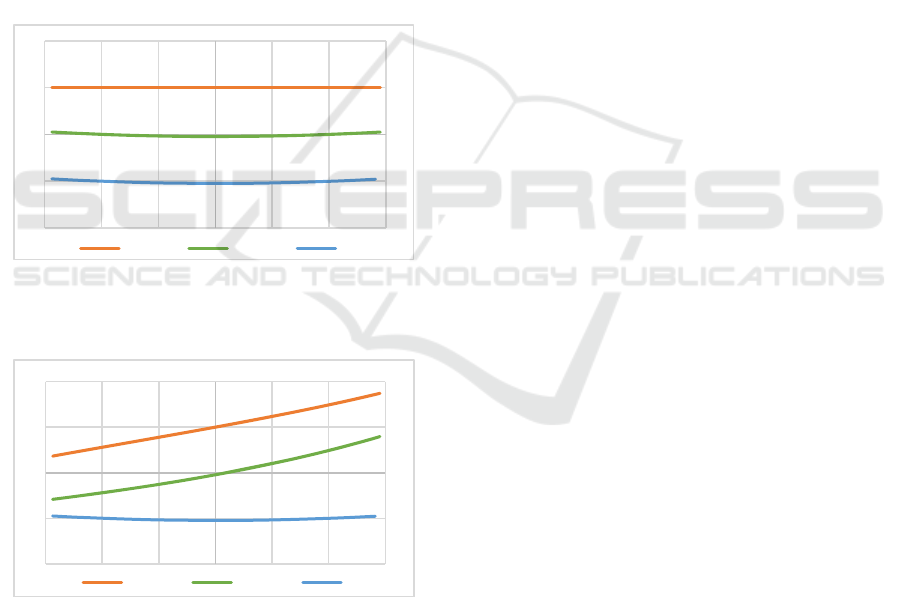
of 5 Nm and the pressures in the chambers

corresponding to profile A. The figure shows the

variation of the gravitational moment in the position

of the joint with deviations q = [0.436;0.436] rad. The

resultant moment at the joint according to (19) is also

shown in the graph. With small deviations, it

oscillates around a zero value, ensuring transparency

of the interaction with the patient. Compensating for

larger or smaller gravity moments with this pressure

profile also results in low resistive forces.

In the 'robot in charge' mode, when the

exoskeleton has to implement not only compensation

but also the desired movement, it is appropriate to

apply a pressure profile similar to the proposed

profile C. Figure 9 shows a case when with a torque

in the joint of 5 Nm and pressure profile C, the same

gravity loads are compensated. Transparency here is

lower. Deviations from the set position lead to

resistance with significant torque deviations.

Figure 8: Joint torques deviations after gravity

compensation with pressures in the chambers

corresponding to profile A.

Figure 9: Joint torques deviations after gravity

compensation with pressures in the chambers

corresponding to profile: C.

5 CONCLUSIONS

The work studies an exoskeleton on the upper limb

intended for rehabilitation and training. A pneumatic

drive with a wide range of control pressure is

available to meet the requirements of rehabilitation

exoskeletons for transparency on the one hand and

efficiency on the other. Cylinder chamber pressures

both higher and lower than atmospheric are used. The

development of a pneumatic drive that allows

simultaneous adjustment of stiffness and torque in the

joints of the exoskeleton is included in the work. The

work presents the structure of the exoskeleton and a

model of pneumatic actuation in the joints of the

exoskeleton. Equations are derived for the torque and

joint stiffness resulting from the elasticity of the air in

the closed chambers of the pneumatic cylinders. In

the work, an approach for adjusting the stiffness at a

certain position of the joint is proposed. In this

position, the joint torque is varied by creating

pressure profiles in the two chambers, so that the joint

stiffness is adjusted in addition to the joint torque. A

characteristic of the proposed profiles is that the

minimum stiffness is generated not at zero value, but

at an average value of the joint torque. To compensate

the gravity loads by the pneumatic drive in a certain

position, it is appropriate to use the moment

corresponding to the lowest stiffness. Then

transparency in this position will be best. An example

of compensation for gravity when providing

transparency through pneumatic activation is shown

in the work.

ACKNOWLEDGEMENTS

This research was supported by the Operational

Program "Science and education for smart growth"

through the project “MIRACle”, № BG05M2OP001-

1.002-0011 to which the authors would like to express

their deepest gratitude.

REFERENCES

Manna S. K., Dubey V. N., (2018). Comparative study of

actuation systems for portable upper limb exoskeletons,

Medical Engineering and Physics, 60, 1–13.

Jarrasse, N., T. Proietti, et al., (2014). Robotic

Exoskeletons: A Perspective for the Rehabilitation of

Arm Coordination in Stroke Patients, Frontiers in

Human Neuroscience, Vol.8, Art.947, 1-13.

Veneman, J.F., R. Ekkelenkamp, et al., (2006). A series

elastic- and bowden-cable-based actuation for use as

torque actuator in exoskeleton-type robots, The Int.

Journ. of Rob. Research, vol. 25(3), 261-281.

Courtois G., Chevrie J., Dequidt A., Bonnet X. and Pudlo

P. (2021). Design of a Rehabilitation Exoskeleton with

Impedance Control: First Experiments. Proc.of the

-10

-5

-0,45 -0,30 -0,15 0,00 0,15 0,30 0,45

q[rad]

[Nm]

Qp Qh Qg

-10

-5

-0,45 -0,30 -0,15 0,00 0,15 0,30 0,45

q[rad]

[Nm]

Qp Qh Qg

Joint Stiffness Adjustment of a Pneumatic Driven Exoskeleton

367

18th Int. Conf. on Informatics in Control, Automation

and Robotics – ICINCO 2021, 469-476.

Morales R., et al., (2011). Pneumatic robotic systems for

upper limb rehabilitation, Med. Biol. Eng. Comput. 49,

1145–1156.

Yang D., M. S. Verma, E. Lossner, D. Stothers, G. M.

Whitesides, (2017). Negative-pressure soft linear

actuator with a mechanical advantage. Adv. Mater.

Technol., vol.2, issue 1, 1600164, 1-6.

Matthew A., Robertson and Jamie Paik, (2017). New soft

robots really suck: Vacuum-powered systems empower

diverse capabilities. Science Robotics, vol. 2, Issue 9,

doi: 10.1126/scirobotics.aan6357, 1-27.

Tawk, C., Spinks, G. M., in het Panhuis, M. & Alici, G.

(2019). 3D Printable Linear Soft Vacuum Actuators:

Their Modeling, Performance Quantification and

Application in Soft Robotic Systems. IEEE/ASME

Transactions on Mechatronics, 24 (5), 2118-2129.

Chakarov D., Veneva I., Tsveov M., Mitrouchev P., Venev

P. (2019), Design of a Two Arms Exoskeleton as Haptic

Device for Virtual Reality Applications, Lecture Notes

in Mech. Eng., Springer Nature, Chapter 25, 252-262.

Chakarov, D., Veneva, I., Venev, P. (2022). Comparative

Study of a Vacuum Powered Upper Limb Exoskeleton,

Pros. of the 19 th Int. Conf. on Informatics in Control,

Automation and Robotics, ICINCO 2022, 403-410.

Czmerk, A., A. Bojtos, (2017). Stiffness investigation of

pneumatic cylinders, 59th Ilmenau Scientific

Colloquium, Technische Universität Ilmenau, 11 – 15

September, 2017, URN: urn:nbn:de:gbv:ilm1-

2017iwk-148:6, 1-7.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

368