Approximate Homomorphic Pre-Processing for CNNs
Shabnam Khanna and Ciara Rafferty
a
CSIT, Queen’s University Belfast, U.K.
Keywords:
Homomorphic Evaluation, Approximate Computing, ReLU, Convolutional Neural Networks.
Abstract:
Homomorphic encryption (HE) allows computations on encrypted data, making it desirable for use in privacy-
preserving data analytics. However, HE function evaluation is computationally intensive. Approximate
computing (AC) allows a trade-off between accuracy, memory/energy usage and running time. Polynomial
approximation of the Rectified Linear Unit (ReLU) function, a key CNN activation function, is explored and
AC techniques of task-skipping and depth reduction are applied. The most accurate ReLU approximations
are implemented in nGraph-HE’s Cryptonets CNN using a SEAL backend, resulting in a minimal decrease in
training accuracy of 0.0011, no change in plaintext classification accuracy, and a speed-up of 47%.
1 INTRODUCTION
Data privacy and security is ever more vital with per-
sonal data stored on the cloud. Homomorphic encryp-
tion (HE) enables computation directly on encrypted
data, reducing risk of privacy-loss. HE has great po-
tential for privacy-preserving shared computation and
secure outsourced analysis. Despite progress in re-
cent years regarding computations on encrypted data
((Graepel et al., 2012), (Chen et al., 2018),(Boemer
et al., 2019), (Chou et al., 2020)), homomorphic eval-
uation is much less efficient than unencrypted data
evaluation. Moreover, non-polynomial function eval-
uation is non-trivial, and often not possible in many
HE libraries, where functions typically need to be in
polynomial form.
Many ML applications use non-polynomial func-
tions, e.g. logistic regression- or classification-based
neural networks (NNs) (Chen et al., 2018), (Chou et al.,
2020). Neural networks consist of many layers, each
containing non-polynomial functions, e.g. logistic,
exponential, and sine functions, often approximated
as Taylor functions when evaluated homomorphically
(Cheon et al., 2017). Conventionally, higher degree
Taylor polynomials result in a higher accuracy levels,
developing into inefficient, larger depth calculations.
This research investigates non-polynomial function
approximation, to balance performance and accuracy.
Specifically, the Rectified Linear Unit (ReLU) function
is targeted, used in Convolutional Neural Networks
(CNNs), and the impact of applying homomorphic-
a
https://orcid.org/0000-0002-3670-366X
friendly, AC-adapted approximations of ReLU to an
(unencrypted) CNN for image classification is consid-
ered. In this research the approximate HE scheme,
CKKS (Cheon et al., 2017), is used due to its compu-
tation expressed as floating point arithmetic.
This paper is structured as follows: Section 2 de-
tails approximate computing. Section 3 introduces
polynomial approximations of ReLU and AC-adapted
approaches implemented homomorphically. Section 4
deploys the most accurate approximations in an open-
source CNN to determine impact on accuracy.
2 AC TECHNIQUES
One main motivation to deploy AC techniques is to en-
sure energy-efficient technology (Barua and Mondal,
2019). Applications where this performance-accuracy
trade-off is acceptable include machine learning, sig-
nal processing, and big data analytics (Barua and Mon-
dal, 2019). In (Khanna and Rafferty, 2020), task skip-
ping and depth reduction are used to adapt logistic
and exponential functions, represented polynomially
using Taylor series approximation and evaluated ho-
momorphically using CKKS in the Microsoft SEAL
Library (SEAL, 2018). This involved skipping the
highest order term, skipping lower order terms, reduc-
ing the depth by replacing the highest order term with
the highest order term in the depth below. For the ex-
ponential function, the depth reduced approximation
had an average error of 2.42 x 10
−5
compared with
an average error of 0.333321 to the Taylor exponen-
710
Khanna, S. and Rafferty, C.
Approximate Homomorphic Pre-Processing for CNNs.
DOI: 10.5220/0012085400003555
In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 710-715
ISBN: 978-989-758-666-8; ISSN: 2184-7711
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

tial function approximation with no adaptations, with
a 35% speed up. For the logistic function, skipping
the highest order term ( x
9
), provided a 45.5% speed
up with an average error of 2.08 x 10
−6
as opposed
to 1.52 x 10
−7
when no AC technique is applied to
its Taylor series approximation. In this research the
depth reduction process is formalised and applied to
another important non-linear function, ReLU, given its
significant usage in CNNs. Our approach is as follows:
1. Task Skipping (TS): All but the highest and lowest
two terms of the approximation are skipped.
2. Depth Reduction (DR): The MATLAB polyfit
function is used to find the depth reduced approxi-
mation (Mathworks, 2021), using least squares to
approximate a polynomial.
3 ReLU
A CNN is made up of several layers, including an acti-
vation layer, which takes a single number as input and
evaluates a non-linear mathematical operation, adding
non-linearity into the network and enabling complex
predictions. Many non-linear functions, such as Sig-
moid, hyperbolic tangent and Softmax, can be used in
an activation layer. One important activation function
is ReLU , defined as: f (x) = max(0, x) (Hesamifard
et al., 2019). Since non-linear functions must be repre-
sented polynomially for homomorphic evaluation, this
research follows (Chabanne et al., 2017) and (Hesam-
ifard et al., 2019) for polynomial approximations of
ReLU. AC techniques from Section 2 are applied to
these approximations, comparing run-time and accu-
racy. Although the CNN input values are in the interval
[0,255], they are not necessarily the ReLU input val-
ues. Scaling and batch normalisation processes are
used when working with inputs for CNN layers; a
smaller input range is used, assuming that inputs to the
ReLU layer can be scaled.
Cryptonets (Dowlin et al., 2016) provides an early
research into homomorphic CNNs, using the MNIST
dataset classification (LeCun et al., 1998). (Chabanne
et al., 2017) use “polyfit” in Python and the Taylor
expansion of Softplus as polynomial approximations
of ReLU with a classification accuracy of 99.30% com-
pared to the Cryptonets accuracy of 98.95% (Dowlin
et al., 2016). (Hesamifard et al., 2019) list five meth-
ods to approximate ReLU: Numerical analysis, Taylor
Series, Standard Chebyshev polynomials, Modified
Chebyshev polynomials and their approach based on
the derivative of ReLU. They show an encrypted re-
sult of classification accuracy of 99.52% and a run-
time of 320s compared to 697s in Cryptonets (Dowlin
et al., 2016). Following this, 12 ReLU approxima-
tions are used in this research, as follows: 5 approx-
imations of different orders using “polyfit” from the
Python numpy package (community, 2020); 3 approxi-
mations derived from Taylor polynomials of Softplus,
f (x) = ln(1 + e
x
) ; and 4 Chebyshev approximations
with input range [0, 250].
All 12 approximations are implemented in PAL-
ISADE, with approximations of order at least 4 and
8 being depth reduced and task skipped respectively.
Table 1 shows the performance and average error of
these approximations. To standardise the methodology
for obtaining DR polynomial approximations and max-
imise accuracy, MATLAB polyfit is used (Mathworks,
2021), where the highest power required for one depth
below the actual depth of the approximation is spec-
ified. For TS approximations (applied to Chebyshev
polynomial approximations only), skipping various
terms were attempted to find the optimal combination.
Note subscript notations
DR
(x) and
T S
(x) correspond
to the DR and TS approximations of the preceding
equation. Equation numbers correspond to those in
Table 1. Each coefficient is defined (and rounded) to
2 decimal places for neatness. However, exact coeffi-
cient values are used in the evaluation.
3.1 Polyfit
Using “polyfit” in Python (community, 2020), as in
(Chabanne et al., 2017) give the following approxima-
tions, with equations 4 and 6 being the depth-reduced
approximations of equations 3 and 5 respectively.
a(x) ≈ 0.20 + 0.50x + 0.20x
2
(1)
b(x) ≈ 0.20 + 0.50x + 0.20x
2
− 0.02x
3
(2)
c(x) ≈ 0.15 + 0.50x + 0.30x
2
− 0.00x
3
− 0.04x
4
(3)
c
DR
(x) ≈ 2.34e+06 − 1.84e+05x
+ 3.24e+03x
2
− 19.79x
3
(4)
d(x) ≈ 0.15 + 0.50x + 0.30x
2
+ 0.00x
3
− 0.02x
4
(5)
d
DR
(x) ≈ 1.01e+06 − 7.96e+04x
+ 1.40e+03x
2
− 8.57x
3
(6)
e(x) ≈ 0.12 + 0.5x + 0.37x
2
− 0.04x
4
+ 0.00x
6
(7)
3.2 Taylor Series
The Taylor expansion of the Softplus function, f (x) =
ln(1+e
x
) , provides a good approximation of the ReLU
function (Chabanne et al., 2017). ReLU approxima-
tions in Equations 8 to 11 with equations 10 and 12
being the DR approximations of equations 9 and 11 re-
spectively. All these approximations using the Taylor
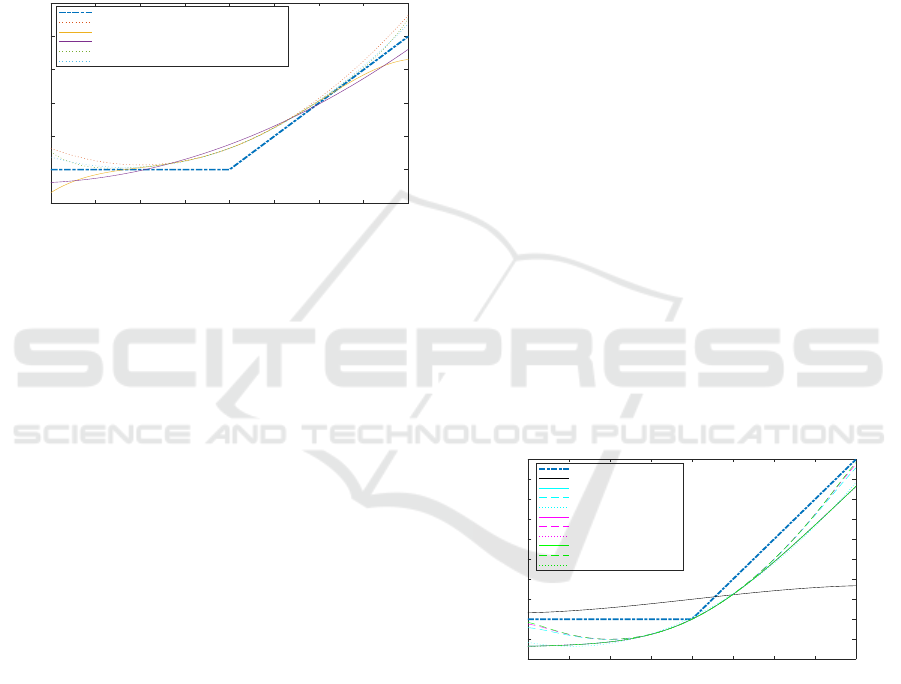
expansion of Softplus are shown in Figure 1.
Approximate Homomorphic Pre-Processing for CNNs
711

f (x) ≈ 0.64 + 0.5x + 0.13x
2
(8)
g(x) ≈ 0.64 + 0.5x + 0.13x
2
− 0.01x
4
(9)
g
DR
(x) ≈ 3.14e+05 − 2.46e+04x
+ 4.35e+02x
2
− 2.65x
3
(10)
h(x) ≈ 0.64 + 0.5x + 0.13x
2
− 0.01x
4
+ 0.00x
6
(11)
h
DR
(x) ≈ −3.92e+09 + 2.77e+08x
− 4.08e+06x
2
+ 1.66e+04x
3
(12)
-4 -3 -2 -1 0 1 2 3 4
Input Value
-1
0
1
2
3
4
5
Evaluation of ReLU
ReLU Exact
f - Taylor expansion of Softplus, order 2
g - Taylor expansion of Softplus, order 4
gDR - Taylor expansion of Softplus, order 3
h - Taylor expansion of Softplus, order 6
hDR - Taylor expansion of Softplus, order 3
Figure 1: Taylor expansions of Softplus, along with the exact
ReLU function and the DR approximations.
3.3 Chebyshev Approximations
Chebyshev polynomial approximations are obtained
using the approach outlined in (Hesamifard et al.,
2017), using the Sigmoid function to approximate
ReLU. The authors of (Hesamifard et al., 2017) per-
form polynomial interpolation to approximate the Sig-
moid function using the roots of Chebyshev polynomi-
als. In this research the roots of a standard Chebyshev
polynomial are used to obtain Chebyshev approxima-
tions of ReLU for degrees 4, 8, 12, 16 polynomials in
the input range [0, 250]. The assumption is that any
input can be scaled as close to this input range as possi-
ble. DR and TS are applied to Chebyshev polynomial
approximations of orders 8, 12 and 16. For TS, skip-
ping all but the largest order term, the x , x
2
, and the
(in this case non-existent) constant term provided the
most accurate TS approximations of the Chebyshev
approximations of ReLU. The Chebyshev polynomials
and their DR and RS approximations are defined as
follows (as in Figure 2.):
- Chebyshev order 4 approximation:
i(x) ≈(5.00e+40) ∗ (1.0e-41)x + (1.0e-41) ∗ (1.14e+40)x
2
+ (1.0e-41) ∗ (7247)x
3
− (1.0e-41) ∗ (1.81e+38)x
4
(13)
- Chebyshev order 8 j
O
(x) with depth-DR, j
DR
(x) and
TS, j
T S
(x) approximations:
j
O
(x) ≈ 0.50x + 0.12x
2
− 7.50e-16x
3
− 0.00x
4
− 5.96e-18x
5
+ 0.00x
6
− 1.98e-19x
7
− 3.05e-6x
8
(14)
j
DR
(x) ≈ 0.05 + 0.50x + 0.08x
2
− 8.95e-16x
3
(15)
j
T S
(x) ≈ 0.50x + 0.12x
2
− 0.00x
8
(16)
- Chebyshev order 12 k
O
(x) with DR, k
DR
(x) and
TS, k
T S
(x) approximations:
k
O
(x) ≈ 0.50x + 0.13x
2
+ 3.54e-18x
3
− 0.01x
4
+ 1.19e-19x
5
+ 0.00x
6
− 1.26e-19x
7
− 0.00x
8
+ 8.11e-21x
9
+ 4.93e-72x
10
− 1.92e-22x
11
− 7.09e-9x
12
(17)
k
DR
(x) ≈ 0.01 + 0.50x + 1.12e-11x
2
− 3.62e-17x
3
− 0.02x
4
(18)
k
T S
(x) ≈ 0.50x + 0.13x
2
− 7.09e-9x
12
(19)
- Chebyshev order 16 l
O
(x) with DR, l
DR
(x) and TS,
l
T S
(x) approximations:
l
O
(x) ≈ 0.50x + 0.13x
2
− 5.94e-17x
3
− 0.01x
4
+ 2611e-17x
5
+ 3.40e-4x
6
− 5.81e-18x
7
− 2.32e-5x
8
+ 6.99e-19x
9
+ 1.37e-6x
10
− 4.75e-20x
11
− 5.93e-8x
12
+ 1.71e-217x
13
+ 1.57e-9x
14
− 2.52e-23x
15
− 1.86e-11x
16
(20)
l
DR
(x) ≈ 0.00 + 0.5x + 0.12x
2
− 6.52e-17x
3
− 0.00x
4
− 2.77e-19x
5
7.79e-05x
6
+ 2.23e-19x
7
(21)
l
T S
(x) ≈ 0.50x − 0.13x
2
− 1.86e-11x
16
(22)
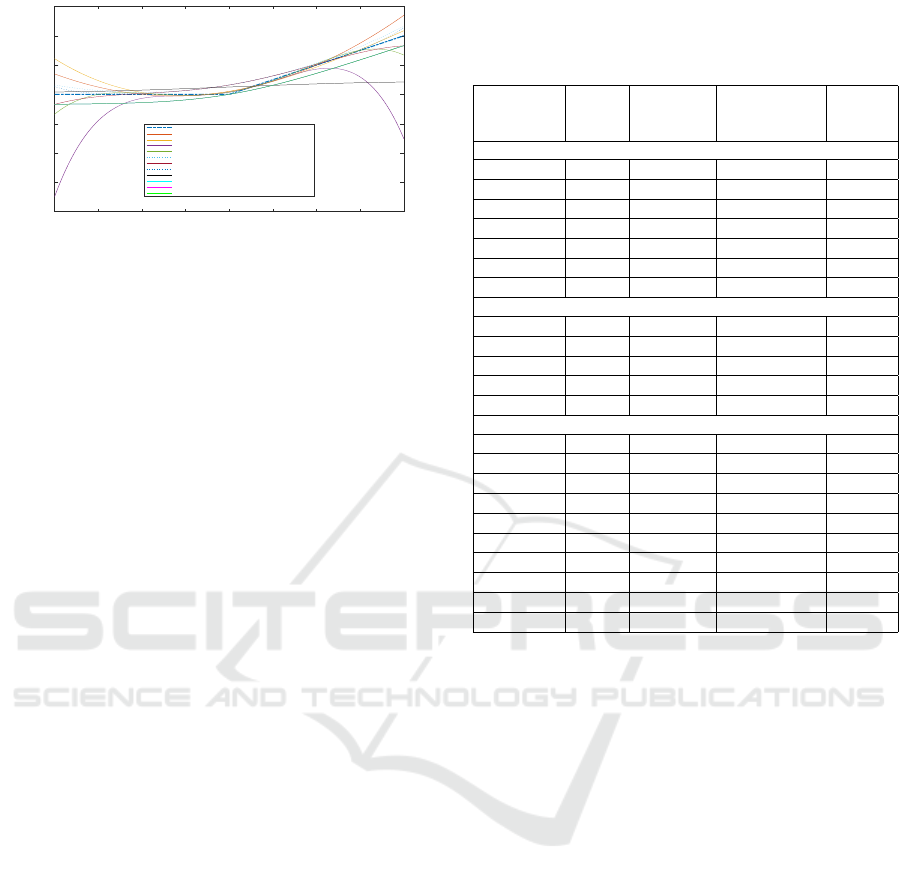
-4 -3 -2 -1 0 1 2 3 4
Input Value
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
Evaluation of ReLU
ReLU Exact
i - Chebyshev, order 4
j - Chebyshev, order 8
jTS - Chebyshev, order 8
jDR - Chebyshev, order 3
k - Chebyshev, order 12
kTS - Chebyshev, order 12
kDR - Chebyshev, order 3
l - Chebyshev, order 16
lTS - Chebyshev, order 16
lDR - Chebyshev, order 7
Figure 2: Chebyshev polynomial approximations, with the
exact ReLU function and TS and DR approximations.
All 12 original approximations (equations 1, 2,
3, 5, 7, 9, 11, 13, 14, 17, 20) are shown in Figure
3. The Chebyshev approximations are more accurate
than other approaches, with the most accurate being
the largest order (16) Chebyshev approximation. Thus,
this is the selected approximation for use in the CNN.
Before applying to a CNN, the ReLU approximations
are implemented in PALISADE to analyse the perfor-
mance/accuracy trade off.
SECRYPT 2023 - 20th International Conference on Security and Cryptography
712

-4 -3 -2 -1 0 1 2 3 4
Input Value
-8
-6
-4
-2
0
2
4
6
Evaluation of ReLU
ReLU Exact
a - Python Polyfit, order 2
b - Python Polyfit, order 3
c - Python Polyfit, order 4
d - Python Polyfit, order 5
e - Taylor expansion of Softplus, order 2
f - Taylor expansion of Softplus, order 4
g - Taylor expansion of Softplus, order 6
h - Chebyshev, order 4
i - Chebyshev, order 8
j - Chebyshev, order 12
k - Chebyshev, order 16
Figure 3: A figure showing all 12 ‘original’ polynomial
approximations of, and the exact the ReLU function.
3.4 Implementation of ReLU
Approximations in PALISADE
This research was implemented on a Linux VM run-
ning on an Intel Core i5-8250U CPU using the CKKS
HE scheme in the Palisade library v1.10.5 (Palisade,
2021). All values in this section are provided to 4 dec-
imal places. The ring size used is 32768 with 8192 in-
put values in the range [-4,4] and other parameters set
to allow 128-bit security according to the HE Standard
(Albrecht et al., 2018). The ReLU approximations out-
lined in Section 3 are implemented and analysed with
respect to accuracy vs performance. The input of raw
form images will always be consistent (input values
between 0 and 255), but change after each CNN func-
tion evaluation, and when evaluated homomorphically,
the inputs per layer are unknown in their raw form and
as they change vastly layer-by-layer. Thus, having an
approach to standardise the input values is important.
Since the actual error for each input value varies
significantly, the average error calculated across the
input range as absolute errors is provided, the impact
of this when running in a CNN may differ. The eval-
uation error is defined as the average error across the
input range for the evaluation of the relevant approx-
imation as compared to the evaluation of the exact
ReLU function. Note two points regarding average
error and amortised running time. Firstly, the ring size
used enables all approximations to be evaluated to the
estimated precision of around 39 bits. However, this
small ring size does pose a larger evaluation error. To
maintain the same parameter settings (including de-
cryption bit accuracy) for all 12 approaches, without
changing the security setting, requires the ring size to
be set as 2048 and thus the slot size (HE batch size)
is 1024. Increasing the ring and slot size significantly
decreases the average evaluation error, however this
impacts on the security level and requires further study.
The performance run-time is the time taken when eval-
uating homomorphically and represented as amortised
run-time, i.e. the run-time per each input value. Since
Table 1: Table shows amortised run-time (milliseconds) and
average error for HE implementation for ReLU approxima-
tions implemented in PALISADE. The amortised run-time
for non-HE implementation is omitted as it is instantaneous.
Equation Degree
Amortised
Run-time
Average
Error
(non-HE)
Average
Error
(HE)
Polyfit approximations
1 2 50.5 ms 1.7031 x 10
−4
0.3134
2 3 99.2 ms 4.1638 x 10
−5
0.3256
3 4 143.1 ms 8.5913 x 10
−4
1.2198
4 (3 DR) 3 97.1 ms 5.8239 x 10
−4
1.5744
5 5 142.6 ms 1.6167 x 10
−4
0.1695
6 (5 DR) 3 97.4 ms 4.1846 x 10
−5
0.2565
7 6 147.4 ms 1.8176 x 10
−5
0.0847
Taylor Series approximations
8 2 48.7 ms 7.8015 x 10
−5
0.3020
9 4 100.1 ms 8.4485 x 10
−5
0.2503
10 (9 DR) 3 96.5 ms 4.3796 x 10
−5
0.2840
11 6 146.9 ms 6.5515 x 10
−5
0.2121
12 (11 DR) 3 96.2 ms 4.5544 x 10
−5
0.2129
Chebyshev approximations
13 4 92.6 ms 3.8584 x 10
−4
0.8359
14 8 233.3 ms 8.2333 x 10
−5
0.4877
15 (14 DR) 3 96.4 ms 7.0558 x 10
−5
0.4896
16 (14 TS) 8 128.9 ms 2.5636 x 10
−5
0.3576
17 12 306.7 ms 8.2396 x 10
−5
0.4880
18 (17 DR) 4 139.1 ms 8.4559 x 10
−5
0.4880
19 (17 TS) 12 158.7 ms 1.4595 x 10
−5
0.3419
20 16 393.8 ms 8.2397 x 10
−5
0.4897
21 (20 DR) 7 219.5 ms 8.2395 x 10
−5
0.4885
22 (20 TS) 16 166.5 ms 9.7406 x 10
−6
0.3402
the run-time for each function evaluation is roughly the
same, no matter the slot size, understanding the total
run-time across all input slots may be more useful.
In Table 1 the equation number ‘ m ( n DR/TS)’,
where m, n are numbers, is read as equation m , which is
equation n with depth-reduction (DR) or task skipping
(TS), e.g. equation 4 (3 DR) is equation 4, the depth-
reduced approximation of equation 3.
Comparing the trends between the evaluation of
the TS, DR and ‘original’ approximations: Although
the TS approach has the same polynomial order as
the ‘original’ approximation, evaluation run-time is
nearly halved, running similarly as DR versions. The
TS approach skips every term between the x
2
and the
highest powered term of the original approximation
and the DR approach uses ‘polyfit’ in MATLAB to
find an approximation as close to the original evalua-
tion as possible but at a lower computational depth. As
Table 1 shows, the DR approximations have similar av-
erage error when compared to original approximations.
However, unexpectedly, every TS approximation is, on
average, more accurate than the original and the DR
polynomial approximations. When evaluating the TS
approximations (unencrypted) the average accuracy
is more than double the average accuracy of the orig-
inal polynomial approximation yet when evaluating
Approximate Homomorphic Pre-Processing for CNNs
713

homomorphically is around a third more accurate than
the original approximation. Figure 2 supports these
conclusions across the input range.
It is important to remember that for performance
(non-HE), only the approximation affects the error, yet
when the same polynomial is evaluated homomorphi-
cally, in addition to the run-time error, there exists an
error created by the CKKS scheme itself. Thus the
analysis focuses on comparing the average errors for
the ‘original’ approximations with the approximations
adapted with AC techniques, rather than comparing
the encrypted vs unencrypted average errors.
Figures 1, 2 and 3 provide a more detailed overview
of errors across the input range than the average evalu-
ation error in Table 1. Table 1 shows that for the first
and second set of approximations, (Python polyfit and
Taylor expansion of Softplus), when DR is applied
to approximations 3 and 5 and 9 and 11, the average
evaluation error on unencrypted evaluation is smaller
than the error of the original approximation. How-
ever, when evaluated homomorphically, the average
error is much larger than the original error, due to the
additional error in the approximate HE scheme itself.
For the Chebyshev approximations, and higher order
approximations, the DR approximations provide a sim-
ilar or slightly larger, average error. However, the TS
approximations provide a slightly smaller evaluation
error than the ‘original’ approximation, makings the
TS approximations favourites to implement.
4 APPROXIMATION OF ReLU
FOR CNNs
To demonstrate the impact of using ReLU approxi-
mations on an application, the Cryptonets network
(Dowlin et al., 2016) is targeted, implemented in Intel’s
nGraph-HE (Boemer et al., 2019), where the original
x
2
activation function replaced with the ReLU function.
This research applies the approaches from Section 3
to this specific Cryptonets CNN for image classifica-
tion; The implementation of ReLU in Section 3 is on
input ranges [-4,4], however for the CNN used in this
section, the input range is [-255, 255], to maintain the
CNN structure without adding extra scale layers, and
enable fair comparison with previous research. Thus,
the Chebyshev polynomial has changed, as it is input
dependent. However the Chebyshev polynomials re-
main the most accurate ReLU approximations over
the input range. Table 1 and Figure 2 show that the
larger order Chebyshev polynomials and the larger or-
der Taylor expansion of SoftPlus are more accurate
ReLU approximations. DR and TS are applied to all
Chebyshev polynomials (orders 8, 12, 16) and Table 1
and Figure 2 show that TS approximations had higher
evaluation accuracy than DR approximations.
4.1 Results: ReLU CNN Approximations
This research was implemented on a Linux VM run-
ning on an Intel Core i5-8250U CPU using the CKKS
HE scheme in SEAL (SEAL, 2018), and Cryptonets
(Dowlin et al., 2016) implementated in nGraph HE
(Boemer et al., 2019). All figures are provided to 4
decimal places. Table 2 shows results when the Cheby-
shev order 16 approximation of ReLU and TS and
DR versions, were applied to the Cryptonets CNN
(Dowlin et al., 2016) in nGraph-HE (Boemer et al.,
2019) for image classification. This change was made
in all ReLU layers, a total of 4 layers. Table 2 gives
average CNN values after 5 runs for each approach.
The aim is to have the lowest possible reduction in ac-
curacy, assuming an acceptable reduction in accuracy
of 0.5% - 1% These implementations were trained in
unencrypted form and then tested again using unen-
crypted data, using a SEAL backend - an approach
recommended for debugging (Boemer et al., 2019).
Table 2: Classification accuracy and run-time of ReLU ap-
proximations (average over 5 runs), based on the Chebyshev
order 16 approximation, applied to the Cryptonets CNN im-
plemented in nGraph-HE.
Chebyshev 16: No change
Task
Skipping
Depth
Reduction
(x
7
)
Depth
Reduction
(x
3
)
Classification Accuracy 0.9900 1.0000 0.9600 0.1500
Train (Test) Accuracy 0.9838 0.9827 0.9169 0.1028
Train (Test) Loss 0.0491 0.0541 0.2939 2.3050
Run-time (Train) µs 390.0 201.0 259.0 193.0
Run-time (Test-HE (CPU)) 237.0 84.0 133.0 86.0
% Speed-up (Train) N/A 48% 34% 51%
% Speed-up (Test-HE (CPU)) N/A 46% 29% 29%
Compared to the approximations evaluated in PAL-
ISADE, where TS approximations had a higher evalu-
ation accuracy than DR approximations, when applied
to the CNN the DR approximations provide a higher
classification accuracy. This may be because, firstly,
these results have high variance and need more runs
for a stable average, and secondly, the TS approxima-
tion provides a more accurate CNN classification when
used in place of ReLU. These conclusions should be
understood cautiously; due to the structure of vary-
ing CNNs, different ReLU approximations could fare
better in terms of performance. Following Table 1,
although DR approximations have a faster run-time,
the accuracy is unacceptably low. Thus, the TS ReLU
approximation fares best in terms of accuracy and per-
formance speed-up. Considering the estimated perfor-
mance details of an encrypted CNN given in (Hesam-
ifard et al., 2019), and the impact of DR and TS on
encrypted ReLU, shown in Tables 1 and 2, the perfor-
SECRYPT 2023 - 20th International Conference on Security and Cryptography
714

mance of approximated ReLU can be estimated to be
slightly faster than the 320s taken in (Hesamifard et al.,
2019) with a slight accuracy reduction.
5 CONCLUSIONS
This research proposed novel approximations of ReLU
to ensure efficient homomorphic evaluation targeting
CNNs. For unencrypted ReLU approximation, the
most accurate approximation is Chebyshev order 16
(TS). If speed is prioritised, DR Chebyshev approxima-
tions orders 8 and 12 are recommended. The DR ap-
proximation of the Taylor expansion of Softplus (order
4) is also suitable. For encrypted ReLU approximation,
TS Chebyshev polynomial approximations orders 8,
12, 16 provide significant speed-up. When applying
Chebyshev approximations (order 16, with DR and
TS) to the CNN, after 5 runs of training and classi-
fying, the TS approximation, equation 22, provides a
48% speed-up in training run-time and a 0.0011 aver-
age decrease in classification accuracy. Overall, using
TS and DR approximations in CNNs do not have sig-
nificant negative impact on accuracy and performance.
This research demonstrates significant opportunities
for acceleration of HE evaluation using AC techniques,
sacrificing minimal accuracy and helping realise the
potential of HE for large scale data analytics.
ACKNOWLEDGEMENTS
This research was supported partly by a Thales UK
placement - thanks to Adrian Waller and Naomi Farley
for their support.
REFERENCES
Albrecht, M., Chase, M., Chen, H., Ding, J., Goldwasser,
S., Gorbunov, S., Halevi, S., Hoffstein, J., Laine, K.,
Lauter, K., Lokam, S., Micciancio, D., Moody, D.,
Morrison, T., Sahai, A., and Vaikuntanathan, V. (2018).
Homomorphic Encryption Security Standard. Tech-
nical report, HomomorphicEncryption.org, Toronto,
Canada.
Barua, H. B. and Mondal, K. C. (2019). Approximate Com-
puting: A Survey of Recent Trends—Bringing Green-
ness to Computing and Communication. Journal of
The Institution of Engineers (India): Series B.
Boemer, F., Lao, Y., Cammarota, R., and Wierzynski, C.
(2019). ngraph-he: a graph compiler for deep learning
on homomorphically encrypted data. In Palumbo, F.,
Becchi, M., Schulz, M., and Sato, K., editors, Pro-
ceedings of the 16th ACM International Conference on
Computing Frontiers, CF 2019, Alghero, Italy, April
30 - May 2, 2019, pages 3–13. ACM.
Chabanne, H., de Wargny, A., Milgram, J., Morel, C., and
Prouff, E. (2017). Privacy-preserving classification
on deep neural network. IACR Cryptol. ePrint Arch.,
2017:35.
Chen, H., Gilad-Bachrach, R., Han, K., Huang, Z., Jalali, A.,
Laine, K., and Lauter, K. (2018). Logistic regression
over encrypted data from fully homomorphic encryp-
tion. BMC Medical Genomics, 11(4).
Cheon, J. H., Kim, A., Kim, M., and Song, Y. S. (2017).
Homomorphic Encryption for Arithmetic of Approx-
imate Numbers. In Takagi, T. and Peyrin, T., editors,
Advances in Cryptology - ASIACRYPT 2017 - 23rd
International Conference on the Theory and Applica-
tions of Cryptology and Information Security, Hong
Kong, China, December 3-7, 2017, Proceedings, Part
I, volume 10624 of Lecture Notes in Computer Science,
pages 409–437. Springer.
Chou, E., Gururajan, A., Laine, K., Goel, N., Bertiger, A.,
and Stokes, J. (2020). Privacy-Preserving Phishing
Web Page Classification Via Fully Homomorphic En-
cryption. pages 2792–2796.
community, T. S. (2008-2020). numpy.polyfit.
https://numpy.org/doc/stable/reference/generated/
numpy.polyfit.html.
Dowlin, N., Gilad-Bachrach, R., Laine, K., Lauter, K.,
Naehrig, M., and Wernsing, J. (2016). CryptoNets:
Applying Neural Networks to Encrypted Data with
High Throughput and Accuracy. Technical Report
MSR-TR-2016-3.
Graepel, T., Lauter, K., and Naehrig, M. (2012). ML Con-
fidential: Machine Learning on Encrypted Data. In
Proceedings of the 15th International Conference on
Information Security and Cryptology, ICISC’12, page
1–21, Berlin, Heidelberg. Springer-Verlag.
Hesamifard, E., Takabi, D., and Ghasemi, M. (2017). Cryp-
toDL: Deep Neural Networks over Encrypted Data.
Hesamifard, E., Takabi, H., and Ghasemi, M. (2019). Deep
Neural Networks Classification over Encrypted Data.
In Proceedings of the Ninth ACM Conference on Data
and Application Security and Privacy, CODASPY ’19,
page 97–108, New York, NY, USA. Association for
Computing Machinery.
Khanna, S. and Rafferty, C. (2020). Accelerating Homo-
morphic Encryption using Approximate Computing
Techniques. In Samarati, P., di Vimercati, S. D. C.,
Obaidat, M. S., and Ben-Othman, J., editors, Proceed-
ings of the 17th International Joint Conference on e-
Business and Telecommunications, ICETE 2020 - Vol-
ume 2: SECRYPT, Lieusaint, Paris, France, July 8-10,
2020, pages 380–387. ScitePress.
LeCun, Y., Cortes, C., and Burges, C. J. (1998). The MNIST
database of handwritten digits.
Mathworks (2006-2021). polyfit. https://www.mathworks.
com/help/matlab/ref/polyfit.html.
Palisade (2021). PALISADE (version 1.10.6). https:
//palisade-crypto.org/.
SEAL (2018). Simple Encrypted Arithmetic Library (release
3.1.0). https://github.com/Microsoft/SEAL. Microsoft
Research, Redmond, WA.
Approximate Homomorphic Pre-Processing for CNNs
715