Robust Three-Factor Lightweight Authentication Based on Extended
Chaotic Maps for Portable Resource-Constrained Devices
Arijit Karati
a
, Yu-Sheng Chang and Ting-Yu Chen
Department of Computer Science and Engineering, National Sun Yat-sen University, Kaohsiung, Taiwan, Republic of China
Keywords:
Authentication, Key Agreement, Extended Chaotic Maps (ECM), Physically Unclonable Function (PUF),
Security and Privacy, Lightweight Cryptography.
Abstract:
Public-key based authentication and key agreement (AKA) protocols have attracted considerable interest in
providing secure access for various application scenarios. Although three-factor AKA (3FAKA) offers higher
security than one- or two-factor ones, most existing 3FAKA are vulnerable, or their safety is reduced to the
security of one- or two-factor authentication. Thus, finding a balance between security and usability and coun-
tering cloning risks with robust three-factor authentication is an ongoing problem. To mitigates such issues,
we propose a lightweight 3FAKA for mobile devices. The suggested 3FAKA employs the physical unclon-
able function to withstand device cloning attacks and extended chaotic maps to preserve lightweight processes
while ensuring essential cryptographic traits, such as unpredictability, unrepeatability, and uncertainty. It is
secure under the intractability of extended chaotic maps computational Diffie-Hellman problem. Performance
analysis exhibits that our protocol provides a comprehensive set of security and functional aspects accounting
for adequate computation, storage, and communication costs compared to state-of-the-art alternatives.
1 INTRODUCTION
With the rapid advancement of technology, mobile
applications are becoming increasingly popular. One
such application is the intelligent healthcare system,
where patient health conditions are further improved
via continuous monitoring of patient data stored on
the remote server. The identity authentication and key
agreement (AKA) gains wide attention in providing
safe access (Trivedi and Patel, 2021) in this setting.
Specifically, the three-factor AKA (3FAKA) provides
higher security than one- or two-factor authentication
(1FA or 2FA) and is fit for healthcare applications.
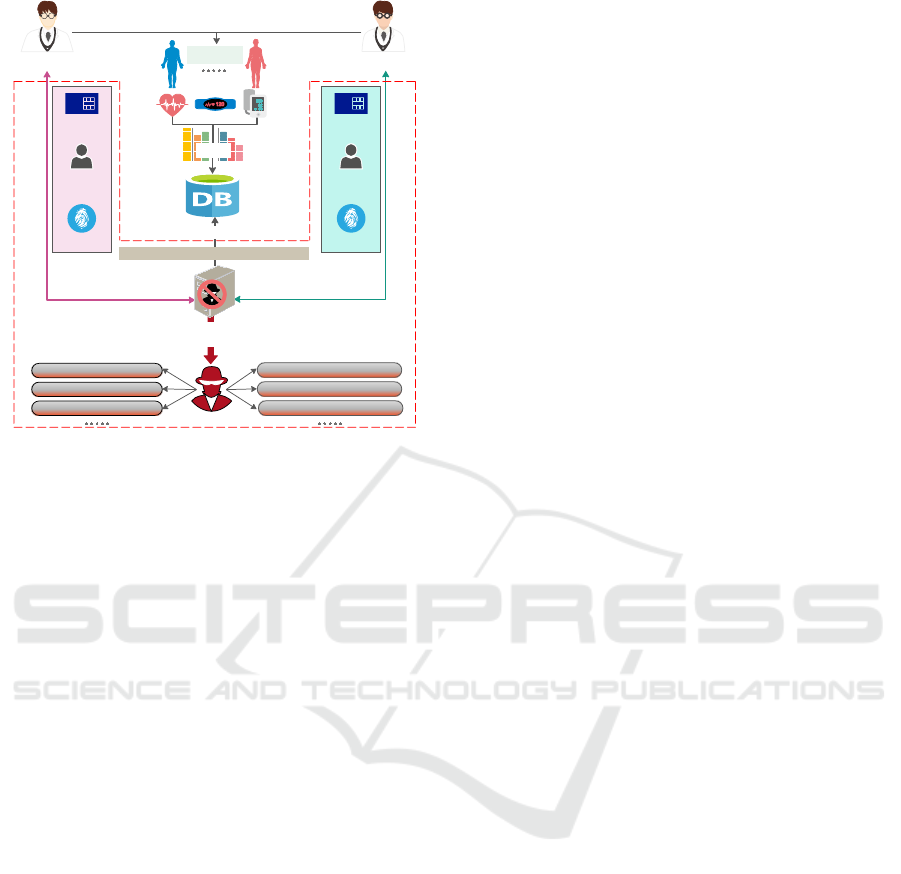
Figure 1 depicts a situation in which patients’
data, such as heart rate, blood pressure, or body tem-
perature, are collected using multiple body-mounted
sensors and stored in the medical database. By col-
lecting such data, a supervising doctor accesses the
database containing his/her patients’ information for
diagnostic reference, allowing him/her to make a
timely and accurate medical decision. Also, each pa-
tient’s information could be accessible to other re-
sponsible divisions. Here, each doctor accesses pa-
tients’ data through robust authentication with secret
credentials (smart card, ID and password, and bio-
a
https://orcid.org/0000-0001-5605-7354
metrics), followed by attribute-based access control
(ABAC) strategy (Hu et al., 2013). However, there
could be various attacks due to improper authenti-
cation. For example, the patient’s rights and health
may be risked if an outside foe or a malevolent in-
sider illegally accesses the database and tampers sen-
sitive data. Although AKA mitigates these issues
(Roy et al., 2021), most recent 3FAKA systems are
vulnerable, or their security is reduced to 1FA or 2FA,
making them inadequate for practical use. Thus, bal-
ancing security, usability, and device cloning threats
with valid 3FAKA is a persistent challenge.
1.1 Security Requirements
3FAKA should support below critical traits between
user U and the server S in the presence of a foe A:
F1 (User anonymity): The U can access system and
being identified uniquely by S while A cannot iden-
tify U during public communication.
F2 (Untraceability): It allows S to identify the source
of an openly conveyed message while A cannot do it.
F3 (Mutual authentication): It is a critical property
that enables S to identify U and vice versa.
F4 (Session key agreement): It offers both S and U to
Karati, A., Chang, Y. and Chen, T.
Robust Three-Factor Lightweight Authentication Based on Extended Chaotic Maps for Portable Resource-Constrained Devices.
DOI: 10.5220/0012077600003555
In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 673-682
ISBN: 978-989-758-666-8; ISSN: 2184-7711
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
673

Patients
Data
Desynchronization
Authentication replay
Smart card stolen
Private information theft
Man-in-the-middle assault
Verification table hack
pass the authentication by 3
factors under ABAC model
pass the authentication by 3
factors under ABAC model
try to access database to get and tamper sensetive data that may malipulate
doctor's decision and endanger the patient's health condition
Biometric
ID and
Password
Smart card
Biometric
ID and
Password
Smart card
Doctor B
Doctor A
ABAC
acces s the DB to obtain certain patients' data
treatment for patients under specific doctor's supervision (sharable data)
Figure 1: A typical patient data access under mixed
threat scenarios where attackers use public parameters and
information-sharing flaws to sabotage medical services.
Robust authentication (red box) prevents data invasion.
persuade a specific key for a single session.
F5 (Revoking smart cards remotely): It permits S to
revoke smart card of a suspected U remotely.
F6 (Dynamic User Addition Feature): A may occa-
sionally physically seize some Us’ credentials due to
a hostile environment. Therefore, allowing dynamic
user addition (canceling ID but not the credentials en-
act) in the network is crucial to maintain safe services.
Besides, 3FAKA should withstand below attacks:
A1 (Resistant to desynchronization attack): Upon ef-
fective authentication, the database stows certain val-
ues. The smart card may simultaneously alter specific
values to sync the database, which aids U for the next
login. During synchronization, A blocks communica-
tion and gains system access in the future. One should
restrict such attacks or avoid synchronization.
A2 (Immune to stolen-data-and-password attack): A
cannot access the system even if U ’s password and
data on the smartcard are known to A.
A3 (Resistant to replay attack): Valid data transmis-
sion in a replay attack is repeated maliciously, fraud-
ulently, or delayed for system access. This kind of
attack will be detected and refused.
A4 (Resistant to man-in-the-middle attack): A sends
and modifies messages between two parties who be-
lieve they are directly communicating in secret. Thus,
only S and U use the same session key, regardless
of the connection’s weakness. Besides, A can only
change the message after first informing S and U .
A5 (Resist stolen smartcard and biometric/password
attack): Even if A has U’s smart card, A cannot pre-
tend himself/herself as a specific U to access S .
A6 (Stolen Verifier Table Attack): Most protocols
hold verifier tokens (such as hashed passwords) on S ,
which is vulnerable to attack, rather than the users’
real passwords or secret keys.
Note, we do not consider network traffic related at-
tacks, such as jamming attack.
1.2 Related Works
Due to the open nature of wireless networks, an at-
tacker may intercept, replay, and even modify shared
data (Karati et al., 2021). In 2014, a 3FAKA pro-
tocol (Islam, 2014) was devised based on extended
chaotic maps (ECM) and showed its security against
various known attacks, such as smartcard loss attacks,
while maintaining the three-factor security properties.
However, the authors (Jiang et al., 2016) noted that
the work (Islam, 2014) is susceptible to offline pass-
word guessing, smart card loss attacks, and biomet-
ric leaks due to incorrect password timely inspection
mechanisms. To overcome the drawbacks, they de-
vised a new 3FAKA with fuzzy verification (Jiang
et al., 2016). In 2018, the authors (Das et al., 2018)
developed a PUF-based authentication for wearable
devices which necessitates a substantial number of
computing operations and a longer execution time.
Subsequently, the authors in (Roy et al., 2018) pro-
posed a chaotic map-based anonymous authentication
protocol with the fuzzy extractor for crowdsourcing
Internet of Things (IoT); however, its verifier token
was vulnerable to performing offline password guess-
ing. In the multi-server setting, the authors (Chatter-
jee et al., 2018) designed a 3FAKA using the Cheby-
shev chaotic map, cryptographic hash, and symmet-
ric key encryption/decryption. However, it does not
provide proper three-factor security: the explicit pass-
word verifier enables attackers to guess passwords
and identities offline when the other two factors (bio-
metric and smart card) are compromised (Qiu et al.,
2022). Shortly thereafter, a 3FAKA protocol is sug-
gested in (Jiang et al., 2019) for cloud-assisted wear-
able devices based on the fuzzy extractor; however,
it cannot provide PFS and X-security. In 2020, the
authors in (Jiang et al., 2020) introduced a cloud-
centric 3FAKA protocol that withstands many secu-
rity measures, such as user anonymity, password con-
fidentiality, and prompt typo detection. In addition,
an IoT-based three-factor authentication method was
developed in (Wang et al., 2020) to secure the system
against all session key disclosure threats. Nonethe-
less, an enhanced anonymous authentication scheme
SECRYPT 2023 - 20th International Conference on Security and Cryptography
674

for smart home was introduced by (Banerjee et al.,
2020). In 2021, the authors in (Masud et al., 2021)
presented a lightweight user authentication strategy
for IoT-based healthcare to defend the network from
impersonation and replay assaults and ensure data pri-
vacy and anonymity. Later, the authors in (Fakroon
et al., 2021) applied PUF to safeguard IoT edge de-
vices against cloning attacks and gave a logical anal-
ysis utilizing Burrows-Abadi-Needham (BAN) logic.
Further, a mutual three-factor authentication using
PUF was designed in (Kwon et al., 2021). It resists
replay and man-in-the-middle attacks using AVISPA.
The authors in (Yu et al., 2021) suggested an ECM-
based AKA system resistant to verifier attacks for a
multi-server scenario. Later, the authors in (Saqib
et al., 2022) introduced a three-factor authentication
system based on identity, password, and a digital sig-
nature mechanism for IoT-driven critical applications.
It resists cryptographic attacks, such as man-in-the-
middle, replay, and publisher impersonation attacks.
In 2022, a fast authentication for charging elec-
tric vehicles (EVs) was devised utilizing the ECM op-
eration (Wang et al., 2022). The protocol ensured
user anonymity while defending against insider as-
saults. Later, a blockchain-based privacy-preserving
multi-factor device authentication was introduced for
the cross-domain industrial IoT resistant to various
known threats, including impersonation and replay
attacks (Zhang et al., 2022). However, the scheme
is vulnerable to user and server impersonation, data
leakage, user traceability, and user revocation flaws
(Ryu et al., 2022). Further, a three-factor authentica-
tion based on configurable ring oscillator (CRO)-PUF
was presented by (Wang et al., 2023) that resists ma-
chine and password guessing attacks.
1.3 Motivation and Our Methodology
Technology for verifying identities has developed in
numerous directions to accommodate comprehensive
use cases. Every single approach to verification has
its own set of flaws. Besides, most currently used
authentication solutions do not provide adequate se-
curity to withstand modern assaults. Some systems
based on single-factor (password-based) authentica-
tion (or reduced to single-factor) do not follow model
security criteria. Nevertheless, many methods are se-
cure yet inefficient due to inadequate cryptographic
operations. This work suggests an efficient scheme
for consumer devices to prevent sensitive data leak-
age. In the proposed scheme, we employ the chaotic
map operation, which is feasible and more efficient
than scalar multiplication and modular exponentia-
tion. We achieve specific cryptographic traits, in-
cluding unpredictability, non-repetition, and uncer-
tainty. In addition, we use physically unclonable
functions (PUFs) to provide hardware-based security
through hardware fingerprints, which are essential for
lightweight device authentication. It may be noted
that the PUFs have specific characteristics, includ-
ing randomness and physical unclonability, which in-
crease the importance of the smart card’s hardware
entity. Thus, as long as the PUF readings are unavail-
able, capturing smartcard data and other secret infor-
mation is insufficient for successful authentication.
1.4 Our Contributions
We design a safe 3FAKA protocol for low-power de-
vices. Given the importance of hardware function, it
offers a viable security solution. Within the context
of this framework, we contribute the following:
• The system incorporates the ECM features to en-
able robust mutual authentication and session key
agreement in lightweight devices.
• The suggested system uses PUFs to enhance the
smartcard’s hardware security and provides low-
powered device-coupled authentication. Besides,
it uses the Fuzzy Extractor to combat the grow-
ing prevalence of biometric verification in soft-
ware and hardware to enhance usability.
• Under the chaotic-map computational Diffie-
Hellman problem (CMCDHP), the scheme meets
critical security aspects, such as mutual authen-
tication, user anonymity, tight session key agree-
ment, and untraceability. Besides, it resists desyn-
chronization, stolen data and passwords, man-in-
the-middle, replay, and stolen smartcard attacks.
• We estimate the efficacy of our scheme in authen-
tication delay, transmission, and storage costs.
2 TECHNICAL PRELIMINARIES
This section describes the necessary backgrounds for
comprehending the proposed work.
2.1 Fuzzy Extractor
With the prevalence of smart gadgets supporting bio-
metric operations, the invariable traits of clients are
gaining increasing attention. As a third authentication
factor, biometrics such as fingerprints, facial char-
acteristics, and iris are utilized to increase security.
To improve usability, biometrics are stabilized with a
fuzzy extractor so that the server can identify the user
Robust Three-Factor Lightweight Authentication Based on Extended Chaotic Maps for Portable Resource-Constrained Devices
675

with an acceptable tolerance for error. A fuzzy ex-
tractor comprises two below functions, where l is the
bit-length of the output string, χ is error tolerance, and
M ∈ {0,1}
v
is the set of positive integers:
• GEN(·): This probabilistic algorithm inputs a bio-
metric B
i
∈ M and outputs a secret σ
i
∈ {0,1}
l
and
a support token T
i
, where GEN(B
i
) = {σ
i
,T
i
}.
• REP(·,·): This deterministic algorithm inputs T
i
,
noisy biometric B
l
i
∈ M and χ related to B
i
, repro-
ducing the biometric key σ
i
. Moreover, we have
REP(B
l
i
,T
i
) = σ
i
where d(B
i
,B
l
i
) ≤ χ is satisfied.
2.2 Physical Unclonable Functions
A physical unclonable function (PUF) is a chaotic
system that maps a given set of challenges to a set
of responses based on the device’s microstructure.
Cloning a PUF has proven extremely difficult, if not
impossible. The functionality of Arbiter PUF may
be modeled using an additive linear delay model
(R
¨
uhrmair et al., 2010). The total delay in each step
is ∆ =
⃗
W
T
⃗
Φ, where
⃗
W is a feature vector represent-
ing the propagation delay of each MUX and
⃗
Φ is a
function of n-bit challenge C= {c
i
}.
⃗
Φ is denoted as:
⃗
Φ(
⃗
C) =

⃗
Φ
1
(
⃗
C),
⃗
Φ
2
(
⃗
C),
⃗
Φ
3
(
⃗
C), ··· ,
⃗
Φ
n
(
⃗
C), 1

T
(1)
where
⃗
Φ
j
(
⃗
C) =
∏
n
i= j
(i−2c
i
),∀ j ∈ [1,k]. If ∆ > 0, the
output r of Arbiter PUF is 1; else, 0. For convenience,
use e = (2 ∗r) −1 to denote e = sgn (∆) = sgn(
⃗
W
T
⃗
Φ),
where sgn is a sign function. An XOR PUF with l
individual Arbiter PUFs is denoted by l-COR PUF.
The individual outputs of Aribiter PUF is denoted by
e
i
∈ {−1,1}, where i ∈ [0,l − 1]. The l-stage XOR
gate is used to XOR all e
i
to get the final response
e
XOR
=
l−1
∏
i=0
(e
i
) (2)
Consider each Arbiter PUF with a unique delay vector
⃗
W
i
shares Φ. Then, we have e
XOR
= sgn(
∏
l−1
i=0
⃗
W
T
⃗
φ).
Moreover, based on the integrated circuit (IC) fea-
tures, a PUF
1
generates unique challenge-response
pair R = PUF(C), where R is a response to a unique
challenge C. An integrated PUF is a d-bit PUF com-
posed of d PUFs, each responding with a single bit.
The properties of an ideal d-bit PUF are as follows:
Fact 1. For C
1
in two PUF
1
and PUF
2
, the Hamming
distance HD(PUF
1
(C
1
),PUF
2
(C
1
)) ≈ d/2.
Fact 2. For two distinct challenges C
1
and C
2
, we
have HD(PUF
1
(C
1
),PUF
2
(C
2
)) ≈ d/2.
1
While PUF is reliant on the features of the IC, its reac-
tion may vary owing to environmental factors.
Fact 3. For a random challenge C
1
, we have the
Hamming distance HD(PUF
1
(C
1
),PUF
′
1
( C
1
)) = 0.
(note, tampered PUF
′
1
contains a d/10 bit error.)
Fact 4. HD(PUF
1
(C
1
),PUF
1
(C
2
)) ≈ d/2 for any d-
bit PUF
1
with any two challenges C
1
and C
2
.
The proposed solution depends on the notion that
these features of PUFs may be exploited to create
physically secure protocols for device authentication.
2.3 Extended Chaotic Maps
Given n ∈ Z
+
and −1 ≤ x ≤ 1, the Chebyshev chaotic
polynomial (CCP) T
n
(x) : [−1,1] → [−1,1] is defined
as T
n
= cos(n · cos
−1
(x)), or
T
n
(x) =





1, if n = 0
x, if n = 1
2xT
n−1
(x) − T
n−2
(x), if n ≥ 2.
(3)
The CCP satifies the semi-group property:
T
r
(T
s
(x)) = T
s
(T
r
(x)) = cos(rs · cos
−1
(x)) for r,s ∈ N.
However, CCP based public key cryptography is not
secure. Later, (Zhang, 2008) defined the extended
Chebyshev polynomial as T
n
= 2xT
n−1
(x) − T
n−2
(x)
mod p, ∀n ≥ 2 that holds the semi-group property in
interval (−∞,+∞), where p is a large prime.
Definition 1 (Extended Chaotic Map). Given prime p
and x ∈ (−∞, +∞), the extended Chebyshev polyno-
mial holds T
r
(T
s
(x)) ≡ T
s
(T
r
(x)) ≡ T
rs
(x) (mod p).
Definition 2 (Chaotic map discrete logarithm prob-
lem (CMDLP)). Given x and y, it is infeasible for A
to find r such that T
r
(x) = y. The advantage of A is:
ε
CMDLP
A
= Pr[A(x,y) = r : r ∈ Z
∗
p
,y = T
r
(x) % p] (4)
Definition 3 (Chaotic map computational Diffie-Hell-
man problem (CMCDHP)). Given (x, T
s
, T
m
), it is in-
feasible for A to find T
ms
(x). The advantage of A is:
ε
CMCDHP
A
= Pr[A(x,T
s
,T
m
) = r : r ≡ T
ms
(x) % p] (5)
3 OUR CONSTRUCTION
Table 1 introduces necessary notations. We presume
there must be a device capable of extracting biomet-
rics features and a smart card capable of performing
PUF and storing user-specific tokens. The proposed
scheme comprises the six phases listed below:
3.1 System Setup
This phase is executed by the server S to initialize
specific parameters prior to user registration and other
SECRYPT 2023 - 20th International Conference on Security and Cryptography
676

associated actions. It sets a large prime p ≡ 3 (mod 4)
and considers an admissible ECM as T
x
(y) where
x,y ∈ Z
∗
p
. Besides, it selects a one-way hash function
H(·) ∈ H . Now, it generates a high entropy secret key
s at random for performing standard symmetric en-
cryption SE[·] and decryption SD[·]. Then, it chooses
a list L(ID,Valid CID), which is initially empty. To
protect against thefts for actual ID and Valid CID at
the server side, S adopts a honey-list L
′
as shown in
(Juels and Ristenpart, 2014) to safeguard L against
potential attackers. After successful authentication,
we assume that S employs the ABAC model to deter-
mine user authorization over sensitive data.
3.2 User Registration
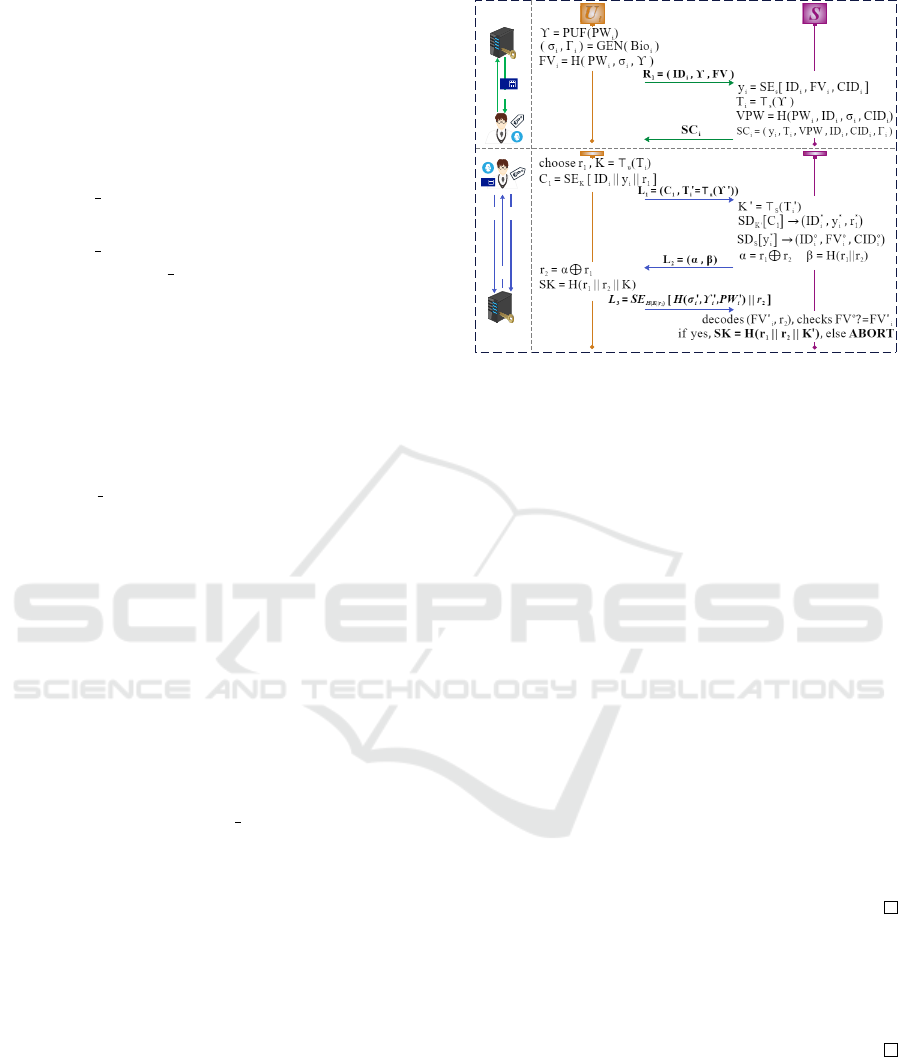
As depicted in Fig. 2, on a viable request from a user
U
i
, the S provides an initially empty smartcard SC
i
de-
pending on U
i
’s level. Now, U
i
selects PW
i
and gen-
erates γ = PUF(PW
i
). Next, it provides a biometric
sample Bio
i
and generates σ
i
with the fuzzy extractor
as (σ
i
,Γ
i
) = GEN(Bio
i
). Besides, it computes fea-
ture value FV
i
= H(PW
i
,σ
i
,γ). Finally, U
i
sends the
R
1
= (ID
i
,γ, FV
i
) to the server S .
Upon obtaining R
1
, S ABORTs the session if ID
i
∈
L. Otherwise (i.e., ID
i
/∈ L ), S assigns a token CID
i
where CID
i
= 1 and inserts (ID
i
,1) ∈ L. Now, S gen-
erates y
i
= SE
s
[ID
i
,FV
i
,CID
i
] and an access token
T
i
= T
s
(γ). Consequently, it updates honey-list L
′
.
Finally, S updates SC
i
that contains (y
i
,T
i
,ID
i
,CID
i
).
Now, U
i
generates VPW = H(PW
i
,ID
i
,σ
i
,CID
i
)
and updates the received smart card as SC
i
=
(y
i
,T
i
,V PW, ID
i
,CID
i
,Γ
i
). The communications be-
tween U
i
and S occur securely.
3.3 Authentication and Key Agreement
U
i
→ S : When U
i
wants to access the system,
he/she provides his/her ID, password, and biomet-
rics to compute γ
′
= PUF(PW
′
i
), σ
′
i
= REP(Bio
′
i
,Γ
i
).
Next, U
i
generates V PW
′
= H(PW
′
i
,ID
i
,σ
′
i
,CID
i
)
and checks whether password and biometrics are cor-
rect as V PW
′
?
= V PW. Then, U
i
computes K = T
u
(T
i
)
and chooses r
1
at random. Next, it performs sym-
metric key encryption by C
1
= SE
K
[ID
i
||y
i
||r
1
]. After
that, U
i
sends L
1
= (C
1
,T
′
i
= T
u
(γ
′
)) to S.
S → U
i
: Once S receives L
1
, it computes K
′
=
T
s
(T
′
i
) to decrypt C
1
and further y
∗
as
SD
K
′
[C
1
] −→ (ID
∗
i
,y
∗
i
,r
∗
1
) (6)
SD
s
[y
∗
i
] −→ (ID
o
i
,FV
o
i
,CID
o
i
) (7)
Now, S checks whether ID
o
i
?
= ID
∗
i
exists in L. If it
does not exist or (CID
o
i
̸= Valid
CID
i
), S terminates
Table 1: List of useful notations.
Notation Description
p A sufficiently large prime holds 3 mod 4
ID
i
,PW
i
Identity and password of user U
i
Bio
i
Biometric data of user U
i
σ
i
Reproducible data generated by GEN(·)
Γ
i
Assisting token to output σ
i
by REP(·)
γ An error-tolerant PUF response
T
x
(y) Extended chaotic map T for input (x, y)
y
i
S derived token for U
i
with secret s
SE
x
[M] Symmetric encoding of M for secret x
SD
x
[C] Symmetric decoding of C for secret x
H(·) Secure cryptographic hash function
PUF(·) Physical unclonable function for SC
i
A ⊕ B Bit-wise XOR operation A and B
A||B Concatenation between A and B
the session. If it exists with Valid CID
i
= −1, then S
ABORTs the session notifying U
i
that the SC
i
has ex-
pired. Otherwise, S chooses r
2
at random and masks
it as α = r
1
⊕ r
2
. Then, it computes β = H(r
1
||r
2
),
and sends L
2
= (α,β) back to U
i
.
U
i
→ S : On receiving L
2
= (α, β), U
i
discloses
r
2
= α ⊕ r
1
and verifies whether β
?
= H(r
2
||r
1
) for re-
sisting replay attack. Finally, U
i
performs symmetric
encryption and sends L
3
to S where
L
3
= SE
H(K||r
2
)
[H(σ
′
i
,γ
′
i
,PW
′
i
)||r
2
] (8)
Since S has knowledge of K
′
and r
2
, it reveals
cleartext ← SD
H(K
′
||r
2
)
[L
3
]. Next, it checks whether
FV
o
i
?
= FV
′
i
. If it holds, S generates the session key
as SK = H(r
1
||r
2
||K
′
). Note that U
i
can compute SK.
Finally, S allows U
i
accessing sensitive data based on
ABAC (Hu et al., 2013) for traced ID
i
, and SK is used
for any data exchange between S and U
i
.
3.4 User Password Update
When U
i
wants to change his/her password PW
i
, U
i
must pass the authentication successfully to commu-
nicate with S with the session key SK. For this, U
i
fol-
lows the steps outlined in Section 3.3. Now, it chooses
a password PW
i
new
complies with password rules and
sets γ
new
i
= PUF(PW
i
new
) and updates feature value
as FV
i
= H(PW
i
new
,σ
′
i
,γ
new
i
). When S reveals γ
i
and
FV
new
i
using symmetric decryption for key SK, it up-
dates CID
new
i
=Valid CID+1 to record the times that
U
i
changes the password. Then, S generates
y
new
i
= SE
s
[ID
i
,FV
new
i
,CID
new
i
] (9)
Next, it computes Ts(γ
new
i
) and updates the smartcard
data SC
∗
= (y
i
∗
,T
s
(γ
∗
i
),ID
i
,CID
i
∗
) securely with SK.
Now, U
i
sets V PW
new
i
= H(PW
new
i
,ID
i
,σ
′
i
,CID
new
i
).
The smartcard data will eventually be refreshed as
SC
new
i
= (y
new
i
,Ts(γ
new
i
),V PW
new
i
,ID
i
,CID
new
i
,Γ
i
).
Robust Three-Factor Lightweight Authentication Based on Extended Chaotic Maps for Portable Resource-Constrained Devices
677

3.5 Dynamic Device Addition
At this phase, a device is considered an end user. As-
sume U
new
i
has to be added to the network after the
first deployment. U
new
i
first sends ID
i
new
,γ
new
i
,FV
new
i
to S. If ID
i
new
does not already exist in L, then S al-
lows U
new
i
to execute the registration phase. However,
if ID
i
new
∈ L, then the following actions are taken:
• If Valid CID
i
= −1 which indicates that U
i
new
has
been revoked, S aborts the session of U
i
new
.
• If Valid CID
i
= 0 (expired smartcard), then S sets
CID
i
new
= Valid CID
i
+ 1. Next, S issues a new
SC
i
new
for user identifier γ
i
new
= PUF
i
new
(PW
i
new
)
and FV
i
new
= H(σ
new
i
,γ
i
new
,PW
new
i
). Next, S de-
codes y
i
from expired SC
old
i
and checks CID
i
?
=
CID
i
new
. If it holds, S collects y
new
i
= SE
s
(ID
new
i
,
FV
new
i
,CID
new
i
) and sets SC
new
i
= (y
new
i
,T
s
(γ
new
i
),
ID
new
i
, CID
new
i
). Now, U
new
i
sets new VPW
new
i
=
H(PW
new
i
,ID
new
i
,σ
i
,CID
new
i
) and updates SC
new
i
as {y
new
i
,T
s
(γ
new
i
),V PW
new
i
,ID
new
i
,CID
new
i
,Γ
i
}.
• If Valid
CID
i
= 1, then U
i
already exists and at-
tempts to add itself again. For this, S permits
U
i
new
to execute the Password Change phase.
3.6 User Revocation
When an identity has been tracked for malicious con-
duct, one of the most pressing concerns is how to re-
voke its login credentials. Tracking hazardous behav-
iors may be discovered by repeatedly providing incor-
rect credentials, ABAC, L
′
, or smart behavior analy-
sis, which is not the focus of this work. We enable S
to revoke U
i
’s authentication credentials remotely. To
do this, S authentically access its own maintained L
and updates tuple (ID
i
,Valid CID) to (ID
i
,−1).
4 SECURITY DISCUSSION
Our 3FAKA achieves several security properties as
mentioned in Section 1.1. Here, we consider S as a
trusted entity while the attacker A is a vulnerable en-
tity. The PUF with the SC is considered a System
on Chip (SoC). Any attempt to tamper or separate the
PUF from a SC renders the PUF useless (Kirkpatrick
et al., 2014). Besides, the communication between SC
and PUF is considered secure (Aman et al., 2018).
Lemma 1. The response (R) of a PUF cannot be en-
visioned. The advantage of A in finding R is 1/2
n
.
Proof. An admissible PUF function is defined as
PUF : {0,1}
m
→ {0,1}
n
for some positive integers m
REGISTRATION
PHASE
AUTHENTICATION
PHASE
SC
i
L
1
L
2
L
3
Figure 2: Registration and authentication of our 3FAKA.
and n. The security of a PUF can be modeled using a
game G
PUF
A
between a challenger S and a probabilis-
tic polynomial-time (PPT) algorithm run by adversary
A. The details are provided below:
T1: A sends a random challenge C
i
to S . The S reveals
R
i
= PUF(C
i
) to A. This is an adaptive process
executed t
1
times.
C: The S chooses a challenge C
x
at random (not
queried by A before). Then, it sends C
x
to A while
keeps R
x
= PUF(C
x
) safely.
T2: A can send any query C
j
to S where C
j
̸= C
x
and
C
j
̸= C
i
. The S reveals R
j
= PUF(C
j
) to A. This
is an adaptive process executed t
2
times where the
total number of queries is q = t
1
+t
2
.
G: A outputs its guess R
∗
to S for the challenge C
x
and wins the game if R
∗
= R
x
.
A wins the above game with an advantage ε
PUF
A
=
Pr[R
∗
← A(C
x
,(C
i
,R
i
)) : C
x
̸= C
i
∈[1,q]
∧ R
∗
= R
x
].
However, each PUF responds uniquely and cannot be
cloned (Kirkpatrick et al., 2014). Thus, A guesses
R
x
∈
R
{0,1}
n
. Hence, A has ε
PUF
A
= 1/2
n
.
Theorem 1. Our 3FAKA protocol supports critical
security traits, namely user anonymity, untraceability,
mutual authentication, and session key agreement.
Proof. The theorem follows when Lemmas 2-5 ac-
cording to Definitions 2-3 and Lemma 1 are hold.
Lemma 2 (F1). The proposed 3FAKA protocol main-
tains strong user anonymity.
Proof. Valid U
i
and server S exchange ⟨L
1
,L
2
,L
3
⟩
during authentication. To violate user anonymity, A
must trace the user identifier hidden in L
1
= (C
1
,T
′
i
).
Specifically, A needs to decrypt C
1
= SE
K
[ID
i
||y
i
||r
1
]
SECRYPT 2023 - 20th International Conference on Security and Cryptography
678

encrypted with K = T
u
(T
s
(γ)). Although A has T
′
i
=
T
u
(γ), it cannot divulge K since the server secret s is
unavailable. As C
1
is seen as a secure trapdoor for K;
user identification is infeasible and only visible to S
who issued SC
i
to U
i
. Hence, the suggested protocol
achieved strong user anonymity.
Lemma 3 (F2). The 3FAKA supports untraceability.
Proof. Even though A cannot uniquely identify a
user during authentication, it may determine the rel-
evance between the user and data. This can be ac-
complished by monitoring the channel and record-
ing the relationship between anonymous ID and data
AR
1
= ⟨L
1
,L
2
,L
3
⟩ is coming from which anonymous
ID. The suggested protocol randomizes each L
j
dur-
ing each session. Even if the same Ui initiates sev-
eral authentication requests (AR
1
,· ·· ,AR
n
) at differ-
ent times, A cannot trace such AR
i
belongs to the
same anonymous U
i
. To achieve randomization in
AR
i
, U
i
generates L
1
for some u, r
1
chosen at random
and L
3
with a random secret key K. Besides, S gen-
erates L
2
with some random r
2
. One may observe
that u,r
1
,r
2
,K are random data for different sessions.
Hence, our scheme meets untraceability.
Lemma 4 (F3). The proposed 3FAKA protocol main-
tains strong mutual authentication.
Proof. During login, U
i
sends L
1
= (C
1
,T
′
i
= T
u
(γ))
to S . Notably, we incorporate U
i
’s identity ID
i
, iden-
tification token y
i
and and random r
1
, then utilize key
K = T
u
(T
s
(γ)) to generate C
1
= SE
K
(ID
i
||y
i
||r
1
) to
S . With secret s, S generates K
′
= T
s
(T
u
(γ)) and
discloses ID
i
,y
i
and r
1
from C
1
to authenticate U
i
.
Due to the hardness of CMCDHP, one may note that
A cannot generate K
′
even if it reveals hard token
T
s
(γ). Following that, S computes α = r
1
⊕ r
2
and
β = H(r
1
||r
2
) for some r
2
. Finally, it returns L
2
=
(α,β) to U
i
. Now, U
i
can authenticate S if it receives
r
1
details from L
2
. This is because r
1
can be derived
from C
1
by the S with secret s. On receiving L
2
, U
i
finds S’s credibility through β. Besides, S finds U
i
’s
credibility when it receives valid FV
i
through L
3
. Fur-
ther, A cannot disclose any sensitive information that
allows A to authenticate on behalf of S and U
i
. Thus,
our scheme meets mutual authentication.
Lemma 5 (F4). Our 3FAKA protocol achieves strong
session key agreement during authentication.
Proof. The strong key agreement relies on the fact
that S and U
i
agree on some session-dependant ran-
dom tokens that are never transmitted as cleartext
throughout authentication exchange for a particular
session. On viable authentication, both S and U
i
agree
on the same session key SK = H(r
1
||r
2
||K), where r
1
and r
2
are random tokens generated by U
i
and S re-
spectively and K is session-dependant symmetric key
generated as T
s
(T
u
(γ)) using U
i
’s nonce u and S ’s se-
cret s. Besides, S agrees on r
1
to send its nonce r
2
in
L
2
. Similarly, when receives r
1
details in L
2
, U
i
agrees
on r
2
to send L
3
. When S reveals FV
i
from L
3
and au-
thenticate it, then S agrees on SK. Thus, the suggested
protocol achieves the session key agreement.
Lemma 6 (F5). The proposed 3FAKA protocol re-
vokes the issued cards remotely.
Proof. Since S controls L, it may officially revoke a
smart card SC
i
by setting Valid CID
i
= −1 of a par-
ticular user U
i
. It impedes A’s capability to authenti-
cate successfully. Because CID
i
and Valid CID
i
are
distinct, A cannot pass authentication. Hence, our
method remotely revokes the smartcard.
Theorem 2. The proposed 3FAKA protocol resists es-
sential security attacks for lightweight devices.
Proof. The theorem follows when Lemmas 6-11 ac-
cording to Definitions 2-3 and Lemma 1 are hold.
Lemma 7 (A1). The proposed 3FAKA protocol is re-
sistant to desynchronization attacks.
Proof. Synchronization of server-side data, including
PUF responses and hash-chain values, is frequent in
many authentications and key agreement systems. So,
several potential vulnerabilities exist due to the sever-
ity of data synchronization. The proposed solution,
however, avoids the possibility of covert data updates
occurring with each user authentication. Hence, our
technique withstands desynchronization attacks.
Lemma 8 (A2). The proposed 3FAKA protocol with-
stands stolen-data-and-password attacks.
Proof. Suppose that A has access to U
i
’s password
PW
i
and the smartcard SC
i
data. Because of the PUF
characteristics and the unavailability of nonce r
1
, A
can still not access the system. In particular, A re-
quires token γ = PUF
i
(PW
i
). According to Lemma 1,
if A cannot obtain PUF
i
, the probability of achieving
the correct γ is 1/2
|γ|
, which corresponds to guessing a
nonce with high-entropy. Thus, the suggested scheme
resists stolen-data-and-password assaults.
Lemma 9 (A3). The proposed 3FAKA protocol is se-
cure against replay attacks.
Proof. Assume that A tries to replay any of L
1
, L
2
,
and L
3
sent in session S
i
to another session S
j
. If A
replays L
1
, then it cannot continue sending L
3
as it
cannot reveal r
2
due to the unavailability of r
1
hidden
in L
1
. Besides, it cannot reveal r
1
due to the hardness
Robust Three-Factor Lightweight Authentication Based on Extended Chaotic Maps for Portable Resource-Constrained Devices
679

Table 2: Security functionalities comparisons of the existing schemes.
Scheme
Security Traits (symbols as in Section 1.1)
F1 F2 F3 F4 F5 F6 A1 A2 A3 A4 A5 A6
W1 (Jiang et al., 2019)
W2 (Zhou et al., 2019)
W3 (Banerjee et al., 2020)
W4 (Kwon et al., 2021)
W5 (Qiu et al., 2022)
W6 (Wang et al., 2023)
Our 3FAKA scheme
of symmetric trapdoor C
1
. Similarly, if A replays L
2
,
then U
i
can detect it due incorrect r
1
details in L
2
.
Nonetheless, replaying L
3
will not be successful as
S can detect it for incorrect r
2
. In the proposed pro-
tocol, S and U produce challenge tokens containing
random integers based on the random responses from
each entity during each session. Hence, the suggested
protocol is resistant to replay assaults.
Lemma 10 (A4). The proposed 3FAKA protocol safe-
guards against a man-in-the-middle attack.
Proof. Assume that A tries to alter the data sent by U
i
during the session. If A wants to alter L
1
= (C
1
,T
′
i
)
where C
1
= SE
K
[ID
i
||y
i
||r
1
] and T
′
i
= T
u
(γ). Sup-
pose A tries to send C
′
1
= SE
K
[ID
j
||y
j
||r
1
] for ID
j
along with T
′
i
. However, computation of a valid
y
j
requires S ’s secret s. For a random y
∗
j
, S de-
tects ID
j
̸= ID
∗
j
(← SD
s
[y
∗
i
]). Thus, successful mod-
ification in L
1
is not feasible. Similarly, any data
tampering in L
2
= (α = r
1
⊕ r
2
,β = H(r
1
||r
2
)) and
L
3
= SE
H(K||r
2
)
[H(σ
∗
,γ
∗
,PW
∗
)||r
2
] is hard due to the
CMCDHP assumption and Lemma 1. Besides, such
changes will be detected by U
i
with r
1
and S with
r
2
, respectively. Hence, the suggested protocol safe-
guards against the man-in-the-middle attack.
Lemma 11 (A5). The proposed 3FAKA protocol is
resistant to a stolen smartcard and password attack.
Proof. Suppose A has stolen U
i
s smartcard SC
i
=
(y
i
,T
i
,V PW, ID
i
,CID
i
,Γ
i
) and use it on behalf of U
i
to access the system. To pass authentication by
S , A uses SC
i
and generates L
1
= (C
1
,T
′
i
) where
C
1
= SE
K
[ID
i
||y
i
||a
1
] and T
′
i
= T
a
(γ
i
) for some a
and γ
i
= PUF
i
(PW
i
). Clearly, S accepts L
1
and
A may receive r
2
. However, A cannot produce
a valid L
3
due to the unavailability of biometric
Bio
i
. If it tries to tamper it and compute as L
3
=
SE
H(K||r
2
)
[H(σ
f
i
ake,γ
i
,PW
i
)||r
2
], then S easily detect
such issue as FV
i
decrypted from y
i
does not match
with H(σ
f ake
i
,γ
i
,PW
i
)||r
2
]. Hence, our scheme resists
the stolen smartcard-and-password attack.
Lemma 12 (A6). The proposed 3FAKA protocol is
resistant to stolen verifier table attack.
Proof. A stolen-verifier attack occurs when A obtains
a password or secret verifier from S to impersonate a
legitimate user. Our 3FAKA employs a database, say
D, to assign IDs and Valid CIDs to users. D stores
no passwords and checks if a user is revoked during
authentication. Thus, updating D for each authentica-
tion request is nonessential. Even if A breaches D se-
curity, it cannot mimic U
i
during user authentication.
Thus, our 3FAKA resists stolen verifier attacks.
5 PERFORMANCE DISCUSSION
Table 2 compares the security features of the related
schemes. One may note that the proposed 3FAKA
achieves comprehensive security properties compared
to others. Our protocol could be implemented with
a lightweight 128-bit ASCON or AES cryptosystem
with standard SHA-2 algorithms. Table 3 compares
our scheme with existing related schemes considering
specific overheads as discussed below.
5.1 Registration and Authentication
For user registration, U
i
executes one PUF(·), one
FE
GEN
, and two H(·) operations while server S runs
one SE(·) and one T
·
(·). Thus, the registration cost is
estimated as C
reg
= T
PUF
+ T
FE
+ T
ECM
+ 2T
H
+ T
SE
.
During an interactive authentication process in our
3FAKA, U
i
requires one PUF(·), one FE
REP
, one
T
·
(·), five H(·), two SE(·) and three SD(·). Thus,
the user’s burden is C
1
= T
PUF
+T
FE
+T
ECM
+4T
H
+
2T
SE
. On the other hand, S needs one T
·
(·), three
H(·), and three SD(·) operations. Thus, the server’s
load is C
2
= T
ECM
+ 3T
H
+ 3T
SD
. Hence, the over-
all authentication overhead is considered as C
auth
=
C
1
+C
2
= T
PUF
+T
FE
+2T
ECM
+7T
H
+2T
SE
+3T
SD
.
Further, W1 requires one T
FE
and three T
H
op-
erations during registration. Thus the overhead is
T
FE
+ 3T
H
. Besides, it runs one T
FE
and twenty T
H
during user authentication. Thus, the overhead is
T
FE
+ 20T
H
. Similarly, one may compute costs for
W2-W5. Work W6 uses PUF to provide hardware se-
curity. It takes one T
PUF
, one T
FE
, and six T
H
to reg-
SECRYPT 2023 - 20th International Conference on Security and Cryptography
680

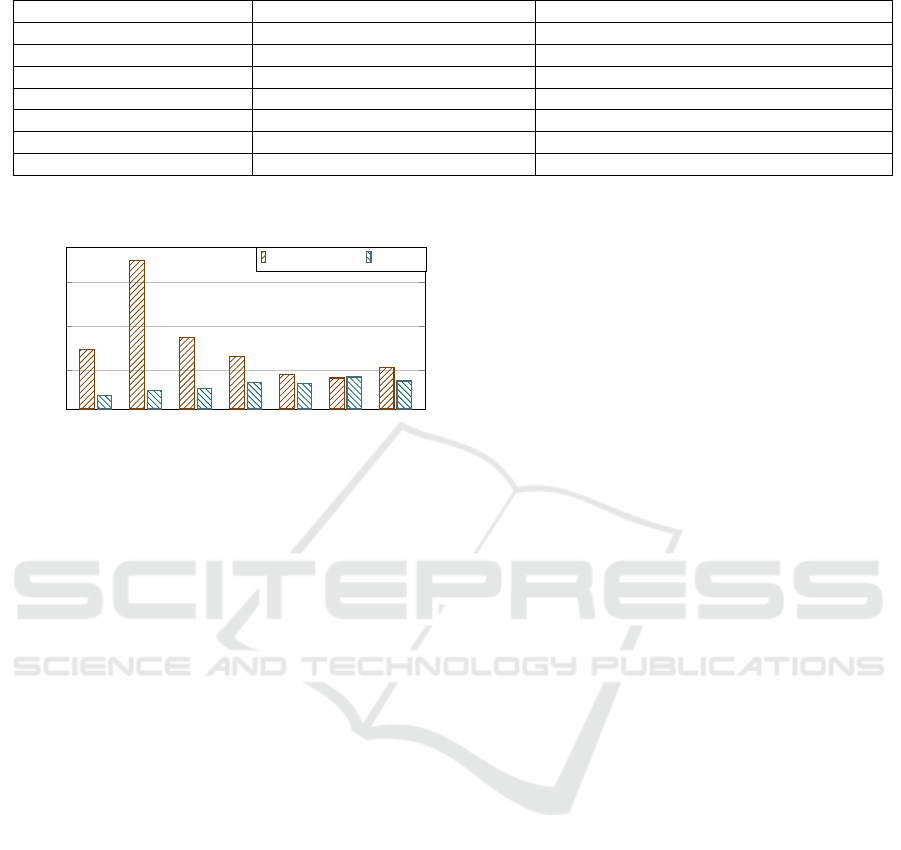
Table 3: Computation cost comparisons of related schemes.
Scheme Registration Overhead Authentication Overhead
W1 (Jiang et al., 2019) T
FE
+ 3T
H
T
FE
+ 20T
H
W2 (Zhou et al., 2019) 5T
H
42T
H
W3 (Banerjee et al., 2020) T
FE
+ 4T
H
T
FE
+ 25T
H
W4 (Kwon et al., 2021) T
FE
+ 5T
H
2T
FE
+ T
PUF
+ 32T
H
W5 (Qiu et al., 2022) T
FE
+ T
ECM
+ 4T
H
T
FE
+ 6T
ECM
+ 19T
H
W6 (Wang et al., 2023) T
PUF
+ T
FE
+ 6T
H
3T
PUF
+ 2T
BP
+ T
FE
+ 12T
H
+ 3T
PEA
Our 3FAKA Scheme T
PUF
+ T
ECM
+ T
FE
+ 2T
H
+ T
SE
T
PUF
+ 2T
ECM
+ T
FE
+ 7T
H
+ 2T
SE
+ 3T
SD
T
PUF
: Time to execute one PUF(·); T
FE
: Time to run either GEN(·) or REP(·); T
ECM
: Time to execute one T
·
(·); T
SE
: Cost for one SE(·)
T
SD
: Cost for one SD(·); T
H
: Cost for one H(·); T
BP
: Cost for one bilinear pairing operation; T
PEA
: Paillier Ecrypt/Decrypt operation.
W1 W2 W3 W4 W5 W6 Ours
200
400
600
Size (Bytes-B)
Communication Storage
Figure 3: Computational and storage costs comparison.
ister a user. Thus, the total cost is T
PUF
+ T
FE
+ 6T
H
.
Besides, it considers three T
PUF
, two T
BP
, one T
FE
twelve T
H
and three T
PEA
. Hence, the overhead is
considered as T
PUF
+ 2T
BP
+ T
FE
+ 12T
H
+ 3T
PEA
.
5.2 Token Transmission and Storage
During authentication, several data as authentication
tokens are transmitted. To measure the various costs,
we approximate the length of the security parameters
as follows: |ID
i
| = 16 bytes (B), |Z
∗
p
| = 20 B, hash
|h| = 32 B, random |r| = 16 B and each component is
of 16 B in the output of the function GEN(·). Authen-
tication is valid when all L
1
,L
2
,L
3
are successfully
transmitted. The U
i
initiates L
1
= (C
1
,T
′
i
), where C
1
is a 96 B ciphertext and T
′
i
is an element in Z
∗
p
. Thus,
U
i
sends |L
1
| = 116 B. Now, S sends L
2
= (α, β)
where α is 16 B masked data and β = 32 B integrity
token. Finally, U
i
sends L
3
which is of 48 B. Hence,
the overall, token transmission overhead is considered
as |L| = |L
1
| + |L
2
| + |L
3
| = 116 + 48 + 48 = 212 B.
On successful interactive registration, U
i
holds a
smart card as SC
i
= (y
i
,T
i
,V PW, ID
i
,CID
i
,Γ
i
) where
y
i
is a 64 B ciphertext, T
i
is 20 B trapdoor, and Γ
i
is
16 B featured value. Thus, the SC
i
requires approxi-
mately 150 B to store essential security tokens.
Although the computation cost in our 3FAKA, as
shown in Table 3, is high compared to some of the
others, the growth is nominal for real-time applica-
tions. Besides, Fig. 3 depicts the comparisons of
transmission and storage costs between the schemes.
Despite W5 and W6 incurring lesser overheads, they
fail to achieve comprehensive security traits as men-
tioned in Table 2. Hence, the suggested 3FAKA is an
effective alternative for achieving all the F1-F6 and
A1-A6 security traits with adequate overheads.
6 CONCLUSION AND FUTURE
RESEARCH DIRECTION
This paper provides a novel secure three-factor au-
thentication and key agreement based on extended
chaotic maps and physical unclonable functions. It
accomplishes several security features, including mu-
tual authentication, session key agreement, dynamic
device addition, user anonymity, efficient revocation,
user untraceability, and remote smartcard revocation.
Under the CMCDHP assumption, it is immune to
various attacks, including device cloning, traceabil-
ity, desynchronization, stolen data and passwords,
replay, man-in-the-middle, and stolen smartcard at-
tacks. Thus, the suggested protocol provides ample
operational security while considering adequate com-
putation, storage, and transmission costs.
Although it offers a broad set of features, the used
fuzzy extractor may require more storage and pro-
cessing power. In the future, we will focus on secure
multi-factor authentication minimizing these issues in
a trust-less multi-server scenario.
ACKNOWLEDGEMENTS
This work was supported by the National Science and
Technology Council under grant 111-2222-E-110 -
008 and by the CANSEC-LAB@NSYSU in Taiwan.
REFERENCES
Aman, M. N., Sikdar, B., Chua, K. C., and Ali, A. (2018).
Low power data integrity in IoT systems. IEEE Inter-
net of Things Journal, 5(4):3102–3113.
Robust Three-Factor Lightweight Authentication Based on Extended Chaotic Maps for Portable Resource-Constrained Devices
681

Banerjee, S., Odelu, V., Das, A. K., Chattopadhyay, S., and
Park, Y. (2020). An efficient, anonymous and robust
authentication scheme for smart home environments.
Sensors, 20(4):1215.
Chatterjee, S., Roy, S., Das, A. K., Chattopadhyay, S.,
Kumar, N., and Vasilakos, A. V. (2018). Secure
biometric-based authentication scheme using cheby-
shev chaotic map for multi-server environment. IEEE
Trans Dependable Secure Comput, 15(5):824–839.
Das, A. K., Wazid, M., Kumar, N., Khan, M. K., Choo,
K.-K. R., and Park, Y. (2018). Design of secure and
lightweight authentication protocol for wearable de-
vices environment. IEEE Journal of Biomedical and
Health Informatics, 22(4):1310–1322.
Fakroon, M., Gebali, F., and Mamun, M. (2021). Multifac-
tor authentication scheme using physically unclonable
functions. Internet of Things, 13:100343.
Hu, V. C., Ferraiolo, D., Kuhn, R., Friedman, A. R.,
Lang, A. J., Cogdell, M. M., Schnitzer, A., Sandlin,
K., Miller, R., Scarfone, K., et al. (2013). Guide
to attribute based access control (ABAC) definition
and considerations (draft). NIST special publication,
800(162):1–54.
Islam, S. (2014). Provably secure dynamic identity-based
three-factor password authentication scheme using ex-
tended chaotic maps. Nonlinear Dyn., 78(3):2261–
2276.
Jiang, Q., Qian, Y., Ma, J., Ma, X., Cheng, Q., and Wei, F.
(2019). User centric three-factor authentication proto-
col for cloud-assisted wearable devices. Int. J. Com-
mun. Syst., 32(6):e3900.
Jiang, Q., Wei, F., Fu, S., Ma, J., Li, G., and Ale-
laiwi, A. (2016). Robust extended chaotic maps-based
three-factor authentication scheme preserving biomet-
ric template privacy. Nonlinear Dyn., 83(4):2085–
2101.
Jiang, Q., Zhang, N., Ni, J., Ma, J., Ma, X., and Choo,
K.-K. R. (2020). Unified biometric privacy preserv-
ing three-factor authentication and key agreement for
cloud-assisted autonomous vehicles. IEEE Trans. on
Vehicular Technology, 69(9):9390–9401.
Juels, A. and Ristenpart, T. (2014). Honey encryption: Se-
curity beyond the brute-force bound. In Advances
in Cryptology–EUROCRYPT 2014: 33rd Annual Intl.
Conf. on the Theory and Applications of Crypto-
graphic Techniques, Copenhagen, Denmark, May 11-
15, 2014. Proceedings 33, pages 293–310. Springer.
Karati, A., Fan, C.-I., and Zhuang, E.-S. (2021). Reliable
data sharing by certificateless encryption supporting
keyword search against vulnerable KGC in industrial
internet of things. IEEE Trans. on Industrial Infor-
matics, 18(6):3661–3669.
Kirkpatrick, M. S., Kerr, S., and Bertino, E. (2014). System
on chip and method for cryptography using a physi-
cally unclonable function. US Patent 8,750,502.
Kwon, D., Park, Y., and Park, Y. (2021). Provably secure
three- factor-based mutual authentication scheme with
PUF for wireless medical sensor networks. Sensors,
21(18):6039.
Masud, M., Gaba, G. S., Choudhary, K., Hossain,
M. S., Alhamid, M. F., and Muhammad, G. (2021).
Lightweight and anonymity-preserving user authenti-
cation scheme for IoT-based healthcare. IEEE Inter-
net of Things Journal, 9(4):2649–2656.
Qiu, S., Wang, D., Xu, G., and Kumari, S. (2022). Prac-
tical and provably secure three-factor authentication
protocol based on extended chaotic-maps for mobile
lightweight devices. IEEE Trans Dependable Secure
Comput, 19(2):1338–1351.
Roy, S., Chatterjee, S., Das, A. K., Chattopadhyay, S.,
Kumari, S., and Jo, M. (2018). Chaotic map-based
anonymous user authentication scheme with user bio-
metrics and fuzzy extractor for crowdsourcing internet
of things. IEEE IOT Journal, 5(4):2884–2895.
Roy, S., Das, D., Mondal, A., Mahalat, M. H., Roy, S., and
Sen, B. (2021). PUF based lightweight authentica-
tion and key exchange protocol for IoT. In SECRYPT,
pages 698–703.
R
¨
uhrmair, U., Sehnke, F., S
¨
olter, J., Dror, G., Devadas,
S., and Schmidhuber, J. (2010). Modeling attacks on
physical unclonable functions. In Proceedings of the
17th ACM conference on Computer and Communica-
tions Security (ACM-CCS), pages 237–249.
Ryu, J., Kang, D., and Won, D. (2022). Improved secure
and efficient chebyshev chaotic map-based user au-
thentication scheme. IEEE Access, 10:15891–15910.
Saqib, M., Jasra, B., and Moon, A. H. (2022). A lightweight
three factor authentication framework for iot based
critical applications. Journal of King Saud University-
Computer and Info. Sciences, 34(9):6925–6937.
Trivedi, H. S. and Patel, S. J. (2021). Privacy preserving
scalable authentication protocol with partially trusted
third party for distributed internet-of-things. In SE-
CRYPT, pages 812–818.
Wang, F., Xu, G., Xu, G., Wang, Y., and Peng, J. (2020). A
robust IoT-based three-factor authentication scheme
for cloud computing resistant to session key exposure.
Wirel Commun Mob Comput, 2020.
Wang, W., Han, Z., Alazab, M., Gadekallu, T. R., Zhou,
X., and Su, C. (2022). Ultra super fast authentication
protocol for electric vehicle charging using extended
chaotic maps. IEEE Trans. on Industry Applications,
58(5):5616–5623.
Wang, Z., Deng, D., Hou, S., Guo, Y., and Li, S. (2023). De-
sign of three-factor secure and efficient authentication
and key-sharing protocol for IoT devices. Computer
Communications.
Yu, Y., Taylor, O., Li, R., and Sunagawa, B. (2021).
An extended chaotic map-based authentication and
key agreement scheme for multi-server environment.
Mathematics, 9(8):798.
Zhang, L. (2008). Cryptanalysis of the public key encryp-
tion based on multiple chaotic systems. Chaos, Soli-
tons & Fractals, 37(3):669–674.
Zhang, Y., Li, B., Wu, J., Liu, B., Chen, R., and Chang, J.
(2022). Efficient and privacy-preserving blockchain-
based multifactor device authentication protocol for
cross-domain IIoT. IEEE IOT J., 9(22):22501–22515.
Zhou, L., Li, X., Yeh, K.-H., Su, C., and Chiu, W.
(2019). Lightweight IoT-based authentication scheme
in cloud computing circumstance. Future Generation
Computer Systems, 91:244–251.
SECRYPT 2023 - 20th International Conference on Security and Cryptography
682